Цели урока:
Планируемые результаты:
личностные:
метапредметные:
предметные:
УУД общенаучные:
УУД личностные:
Оборудование: учебник, интерактивная доска, смайлики, модели фигур, развёртки фигур, светофоры индивидуальные, прямоугольники -средства обратной связи, Толковый словарь.
Тип урока: изучение нового материала.
Методы: словесные, исследовательские, наглядные, практические.
Формы работы: фронтальная, групповая, парная, индивидуальная.
Утром солнышко взошло.
Новый день нам принесло.
Сильными и добрыми
Новый день встречаем мы.
Вот мои руки, я раскрываю
Их навстречу солнцу.
Вот мои ноги, они твердо
Стоят на земле и ведут
Меня верной дорогой.
Вот моя душа, я раскрываю
Её навстречу людям.
Наступи, новый день!
Здравствуй, новый день!
2. Актуализация знаний.
Создадим хорошее настроение. Улыбнитесь мне и друг другу, садитесь!
Чтобы дойти до цели, надо прежде всего идти.
Перед вами высказывание, прочитайте. Что означает это высказывание?
(Чтобы чего-то добиться, нужно что-то делать)
— И действительно, ребята, попадающим в цель может стать только тот, кто настраивает себя на собранность и организованность своих действий. И вот я надеюсь, что мы с вами на уроке достигнем своей цели.
— Начнем наш путь к достижению цели сегодняшнего урока.
3. Подготовительная работа.
— Посмотрите на экран. Что вы видите? (Геометрические фигуры)
Назовите эти фигуры.
— Какое задание, вы можете предложить своим одноклассникам? (разделите фигуры на группы)
— У вас на партах лежат карточки с этими фигурами.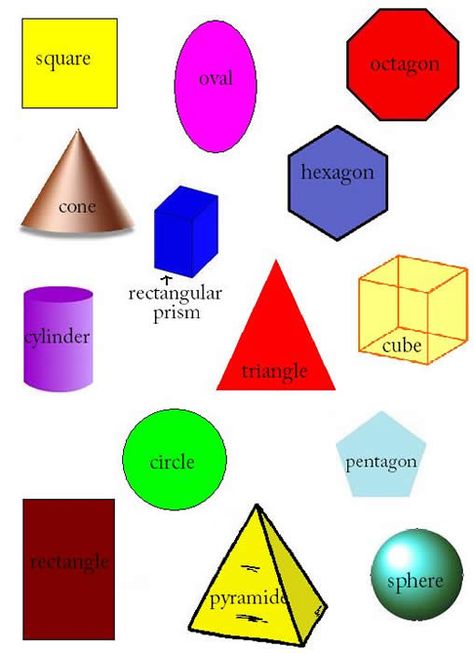
Выполните это задание в парах.
— По какому признаку вы разделили эти фигуры?
— С какими фигурами мы уже работали? Что учились находить у них? Какие фигуры встречаются нам на геометрии впервые?
— Какая же тема нашего урока? (Учитель добавляет слова на доске: объёмные, на доске появляется тема урока: Объёмные геометрические фигуры.)
— Чему мы должны научиться на уроке?
4. «Открытие» нового знания в практической исследовательской работе.
(Учитель показывает куб и квадрат.)
— Чем они похожи?
— Можно ли сказать, что это одно и тоже?
— Чем же отличается куб от квадрата?
— Давайте проведём опыт. (Ученики получают индивидуальные фигуры – куб и квадрат.)
— Попробуем приложить квадрат к плоской поверхности порты. Что видим? Он весь (целиком) лёг на поверхность парты? Вплотную?
! Как назовём фигуру, которую можно целиком расположить на одной плоской поверхности? (Плоской фигурой.
)
— Можно ли куб полностью (весь) прижать к парте? Проверим.
— Можно ли назвать куб плоской фигурой? Почему? Есть ли пространство между рукой и партой?
! Значит, что мы можем сказать о кубе? (Занимает определённое пространство, является объёмной фигурой.)
ВЫВОДЫ: Чем же отличаются плоские и объёмные фигуры? (Учитель вывешивает на доске выводы.)
ПЛОСКИЕ
ОБЪЁМНЫЕ
Объёмные фигуры: пирамида, куб, цилиндр, конус, шар, параллелепипед.
4. Открытие новых знаний.
1. Назовите фигуры, изображенные на рисунке.
— Какую форму имеют основания этих фигур?
— Какие еще формы можно увидеть на поверхности куба и призмы?
2. Фигуры и линии на поверхности объемных фигур имеют свои названия.
— Предложите свои названия.
— Боковые стороны, образующие плоскую фигуру называются гранями. А боковые линии – рёбра. Углы многоугольников – вершины. Это элементы объемных фигур.
— Ребята, а как вы думаете, как называются такие объемные фигуры, у которых много граней? Многогранники.
Работа с тетрадями: чтение нового материала
Соотнесение реальных объектов и объёмных тел.
— А теперь подберите для каждого предмета ту объёмную фигуру, на которую он похож.
+ Коробка – параллелепипед.
5. Физминутка.
1. Представьте себе большой шар, погладьте его со всех сторон. Он большой, гладкий.
(Ученики «обхватывают» руками и гладят воображаемый шар.
)
А теперь представьте себе конус, дотроньтесь до его вершины. Конус растёт вверх, вот он уже выше вас. Допрыгните до его вершины.
Представьте, что вы внутри цилиндра, похлопайте по его верхнему основанию, потопайте по нижнему, а теперь руками по боковой поверхности.
Цилиндр стал маленькой подарочной коробочкой. Представьте, что вы сюрприз, который находится в этой коробочке. Я нажимаю кнопку и… сюрприз выскакивает из коробочки!
6. Групповая работа:
(Каждая группа получает одну из фигур: куб, пирамиду, параллелепипед.Полученную фигуру дети изучают, выводы записывают в подготовленную учителем карточку.)
Группа 1. (Для изучения параллелепипеда)
| Эта объемная фигура называется ______________ . Их ровно ______________ . Еще у этой фигуры есть углы – вершины, их ______________ .  |
Группа 2. (Для изучения пирамиды)
| Эта объемная фигура называется ______________ . Его стороны (грани) похожи на плоскую фигуру ______________ . Их ровно ______________ . Еще у этой фигуры есть углы – вершины, их ______________ . |
Группа 3. (Для изучения куба)
| Эта объемная фигура называется ______________ . Его стороны (грани) похожи на плоскую фигуру ______________ . Их ровно ______________ . Еще у этой фигуры есть углы – вершины, их ______________ . |
Далее каждая группа выступает, представляя свою объемную фигуру другим.
7. Решение кроссворда
8. Итог урока. Рефлексия деятельности.
Решение кроссворда в презентации
— Что нового вы для себя сегодня открыли?
+ Все геометрические фигуры можно разделить на объёмные и плоские.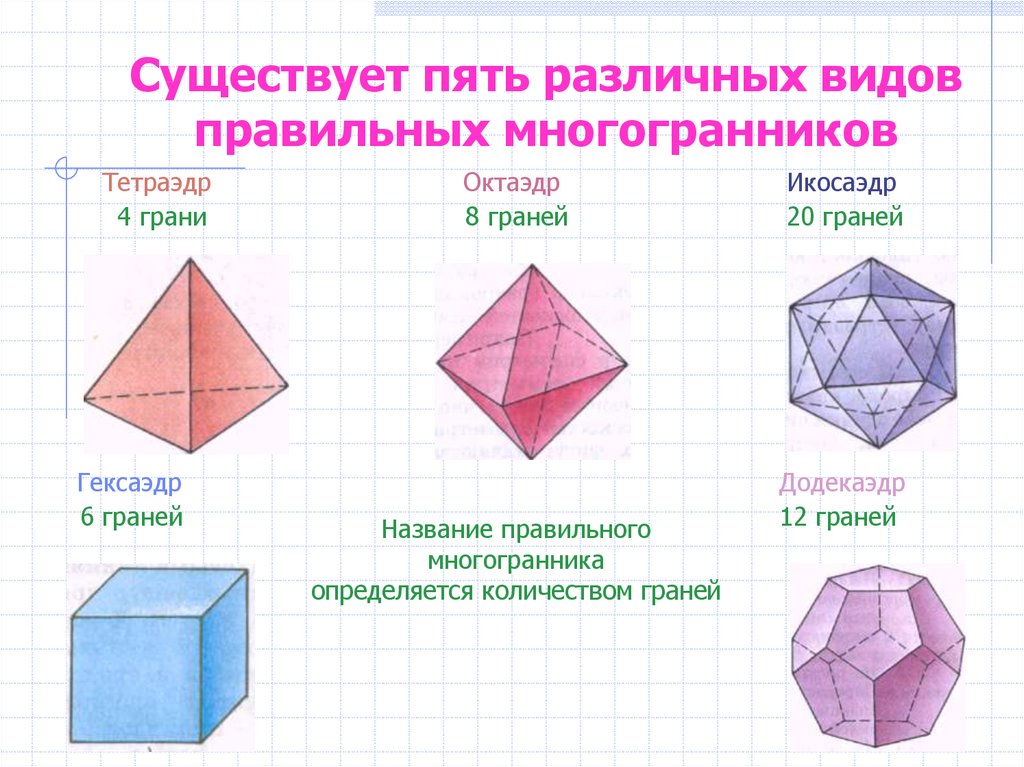
+ А я узнал названия объёмных фигур
Каждый из нас — и взрослый, и ребенок — замечал, как много геометрических фигур существует вокруг нас. Мы встречаемся с ними везде, во всех окружающих нас предметах. Где же встречаются геометрические фигуры в нашей жизни?
Каждый из нас — и взрослый, и ребенок — замечал, как много геометрических фигур существует вокруг нас. Мы встречаемся с ними везде, во всех окружающих нас предметах.
Люди давно заинтересовались разнообразием геометрических фигур. Ещё для первобытных людей важную роль играла форма окружавших их предметов. Овладевая миром, люди знакомились с простейшими геометрическими формами. Сначала они изготавливали орудия труда относительно правильной формы, потом научились их совершенствовать. Специальных названий для геометрических фигур тогда, конечно, не было. Их придумали значительно позже. Когда люди стали строить дома, им пришлось ещё глубже разбираться в особенностях разных фигур, чтобы понять, какую форму следует придавать стенам и крыше, какой формы должны быть брёвна или каменные глыбы.
Сам того не зная, человек всё время занимался изучением фигур: женщины, изготавливая одежду, охотники — наконечники для копий или бумеранги сложной формы, рыболовы, делая такие крючки из кости, чтобы рыба с них не срывалась.
И в современном мире без этих знаний не прожить.
Где же встречаются геометрические фигуры в нашей жизни?
Возможно, кто-то считает, что различные линии фигуры «водятся» только в книгах учёных математиков. Однако, если посмотреть вокруг, становится понятно, что многие предметы имеют форму, похожую на основные геометрические фигуры. Просто мы не всегда это замечаем. Немало замечательных геометрических фигур встречается в окружающей нас природе. Поле имеет форму прямоугольника, река — кривой линии, озеро — круга, кристалл соли — форму куба, обычная горошинка, капелька росы — форму шара. Красивы и разнообразны многогранники — кристаллы горного хрусталя. Но и в привычной жизни основные геометрические фигуры тоже повсюду. Это здания, строения, транспорт, интерьер квартиры, даже посуда и предметы одежды.
К примеру, женская юбка — это трапеция, тарелка — круг, дом — квадрат и треугольник, а в трубе — цилиндр.
Знать все фигуры, их виды, названия и свойства очень важно. Систематизирует знания о геометрических фигурах и изучает их свойства математическая наука — геометрия. Наука эта очень важная, её применение просто бесценно во все времена и независимо от профессии. Без знаний геометрии не обходится ни рабочий, ни инженер, ни архитектор, ни художник. И очень важно начать осваивать эту науку в раннем возрасте.
Прекрасным помощником ребёнку в этом станет образовательная платформа iSmart. Основные виды геометрических фигур, их свойства, задачи на нахождение площади фигур и многое другое есть на платформе в разделе «Математика». Тут собраны несколько тысяч заданий на освоение этих тем, не повторяющиеся при многократной отработке. Занимаясь на , школьники начальных классов досконально разберутся в основах геометрии. Это даст им хорошую базу по предмету для учёбы в средних и старших классах.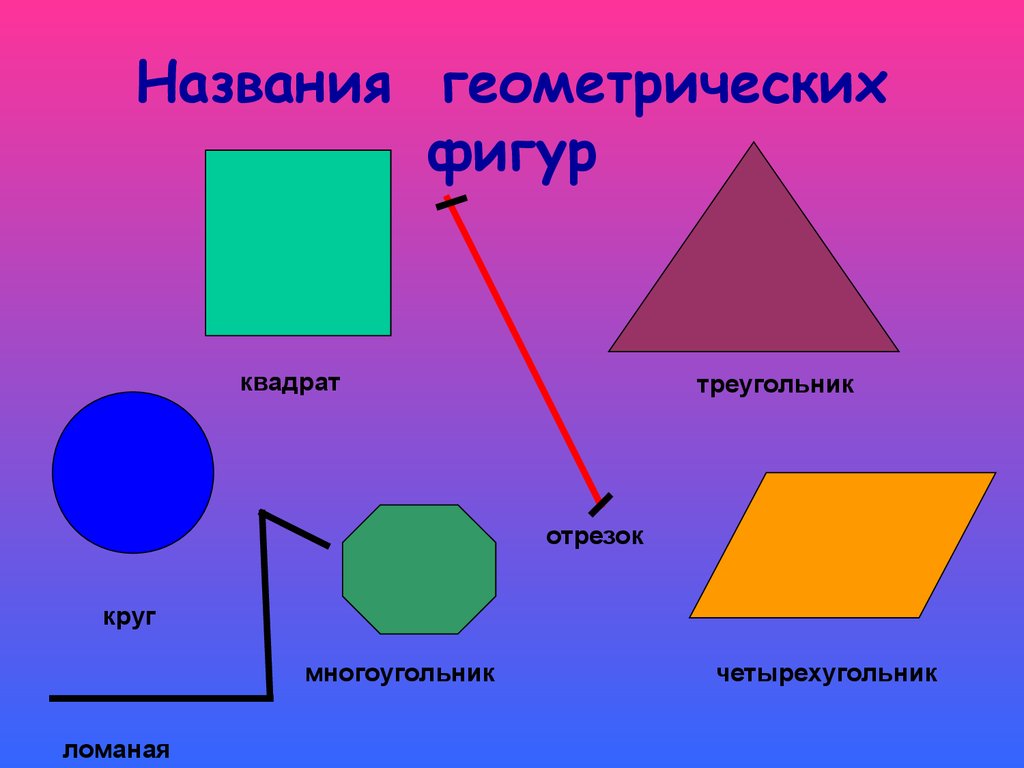
Кроме того, интерактивные задания красочные, интересные, увлекательные.
Итак,
Две основные фигуры — это точка и линия. Скопление точек и линий образует различные геометрические фигуры. Каждая из них индивидуальна, отличается своими параметрами, их формы очень разнообразны. Фигуры бывают простыми и сложными, плоскими и объёмными.
Точка — это самый минимальный, но в то же время самый главный объект в геометрии. Это самая малая геометрическая фигура, но именно она необходима для построения других фигур на плоскости и является основой для всех других фигур. Она не содержит таких свойств, как длина, высота, объём, площадь, не имеет измерительных особенностей и характеристик. Важно только то, где она расположена. Обозначается точка заглавной буквой латинского алфавита либо числом. Например, A, B, C или 1, 2, 3.
Всякая более сложная геометрическая фигура — это множество точек, которые обладают определенным свойством, характерным только для этой фигуры.
Самыми простейшими фигурами являются луч и отрезок.
Линия образуется из множества точек, последовательно расположенных друг за другом и соединённых между собой. Линии бывают замкнутыми и разомкнутыми, прямыми и кривыми, а также ломаными.
Через одну точку можно провести бесконечное число линий, а через две — только одну прямую и множество кривых.
Соединённые между собой точки образуют линии, а соединённые между собой линии — основные геометрические фигуры на плоскости.
Геометрические фигуры бывают плоские или двухмерные (2D) и объёмные пространственные, или трёхмерные (3D). Они ограничены замкнутой поверхностью своей наружной границы.
Если все точки фигуры находятся в одной плоскости, значит, она является плоской. Плоские фигуры, которые знают все: точка, квадрат, прямоугольник, треугольник, круг, полукруг, окружность, овал, ромб, трапеция.
А если у геометрической фигуры все точки не находятся в одной плоскости, то она объёмная. К ним относятся шар, конус, цилиндр, сфера, пирамида и др.
Разберём плоские фигуры.
Треугольник — это фигура, которая образуется, когда три отрезка соединяют три точки, не лежащие на одной прямой. Эти три точки называются вершинами, а отрезки — сторонами.
Есть три вида треугольников:
Треугольники имеют следующие свойства:
Вершины треугольников обозначаются заглавными буквами латинского алфавита: A, B, C и др.
Примеры треугольников:
Окружность — геометрическая фигура, образованная замкнутой кривой линией, все точки которой находятся на одинаковом от центра расстоянии.
Часть плоскости, находящаяся внутри окружности, называется кругом. То есть, окружность — это граница круга. А расстояние от центра окружности до любой точки на ней называется радиусом. Диаметр круга — это отрезок, который соединяет две точки на окружности и проходит через её центр. Диаметр круга равен двум его радиусам.
Прямоугольник — это фигура, состоящая из четырёх сторон и четырёх прямых углов, у которой:
Квадрат — это тот же прямоугольник, у которого:
Четырёхугольник, у которого две стороны параллельны, а две — нет, называется трапецией. Если сумма длин оснований трапеции равна сумме длин боковых сторон, в неё можно вписать окружность.
Параллелограмм — четырёхугольник, противоположные стороны которого попарно параллельны.
Ромб — это параллелограмм с равными сторонами.
Параллелограмм имеет следующие свойства:
Все геометрические фигуры имеют свои характеристики и собственную величину. Самыми распространёнными являются такие величины как площадь и периметр. Они используются в повседневной жизни, в строительстве и в других областях. Например, во время ремонта или нового строительства, количество необходимых материалов и объём работ не определить, не вычислив заранее площадь и периметр.
Периметром называется замкнутая граница плоской геометрической фигуры, которая отделяет её внутреннюю область от внешней. Периметр есть у любой замкнутой геометрической фигуры:
На рисунке периметры выделены красной линией. Периметр окружности часто называют длиной.
Периметр измеряется в единицах измерения длины: мм, см, дм, м, км.
Обозначается заглавной латинской P.
Площадь — это часть плоскости, занимаемая замкнутой плоской геометрической фигурой, то есть та часть плоскости, которая находится внутри периметра.
Именно она даёт нам основную информацию о её размере. Любая плоская замкнутая геометрическая фигура имеет определённую площадь.
На рисунке площади фигур окрашены различными цветами.
Измерить площадь фигуры — значит найти, сколько раз в данной фигуре помещается другая фигура, принятая за единицу измерения. Площадь измеряется в квадратных единицах измерения длины. К единицам измерения площади относятся: мм2, см2, м2, км2 и т. д. S (square) — знак площади.
Периметр — это длина замкнутого контура геометрической фигуры. Можно, конечно, измерить линейкой длины всех сторон и сложить их. Но лучше воспользоваться специальными формулами для вычисления периметра, это значительно упростит задачу.
Для вычисления площади фигуры также потребуется соответствующая формула. К разным фигурам применяются разные формулы. Для вычисления площади стандартных геометрических фигур можно воспользоваться следующими формулами:
Итак, мы перечислили основные и самые распространённые геометрические фигуры и их свойства. Образовательная платформа iSmart поможет вашему ребёнок изучить основные геометрические фигуры, их виды, названия и свойства с помощью увлекательных заданий. Преимущества занятий на умных тренажёрах iSmart:
Кроме того, занятия помогут вам освободить своё время, ведь ребёнок сможет заниматься самостоятельно, а родитель — получать отчёты и наблюдать за динамикой обучения. Метод обучения iSmart основан на последних научных практиках: микрообучение и поведенческий анализ.
Образовательная платформа iSmart предлагает подготовку к контрольным работам, тестам, ВПР, олимпиадам, а также изучение дополнительных предметов, не вошедших в школьную программу.
В количественной химии часто приходится производить объемные измерения с погрешностью порядка 0,1%, одна тысячная часть. Это предполагает использование стеклянной посуды, которая может содержать или доставлять объем, известный до нескольких сотых миллилитра, или около 0,01 мл. Затем можно указать количества больше 10 мл до четырех значащих цифр. Стеклянная посуда, разработанная для такого уровня точности и аккуратности, стоит дорого и требует определенной осторожности и навыков для достижения наилучших результатов. Распространены четыре основных типа мерной посуды: мерный цилиндр, мерная колба, бюретка и пипетка. Они имеют специфическое применение и будут обсуждаться индивидуально. Однако есть некоторые моменты, общие для всех типов. Они включают в себя чистоту и то, как правильно читать тома. Чистота необходима для хороших результатов. Химически чистое стекло поддерживает равномерную водяную пленку, на которой не видны висящие капли.
Рассмотрите мениск на уровне, перпендикулярном вашему глазу, чтобы избежать ошибки.Некоторая мерная стеклянная посуда имеет этикетку « TC 20°C», что означает « содержит при 20°C». Это означает, что при 20°C внутри этой колбы будет точно указанный объем. Если бы вы выливали жидкость, вам нужно было бы выжать из нее каждую каплю, чтобы получить такой объем. В качестве альтернативы, некоторая мерная стеклянная посуда имеет этикетку « TD 20°C», что означает « для доставки при 20°C». Это означает, что при температуре 20°C из сосуда выйдет именно указанный объем, когда содержимому будет позволено вытечь из сосуда. Необязательно высасывать все до последней капли и, по сути, неаккуратно выдувать последнюю каплю из объемной пипетки.
Большинство студентов знакомы с градуированными цилиндрами, которые используются для измерения и дозирования известных объемов жидкостей.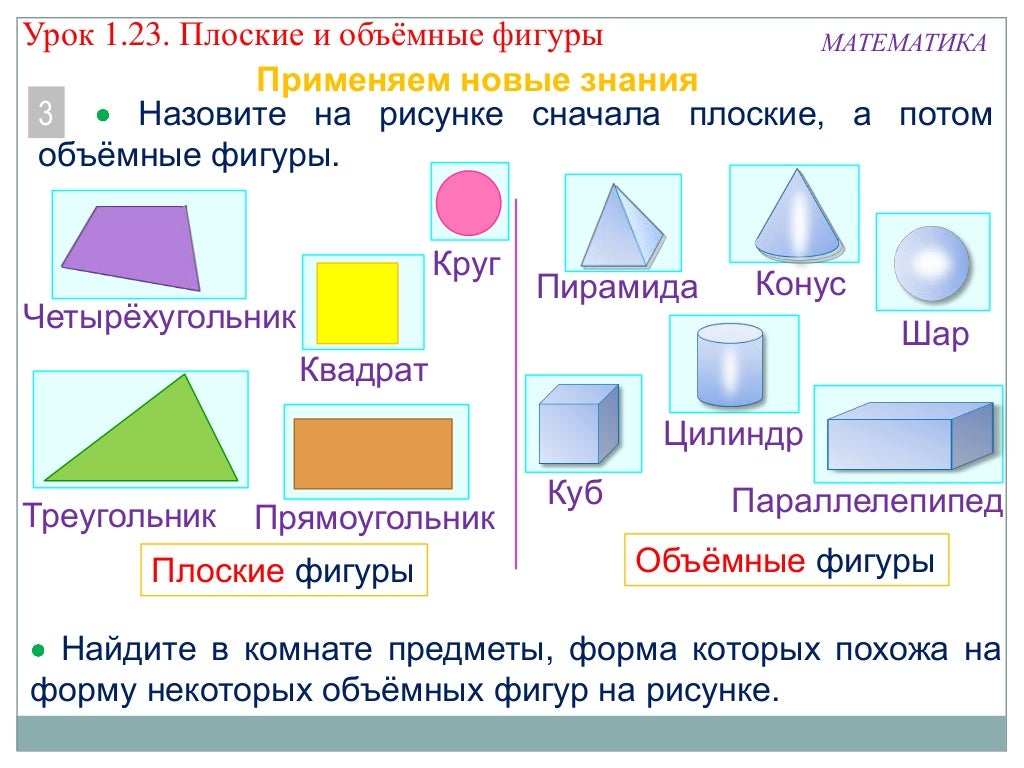
Они изготавливаются так, чтобы содержать измеряемый объем с погрешностью от 0,5 до 1%. Для градуированного цилиндра на 100 мл погрешность составит от 0,5 до 1,0 мл. Измерения, сделанные с помощью градуированного цилиндра, могут быть записаны с точностью до трех значащих цифр.
Рисунок 1
Посмотрите фильм об использовании мерной колбы. Мерная колба, доступная вместимостью от 1 мл до 2 л, предназначена для содержания определенного объема жидкости, обычно с допуском в несколько сотых миллилитра, что составляет около 0,1% от вместимости колбы. На узкой части горлышка колбы выгравирована калибровочная линия. Он заполнен жидкостью, так что нижняя часть мениска находится на этой выгравированной линии. Калибровочная линия специфична для данной колбы; набор колб, рассчитанный на один и тот же объем, будет иметь линии в разных положениях.
Рисунок 2
Мерные колбы используются для приготовления растворов с очень точно известными концентрациями.
Есть два способа сделать это. Можно начать с твердого растворенного вещества или с концентрированного маточного раствора. При работе с твердым раствором материал взвешивают с нужной точностью и осторожно и полностью переносят в мерную колбу. Если растворенное вещество теряется при переносе, фактическая концентрация полученного раствора будет ниже расчетного значения. Поэтому твердое вещество взвешивают в химическом стакане или другой стеклянной посуде, которую можно промыть растворителем, обычно водой, и переносят в колбу. Добавляют дополнительное количество растворителя, но недостаточное для заполнения широкой части колбы. Растворенное вещество растворяют, вращая колбу или закрывая ее пробкой и многократно переворачивая. После растворения растворителя добавляют еще растворителя, чтобы довести объем до отметки на колбе. Последнюю порцию следует добавлять очень осторожно, по каплям, так, чтобы дно мениска оказалось на отметке. Затем колбу закрывают пробкой и несколько раз переворачивают для полного перемешивания раствора.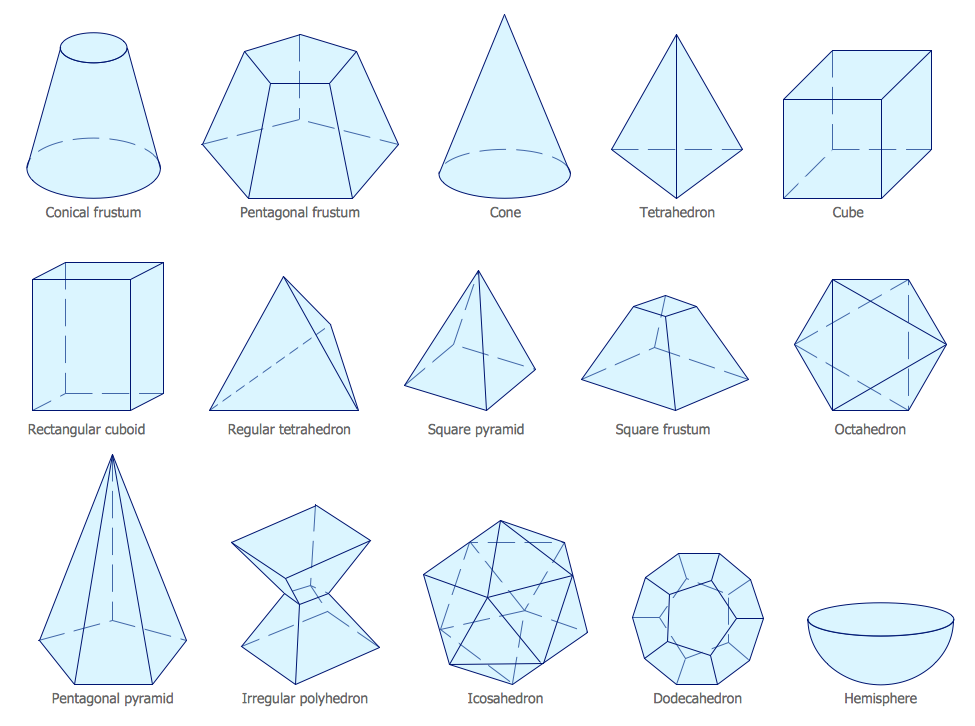
При разбавлении маточного раствора нужный объем раствора переносится в колбу пипеткой. Затем добавляют растворитель, как описано выше. Очевидно, что концентрация исходного раствора должна быть точно известна с точностью до стольких значащих цифр, сколько требуется для разбавленного раствора. Кроме того, передаваемый объем должен быть известен до нужного количества значащих цифр. Никогда заполните мерную колбу растворителем и затем добавьте растворенное вещество. Это приводит к переполнению колбы, и объем не будет точно известен. Иногда полезно иметь в колбе немного растворителя перед добавлением растворенного вещества. Это хорошая практика при работе с летучими растворенными веществами. Мерные колбы не используют для хранения растворов. После того, как раствор приготовлен, его переливают в чистую маркированную бутыль или химический стакан. Затем колбу промывают и хорошо ополаскивают. Последние несколько полосканий должны быть деионизированной водой.
Бюретка представляет собой длинную узкую трубку с запорным краном в основании.
Он используется для точного дозирования переменных объемов жидкостей или растворов. Он градуирован с шагом 0,1 мл, с отметкой 0,00 мл вверху и отметкой 50,00 мл внизу. Обратите внимание, что метки не доходят до запорного крана. Следовательно, бюретка фактически вмещает более 50,00 мл раствора. Также доступны бюретки емкостью 25,00 мл и 10,00 мл.
Рисунок 3
Посмотрите фильм о чистке и кондиционировании бюретки. Для оптимальной точности и предотвращения загрязнения бюретка должна быть чистой. Для проверки бюретки на чистоту закройте ее запорный кран и налейте в нее небольшой объем (5–10 мл) деионизированной воды. Держите бюретку под наклоном, почти параллельно поверхности стола. Медленно вращайте бюретку и дайте жидкости покрыть ее внутреннюю поверхность. Затем держите его вертикально; жидкость должна оседать на дно бюретки слоями, не оставляя капель на внутренних стенках. Если на стенках образуются капли, промойте внутреннюю часть мыльным раствором и ополосните дистиллированной или деионизированной водой.
Повторите тест на чистоту. Непосредственно перед использованием бюретку следует «кондиционировать», чтобы убедиться, что вода, прилипшая к внутренним стенкам, удалена. Добавьте ~ 5 мл жидкости, которая будет использоваться в бюретку. Промойте стенки бюретки, затем слейте жидкость через запорный кран. Повторите со вторым объемом жидкости. Теперь бюретку можно заполнить раствором. Делайте это осторожно и избегайте попадания пузырьков воздуха в трубку. Вам может понадобиться небольшая воронка. Уровень жидкости может быть выше отметки 0,00 мл. Зафиксируйте заполненную бюретку, если это не было сделано до заполнения; иногда легче держать бюретку во время наполнения. Откройте запорный кран и слейте достаточное количество жидкости, чтобы заполнить кончик бюретки. Держите под рукой стакан для раствора отходов для этой и подобных операций. В трубке и на кончике бюретки не должно быть пузырей. Это приведет к ошибкам объема. Если в пробирке есть пузырьки, осторожно постучите по бюретке, чтобы освободить их.
Используйте запорный кран, чтобы вытолкнуть пузырьки из наконечника. Может возникнуть необходимость опорожнить и наполнить бюретку. Посмотрите фильм о титровании. Когда бюретка станет чистой и без пузырьков, слейте жидкость до тех пор, пока мениск (нижняя часть изогнутой поверхности жидкости) не окажется на отметке 0,00 мл или чуть ниже. Нет необходимости выравнивать мениск точно по отметке 0,00 мл, поскольку желаемым измерением является разница между начальным и конечным объемами. Если на кончике бюретки осталась капля жидкости, удалите ее, осторожно коснувшись кончиком стеклянной поверхности, например края стакана для отходов, или протерев салфеткой Kimwipe. Объем капли составляет около 0,1 мл, что соответствует объему деления бюретки. Найдите дно мениска и измерьте уровень жидкости в бюретке с точностью до 0,01 мл в этой точке. Это потребует небольшой практики. Помните, вы читаете сверху вниз. Запишите это значение как начальный объем. Хотя сложно «читать между строк», помните, что последняя цифра измерения, как ожидается, будет иметь некоторую неопределенность! Одна пятая (1/5) деления (0,02 мл) может быть оценена воспроизводимо, если мениск находится между калибровочными метками после небольшой практики.
Теперь дозируйте жидкость, которая вам нужна. Если вы используете бюретку для измерения заданного количества жидкости, определите, какими должны быть окончательные показания, чтобы получить это количество. Медленно перелейте жидкость в приемный сосуд. Помните, что в чистой бюретке вода будет покрывать внутренние стенки и медленно стекать. После закрытия запорного крана улавливайте любые висящие капли в приемном сосуде. На данный момент это часть измерения, поэтому не собирайте его в контейнер для отходов. Подождите несколько секунд, пока мениск не стабилизируется, затем считайте и запишите окончательный объем с точностью до 0,01 мл. Разница между начальным и конечным показаниями и есть дозированный объем. При использовании бюретки легче работать с точным дозированным объемом, чем пытаться дозировать точный объем. Планируйте свою работу с учетом этого. Хотя бюретки иногда используются в качестве дозаторов, они гораздо чаще используются в процедурах, называемых титрованием. При титровании пытаются определить точку эквивалентности как можно точнее.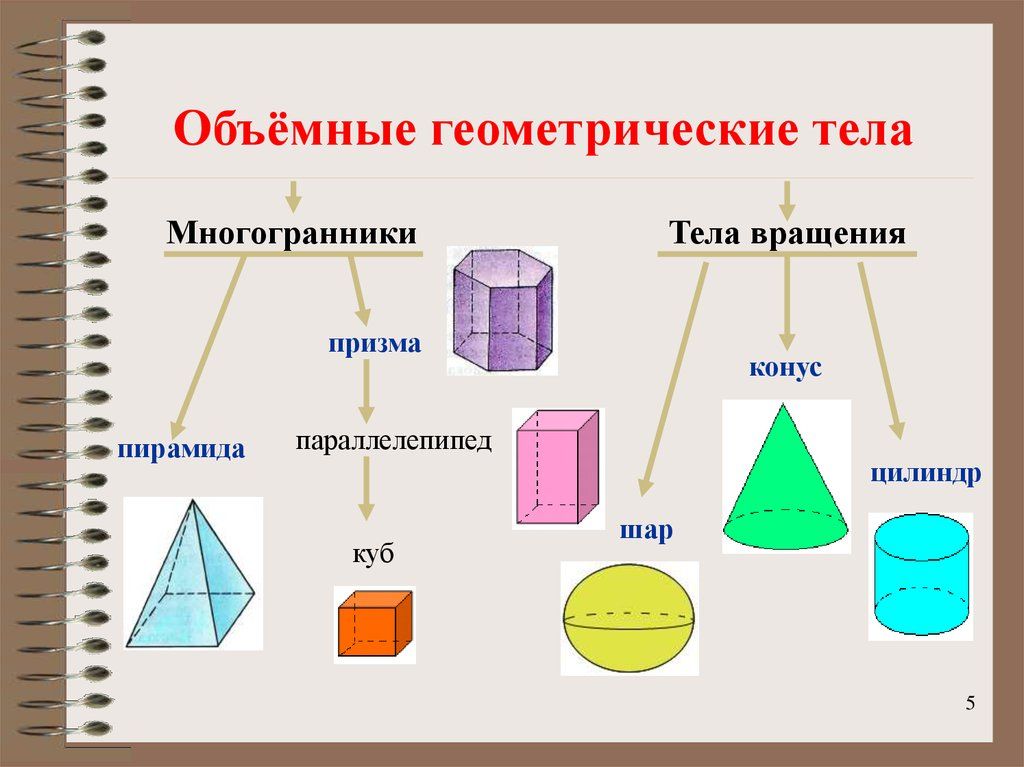
Обычно это первое стойкое изменение цвета индикатора. Немного потренировавшись, можно вводить фракции капель (менее 0,1 мл) в сосуд для титрования и воспроизводить результаты с точностью до 0,10 мл или меньше. Посмотрите фильм про чистку бюретки. По окончании использования бюретки слейте оставшуюся жидкость и тщательно очистите ее. Закончите несколькими промывками деионизированной водой, включая запорный кран и наконечник. Если раствор засыхает в бюретке, его очень трудно удалить. Зажмите бюретку в зажиме бюретки вверх дном с открытым запорным краном, чтобы она высохла для следующего лабораторного сеанса.
Посмотрите фильм о технике пипетирования. Пипетки предназначены для подачи известного объема жидкости. Их объем варьируется от менее 1 мл до примерно 100 мл. Существует несколько типов, которые различаются точностью и типом задачи, для которой они оптимальны.
Рисунок 4
Этот тип пипетки представляет собой узкую трубку с «пузырем» в центре, сужающимся наконечником для подачи жидкости и единственной градуировкой в верхней части (напротив сужающегося конца) трубки. Волюметрические пипетки, иногда называемые пипетками для переноса, являются наиболее точными пипетками. Обычно они дают указанный объем ±0,1%, погрешность в несколько сотых миллилитра.
Они очень похожи на бюретки и могут использоваться для титрования малых объемов. Однако это требует достаточной практики. Перед использованием пипетку следует несколько раз промыть деионизированной водой.
Если капли воды остались внутри, попробуйте очистить пипетку теплым мыльным раствором, а затем несколько раз промыть деионизированной водой. Пипетку следует «кондиционировать» после очистки. Во-первых, получить небольшой объем раствора для дозирования в химический стакан или колбу. Никогда не пипетируйте прямо из бутыли с маточным раствором! Поскольку вы можете загрязнить этот раствор, планируйте отказаться от него после завершения кондиционирования. Наберите небольшой объем раствора в пипетку, затем поверните пипетку в сторону (параллельно столешнице) и медленно вращайте ее, чтобы покрыть внутреннюю поверхность. Затем дайте раствору полностью слив. Теперь пипетка готова для переноса нужной жидкости. Наполнение пипетки требует небольшой практики; Вы можете попробовать это несколько раз с деионизированной водой после очистки. Используйте для этой цели грушу для пипетки — ни в коем случае не рот! Колба имеет коническое резиновое уплотнение. Он не должен и никогда плотно прилегать к верхней части пипетки.
Держите лампочку напротив верхней части трубки, достаточно крепко, чтобы обеспечить герметичность. Сожмите и удерживайте грушу в сжатом виде, опустите кончик пипетки в интересующий раствор и медленно ослабьте давление на грушу. Когда жидкость поднимется немного выше калибровочной метки на горлышке, быстро снимите грушу и плотно прижмите палец (обычно большой или указательный) к верхней части пипетки. Слегка покачивая или вращая пальцем, раствор должен стекать до тех пор, пока нижняя часть мениска не окажется на калибровочной отметке. Удалите все капли, висящие на наконечнике, осторожно коснувшись наконечником стеклянной поверхности, например стакана для отработанного раствора. Содержимое пипетки теперь можно слить в нужный контейнер. Вставьте кончик пипетки в емкость, уберите палец и дайте жидкости вытечь из пипетки. В мерной пипетке будет одна оставшаяся капля, которую следует «прикоснуться», осторожно прикоснувшись кончиком пипетки к внутреннему краю контейнера. Небольшой объем жидкости останется в пипетке и должен оставаться там.
Из серологических пипеток должна быть удалена вся жидкость из пипетки, как правило, при легком нажатии резиновой грушей. Градуированные пипетки (серологические или Мора) немного сложнее в использовании, чем мерные пипетки, потому что существует больше вариантов их заполнения и считывания. Изучите такую пипетку, прежде чем использовать ее, и продумайте, что вы будете с ней делать. Многие градуированные пипетки имеют две шкалы. Одна шкала имеет самые высокие значения по направлению к дозирующему наконечнику и читается как бюретка. Другой имеет самые низкие значения вблизи дозирующего наконечника. Это легче прочитать при наборе жидкости в пипетку для переливания в другой сосуд. После использования пипетки несколько раз промойте ее деионизированной водой. Набрать полный объем и дать стечь. Если вы используете пипетку повторно для нескольких аликвот (образцов) одного и того же раствора, не промывайте пипетку между использованиями. Вам просто нужно будет каждый раз его кондиционировать.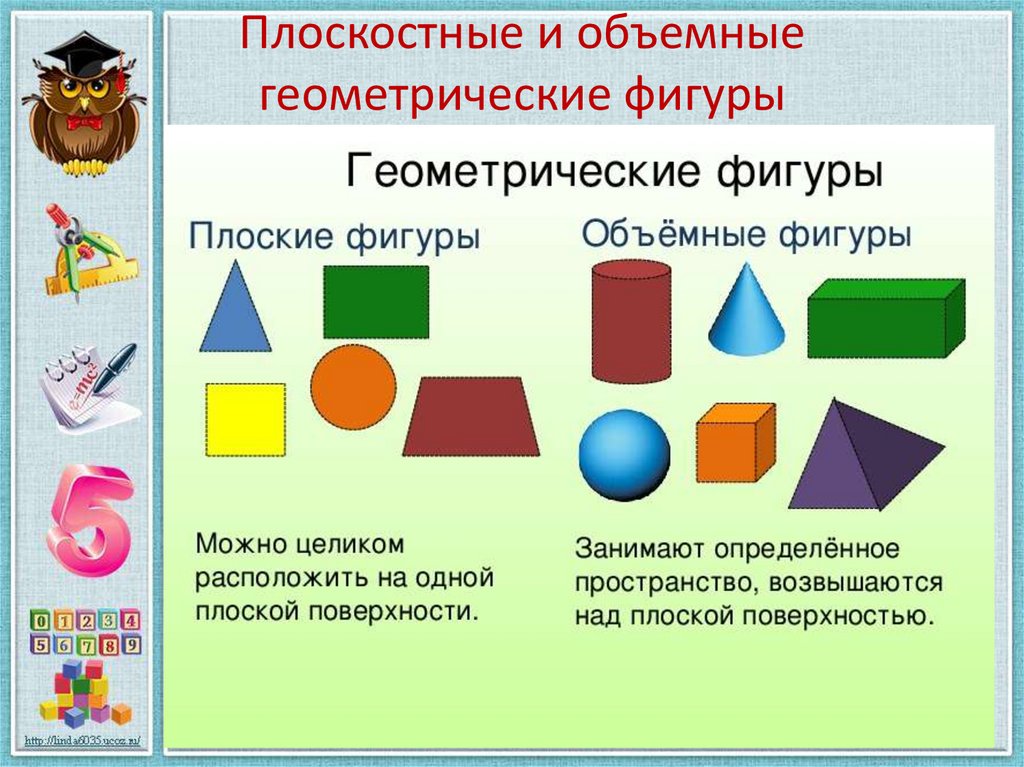
Очистите его, когда закончите, или перед началом работы с другим раствором.
Как показывает предыдущее обсуждение, точность большинства мерных стеклянных сосудов составляет несколько сотых долей миллилитра, и они сконструированы таким образом, чтобы внимательный оператор мог воспроизвести измерения с такой точностью. Таким образом, измерения, сделанные с помощью мерной посуды, сообщаются с точностью до 0,01 мл. В зависимости от используемых объемов, три или четыре значащие цифры могут быть показаны в таблицах данных и учтены в расчетах.
org/ListItem»> Объемные векторыТип лицензии определяет, как вы можете использовать этот образ.
| Станд. | Экспл. | |
|---|---|---|
| Печатный / редакционный | ||
| Графический дизайн | ||
| Веб-дизайн | ||
| Социальные сети | ||
| Редактировать и изменять | ||
| Многопользовательский | ||
| Предметы перепродажи | ||
| Печать по запросу |
Хотите, чтобы это векторное изображение было только у вас? Эксклюзивный выкуп обеспечивает все права этого вектора.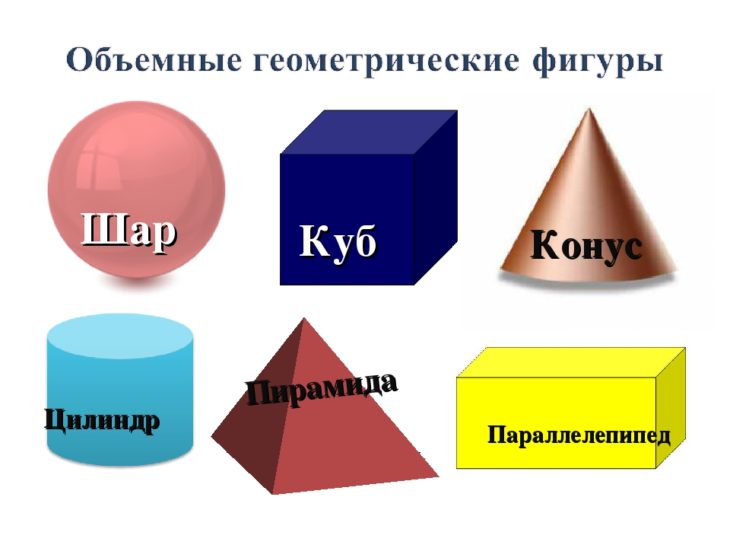
Мы удалим этот вектор из нашей библиотеки, а художник прекратит продажу работ.
Оплатить стандартные лицензии можно тремя способами. Цены $ $ .
| Оплата с помощью | Цена изображения |
|---|---|
| Плата за изображение $ 14,99 Одноразовый платеж | |
| Предоплаченные кредиты $ 1 Загружайте изображения по запросу (1 кредит = 1 доллар США). Минимальная покупка 30р. | |
| План подписки От 69 центов Выберите месячный план. Неиспользованные загрузки автоматически переносятся на следующий месяц. | |
Существует два способа оплаты расширенных лицензий.
