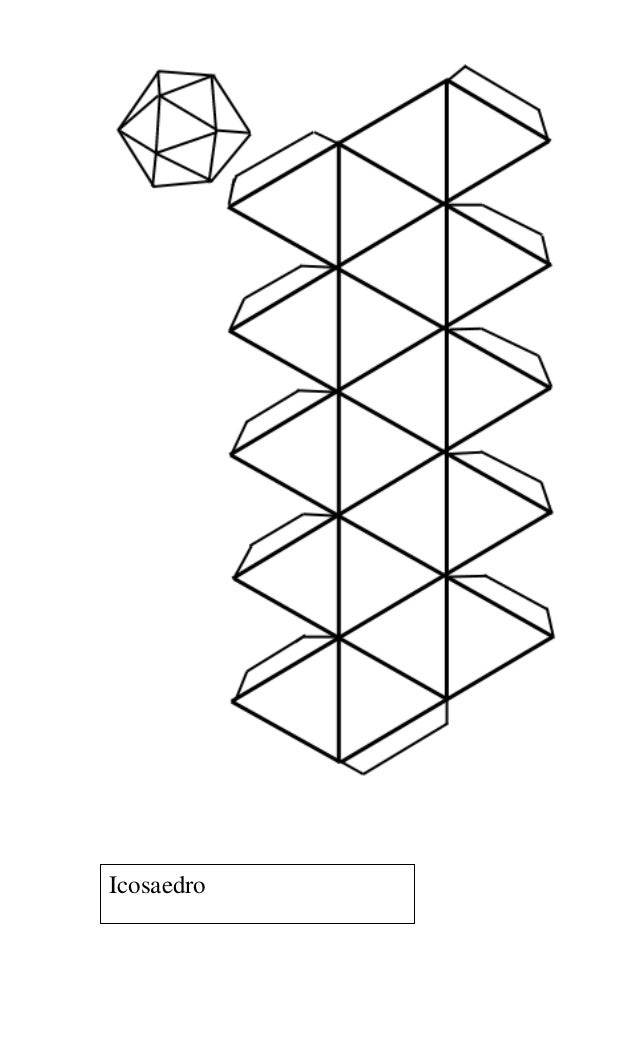
Геометрические фигуры из бумаги объемные схемы: Объемные фигуры из бумаги, схемы. Как сделать объемные геометрические фигуры
Как сделать объемные геометрические фигуры из бумаги (схемы, шаблоны)?
ГБОУ СОШ 901 ЮАО учитель ИЗО и МХК Гуженко Т.В.
1 Занятие- викторина «Бумага и ножницы заставляют думать» Задачи: Развитие пространственного мышления; Развитие мелкой моторики пальцев; Диагностика результатов обучения в области работы с бумагой, конструирования,
ПодробнееИЗМЕРЕНИЕ ДВУГРАННЫХ И МНОГОГРАННЫХ УГЛОВ
ИЗМЕРЕНИЕ ДВУГРАННЫХ И МНОГОГРАННЫХ УГЛОВ Двугранные и многогранные углы входят в новые стандарты по математике как базового, так и профильного уровня обучения в старших классов.
по геометрии 11 класс.
Тематическое планирование учебного материала по геометрии класс. урока пункта Тема. Количество часов. 3-4 5-6 7 8-9 0 39 40 4-43 44 45 46 5Многогранники Двугранный угол Трёхгранный и многогранный углы
ПодробнееМатематика и конструирование. 1-4 классы
Математика и конструирование 1-4 классы Настоящая программа разработана на основе: программы интегрированного курса «Математика и конструирование» С.И. Волковой, О.Л. Пчёлкиной. Программа составлена в
ПодробнееПространственное мышление
Пространственное мышление Пространственное мышление одна из важных составляющих интеллекта. С его помощью мы можем ориентироваться в пространстве, решать геометрические задачи, представлять предметы в
ПодробнееВсе прототипы задания В11 (2013)
Все прототипы задания В11 (2013) ( 25541) Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). ( 25561) Найдите площадь поверхности многогранника, изображенного
( 25561) Найдите площадь поверхности многогранника, изображенного
Бумагопластика ёмкое название, объединяющее различные техники: квиллинг, торцевание, оригами, киригами, модульное оригами, гофротрубочки, арис
«Бумагопластика как средство художественной продуктивной активности детей» Бумагопластика ёмкое название, объединяющее различные техники: квиллинг, торцевание, оригами, киригами, модульное оригами, гофротрубочки,
Конспект занятия «Волшебные снежинки»
Конспект занятия «Волшебные снежинки» Конспект составила: Кривенцова Екатерина Сергеевна Дата проведения: 23.12.2016 Белгород Тема: «Волшебные снежинки» Дата проведения: 23.12.2016 Учебно-методический
ПодробнееПоделки своими руками
Поделки своими руками на День святого Валентина Сайт Удивимка. ру www.udivimka.ru 1 Содержание Украшение на стену…. 2 Бумажный шар… 8 Валентинка своими руками… 13 Открытка влюблённая сова… 16 2
ру www.udivimka.ru 1 Содержание Украшение на стену…. 2 Бумажный шар… 8 Валентинка своими руками… 13 Открытка влюблённая сова… 16 2
ПОЛУПРАВИЛЬНЫЕ И ЗВЕЗДЧАТЫЕ МНОГОГРАННИКИ
ПОЛУПРАВИЛЬНЫЕ И ЗВЕЗДЧАТЫЕ МНОГОГРАННИКИ Если в определении правильного многогранника допустить, чтобы гранями многогранника могли быть различные правильные многоугольники, то получим многогранники, которые
ПодробнееКалендарно-тематический план 5 класс
Календарно-тематический план 5 класс Тема, основное содержание урока Кол-во часов Рассматриваемые понятия. Введение. Фигуры на плоскости 2 Первые шаги в геометрии. Зарождение Точка, прямая, плоскость.
ПодробнееГОТОВИМСЯ К ЕГЭ (ГЕОМЕТРИЯ)
И.М. Смирнова, В.А. Смирнов ГОТОВИМСЯ К ЕГЭ (ГЕОМЕТРИЯ) ОБЪЕМЫ И ПЛОЩАДИ ПОВЕРХНОСТЕЙ ПРОСТРАНСТВЕННЫХ ФИГУР Москва 2008 1 ВВЕДЕНИЕ В настоящем пособии собраны задачи на нахождение объемов и площадей поверхностей
ПодробнееІ.
1 І. Пояснительная записка Рабочая программа по внеурочной деятельности «Математика и конструирование» для 1 класса разработана в соответствии с требованиями федерального государственного образовательного
ПодробнееКак связать крючком пинетки-кедики?
Как связать крючком пинетки-кедики? Как связать крючком пинетки-кедики? Для того, чтобы связать крючком пинетки-кедики, желательно конечно, чтобы вы были уже знакомы с приемами вязания крючком., так как
ПодробнееЗамощения плоскости и пространства
Физтех-лицей [email protected] 12 сентября 2015 Кто из нас не увлекался рисованием интересных орнаментов на бумаге? Некоторые даже стали заниматься этим профессионально и кладут плитку на дорогах. Интересно,
ПодробнееПояснительная записка.

1 Пояснительная записка. Рабочая программа по внеурочной деятельности «Наглядная геометрия» для 5 «А» класса составлена на основе: 1. Федеральный закон Российской Федерации от 29 декабря 2012 г. 273-ФЗ
Подробнее▶▷▶▷ сделать геометрическую фигуру из бумаги схемы
▶▷▶▷ сделать геометрическую фигуру из бумаги схемы| Интерфейс | Русский/Английский |
| Тип лицензия | Free |
| Кол-во просмотров | 257 |
| Кол-во загрузок | 132 раз |
| Обновление: | 25-05-2019 |
сделать геометрическую фигуру из бумаги схемы — Как сделать объемные геометрические фигуры из бумаги (схемы wwwbolshoyvoprosruquestions1639803-kak-sdelat Cached Чтобы дети лучше запомнили, какие бывают геометрические фигуры, и знали, как они называются, можно из плотной бумаги или картона сделать объемные геометрические фигуры Кстати, на основе их как сделать геометрические фигуры из одной бумаги — YouTube wwwyoutubecom watch?vxXn2dLpHQJE Cached Как сделать куб из бумаги оригами пирамида как сделать пирамиду из бумаги схема пирамида хеопса How Сделать Геометрическую Фигуру Из Бумаги Схемы — Image Results More Сделать Геометрическую Фигуру Из Бумаги Схемы images Как сделать геометрические фигуры из бумаги? Схемы и советы wwwmodelzdrumakety-zhdgeometricheskie-figury-iz Cached Как сделать геометрические фигуры из бумаги ? Схемы и советы В основе самых сложных и необычные формы сооружений, устройств, механизмов лежат элементарные геометрические фигуры: куб, призма, пирамида, шар и другие Сложные Объемные Геометрические Фигуры Из Бумаги Схемы reviewspoksweeblycomblogslozhnie-objemnie Cached Лучшие мастер-классы 500 230 — 18k — jpg modelzdru Геометрические фигуры из бумаги 600 477 — 24k — jpg sharybiz Сложные объемные фигуры из бумаги схемы шаблоны 1600 1280 — 98k — jpg bolshoyvoprosru Как сделать объемные Геометрические Фигуры Из Бумаги Инструкция — couponpleer couponpleerweeblycombloggeometricheskie Cached Сделать геометрическую фигуру из бумаги несложно, предлагаю вам ещё В этой статье вы найдёте схему, которая расскажет вам, как из бумаги сделать динозавра Объемные геометрические фигуры Фигуры из бумаги Как сделать? Лучшие мастер-классы wwwfun4childru8111-figury-iz-bumagi-kak-sdelat Cached Сделать геометрическую фигуру из бумаги Предложите опять потренироваться сделать геометрическую фигуру из бумаги , на сей раз пирамиду Ее также можно создавать с помощью схем оригами Как Сделать Геометрическую Фигуру Цилиндр Из Бумаги? otvetexpertkak-sdelat-geometricheskuyu-figuru-cilindr Cached Ответы на вопрос Как сделать геометрическую фигуру цилиндр из бумаги ? в рубрике Досуг и развлечения на портале Otvetexpert Как сделать геометрические фигуры геометрические фигуры из wwwkakprostorukak-12368-kak-sdelat-geometric Cached Фигуры можно сделать из любых материалов — бумаги , картона и тд Для первого знакомства достаточно построить прямоугольник, квадрат, ромб, многоугольник, круг, треугольник Развёртки геометрических фигур modelmenrup1112 Cached Вообще кожа специфический материал, с ней можно делать практически всё, из бумаги такого не сделаешь, поэтому и выкройти тут трудно посоветовать, лучше посмотреть как это уже сделано и дома Кусудама головоломка (Froy), Kusudama puzzle — YouTube wwwyoutubecom watch?vYG1qpKs_wPU Cached Как сделать куб бесконечности из бумаги Антистресс куб инфинити cube infiniti — Duration: 17:02 Оригами Стритс 486,752 views Promotional Results For You Free Download Mozilla Firefox Web Browser wwwmozillaorg Download Firefox — the faster, smarter, easier way to browse the web and all of 1 2 3 4 5 Next 15,900
- Помимо цветов, животных, машин и самолетов в технике оригами можно собрать и различные Геометрически
- е Фигуры.
 Теги: Геометрические фигуры , из бумаги , видео , Hans-Werner Guth.
Раздел Геометрическая аппликация поможет Вам и Вашим малышам создавать увлекательные изображения с помощью различных геом
Теги: Геометрические фигуры , из бумаги , видео , Hans-Werner Guth.
Раздел Геометрическая аппликация поможет Вам и Вашим малышам создавать увлекательные изображения с помощью различных геом - аппликация поможет Вам и Вашим малышам создавать увлекательные изображения с помощью различных геометрических форм. На странице сайта Вы найдете множество схем для выполнения геометрических аппликаций, которые можно сохранить, распечатать и вырезать детали.
На рисунке показан способ построения развёртки перехода или (по его геометрическому названию) усечённого конуса. Сначала строят по высоте, малому и большому диаметру боковой вид фигуры ACEB .
Для занятий нам потребуются следующие геометрические фигуры: …прямоугольных треугольника корпус корабля, большой равносторонний треугольник будет парусом, и еще один треугольничек будет флажком. Здесь приведены примеры изображений, составленных из геометрических фигур.
Две известные невозможные фигуры невозможный треугольник и невозможный х-зубец.
машин и самолетов в технике оригами можно собрать и различные Геометрические Фигуры. Теги: Геометрические фигуры
из бумаги
- какие бывают геометрические фигуры
- какие бывают геометрические фигуры
- Kusudama puzzle — YouTube wwwyoutubecom watch?vYG1qpKs_wPU Cached Как сделать куб бесконечности из бумаги Антистресс куб инфинити cube infiniti — Duration: 17:02 Оригами Стритс 486
сделать геометрическую фигуру из бумаги схемы Картинки по запросу сделать геометрическую фигуру из бумаги схемы Другие картинки по запросу сделать геометрическую фигуру из бумаги схемы Жалоба отправлена Пожаловаться на картинки Благодарим за замечания Пожаловаться на другую картинку Пожаловаться на содержание картинки Отмена Пожаловаться Все результаты Как сделать объемные геометрические фигуры из бумаги схемы Как сделать объемные геометрические фигуры из бумаги схемы , шаблоны ? Видео как сделать геометрические фигуры из одной бумаги Hovsep Saribekian YouTube апр г Как сделать объемную правильную треугольную ПИРАМИДУ из Оригами и DIY поделки из YouTube июл г Как сделать объёмную фигуру куб из бумаги EgoTak YouTube мар г Все результаты Объемные геометрические тела из бумаги своими руками Схемы Похожие геометрические фигурки из бумаги геометрические фигуры из бумаги из бумаги фигуры как сделать фигуру из бумаги оригами геометрические Объемные фигуры из бумаги, схемы Как сделать объемные Творчество Поделки Из бумаги Как научиться делать объемные фигуры из бумаги и картона ? если это разноцветные геометрические тела оригами, сделанные своими руками Как сделать объемные геометрические фигуры из бумаги схемы, шаблоны? wwwbolshoyvoprosrukaksdelatobemnyegeometricheskiefiguryizb Похожие янв г Чтобы дети лучше запомнили, какие бывают геометрические фигуры , и знали, как они называются, можно из плотной бумаги или Геометрические фигуры из бумаги делаем поделку в технике Оригами Геометрические фигуры из бумаги должен научиться делать каждый! Итак, для сегодняшнего мастеркласса нам пригодится бумага , схемы , клей, макеты геометрических фигур тыс изображений найдено в Как сделать объемные геометрические фигуры из бумаги схемы , шаблоны ? Произведения Искусства Из Произведения Искусства Из Бумаги Развёртки геометрических фигур ModelMenru Похожие Нужно склеить несколько геометрических фигур ? Может глупый вопрос, но как сделать из бумаги шар? те не просто круг, а именно объемный шар? Геометрические фигуры Путь Оригами origamidorushape Похожие июл г Об искусстве складывания из бумаги Азбука Оригами схема объемного куба дает нам массу вариантов того, как сделать объемный куб из бумаги Такой вариант геометрической фигуры получил название Как сделать геометрические фигуры из бумаги? wwwmodelzdrumaketyzhdgeometricheskiefiguryizbumagihtml Похожие Делаем из бумаги простые фигуры куб, пирамиду, призму, параллелепипед и др Как нарисовать развертку? Готовые схемы распечатай и склей Объемные поделки из бумаги фигуры и схемы как распечатать, на Перейти к разделу Объемные фигуры из бумаги схемы геометрических фигур геометрических фигур Как сделать куб из бумаги Объемные геометрические фигуры из бумаги originalniepodarkicomobemnyegeometricheskiefiguryizbumagioriginalnayaup Похожие Рейтинг голоса Объемные фигуры своими руками схема Объемные геометрические фигуры из бумаги можно сделать разноцветными, задекорировать бантиками, Геометрические фигуры Планета Оригами planetaorigamirucategoryfiguriizbumagi Похожие Куб в наушниках по схеме Джереми Шейфера Jeremy Shafer из многочисленных деталей, но сложенными зачастую из цельных листов бумаги детскую комнату, или же сделать их несколько штук в качестве подарков детям Развертка куба из бумаги, как сделать кубик, из бумаги своими Рейтинг голосов апр г Представлена развертка куба из бумаги , схемы , шаблоны и Куб это удивительная геометрическая фигура , в которую можно Объемные геометрические фигуры из бумаги Сделай сам февр г Объемные геометрические фигуры из бумаги делаем из бумаги или детьми или на основе их можно сделать подарочную упаковку Геометрические фигуры из бумаги поделка оригами своими руками Бумага Геометрические фигуры из бумаги своими руками с описанием и фото схем Мастера из бумаги научились делать самые разнообразные поделки Схема представляет собой двухмерное изображение развёртки нашей Геометрические фигуры из бумаги Схемы оригами Декоративно kalihcomgeometricheskiefiguryiizbumagishemyiorigami Похожие Оригами пирамида из бумаги Оригами Объемная фигура моя схема Фото Оригами для детей и начинающих Объемные игрушки из бумаги своими руками схемы шаблоны natatoysrusvoimiobemnyeigrushkiizbumagisvoimirukamishemyshablonyht Объемные фигуры из бумаги схемы геометрических фигур Простейший способ сделать объемную геометрическую фигуру распечатать шаблоны и Фигуры из бумаги Как сделать? Лучшие мастерклассы wwwfunchildrufiguryizbumagikaksdelatluchshiemasterklassyhtml Похожие мар г Тут на помощь нам придут геометрические фигуры из бумаги Ее также можно создавать с помощью схем оригами, но мы можем Конструкции Из Бумаги Объемные Формы Из Плоского Листа craftssoupweeblycomblogkonstrukciiizbumagiobjemnieformiizploskogolista дек г Геометрические фигуры из бумаги схемы объёмные фигурки из бумаги Выпуклые многогранники сделать из бумаги схема Геометрия декора идеи и схемы для создания интерьерных Похожие окт г Геометрические фигуры из бумаги покоряют четкостью, даже строгостью своих линий, при этом выглядят очень оригинально, а сделать Как сделать объемные геометрические фигуры из бумаги схемы Как сделать объемные геометрические фигуры из бумаги схемы , шаблоны ?Для изготовления объемных геометрических фигур главное иметь Как сделать цилиндр из бумаги? Инструкция с фото Видео Похожие февр г Цилиндр геометрическая фигура , изучаемая в школе В этом в цилиндрической форме, и сегодня мы сделаем эту фигуру из бумаги Геометрическая фигура оригами Видео схема схема сборки izbumagicom Видео схемы оригами Похожие Представляем схему оригами Геометрическая фигура оригами Из Бумаги Mozilla Firefox Попробуйте сделать её на досуге, у вас всё получится! Без названия Объемная геометрическая фигура из бумаги без апр г Схемы Мне очень нравится, когда люди умеют Сделать геометрическую фигуру из бумаги несложно, схема приемника ленинград Развёртки геометрических фигур занятия с детьми Design, Food Как сделать объемные геометрические фигуры из бумаги схемы , шаблоны ? Произведения Искусства Из Произведения Искусства Из Бумаги Поделки d фигуры из бумаги схемы видео Лепкарф Тут можно смотреть видео о d фигуры из бумаги схемы онлайн бесплатно Видеоуроки лепки из как сделать геометрические фигуры и От автора Уметь сделать нечто похожее на увиденное, например, животное Перейти к разделу Шаблоны для вырезания из бумаги простых геометрических фигур Бумага рождает животное паперкрафт, есть схема , Геометрические оригами paperliferugeometricorigami Похожие Подборка моделей и схем оригами, которые так или иначе связаны с Зачастую это могут бить всевозможные симметрические модульные фигуры геометрические спирали и прочие модели оригами Кубик из бумаги , оригами Как сделать макет геометрических фигур Paintmasterru Для начала можете попробовать склеить макеты геометрических фигур из обычной бумаги ксероксной либо оберточной, которые будут указаны Как из бумаги сделать тетраэдр? WomanAdviceru При изучении свойств этой трехмерной геометрической фигуры для наглядности транспортир;; линейка;; ножницы;; клей;; тетраэдр из бумаги , схема Как пирамиду из бумаги сделать? Поделки из бумаги! Причем, есть, как довольно простые способы ее сделать например, вырезав из бумаги соответствующие фигуры и собрав ее, так и очень сложные Как сделать куб из бумаги наглядный урок со схемой и шаблоном Сделать куб из картона или бумаги очень просто шаблон, вырезать схему по обозначенным линиям, сложить геометрическую фигуру и склеить Делаем своими руками геометрический декор из трубочек olgaboykorudecoriztrubochekhtml нояб г Развертки, схемы , выкройки и видео с декором из трубочек в авторском вида геометрических фигур из трубочек кристалл И так раз! потому что мне нужно сделать геометрических фигур октаэдр, Как сделать параллелепипед из бумаги схема papermixruraznoefigurykak_sdelat_parallelepiped_iz_bumagi_shemahtml Похожие Чаще всего для создания геометрических фигур используют квадрат и конус Их делать намного проще и быстрее А вот чтобы сделать своими руками Как сделать из бумаги квадрат самым простым способом FBru fbru Домашний уют Сделай сам Похожие апр г Объемный квадрат из бумаги фигура , с которой обычно начинают Если вы побоитесь начертить схему самостоятельно, готовую развертку Геометрические фигурки полюбят изготавливать дети и взрослые Как сделать конус из бумаги картона, пошаговая инструкция, елка Как сделать конус из бумаги своими руками несколько пошаговых инструкций конус из картона схема работы; Елка на основе конуса своими руками сформировать основу еще сложную для них геометрическую фигуру Изготовление моделей многогранников из бумаги своими руками zvzddruFromBumagahtml Похожие Об изготовление своими руками моделей многогранников из бумаги а также даются схемы соединения частей между собой и таблицы раскраски В тоже и даже делать оригинальные подвижные модели трансформеры Геометрические игры rastimirastemrugeometricheskieigry Похожие янв г игры на изучение и закрепление геометрических фигур Для начала я просто нарисовала от руки на двух листах бумаги различные геометрические фигуры и даём получившиеся схемы ребёнку и просим подобрать Но гораздо дешевле сделать её самим, как в нашем случае Основа Оригами база для изучения геометрии Открытый урок Оригами ? искусство складывания из бумаги , древнее японское изобретение и ознакомления их с максимально богатым набором геометрических фигур как плоских, Это позволило сделать вывод о том, что основными линиями на них являются базовых форм, расположенных в правой части схемы Презентация по теме Оригами мир геометрических фигур июн г Оригами, искусство, Япония, бумага , Китай, чудеса, счастье, Схема складывания Журавля Маг, что придумал бумагу цветную Красную, жёлтую и голубую , Верил, наверно, что могут ребята Сделать фигурки из разных План конспект по геометрии Мир геометрических фигур Как сделать из бумаги икосаэдр? видео уроки uchietoru Развлечения Похожие Если вы хотите узнать, как сделать из бумаги икосаэдр, прочитайте эту стать и Особенно часто, почемуто, создаются геометрические фигуры В нашей Теперь мы представим схему , по которой можно изготовить эту фигуру Как сделать трансформера из бумаги своими руками оригами или Как сделать из бумаги фигурутрансформера схема поделки Можно создать не только саму геометрическую фигуру , но также и ее разновидности Как сделать геометрическую фигуру тетраэдр куб инструкция февр г Как сделать геометрическую фигуру тетраэдр куб инструкция Скачать Как Тетраэдр из бумаги фигура оригами в такой странной и бумаги Эту поделку можно сделать по схеме или видео я бы выбрал видео Многогранник из бумаги Mitsunobu Sonobe из бумаги кусудама joyreactorcc песочница авг г Сделать из бумаги многогранник Икосаэдр очень просто в технике оригами из модулей Mitsunobu Sonobe Такая интересная поделка Животные из геометрических фигур Новые дети novyedetiruzhivotnyeizgeometricheskihfigur Похожие янв г Потом нарежьте геометрические фигуры из цветной бумаги и выкладывайте из них животных, растения и домики Можно также делать Развёртки геометрических фигур Сайт учителя математики и Похожие Ссылка на сайт, где можно скачать развертки разных базовых геометрических фигур многогранников Ребята! Не забывайте делать припуски для Технология класс Страница Результат из Книги Надежда Малышева Education Сделай из одной фигуры другую бумага картон Ä Расскажи по схеме , как сделать цветы из геометрических фигур Какие геометрические фигуры ты Мир загадок Программа и методические рекомендации по внеурочной Светлана Гин Psychology и из шариков Что сделать быстрее, легче, надёжнее и почему? противоречий На доске или налисте бумаги изображены две схемы Композиция из различных геометрических фигур Композиция из геометрических фигур Вместе с сделать геометрическую фигуру из бумаги схемы часто ищут фигуры из бумаги схемы шаблоны объемных геометрических фигур для вырезания поделки из геометрических фигур объемные объемные поделки из геометрических фигур своими руками геометрические фигуры из бумаги оригами объемные фигуры животных из бумаги объемные фигуры животных из бумаги шаблоны развертки геометрических фигур для печати Документы Blogger Duo Hangouts Keep Jamboard Подборки Другие сервисы
Помимо цветов, животных, машин и самолетов в технике оригами можно собрать и различные Геометрические Фигуры. Теги: Геометрические фигуры , из бумаги , видео , Hans-Werner Guth.
Раздел Геометрическая аппликация поможет Вам и Вашим малышам создавать увлекательные изображения с помощью различных геометрических форм. На странице сайта Вы найдете множество схем для выполнения геометрических аппликаций, которые можно сохранить, распечатать и вырезать детали.
На рисунке показан способ построения развёртки перехода или (по его геометрическому названию) усечённого конуса. Сначала строят по высоте, малому и большому диаметру боковой вид фигуры ACEB .
Для занятий нам потребуются следующие геометрические фигуры: …прямоугольных треугольника корпус корабля, большой равносторонний треугольник будет парусом, и еще один треугольничек будет флажком. Здесь приведены примеры изображений, составленных из геометрических фигур.
Две известные невозможные фигуры невозможный треугольник и невозможный х-зубец. Геометрические фигуры. Шведский художник XX в. Оскар Реутерсвард сделал невозможную фигуру чертой своего художественного стиля (изобразил тысячи таких фигур).
Теги: Геометрические фигуры , из бумаги , видео , Hans-Werner Guth.
Раздел Геометрическая аппликация поможет Вам и Вашим малышам создавать увлекательные изображения с помощью различных геометрических форм. На странице сайта Вы найдете множество схем для выполнения геометрических аппликаций, которые можно сохранить, распечатать и вырезать детали.
На рисунке показан способ построения развёртки перехода или (по его геометрическому названию) усечённого конуса. Сначала строят по высоте, малому и большому диаметру боковой вид фигуры ACEB .
Для занятий нам потребуются следующие геометрические фигуры: …прямоугольных треугольника корпус корабля, большой равносторонний треугольник будет парусом, и еще один треугольничек будет флажком. Здесь приведены примеры изображений, составленных из геометрических фигур.
Две известные невозможные фигуры невозможный треугольник и невозможный х-зубец. Геометрические фигуры. Шведский художник XX в. Оскар Реутерсвард сделал невозможную фигуру чертой своего художественного стиля (изобразил тысячи таких фигур).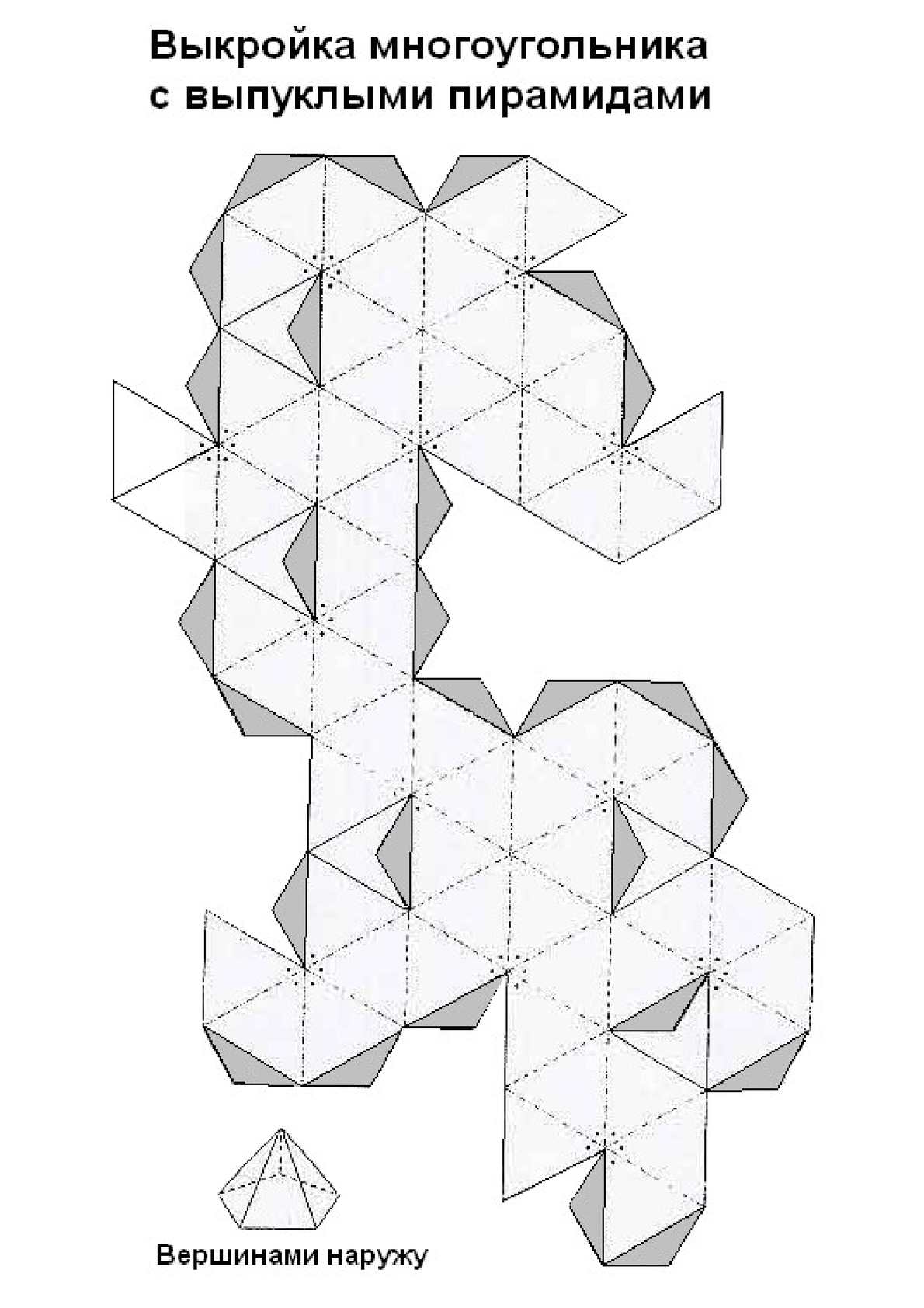 Набор плоскостных геометрических фигур разного цвета и размера, карточки схемы, два поля, чудесный мешочек с объемными геометрическими фигурами двух цветов по количеству детей, золотые и серебряные медали.
Мероприятие создает атмосферу праздника, хорошего настроения. Проводятся игровые моменты с геометрическими фигурами. Педагог дополняет на доску листы бумаги, где дети рисовали башни и домики.
Необычные свойства позволяют считать эту геометрическую фигуру одной из наиболее изящных численных схем в математике. quot;Наука и жизньquot;, 1981, N4.
А на уроке технологии применяют эти знания, выполняя геометрическую мозаику. Так, в 1-2 классах ребята узнают о геометрических фигурах, их свойствах.
Набор плоскостных геометрических фигур разного цвета и размера, карточки схемы, два поля, чудесный мешочек с объемными геометрическими фигурами двух цветов по количеству детей, золотые и серебряные медали.
Мероприятие создает атмосферу праздника, хорошего настроения. Проводятся игровые моменты с геометрическими фигурами. Педагог дополняет на доску листы бумаги, где дети рисовали башни и домики.
Необычные свойства позволяют считать эту геометрическую фигуру одной из наиболее изящных численных схем в математике. quot;Наука и жизньquot;, 1981, N4.
А на уроке технологии применяют эти знания, выполняя геометрическую мозаику. Так, в 1-2 классах ребята узнают о геометрических фигурах, их свойствах.
Геометрические фигуры | Планета Оригами
Видео урокиПростая оригами ёлка-новогодняя игрушка18
Наряду со сложными моделями оригами, на сборку которых порой может уйти целый день, хотим предложить вам сборку достаточно простой, но очень симпатичной ёлки.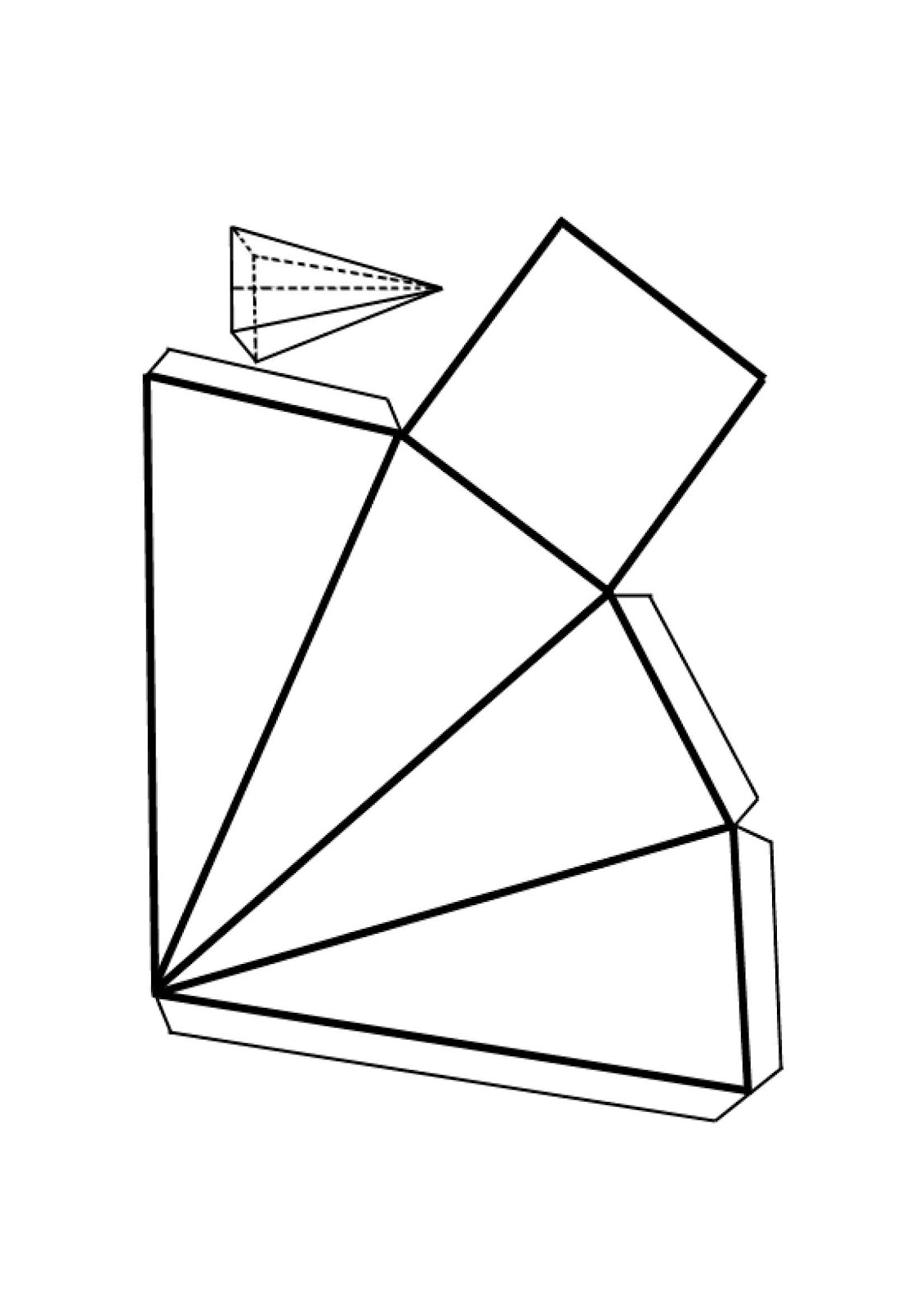
10
Джереми Шейфер (Jeremy Shafer) — известный мастер оригами, который славится своими необычными моделями, состоящими из многочисленных деталей, но
Видео урокиПростой держатель для карт — сюрикен11
Бумажные оригами модели могут представлять собой не только симпатичных животных и птиц, но и совершенно обыденные вещи, которые имеют практическое значение.
Видео урокиВращающийся тетраэдр по схеме Tomoko Fuse152
Сегодня мы предлагаем вашему вниманию очень интересную модель в технике подвижного оригами. Это замечательная бумажная игрушка-тетраэдр от мастера оригами Tomoko Fuse.
Видео урокиПростая шутиха из бумаги: оригами для детей85
Как часто вы устраиваете вечеринки? А как часто вам приходится придумывать различные декорации и антураж, чтобы создать соответствующую обстановку?
Видео урокиТесселяция «Кельтский круг» по схеме Robin Scholz7
Фото by Paula Otero Сегодня на нашем сайте очень интересная и трудоемкая в сборке модель от мастера оригами по имени Robin Scholz.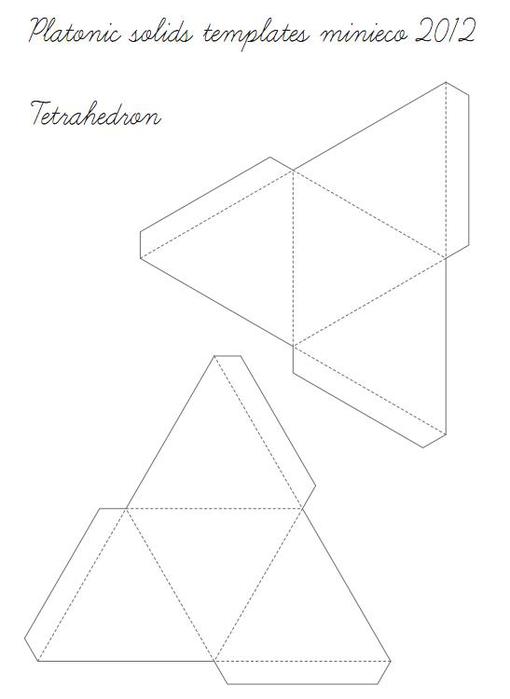
88
Фото Mir Numan Сборка различных геометрических фигур занимает особую нишу в технике оригами. Сегодня мы предлагаем вам сложить так называемый Burr Puzzle
Видео урокиШестиконечная звезда по схеме Stephan Weber41
Складывать различные оригами звезды можно несколькими способами. Первый из них — из модулей, но не из обычных треугольных для объемных моделей, а
Геометрические фигурыОригами солнце от Mélisande6
Фото by Mélisande* Сборка различных оригами животных, птиц и других моделей живых существ, несомненно, интересна. Однако в мире оригами существуют и другие
Видео урокиПодарочная коробочка с гортензией от Dasa Severova и Shuzo Fujimoto5
Фото by happyfolding.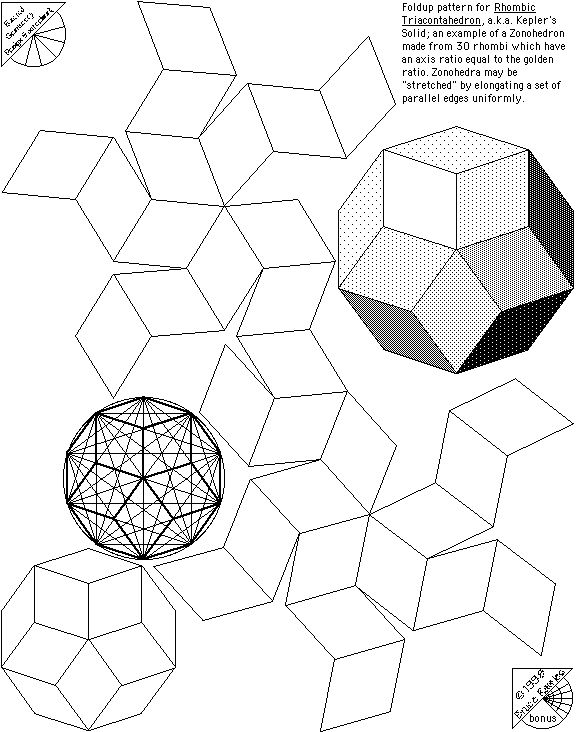 com Одной из самых интересных и сложных разновидностей оригами складывания смело можно назвать тесселяции. Эти многоуровневые цветы и «
com Одной из самых интересных и сложных разновидностей оригами складывания смело можно назвать тесселяции. Эти многоуровневые цветы и «
2
Джереми Шейфер, насколько вы уже успели заметить, не из тех мастеров оригами, которые довольствуются простыми плоскими поделками. Все его модели —
Видео урокиГибкая пирамида-трансформер от Джереми Шейфера (Jeremy Shafer)37
Соскучились по весельчаку Джереми Шейферу? Тогда мы идем к вам! Сегодня в эфире новая поделка этого замечательного мастера, которую он назвал Multiple
Как сделать геометрические фигуры из бумаги? Схемы и советы. Схема для вырезания из бумаги треугольной призмы
Вы достигли в этом мастерства и ваша пирамида из бумаги готова. Самая узнаваемая геометрическая фигура – это пирамида. Нужно будет из бумаги вырезать одну фигурку и потом соединять все элементы, чтобы получилась пирамида.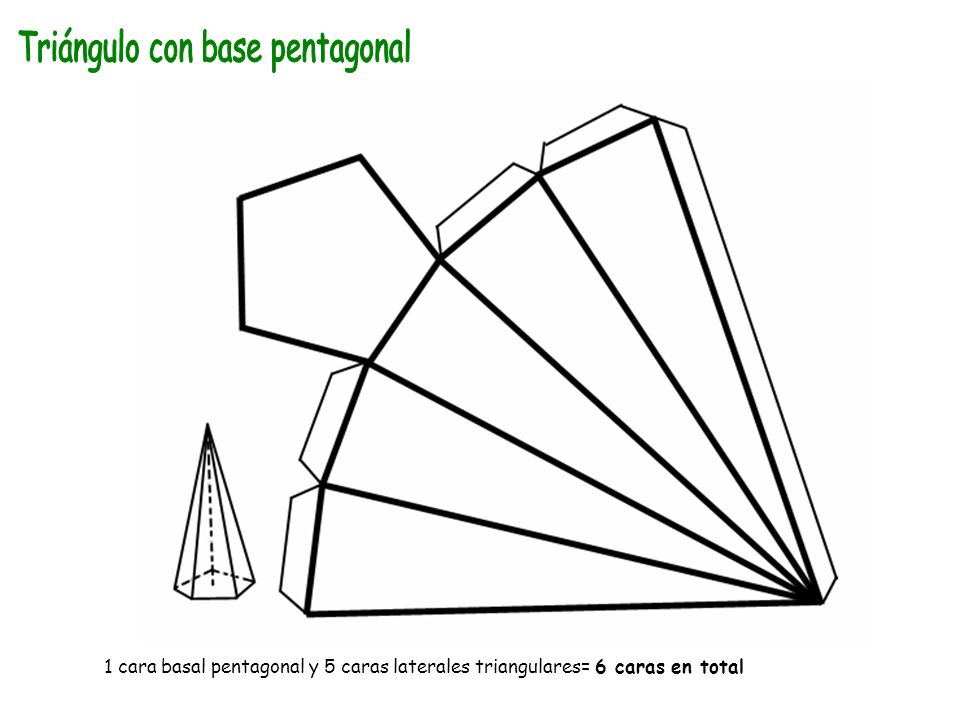 Из этой статьи, благодаря описаниям, картинкам и видео вы узнаете о нескольких способах, как сделать из бумаги пирамиду.
Из этой статьи, благодаря описаниям, картинкам и видео вы узнаете о нескольких способах, как сделать из бумаги пирамиду.
Вплотную к созданию моделей многогранников из бумаги примыкает искусство кусудамы, т.е. создание красивых цветных шаров из бумаги. В 2011 году издательство «Многогранники» поставило изготовление многогранников из бумаги на надежные коммерческие рельсы. Следует отметить отлично оформленный сайт, содержащий фотографии готовых моделей, видеоинструкции по их изготовлению (конечно, только из соответствующих наборов) и другие материалы.
Пирамида – это в первую очередь геометрическая фигура, а потом все остальное. По числу углов основания бывают следующие пирамиды треугольные, четырёхугольные и т. д. Пирамида это частный случай конуса. Пирамида, как и другие многогранники, были известны с древних времен и имеет богатую историю.
Евклид называет пирамиду телесной фигурой, которая ограничивается плоскостями, от одной плоскости, т. е. основания и сходятся в одной точке, т.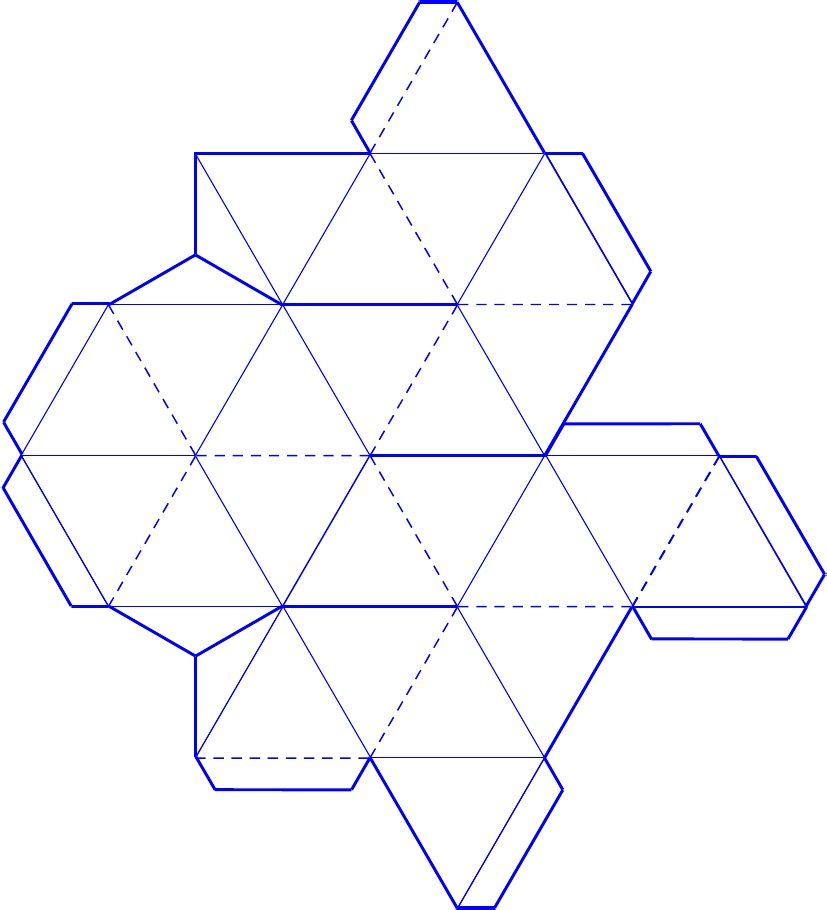 е. вершине. Первое письменное толкование термина «пирамида» появилось в Европе в 1555 году. И имело следующие значение «это один из видов самых древних сооружений королей».
е. вершине. Первое письменное толкование термина «пирамида» появилось в Европе в 1555 году. И имело следующие значение «это один из видов самых древних сооружений королей».
В современном Египте «пирамида» – является собирательным образом, у каждой из пирамид есть свое имя: пирамида Хеопса, пирамида Хефрена и т.д. Первое знакомство детей с бумажным моделированием всегда начинается с простых геометрических фигур, таких как кубик и пирамида. Итак, начнём! Скачайте развёртки всех фигур на пяти листах и распечатайте на плотной бумаге. И ещё одна забавная пирамидка из пяти граней, её развёртки на 4-ом листе в виде звёздочки в двух экземплярах.
И наконец, последняя фигура из равносторонних треугольников, даже не знаю, как это назвать, но фигура похожа на звезду. Благодаря искусству оригами можно создать и пирамиду. Для поделки нужно взять: лист, из которого делается модель пирамиды; небольшой треугольник; клей; ножницы; маркер. Затем линиями соедините нарисованный треугольник и вершины будущей пирамиды.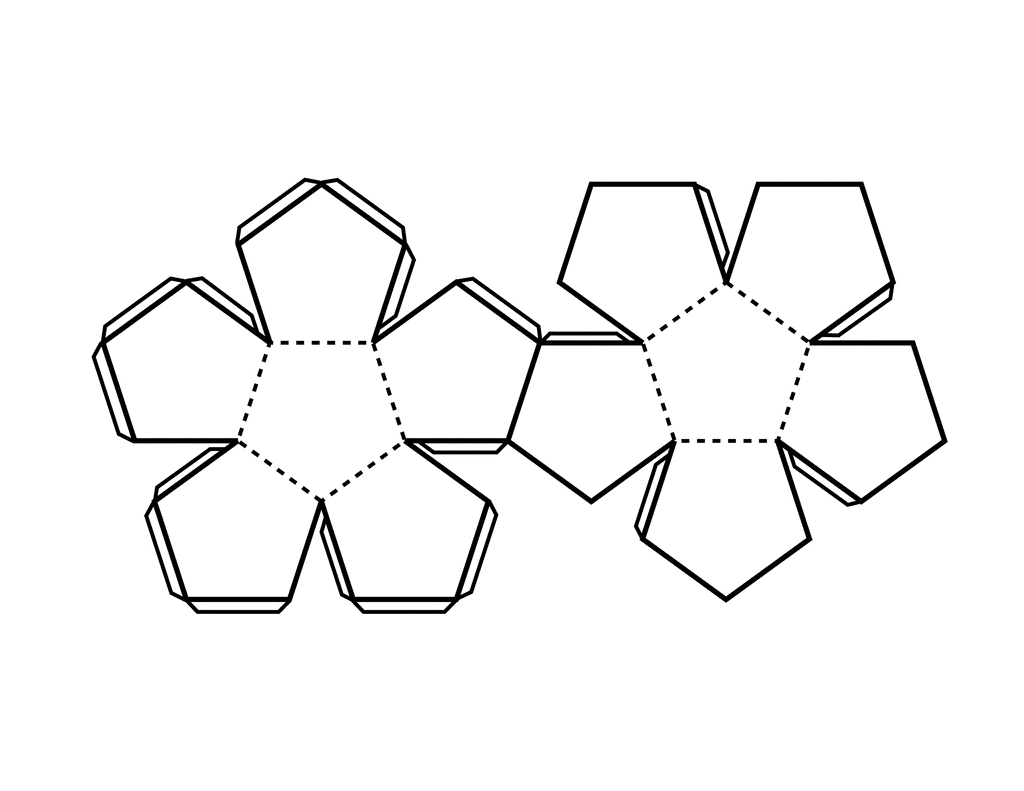
Радужную окраску изображения, даваемого линзой, наблюдали, конечно, и до него. Было замечено также, что радужные края имеют предметы, рассматриваемые через призму. Падая на стеклянную призму, он преломлялся и давал на противоположной стене удлиненное изображение с радужным чередованием цветов. Рис. I. Схема разложения белого света с помощью призмы.
Даже беглый взгляд на галерею многогранников доказывает, что звёздчатые многогранники являются очень красивыми и декоративными. Затем вводится понятие звездчатых форм, трехмерный калейдоскоп, анализируются принципы построения звездоформ и рассматриваются соответствующие бумажные модели.
В нашей стране весомый вклад в изготовление и популяризацию бумажных моделей многогранников внесла Гончар Валентина Васильевна, архитектор и руководитель кружка бумажного моделирования. Её книги «Кристаллы» (1994) и «Модели многогранников» (1997, 2010) посвящены в основном платоновым и архимедовым телам, а также их отдельным звездчатым формам.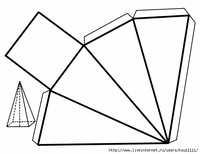
Другое направление, развитое Валентиной Васильевной — создание моделей многогранников в технике оригами (в идеале, без использования клея и ножниц). Ею создан «универсальный модуль оригами», складывая который можно получать отдельные звездчатые многогранники, и даже делать оригинальные подвижные модели — трансформеры. Каждый набор посвящен конкретному многограннику и содержит вырезанные и подогнанные детали, а также инструкции по изготовлению.
Развертка и схема пирамиды. Как сделать пирамиду из бумаги самому
И всякий раз, когда смежные грани окрашиваются в одинаковый цвет, можно упростить изготовление модели, уменьшив количество заготовок и клеевых соединений. Впрочем, зачастую упрощенно раскрашенные или даже одноцветные бумажные модели многогранников весьма эффектны.
Согласитесь, вы намного быстрее догадаетесь, о чем идет речь, если услышите слово «пирамида». Услышав же слова додекаэдр, тетраэдр, гексаэдр, октаэдр или икосаэдр призадумаетесь, и будете вспоминать, как они выглядят и что из себя представляют.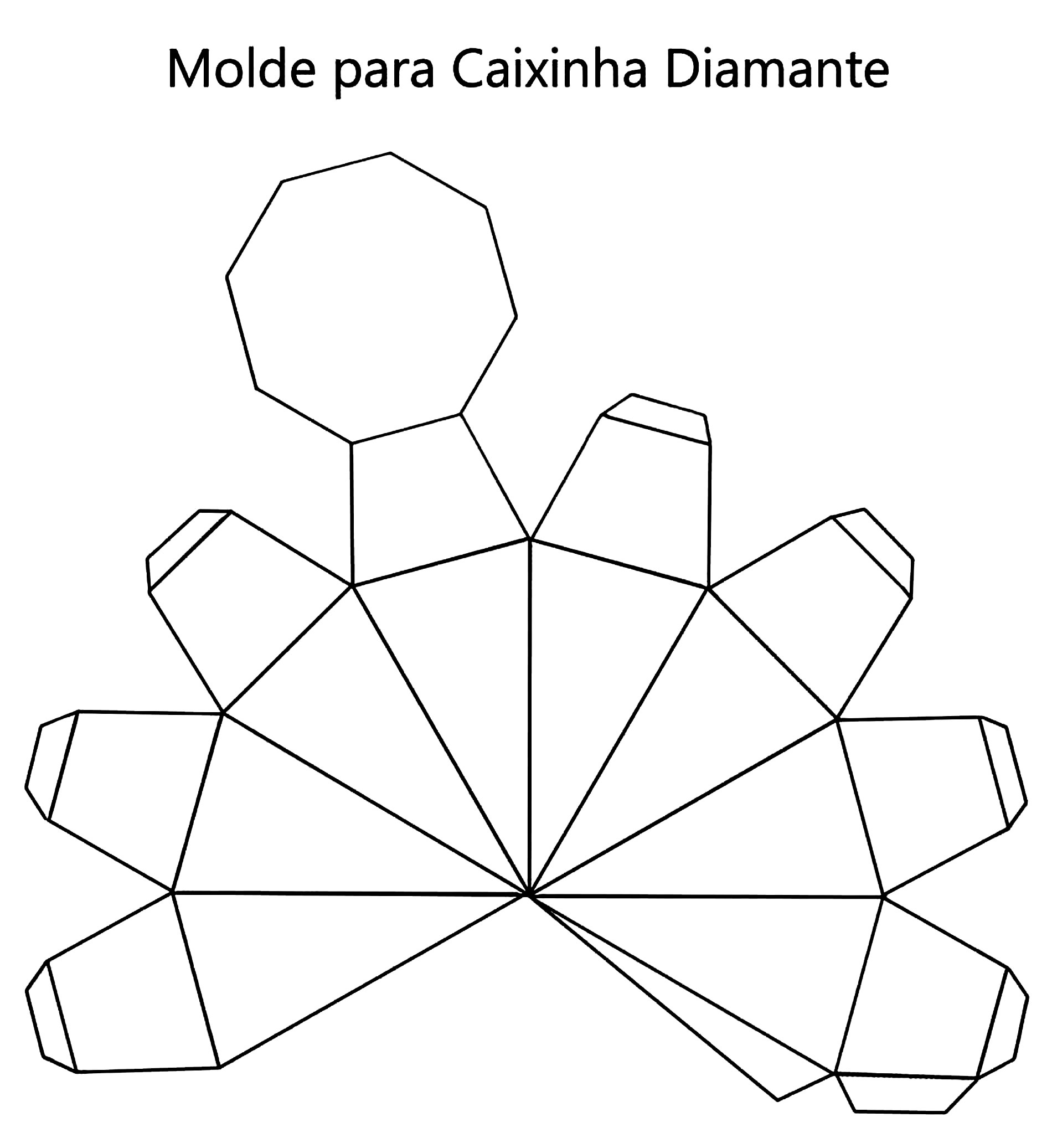
Слово пирамида имеет много значений. Еще в Древней Греции словом «пирамис» называли пшеничный пирог, напоминавший форму египетских пирамид. Затем это слово стало означать сложный термин «монументальную структуру имеющая квадратную площадь в основании с наклонными сторонами, встречающимися на вершине». Начало геометрии пирамиды было положено в Древнем Египет и Вавилоне, хотя самое активное развитие оно получило в Древней Греции.
Пирамида в данном случае делается из квадратного листа бумаги путем некоторых действий. Постепенно из бумаги начнет проявляться пирамиду, которую мы так хотели собрать. После прочтения книги Веннинджера вы научитесь самостоятельно проектировать новые звездчатые формы и изготавливать их модели из бумаги. В книге приводятся трафареты и шаблоны для вырезания из бумаги составных частей будущей модели (заготовок), а также даются схемы соединения частей между собой и таблицы раскраски.
Призма – объемная фигура, многогранник, видов которого дюже много: положительные и неправильные, прямые и наклонные.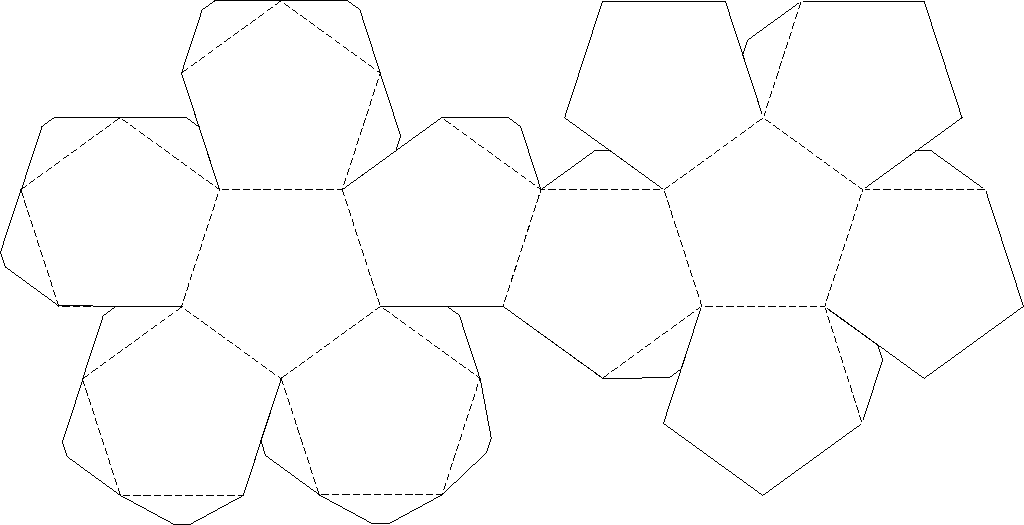 По фигуре, лежащей в основании, призма бывает от треугольной до многоугольной. Проще каждого сделать прямую призму, а вот над наклонной надобно немножко огромнее потрудиться.
По фигуре, лежащей в основании, призма бывает от треугольной до многоугольной. Проще каждого сделать прямую призму, а вот над наклонной надобно немножко огромнее потрудиться.
Вам понадобится
- – циркуль;
- – линейка;
- – карандаш;
- – ножницы;
- – клей;
- – бумага либо картон.
Инструкция
1. Начертите основания призмы, в данном случае это будут 2 шестиугольника. Для того, дабы начертить верный шестиугольник воспользуйтесь циркулем. Нарисуйте им круг, и с подмогой этого же радиуса поделите окружность на шесть частей (у верного шестиугольника стороны равны радиусу описанной окружности). Получившаяся фигура напоминает ячейку пчелиной соты. Неверный шестиугольник начертите произвольно, но с подмогой линейки.
2. Сейчас приступайте к проектированию «выкройки». Стенками призмы являются параллелограммы, и вам необходимо их начертить. В прямой модели параллелограммом будет легкой прямоугольник. И его ширина будет неизменно равна стороне шестиугольника, лежащего в основании призмы. При верной фигуре в основании, все грани призмы будут равны между собой. При неправильной – всей стороне шестиугольника будет соответствовать только один параллелограмм (одна боковая грань), подходящий по размеру. При этом следите за последовательностью размеров граней.
И его ширина будет неизменно равна стороне шестиугольника, лежащего в основании призмы. При верной фигуре в основании, все грани призмы будут равны между собой. При неправильной – всей стороне шестиугольника будет соответствовать только один параллелограмм (одна боковая грань), подходящий по размеру. При этом следите за последовательностью размеров граней.
3. На горизонтальной прямой ступенчато отложите 6 отрезков, равных стороне основания шестиугольника. Из полученных точек проведите перпендикулярные линии требуемой высоты. Концы перпендикуляров объедините 2-й горизонтальной линией. У вас получилось 6 прямоугольников, объединенных совместно.
4. Пристройте к нижней и верхней стороне одного из прямоугольников 2 сконструированных ранее шестиугольника. К любому основанию, если он положительный, и к соответствующему по длине, если шестиугольник неверный. Обведите силуэт сплошной линией, а линии сгиба внутри фигуры – пунктирной. У вас получилась развертка поверхности прямой призмы.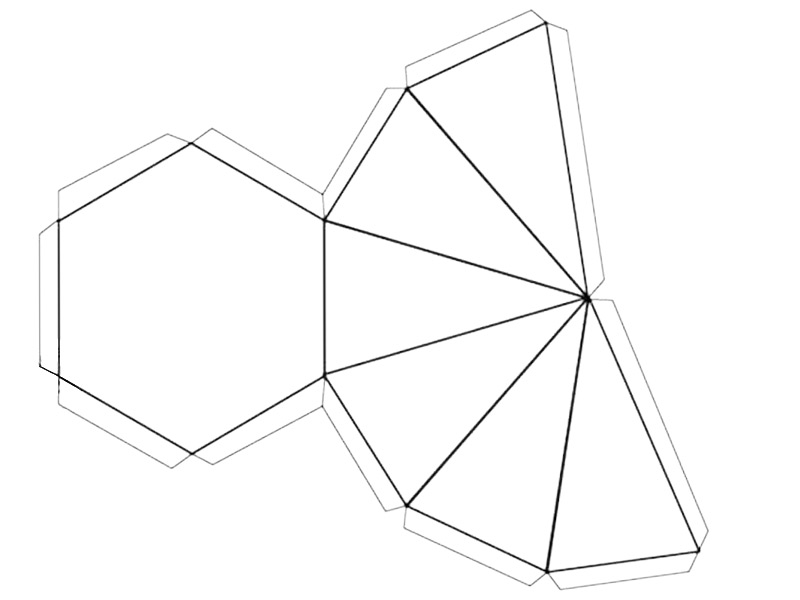
5. Для создания наклонной призмы основания оставьте такими же. Начертите сторону-параллелограмм, которая будет являться одной из граней. Таких граней должно быть шесть, как вы помните. Дабы сейчас начертить развертку наклонной призмы, надобно расположить шесть параллелограммов в дальнейшем порядке: три по возрастанию, так, дабы их косые стороны образовали одну линию, дальше три по убыванию с тем же условием. Крутизна получившейся линии прямо пропорциональна градусу наклона призмы.
6. К пяти прямоугольникам в развертке пририсуйте небольшие трапециевидные захлесты на коротких сторонах для склеивания фигуры, а также на одной свободной длинной стороне. Вырежете заготовку для призмы совместно с захлестами и склейте модель.
Призма – это прибор, тот, что разделяет типичный свет на отдельные цвета: алый, оранжевый, желтый, зеленый, голубой, синий, фиолетовый. Это светопроницаемый объект, с плоской поверхностью, которая преломляет световые волны в зависимости от их длин и вследствие этому разрешает увидеть свет в различных цветах.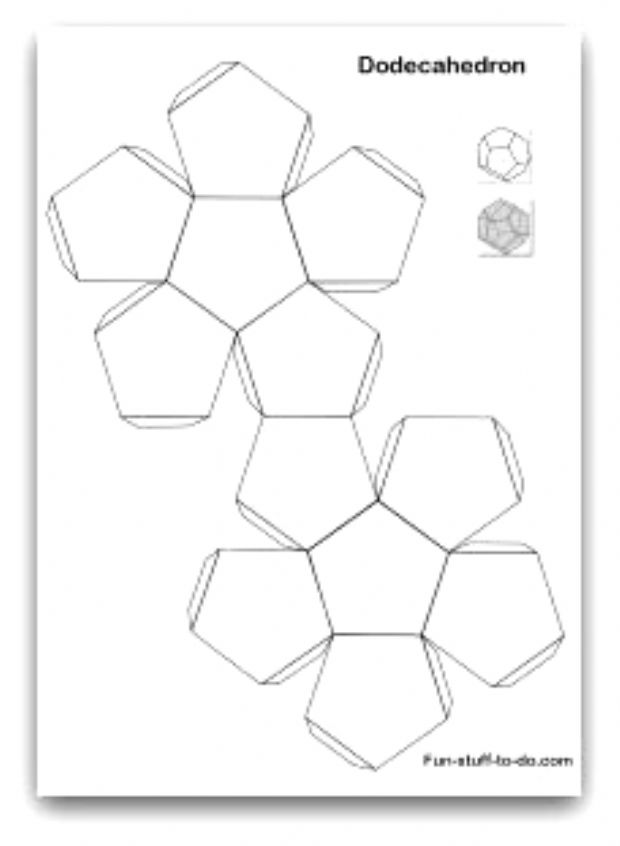 Сделать призму самосильно достаточно легко.
Сделать призму самосильно достаточно легко.
Вам понадобится
- Два листа бумаги
- Фольга
- Стакан
- Компакт Диск
- Кофейный столик
- Фонарик
- Булавка
Инструкция
1. Призму дозволено сделать из простого стакана. Наполните стакан водой чуть огромнее чем наполовину. Разместите стакан на край кофейного столика так, дабы примерно половина дна стакана повисла в воздухе. При этом следите, дабы стаканчик стоял на столе устойчиво.
2. Положите два листа бумаги один за одним рядом с кофейным столом. Включите фонарь и посветите лучиков света через стакан, так, дабы он падал на бумагу.
3. Регулируйте расположение фонаря и бумаги до тех пор пока не увидите на листах радугу – так ваш луч света раскладывается на спектры.
Видео по теме
Базовым навыком художника в академическом рисунке является знание изображать на плоскости простейшие объемные геометрические формы – куб, призму , цилиндр, конус, пирамиду и шар.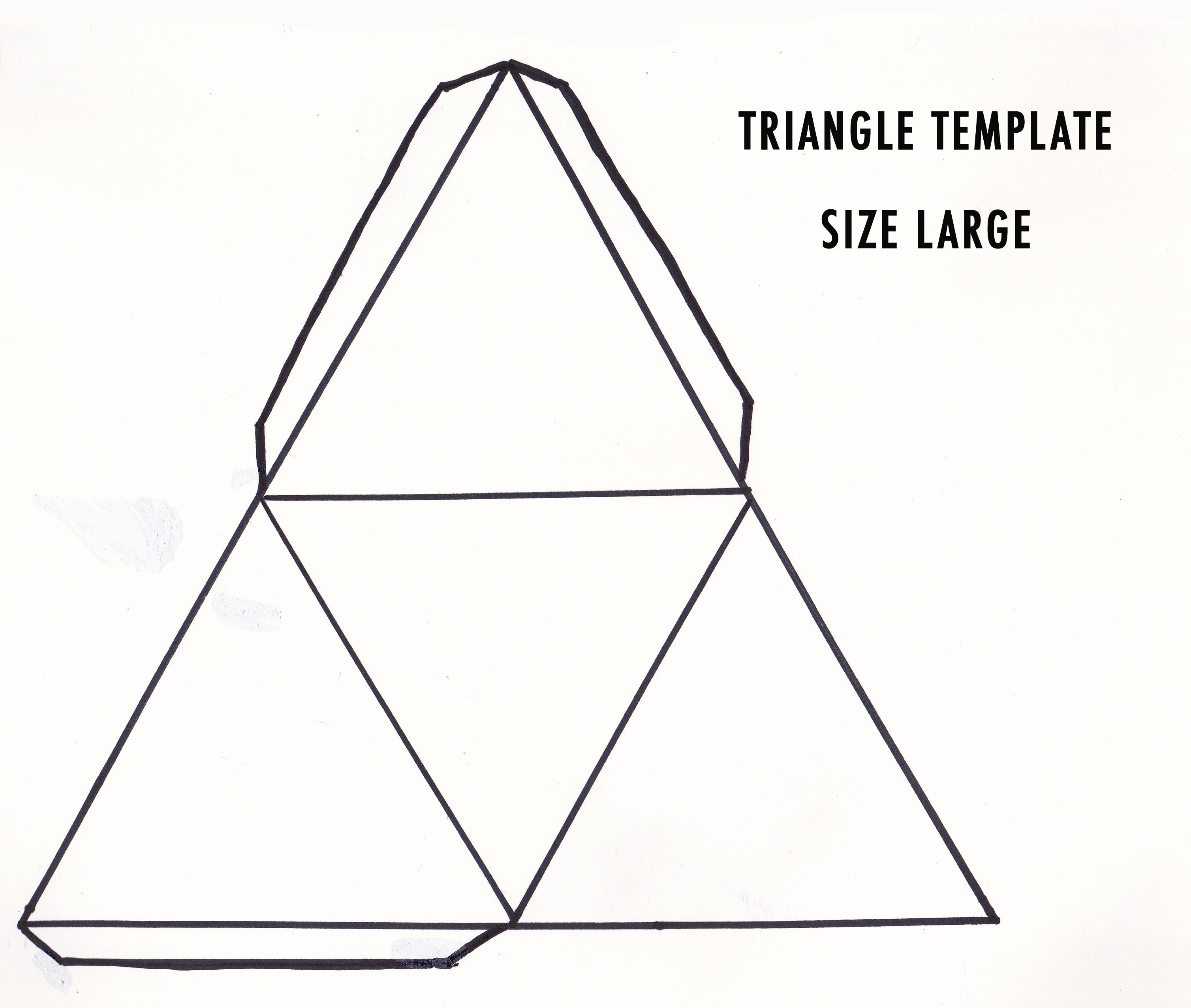 Владея этим навыком, дозволено выстраивать больше трудные, комбинированные объемные формы архитектурных и прочих объектов. Призма – это многогранник, две грани (основания) которого имеют идентичную форму и параллельны друг другу. Боковые грани призмы являются параллелограммами. По числу боковых граней призмы могут быть 3-, четырехгранными и т.д.
Владея этим навыком, дозволено выстраивать больше трудные, комбинированные объемные формы архитектурных и прочих объектов. Призма – это многогранник, две грани (основания) которого имеют идентичную форму и параллельны друг другу. Боковые грани призмы являются параллелограммами. По числу боковых граней призмы могут быть 3-, четырехгранными и т.д.
Вам понадобится
- – бумага для рисования;
- – примитивные карандаши;
- – мольберт;
- – призма либо предмет, имеющий форму призмы (деревянный брусок, коробка, шкатулка, деталь детского конструктора и т.п.), желанно белого цвета.
Инструкция
1. Возвести призму дозволено, вписав ее либо в параллелепипед, либо в цилиндр. Стержневой трудностью при рисовании призмы является положительное построение формы 2-х граней ее основания. При рисовании призмы, лежащей на одной из боковых граней, появляется добавочная трудность соблюдения законов перспективы, от того что в таком расположении становится приметным перспективное сокращение боковых граней.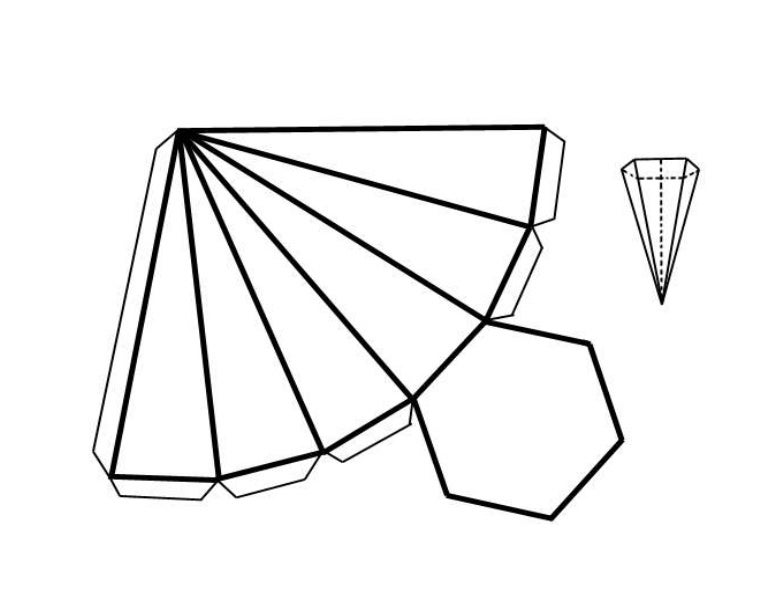
2. Рисование вертикально расположенной призмы начните с обозначения ее центральной оси – вертикальной линии, проведенной посередине листа. На линии оси подметьте центр верхней (видимой) грани основания и проведите через эту точку горизонтальную линию. Определите соотношение высоты и ширины призмы способом визирования: посмотрите на натуру, прикрыв один глаз, и, держа карандаш в вытянутой руке на ярусе глаз, подметьте пальцем на карандаше видимую с вашей точки зрения ширину призмы и мысленно уложите это расстояние по линии высоты призмы определенное число раз (сколько получится).
3. Отмеривая отрезки карандашом теснее на рисунке, подметьте ширину и высоту призмы точками на 2-х нарисованных ранее линиях, соблюдая полученное соотношение. Нарисуйте эллипс вокруг центра верхней грани. Усердствуйте верно передать его воображаемую форму, глядя на натуру. Нарисуйте приблизительно такой же эллипс (но менее сплюснутый) и в плоскости нижней грани основания призмы. Полученные эллипсы объедините двумя вертикальными линиями.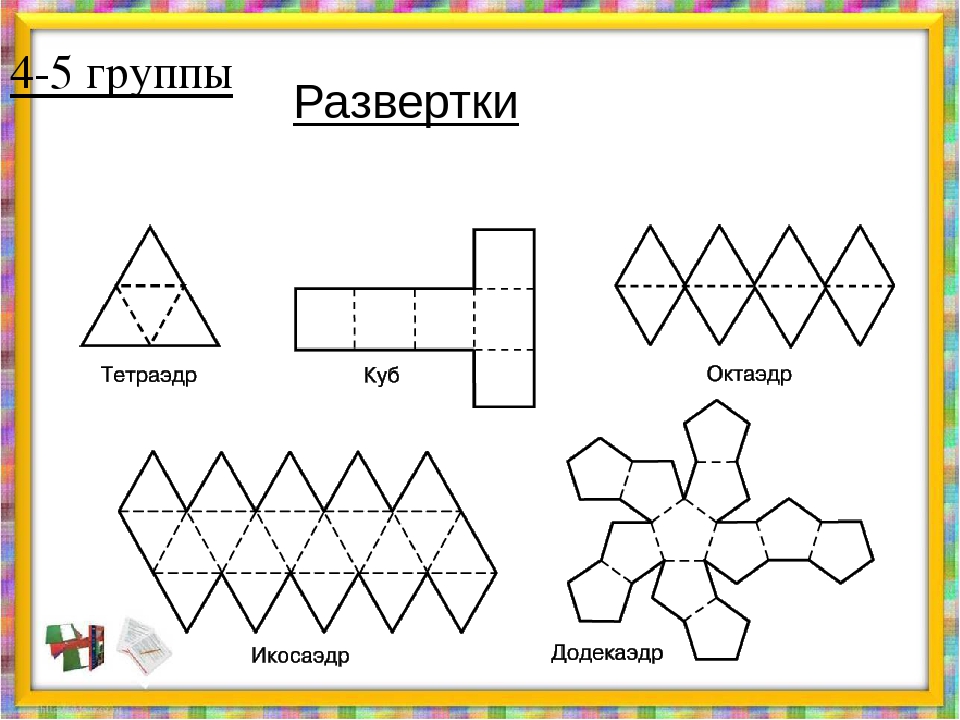
4. Сейчас на верхнем эллипсе необходимо подметить отрезки пересечения боковых граней и ее оснований. Глядя на натуру, подметьте точки – вершины многоугольника – лежащего в основании призмы, как вы их видите, и ступенчато объедините их между собой. Из этих точек проведите линии вниз до пересечения с нижним эллипсом. Полученные точки пересечения так же объедините. При последующем рисовании грани, заметные с выбранной точки зрения, стираются либо заштриховываются, следственно все вспомогательные линии построения рисуйте без нажима.
5. Лежащую на боку призму нарисуйте с подмогой вспомогательного параллелепипеда. Ориентируясь на натуру, вычертите параллелепипед, соблюдая тезисы перспективы – линии боковых ребер при их мысленном продолжении до линии горизонта, находящейся неизменно на ярусе глаз зрителя, сходятся в одной точке. Следственно далекая от нас (заметная) грань будет немножко поменьше передней. При определении соотношений сторон параллелепипеда пользуйтесь способом «вытянутой руки» (либо визирования).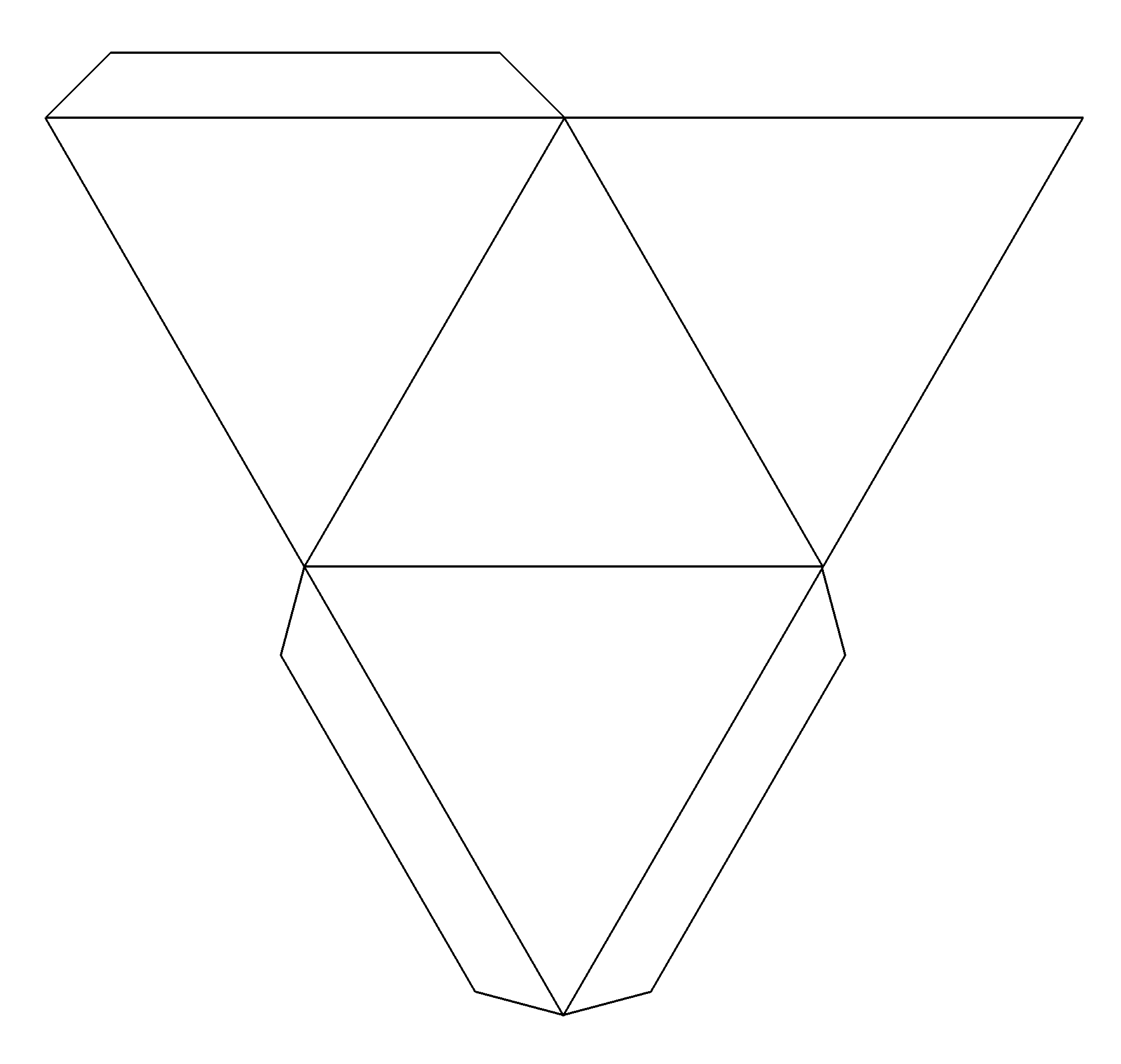
6. На передней и задней квадратных гранях подметьте вершины многоугольников, лежащих в основании призмы, и постройте их. Объедините эти точки попарно на 2-х гранях – нарисуйте боковые ребра призмы. Удалите непотребные линии. Больше близкие к вам линии ребер и углы призмы выделите пожирнее, а удаленные обозначьте легкими линиями.
7. Глядя на натуру, определите угол падения света, самую ясную, самую затененную грани и с подмогой штриховки различной интенсивности передайте эти световые соотношения в рисунке. Нарисуйте падающую от предмета тень. Рубеж соприкосновения призмы и стола подчеркните самой темной линией. Обратите внимание, что на самую затененную грань призмы снизу падает свет, отраженный от поверхности стола (рефлекс), и чуть приметно ее освещает. При наложении штриховки на эту грань учтите данный результат и в месте рефлекса наложите менее насыщенный тон.
Видео по теме
Призма – это многогранник, образованный любым финальным числом граней, две из которых – основания – непременно обязаны быть параллельны.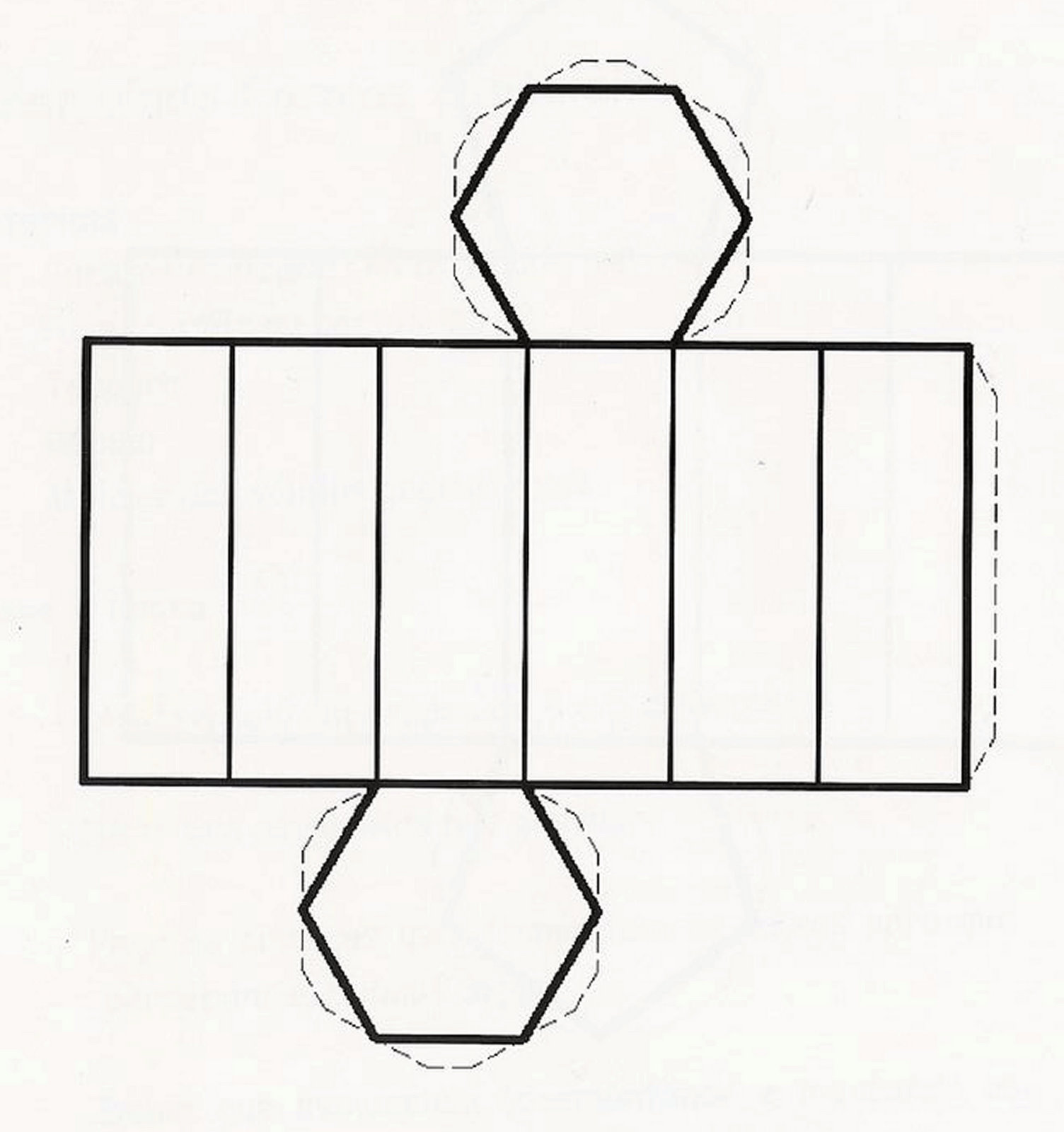 Любая прямая линия, проведенная перпендикулярно основаниям, содержит соединяющий их отрезок, называемый высотой призмы. Если все боковые грани примыкают к обоим основаниям под углом в 90°, призма именуется прямой .
Любая прямая линия, проведенная перпендикулярно основаниям, содержит соединяющий их отрезок, называемый высотой призмы. Если все боковые грани примыкают к обоим основаниям под углом в 90°, призма именуется прямой .
Вам понадобится
- Чертеж призмы, карандаш, линейка.
Инструкция
1. В прямой призме всякое боковое ребро по определению перпендикулярно основанию. А расстояние между параллельными плоскостями боковых граней идентично в всякий точке, в том числе и в тех точках, где боковое ребро примыкает к ним. Из этих 2-х обстоятельств вытекает, что длина ребра всякий боковой грани прямой призмы равна высоте этой объемной фигуры. Значит, если у вас есть чертеж, на котором изображен такой многогранник, на нем теснее присутствуют отрезки (ребра боковых граней), весь из которых дозволено обозначить и как высоту призмы. Если это не запрещено условиями задания, примитивно обозначьте всякое боковое ребро как высоту, и задача будет решена.
2. Если требуется провести на чертеже несовпадающую с боковыми ребрами высоту, начертите параллельный любому из этих ребер отрезок, соединяющий основания. Не неизменно это дозволено сделать «на глаз», следственно постройте две вспомогательные диагонали на боковых гранях – объедините пару всяких углов на верхнем и соответствующую им пару на нижнем основании. После этого отмерьте на верхней диагонали всякое комфортное расстояние и поставьте точку – это будет пересечение высоты с верхним основанием. На нижней диагонали отмерьте верно такое же расстояние и поставьте вторую точку – пересечение высоты с нижним основанием. Объедините эти точки отрезком, и построение высоты прямой призмы будет завершено.
3. Призма может быть изображена с учетом перспективы, то есть длины идентичных ребер фигуры могут иметь на рисунке различную длину, боковые грани могут примыкать к основаниям под различными и не неукоснительно прямыми углами и т.д. В этом случае, дабы верно соблюсти пропорции, действуйте так же, как описано в предыдущем шаге, но точки на верхней и нижней диагоналях ставьте верно в их серединах.
Детально – как сложить лист бумаги и вырезать прекрасную снежинку.
Вам понадобится
- Лист бумаги, у меня – обыкновенный лист А4, отменнее брать огромные салфетки
- Ножницы
Инструкция
1. Сворачиваем лист поперек вдвое
2. Сейчас по вдвое, лишь для того, дабы обнаружить середину
3. Заворачиваем края бумаги, сложенной вдвое, поочередно – видно как на фото
4. Следим, дабы листик загнулся равномерно, и концы доставали до сгибов.
5. Сейчас сворачиваем вдвое полученный конвертик. Необходимо потренироваться, дабы добиться того, дабы внешний край листа доходил ровно до сгиба.
6. Пока навыка нет, класснее рисовать приблизительный силуэт снежинки заблаговременно.
7. Аккуратненько вырезаем по силуэту.
8. Старательно разворачиваем.
Обратите внимание!
Помните, что невозможно делать сквозной разрез, снежинка распадется на части.
Полезный совет
Чем тоньше бумага, тем проще вырезать снежинку. Дозволено делать снежинки и из фольги.
Обратите внимание!
В развертке наклонной призмы не чертите ее грани под слишком огромным углом, напротив модель будет неустойчивой.
Призма — это геометрическое тело, многогранник, основаниями которого являются равные многоугольники, а боковыми гранями — параллелограммы. Для непосвященного, возможно, это звучит несколько устрашающе. И, когда вашему ребенку на урок геометрии надо принести призму, собственноручно изготовленную дома, вы пребываете в растерянности, не зная как помочь своему любимому чаду. На самом деле все не так уж и сложно и, воспользовавшись нашими советами, как сделать призму, вы достойно справитесь с этой проблемой.
Как сделать призму из бумаги
Сразу условимся, что делать мы будем прямую призму, то есть призму, у которой боковые ребра будут перпендикулярны основаниям. Сделать же наклонную призму из бумаги весьма проблематично (подобные макеты обычно выполняются из проволоки).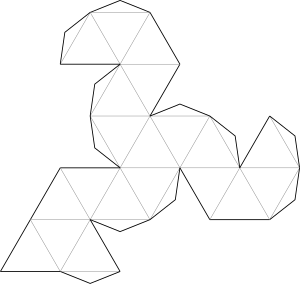
Мы уже знаем, что в основаниях призмы лежат два одинаковых многоугольника. Поэтому нашу работу начнем именно с них. Простейший из многоугольников – треугольник. Значит, и призму сначала будем делать треугольную.
Как сделать треугольную призму
Нам понадобится плотная белая бумага для черчения, карандаш, транспортир, циркуль, линейка, ножницы и клей.
Чертим треугольник, можно любой, но чтобы наша призма получилась особенно красивой, треугольник сделаем равносторонний. Такая призма в геометрии называется «правильная». Выбираем на свое усмотрение величину стороны треугольника, допустим 10 см. Линейкой откладываем этот отрезок на бумаге и транспортиром отмеряем угол в 60 ∗ от одного конца нашего отрезка.
Проводим наклонную линию. На ней при помощи линейки откладываем 10 см от конца отрезка. Таким образом, мы нашли третью вершину треугольника. Соединяем эту точку с концами начального отрезка и равносторонний треугольник готов. Его можно вырезать. Аналогично делаем второй треугольник, или аккуратно обводим на бумаге контуры первого.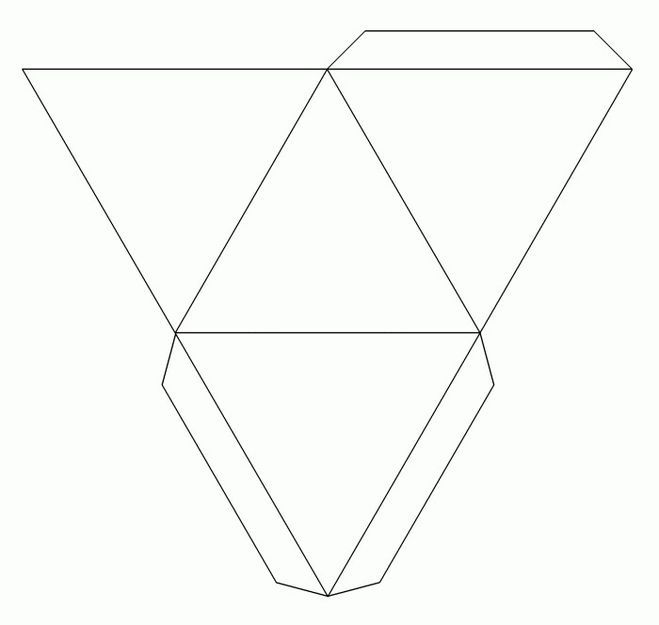 Ну вот, два основания у нас уже есть.
Ну вот, два основания у нас уже есть.
Делаем боковые грани. Решаем, какая у призмы будет высота. Допустим, 20 см. Чертим прямоугольник, у которого величина одной стороны это высота призмы (в нашем случае – 20 см), а вторая сторона равна величине стороны основания, умноженной на количество этих сторон (у нас: 10 см х 3 = 30 см).
На длинных сторонах делаем отметки через каждые 10 см. Соединяем противоположные отметки прямыми линиями. По ним потом надо будет аккуратно согнуть бумагу. Это — боковые ребра нашей призмы. Намечаем узкие припуски для склеивания по двум длинным и одной короткой стороне прямоугольника (достаточно полосок шириной 1 см). Вырезаем прямоугольник вместе с припусками, аккуратно отгибаем их по разметке. Сгибаем ребра.
Начинаем сборку. Склеиваем прямоугольник по боковой грани в трубу треугольного сечения. Сверху и снизу на отогнутые припуски наклеиваем треугольники-основания. Призма готова.
Вдаваться в подробности вопроса как сделать призму из картона, пожалуй, не стоит.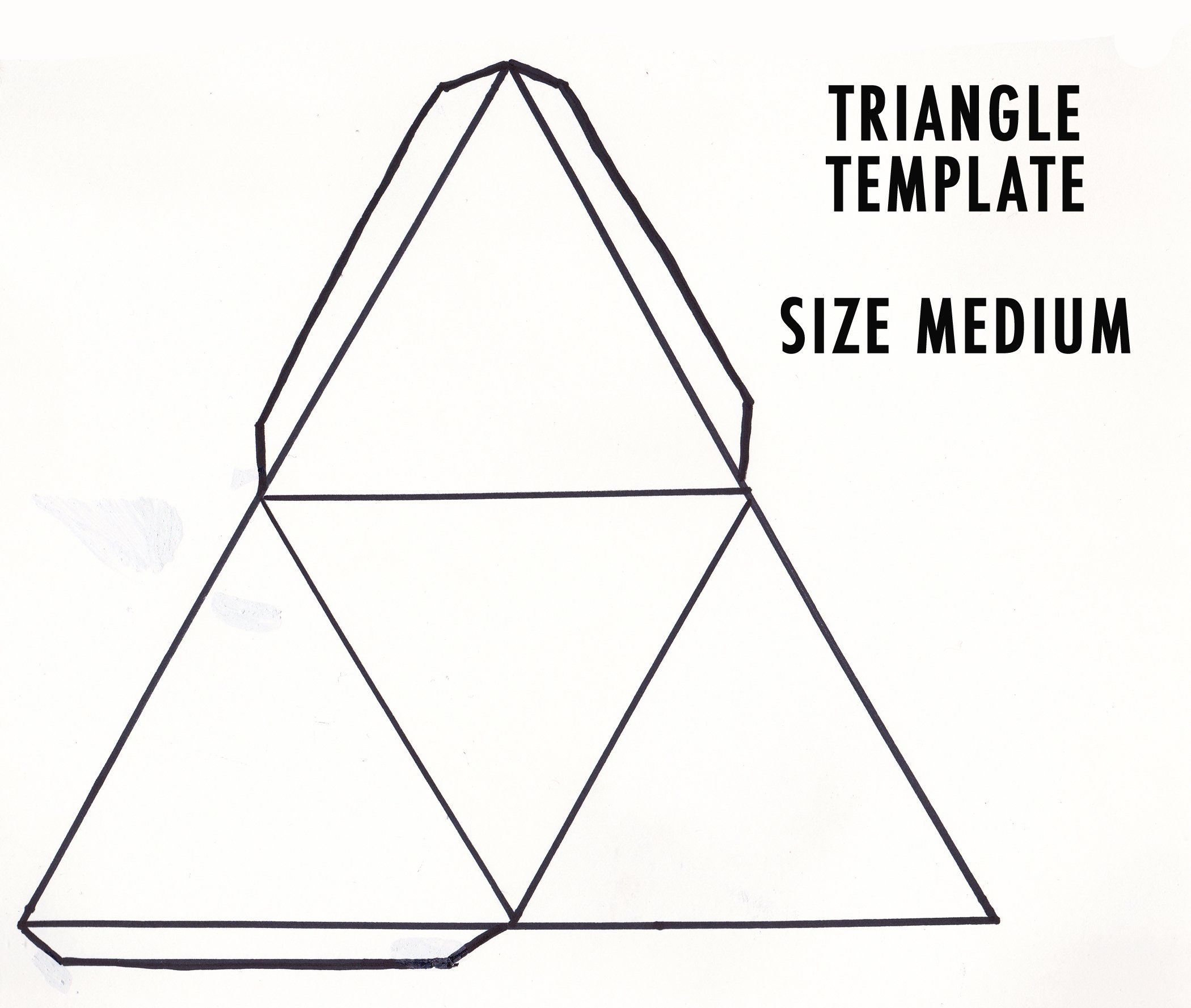 Весь алгоритм сборки остается таким же, только бумагу замените тонким картоном. Меняя количество сторон у многоугольников основания, вы теперь самостоятельно сможете сделать и пяти- и шестиугольную призму.
Весь алгоритм сборки остается таким же, только бумагу замените тонким картоном. Меняя количество сторон у многоугольников основания, вы теперь самостоятельно сможете сделать и пяти- и шестиугольную призму.
Большой выбор развёрток простых геометрических фигур.
Первое знакомство детей с бумажным моделированием всегда начинается с простых геометрических фигур, таких как кубик и пирамида. Не у многих получается склеить кубик с первого раза, иногда требуется несколько дней, чтобы сделать поистине ровный и безупречный куб. Более сложные фигуры цилиндр и конус требуют в несколько раз больше усилий нежели простой кубик. Если вы не умеете аккуратно клеить геометрические фигуры, значит и за сложные модели вам ещё рано браться. Займитесь сами и научите своих детей клеть эти «азы» моделирования по готовым развёрткам.
Для начала я, конечно же, предлагаю научиться клеить обычный кубик. Развёртки сделаны для двух кубиков, большого и маленького. Более сложной фигурой является маленький кубик потому, как клеить его сложнее, чем большой.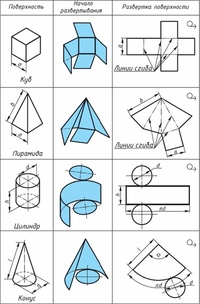
Итак, начнём! Скачайте развёртки всех фигур на пяти листах и распечатайте на плотной бумаге. Перед тем, как печатать и клеить геометрические фигуры обязательно ознакомьтесь со статьёй о том, как выбрать бумагу и как вообще правильно вырезать, сгибать и клеить бумагу.
Для более качественной печати советую использовать программу AutoCAD, и даю вам развёртки для этой программы , а также читайте, как распечатывать из автокада . Вырежьте развёртки кубиков с первого листа, по линиям сгиба обязательно проведите иголкой циркуля под железную линейку, чтобы бумага хорошо сгибалась. Теперь можно начинать клеить кубики.
Для экономии бумаги и на всякий пожарный я сделал несколько развёрток маленького кубика, мало ли вам захочется склеить не один кубик или что-то не получится с первого раза. Ещё одна несложная фигура это пирамида, её развёртки найдёте на втором листе. Подобные пирамиды стоили древние египтяне, правда не из бумаги и не таких маленьких размеров:)
А это тоже пирамида, только в отличие от предыдущей у неё не четыре, а три грани.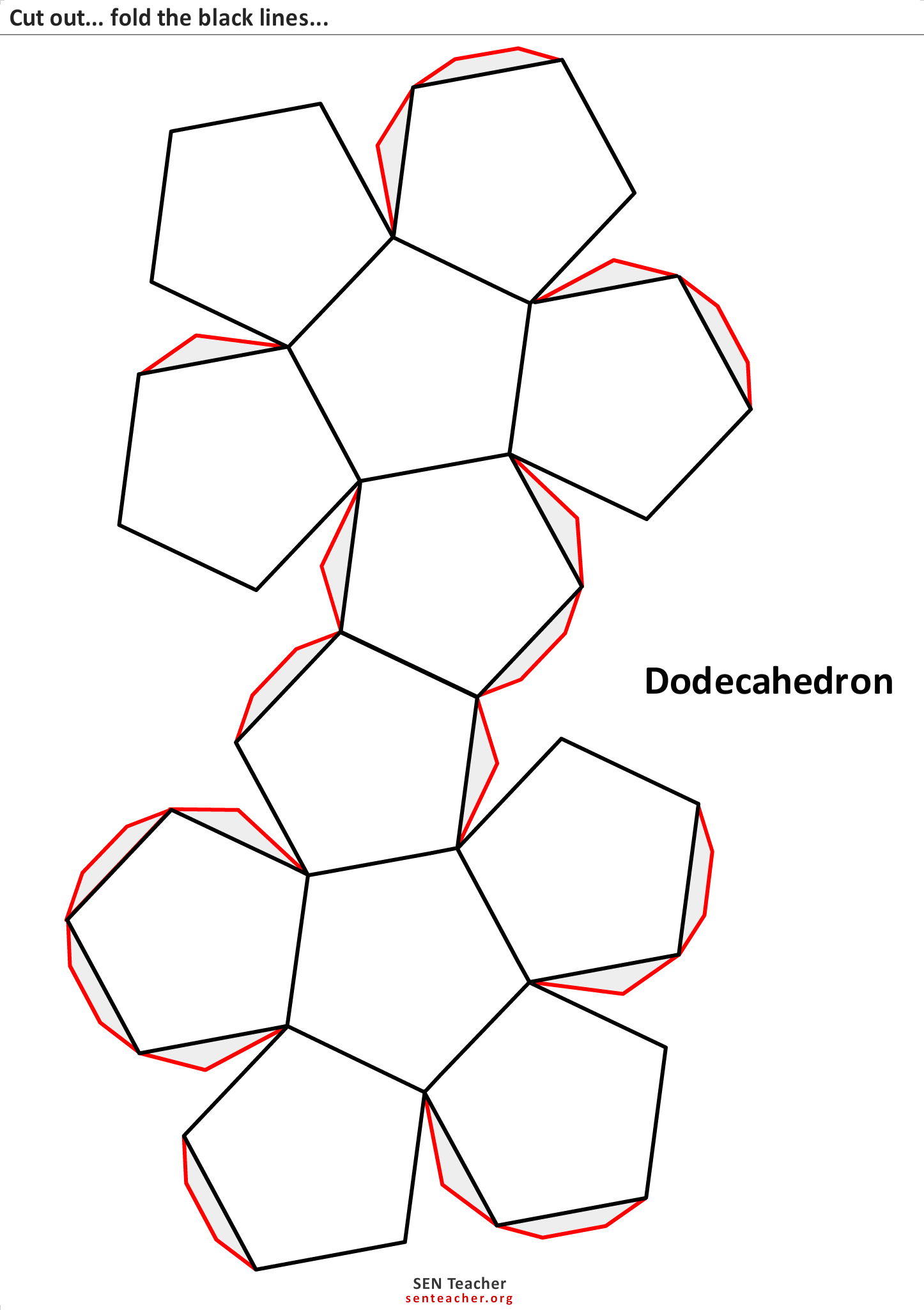
Развёртки трёхгранной пирамиды на первом листе для печати.
И ещё одна забавная пирамидка из пяти граней, её развёртки на 4-ом листе в виде звёздочки в двух экземплярах.
Более сложная фигура это пятигранник, хотя пятигранник сложнее начертить, нежели склеить.
Развёртки пятигранника на втором листе.
Вот мы и добрались до сложных фигур. Теперь придётся поднапрячься, склеить такие фигуры нелегко! Для начала обычный цилиндр, его развёртки на втором листе.
А это более сложная фигура по сравнению с цилиндром, т.к. в её основании не круг, а овал.
Развёртки этой фигуры на втором листе, для овального основания сделано две запасных детали.
Чтобы аккуратно собрать цилиндр его детали нужно клеить встык. С одной стороны дно можно приклеить без проблем, просто поставьте на стол заранее склеенную трубку, положите на дно кружок и залейте клеем изнутри. Следите, чтобы диаметр трубы и круглого дна плотно подходили друг к другу, без щелей, иначе клей протечёт и всё приклеится к столу. Второй кружок приклеить будет сложнее, поэтому приклейте внутри вспомогательные прямоугольники на расстоянии толщины бумаги от края трубы. Эти прямоугольники не дадут упасть основанию внутрь, теперь вы без проблем приклеете кружок сверху.
Второй кружок приклеить будет сложнее, поэтому приклейте внутри вспомогательные прямоугольники на расстоянии толщины бумаги от края трубы. Эти прямоугольники не дадут упасть основанию внутрь, теперь вы без проблем приклеете кружок сверху.
Цилиндр с овальным основанием можно клеить также как и обычный цилиндр, но он имеет меньшую высоту, поэтому тут проще вставить внутрь гармошку из бумаги, а наверх положить второе основание и по краю приклеить клеем.
Теперь очень сложная фигура — конус. Его детали на третьем листе, запасной кружок для днища на 4-ом листе. Вся сложность склеивания конуса в его острой вершине, а потом ещё будет очень сложно приклеить дно.
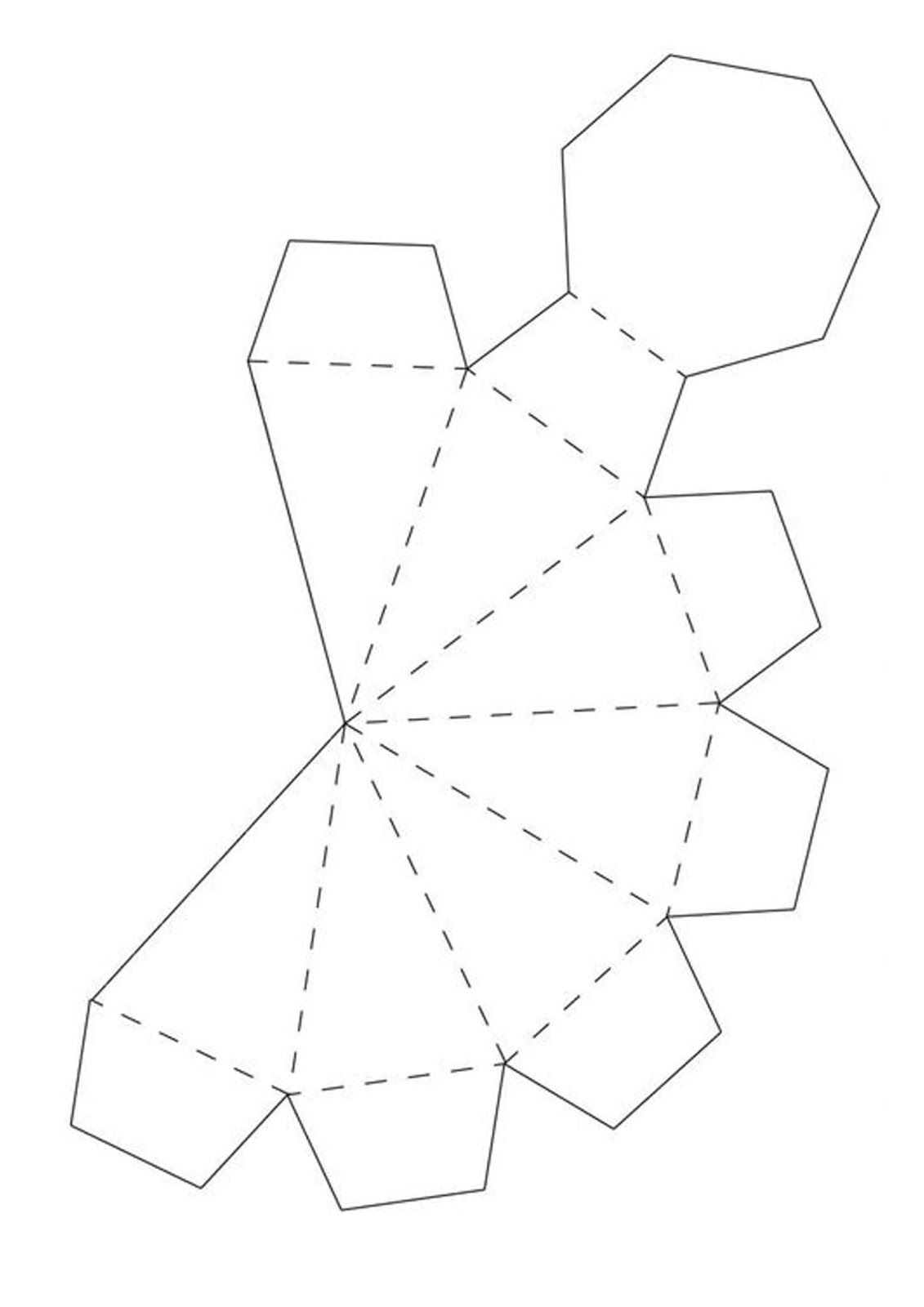
Сложная и одновременно простая фигура это шар. Шар состоит из 12-ти пятигранников, развёртки шара на 4-ом листе. Сначала клеится две половинки шара, а потом обе склеиваются вместе.
Довольно интересная фигура — ромб, её детали на третьем листе.
А теперь две очень похожие, но совершенно разные фигуры, их отличие только в основании.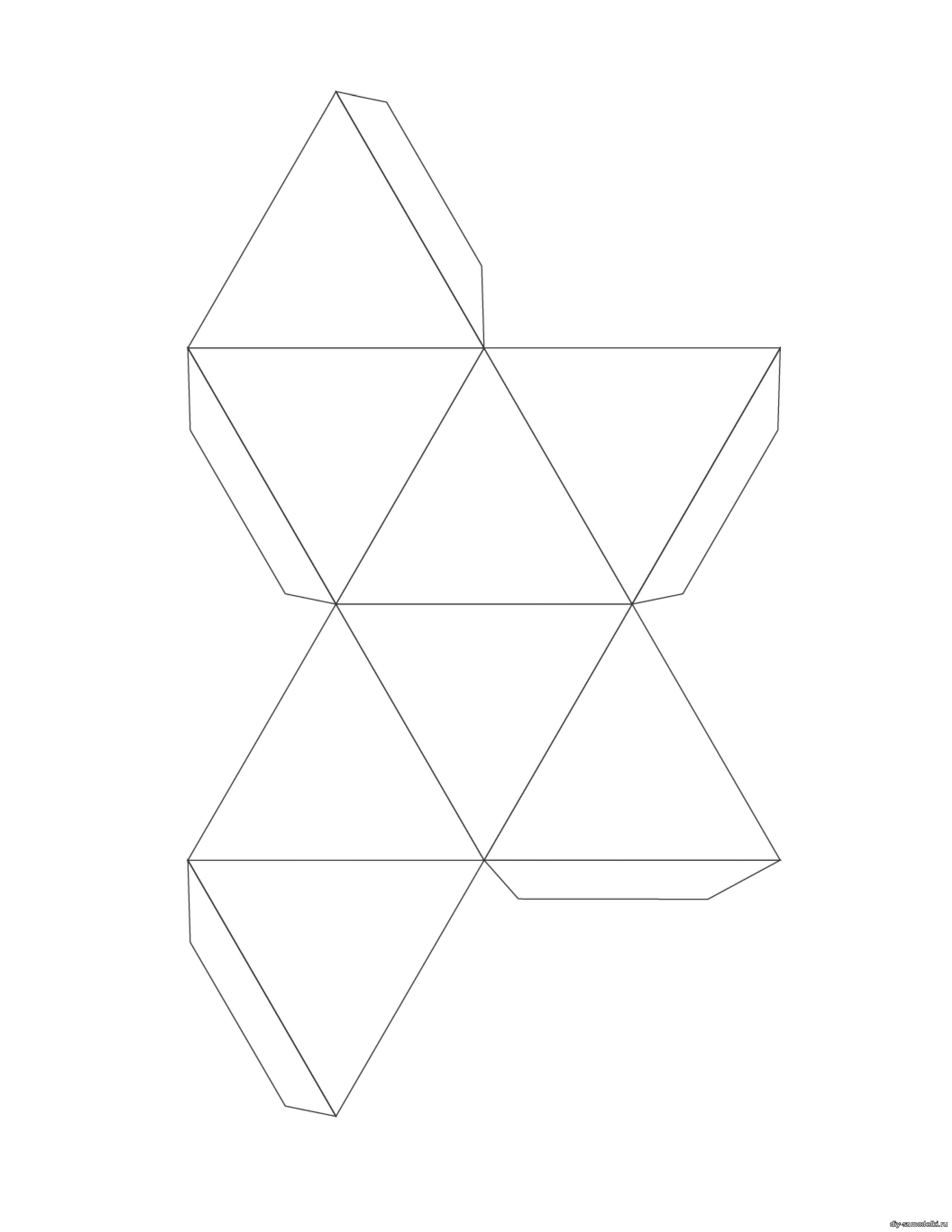
Когда склеите эти обе фигуры, то не сразу поймёте, что это вообще такое, они получились какие-то совсем невосприимчивые.
Ещё одна интересная фигурка это тор, только он у нас очень упрощён, его детали на 5-ом листе.
И наконец, последняя фигура из равносторонних треугольников, даже не знаю, как это назвать, но фигура похожа на звезду. Развёртки этой фигуры на пятом листе.
На сегодня это всё! Я желаю вам успехов в этой нелёгкой работе!
В основе геометрического тела – призмы лежат многоугольники, а каждая боковая грань – параллелограмм. Непосвященный, возможно, немного испугался. Но если вашего ребенка просят прийти на урок с призмой, вы, естественно, захотите помочь ему и объяснить, как сделать призму из бумаги.
Начнем с изготовления прямой призмы. В этой призме боковые ребра перпендикулярны основаниям. Наиболее проста в изготовлении своими руками призма из бумаги с тремя гранями, так как в ее основаниях лежат простейшие из многоугольников – треугольники.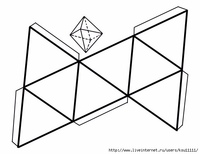 Изготовим «правильную» призму. У нее основания представлены равносторонними треугольниками.
Изготовим «правильную» призму. У нее основания представлены равносторонними треугольниками.
Продумаем, какая по высоте будет наша треугольная призма из бумаги. Начертим прямоугольник-с одной стороной, равной высоте, а другой — равной длине периметру треугольника в основании. Полученный прямоугольник разделим параллельными прямыми на три равные части. От углов прямоугольника, находящегося в середине, циркулем проведем окружности с радиусом, равным стороне нашего треугольника в основании. Где окружности пересекутся за пределами первоначального прямоугольника, поставим точки и соединим их с центрами окружностей. Мы должны получить фигуру, изображенную в середине рисунка. Далее фигуру вырезаем с небольшими припусками для склеивания, сгибаем по имеющимся прямым линиям и получаем готовую призму.
По какому шаблону изготавливается призма из бумаги с четырьмя гранями, наглядно демонстрирует схема на рисунке.
Шестиугольная призмаПример заготовки для пятигранной призмы представлен на рисунке. Здесь высота пирамиды 10 см, длина сторон у пятигранника в основании по 3 см. Похожим образом может быть изготовлена шестиугольная призма из бумаги, но в ее основании лежит шестиугольник.
Здесь высота пирамиды 10 см, длина сторон у пятигранника в основании по 3 см. Похожим образом может быть изготовлена шестиугольная призма из бумаги, но в ее основании лежит шестиугольник.
Наклонная призма из бумаги представлена на этом рисунке. Ее боковые грани находятся под углом к основанию. Такую призму можно изготовить по шаблону-развертке.
математических формул для основных фигур и трехмерных фигур
В математике (особенно в геометрии) и естественных науках вам часто нужно рассчитывать площадь поверхности, объем или периметр различных форм. Будь то сфера или круг, прямоугольник или куб, пирамида или треугольник, каждая форма имеет определенные формулы, которым вы должны следовать, чтобы получить правильные измерения.
Мы собираемся изучить формулы, которые понадобятся вам для определения площади поверхности и объема трехмерных фигур, а также площади и периметра двухмерных фигур.Вы можете изучить этот урок, чтобы изучить каждую формулу, а затем сохранить ее для быстрого ознакомления в следующий раз, когда она вам понадобится. Хорошая новость заключается в том, что в каждой формуле используются одни и те же базовые измерения, поэтому изучение каждого нового становится немного проще.
Хорошая новость заключается в том, что в каждой формуле используются одни и те же базовые измерения, поэтому изучение каждого нового становится немного проще.
Площадь и объем сферы
Д. РасселТрехмерный круг известен как сфера. Чтобы рассчитать площадь поверхности или объем сферы, вам необходимо знать радиус ( r ). Радиус — это расстояние от центра сферы до края, которое всегда одинаково, независимо от того, от каких точек на краю сферы вы измеряете.
Когда у вас есть радиус, формулы довольно просто запомнить. Как и в случае с окружностью круга, вам нужно будет использовать число пи ( π ). Обычно вы можете округлить это бесконечное число до 3,14 или 3,14159 (принятая дробь — 22/7).
- Площадь поверхности = 4πr 2
- Объем = 4/3 πr 3
Площадь поверхности и объем конуса
Д. Рассел Конус — это пирамида с круглым основанием, имеющая наклонные стороны, которые встречаются в центральной точке. Чтобы рассчитать его площадь поверхности или объем, необходимо знать радиус основания и длину стороны.
Чтобы рассчитать его площадь поверхности или объем, необходимо знать радиус основания и длину стороны.
Если вы этого не знаете, вы можете найти длину стороны ( s ), используя радиус ( r ) и высоту конуса ( h ).
После этого вы можете найти общую площадь поверхности, которая является суммой площади основания и площади стороны.
- Площадь основания: πr 2
- Площадь стороны: πrs
- Общая площадь поверхности = πr 2 + πrs
Чтобы найти объем сферы, вам нужны только радиус и высота.
Площадь поверхности и объем цилиндра
Д. Рассел Вы обнаружите, что работать с цилиндром намного проще, чем с конусом. Эта форма имеет круглое основание и прямые параллельные стороны. Это означает, что для определения его площади поверхности или объема вам понадобятся только радиус ( r ) и высота ( h ).
Тем не менее, вы также должны учитывать, что есть и верх, и низ, поэтому радиус необходимо умножить на два для площади поверхности.
- Площадь поверхности = 2πr 2 + 2πrh
- Объем = πr 2 ч
Площадь и объем прямоугольной призмы
Д. РасселПрямоугольник в трех измерениях становится прямоугольной призмой (или коробкой). Когда все стороны равны, он становится кубом. В любом случае для определения площади поверхности и объема требуются одни и те же формулы.
Для них вам нужно знать длину ( л ), высоту ( х ) и ширину ( х ).С кубом все три будут одинаковыми.
- Площадь поверхности = 2 (слева) + 2 (lw) + 2 (белый)
- Объем = lhw
Площадь и объем пирамиды
Д. Рассел С пирамидой с квадратным основанием и гранями из равносторонних треугольников работать сравнительно легко.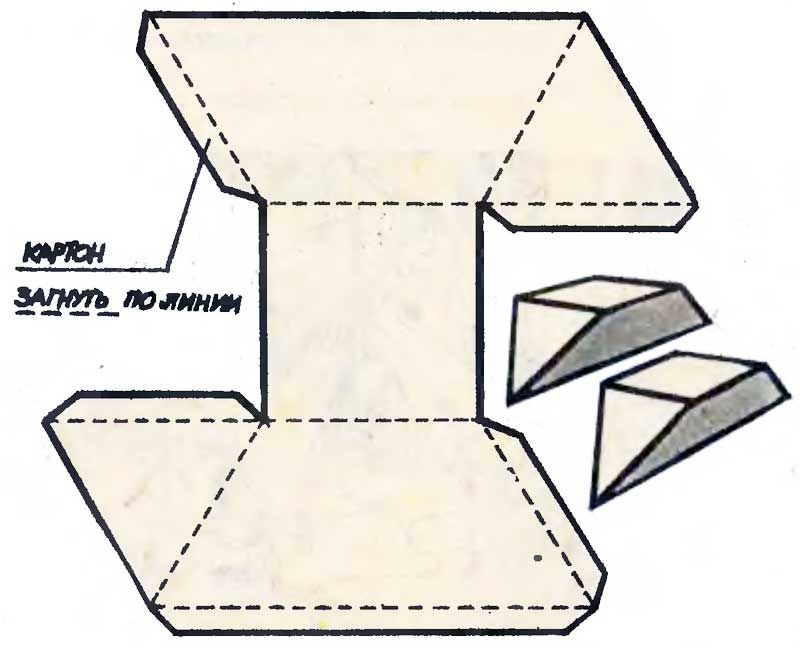
Вам нужно будет знать размер одной длины основания ( b ). Высота ( х ) — это расстояние от основания до центральной точки пирамиды.Сторона ( s ) — это длина одной грани пирамиды от основания до верхней точки.
- Площадь поверхности = 2bs + b 2
- Объем = 1/3 млрд 2 ч
Другой способ вычислить это — использовать периметр ( P ) и площадь ( A ) базовой формы. Это можно использовать для пирамиды с прямоугольным, а не квадратным основанием.
- Площадь поверхности = (½ x P x s) + A
- Объем = 1/3 Ач
Площадь поверхности и объем призмы
Д.Рассел Когда вы переключаетесь с пирамиды на равнобедренную треугольную призму, вы также должны учитывать длину ( l ) формы. Запомните сокращения для основания ( b ), высоты ( h ) и стороны ( s ), потому что они необходимы для этих расчетов.
- Площадь поверхности = bh + 2ls + lb
- Объем = 1/2 (bh) л
Однако призма может быть любой формы. Если вам нужно определить площадь или объем нечетной призмы, вы можете полагаться на площадь ( A ) и периметр ( P ) базовой формы.Часто в этой формуле будет использоваться высота призмы или глубина ( d ), а не длина ( l ), хотя вы можете видеть любое сокращение.
- Площадь поверхности = 2A + Pd
- Объем = Ad
Площадь сектора круга
Д. РасселПлощадь сектора круга может быть вычислена в градусах (или радианах, как это чаще всего используется в расчетах). Для этого вам понадобятся радиус ( r ), пи ( π ) и центральный угол ( θ ).
- Площадь = θ / 2 r 2 (в радианах)
- Площадь = θ / 360 πr 2 (в градусах)
Площадь эллипса
Д. Рассел
РасселЭллипс также называют овалом и по сути представляет собой удлиненный круг. Расстояния от центральной точки до стороны непостоянны, что делает формулу для определения его площади немного сложной.
Чтобы использовать эту формулу, вы должны знать:
- Полу-ось ( a ): кратчайшее расстояние между центральной точкой и краем.
- Большая полуось ( b ): наибольшее расстояние между центральной точкой и краем.
Сумма этих двух точек остается постоянной. Вот почему мы можем использовать следующую формулу для вычисления площади любого эллипса.
Иногда вы можете увидеть эту формулу, записанную как r 1 (радиус 1 или малая полуось) и r 2 (радиус 2 или большая полуось), а не a и b .
Площадь и периметр треугольника
Треугольник — одна из самых простых фигур, и вычислить периметр этой трехсторонней формы довольно просто.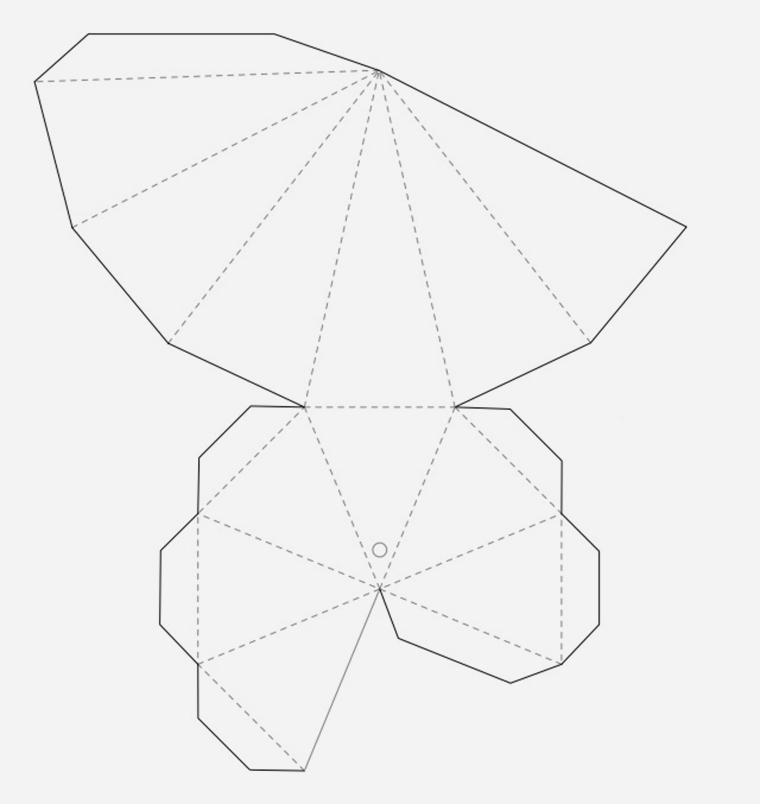 Вам нужно будет знать длину всех трех сторон ( a, b, c ), чтобы измерить полный периметр.
Вам нужно будет знать длину всех трех сторон ( a, b, c ), чтобы измерить полный периметр.
Чтобы узнать площадь треугольника, вам понадобится только длина основания ( b ) и высота ( h ), которая измеряется от основания до вершины треугольника. Эта формула работает для любого треугольника, независимо от того, равны ли стороны или нет.
Площадь и окружность круга
Подобно сфере, вам нужно знать радиус ( r ) круга, чтобы узнать его диаметр ( d ) и длину окружности ( c ). Имейте в виду, что круг — это эллипс, у которого одинаковое расстояние от центральной точки до каждой стороны (радиуса), поэтому не имеет значения, где на краю вы измеряете.
- Диаметр (d) = 2r
- Окружность (c) = πd или 2πr
Эти два измерения используются в формуле для вычисления площади круга.Также важно помнить, что отношение длины окружности к ее диаметру равно пи ( π ).
Площадь и периметр параллелограмма
У параллелограмма есть два набора противоположных сторон, идущих параллельно друг другу. Форма четырехугольная, поэтому у нее четыре стороны: две стороны одной длины ( a ) и две стороны другой длины ( b ).
Чтобы узнать периметр любого параллелограмма, используйте эту простую формулу:
Когда вам нужно найти площадь параллелограмма, вам понадобится высота ( х ).Это расстояние между двумя параллельными сторонами. База ( b ) также обязательна, это длина одной из сторон.
Имейте в виду, что b в формуле площади не то же самое, что b в формуле периметра. Вы можете использовать любую из сторон, которые были объединены в пары как a и b при вычислении периметра, хотя чаще всего мы используем сторону, перпендикулярную высоте.
Площадь и периметр прямоугольника
Прямоугольник тоже четырехугольник.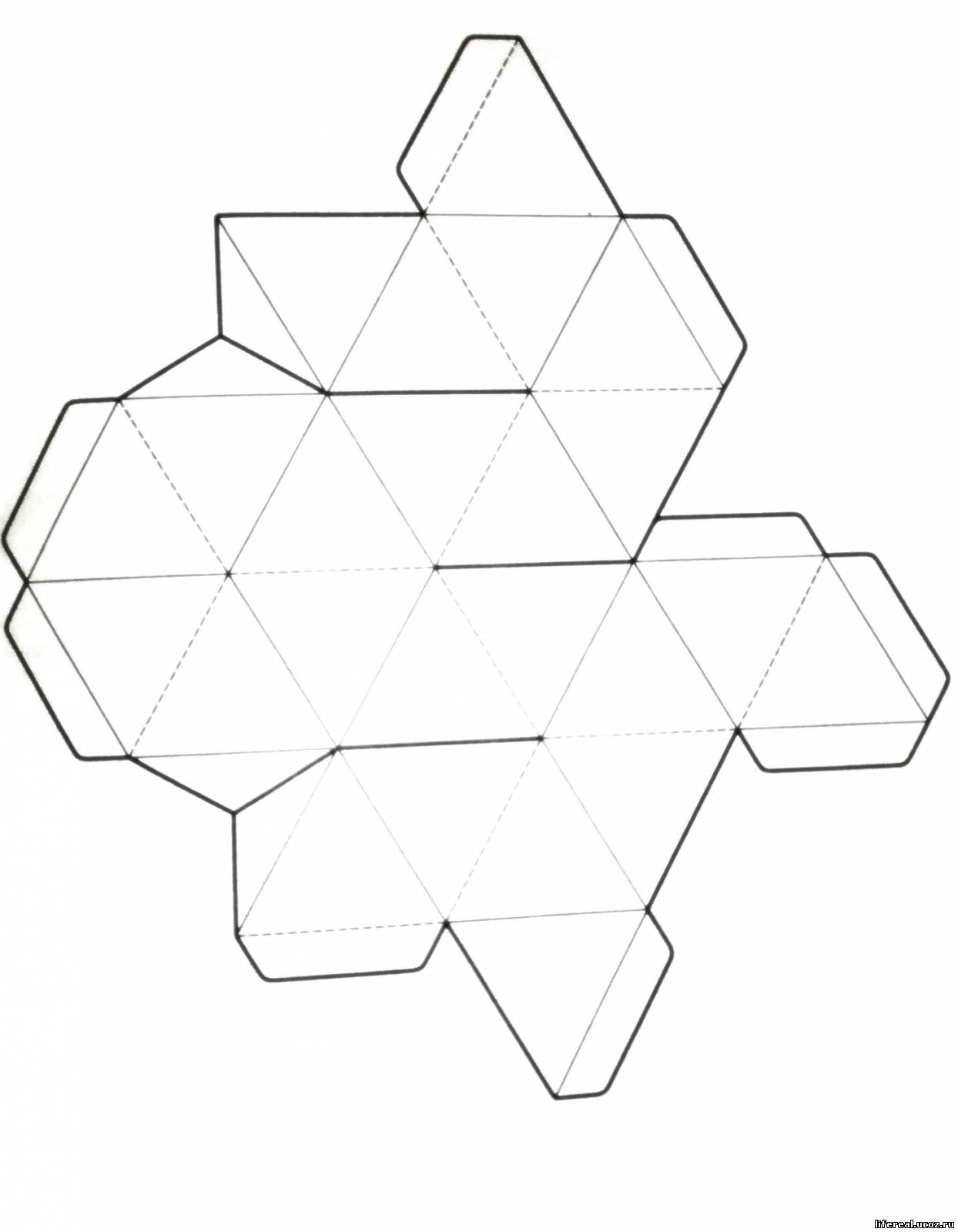 В отличие от параллелограмма, внутренние углы всегда равны 90 градусам. Кроме того, стороны, противоположные друг другу, всегда будут иметь одинаковую длину.
В отличие от параллелограмма, внутренние углы всегда равны 90 градусам. Кроме того, стороны, противоположные друг другу, всегда будут иметь одинаковую длину.
Чтобы использовать формулы для периметра и площади, вам необходимо измерить длину прямоугольника ( l ) и его ширину ( w ).
- Периметр = 2h + 2w
- Площадь = h x w
Площадь и периметр квадрата
Квадрат даже проще, чем прямоугольник, потому что это прямоугольник с четырьмя равными сторонами.Это означает, что вам нужно знать длину только одной стороны ( s ), чтобы определить ее периметр и площадь.
Площадь и периметр трапеции
Трапеция — это четырехугольник, который может показаться сложной задачей, но на самом деле это довольно просто. У этой формы только две стороны параллельны друг другу, хотя все четыре стороны могут быть разной длины. Это означает, что вам нужно знать длину каждой стороны ( a, b 1 , b 2 , c ), чтобы найти периметр трапеции.
- Периметр = a + b 1 + b 2 + c
Чтобы найти площадь трапеции, вам также понадобится высота ( х ). Это расстояние между двумя параллельными сторонами.
Площадь и периметр шестиугольника
Шестигранный многоугольник с равными сторонами — это правильный шестиугольник. Длина каждой стороны равна радиусу ( r ). Хотя это может показаться сложной формой, вычисление периметра — это простой вопрос умножения радиуса на шесть сторон.
Определить площадь шестиугольника немного сложнее, и вам придется запомнить эту формулу:
Площадь и периметр восьмиугольника
Правильный восьмиугольник похож на шестиугольник, но у этого многоугольника восемь равных сторон. Чтобы найти периметр и площадь этой формы, вам понадобится длина одной стороны ( a ).
- Периметр = 8a
- Площадь = (2 + 2√2) a 2
бесплатных онлайн-ресурсов по 3D-фигурам
Ресурсы по 3D-фигурам
3D-фигуры — это твердые объекты, имеющие три измерения.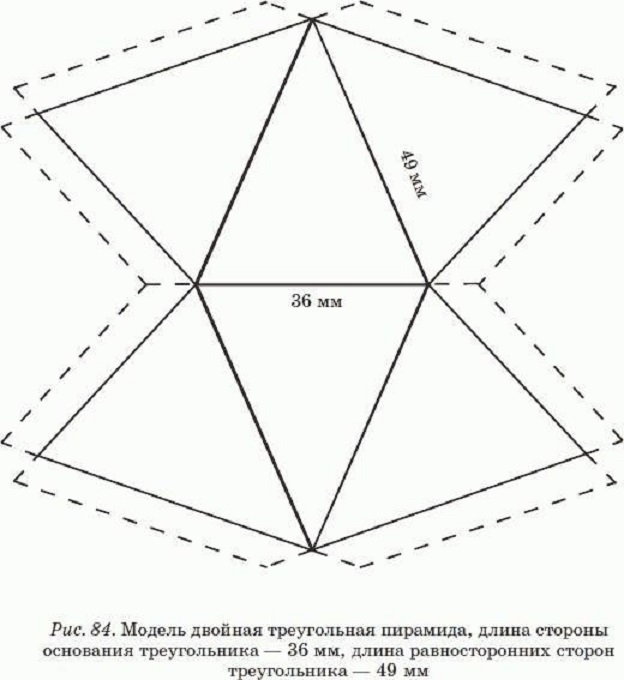 Это длина, ширина и высота. В то время как 2D-фигуры являются плоскими, 3D-фигуры имеют большую глубину. Футбольный мяч — это трехмерная форма, также известная как сфера, а круг на листе бумаги — это двумерная форма. Чтобы узнать больше о различных именах и свойствах трехмерных фигур, см. Наши ресурсы ниже.
Это длина, ширина и высота. В то время как 2D-фигуры являются плоскими, 3D-фигуры имеют большую глубину. Футбольный мяч — это трехмерная форма, также известная как сфера, а круг на листе бумаги — это двумерная форма. Чтобы узнать больше о различных именах и свойствах трехмерных фигур, см. Наши ресурсы ниже.
Начало работы с 3D-фигурами
Поначалу с 3D-фигурами может быть сложно работать, потому что они имеют странные имена и свойства, которые отличаются от знакомых 2D-форм.Мы составили список некоторых свойств обычных 3D-форм и общих уравнений, которые можно использовать при работе с 3D-фигурами.| 3D-форма | Свойства | Объем | Площадь поверхности |
|---|---|---|---|
| Сфера | У нее нет ребер или вершин (углов) У нее одна поверхность Все идеально симметричны на поверхности одинаковое расстояние «r» от центра | 4 ⁄ 3 × π × r 3 | 4 × π × r 2 |
| Цилиндр | Имеет плоскую основание и плоская верхняя часть Основание такое же, как и верхняя часть Имеет одну изогнутую сторону | π × r 2 × h | 2 × π × r × (r + h) |
| Конус | Имеет плоское основание Имеет одну изогнутую сторону | 1 ⁄ 3 × π × r 2 × h | π × r × (r + s) |
| Куб | Имеет 6 Грани, каждая с 4 гранями (квадратная) Имеет 12 граней У нее 8 вершин (угловые точки), каждая из которых совпадает с 3 кромками | (длина кромки) 3 | 6 × (длина кромки) 2 |
| Треугольная призма | Она имеет одинаковые концы (треугольники ) и плоские грани Он имеет одинаковое поперечное сечение по всей длине | Площадь основания × длина | 2 × площадь основания + периметр основания × длина |
Теперь, когда у вас есть список некоторых распространенных трехмерных фигур, погрузитесь в наши ресурсы, чтобы узнать, как применять эти и другие формы, или перейдите на нашу страницу объема, чтобы узнать, как рассчитать, какую площадь занимают эти трехмерные формы.
Изучение геометрии с маленькими детьми
После некоторых экспериментов маленькая Эми вставляет квадратный блок в квадратное отверстие. Это подходит! Она пытается снова. Успех — прекрасное чувство! Наблюдая за этим вдумчивым исследованием, мы можем спросить себя: что этот ребенок знает о формах? Что она изучает? Что еще она узнает в дошкольном учреждении? Чему она могла бы научиться, если бы у нее была возможность?
Маленькие дети спонтанно «занимаются» математикой в игре, в своей жизни. Мы все видели, как дошкольники изучают формы и узоры, рисуют и создают геометрические узоры, с радостью узнавая и называя определенные формы, которые они видят.Это геометрия — одна из самых естественных и увлекательных областей математики, которую нужно развивать с маленькими детьми!
Обогащение детского опыта В дошкольном возрасте интуитивные знания детей в геометрии часто превышают их численные навыки. Опираясь на сильные стороны и интересы, которые уже присутствуют, мы можем развивать постоянный энтузиазм в отношении математики и обеспечивать логический контекст для развития представлений о числах.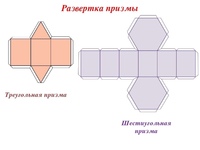
Учитель предлагает двум девочкам использовать свои тела, чтобы вместе создавать фигуры.Они садятся лицом друг к другу и разводят ноги. Соприкоснувшись ногами, они создают алмаз. Другой ребенок смотрит, видит ромбовидную фигуру и предлагает: «Если мы поместим кого-нибудь внутрь, мы сможем сделать два треугольника». Сразу же они просят Рея — самого маленького ребенка в группе — сжаться и лечь посередине. Оно работает! Разделенный пополам ромб образует два треугольника.
Мишель говорит, что есть фигура с шестью сторонами, и хочет попробовать сделать одну из них. Другой ребенок даже знает, что это называется шестиугольником.После краткого обсуждения Мишель собирает вместе еще пятерых детей. Под ее руководством все ложатся на пол и вместе создают шестигранную форму.
Построение геометрического воображения Дети учатся создавать мысленные образы-картинки, которые они могут нести в уме. Маленькие дети имеют тенденцию формировать статические образы — «неподвижные» мысленные образы, к которым они могут обращаться. Дети старшего возраста учатся формировать динамические изображения, которые они могут перемещать или изменять. Например: пятилетний Брайан смотрит на клетку с песчанками, пытаясь понять, поместится ли она в кузове машины его матери.Он так думает и в тот же день обнаруживает, что прав. Формирование геометрического воображения детей — важная часть изучения пространственных отношений и изучения математики. Итак, давайте посмотрим, как мы можем помочь детям учиться, работая с фигурами, изображениями, навигацией и картами.
Дети старшего возраста учатся формировать динамические изображения, которые они могут перемещать или изменять. Например: пятилетний Брайан смотрит на клетку с песчанками, пытаясь понять, поместится ли она в кузове машины его матери.Он так думает и в тот же день обнаруживает, что прав. Формирование геометрического воображения детей — важная часть изучения пространственных отношений и изучения математики. Итак, давайте посмотрим, как мы можем помочь детям учиться, работая с фигурами, изображениями, навигацией и картами.
Имейте в виду, что к шести годам дети часто имеют устойчивые, но ограниченные представления о формах. Например, четырехлетняя Тина говорит своему учителю: «Это не квадрат. Он слишком большой. Квадрат выглядит так.«Ее одноклассник Чарли добавляет:« Треугольники должны быть такими ». Это не треугольник. Это слишком перевернуто ». Вы можете расширить понимание детей, поделившись и узнав различные примеры — квадраты разных размеров или треугольники, которые являются« длинными »,« тощими »,« толстыми »и повернуты во многих направлениях. поощрять более глубокое осмысление форм не только посредством практических занятий и обсуждений, но и с помощью книжек с картинками. Например, в «Жадном треугольнике» Мэрилин Бернс (Scholastic Inc.), треугольнику так наскучивает быть той же старой формой, что он просит у переключателя формы еще одну сторону и еще один угол. Тогда он становится четырехугольником. После того, как мы потребовали больше сторон и углов и превратились в пятиугольник, шестиугольник и т. Д., Фигура в конце концов узнает, что быть треугольником — самое интересное. Это отличное введение в создание фигур с другими формами.
поощрять более глубокое осмысление форм не только посредством практических занятий и обсуждений, но и с помощью книжек с картинками. Например, в «Жадном треугольнике» Мэрилин Бернс (Scholastic Inc.), треугольнику так наскучивает быть той же старой формой, что он просит у переключателя формы еще одну сторону и еще один угол. Тогда он становится четырехугольником. После того, как мы потребовали больше сторон и углов и превратились в пятиугольник, шестиугольник и т. Д., Фигура в конце концов узнает, что быть треугольником — самое интересное. Это отличное введение в создание фигур с другими формами.
Как мы можем побудить детей продолжать создавать статические, а затем динамические изображения? Основу составляет манипулятивная работа с фигурами, такими как блоки, головоломки и танграммы.У детей должно быть достаточно времени для изучения этих материалов и работы с ними. Далее родим детей:
- Делайте головоломки, где можно увидеть только очертания нескольких частей.
 Затем попросите их найти способы заполнить контур, создавая кусочки головоломки, используя свой собственный набор танграм.
Затем попросите их найти способы заполнить контур, создавая кусочки головоломки, используя свой собственный набор танграм. - Попробуйте упражнения с быстрым изображением. Нарисуйте на листе бумаги простой набор фигур. Затем дайте детям короткий взгляд и снова закройте изображение. Например, вы можете нарисовать квадрат, разделенный на два маленьких квадрата и прямоугольник.После того, как дети быстро посмотрят, попросите их поделиться увиденным. Вы услышите множество разных ответов, от описания форм до сравнения с вещами, которые формы напоминают детям, например, шашками или кубиками. На самом деле нет никаких неправильных ответов, а занятие и обсуждение заставят детей больше задуматься о формах и том, что они видят. (Попросите детей старшего возраста использовать разные способы передвижения, рисования, построения с помощью зубочисток и т. Д., Чтобы представить то, что они видели во время быстрых действий с изображениями.)
Юнит-блоки открывают окно в геометрию детских игр. Они позволяют детям исследовать мир, в котором объекты имеют предсказуемое сходство и взаимосвязь, и вдохновляют детей на создание форм и структур, основанных на математических отношениях. Например, детям приходится бороться с такими понятиями, как отношения длины, чтобы найти блоки, которые будут работать при создании крыши для их здания, и эквивалент при замене двух более коротких блоков на один длинный.Дети также принимают во внимание рост, площадь и объем, когда они создают и исследуют важные интуитивные идеи. Вот несколько предложений о том, как вы можете способствовать этому росту:
Они позволяют детям исследовать мир, в котором объекты имеют предсказуемое сходство и взаимосвязь, и вдохновляют детей на создание форм и структур, основанных на математических отношениях. Например, детям приходится бороться с такими понятиями, как отношения длины, чтобы найти блоки, которые будут работать при создании крыши для их здания, и эквивалент при замене двух более коротких блоков на один длинный.Дети также принимают во внимание рост, площадь и объем, когда они создают и исследуют важные интуитивные идеи. Вот несколько предложений о том, как вы можете способствовать этому росту:
- Поощряйте детей обсуждать свои мысли и помогайте им выражать словами свои действия. Например, трое дошкольников строили башни и спорили, чья из них самая большая. Используя жесты, а также слова, их учитель спросил их, имеют ли они в виду, чья башня была «самой высокой» или «самой широкой» или в чьем здании было больше всего блоков.Собралась небольшая толпа, чтобы послушать и высказать свое мнение, и все были удивлены, обнаружив, что в самой высокой башне не было больше всего блоков.
 Другими словами, вы используете детский конструкторский опыт, чтобы помочь им научиться различать разные величины, такие как высота, площадь и объем.
Другими словами, вы используете детский конструкторский опыт, чтобы помочь им научиться различать разные величины, такие как высота, площадь и объем. - Вовлеките детей в обсуждения, которые побуждают их задуматься о сходствах и различиях между используемыми ими блоками и структурами, которые они создают.
- Во время игры с блоками ищите возможности предложить детям попробовать различные задания, например: расположить квадратные и прямоугольные блоки по длине; использование «более коротких» блоков для изготовления стены, равной длине самого длинного блока; сделать как можно больше полов различной формы (прямоугольной); и сделать квадратную коробку из четырех блоков.
Помните: Эти и им подобные упражнения не предназначены для определения способностей детей к математике или определения количества правильных и неправильных ответов, которые они придут. Напротив, они дают возможность изучить свойства математики и побудить детей к логическому, творческому и критическому мышлению. Все будут в разных местах в процессе обучения математике, поэтому наша задача — убедиться, что каждый чувствует себя способным и никто не чувствует себя неадекватным или обделенным.
Все будут в разных местах в процессе обучения математике, поэтому наша задача — убедиться, что каждый чувствует себя способным и никто не чувствует себя неадекватным или обделенным.
Маленькие дети рано учатся передвигаться — с этим согласны все взрослые, ответственные за их уход. Что, однако, они могут понять математически о месте и движении? Разумно ли думать о том, чтобы дошкольники составляли и использовали карты? Хотя это может показаться неприемлемым с точки зрения развития, исследования показали, что это не так. Вот факты:
- Многие трехлетние дети могут создавать простые, но содержательные карты с пейзажными игрушками, такими как дома, машины и деревья.Некоторые тройки могут даже воспроизвести комнату в миниатюре, используя блоки, игрушки и другой реквизит.
- Многие старшие дошкольники знают об относительных расстояниях между ориентирами. Например, четырехлетняя Андреа знала, что между ее домом и домом бабушки дальше, чем между ее домом и знаком «Стоп».
- Многие дети также могут указывать местоположения на маршруте. Например, вы гуляете с ребенком в магазине. Вы выходите из дома, поворачиваете направо, идете один квартал по улице, снова поворачиваете направо и идете еще один квартал до магазина.Вернувшись домой, спросите ребенка, где находится магазин. Даже не пройдя по маршруту «по прямой», ребенок указывает по диагонали в сторону магазина.
- Когда им было предложено выучить маршрут через игровой домик с шестью комнатами, четырехлетние дети, предварительно изучившие карту, выучили маршрут быстрее, чем те, кто этого не сделал.
Это не означает, что маленькие дети умеют читать карты, но это означает, что они обладают впечатляющими начальными способностями, изучение которых может быть забавным и увлекательным.Вот несколько действий для этого:
Где мы? Предложите детям вырезать фигурки из фетра для игр на открытом воздухе, например, деревья, стол для пикника, качели, песочницу и так далее.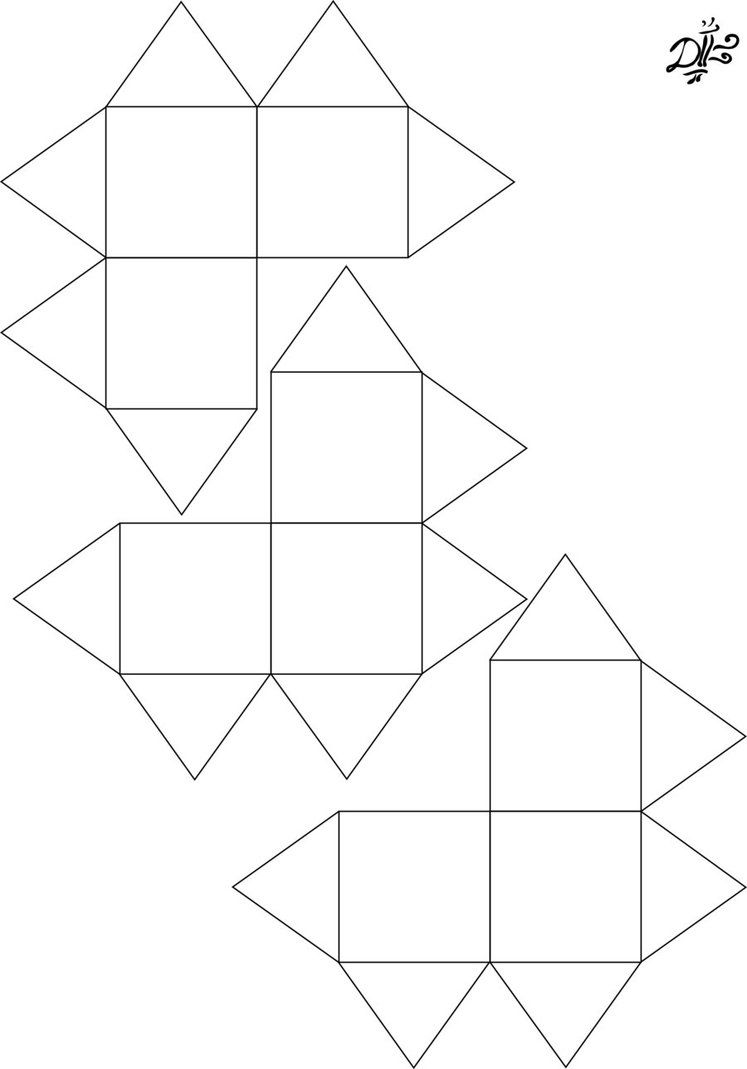 Предложите им разложить фигуры на войлочной доске, чтобы составить простую карту открытой местности. (То же самое можно сделать и в вашем классе.) Вовлеките детей в обсуждение того, как перемещение предмета, например стола, может изменить карту окружающей среды. Предложите детям фигурки из фетра и предложите им расположиться на карте рядом с местом, которое им больше всего нравится играть.
Предложите им разложить фигуры на войлочной доске, чтобы составить простую карту открытой местности. (То же самое можно сделать и в вашем классе.) Вовлеките детей в обсуждение того, как перемещение предмета, например стола, может изменить карту окружающей среды. Предложите детям фигурки из фетра и предложите им расположиться на карте рядом с местом, которое им больше всего нравится играть.
Многие маленькие дети готовы изучать направления окружающей среды, такие как «сверху», «сверху» и «сзади», и развивать такие навигационные идеи, как «вперед», «назад», «идти в сторону» и «поворачивать». » Чтобы способствовать этому обучению, помогите детям изобразить эти концепции на простых картах. Например, попросите детей использовать малярный скотч и помочь вам обозначить путь от двери до корзины для мусора. Затем вместе создайте карту своего пути. Вы можете сфотографировать дверь и мусорную корзину и вместе решить, где приклеить каждую на большом листе бумаги.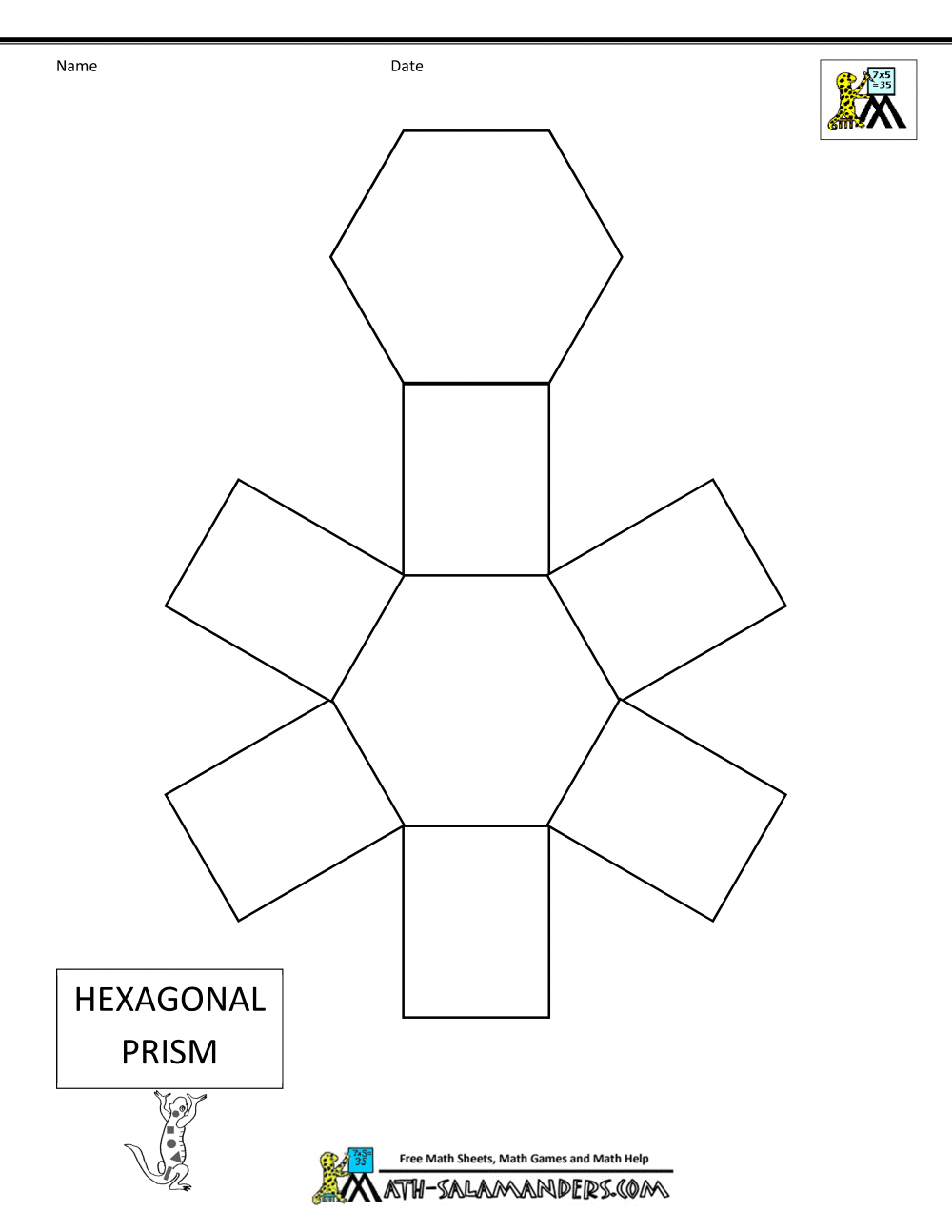 Затем найдите и перечислите предметы, которые появляются на пути, например стол и мольберты. Вместе проиллюстрируйте каждый на карте в соответствующем месте. Дети также могут использовать блоки, различные предметы и игрушки по комнате для создания наглядных карт отдельных частей класса, всего класса или вашей игровой площадки на открытом воздухе. Когда дети научатся создавать карты, некоторые могут захотеть поработать над более сложными картами.
Затем найдите и перечислите предметы, которые появляются на пути, например стол и мольберты. Вместе проиллюстрируйте каждый на карте в соответствующем месте. Дети также могут использовать блоки, различные предметы и игрушки по комнате для создания наглядных карт отдельных частей класса, всего класса или вашей игровой площадки на открытом воздухе. Когда дети научатся создавать карты, некоторые могут захотеть поработать над более сложными картами.
Предоставьте детям возможность исследовать перспективу.Сделайте несколько фотографий здания школы с разных ракурсов и оставьте их, чтобы дети могли посмотреть и подумать. Выберите несколько игровых построек снаружи и сфотографируйте каждую с разных точек зрения. Смешайте фотографии и дайте детям возможность отсортировать их по структуре. Поощряйте каждого ребенка рисовать структуру блока другого ребенка с разных точек зрения. Разместите рисунки, чтобы дети могли наблюдать и сравнивать. Вы также можете сфотографировать структуры с разных точек зрения и предложить детям найти точку обзора, с которой была сделана каждая фотография.
Проводите простую охоту на мусорщиков на открытом воздухе, чтобы дети могли практиковаться в том, чтобы давать и следовать указаниям и подсказкам.
Помните: Геометрические идеи преподают повсюду. Материалы в магазинах игрушек, магазинах товаров для учителей и каталогах, а также телепрограммы пытаются научить детей формам. По мере поиска ресурсов ищите те, которые знакомят детей с самыми разными формами, а не только с треугольниками, прямоугольниками и квадратами.Покажите различные примеры каждой формы.
Геометрия может быть самой интересной и самой естественной математикой для изучения с дошкольниками, опираясь на их существующие сильные стороны, когда они узнают о структуре форм и пространства. Но мы все должны помнить, что дети усваивают эти идеи наиболее эффективно через активное взаимодействие с игрушками, кубиками, головоломками, манипуляторами, рисунками, компьютерами — и вами!
Примечание автора: Время на подготовку этого материала было частично предоставлено Национальным научным фондом, грант NSF MDR-8954664, «Исследование развития элементарного детского геометрического мышления в компьютерной и некомпьютерной среде» и грант Национального научного фонда. номер ESI-9730804, «Строительные блоки — основы математического мышления, от подготовительного до второго класса: разработка материалов на основе исследований».«Любые мнения, выводы, выводы или рекомендации, выраженные в этой публикации, принадлежат автору и не обязательно отражают точку зрения Национального научного фонда.
номер ESI-9730804, «Строительные блоки — основы математического мышления, от подготовительного до второго класса: разработка материалов на основе исследований».«Любые мнения, выводы, выводы или рекомендации, выраженные в этой публикации, принадлежат автору и не обязательно отражают точку зрения Национального научного фонда.
Вот список замечательных книг по математике, которыми можно поделиться со своим классом.
Как летит ворона Гейл Хартман, иллюстрация Харви Стивенсона
Бэби Боп открывает формы Стивена Уайта, иллюстрировано Ларри Дастом
Изменения, изменения Пэт Хатчинс
История деда Тана Энн Томперт, иллюстрация Роберта Эндрю Паркера
Давайте изучим формы с помощью Shapely-CAL от S.Келлер и И. Гольдберг
Игра в фигуры Пол Роджерс
Форма вещей Д.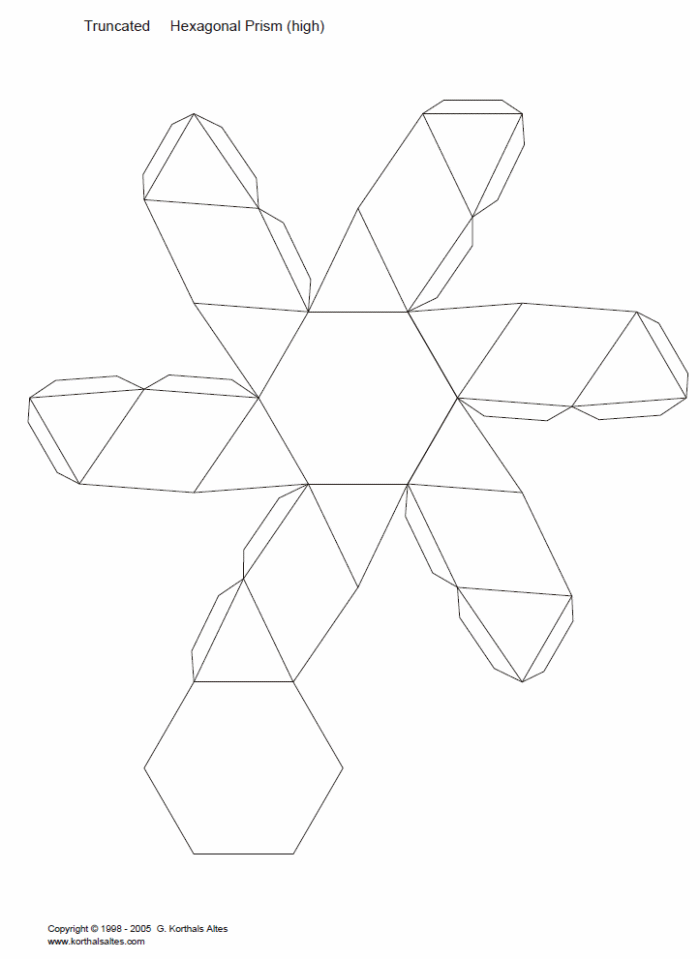 А. Доддс
А. Доддс
Кто сказал красный? Мэри Сертоза
Что бывает в комбинациях 2, 3 и 4? Сюзанна Акер
Планы уроков по геометрии
Планы уроков по геометрииПланы уроков по геометрии
- 3-D Рисование и геометрия — в этом геометрическом блоке вы увидите несколько разных типы трехмерных рисунков и научитесь делать эти рисунки самостоятельно.Ты также исследует множество интересных профессий, в которых используются эти методы, от архитектуры до фильмов.
- Площадь треугольника — учащиеся узнают и применяют формулу чтобы найти площадь треугольника.
- Buckyballs- Студенты, задающиеся вопросом, почему мы изучаем многогранники, могут найти одну причину: просматривая информацию в ссылках на Buckyballs.
- Классификация
и построение углов — учащиеся исследуют, классифицируют и определяют
различные типы углов (острый, прямой, тупой и прямой), которые
происходят в окружающем их мире.
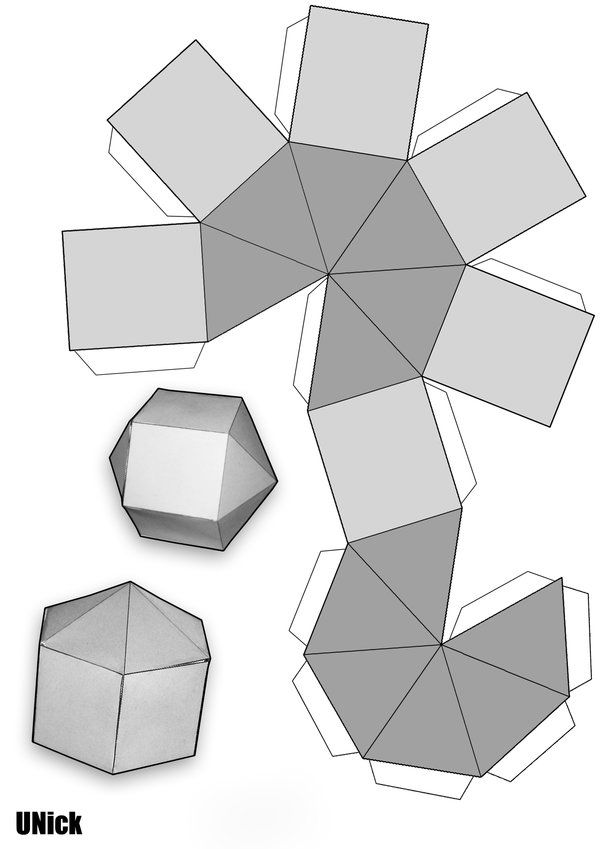 Этот план урока — второй урок
в серии по геометрии.
Этот план урока — второй урок
в серии по геометрии. - Создание Тесселяции — изучите историю мозаики; тогда используйте искусство и геометрия для создания оригинальной мозаики.
- кристаллов: Кристаллография и системы — Студенты, изучающие многогранник, пользуются видеть структуры такими, какими они являются в реальном мире. Кристаллические структуры можно разделить на семь кристаллических систем.
- Дизайн с кругами- В исламской культуре круг — это единица измерения.Круг основа для организации пространства. Это отправная точка в архитектуре, поэзия, музыка и даже каллиграфия.
- Но это Не честно! — Студенты решают задачи с использованием дробей на практике мероприятия и соответствующая литература.
- Координата Геометрия — учащийся сможет определить положение по координате плоскость при задании координат (наведение, карандаш или манипуляция).
- EggMath-
Форма яйца, включающая обсуждение поверхностей вращения
и методы рисования овалов на плоскости.

- Геометрия Евклида: История и практика — серия междисциплинарных уроков по Элементы Евклида были исследованы и написаны классицистом Алексом Пирсоном. в Епископальной академии в Мерионе, штат Пенсильвания.
- Объясните перемену — урок будет можно представить, рассматривая наклон как скорость изменения, как обсуждалось ранее в классе.
- Исследование Площадь / периметр через координатную геометрию — учащиеся узнают о площадь и периметр через координатную геометрию.Использование детских литература, практические манипуляторы и Интернет будут включены.
- Колесо обозрения- Физические устройства можно моделировать с использованием динамической геометрии. Жизненно важный инструмент для движущиеся объекты в модели — это изометрии или сохраняющие расстояние трансформации. Эта модель колеса обозрения является хорошим примером.
- Находка Периметр — приложение геометрии TLWD с использованием формулы для найти периметр.
- Этаж
Круги — учащиеся будут отображать число в виде площади прямоугольника.
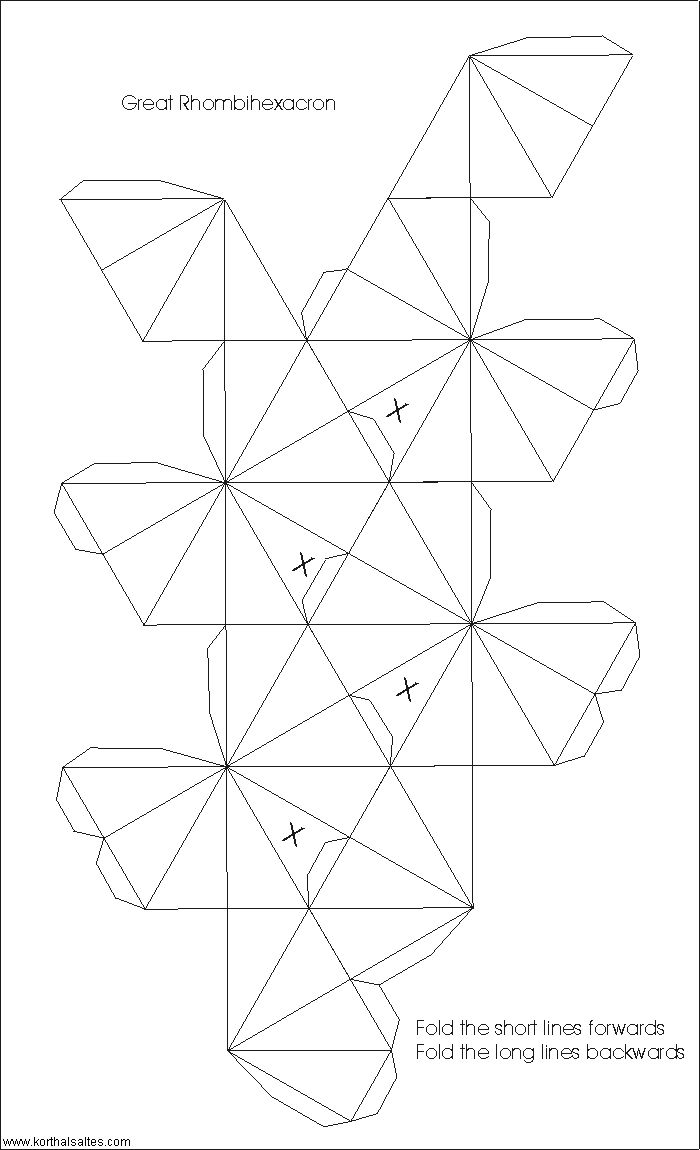 Студенты сделают как можно больше прямоугольных композиций для каждого
цифра дана.
Студенты сделают как можно больше прямоугольных композиций для каждого
цифра дана. - Geo Jammin ‘ Автор DeSign — Учитель и ученики — динамичный дуэт, ищущий геометрию Веб-сайт для определения слов из геометрического словаря, записи их на лоскутное одеяло Стена Слов и танцуй их вместе. Слова отображаются, чтобы взять характеристики различных шаблонов проектирования.
- Geo Jammin ‘ By DeSign 2 — последовательность рисунков, выполненных учителем, ведет учащимся создавать ассоциации с нарисованным объектом и геометрией содержание, изученное на предыдущих уроках.Через вопросы ученики разблокируют Квадрант 1 координатной плоскости и новые словарные слова.
- Geo Jammin ‘ By DeSign 3 — Знание геометрии переносится в лес в студенческие годы прогуляйтесь по территории школы в поисках симметрии в природе. Их находки возвращаются в класс, сохраняются нажатием, а затем используются как в центре сюжета, созданного учащимся.
- Geo Jammin ‘
By DeSign 4 — Геометрическая бумага используется в качестве сетки для координатной геометрии,
сделать привычную арену для выполнения самого необычного задания.
 Письма
присваивается каждой точке. Задача состоит в том, чтобы расшифровать каждое слово, используя заданные
координаты, а затем проиллюстрировать каждую танграммами.
Письма
присваивается каждой точке. Задача состоит в том, чтобы расшифровать каждое слово, используя заданные
координаты, а затем проиллюстрировать каждую танграммами. - Геометрический факторинг
- Геометрия и самолеты — учащиеся смогут описывать фигуры, используя с точки зрения геометрии.
- Геометрия 2D-фигуры — спросите учащихся, хочу ли я классифицировать фигуры по их количеству. углов, формы которых будут принадлежать где.
- Геометрия Geopardy — интересный способ попрактиковаться и изучить геометрический материал.
- Геометрия введение в 3D-формы — учащиеся заметят разницу между 2D и 3D формами.
- Геометрия Библиотека — студенты пишут и иллюстрируют книги, чтобы сделать классную библиотеку. курсов по математике. Это отличный обзор математического теста FCAT.
- Геометрия
Манипулятивно — используйте круги для построения правильных многоугольников. Используйте круги.
для определения вращательной и отражательной симметрии.
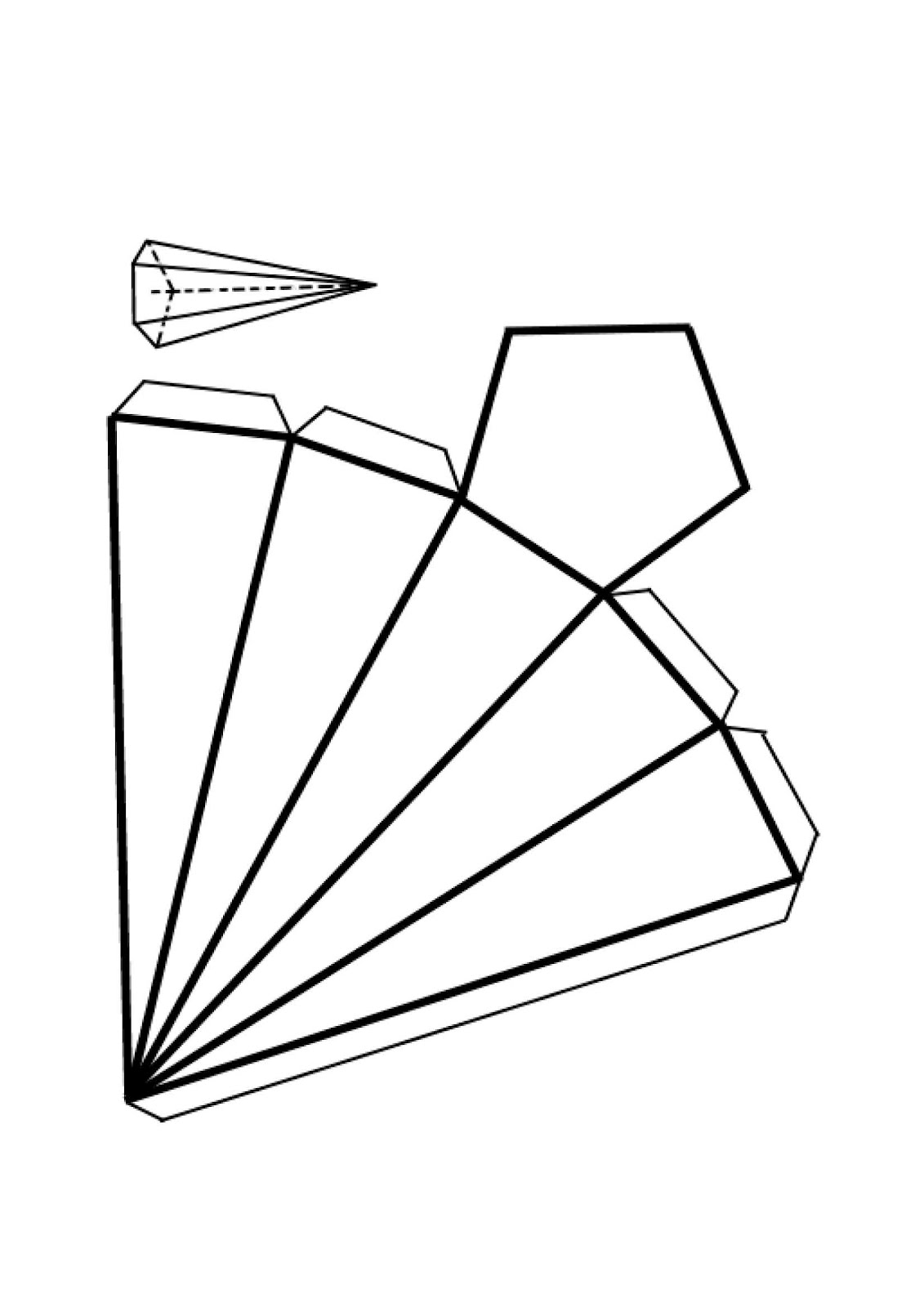
- Геометрия в африканском искусстве — анализируйте произведения искусства с точки зрения геометрических форм и формы.
- Геометрия в природе — учащиеся исследуют, как окружность, диаметр, и отношение Пи круга связаны. Студенты будут также определите возраст дерева, посчитав летние годичные кольца.
- Геометрия Охота за мусором — учащиеся находят предметы повседневного пользования, которые представляют собой геометрические фигуры. цифры. Затем ученики должны доказать, что объект действительно имеет форму. Студенты также находят периметр, площадь, площадь поверхности, объем, окружность. выбранных объектов.
- Геометрия Преобразования — студенты поймут концепции отражения и перевод как преобразования точек, линий и объектов.
- Геометрия: Тесселяции — студенты применяют знания об отражениях, вращениях, и переводы при создании тесселяции.
- Геометрия Задания
- Интернет
Field Trip on Fractions and Geometry — Этот урок посвящен фракциям / геометрии.
 как это касается деталей и целых.
как это касается деталей и целых. - Введение в геометрию для учеников начальной школы — эти уроки предназначены для маленьких детей через введение в геометрию.Дети научатся распознавать форм и создания узоров, а также изучит пространственные отношения и симметрия.
- Это модно быть Квадратом — Опишите, классифицируйте и сравните отношения среди четырехугольников, включая квадрат, прямоугольник, ромб, параллелограмм, и трапеция.
- Широта и долгота: география и геометрия! — Этот урок объединяет области геометрии и географии. Студенты научатся определять местоположение на картах и диаграммах с использованием координат широты и долготы.
- Магические квадраты- Студенты часто считают, что «математику» «написал» один человек. На этих страницах вы обнаружите, что математическая игра «Магический квадрат» существовали на протяжении всей истории и во многих различных частях мира. Математика вокруг нас, и ваш разум увидит это, когда вы будете готовы!
- Имя
этот полигон! — Студенты смогут определить и описать
Полигоны с помощью Geoboard и манипуляций с партнером.
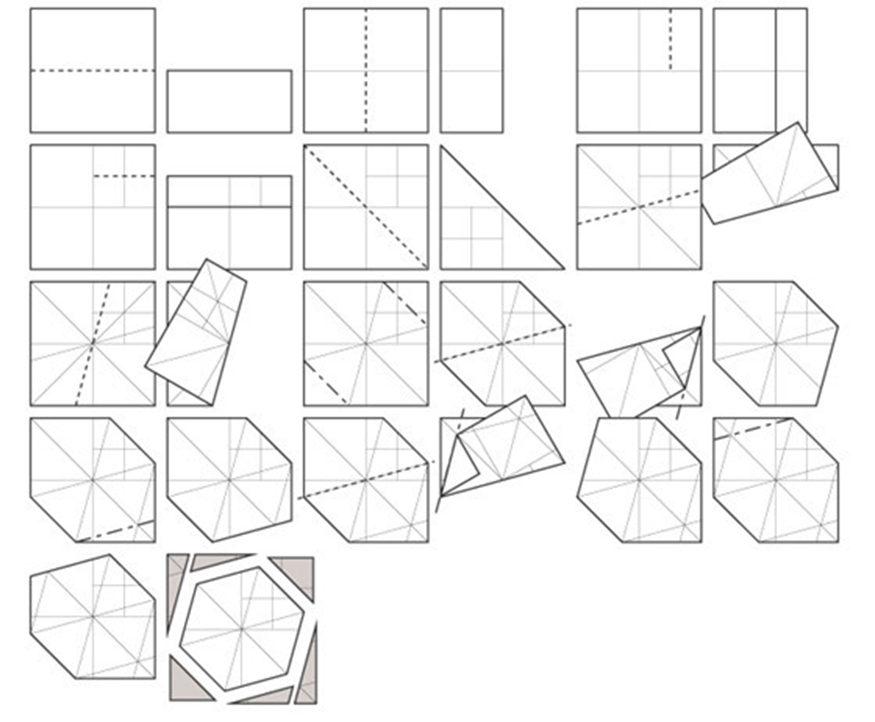
- Номер отрезков и вершин линии — учащиеся узнают конус, сфера, куб, прямоугольная призма и цилиндр и укажите количество вершин, грани и ребра / отрезки линий.
- Параллельно & Пересекающиеся отрезки, лучи и линии — для ориентации детей поскольку они моделируют и рисуют параллельные и пересекающиеся сегменты многоугольников, лучи и линии.
- Точка, Линия, плоскость — учащиеся научатся работать с точками, чтобы построить линии. которые затем превращаются в самолеты. Это упражнение помогает ученикам развить свои дизайнерские идеи.
- очков, Сегменты линии — учащиеся смогут распознать точку, сегмент линии, линия и луч.
- Многогранник в классе- .Представленный здесь блок использует найденные цели в Блоке 14 интерактивной математики Гленко, но разработан так, чтобы учащиеся могли уделять дополнительное время определенным математическим идеи.
- Проверка
Конгруэнтность треугольника — критическое и логическое мышление при решении конгруэнтности
основан на использовании двухколоночных доказательств для отображения мыслительного процесса
логичным и упорядоченным образом.
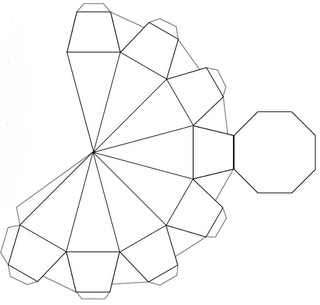
- Нечетный Геометрические формы — учащиеся узнают все 2D и 3D формы, которые они атрибуты и свойства.
- Quandaries, Болота и четырехугольники — учащиеся классифицируют, переворачивают, скользят и поверните некоторое количество четырехугольников. Практические манипуляторы и решение проблем шаги используются для изучения этих четырехсторонних многоугольников. Этот план — пятое в серии уроков по геометрии.
- Резюме по геометрии — учащиеся будут лучше понимать основы геометрии сроки, и может производить продукт по запросу, используя бумагу и карандаш метод, так и с помощью тактильного метода.
- Формы / Пространство и геометрия — учащиеся узнают больше о своих способностях и фантазии.
- Сторона Длины треугольников — этот урок знакомит с разносторонней, равнобедренной и и равносторонние треугольники и их различия.
- Сходства
— Главный результат заключается в том, чтобы учащиеся могли быстро показать
разница между похожими и совпадающими фигурами.
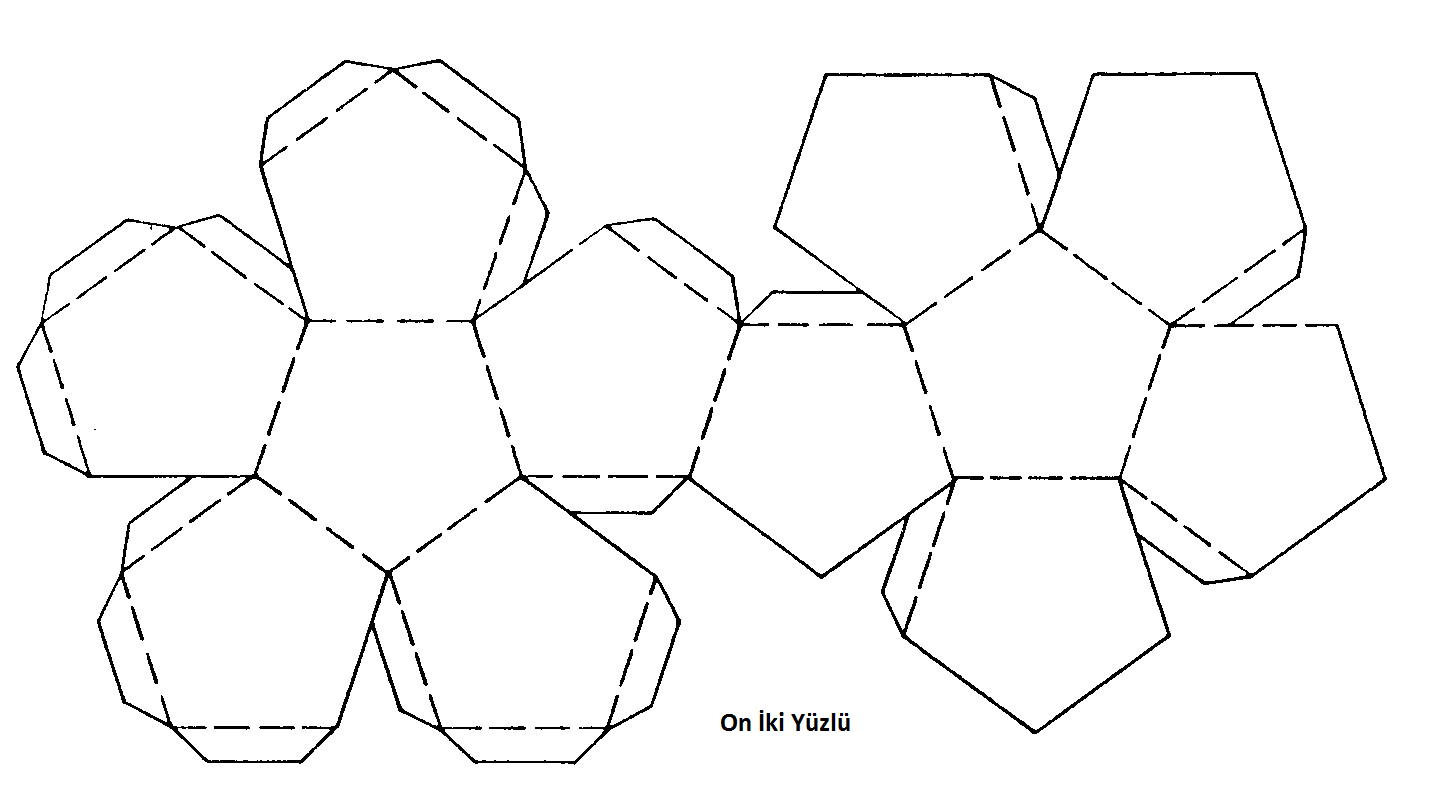
- Учеба Многогранники — Иногда в математике мы изучаем абстрактные идеи. и трудно увидеть, но многогранность видна! Кристаллы реальный мир примеры многогранников. Соль, которую вы посыпаете своей едой, — это кристалл в форме куба.
- Поверхность Площадь геометрических фигур — в этом разделе учащиеся будут применять свои знание площади обычных геометрических фигур для определения поверхности площадь общей пространственной фигуры.
- Симметрия и использование географических досок — студенты создадут валентинки Дневная карта с использованием симметрии.
- Танаграм Человек — TLW создает различные типы треугольников, используя данные измерения и классифицируйте каждый треугольник по углам и длине линий.
- Tangrams- Это модуль для классов с 4 по 6 использует танграммы для вычисления площади многоугольников без формул.В процессе этого условия совпадающие и подобные вводятся.
- Дразнящий
Тесселяции — этот модуль объединяет математику с такими предметами, как язык.
искусство и художественное образование. На протяжении всей нашей деятельности мы просили студентов ответить на концепции тесселяции. Они напишут определения и оценить, насколько хорошо их группы работали вместе.
- Тесселяция Учебники — Учебники и шаблоны для создания ваших собственных мозаик.
- Здание Блоки геометрии — учащиеся изучают геометрические строительные блоки в реальный мир для описания характеристик и отношений точек, линий, отрезков, лучей и плоскостей.Это первый урок план в серии уроков по геометрии.
- Веселье Многоугольник — студенты используют практические манипуляторы для изучения и описания свойства и атрибуты основного многоугольника: треугольники.
- Самолет! Самолет! — Учащиеся рисуют, описывают и классифицируют построенные полигоны из точек, линий, отрезков и лучей в двухмерной плоскости.
- Трехмерный Объекты. Учащиеся смогут определять объекты, которые находятся в формы прямоугольной призмы, цилиндра и овала.
- Понимание Геометрические фигуры — Где я могу найти геометрические фигуры в моем окружении?
- Понимание
Перспектива — сформулируйте и расшифруйте форму и пространство в приложении
основных принципов перспективы и геометрии.
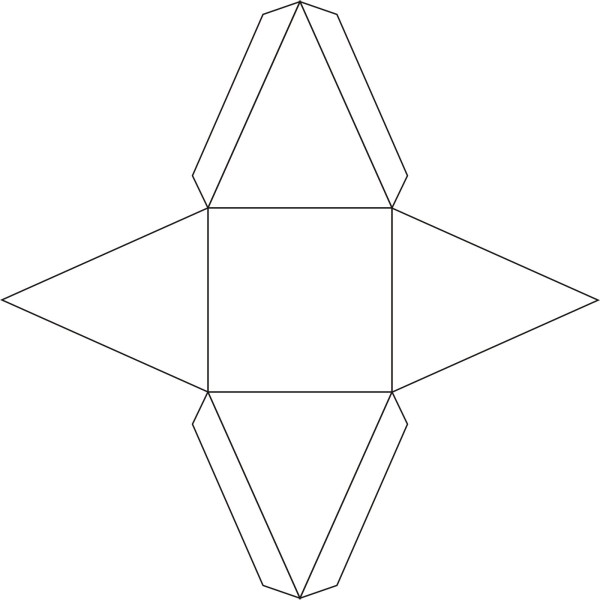
- Использование Транспортир — Как мы можем оценить измерение углов?
Площадь поверхности и объем трехмерных фигур
В этом разделе мы вычисляем объем и площадь поверхности 3-D фигур, таких как кубов , кубов , призм и цилиндров .
| Куб | Объем = x ³ Площадь поверхности = 6 x ² | |
| Кубоид | Объем = xyz Площадь поверхности = 2 xy + 2 xz + 2 yz | |
| Цилиндр | Объем = π r ² h Площадь криволинейной поверхности = 2 π rh Площадь каждого конца = π r ² Общая площадь поверхности = 2 π rh + 2 π r ² | |
| Призма | Призма имеет однородное поперечное сечение Объем = площадь поперечного сечения × длина = А л |
Упражнения
Вопрос 5 На схеме показан деревянный брусок, в котором просверлено отверстие.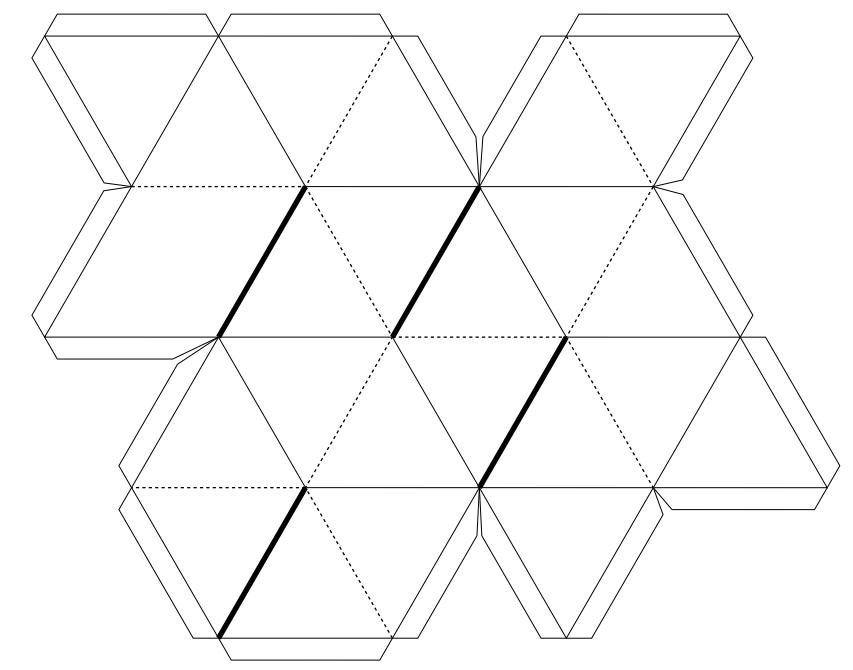 Диаметр отверстия 2 см.
Диаметр отверстия 2 см.
Вычислите объем этого твердого тела, дав правильный ответ с точностью до 2 знаков после запятой.
Объем = блок — отверстие = 4 × 6 × 6 — 1² × π × 6 = 144 — 6 π = 125,15 (до 2 d.p.)
Вопрос 7 На схеме показано сечение трубы длиной 50 см.
Внутренний диаметр трубы составляет 20 см, а внешний — 30 см.
(а)
(б)
| Общая площадь поверхности | = 2 × (15² — 10²) × π + 30 π × 50 + 20 π × 50 |
| = 250 π + 1500 π + 1000 π = 2750 π | |
| = 8639,379797 см² = 8640 см² (до 3 SF) |
Цилиндр имеет диаметр 12 см и площадь изогнутой поверхности 132 π или 415 см² (до 3 значащих цифр).
Вопрос 12(а)
(б)
Ящик стандартного размера содержит достаточно соли, чтобы заполнить 10 солонок.
(в)
Вопрос 13(а)
(б)
Каков объем этой призмы?
Площадь поперечного сечения = × основание × высота = × 6 × 8 = 24 см²
Объем призмы = площадь поперечного сечения × длина = 24 × 7 = 168 см³
(в)
Призмы A и B имеют одинаковую площадь поперечного сечения.
Заполните таблицу:
Геометрия + компьютерная визуализация / моделирование
Введение
Студенты узнают, что компьютерные программы могут использоваться для облегчения и автоматизации таких задач, как рисование фигуры или построение линии. Используя графический интерфейс программирования, такой как Scratch или Snap !, учащиеся напишут простые программы, которые рисуют двухмерные геометрические объекты на экране. Студенты получат базовые знания об основных геометрических принципах точек, линий и плоскостей.По мере построения геометрических объектов на экране они узнают основные свойства некоторых многоугольников (включая, помимо прочего, треугольники и четырехугольники).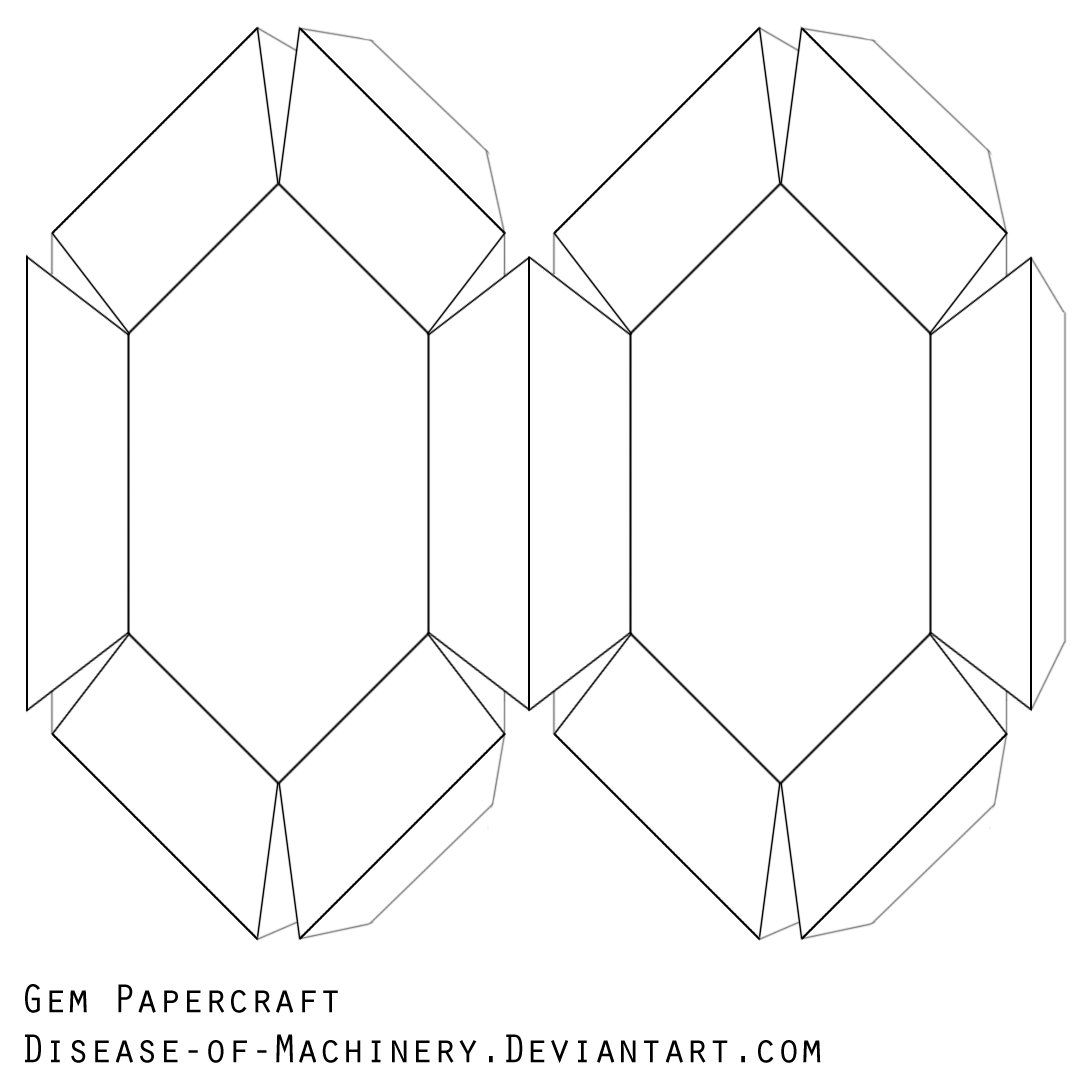 Учащиеся продемонстрируют свое понимание этих свойств, когда они запрограммируют компьютер для построения двумерных правильных многоугольников, используя количество углов и их меры в качестве входных данных.
Учащиеся продемонстрируют свое понимание этих свойств, когда они запрограммируют компьютер для построения двумерных правильных многоугольников, используя количество углов и их меры в качестве входных данных.
- Студенты начнут с программирования цифрового «пера», чтобы рисовать четыре точки в виде углов на плоскости с заданными координатами. Затем студенты будут программно строить линии, которые приведут к построению треугольников и четырехугольников с использованием заданных точек и углов поворота на требуемые градусы для создания правильных многоугольников.
- Затем учащиеся узнают о функциях зацикливания, которые автоматизируют рисование треугольника, квадрата и других правильных многоугольников путем повторения рисования каждой стороны и вращения пера. Функции будут отражать понимание геометрической конструкции и атрибутов правильного многоугольника, включая команды, требующие ввода соответствующего количества раз, когда линия должна быть нарисована, и соответствующего количества градусов, на которые перо должно повернуться, чтобы закрыть многоугольник.
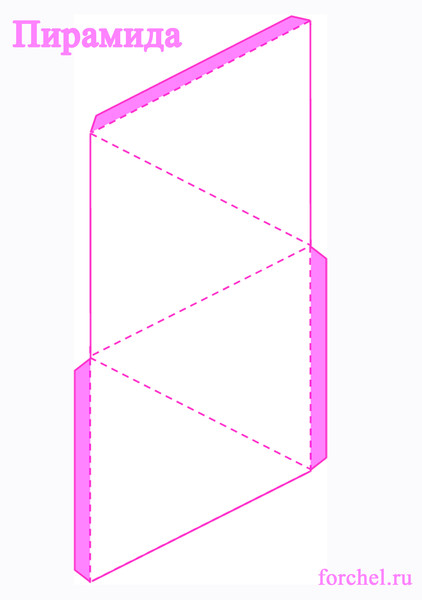
- Затем учащиеся узнают о вводе с клавиатуры или подсказках, например о количестве сторон от 3 до 12 и длине каждой стороны, чтобы получить действительные вводы от пользователя. Наконец, студенты смогут написать свою собственную программу, предлагающую пользователям ввести количество сторон и длину каждой стороны, а затем нарисовать этот многоугольник на экране с правильными углами и размерами. Эта программа требует понимания того, как вычислять углы правильного многоугольника с учетом количества сторон.Расширение: напишите программу, которая принимает строковое значение (слово) и преобразует его в многоугольник определенных размеров.
Площади выпуклых четырехугольников и треугольников
- Учащиеся напишут программу для вычисления площади четырехугольника в квадратных единицах. Это задание также научит студентов концепциям переменных и операторам if / else, используемым в компьютерном программировании. Во-первых, учащиеся расширят программу в упражнении, которое рисует квадрат, чтобы нарисовать прямоугольник заданной длины и ширины.
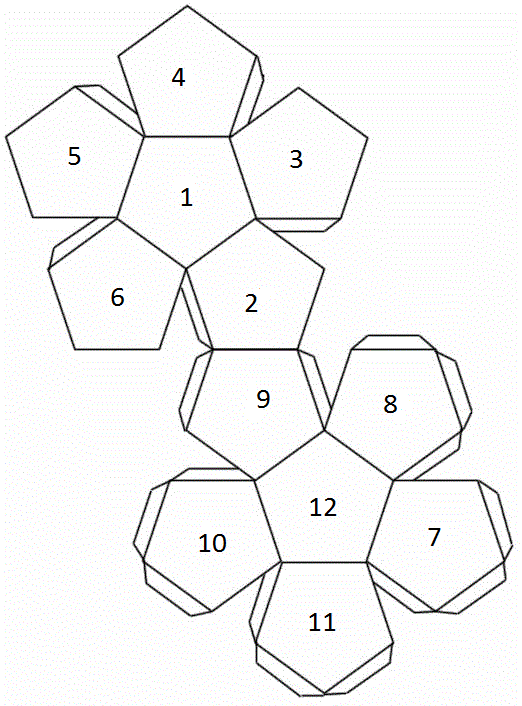 Используя Scratch или синтаксический язык, такой как Python или JavaScript, учащиеся определяют две переменные, например, «b» и «h», и еще одну пустую переменную, называемую «область». Запрашивая пользователя, программа примет первый ввод как длину, а второй как ширину. Затем программа выведет площадь рисунка либо в командную строку, либо выведет.
Используя Scratch или синтаксический язык, такой как Python или JavaScript, учащиеся определяют две переменные, например, «b» и «h», и еще одну пустую переменную, называемую «область». Запрашивая пользователя, программа примет первый ввод как длину, а второй как ширину. Затем программа выведет площадь рисунка либо в командную строку, либо выведет. - Затем учащиеся пишут программу, которая вычисляет площади следующих многоугольников: треугольника, параллелограмма, трапеции, прямоугольника и ромба.Программа предложит пользователю ввести имя многоугольника из списка, а затем с помощью оператора if / else повторно попросит пользователя ввести другую базу в случае выбора трапеции. Если это не трапеция, то программа запустит функцию «вычислить площадь», которая примет входные данные о том, какая форма была выбрана, применит соответствующую формулу и вернет это вычисленное значение пользователю в таком заявлении, как: «Площадь ваша трапеция — 56 кв. единиц ». Цель этого задания — развить у учащихся понимание оператора if / else, используя обзор основных формул области.
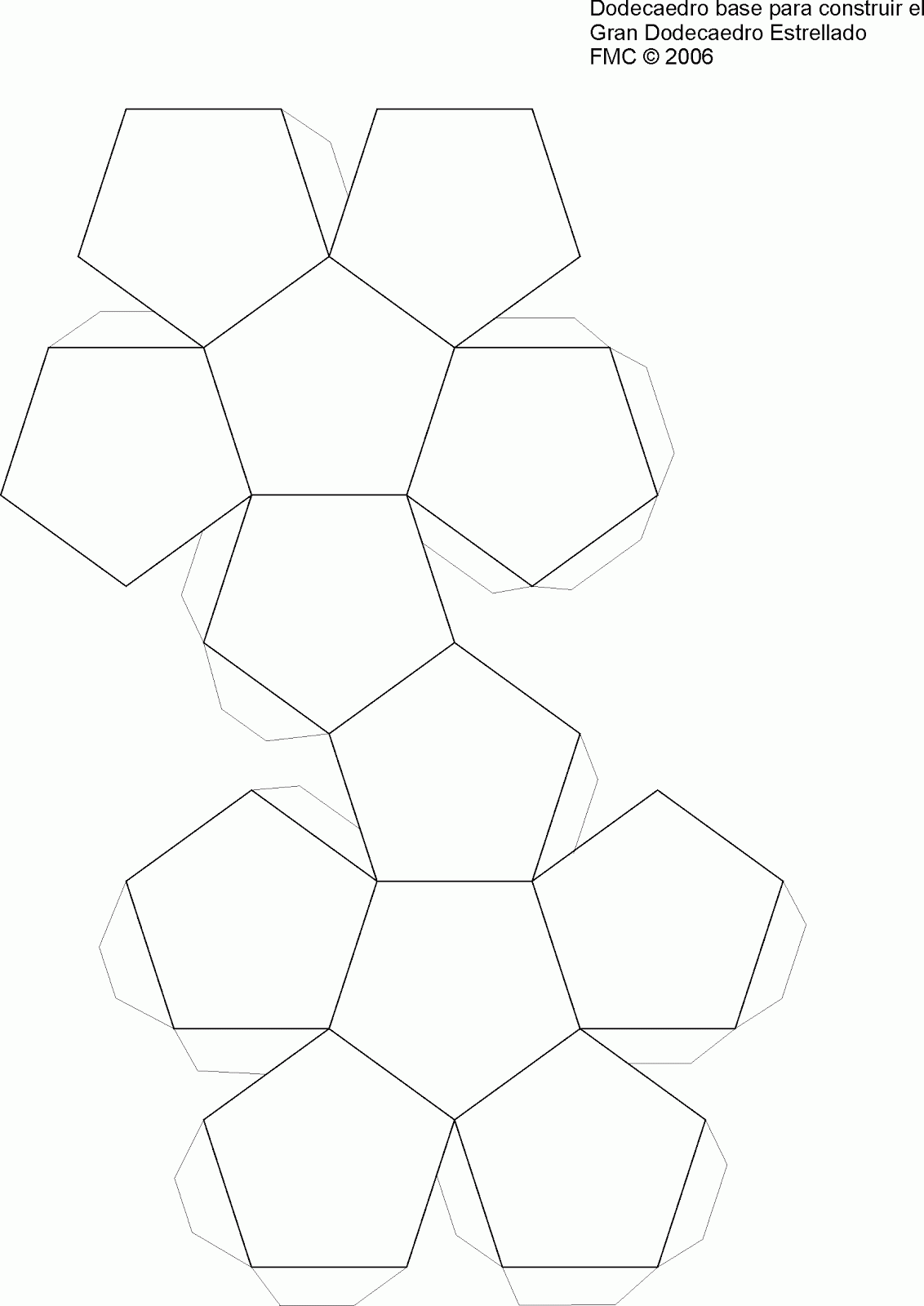 Расширение этой программы будет фактически рисовать многоугольник на экране И вычислять площадь.
Расширение этой программы будет фактически рисовать многоугольник на экране И вычислять площадь. - Наконец, ученики будут использовать квадратный спрайт 10 на 10 пикселей в Scratch или Snap !, и программно вычислить, сколько квадратов необходимо для заполнения большего заданного прямоугольника. Учащийся расширит свои знания о циклах, включив вложенные циклы, чтобы решить задачу заполнения прямоугольника квадратными плитками. Программа должна отслеживать количество плиток, которые используются для заполнения фигуры переменной площади, а затем выводить или печатать на экран площадь в квадратных единицах.
Круги
В этом упражнении учащиеся будут создавать динамические компьютерные симуляции, чтобы продемонстрировать свое понимание сходства всех кругов. Используя выбранный язык программирования, студенты сначала напишут программу, которая рисует круг после того, как пользователю будет предложено ввести радиус. Затем студенты изучат различные типы пользовательских интерфейсов для настройки или изменения значения переменной, такие как ползунок, кнопки или текстовые поля, и выберут один метод, который лучше всего подходит для создания программы, позволяющей пользователю динамически изменять размер круга на экране, настраивая интерфейс. Программа должна автоматически обновляться, когда пользователь изменяет или обновляет ввод через интерфейс. Расширение: симуляция должна затем анимироваться для отображения радиуса, центра, диаметра и касательной круга, где радиус пересекает круг, когда пользователь взаимодействует с другими кнопками или интерфейсом в программе.
Программа должна автоматически обновляться, когда пользователь изменяет или обновляет ввод через интерфейс. Расширение: симуляция должна затем анимироваться для отображения радиуса, центра, диаметра и касательной круга, где радиус пересекает круг, когда пользователь взаимодействует с другими кнопками или интерфейсом в программе.
Программирование визуализации подобных треугольников
В этом упражнении учащиеся напишут программу, которая покажет, как треугольник расширяется через заданный центр и масштабный коэффициент.В программе учащиеся сначала построят неравносторонний треугольник, применив свойства треугольников, чтобы гарантировать, что с учетом набора из трех длин сторон и трех угловых размеров полученный многоугольник будет образовывать треугольник. Затем, используя заданные пользователем значения для центра растяжения и масштабного коэффициента через запрограммированную подсказку, программа должна сгенерировать преобразованный треугольник. Наконец, программа должна включать проверку, которая включает определение подобия, чтобы убедиться, что два треугольника подобны.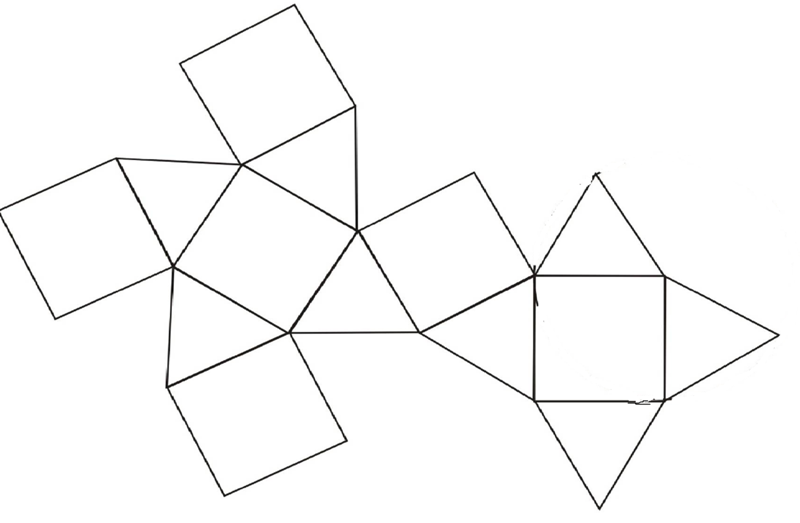
3-5 Объемные текстуры — 3D геометрическое моделирование
Последняя тема этой недели — объемные текстуры. Предлагаемая здесь работа — это объемные иллюстрации, проектирование 3D-модели с внутренними текстурами. Итак, мотивация здесь. Таким образом, мы можем видеть тщательно разработанную трехмерную иллюстрацию, показывающую сложные внутренние структуры. И такие виды иллюстраций очень сложно создать, и кроме того, особенно сложно сделать возможным интерактивное рисование такого рода иллюстраций, когда вы вырезаете объект, так что это цель.Итак, цель состоит в том, чтобы создать «вырезанные» 3D-модели. У вас есть трехмерная геометрия, и всякий раз, когда вы режете, вы получаете красивое поперечное сечение, это наша цель. И проблема в том, что это сделать очень сложно. Традиционные, стандартные 3D-модели — это просто модели поверхности, внутри ничего нет, если вырезать, то пусто. Если вам нужна внутренняя структура, вам, вероятно, понадобится объемная информация.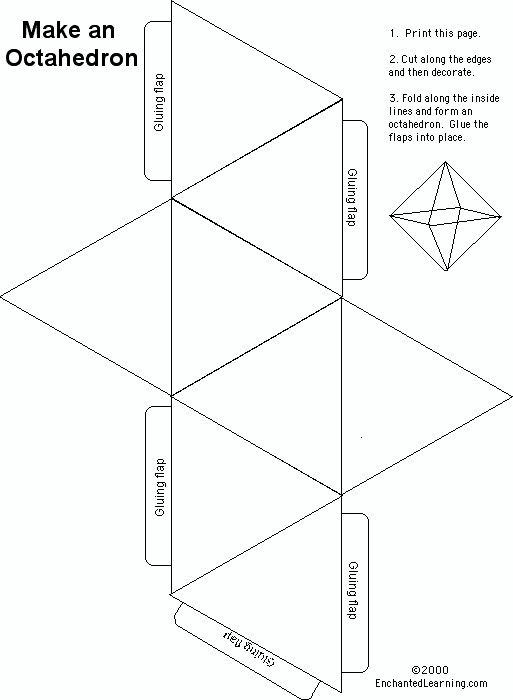 Однако объемную информацию очень сложно создать. По сути, вы должны раскрасить отдельные ячейки бокса в пространстве x, y, z один за другим.указание цветов. Это очень, слишком сложно. И вы также можете использовать компьютерные томографы или МРТ для сканирования, но они просто дают вам значения интенсивности, а красивые цвета не назначаются, и это проблема, которую мы решаем, и основная идея заключается в использовании техники синтеза текстур. Итак, как только пользователь вырезает модель, в настоящее время внутри ничего нет. Но на этапе моделирования пользователь-дизайнер определяет, какие элементы текстуры использовать для создания поперечного сечения. Использование этой информации или системы подсказок в реальном времени позволяет синтезировать реалистичную текстуру.Итак, с точки зрения пользователей, похоже, что внутри есть существующая текстура. Это идея. Разрешите показать вам видео. [BLANK_AUDIO] Итак, вот обзор системы. Таким образом, вы предоставляете входное изображение, а затем, как только пользователь вырезает 3D-модель.
Однако объемную информацию очень сложно создать. По сути, вы должны раскрасить отдельные ячейки бокса в пространстве x, y, z один за другим.указание цветов. Это очень, слишком сложно. И вы также можете использовать компьютерные томографы или МРТ для сканирования, но они просто дают вам значения интенсивности, а красивые цвета не назначаются, и это проблема, которую мы решаем, и основная идея заключается в использовании техники синтеза текстур. Итак, как только пользователь вырезает модель, в настоящее время внутри ничего нет. Но на этапе моделирования пользователь-дизайнер определяет, какие элементы текстуры использовать для создания поперечного сечения. Использование этой информации или системы подсказок в реальном времени позволяет синтезировать реалистичную текстуру.Итак, с точки зрения пользователей, похоже, что внутри есть существующая текстура. Это идея. Разрешите показать вам видео. [BLANK_AUDIO] Итак, вот обзор системы. Таким образом, вы предоставляете входное изображение, а затем, как только пользователь вырезает 3D-модель.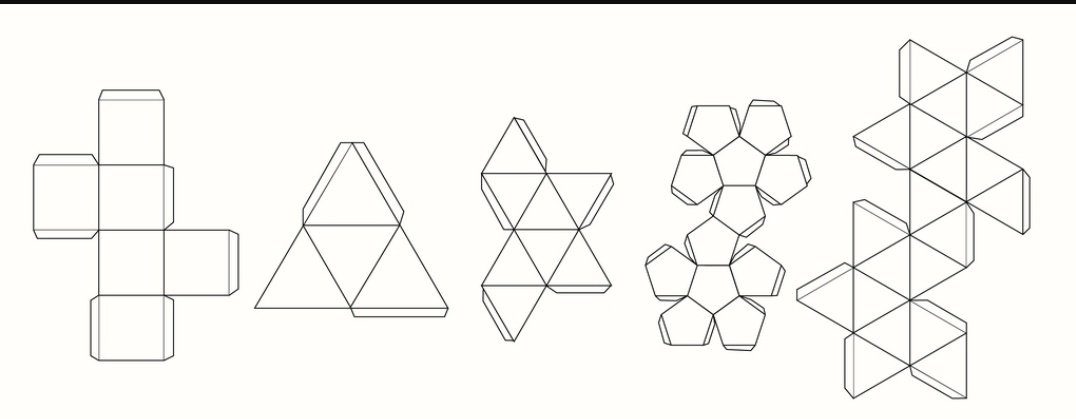 Изначально пусто. Но система автоматически синтезирует поперечное сечение, используя технику синтеза текстур. Итак, позвольте мне сначала показать вам пользовательский интерфейс для просмотра. Итак, вот входная трехмерная форма, пользователь вырезает форму, и система мгновенно синтезирует поперечное сечение, и вы получаете этот результат.А если вырезать по-другому, получится другая текстура. Таким образом, с точки зрения пользователей, похоже, что он имеет трехмерные плотные текстуры. Но с системной точки зрения это просто рисует поперечные сечения. Вот огурец, если его разрезать, везде поперечное сечение. Итак, это был интерфейс просмотра, а теперь мы показываем интерфейс моделирования. Итак, моделирование начинается с данной трехмерной модели поверхности, внутри ничего нет, только поверхность. И мы научим, как синтезировать внутреннюю текстуру в системе, чтобы пользователь сначала вырезал, пример поперечного сечения, а потом уже ничего внутри.Затем пользователь указывает, какой тип текстуры вы будете использовать: изотопную, ориентационную, слоистую или ориентированную.
Изначально пусто. Но система автоматически синтезирует поперечное сечение, используя технику синтеза текстур. Итак, позвольте мне сначала показать вам пользовательский интерфейс для просмотра. Итак, вот входная трехмерная форма, пользователь вырезает форму, и система мгновенно синтезирует поперечное сечение, и вы получаете этот результат.А если вырезать по-другому, получится другая текстура. Таким образом, с точки зрения пользователей, похоже, что он имеет трехмерные плотные текстуры. Но с системной точки зрения это просто рисует поперечные сечения. Вот огурец, если его разрезать, везде поперечное сечение. Итак, это был интерфейс просмотра, а теперь мы показываем интерфейс моделирования. Итак, моделирование начинается с данной трехмерной модели поверхности, внутри ничего нет, только поверхность. И мы научим, как синтезировать внутреннюю текстуру в системе, чтобы пользователь сначала вырезал, пример поперечного сечения, а потом уже ничего внутри.Затем пользователь указывает, какой тип текстуры вы будете использовать: изотопную, ориентационную, слоистую или ориентированную. Затем, если пользователь выбирает многослойную текстуру, система просит пользователя указать образцы текстур. Скажите «Перетащите изображение» сюда, и пользователь перетащит фотографию мяса. И пользователь учит, какую часть изображения использовать. Это снаружи, это внутри, и вы получите это. Кроме того, пользователь указывает, есть ли эталонный 3D-объем внутри и снаружи. И вы учите, какая часть 3D-модели находится внутри или снаружи.С этими соответствиями теперь система получает достаточно информации, а затем синтезирует изображение, так что это ваше моделирование. А затем, учитывая эту информацию, теперь мы можем использовать наш разрез в разных местах, система синтезирует соответствующую текстуру. [BLANK_AUDIO] В этой системе мы поддерживали три типа, три типа. Итак, первый изотропный, так что есть ориентация. Итак, самый простой, например, сосиски или бисквит, картофель и другие. Вы просто выбираете тип, а затем перетаскиваете отдельную текстуру, без ориентации.И затем система автоматически запускается, вот так.
Затем, если пользователь выбирает многослойную текстуру, система просит пользователя указать образцы текстур. Скажите «Перетащите изображение» сюда, и пользователь перетащит фотографию мяса. И пользователь учит, какую часть изображения использовать. Это снаружи, это внутри, и вы получите это. Кроме того, пользователь указывает, есть ли эталонный 3D-объем внутри и снаружи. И вы учите, какая часть 3D-модели находится внутри или снаружи.С этими соответствиями теперь система получает достаточно информации, а затем синтезирует изображение, так что это ваше моделирование. А затем, учитывая эту информацию, теперь мы можем использовать наш разрез в разных местах, система синтезирует соответствующую текстуру. [BLANK_AUDIO] В этой системе мы поддерживали три типа, три типа. Итак, первый изотропный, так что есть ориентация. Итак, самый простой, например, сосиски или бисквит, картофель и другие. Вы просто выбираете тип, а затем перетаскиваете отдельную текстуру, без ориентации.И затем система автоматически запускается, вот так.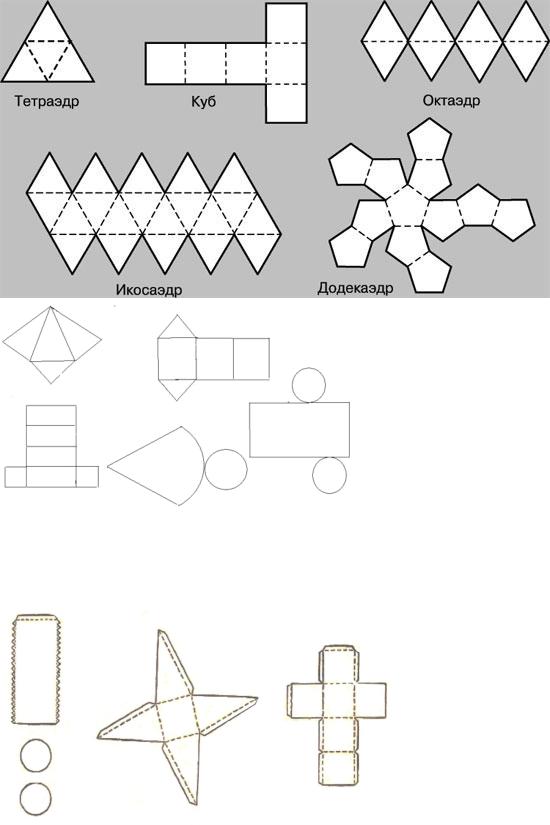 Второй — слоистая структура, например, морковь, или лепешки, и другие. И это тоже слоистая структура. А вот выберите текстуру слоя, а затем получите изображение. Как я уже сказал, как мы уже видели, пользователь указывает внутри или снаружи. Или сверху и снизу, и вам также нужно указать то же самое для 3D-геометрии. Верх и низ. И теперь мы знаем соответствие между эталонным изображением и трехмерной геометрией, и затем система начинает синтезировать текстуру нашего шоколадного торта.То же самое для моркови, пользователь указывает внутри, снаружи и внутри, снаружи для трехмерной формы. А затем система синтезирует форму, текстуру. Последний — это ориентированная текстура, как у этой формы бамбука. Волокна бамбука имеют определенную ориентацию. Поэтому в этом случае пользователю необходимо указать ориентацию волокон. Таким образом, пользовательский ввод — это двухмерная текстура горизонтального разреза, затем вы получаете трехмерную объемную ссылку, а затем пользователь указывает ориентацию.
Второй — слоистая структура, например, морковь, или лепешки, и другие. И это тоже слоистая структура. А вот выберите текстуру слоя, а затем получите изображение. Как я уже сказал, как мы уже видели, пользователь указывает внутри или снаружи. Или сверху и снизу, и вам также нужно указать то же самое для 3D-геометрии. Верх и низ. И теперь мы знаем соответствие между эталонным изображением и трехмерной геометрией, и затем система начинает синтезировать текстуру нашего шоколадного торта.То же самое для моркови, пользователь указывает внутри, снаружи и внутри, снаружи для трехмерной формы. А затем система синтезирует форму, текстуру. Последний — это ориентированная текстура, как у этой формы бамбука. Волокна бамбука имеют определенную ориентацию. Поэтому в этом случае пользователю необходимо указать ориентацию волокон. Таким образом, пользовательский ввод — это двухмерная текстура горизонтального разреза, затем вы получаете трехмерную объемную ссылку, а затем пользователь указывает ориентацию. Итак, здесь пользователь рисует здесь линии, а затем здесь автоматически создается ориентация, и система синтезирует текстуру по этой ориентации.[BLANK_AUDIO] Так что это немного сложно увидеть в этой презентации, но я надеюсь, вы видите, горизонтальные длинные линии здесь и много точек здесь и так далее. А вот пример моделирования, так что у вас есть трехмерная модель зуба. Вначале внутри ничего нет, потом вы берете фотографию, иллюстрацию, затем кладете, задаете взаимосвязи, и тогда вы получаете объемную фактуру для зуба. Вот и все. А вот пара результатов, например, огурец, пончик, бамбук или зуб.И, как я уже сказал, на этапе моделирования пользователь указывает, как вставить изображение в 3D-модель в поперечном сечении, указав снаружи, внутри и так далее. И алгоритм такой. Итак, для эталонного изображения пользователь указывает внутреннюю и внешнюю стороны, а затем вы вычисляете контрольную карту, своего рода распределение расстояния изнутри. И тогда вы также получите такую же контрольную карту для поперечного сечения.
Итак, здесь пользователь рисует здесь линии, а затем здесь автоматически создается ориентация, и система синтезирует текстуру по этой ориентации.[BLANK_AUDIO] Так что это немного сложно увидеть в этой презентации, но я надеюсь, вы видите, горизонтальные длинные линии здесь и много точек здесь и так далее. А вот пример моделирования, так что у вас есть трехмерная модель зуба. Вначале внутри ничего нет, потом вы берете фотографию, иллюстрацию, затем кладете, задаете взаимосвязи, и тогда вы получаете объемную фактуру для зуба. Вот и все. А вот пара результатов, например, огурец, пончик, бамбук или зуб.И, как я уже сказал, на этапе моделирования пользователь указывает, как вставить изображение в 3D-модель в поперечном сечении, указав снаружи, внутри и так далее. И алгоритм такой. Итак, для эталонного изображения пользователь указывает внутреннюю и внешнюю стороны, а затем вы вычисляете контрольную карту, своего рода распределение расстояния изнутри. И тогда вы также получите такую же контрольную карту для поперечного сечения. из информации или обозначений, данных трехмерной форме. А затем, учитывая эти две информации, система генерирует синтезированное сечение, используя алгоритм синтеза текстур.И позвольте мне вкратце описать алгоритм синтеза текстур. Синтез текстур — очень популярный метод в компьютерной графике. И он генерирует более крупную текстуру из входной меньшей текстуры. Оригинальная статья была опубликована в 99 году, и основная идея очень и очень проста. Итак, чтобы синтезировать новую текстуру из каждого отдельного пикселя, вы просто ищите аналогичный контекстный пиксель в ссылке. И если вы найдете наиболее похожий, просто выберите цвет или пиксель более похожий на текущий кадр.Итак, просто повторяя это много раз, начиная со случайного поля, вы получаете очень и очень реалистичную текстуру. И этот прием очень часто используется и в последнее время уже используется в коммерческих продуктах. Так что да, оригинальная статья была опубликована в 2004 году под названием «Объемные иллюстрации и синтез текстур», много статей, но оригинальной бумагой был «Синтез текстур» в ICCV, ’99.
из информации или обозначений, данных трехмерной форме. А затем, учитывая эти две информации, система генерирует синтезированное сечение, используя алгоритм синтеза текстур.И позвольте мне вкратце описать алгоритм синтеза текстур. Синтез текстур — очень популярный метод в компьютерной графике. И он генерирует более крупную текстуру из входной меньшей текстуры. Оригинальная статья была опубликована в 99 году, и основная идея очень и очень проста. Итак, чтобы синтезировать новую текстуру из каждого отдельного пикселя, вы просто ищите аналогичный контекстный пиксель в ссылке. И если вы найдете наиболее похожий, просто выберите цвет или пиксель более похожий на текущий кадр.Итак, просто повторяя это много раз, начиная со случайного поля, вы получаете очень и очень реалистичную текстуру. И этот прием очень часто используется и в последнее время уже используется в коммерческих продуктах. Так что да, оригинальная статья была опубликована в 2004 году под названием «Объемные иллюстрации и синтез текстур», много статей, но оригинальной бумагой был «Синтез текстур» в ICCV, ’99. И если вы хотите теперь недавние, то самым известным является PatchMatch. Опубликовано в 2009 году, и в настоящее время используется в Photoshop и других приложениях.И есть еще пара новейших методов синтеза трехмерных текстур, таких как синтез твердых текстур. А также многослойные сплошные текстуры, так что они могут быть
Вам интересно. Спасибо. Итак, это конец 3D-моделирования. Мы представили привлекательный интерфейс, моделирование на основе эскизов, управление формой с помощью кривых и объемные текстуры и позволили мне вернуться к первоначальному обсуждению. Таким образом, проблема в 3D-моделировании состоит в том, как дополнить недостающую информацию, в основном значения глубины или z. Подход заключается в разработке пользовательского интерфейса и алгоритма автоматического вывода, использующего знания конкретной предметной области.Итак, в примерах, которые мы показываем сегодня, вы знаете, что для моделирования архитектуры мы использовали жестко запрограммированные правила проектирования для архитектурных моделей.
И если вы хотите теперь недавние, то самым известным является PatchMatch. Опубликовано в 2009 году, и в настоящее время используется в Photoshop и других приложениях.И есть еще пара новейших методов синтеза трехмерных текстур, таких как синтез твердых текстур. А также многослойные сплошные текстуры, так что они могут быть
Вам интересно. Спасибо. Итак, это конец 3D-моделирования. Мы представили привлекательный интерфейс, моделирование на основе эскизов, управление формой с помощью кривых и объемные текстуры и позволили мне вернуться к первоначальному обсуждению. Таким образом, проблема в 3D-моделировании состоит в том, как дополнить недостающую информацию, в основном значения глубины или z. Подход заключается в разработке пользовательского интерфейса и алгоритма автоматического вывода, использующего знания конкретной предметной области.Итак, в примерах, которые мы показываем сегодня, вы знаете, что для моделирования архитектуры мы использовали жестко запрограммированные правила проектирования для архитектурных моделей.