Фигура – это произвольное множество точек на плоскости. Точка, прямая, отрезок, луч, треугольник, круг, квадрат и так далее – всё это примеры геометрических фигур.
Точка – основное понятие геометрии, это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса.
Линия – это множество точек, последовательно расположенных друг за другом. У линии измеряют только длину. Ширины и толщины она не имеет.
Прямая линия – это линия, которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороны.
Луч – это часть прямой линии, которая имеет начало, но не имеет конца, её можно бесконечно продолжать только в одну сторону.
Отрезок – это часть прямой линии, ограниченная двумя точками. Отрезок имеет начало и конец, поэтому можно измерить его длину.
Кривая линия – это плавно изгибающаяся линия, которая определяется расположением составляющих её точек.
Ломаная линия – это фигура, которая состоит из отрезков, последовательно соединенных своими концами.
Вершины ломаной – это
Звенья ломаной – это отрезки, из которых состоит ломаная. Количество звеньев ломаной всегда на 1 меньше, чем количество вершин ломаной.
Незамкнутая линия – это линия, концы которой не соединены вместе.
Замкнутая линия – это линия, концы которой соединены вместе.
Многоугольник – это замкнутая ломанная линия. Вершины ломаной называются вершинами многоугольника, а отрезки — сторонами многоугольника.
Цели урока :
Планируемые результаты:
личностные:
метапредметные:
предметные:
УУД общенаучные :
УУД личностные :
Оборудование : учебник, интерактивная доска, смайлики, модели фигур, развёртки фигур, светофоры индивидуальные, прямоугольники -средства обратной связи, Толковый словарь.
Тип урока : изучение нового материала.
Методы : словесные, исследовательские, наглядные, практические.
Формы работы : фронтальная, групповая, парная, индивидуальная.
1. Организация начала урока.
Утром солнышко взошло.
Новый день нам принесло.
Сильными и добрыми
Новый день встречаем мы.
Вот мои руки, я раскрываю
Их навстречу солнцу.
Вот мои ноги, они твердо
Стоят на земле и ведутМеня верной дорогой.
Вот моя душа, я раскрываю
Её навстречу людям.
Наступи, новый день!
Здравствуй, новый день!
2. Актуализация знаний.
Создадим хорошее настроение. Улыбнитесь мне и друг другу, садитесь!
Чтобы дойти до цели, надо прежде всего идти.
Перед вами высказывание, прочитайте. Что означает это высказывание?
(Чтобы чего-то добиться, нужно что-то делать)
И действительно, ребята, попадающим в цель может стать только тот, кто настраивает себя на собранность и организованность своих действий. И вот я надеюсь, что мы с вами на уроке достигнем своей цели.
Начнем наш путь к достижению цели сегодняшнего урока.
3. Подготовительная работа.
Посмотрите на экран. Что вы видите? (Геометрические фигуры)
Назовите эти фигуры.
Какое задание, вы можете предложить своим одноклассникам? (разделите фигуры на группы)
У вас на партах лежат карточки с этими фигурами. Выполните это задание в парах.
По какому признаку вы разделили эти фигуры?
С какими фигурами мы уже работали? Что учились находить у них? Какие фигуры встречаются нам на геометрии впервые?
Какая же тема нашего урока? (Учитель добавляет слова на доске: объёмные, на доске появляется тема урока: Объёмные геометрические фигуры.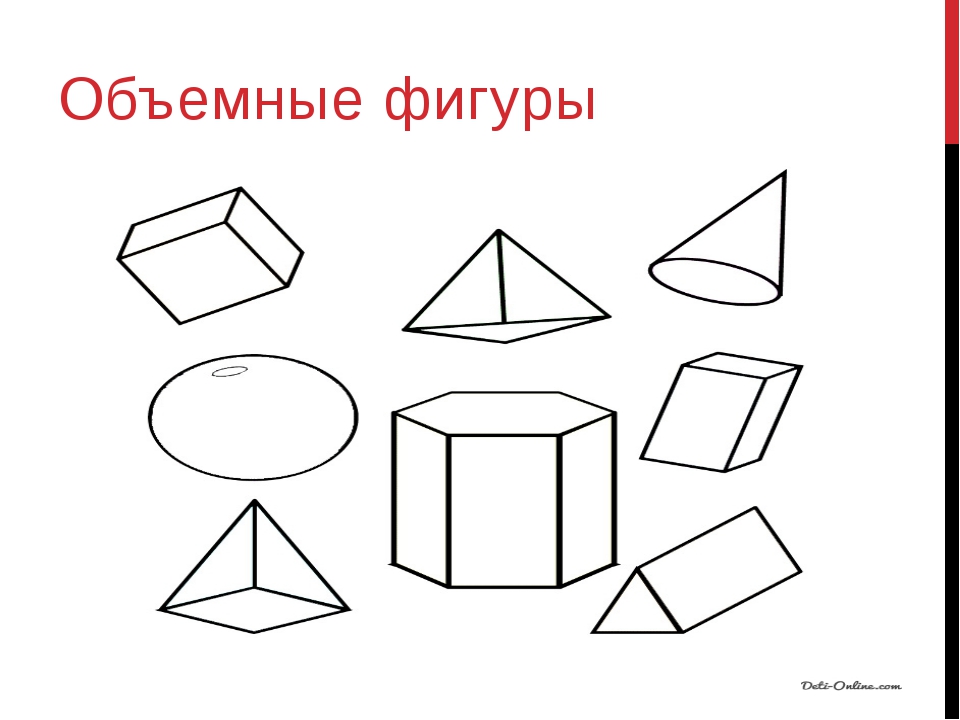
)
Чему мы должны научиться на уроке?
4. «Открытие» нового знания в практической исследовательской работе.
(Учитель показывает куб и квадрат.)
Чем они похожи?
Можно ли сказать, что это одно и тоже?
Чем же отличается куб от квадрата?
Давайте проведём опыт. (Ученики получают индивидуальные фигуры – куб и квадрат.)
Попробуем приложить квадрат к плоской поверхности порты. Что видим? Он весь (целиком) лёг на поверхность парты? Вплотную?
! Как назовём фигуру, которую можно целиком расположить на одной плоской поверхности? (Плоской фигурой.)
Можно ли куб полностью (весь) прижать к парте? Проверим.
Можно ли назвать куб плоской фигурой? Почему? Есть ли пространство между рукой и партой?
! Значит, что мы можем сказать о кубе? (Занимает определённое пространство, является объёмной фигурой.)
ВЫВОДЫ: Чем же отличаются плоские и объёмные фигуры? (Учитель вывешивает на доске выводы.)
ОБЪЁМНЫЕ
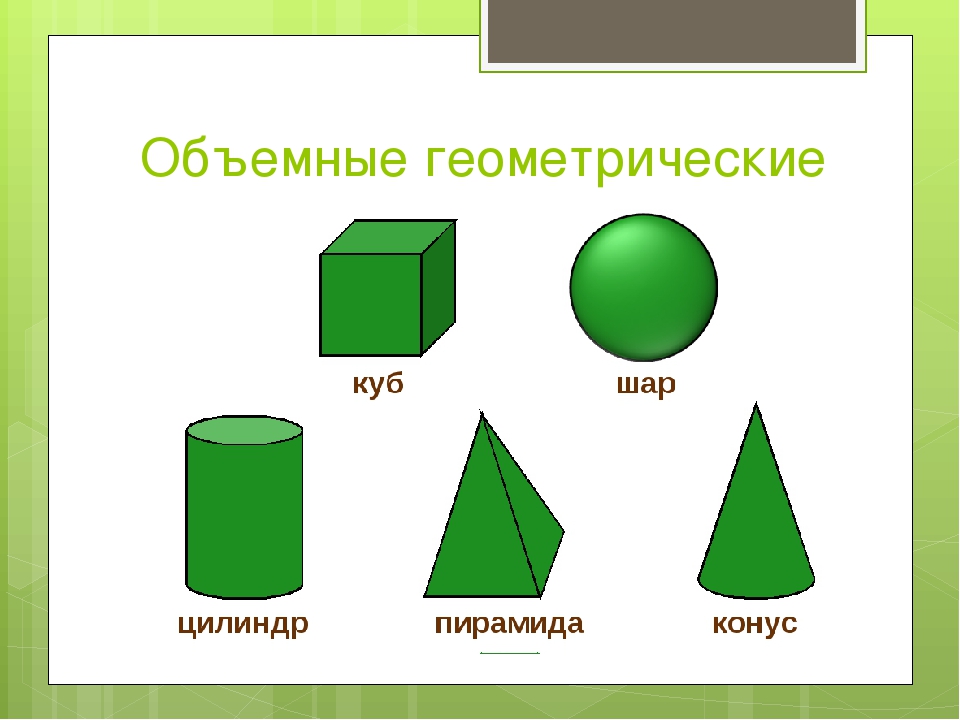
Объёмные фигуры: пирамида, куб, цилиндр, конус, шар, параллелепипед.
4. Открытие новых знаний.
1. Назовите фигуры, изображенные на рисунке.
Какую форму имеют основания этих фигур?
Какие еще формы можно увидеть на поверхности куба и призмы?
2. Фигуры и линии на поверхности объемных фигур имеют свои названия.
Предложите свои названия.
Боковые стороны, образующие плоскую фигуру называются гранями. А боковые линии – рёбра. Углы многоугольников – вершины. Это элементы объемных фигур.
Ребята, а как вы думаете, как называются такие объемные фигуры, у которых много граней? Многогранники.
Работа с тетрадями: чтение нового материала
Соотнесение реальных объектов и объёмных тел.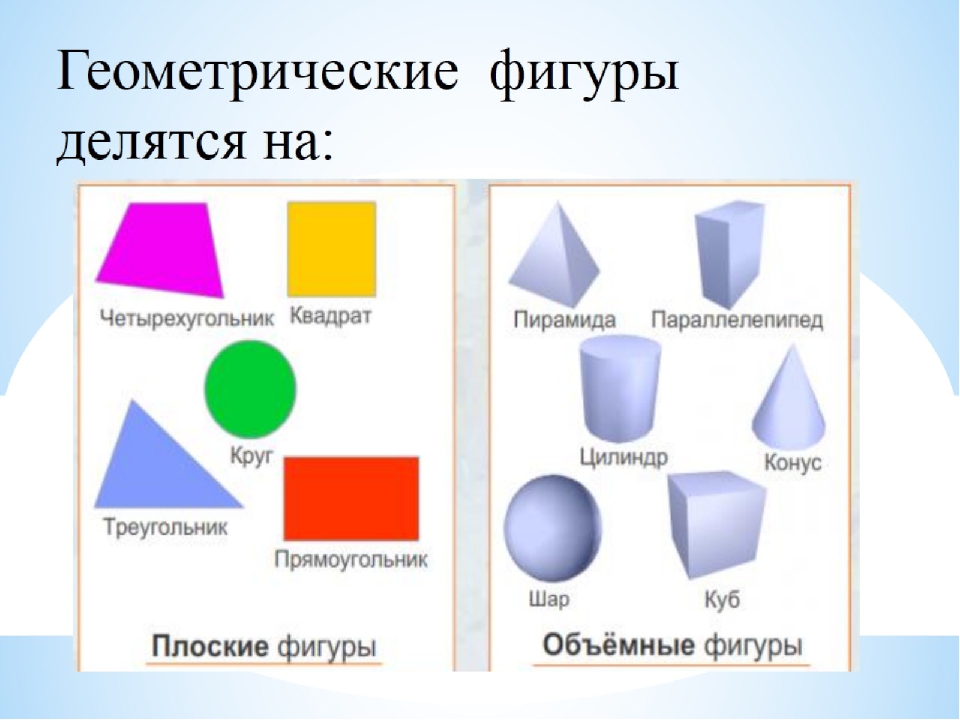
А теперь подберите для каждого предмета ту объёмную фигуру, на которую он похож.
Коробка – параллелепипед.
5. Физминутка.
1. Представьте себе большой шар, погладьте его со всех сторон. Он большой, гладкий.
(Ученики «обхватывают» руками и гладят воображаемый шар.)
А теперь представьте себе конус, дотроньтесь до его вершины. Конус растёт вверх, вот он уже выше вас. Допрыгните до его вершины.
Представьте, что вы внутри цилиндра, похлопайте по его верхнему основанию, потопайте по нижнему, а теперь руками по боковой поверхности.
Цилиндр стал маленькой подарочной коробочкой. Представьте, что вы сюрприз, который находится в этой коробочке. Я нажимаю кнопку и… сюрприз выскакивает из коробочки!
6. Групповая работа :
(Каждая группа получает одну из фигур: куб, пирамиду, параллелепипед.Полученную фигуру дети изучают, выводы записывают в подготовленную учителем карточку .)
Группа 1. (Для изучения параллелепипеда)
Группа 2. (Для изучения пирамиды)
Группа 3. (Для изучения куба)
7. Решение кроссворда
8. Итог урока. Рефлексия деятельности.
Решение кроссворда в презентации
Что нового вы для себя сегодня открыли?
Все геометрические фигуры можно разделить на объёмные и плоские.
А я узнал названия объёмных фигур
Геометрические фигуры
Геометрические фигуры – это совокупность множества точек, линий, поверхностей или тел, которые расположены на поверхности, плоскости или пространстве и формирует конечное количество линий.
Термин «фигура» в какой-то степени формально применяется к множеству точек, но как правило фигурой принято называть такие множества, которые расположенные на плоскости и ограничиваются конечным числом линий.
Точка и прямая — это основные геометрические фигуры, расположенные на плоскости.
К самым простым геометрическим фигурам на плоскости принадлежат — отрезок, луч и ломаная линия.
Геометрия – это такая математическая наука, которая занимается изучением свойств геометрических фигур. Если дословно перевести на русский язык термин «геометрия», то он обозначает «землемерие», так как в стародавние времена основной задачей геометрии, как науки, стало измерение расстояний и площадей на поверхности земли.
Практическое применение геометрии бесценно во все времена и независимо от профессии. Без знаний геометрии не может обойтись ни рабочий, ни инженер, ни архитектор и даже художник.
В геометрии есть такой раздел, который занимается изучением различных фигур на плоскости и называется планиметрия.
Вам уже известно, что фигурой называют произвольное множество точек, находящиеся на плоскости.
К геометрическим фигурам принадлежат: точка, прямая, отрезок, луч, треугольник, квадрат, круг и другие фигуры, которые изучает планиметрия.
Из выше изученного материала вам уже известно, что точка относится к главным геометрическим фигурам. И хотя это самая малая геометрическая фигура, но она необходима для построения других фигур на плоскости, чертеже или изображении и является основой для всех остальных построений. Ведь построение более сложноватых геометрических фигур складывается из множества точек, характерных для данной фигуры.
В геометрии точки обозначают прописными буквами латинского алфавита, например, такими, как: А, В, С, D ….
А теперь подведем итог, и так, с математической точки зрения, точка является таким абстрактным объектом в пространстве, который не имеет объема, площади, длины и других характеристик, но остается одним из фундаментальных понятий в математике.
Точка – это такой нульмерный объект, которые не имеет определения. По определению Евклида, точкой называют то, что невозможно определить.
Как и точка, прямая относится к фигурам на плоскости, которая не имеет определения, так как состоит из бесконечного множества точек, находящихся на одной линии, которая не имеет ни начала ни конца. Можно утверждать, что прямая линия бесконечна и не имеет предела.
Если же прямая начинается и заканчивается точкой, то она уже не является прямой и называется отрезком.
Но иногда прямая, с одной стороны имеет точку, а с другой нет. В таком случае прямая превращается в луч.
Если же взять прямую и на ее средине поставить точку, то она разобьет прямую на два противоположно направленных луча. Данные лучи являются дополнительными.
Если же перед вами несколько отрезков, соединенных между собой так, что конец первого отрезка становиться началом второго, а конец второго отрезка — началом третьего и т. д., и эти отрезки находятся не на одной прямой и при соединении имеют общую точку, то такая цепочка является ломаной линией.
Задание
Какая ломаная линия называется незамкнутой?
Как обозначается прямая?
Как называется ломаная линия, у которой четыре замкнутых звена?
Какое название имеет ломаная линия с тремя замкнутыми звеньями?
Когда конец последнего отрезка ломаной совпадает с началом 1-го отрезка, то такую ломаную линию называют замкнутой. Примером замкнутой ломаной является любой многоугольник.
Как точка и прямая, так и плоскость является первичным понятием, не имеет определения и у нее нельзя увидеть ни начала, ни конца. Поэтому, при рассмотрении плоскости, мы рассматриваем только ту ее часть, которая ограничивается замкнутой ломаной линией. Таким образом, плоскостью можно считать любую гладкую поверхность. Этой поверхностью может быть лист бумаги или стола.
Фигура, которая имеет два луча и вершину, называется углом. Место соединения лучей, является вершиной этого угла, а его сторонами считаются лучи, которые этот угол образуют.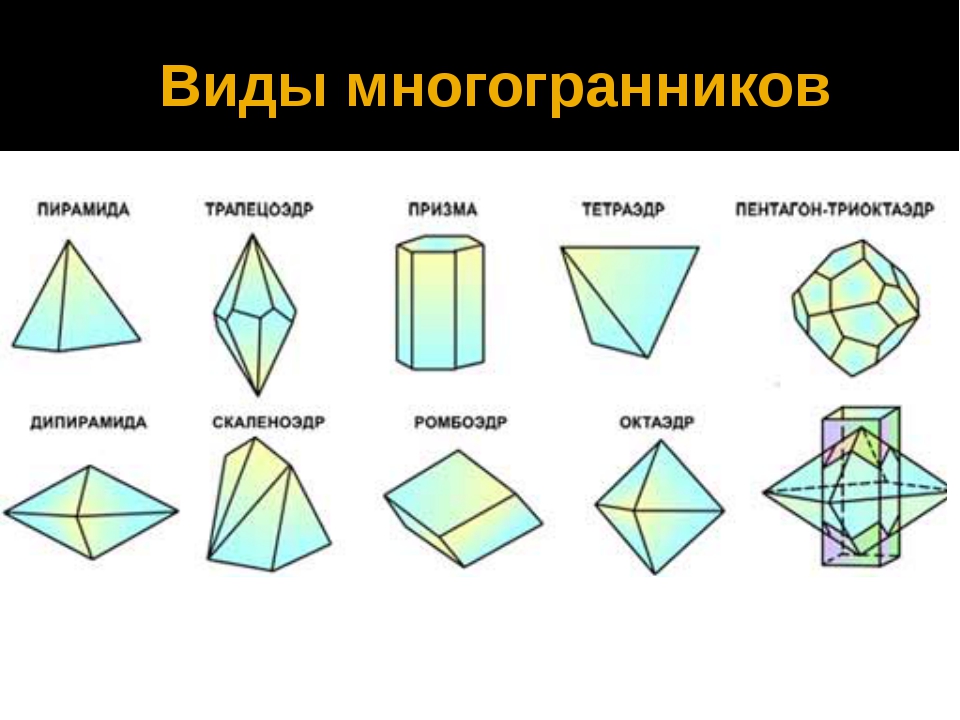
Задание:
1. Как в тексте обозначают угол?
2. Какими единицами можно измерить угол?
3. Какие бывают углы?
Параллелограмм — это четырехугольник, противолежащие стороны которого попарно параллельны.
Прямоугольник, квадрат и ромб являются частными случаями параллелограмма.
Параллелограмм, имеющий прямые углы равные 90 градусам, является прямоугольником.
Квадрат — это тот же параллелограмм, у него и углы и стороны равны.
Что до определения ромба, то это такая геометрическая фигура, все стороны которого равны.
Кроме того, следует знать, что любой квадрат является ромбом, но не каждый ромб может быть квадратом.
При рассмотрении такой геометрической фигуры, как трапеция, можно сказать, что в частности она, как и четырехугольник имеет одну пару параллельных противолежащих сторон и является криволинейной.
Окружность — геометрическое место точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное ненулевое расстояние, называемое её радиусом.
Также к простым геометрическим фигурам принадлежит и уже изучаемый вами треугольник. Это один из видов многоугольников, у которого часть плоскости ограничена тремя точками и тремя отрезками, которые соединяют эти точки попарно. Любой треугольник имеет три вершины и три стороны.
Задание: Какой треугольник называют вырожденным?
К многоугольникам относятся геометрические фигуры разных форм, у которых замкнутая ломаная линия.
В многоугольнике все точки, которые соединяют отрезки, являются его вершинами. А отрезки, из которых состоит многоугольник, являются его сторонами.
А известно ли вам, что возникновение геометрии уходит в глубину веков и связано с развитием различных ремесел, культуры, искусства и наблюдением за окружающим миром.
Да и название геометрических фигур является тому подтверждением, так как их термины, возникли не просто так, а благодаря своей схожести и подобию.
Ведь термин «трапеция» в переводе с древнегреческого языка от слова «трапезион» обозначает столик, трапеза и другие производные слова.
«Конус» произошел от греческого слова «конос», что в переводе звучит, как сосновая шишка.
«Линия» имеет латинские корни и происходит от слова «линум», в переводе это звучит, как льняная нить.
А знаете ли вы, что если взять геометрические фигуры с одинаковым периметром, то среди них обладателем самой большой площади оказался круг.
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
Геометрия — одна из важнейших компонент математического образования, необходимая для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, а также для эстетического воспитания. Изучение геометрии вносит вклад в развитие логического мышления, формирование навыков доказательства.
В курсе геометрии 7 класса систематизируются знания о простейших геометрических фигурах и их свойствах; вводится понятие равенства фигур; вырабатывается умение доказывать равенство треугольников с помощью изученных признаков; вводится класс задач на построение с помощью циркуля и линейки; вводится одно из важнейших понятий — понятие о параллельных прямых; рассматриваются новые интересные и важные свойства треугольников; рассматривается одна из важнейших теорем в геометрии — теорема о сумме углов треугольника, которая позволяет дать классификацию треугольников по углам (остроугольный, прямоугольный, тупоугольный).
На протяжении занятий, особенно при переходе от одной части занятия к другой, смене деятельности встает вопрос о поддержании интереса к занятиям.
Таким образом, актуальным становится вопрос о применении на занятиях по геометрии задач, в которых есть условие проблемной ситуации и элементы творчества . Таким образом, целью данного исследования является систематизация заданий геометрического содержания с элементами творчества и проблемных ситуаций.
Объект исследования : Задачи по геометрии с элементами творчества, занимательности и проблемных ситуаций.
Задачи исследования: Проанализировать существующие задачи по геометрии, направленные на развитие логики, воображения и творческого мышления. Показать, как занимательными приемами можно развить интерес к предмету.
Теоретическая и практическая значимость исследования состоит в том, что собранный материал может быть использован в процессе дополнительных занятий по геометрии, а именно на олимпиадах и конкурсах по геометрии.
Объем и структура исследования:
Исследование состоит из введения, двух глав, заключения, библиографического списка, содержит 14 страниц основного машинописного текста, 1 таблицу, 10 рисунков.
Глава 1. ПЛОСКИЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
1.1. Основные геометрические фигуры в архитектуре зданий и сооружений
В окружающем нас мире существует множество материальных предметов разных форм и размеров: жилые дома, детали машин, книги, украшения, игрушки и т. д.
В геометрии вместо слова предмет говорят геометрическая фигура, при этом разделяя геометрические фигуры на плоские и пространственные. В данной работе будет рассмотрен один из интереснейших разделов геометрии — планиметрия, в которой рассматриваются только плоские фигуры. Планиметрия (от лат. planum — «плоскость», др.-греч. μετρεω — «измеряю») — раздел евклидовой геометрии, изучающий двумерные (одноплоскостные) фигуры, то есть фигуры, которые можно расположить в пределах одной плоскости. Плоской геометрической фигурой называется такая, все точки которой лежат на одной плоскости.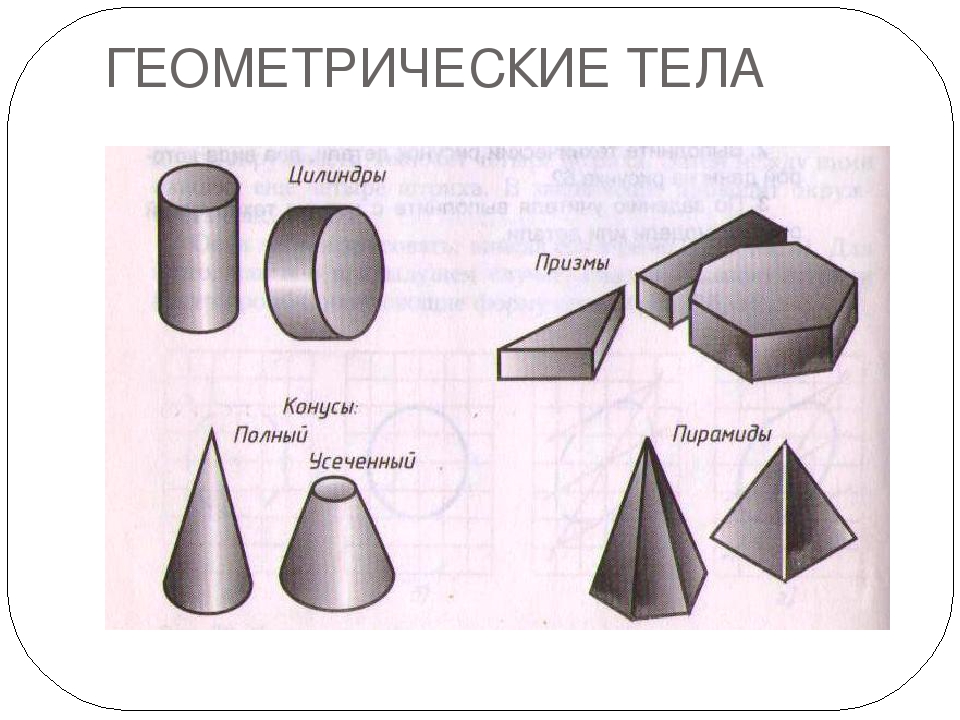
Представление о такой фигуре даёт любой рисунок, сделанный на листе бумаги.
Но прежде, чем рассматривать плоские фигуры, необходимо познакомиться с простыми, но очень важными фигурами, без которых плоские фигуры просто не могут существовать.
Самой простой геометрической фигурой является точка. Это одна из главных фигур геометрии. Она очень маленькая, но ее всегда используют для построения различных форм на плоскости. Точка — это основная фигура для абсолютно всех построений, даже самой высокой сложности. С точки зрения математики точка — это абстрактный пространственный объект, не обладающий такими характеристиками, как площадь, объем, но при этом остающийся фундаментальным понятием в геометрии.
Прямая — одно из фундаментальных понятий геометрии.При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии (евклидовой). Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить, как линию, путь вдоль которой равен расстоянию между двумя точками.
Прямые в пространстве могут занимать различные положения, рассмотрим некоторые из них и приведем примеры, встречающиеся в архитектурном облике зданий и сооружений (табл. 1):
Таблица 1
Параллельные прямые | Свойства параллельных прямых | |
Если прямые параллельны, то их одноименные проекции параллельны: | Ессентуки, здание грязелечебницы (фото автора) | |
Пересекающиеся прямые | Свойства пересекающихся прямых | Примеры в архитектуре зданий и сооружений |
Пересекающиеся прямые имеют общую точку, то есть точки пересечения их одноименных проекций лежат на общей линии связи: | Здания «горы» на Тайване https://www. | |
Скрещивающиеся прямые | Свойства скрещивающихся прямых | Примеры в архитектуре зданий и сооружений |
Прямые, не лежащие в одной плоскости и не параллельные между собой, являются скрещивающимися. Ноне является общей линией связи. Если пересекающиеся и параллельные прямые лежат в одной плоскости, то скрещивающиеся прямые лежат в двух параллельных плоскостях. | Робер, Гюбер — Вилла Мадама под Римом https://gallerix.ru/album/Hermitage-10/pic/glrx-172894287 |
1.2. Плоские геометрические фигуры. Свойства и определения
Наблюдая за формами растений и животных, гор и извилинами рек, за особенностями ландшафта и далекими планетами, человек заимствовал у природы ее правильные формы, размеры и свойства. Материальные потребности побуждали человека строить жилища, изготавливать орудия труда и охоты, лепить из глины посуду и прочее. Все это постепенно способствовало тому, что человек пришел к осознанию основных геометрических понятий.
Четырехугольники:
Параллелограмм (др.-греч. παραλληλόγραμμον от παράλληλος — параллельный и γραμμή — черта, линия) — это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых.
Признаки параллелограмма:
Четырёхугольник является параллелограммом, если выполняется одно из следующих условий: 1. Если в четырёхугольнике противоположные стороны попарно равны, то четырёхугольник — параллелограмм. 2. Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник — параллелограмм. 3. Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник — параллелограмм.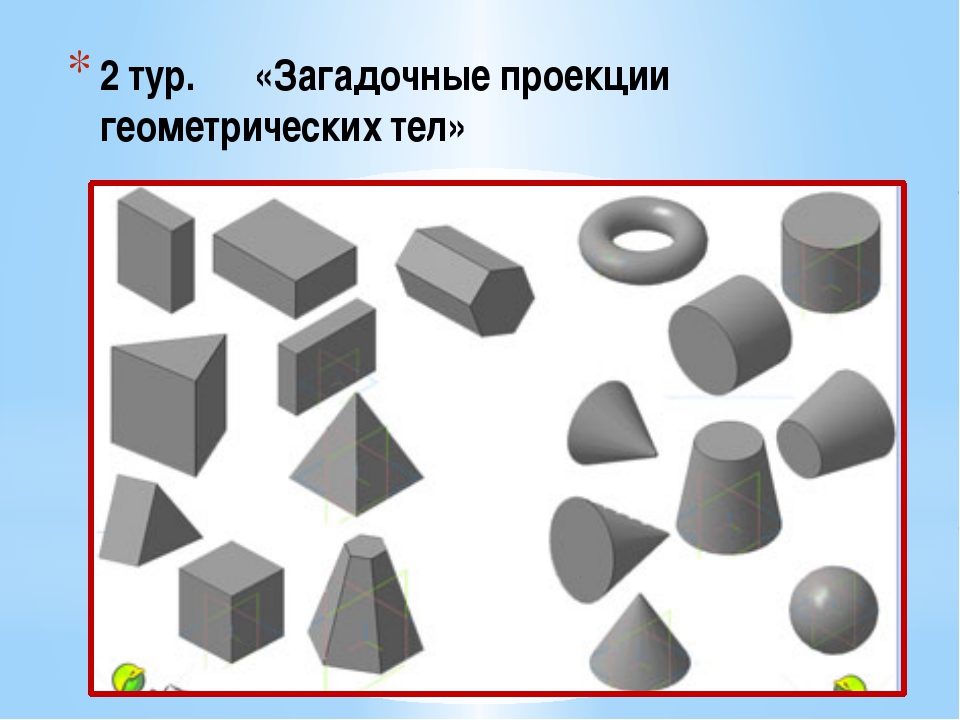
Параллелограмм, у которого все углы прямые, называется прямоугольником.
Параллелограмм, у которого все стороны равны, называется ромбом.
Трапеция— это четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.
Треугольник — это простейшая геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Указанные три точки называются вершинами треугольника , а отрезки — сторонами треугольника. Именно в силу своей простоты треугольник явился основой многих измерений. Землемеры при своих вычислениях площадей земельных участков и астрономы при нахождении расстояний до планет и звезд используют свойства треугольников. Так возникла наука тригонометрия — наука об измерении треугольников, о выражении сторон через его углы. Через площадь треугольника выражается площадь любого многоугольника: достаточно разбить этот многоугольник на треугольники, вычислить их площади и сложить результаты. Правда, верную формулу для площади треугольника удалось найти не сразу.
Особенно активно свойства треугольника исследовались в XV-XVI веках. Вот одна из красивейших теорем того времени, принадлежащая Леонарду Эйлеру:
Огромное количество работ по геометрии треугольника, проведенное в XY-XIX веках, создало впечатление, что о треугольнике уже известно все.
Многоуго́льник — это геометрическая фигура, обычно определяемая как замкнутая ломаная.
Круг — геометрическое место точек плоскости, расстояние от которых до заданной точки, называемой центром круга, не превышает заданного неотрицательного числа, называемого радиусом этого круга. Если радиус равен нулю, то круг вырождается в точку.
Существует большое количество геометрических фигур, все они отличаются параметрами и свойствами, порой удивляя своими формами.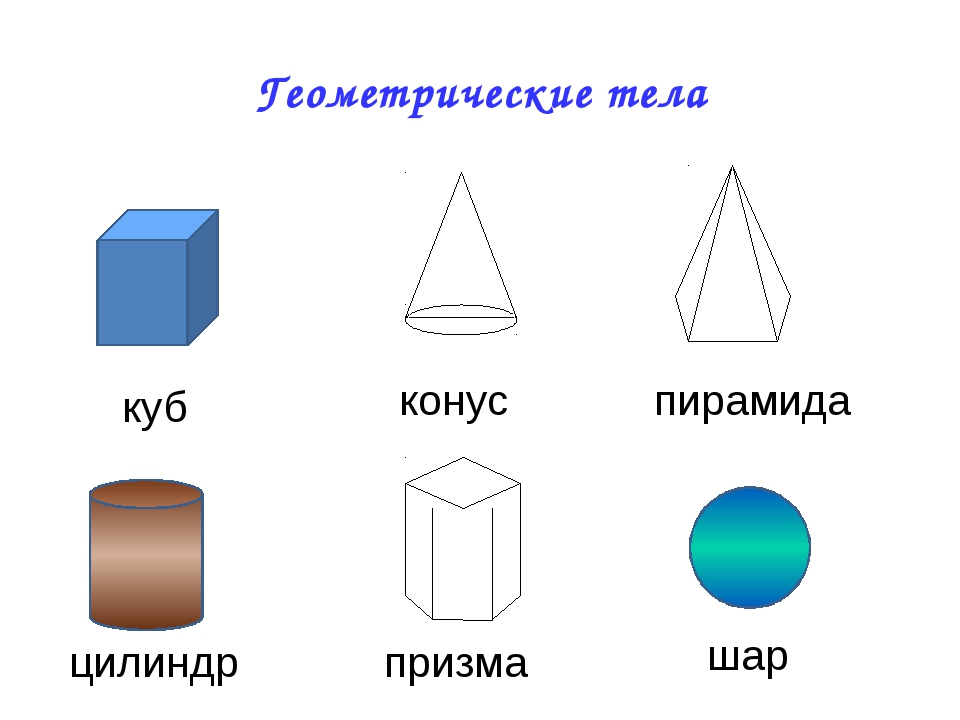
Чтобы лучше запомнить и отличать плоские фигуры по свойствам и признакам, я придумал геометрическую сказку, которую хотел бы представит вашему вниманию в следующем параграфе.
Глава 2. ЗАДАЧИ-ГОЛОВОЛОМКИ ИЗ ПЛОСКИХ ГЕОМЕТРИЧЕСКИХ ФИГУР
2.1.Головоломки на построение сложной фигуры из набора плоских геометрических элементов.
Изучив плоские фигуры, я задумался, а существуют какие-нибудь интересные задачи с плоскими фигурами, которые можно использовать в качестве заданий-игр или заданий-головоломок. И первой задачей, которую я нашел, была головоломка «Танграм».
Это китайская головоломка. В Китае ее называют «чи тао ту», т.е умственная головоломка из семи частей. В Европе название «Танграм» возникло, вероятнее всего, от слова «тань», что означает «китаец» и корня «грамма» (греч. — «буква»).
Для начала необходимо начертить квадрат 10 х10 и разделить его на семь частей: пять треугольников 1-5 , квадрат 6 и параллелограмм 7 . Суть головоломки состоит в том, чтобы, используя все семь частей, сложить фигурки, показанные на рис.3.
Рис.3. Элементы игры «Танграм» и геометрические фигуры
Рис.4. Задания «Танграм»
Особенно интересно составлять из плоских фигур «образные» многоугольники, зная лишь очертания предметов (рис.4). Несколько таких заданий-очертаний я придумал сам и показал эти задания своим одноклассникам, которые с удовольствием принялись разгадывать задания и составили много интересных фигур-многогранников, похожих на очертания предметов окружающего нас мира.
Для развития воображения можно использовать и такие формы занимательных головоломок, как задачи на разрезание и воспроизведение заданных фигур.
Пример 2. Задачи на разрезание (паркетирование) могут показаться, на первый взгляд, весьма многообразными. Однако в большинстве в них используется всего лишь несколько основных типов разрезаний (как правило, те, с помощью которых из одного параллелограмма можно получить другой).
Рассмотрим некоторые приёмы разрезаний. При этом разрезанные фигуры будем называть многоугольниками.
Рис. 5. Приёмы разрезаний
На рис.5 представлены геометрические фигуры, из которых можно собрать различные орнаментальные композиции и составить орнамент своими руками.
Пример 3. Еще одна интересная задача, которую можно самостоятельно придумать и обмениваться с другими учениками, при этом кто больше соберет разрезанные фигуры, тот объявляется победителем. Задач такого типа может быть достаточно много. Для кодирования можно взять все существующие геометрические фигуры, которые разрезаются на три или четыре части.
Рис.6.Примеры задач на разрезание:
—— — воссозданный квадрат; — разрез ножницами;
Основная фигура
2.2.Равновеликие и равносоставленные фигуры
Рассмотрим еще один интересный прием на разрезание плоских фигур, где основными «героями» разрезаний будут многоугольники. При вычислении площадей многоугольников используется простой прием, называемый методом разбиения.
Вообще многоугольники называются равносоставленными, если, определенным образом разрезав многоугольник F на конечное число частей, можно, располагая эти части иначе, составить из них многоугольник Н.
Отсюда вытекает следующая теорема: равносоставленные многоугольники имеют одинаковую площадь, поэтому они будут считаться равновеликими.
На примере равносоставленных многоугольников можно рассмотреть и такое интересное разрезание, как преобразование «греческого креста» в квадрат (рис.7).
Рис.7. Преобразование «греческого креста»
В случае мозаики (паркета), составленной из греческих крестов, параллелограмм периодов представляет собой квадрат. Мы можем решить задачу, накладывая мозаику, составленную из квадратов, на мозаику, образованную с помощью крестов, так, чтобы при этом конгруэнтные точки одной мозаики совпали с конгруэнтными точками другой (рис.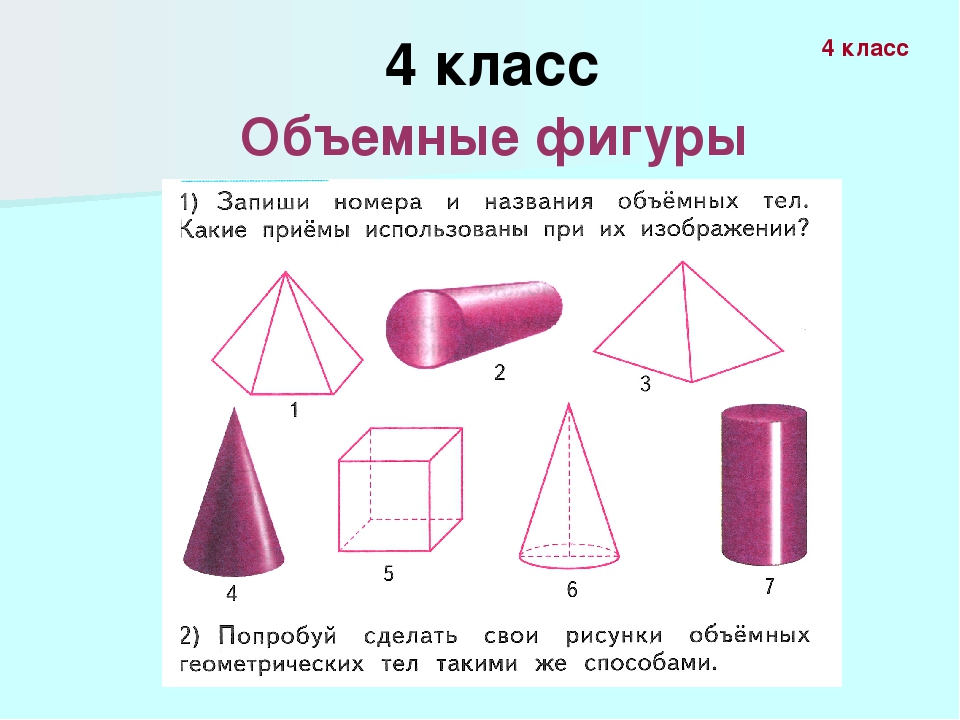
8).
На рисунке конгруэнтные точки мозаики из крестов, а именно центры крестов, совпадают с конгруэнтными точками «квадратной» мозаики — вершинами квадратов. Параллельно сдвинув квадратную мозаику, мы всегда получим решение задачи. Причем, задача имеет несколько вариантов решений, если при составлении орнамента паркета используется цвет.
Рис.8. Паркет, собранный из греческого креста
Еще один пример равносоставленных фигур можно рассмотреть на примере параллелограмма. Например, параллелограмм равносоставлен с прямоугольником (рис.9).
Этот пример иллюстрирует метод разбиения, состоящий в том, что для вычисления площади многоугольника пытаются разбить его на конечное число частей таким образом, чтобы из этих частей можно было составить более простой многоугольник, площадь которого нам уже известна.
Например, треугольник равносоставлен с параллелограммом, имеющим то же основание и вдвое меньшую высоту. Из этого положения легко выводится формула площади треугольника.
Отметим, что для приведенной выше теоремы справедлива и обратная теорема: если два многоугольника равновелики, то они равносоставлены.
Эту теорему, доказанную в первой половине XIX в. венгерским математиком Ф.Бойяи и немецким офицером и любителем математики П.Гервином, можно представить и в таком виде: если имеется торт в форме многоугольника и многоугольная коробка, совершенно другой формы, но той же площади, то можно так разрезать торт на конечное число кусков (не переворачивая их кремом вниз), что их удастся уложить в эту коробку.
Заключение
В заключении отмечу, что задач на плоские фигуры достаточно представлено в различных источниках, но интерес представили для меня те, на основании которых мне пришлось придумывать свои задачи-головоломки.
Ведь решая такие задачи, можно не просто накопить жизненный опыт, но и приобрести новые знания и умения.
В головоломках при построении действий-ходов используя повороты, сдвиги, переносы на плоскости или их композиции, у меня получились самостоятельно созданные новые образы, например, фигурки-многогранники из игры «Танграм».
Известно, что основным критерием подвижности мышления человека является способность путём воссоздающего и творческого воображения выполнить в установленный отрезок времени определенные действия, а в нашем случае — ходы фигур на плоскости. Поэтому изучение математики и, в частности, геометрии в школе даст мне еще больше знаний, чтобы в дальнейшем применить их в своей будущей профессиональной деятельности.
Библиографический список
1. Павлова, Л.В. Нетрадиционные подходы к обучению черчению: учебное пособие/ Л.В. Павлова. — Нижний Новгород: Изд-во НГТУ, 2002. — 73 с.
2. Энциклопедический словарь юного математика /Сост. А.П. Савин. — М.: Педагогика, 1985. — 352 с.
3.https://www.srops.ru/novosti_otrasli/2015_11_11_pervoe_zdanie_iz_grandioznogo_proekta_big_v_tayvane
4.https://www.votpusk.ru/country/dostoprim_info.asp?ID=16053
Приложение 1
Анкета-опросник для одноклассников
1. Знаете ли вы, что такое головоломка «Танграм»?
2. Что такое «греческий крест»?
3. Было бы вам интересно узнать, что такое «Танграм»?
4. Было бы вам интересно узнать, что такое «греческий крест»?
Было опрошено 22 ученика 8 класса. Результаты: 22 ученика не знают, что такое «Танграм» и «греческий крест». 20-ти ученикам было бы интересно узнать о том, как с помощью головоломки «Танграм», состоящая из семи плоских фигур, получить более сложную фигуру. Результаты опроса обобщены на диаграмме.
Приложение 2
Элементы игры «Танграм» и геометрические фигуры
Преобразование «греческого креста»
Существует бесконечное множество форм. Формой называют внешнее очертание предмета.
Изучение форм можно начинать с самого раннего детства, обращая внимание своего ребенка на окружающий нас мир, который состоит из фигур (тарелка – круглая, телевизор – прямоугольный).
Уже с двух лет малыш должен знать три простые фигуры – круг, квадрат, треугольник. Сначала он их должен просто показывать, когда вы это просите.
А в три года уже называть их самостоятельно и отличать круг от овала, квадрат от прямоугольника.
Чем больше упражнений на закрепление форм будет выполнено ребенком, тем больше новых фигур он запомнит.
Будущий первоклашка должен знать все простые геометрические фигуры и уметь составлять из них аппликации.
Геометрическая фигура — это эталон, с помощью которого можно определить форму предмета или его частей.
Фигуры разделяют на две группы: плоские фигуры, объемные фигуры.
Плоскими фигурами мы назовем те фигуры, которые расположены в одной плоскости. К ним относятся круг, овал, треугольник, четырёхугольник (прямоугольник, квадрат, трапеция, ромб, параллелограмм) и всевозможные многоугольники.
К объемным фигурам относят: сфера, куб, цилиндр, конус, пирамида. Это те фигуры, которые имеют высоту, ширину и глубину.
Следуйте двум простым советам при объяснении геометрических фигур:
Геометрические фигуры представляют собой комплекс точек, линий, тел или поверхностей. Эти элементы могут располагаться как на плоскости, так и в пространстве, формируя конечное количество прямых.
Термин «фигура» подразумевает под собой несколько множеств точек. Они должны располагаться на одной или нескольких плоскостях и одновременно ограничиваться конкретным числом оконченных линий.
Основными геометрическими фигурами считаются точка и прямая.
Они располагаются на плоскости. Кроме них, среди простых фигур выделяют луч, ломаную линию и отрезок.
Это одна из главных фигур геометрии. Она очень маленькая, но ее всегда используют для построения различных форм на плоскости. Точка — это основная фигура для абсолютно всех построений, даже самой высокой сложности. В геометрии ее принято обозначать буквой латинской алфавита, к примеру, A, B, K, L.
С точки зрения математики точка — это абстрактный пространственный объект, не обладающий такими характеристиками, как площадь, объем, но при этом остающийся фундаментальным понятием в геометрии. Этот нульмерный объект просто не имеет определения.
Это фигура полностью размещается в одной плоскости. У прямой нет конкретного математического определения, так как она состоит из огромного количества точек, располагающихся на одной бесконечной линии, у которой нет предела и границ.
Существует еще и отрезок. Это тоже прямая, но она начинается и заканчивается с точки, а значит, имеет геометрические ограничения.
Также линия может превратиться в направленный луч. Такое происходит, когда прямая начинается с точки, но четкого окончания не имеет. Если же поставить точку посредине линии, то она разобьется на два луча (дополнительных), причем противоположно направленных друг к другу.
Несколько отрезков, которые последовательно соединяются друг с другом концами в общей точке и располагаются не на одной прямой, принято называть ломаной линией.
Геометрические фигуры, названия которых мы рассмотрели выше, считают ключевыми элементами, использующимися при построении более сложных моделей.
Угол — это конструкция, состоящая из вершины и двух лучей, которые выходят из нее. То есть стороны этой фигуры соединяются в одной точке.
Рассмотрим еще одно первичное понятие. Плоскость — это фигура, у которой нет ни конца, ни начала, равно как и прямой, и точки. Во время рассмотрения этого геометрического элемента во внимание берется лишь его часть, ограниченная контурами ломаной замкнутой линии.
Любую гладкую ограниченную поверхность можно считать плоскостью. Это может быть гладильная доска, лист бумаги или даже дверь.
Параллелограмм — это геометрическая фигура, противоположные стороны которой параллельны друг другу попарно. Среди частных видов этой конструкции выделяют ромб, прямоугольник и квадрат.
Прямоугольник — это параллелограмм, у которого все стороны соприкасаются под прямым углом.
Квадрат — это четырехугольник с равными сторонами и углами.
Ромб — это фигура, у которой все грани равны. При этом углы могут быть совершенно разными, но попарно. Каждый квадрат считается ромбом. Но в противоположном направлении это правило действует не всегда. Далеко не каждый ромб является квадратом.
Геометрические фигуры бывают совершенно разными и причудливыми. Каждая из них имеет своеобразную форму и свойства.
Трапеция — это фигура, которая чем-то схожа с четырехугольником. Она имеет две параллельные противоположные стороны и при этом считается криволинейной.
Эта геометрическая фигура подразумевает расположение на одной плоскости точек, равноудаленных от ее центра. При этом заданный ненулевой отрезок принято называть радиусом.
Это простая геометрическая фигура, которая очень часто встречается и изучается.
Треугольник считается подвидом многоугольника, расположенным на одной плоскости и ограниченным тремя гранями и тремя точками соприкосновения. Эти элементы попарно соединены между собой.
Вершинами многоугольников называют точки, соединяющие отрезки. А последние, в свою очередь, принято считать сторонами.
Эти тела имеют нечто общее. Все они ограничиваются замкнутой поверхностью, внутри которой находится множество точек.
Объемные тела изучают не только в геометрии, но и в кристаллографии.
Наверняка вам будет интересно ознакомиться с информацией, предоставленной ниже.
Существует большое количество геометрических фигур. Все они отличаются параметрами, а порой даже удивляют формами.
Чукур Людмила Васильевна
Геометрические фигуры. Особенности восприятия детьми формы предметов и геометрических фигур
«ГЕОМЕТРИЧЕСКАЯ ФИГУРА .
ОСОБЕННОСТИ ВОСПРИЯТИЯ ДЕТЬМИ
Подготовила : ст. воспитатель Чукур Л . В.
1. Понятие «геометрическая фигура » . Особенности развития представлений о форме предметов у детей дошкольного возраста
Одним из свойств окружающих предметов является их форма . Форма предметов получила обобщенное отражение в геометрических фигурах .
Фигура — латинское слово , означает «образ» , «вид» , «начертание» ; это часть плоскости, ограниченная замкнутой линией, или часть пространства, ограниченная замкнутой поверхностью. Этот термин вошел в общее употребление в XII в. До этого чаще употреблялось другое латинское слово — «форма » , также означающее «наружный вид» , «внешнее очертание предмета » .
Наблюдая за предметами окружающего мира , люди заметили, что есть некоторое общее свойство, позволяющее объединить предметы в одну группу . Это свойство было названо геометрической фигурой . Геометрическая фигура – это эталон для определения формы предмета , всякое непустое множество точек; обобщенное абстрактное понятие.
Само определение понятия геометрической фигуры дали древние греки . Они определили , что геометрической фигурой является внутренняя область, ограниченная замкнутой линией на плоскости. Активно это понятие применял в своей работе Евклид. Древние греки классифицировали все геометрические фигуры и дали им названия .
Упоминание о первых геометрических фигурах встречается и у древних египтян и древних шумеров. Учеными-археологами был найден папирусный свиток с геометрическими задачами , в которых упоминались геометрические фигуры . И каждая из них называлась каким-то определенным словом .
Таким образом, представление о геометрии и изучаемых этой наукой фигурах имели люди с давних времен, но название, «геометрическая фигура » и названия всем геометрическим фигурам дали древнегреческие ученые.
В наше время знакомство с геометрическими фигурами начинается с раннего детства и продолжается на всём пути обучения. Дошкольники, познавая окружающий мир, сталкиваются с разнообразием форм предметов , учатся называть и различать их, а затем знакомятся и со свойствами геометрических фигур .
Форма – это внешнее очертание предмета . Множество форм бесконечно .
Представления о форме предметов возникают у детей достаточно рано. В исследованиях Л. А. Венгера выясняется, возможно ли различение формы предметов детьми , у которых еще не сформировался акт хватания . В качестве индикатора он использовал ориентировочную реакцию ребенка в возрасте 3-4 месяцев.
Детям предъявлялись два объемных тела одинакового стального цвета и размера (призма и шар, одно из них подвешивалась над манежем, чтобы угасить ориентировочную реакцию; затем снова подвешивалась пара фигур . На одну из них (призма) реакция угашена, другая (шар) — новая. Малыши обращали взор на новую фигуру и фиксировали ее взглядом в течение более длительного времени, чем старую.
Л. А. Венгер заметил также, что что на геометрической фигуре с изменением пространственной ориентации возникает такое же зрительное сосредоточение, как и на новой геометрической фигуре .
Исследования М. Денисовой и Н. Фигурина показали , что грудной ребенок по форме на ощупь определяет бутылочку , соску, материнскую грудь. Зрительно дети начинают различать форму предметов с 5 месяцев . При этом индикатором различения являются движения рук, корпуса по направлению к экспериментальному объекту и схватывание его (при пищевом подкреплении) .
В других исследованиях выявлено, что, если предметы отличаются цветом , то ребенок 3-х лет выделяет их форму только в том случае , если предмет знаком ребенку из практического опыта (опыт манипуляций, действий) .
Это доказывает и тот факт, что ребенок одинаково узнает прямые и перевернутые изображения (может рассматривать и понимать знакомые картинки, держа книжку «вверх ногами» , предметы , окрашенные в несвойственные цвета (черное яблоко, но квадрат, повернутый на угол, т. е. в виде ромба, не узнает, так как исчезает непосредственное сходство формы предмета , которого нет в опыте.
2. Особенности восприятия детьми дошкольного возраста формы предметов и геометрических фигур
Одним из ведущих познавательных процессов детей дошкольного возраста является восприятие . Восприятие помогает отличить один предмет от другого , выделить какие-то предметы или явления из других похожих на него.
Первичное овладение формой предмета Форма предмета , как таковая, не предмета предшествовать практическим действиям. Действия детей с предметами на разных этапах различны.
Исследования психолога С. Н. Шабалина показывают, что геометрическая фигура воспринимается дошкольниками своеобразно. Если взрослый воспринимает ведро или стакан как предметы , имеющие цилиндрическую форму , то в его восприятие включается знание геометрических форм . У дошкольника происходит обратное явление.
В 3-4 года дети опредмечивают геометрические фигуры , так как они в их опыте представлена нераздельно с предметами , не абстрагированы. Геометрическая фигура воспринимается детьми как картинка , как некоторый предмет : квадрат — это платочек, кармашек; треугольник — крыша, круг — колесо, мячик, два круга рядом — очки, несколько кругов рядом — бусы и т. п.
В 4 года опредмечивание геометрической фигуры возникает только при столкновении ребенка с незнакомой фигурой : цилиндр — это ведро, стаканчик.
В 4-5 лет ребенок начинает сравнивать геометрическую фигуру с предметом : про квадрат говорит «это как платочек» .
В результате организованного обучения дети начинают выделять в окружающих предметах знакомую геометрическую фигуру , сравнивать предмет с фигурой (стаканчик как цилиндр, крыша как треугольник, учится давать правильное название геометрической фигуры и формы предмета , в их речи появляются слова «квадрат» , «круг» , «квадратный» , «круглый» и т. п.
Проблему знакомства детей с геометрическими фигурами и их свойствами следует рассматривать в двух аспектах :
В плане сенсорного восприятия форм геометрических фигур и использования их как эталонов в познании форм окружающих предметов ;
В смысле познания особенностей их структуры , свойств, основных свя-зей и закономерностей в их построении, т.
е. собственно геометри-ческого материала .
Контур предмета это общее начало , которое является исходным как для зрительного, так и для осязательного восприятия . Однако вопрос о роли контура в восприятии формы и формировании целостного образа требует еще дальнейшей разработки.
Первичное овладение формой предмета осуществляется в действиях с ним. Форма предмета , как таковая, не воспринимается отдельно от предмета , она является его неотъемлемым признаком. Специфические зрительные реакции прослеживания контура предмета появляются в конце второго года жизни и начинают предшествовать практическим действиям.
Действия детей с предметами на разных этапах различны. Малыши стремятся, прежде всего, захватить предмет руками и начать манипулировать им. Дети 2,5 лет, прежде чем действовать, довольно подробно зрительно и осязательно — двигательно знакомятся с предметами . Значение практических действий остается главным. Отсюда следует вывод о необходимости руководить развитием перцептивных действий двухлетних детей. В зависимости от педагогического руководства характер перцептивных действий детей постепенно достигает познавательного уровня. Ребенка начинают интересовать различные признаки предмета , в том числе и форма . Однако он еще долго не может выделить и обобщить тот или иной признак, в том числе и форму разных предметов .
Сенсорное восприятие формы предмета должно быть направлено не только на то, чтобы видеть , узнавать формы , наряду с другими его признаками, но уметь, абстрагируя форму от вещи , видеть ее и в других вещах . Такому восприятию формы предметов и ее обобщению и способствует знание детьми эталонов — геометрических фигур . Поэтому задачей сенсорного развития является формирование у ребенка умений узнавать в соответствии с эталоном (той или иной геометрической фигурой ) форму разных предметов .
Экспериментальные данные Л. А. Венгера показали, что возможностью различать геометрические фигуры обладают дети 3-4 месяцев. Сосредоточение взгляда на новой фигуре — свидетельство этому.
Уже на втором году жизни дети свободно выбирают фигуру по образцу из таких пар : квадрат и полукруг, прямоугольник и треугольник. Но различать прямоугольник и квадрат, квадрат и треугольник дети могут лишь после 2,5 лет. Отбор же по образцу фигур более сложной формы доступен примерно на рубеже 4-5 лет, а воспроизведение сложной фигуры осуществляют дети пятого и шестого года жизни.
Под обучающим воздействием взрослых восприятие геометрических фигур постепенно перестраивается. Геометрические фигуры начинают восприниматься детьми как эталоны , с помощью которых познание структуры предмета , его формы и размера осуществляется не только в процессе восприятия той или иной формы зрением , но и путем активного осязания, ощупывания ее под контролем зрения и обозначения словом.
Совместная работа всех анализаторов способствует более точному восприятию формы предметов . Чтобы лучше познать предмет , дети стремятся коснуться его рукой, взять в руки, повернуть; причем рассматривание и ощупывание различны в зависимости от формы и конструкции познаваемого объекта. Поэтому основную роль в восприятии предмета и определении его формы имеет обследование , осуществляемое одновременно зрительным и двигательно-осязательным анализаторами с последующим обозначением словом. Однако у дошкольников наблюдается весьма низкий уровень обследования формы предметов ; чаще всего они ограничиваются беглым зрительным восприятием и поэтому не различают близкие по сходству фигуры (овал и круг, прямоугольник и квадрат, разные треугольники) .
В перцептивной деятельности детей осязательно-двигательные и зрительные приемы постепенно становятся основным способом рас-познавания формы .
Обследование фигур не только обеспечивает целостное их восприятие , но и позволяет ощутить их особенности (характер, направления линий и их сочетания, образующиеся углы и вершины, ребенок учится чувственно выделять в любой фигуре образ в целом и его части. Это дает возможность в дальнейшем сосредоточить внимание ребенка на осмысленном анализе фигуры , сознательно выделяя в ней структурные элементы (стороны, углы, вершины) . Дети уже осознанно начинают понимать и такие свойства, как устойчивость, неустойчивость и др., понимать, как образуются вершины, углы и т. д. Сопоставляя объемные и плоские фигуры , дети находят уже общность между ними («У куба есть квадраты» , «У бруса — прямоугольники, у цилиндра — круги» и т. д.).
Сравнение фигуры с формой того или иного предмета помогает детям понять, что с геометрическими фигурами можно сравнивать разные предметы или их части . Так, постепенно геометрическая фигура становится эталоном определения формы предметов .
3. Особенности обследования и этапы обучения обследованию детьми дошкольного возраста формы предметов и геометрических фигур
Известно, что в основе познания всегда лежит сенсорное обследование, опосредованное мышлением и речью. В исследованиях Л. Венгера с детьми 2-3 лет индикатором зрительного различения формы предметов служили предметные действия ребенка .
По исследованиям С. Якобсон, В. Зинченко, А. Рузской дети 2-4 лет лучше узнавали предметы по форме , когда предлагалось сначала ощупать предмет , а потом найти такой же. Более низкие результаты наблюдались тогда, когда предмет воспринимался зрительно .
Исследования Т. Гиневской раскрывают особенности движений рук при обследовании предметов по форме . Детям завязывали глаза и предлагали ознакомиться с предметом путем осязания .
В 3-4 года – движения исполнительные (катают, стучат, возят) .
Движения немногочисленны, внутри фигуры , иногда (однократно) по осевой линии, много ошибочных ответов, смешение разных фигур . В 4-5 лет – движения установочные (зажимают в руке) . Количество движений увеличивается в два раза; судя по траектории, ориентированы на размер и площадь; крупные, размашистые, обнаруживаются группы близко расположенных фиксаций, относящихся к наиболее характерным признакам фигуры ; дают более высокие результаты. В 5-6лет – движения обследовательские (прослеживание контура, проверка на упругость) . Появляются движения, прослеживающие контур, однако они охватывают наиболее характерную часть контура, другие части оказываются необследованными; движения внутри контура, количество то же, высокие результаты; как и в предыдущий период , наблюдается смешение близких фигур . В 6-7 лет – движения по контуру, пересечение поля фигуры , причем движения сосредотачиваются на наиболее информативных признаках , наблюдаются отличные результаты не только при узнавании, но и при воспроизведении .
Таким образом, для того, чтобы ребенок выделил существенные признаки геометрических фигур , необходимо их зрительное и двигательное обследование. Движения рук организовывают движения глаз и этому детей необходимо научить.
Этапы обучения обследованию
Задача первого этапа обучения детей 3-4 лет — это сенсорное восприятие формы предметов и геометрических фигур .
Второй этап обучения детей 5-6 лет должен быть посвящен формированию системных знаний о геометрических фигурах и развитию у них начальных приемов и способов «геометрического мышления » .
«Геометрическое мышление » вполне возможно развить еще в дошкольном возрасте. В развитии «геометрических знаний » у детей прослеживается несколько различных уровней.
Первый уровень характеризуется тем, что фигура воспринимается детьми как целое , ребенок еще не умеет выделять в ней отдельные элементы, не замечает сходства и различия между фигурами , каждую из них воспринимает обособленно .
На втором уровне ребенок уже выделяет элементы в фигуре и устанавливает отношения как между ними, так и между отдельными фигурами , однако еще не осознает общности между фигурами .
На третьем уровне ребенок в состоянии устанавливать связи между свойствами и структурой фигур , связи между самими свойствами. Переход от одного уровня к другому не является самопроизвольным, идущим параллельно биологическому развитию человека и зависящим от возраста. Он протекает под влиянием целенаправленного обучения, которое содействует ускорению перехода к более высокому уровню. Отсутствие же обучения тормозит развитие. Обучение поэтому следует организовывать так, чтобы в связи с усвоением знаний о геометрических фигурах у детей развивалось и элементарное геометрическое мышление .
Познание геометрических фигур , их свойств и отношений расширяет кругозор детей, позволяет им более точно и разносторонне воспринимать форму окружающих предметов , что положительно отражается на их продуктивной деятельности (например, рисовании, лепке) .
Большое значение в развитии геометрического мышления и про-странственных представлений имеют действия по преобразованию фигур (из двух треугольников составить квадрат или из пяти палочек сложить два треугольника).
Все эти разновидности упражнений развивают пространственные представления и начала геометрического мышления детей , формируют у них умения наблюдать, анализировать, обобщать, выделять главное, существенное и одновременно с этим воспитывают такие качества личности, как целенаправленность, настойчивость.
Итак, в дошкольном возрасте происходит овладение перцептивной и интеллектуальной систематизацией форм геометрических фигур . Перцептивная деятельность в познании фигур опережает развитие интеллектуальной систематизации.
Библиографический список
1. Белошистая А. В. Знакомство с геометрическими понятиями / А . Белошистая // Дошкольное воспитание . — 2008. — № 9. — с. 41- 51
2. Венгер Л. А. Воспитание сенсорной культуры ребенка / Л. А. Венгер Э. Г. Пилюгина, Н. Б. Венгер. — М. : Просвещение, 1988.- 144с.
3. Воспитание и обучение детей пятого года жизни : книга для воспитателя детского сада / (А. Н. Давидчук, Т. И. Осокина, Л. А. Парамонова и др.) ; под ред. В. В. Холмовской. — М. : Просвещение, 1986. — 144 с.
4. Габова М. А. Знакомство детей с геометрическими фигурами / М . А. Габова // Дошкольное воспитание . — 2002. — № 9. — с. 2- 17.
5. Дидактические игры и упражнения по сенсорному воспитанию дошкольников : (пособие для воспитателя детского сада / под ред. Л. А. Венгера). — М. : Просвещение, 1978. — 203 с.
6. Кербс Е. В. Математические досуги / Е. В. Кербс // Ребёнок в детском саду. — 2008. — № 3. — с. 21- 23.
7.Математика в детском саду : (пособие для воспитателя дет . сада / составитель Г. М. Лямина). — М. : Просвещение, 1977. — С. 224 — 228.
8. Метлина Л. С.Математика в детском саду : (пособие для воспитателя дет . сада) / Л. С. Метлина. — М. : Просвещение, 1994. — 256 с.
Геометрические фигуры представляют собой комплекс точек, линий, тел или поверхностей. Эти элементы могут располагаться как на плоскости, так и в пространстве, формируя конечное количество прямых.
Термин «фигура» подразумевает под собой несколько множеств точек. Они должны располагаться на одной или нескольких плоскостях и одновременно ограничиваться конкретным числом оконченных линий.
Основными геометрическими фигурами считаются точка и прямая. Они располагаются на плоскости. Кроме них, среди простых фигур выделяют луч, ломаную линию и отрезок.
Это одна из главных фигур геометрии. Она очень маленькая, но ее всегда используют для построения различных форм на плоскости. Точка — это основная фигура для абсолютно всех построений, даже самой высокой сложности. В геометрии ее принято обозначать буквой латинской алфавита, к примеру, A, B, K, L.
С точки зрения математики точка — это абстрактный пространственный объект, не обладающий такими характеристиками, как площадь, объем, но при этом остающийся фундаментальным понятием в геометрии. Этот нульмерный объект просто не имеет определения.
Это фигура полностью размещается в одной плоскости. У прямой нет конкретного математического определения, так как она состоит из огромного количества точек, располагающихся на одной бесконечной линии, у которой нет предела и границ.
Существует еще и отрезок. Это тоже прямая, но она начинается и заканчивается с точки, а значит, имеет геометрические ограничения.
Также линия может превратиться в направленный луч. Такое происходит, когда прямая начинается с точки, но четкого окончания не имеет. Если же поставить точку посредине линии, то она разобьется на два луча (дополнительных), причем противоположно направленных друг к другу.
Несколько отрезков, которые последовательно соединяются друг с другом концами в общей точке и располагаются не на одной прямой, принято называть ломаной линией.
Геометрические фигуры, названия которых мы рассмотрели выше, считают ключевыми элементами, использующимися при построении более сложных моделей.
Угол — это конструкция, состоящая из вершины и двух лучей, которые выходят из нее. То есть стороны этой фигуры соединяются в одной точке.
Рассмотрим еще одно первичное понятие. Плоскость — это фигура, у которой нет ни конца, ни начала, равно как и прямой, и точки. Во время рассмотрения этого геометрического элемента во внимание берется лишь его часть, ограниченная контурами ломаной замкнутой линии.
Любую гладкую ограниченную поверхность можно считать плоскостью. Это может быть гладильная доска, лист бумаги или даже дверь.
Параллелограмм — это геометрическая фигура, противоположные стороны которой параллельны друг другу попарно. Среди частных видов этой конструкции выделяют ромб, прямоугольник и квадрат.
Прямоугольник — это параллелограмм, у которого все стороны соприкасаются под прямым углом.
Квадрат — это четырехугольник с равными сторонами и углами.
Ромб — это фигура, у которой все грани равны. При этом углы могут быть совершенно разными, но попарно. Каждый квадрат считается ромбом. Но в противоположном направлении это правило действует не всегда. Далеко не каждый ромб является квадратом.
Геометрические фигуры бывают совершенно разными и причудливыми. Каждая из них имеет своеобразную форму и свойства.
Трапеция — это фигура, которая чем-то схожа с четырехугольником. Она имеет две параллельные противоположные стороны и при этом считается криволинейной.
Эта геометрическая фигура подразумевает расположение на одной плоскости точек, равноудаленных от ее центра. При этом заданный ненулевой отрезок принято называть радиусом.
Это простая геометрическая фигура, которая очень часто встречается и изучается.
Треугольник считается подвидом многоугольника, расположенным на одной плоскости и ограниченным тремя гранями и тремя точками соприкосновения. Эти элементы попарно соединены между собой.
Вершинами многоугольников называют точки, соединяющие отрезки. А последние, в свою очередь, принято считать сторонами.
Эти тела имеют нечто общее. Все они ограничиваются замкнутой поверхностью, внутри которой находится множество точек.
Объемные тела изучают не только в геометрии, но и в кристаллографии.
Наверняка вам будет интересно ознакомиться с информацией, предоставленной ниже.
Существует большое количество геометрических фигур. Все они отличаются параметрами, а порой даже удивляют формами.
Маленькие детки готовы учиться везде и всегда. Их юный мозг способен улавливать, анализировать и запоминать столько информации, сколько трудно даже взрослому человеку. То, чему родители должны научить малышей, имеет общепринятые возрастные рамки.
Основные геометрические фигуры и их названия дети должны узнать в возрасте от 3 до 5 лет.
Поскольку все дети разнообучаемы, то эти границы лишь условно приняты в нашей стране.
Геометрия – это наука о формах, размерах и расположении фигур в пространстве. Может создаться впечатление, что это сложно для малышей. Однако предметы изучения этой науки находятся повсюду вокруг нас. Вот почему иметь основные познания в этой области важно и для детей, и для старших.
Чтобы увлечь детей изучением геометрии, можно прибегнуть к веселым картинкам. Дополнительно хорошо бы иметь пособия, которые ребенок сможет потрогать, ощупать, обвести, раскрасить, узнать с закрытыми глазами. Основной принцип любых занятий с детьми – удержание их внимание и развития тяги к предмету с использованием игровых приемов и непринужденной веселой обстановки.
Сочетание нескольких средств восприятия сделает свое дело очень быстро. Воспользуйтесь нашей мини-методичкой, чтобы научить ребенка отличать геометрические фигуры, знать их названия.
Круг – самая первая из всех фигур. В природе вокруг нас многое имеет круглую форму: наша планета, солнце, луна, сердцевина цветка, многие фрукты и овощи, зрачки глаз. Объемный круг – это шар (мячик, клубок)
Начать изучение формы круга с ребенком лучше, рассматривая рисунки, а потом уже подкрепить теорию практикой, дав ребенку подержать что-нибудь круглое в руках.
Квадрат – это фигура, у которой все стороны имеют одинаковую высоту и ширину. Квадратные предметы – кубики, коробки, дом, окно, подушка, табурет и т. п.
Строить из квадратных кубиков всякие домики очень просто. Рисунок квадрата проще сделать на листочке в клетку.
Прямоугольник – родственник квадрата, который отличается тем, что имеет одинаковые противоположные стороны. Так же, как и у квадрата, у прямоугольника все равны 90 градусам.
Можно найти множество предметов, имеющих форму прямоугольника: шкафы, бытовая техника, двери, мебель.
В природе форму треугольника имеют горы и некоторые деревья. Из ближайшего окружения малышей можно привести в пример треугольную крышу дома, различные дорожные знаки.
В форме треугольника были построены некоторые древние сооружения, например храмы и пирамиды.
Овал – это круг, вытянутый с двух сторон. Формой овала обладают, например: яйцо, орехи, многие овощи и фрукты, человеческое лицо, галактики т. д.
Овал в объеме называется эллипсом. Даже Земля сплюснута с полюсов – эллипсовидная.
Ромб – тот же квадрат, только вытянутый, т. е. имеет два тупых угла и пару острых.
Изучать ромб можно с помощью наглядных пособий – нарисованной картинки или объемного предмета.
Геометрические фигуры по названиям запомнить несложно. В игру их изучение для детей можно превратить, применив следующие идеи:
Можно придумать много возможностей научить малышей знать названия геометрических фигур. Все способы хороши: рисунки, игрушки, наблюдения за окружающими предметами. Начните с малого, постепенно усложняя информацию и задания. Вы не ощутите, как пролетит время, а малыш обязательно порадует вас успехами в скором.
Геометрические объемные фигуры — это твердые тела, которые занимают ненулевой объем в евклидовом (трехмерном) пространстве. Эти фигуры изучает раздел математики, который носит название «пространственная геометрия». Знания о свойствах объемных фигур применяются в инженерии и в науках о природе. Рассмотрим в статье вопрос, геометрические объемные фигуры и их названия.
Поскольку эти тела имеют конечную размерность в трех пространственных направлениях, то для их описания в геометрии используют систему из трех координатных осей. Эти оси обладают следующими свойствами:
Говоря о геометрических объемных фигурах и их названиях, следует отметить, что все они принадлежат к одному из 2-х больших классов:
Что касается свойств объемных фигур, то следует выделить два самых важных из них:
Оба свойства для каждой фигуры описываются конкретными математическими формулами.
Рассмотрим ниже самые простые геометрические объемные фигуры и их названия: куб, пирамиду, призму, тетраэдр и шар.
Под геометрической фигурой куб понимают объемное тело, которое образовано 6-тью квадратными плоскостями или поверхностями. Также эту фигуру называют правильный гексаэдр, поскольку она имеет 6 сторон, или прямоугольный параллелепипед, так как он состоит из 3-х пар параллельных сторон, которые взаимно перпендикулярны друг другу. Называют куб и у которой основание является квадратом, а высота равна стороне основания.
Поскольку куб является многогранником или полиэдром, то для него можно применить теорему Эйлера, чтобы определить число его ребер. Зная, что число сторон равно 6, а вершин у куба 8, число ребер равно: Р = С + В — 2 = 6 + 8 — 2 = 12.
Если обозначить буквой «a» длину стороны куба, тогда формулы для его объема и площади поверхности будут иметь вид: V = a 3 и S = 6*a 2 , соответственно.
Пирамида — это полиэдр, который состоит из простого многогранника (основание пирамиды) и треугольников, которые соединяются с основанием и имеют одну общую вершину (вершина пирамиды). Треугольники называются боковыми гранями пирамиды.
Геометрические характеристики пирамиды зависят от того, какой многоугольник лежит в ее основании, а также от того, является ли пирамида прямой или косой. Под прямой пирамидой понимают такую пирамиду, для которой перпендикулярная основанию прямая, проведенная через вершину пирамиды, пересекает основание в ее геометрическом центре.
Одной из простых пирамид является четырехугольная прямая пирамида, в основании которой лежит квадрат со стороной «a», высота этой пирамиды «h». Для этой фигуры пирамиды объем и площадь поверхности будут равны: V = a 2 *h/3 и S = 2*a*√(h 2 +a 2 /4) + a 2 , соответственно. Применяя теорему Эйлера для нее, с учетом того, что число граней равно 5, и число вершин равно 5, получаем количество ребер: Р = 5 + 5 — 2 = 8.
Под геометрической фигурой тетраэдр понимают объемное тело, образованное 4-мя гранями. Исходя из свойств пространства, такие грани могут представлять только треугольники. Таким образом, тетраэдр является частным случаем пирамиды, у которой в основании лежит треугольник.
Если все 4-ре треугольника, образующие грани тетраэдра, являются равносторонними и равными между собой, то такой тетраэдр называется правильным. Этот тетраэдр имеет 4 грани и 4 вершины, число ребер составляет 4 + 4 — 2 = 6. Применяя стандартные формулы из плоской геометрии для рассматриваемой фигуры, получаем: V = a 3 * √2/12 и S = √3*a 2 , где a — длина стороны равностороннего треугольника.
Интересно отметить, что в природе некоторые молекулы имеют форму правильного тетраэдра. Например, молекула метана CH 4 , в которой атомы водорода расположены в вершинах тетраэдра, и соединены с атомом углерода ковалентными химическими связями. Атом углерода находится в геометрическом центре тетраэдра.
Простая в изготовлении форма фигуры тетраэдр используется также в инженерии. Например, тетраэдрическую форму используют при изготовлении якорей для кораблей. Отметим, что космический зонд НАСА, Mars Pathfinder, который совершил посадку на поверхность Марса 4 июля 1997 года, также имел форму тетраэдра.
Эту геометрическую фигуру можно получить, если взять два многогранника, расположить их параллельно друг другу в разных плоскостях пространства, и соединить их вершины соответствующим образом между собой. В итоге получится призма, два многогранника называются ее основаниями, а поверхности, соединяющие эти многогранники, будут иметь форму параллелограммов. Призма называется прямой, если ее боковые стороны (параллелограммы) являются прямоугольниками.
Призма — это полиэдр, поэтому для нее верна Например, если в основании призмы лежит шестиугольник, тогда, количество сторон у призмы равно 8, а количество вершин — 12. Число ребер будет равно: Р = 8 + 12 — 2 = 18. Для прямой призмы высотой h, в основании которой лежит правильный шестиугольник со стороной a, объем равен: V = a 2 *h*√3/4, площадь поверхности равна: S = 3*a*(a*√3 + 2*h).
Говоря о простых геометрических объемных фигурах и их названиях, следует упомянуть шар. Под объемным телом под названием шар понимают тело, которое ограничено сферой. В свою очередь, сфера — это совокупность точек пространства, равноудаленных от одной точки, которая называется центром сферы.
Поскольку шар относится к классу круглых тел, то для него не существует понятия о сторонах, ребрах и вершинах. сферы, ограничивающей шар, находится по формуле: S = 4*pi*r 2 , а объем шара можно вычислить по формуле: V = 4*pi*r 3 /3, где pi — число пи (3,14), r — радиус сферы (шара).
Геометрические фигуры — это замкнутые множества точек на плоскости или в пространстве, которые ограничены конечным числом линий. Они могут быть линейными (1D), плоскими (2D) или пространственными (3D).
Любое тело, имеющее форму, представляет собой совокупность геометрических фигур.
Любую фигуру можно описать математической формулой различной степени сложности. Начиная от простого математического выражения до суммы рядов математических выражений.
Основными математическими параметрами геометрических фигур являются радиусы, длины сторон или граней и углы между ними.
Ниже представлены основные геометрические фигуры, наиболее часто используемые в прикладных расчетах, формулы и ссылки на расчетные программы.
Точка — это базовый объект измерения. Основной и единственной математической характеристикой точки является её координата.
2. Линия
Линия — это тонкий пространственный объект имеющий конечную длину и представляющий собой цепь связанных друг с другом точек. Основной математической характеристикой линии является длина.
Луч — это тонкий пространственный объект имеющий бесконечную длину и представляющий собой цепь связанных друг с другом точек. Основными математическими характеристиками луча являются координата его начала и направление.
Круг — это геометрическое место точек на плоскости, расстояние от которых до его центра, не превышает заданного числа, называемого радиусом этого круга. Основной математической характеристикой круга является радиус.
2. Квадрат
Квадрат — это четырёхугольник, у которого все углы и все стороны равны. Основной математической характеристикой квадрата является длина его стороны.
3. Прямоугольник
Прямоугольник — это четырехугольник, у которого все углы равны 90 градусам (прямые). Основными математичскими характеристиками прямоугольника являются длины его сторон.
4. Треугольник
Треугольник — это геометрическая фигура, образованная тремя отрезками, которые соединяют три точки (вершины треугольника), не лежащие на одной прямой. Основными математическими характеристиками треугольника являются длины сторон и высота.
5. Трапеция
Трапеция — это четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Основными математическими характеристиками трапеции являются длины сторон и высота.
6. Параллелограмм
Параллелограмм — это четырёхугольник, у которого противоположные стороны параллельны. Основными математическими характеристиками параллелограмма являются длины его сторон и высота.
Ромб — это четырехугольник, у которого все стороны, а углы его вершин не равны 90 градусам. Основными математическими характеристиками ромба являются длина его стороны и высота.
8. Эллипс
Эллипс — это замкнутая кривая на плоскости, которая может быть представлена как ортогональная проекция сечения окружности цилиндра на плоскость. Основными математическими характеристиками окружности являются длина его полуосей.
Шар — это геометрическое тело, представляющее собой совокупность всех точек пространства, находящихся от его центра на заданном расстоянии. Основной математической характеристикой шара является его радиус.
Сфера — это оболочка геометрического тела, представляющее собой совокупность всех точек пространства, находящихся от его центра на заданном расстоянии. Основной математической характеристикой сферы является её радиус.
Куб — это геометрическое тело, представляющее собой правильный многогранник, каждая грань которого представляет собой квадрат. Основной математической характеристикой куба является длина его ребра.
4. Параллелепипед
Параллелепипед — это геометрическое тело, представляющее собой многогранник, у которого шесть граней и каждая из них прямоугольник. Основными математическими характеристиками параллелепипеда являются длины его ребер.
5. Призма
Призма — это многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани параллелограммами, имеющими общие стороны с этими многоугольниками. Основными математическими характеристиками призмы являются площадь основания и высота.
Конус — это геометрическая фигура, полученная объединением всех лучей, исходящих из одной вершины конуса и проходящих через плоскую поверхность. Основными математическими характеристиками конуса являются радиус основания и высота.
7. Пирамида
Пирамида — это многогранник, основанием которого является произвольный многоугольник, а боковые грани являются треугольниками, имеющие общую вершину. Основными математическими характеристиками пирамиды являются площадь основания и высота.
8. Цилиндр
Цилиндр — это геометрическая фигура, ограниченная цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её. Основными математическими характеристиками цилиндра являются радиус основания и высота.
Быстро выполнить эти простейшие математические операции можно с помощью наших онлайн программ. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлены все геометрические фигуры, которые наиболее часто встречаются в геометрии для представления объекта или его части на плоскости или в пространстве.
Маленькие детки готовы учиться везде и всегда. Их юный мозг способен улавливать, анализировать и запоминать столько информации, сколько трудно даже взрослому человеку. То, чему родители должны научить малышей, имеет общепринятые возрастные рамки.
Основные геометрические фигуры и их названия дети должны узнать в возрасте от 3 до 5 лет.
Поскольку все дети разнообучаемы, то эти границы лишь условно приняты в нашей стране.
Геометрия – это наука о формах, размерах и расположении фигур в пространстве. Может создаться впечатление, что это сложно для малышей. Однако предметы изучения этой науки находятся повсюду вокруг нас. Вот почему иметь основные познания в этой области важно и для детей, и для старших.
Чтобы увлечь детей изучением геометрии, можно прибегнуть к веселым картинкам. Дополнительно хорошо бы иметь пособия, которые ребенок сможет потрогать, ощупать, обвести, раскрасить, узнать с закрытыми глазами. Основной принцип любых занятий с детьми – удержание их внимание и развития тяги к предмету с использованием игровых приемов и непринужденной веселой обстановки.
Сочетание нескольких средств восприятия сделает свое дело очень быстро. Воспользуйтесь нашей мини-методичкой, чтобы научить ребенка отличать геометрические фигуры, знать их названия.
Круг – самая первая из всех фигур. В природе вокруг нас многое имеет круглую форму: наша планета, солнце, луна, сердцевина цветка, многие фрукты и овощи, зрачки глаз. Объемный круг – это шар (мячик, клубок)
Начать изучение формы круга с ребенком лучше, рассматривая рисунки, а потом уже подкрепить теорию практикой, дав ребенку подержать что-нибудь круглое в руках.
Квадрат – это фигура, у которой все стороны имеют одинаковую высоту и ширину. Квадратные предметы – кубики, коробки, дом, окно, подушка, табурет и т. п.
Строить из квадратных кубиков всякие домики очень просто. Рисунок квадрата проще сделать на листочке в клетку.
Прямоугольник – родственник квадрата, который отличается тем, что имеет одинаковые противоположные стороны. Так же, как и у квадрата, у прямоугольника все равны 90 градусам.
Можно найти множество предметов, имеющих форму прямоугольника: шкафы, бытовая техника, двери, мебель.
В природе форму треугольника имеют горы и некоторые деревья. Из ближайшего окружения малышей можно привести в пример треугольную крышу дома, различные дорожные знаки.
В форме треугольника были построены некоторые древние сооружения, например храмы и пирамиды.
Овал – это круг, вытянутый с двух сторон. Формой овала обладают, например: яйцо, орехи, многие овощи и фрукты, человеческое лицо, галактики т. д.
Овал в объеме называется эллипсом. Даже Земля сплюснута с полюсов – эллипсовидная.
Ромб – тот же квадрат, только вытянутый, т. е. имеет два тупых угла и пару острых.
Изучать ромб можно с помощью наглядных пособий – нарисованной картинки или объемного предмета.
Геометрические фигуры по названиям запомнить несложно. В игру их изучение для детей можно превратить, применив следующие идеи:
Можно придумать много возможностей научить малышей знать названия геометрических фигур. Все способы хороши: рисунки, игрушки, наблюдения за окружающими предметами. Начните с малого, постепенно усложняя информацию и задания. Вы не ощутите, как пролетит время, а малыш обязательно порадует вас успехами в скором.
Фигура – это произвольное множество точек на плоскости. Точка, прямая, отрезок, луч, треугольник, круг, квадрат и так далее – всё это примеры геометрических фигур.
Точка – основное понятие геометрии, это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса.
Линия – это множество точек, последовательно расположенных друг за другом. У линии измеряют только длину. Ширины и толщины она не имеет.
Прямая линия – это линия, которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороны.
Луч – это часть прямой линии, которая имеет начало, но не имеет конца, её можно бесконечно продолжать только в одну сторону.
Отрезок – это часть прямой линии, ограниченная двумя точками. Отрезок имеет начало и конец, поэтому можно измерить его длину.
Кривая линия – это плавно изгибающаяся линия, которая определяется расположением составляющих её точек.
Ломаная линия – это фигура, которая состоит из отрезков, последовательно соединенных своими концами.
Вершины ломаной – это
Звенья ломаной – это отрезки, из которых состоит ломаная. Количество звеньев ломаной всегда на 1 меньше, чем количество вершин ломаной.
Незамкнутая линия – это линия, концы которой не соединены вместе.
Замкнутая линия – это линия, концы которой соединены вместе.
Многоугольник – это замкнутая ломанная линия. Вершины ломаной называются вершинами многоугольника, а отрезки — сторонами многоугольника.
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
Геометрия — одна из важнейших компонент математического образования, необходимая для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, а также для эстетического воспитания. Изучение геометрии вносит вклад в развитие логического мышления, формирование навыков доказательства.
В курсе геометрии 7 класса систематизируются знания о простейших геометрических фигурах и их свойствах; вводится понятие равенства фигур; вырабатывается умение доказывать равенство треугольников с помощью изученных признаков; вводится класс задач на построение с помощью циркуля и линейки; вводится одно из важнейших понятий — понятие о параллельных прямых; рассматриваются новые интересные и важные свойства треугольников; рассматривается одна из важнейших теорем в геометрии — теорема о сумме углов треугольника, которая позволяет дать классификацию треугольников по углам (остроугольный, прямоугольный, тупоугольный).
На протяжении занятий, особенно при переходе от одной части занятия к другой, смене деятельности встает вопрос о поддержании интереса к занятиям. Таким образом, актуальным становится вопрос о применении на занятиях по геометрии задач, в которых есть условие проблемной ситуации и элементы творчества . Таким образом, целью данного исследования является систематизация заданий геометрического содержания с элементами творчества и проблемных ситуаций.
Объект исследования : Задачи по геометрии с элементами творчества, занимательности и проблемных ситуаций.
Задачи исследования: Проанализировать существующие задачи по геометрии, направленные на развитие логики, воображения и творческого мышления. Показать, как занимательными приемами можно развить интерес к предмету.
Теоретическая и практическая значимость исследования состоит в том, что собранный материал может быть использован в процессе дополнительных занятий по геометрии, а именно на олимпиадах и конкурсах по геометрии.
Объем и структура исследования:
Исследование состоит из введения, двух глав, заключения, библиографического списка, содержит 14 страниц основного машинописного текста, 1 таблицу, 10 рисунков.
Глава 1. ПЛОСКИЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
1.1. Основные геометрические фигуры в архитектуре зданий и сооружений
В окружающем нас мире существует множество материальных предметов разных форм и размеров: жилые дома, детали машин, книги, украшения, игрушки и т. д.
В геометрии вместо слова предмет говорят геометрическая фигура, при этом разделяя геометрические фигуры на плоские и пространственные. В данной работе будет рассмотрен один из интереснейших разделов геометрии — планиметрия, в которой рассматриваются только плоские фигуры. Планиметрия (от лат. planum — «плоскость», др.-греч. μετρεω — «измеряю») — раздел евклидовой геометрии, изучающий двумерные (одноплоскостные) фигуры, то есть фигуры, которые можно расположить в пределах одной плоскости. Плоской геометрической фигурой называется такая, все точки которой лежат на одной плоскости. Представление о такой фигуре даёт любой рисунок, сделанный на листе бумаги.
Но прежде, чем рассматривать плоские фигуры, необходимо познакомиться с простыми, но очень важными фигурами, без которых плоские фигуры просто не могут существовать.
Самой простой геометрической фигурой является точка. Это одна из главных фигур геометрии. Она очень маленькая, но ее всегда используют для построения различных форм на плоскости. Точка — это основная фигура для абсолютно всех построений, даже самой высокой сложности. С точки зрения математики точка — это абстрактный пространственный объект, не обладающий такими характеристиками, как площадь, объем, но при этом остающийся фундаментальным понятием в геометрии.
Прямая — одно из фундаментальных понятий геометрии.При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии (евклидовой). Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить, как линию, путь вдоль которой равен расстоянию между двумя точками.
Прямые в пространстве могут занимать различные положения, рассмотрим некоторые из них и приведем примеры, встречающиеся в архитектурном облике зданий и сооружений (табл. 1):
Таблица 1
Параллельные прямые | Свойства параллельных прямых | |
Если прямые параллельны, то их одноименные проекции параллельны: | Ессентуки, здание грязелечебницы (фото автора) | |
Пересекающиеся прямые | Свойства пересекающихся прямых | Примеры в архитектуре зданий и сооружений |
Пересекающиеся прямые имеют общую точку, то есть точки пересечения их одноименных проекций лежат на общей линии связи: | Здания «горы» на Тайване https://www.sro-ps.ru/novosti_otrasli/2015_11_11_pervoe_zdanie_iz_grandioznogo_proekta_big_v_tayvane | |
Скрещивающиеся прямые | Свойства скрещивающихся прямых | Примеры в архитектуре зданий и сооружений |
Прямые, не лежащие в одной плоскости и не параллельные между собой, являются скрещивающимися. Ноне является общей линией связи. Если пересекающиеся и параллельные прямые лежат в одной плоскости, то скрещивающиеся прямые лежат в двух параллельных плоскостях. | Робер, Гюбер — Вилла Мадама под Римом https://gallerix.ru/album/Hermitage-10/pic/glrx-172894287 |
1.2. Плоские геометрические фигуры. Свойства и определения
Наблюдая за формами растений и животных, гор и извилинами рек, за особенностями ландшафта и далекими планетами, человек заимствовал у природы ее правильные формы, размеры и свойства. Материальные потребности побуждали человека строить жилища, изготавливать орудия труда и охоты, лепить из глины посуду и прочее. Все это постепенно способствовало тому, что человек пришел к осознанию основных геометрических понятий.
Четырехугольники:
Параллелограмм (др.-греч. παραλληλόγραμμον от παράλληλος — параллельный и γραμμή — черта, линия) — это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых.
Признаки параллелограмма:
Четырёхугольник является параллелограммом, если выполняется одно из следующих условий: 1. Если в четырёхугольнике противоположные стороны попарно равны, то четырёхугольник — параллелограмм. 2. Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник — параллелограмм. 3. Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник — параллелограмм.
Параллелограмм, у которого все углы прямые, называется прямоугольником.
Параллелограмм, у которого все стороны равны, называется ромбом.
Трапеция— это четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.
Треугольник — это простейшая геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Указанные три точки называются вершинами треугольника , а отрезки — сторонами треугольника. Именно в силу своей простоты треугольник явился основой многих измерений. Землемеры при своих вычислениях площадей земельных участков и астрономы при нахождении расстояний до планет и звезд используют свойства треугольников. Так возникла наука тригонометрия — наука об измерении треугольников, о выражении сторон через его углы. Через площадь треугольника выражается площадь любого многоугольника: достаточно разбить этот многоугольник на треугольники, вычислить их площади и сложить результаты. Правда, верную формулу для площади треугольника удалось найти не сразу.
Особенно активно свойства треугольника исследовались в XV-XVI веках. Вот одна из красивейших теорем того времени, принадлежащая Леонарду Эйлеру:
Огромное количество работ по геометрии треугольника, проведенное в XY-XIX веках, создало впечатление, что о треугольнике уже известно все.
Многоуго́льник — это геометрическая фигура, обычно определяемая как замкнутая ломаная.
Круг — геометрическое место точек плоскости, расстояние от которых до заданной точки, называемой центром круга, не превышает заданного неотрицательного числа, называемого радиусом этого круга. Если радиус равен нулю, то круг вырождается в точку.
Существует большое количество геометрических фигур, все они отличаются параметрами и свойствами, порой удивляя своими формами.
Чтобы лучше запомнить и отличать плоские фигуры по свойствам и признакам, я придумал геометрическую сказку, которую хотел бы представит вашему вниманию в следующем параграфе.
Глава 2. ЗАДАЧИ-ГОЛОВОЛОМКИ ИЗ ПЛОСКИХ ГЕОМЕТРИЧЕСКИХ ФИГУР
2.1.Головоломки на построение сложной фигуры из набора плоских геометрических элементов.
Изучив плоские фигуры, я задумался, а существуют какие-нибудь интересные задачи с плоскими фигурами, которые можно использовать в качестве заданий-игр или заданий-головоломок. И первой задачей, которую я нашел, была головоломка «Танграм».
Это китайская головоломка. В Китае ее называют «чи тао ту», т.е умственная головоломка из семи частей. В Европе название «Танграм» возникло, вероятнее всего, от слова «тань», что означает «китаец» и корня «грамма» (греч. — «буква»).
Для начала необходимо начертить квадрат 10 х10 и разделить его на семь частей: пять треугольников 1-5 , квадрат 6 и параллелограмм 7 . Суть головоломки состоит в том, чтобы, используя все семь частей, сложить фигурки, показанные на рис.3.
Рис.3. Элементы игры «Танграм» и геометрические фигуры
Рис.4. Задания «Танграм»
Особенно интересно составлять из плоских фигур «образные» многоугольники, зная лишь очертания предметов (рис.4). Несколько таких заданий-очертаний я придумал сам и показал эти задания своим одноклассникам, которые с удовольствием принялись разгадывать задания и составили много интересных фигур-многогранников, похожих на очертания предметов окружающего нас мира.
Для развития воображения можно использовать и такие формы занимательных головоломок, как задачи на разрезание и воспроизведение заданных фигур.
Пример 2. Задачи на разрезание (паркетирование) могут показаться, на первый взгляд, весьма многообразными. Однако в большинстве в них используется всего лишь несколько основных типов разрезаний (как правило, те, с помощью которых из одного параллелограмма можно получить другой).
Рассмотрим некоторые приёмы разрезаний. При этом разрезанные фигуры будем называть многоугольниками.
Рис. 5. Приёмы разрезаний
На рис.5 представлены геометрические фигуры, из которых можно собрать различные орнаментальные композиции и составить орнамент своими руками.
Пример 3. Еще одна интересная задача, которую можно самостоятельно придумать и обмениваться с другими учениками, при этом кто больше соберет разрезанные фигуры, тот объявляется победителем. Задач такого типа может быть достаточно много. Для кодирования можно взять все существующие геометрические фигуры, которые разрезаются на три или четыре части.
Рис.6.Примеры задач на разрезание:
—— — воссозданный квадрат; — разрез ножницами;
Основная фигура
2.2.Равновеликие и равносоставленные фигуры
Рассмотрим еще один интересный прием на разрезание плоских фигур, где основными «героями» разрезаний будут многоугольники. При вычислении площадей многоугольников используется простой прием, называемый методом разбиения.
Вообще многоугольники называются равносоставленными, если, определенным образом разрезав многоугольник F на конечное число частей, можно, располагая эти части иначе, составить из них многоугольник Н.
Отсюда вытекает следующая теорема: равносоставленные многоугольники имеют одинаковую площадь, поэтому они будут считаться равновеликими.
На примере равносоставленных многоугольников можно рассмотреть и такое интересное разрезание, как преобразование «греческого креста» в квадрат (рис.7).
Рис.7. Преобразование «греческого креста»
В случае мозаики (паркета), составленной из греческих крестов, параллелограмм периодов представляет собой квадрат. Мы можем решить задачу, накладывая мозаику, составленную из квадратов, на мозаику, образованную с помощью крестов, так, чтобы при этом конгруэнтные точки одной мозаики совпали с конгруэнтными точками другой (рис.8).
На рисунке конгруэнтные точки мозаики из крестов, а именно центры крестов, совпадают с конгруэнтными точками «квадратной» мозаики — вершинами квадратов. Параллельно сдвинув квадратную мозаику, мы всегда получим решение задачи. Причем, задача имеет несколько вариантов решений, если при составлении орнамента паркета используется цвет.
Рис.8. Паркет, собранный из греческого креста
Еще один пример равносоставленных фигур можно рассмотреть на примере параллелограмма. Например, параллелограмм равносоставлен с прямоугольником (рис.9).
Этот пример иллюстрирует метод разбиения, состоящий в том, что для вычисления площади многоугольника пытаются разбить его на конечное число частей таким образом, чтобы из этих частей можно было составить более простой многоугольник, площадь которого нам уже известна.
Например, треугольник равносоставлен с параллелограммом, имеющим то же основание и вдвое меньшую высоту. Из этого положения легко выводится формула площади треугольника.
Отметим, что для приведенной выше теоремы справедлива и обратная теорема: если два многоугольника равновелики, то они равносоставлены.
Эту теорему, доказанную в первой половине XIX в. венгерским математиком Ф.Бойяи и немецким офицером и любителем математики П.Гервином, можно представить и в таком виде: если имеется торт в форме многоугольника и многоугольная коробка, совершенно другой формы, но той же площади, то можно так разрезать торт на конечное число кусков (не переворачивая их кремом вниз), что их удастся уложить в эту коробку.
Заключение
В заключении отмечу, что задач на плоские фигуры достаточно представлено в различных источниках, но интерес представили для меня те, на основании которых мне пришлось придумывать свои задачи-головоломки.
Ведь решая такие задачи, можно не просто накопить жизненный опыт, но и приобрести новые знания и умения.
В головоломках при построении действий-ходов используя повороты, сдвиги, переносы на плоскости или их композиции, у меня получились самостоятельно созданные новые образы, например, фигурки-многогранники из игры «Танграм».
Известно, что основным критерием подвижности мышления человека является способность путём воссоздающего и творческого воображения выполнить в установленный отрезок времени определенные действия, а в нашем случае — ходы фигур на плоскости. Поэтому изучение математики и, в частности, геометрии в школе даст мне еще больше знаний, чтобы в дальнейшем применить их в своей будущей профессиональной деятельности.
Библиографический список
1. Павлова, Л.В. Нетрадиционные подходы к обучению черчению: учебное пособие/ Л.В. Павлова. — Нижний Новгород: Изд-во НГТУ, 2002. — 73 с.
2. Энциклопедический словарь юного математика /Сост. А.П. Савин. — М.: Педагогика, 1985. — 352 с.
3.https://www.srops.ru/novosti_otrasli/2015_11_11_pervoe_zdanie_iz_grandioznogo_proekta_big_v_tayvane
4.https://www.votpusk.ru/country/dostoprim_info.asp?ID=16053
Приложение 1
Анкета-опросник для одноклассников
1. Знаете ли вы, что такое головоломка «Танграм»?
2. Что такое «греческий крест»?
3. Было бы вам интересно узнать, что такое «Танграм»?
4. Было бы вам интересно узнать, что такое «греческий крест»?
Было опрошено 22 ученика 8 класса. Результаты: 22 ученика не знают, что такое «Танграм» и «греческий крест». 20-ти ученикам было бы интересно узнать о том, как с помощью головоломки «Танграм», состоящая из семи плоских фигур, получить более сложную фигуру. Результаты опроса обобщены на диаграмме.
Приложение 2
Элементы игры «Танграм» и геометрические фигуры
Преобразование «греческого креста»
Геометрическая фигура — множество точек на поверхности (зачастую на плоскости), которое образует конечное количество линий.
Основными геометрическими фигурами на плоскости являются точка и прямая линия . Отрезок, луч, ломаная линия — самые простые геометрические фигуры на плоскости.
Точка — мельчайшая геометрическая фигура, являющаяся основой других фигур во всяком изображении либо чертеже.
Каждая более сложная геометрическая фигура есть множество точек, которые обладают определенным свойством, характерное только для этой фигуры.
Прямая линия , либо прямая — это бесконечное множество точек, расположенных на 1-ой линии, которая не имеет начала и конца. На листе бумаги можно увидеть лишь часть прямой линии, т.к. она не имеет предела.
Прямую изображают так:
Часть прямой линии, которая ограничена с 2-х сторон точками, называют отрезком прямой, либо отрезком. Его изображают так:
Луч — это направленная полупрямая, имеющая точку начала и у которой нет конца. Луч изображают так:
Если на прямой поставить точку, то эта точка будет разбивать прямую на 2 противоположно направленных луча. Эти лучи называют дополнительными .
Ломаная линия — несколько отрезков, которые соединены друг с другом таким образом, что конец 1-го отрезка оказывается началом 2-го отрезка, а конец 2-го отрезка — началом 3-го отрезка и так далее, причем соседние (которые имеют 1-ну общую точку) отрезки располагаются на разных прямых. Когда конец последнего отрезка не совпадает с началом 1-го, значит, эта ломаная линия будет называться незамкнутой :
Когда конец последнего отрезка ломаной совпадает с началом 1-го, значит, эта ломаная линия будет замкнутой . Пример замкнутой ломаной — это всякий многоугольник:
Четырехзвенная замкнутая ломаная линия — четырехугольник (прямоугольник) :
Трехзвенная замкнутая ломаная линия —
Масару Ибука в своей книге «После трёх уже поздно» утверждает, что в первые три года жизни у ребенка самый высокий потенциал к обучению и развитию, поэтому бездействие сродни преступлению.
Конечно, нам может казаться, что ребенок слишком мал. Да и чему он может научиться, если не умеет даже говорить? Но мозг ребёнка, как губка, впитывает всю окружающую его информацию. И от родителей зависит, что усвоит ребенок в этом возрасте.
Стоит ли начинать изучать геометрические фигуры в столь раннем возрасте? Безусловно. Ребенок живет в окружении геометрических форм. Знания, которые вы даёте, не должны быть оторваны от вашей повседневной жизни. Мама – проводник малыша в этом мире, и ей совершенно не обязательно иметь ученую степень, чтобы рассказать ребенку, как устроен мир.
Первые три года жизни ребенка – это период развития мозговых клеток, когда образуется прочная база для новых свершений. Уже в 3-4 месяца малыш способен различать формы. Это не означает, что пришла пора заучивать названия геометрических фигур, но мама при разговоре с крохой может стараться употреблять фразы: «А вот и наше любимое круглое блюдце», «Давай посмотрим, что в квадратной коробке» и подобные.
Знание геометрических фигур помогает:
И, конечно же, полученные дошкольником знания послужат ему отличным подспорьем в изучении математики в школе.
Есть немало техник и методик, которые сделают запоминание фигур интересным для детей. Подбор методик будет зависеть от возраста и познаний ребёнка.
При изучении геометрических фигур, важно действовать поэтапно. Начать следует с легких фигур: круг, квадрат, треугольник, ромб, прямоугольник, овал. Знания этих фигур доступны для детей 2-3 лет.
Детки постарше, 4-5 лет, включают в свой лексикон и берут в оборот представления об трапеции, параллелограмме, пентагоне, гексагоне, октагоне, декагоне и других многоугольниках. Они уже умеют анализировать, поэтому с легкостью сравнивают и находят отличия между фигурами.
Старшие дошколята знакомятся с объемными фигурами: цилиндр, пирамида, куб, шар, конус, призма.
Разберем некоторые варианты техник по изучению геометрических фигур:
1. Сортер – ищем «домик» для каждой фигуры. Ребенок не только запомнит фигуры, но и будет развивать мелкую моторику вкупе с мышлением.
2. Лепка. Лепите вместе с малышом геометрические фигуры – лучшего занятия для развития мелкой моторики рук и усидчивости просто не придумаешь.
3. Объемные наклейки и магниты, изображающие геометрические фигуры, тоже могут помочь ребенку закрепить в памяти названия фигур.
4. Ищем половинки. Разрежьте геометрические фигуры на две части, смешайте и предложите малышу найти вторую половину.
5. Аппликации. Также из вырезанных фигур можно составлять геометрическую аппликацию. Например, домик (квадрат + треугольник), ёлочку, машинку.
6. Обводить пунктирные геометрические фигуры.
7. Раскрасить или заштриховать предложенные вами геометрические фигуры.
7. Дорисовать фигуру по образцу.
8. Рисовать фигуры при помощи трафаретов.
9. Послушать сказку, где главные герои — геометрические фигуры, а потом зарисовать услышанное.
10. Положить в непрозрачный мешок фигуры разной формы и предложить на ощупь угадать форму предмета.
11. Отличная игра для развития памяти и внимательности. Взрослый готовит вырезанные фигуры разных цветов и размеров и выкладывает перед малышом. Они обсуждают цвета, называют фигуры, а после взрослый прячет фигуру. Задача ребенка обнаружить и назвать, какой фигуры нет.
12. Выкладывание геометрических фигур при помощи счетных палочек или спичек. Когда ребенок овладеет этим навыком, можно перейти на более сложный уровень — решать задачки. Например, убери одну спичку так, чтобы получился треугольник.
13. Ассоциации. Предложите ребенку назвать предметы, на которые похож круг или прямоугольник.
14. Шнуровки и различные рамки-вкладыши, например, квадраты Никитина, где нужно из нескольких предметов воссоздать квадрат, либо доски Сегена, где необходимо вставить недостающую деталь.
15. Подвижные игры. Например, на асфальте рисуются овал, треугольник, квадрат, прямоугольник. По команде взрослого ребенок должен найти названную фигуру и встать в неё.
16. Видеоматериалы. Существует большое количество мультфильмов и обучающих материалов про геометрические фигуры. Посмотрите видео с малышом и обязательно обсудите увиденное.
17. Найдите в интернете и распечатайте картины, которые художники рисуют геометрическими формами, и предложите ребенку посчитать, сколько здесь кругов, прямоугольников и т. д.
Объемные фигуры можно изучать по аналогии с окружающим предметами (например, мяч = шар). И, конечно же, задействовать изучение предмета через игры:
Изучение геометрических фигур не должно становиться пыткой для ребенка и взрослого. Выбирайте ту методику, которая подходит именно вам. Проявите терпение и изобретательность, и тогда результат не заставит себя долго ждать. Главное, не забывайте поощрять ребенка за его новые открытия и время от времени повторять полученные знания.
Шар — геометрическое тело, его поверхность — сфера.
Шар Сфера
Винтовая линия — объёмная фигура, но это не тело.
Винтовая линия
Пирамида — геометрическое тело, которое ограничено плоскими многоугольниками.
Пирамида Плоские многоугольники
Плоскость
Примеры плоскости в природе:
Поверхность стола Поверхность книг Поверхность воды Пол
В стереометрии так же, как и в планиметрии, определяется равенство двух геометрических тел или фигур.
Две фигуры (или тела) называются равными, если их можно совместить наложением.
Главная величина геометрических тел — это их объём.
Объём геометрического тела — это величина, которая описывает занимающую этим телом часть пространства.
Из определения следует, что объём не зависит ни от местонахождения тела в пространстве, ни от того, как это тело делится на части.
Величину объёма вычисляют, основываясь на аксиомах:
1) равные тела имеют равные объёмы.
2) Объём тела равен сумме объёмов его отдельных частей.
Чтобы объём можно было измерить, т. е. чтобы объём можно было бы выразить в виде числа, необходимо выбрать единицу измерения объёма.
Единица объёма — это объём такого куба, ребро которого равно одной единице длины.
Если ребро куба равно \(1\) \(см\), то его объём обозначается кубическими сантиметрами — см3, если ребро куба равно \(1\) \(м\), то объём обозначается кубическими метрами — м3.
Тела с равными объёмами называются равновеликими.
Равные тела Равновеликие тела
Равные тела с объёмом \(8\) см3 Равновеликие тела с объёмом \(6\) см3
Все равные тела равновелики, но не все равновеликие тела равны.
|
Автор admin На чтение 19 мин. Просмотров 3 Опубликовано
Поскольку эти тела имеют конечную размерность в трех пространственных направлениях, то для их описания в геометрии используют систему из трех координатных осей. Эти оси обладают следующими свойствами:
Говоря о геометрических объемных фигурах и их названиях, следует отметить, что все они принадлежат к одному из 2-х больших классов:
Что касается свойств объемных фигур, то следует выделить два самых важных из них:
Оба свойства для каждой фигуры описываются конкретными математическими формулами.
Рассмотрим ниже самые простые геометрические объемные фигуры и их названия: куб, пирамиду, призму, тетраэдр и шар.
Под геометрической фигурой куб понимают объемное тело, которое образовано 6-тью квадратными плоскостями или поверхностями. Также эту фигуру называют правильный гексаэдр, поскольку она имеет 6 сторон, или прямоугольный параллелепипед, так как он состоит из 3-х пар параллельных сторон, которые взаимно перпендикулярны друг другу. Называют куб и прямоугольной призмой, у которой основание является квадратом, а высота равна стороне основания.
Геометрические характеристики пирамиды зависят от того, какой многоугольник лежит в ее основании, а также от того, является ли пирамида прямой или косой. Под прямой пирамидой понимают такую пирамиду, для которой перпендикулярная основанию прямая, проведенная через вершину пирамиды, пересекает основание в ее геометрическом центре.
Под геометрической фигурой тетраэдр понимают объемное тело, образованное 4-мя гранями. Исходя из свойств пространства, такие грани могут представлять только треугольники. Таким образом, тетраэдр является частным случаем пирамиды, у которой в основании лежит треугольник.
Интересно отметить, что в природе некоторые молекулы имеют форму правильного тетраэдра. Например, молекула метана CH4, в которой атомы водорода расположены в вершинах тетраэдра, и соединены с атомом углерода ковалентными химическими связями. Атом углерода находится в геометрическом центре тетраэдра.
Простая в изготовлении форма фигуры тетраэдр используется также в инженерии. Например, тетраэдрическую форму используют при изготовлении якорей для кораблей. Отметим, что космический зонд НАСА, Mars Pathfinder, который совершил посадку на поверхность Марса 4 июля 1997 года, также имел форму тетраэдра.
Эту геометрическую фигуру можно получить, если взять два многогранника, расположить их параллельно друг другу в разных плоскостях пространства, и соединить их вершины соответствующим образом между собой. В итоге получится призма, два многогранника называются ее основаниями, а поверхности, соединяющие эти многогранники, будут иметь форму параллелограммов. Призма называется прямой, если ее боковые стороны (параллелограммы) являются прямоугольниками.
Источник
Основные геометрические фигуры на плоскости состоят из точек, линий, лучей, отрезков и вершин. У каждого предмета есть свои особенности, свойства и предназначение.
Самый минимальный объект в геометрии — точка. Ее особенность в том, что она не имеет измерительных мер: у нее нет высоты, длины, радиуса. У точки можно определить только ее расположение, которое принято обозначать одной заглавной буквой латинского алфавита.
Из множества точек может получится линия, а из нескольких соединенных между собой линий — геометрические фигуры.
Каждая математическая фигура имеет собственную величину, которую можно измерить при помощи формул и внимательности.
Площадь — это одна из характеристик замкнутой геометрической фигуры, которая дает нам информацию о ее размере. S (square) — знак площади.
Периметром принято называть длину всех сторон многоугольника. Периметр обозначается заглавной латинской P.
Если параметры переданы в разных единицах длины, мы не сможем узнать какая площадь фигуры получится. Чтобы правильно решить задачу, нужно перевести все данные к одной единице измерения.
Популярные единицы измерения
Геометрические тела — часть пространства, которая ограничена замкнутой поверхностью своей наружной границы.
Если все точки фигуры принадлежат одной плоскости, значит она является плоской.
Объемная фигура — геометрическая фигура, у которой все точки не находятся на одной плоскости.
Объемные геометрические фигуры:
В начальной школе дети узнают названия геометрических фигур и учатся различать плоские от объемных. Сейчас мы рассмотрим подробнее некоторые фигуры, разберем их определения и свойства.
На уроках математики в Skysmart дети решают увлекательные задачки в интерактивном формате, рисуют пальцами на онлайн-доске и помогают героям красочных комиксов. Приходите вместе с ребенком на бесплатный вводный урок: познакомимся, покажем, как все устроено на платформе и наметим вдохновляющую программу обучения.
Прямоугольник — четырехугольник, у которого все стороны пересекаются под прямым углом.
Узнать площадь прямоугольника помогут следующие формулы:
Диагональ — это отрезок, который соединяет противоположные стороны фигуры. Он есть во всех фигурах, число вершин которых больше трех.
Периметр прямоугольника — сумма длины и ширины, умноженная на два.
P = 2 * (a + b), где a — ширина, b — высота.
Квадрат — это тот же прямоугольник, у которого все стороны равны.
Найти площадь квадрата легко:
Периметр квадрата — это произведение длины стороны на четыре.
P = 4 * a, где a — длина стороны.
Трапеция — это четырёхугольник, у которого две стороны параллельны, а две не параллельны.
Основное свойство: в трапецию можно вписать окружность, если сумма ее основ равна сумме боковых сторон.
Как найти площадь трапеции:
S = (a + b) : 2 * h, где a, b — два разных основания, h — высота трапеции.
Построить высоту трапеции можно, начертив отрезок так, чтобы он соединил параллельные стороны и пересек их под прямым углом.
Формула периметра для равнобедренной трапеции отличается от прямоугольника тем, что у первого есть две равные стороны.
P = a + b + 2 * c, где a, b — параллельные стороны, c — две длины одинаковых сторон.
Параллелограмм — четырехугольник, противоположные стороны которого попарно параллельны. Определение ромба звучит точно также, поэтому мы их объединили.
Общие формулы расчета площади фигур:
Периметр ромба — это произведение длины стороны на четыре.
P = 4 * a, где a — длина стороны.
Периметр параллелограмма — сумма длины и ширины, умноженная на два.
P = 2 * (a + b), где a — ширина, b — высота.
Треугольник — это когда три отрезка соединяют три точки, не лежащие на одной прямой. Эти три точки принято называть вершинами, а отрезки — сторонами.
Рассчитать площадь треугольника можно несколькими способами по исходным данным, давайте их рассмотрим.
S = 0,5 * a * h, где a — длина основания, h — высота, проведенная к основанию.
Основание может быть расположено иначе, например так:
При тупом угле высоту можно отразить на продолжение основания:
При прямом угле основанием и высотой будут его катеты:
S = 0,5 * a * b * sinα, где a и b — две стороны, sinα — синус угла между ними.
S = (a * b * с) : 4 * R, где a, b и с — стороны треугольника, а R — радиус описанной окружности.
S = p * r, где р — полупериметр треугольника, r — радиус вписанной окружности.
Периметр треугольника — это сумма длин трех его сторон.
P = a + b + c, где a, b, c — длина стороны.
Формула измерения периметра для равностороннего треугольника — это произведение длины стороны на три.
P = 3 * a, где a — длина стороны.
Подружиться с геометрией помогут внимательные учителя-профессионалы Skysmart. Они найдут подход к любому ребенку: объяснят сложную тему, ответят на неловкие вопросы и вдохновят на учебу. А если что-то пойдет не так — учителя можно поменять.
Записывайтесь на бесплатный урок математики и начните заниматься в удовольствие и в комфортном темпе.
Круг — это когда множество точек на плоскости удалены от центра на равном радиусу расстоянии.
Окружность — это граница круга.
Радиус круга — это расстояние от центра окружности до любой ее точки.
Диаметр круга — это отрезок, который соединяет две точки окружности и проходит через её центр. Диаметр круга равен двум его радиусам.
Формулы площади круга:
Периметр круга или длина окружности — это произведение радиуса на два Пи или произведение диаметра на Пи.
L = d * π = 2 * r * π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.
Источник
Любому ребенку нравится делать яркие и объемные поделки. Творчество можно объединить с изучением математики и склеить вместе с детьми геометрические фигуры. Ребенок с интересом проведет время, а дополнительно постигнет основы точной науки. Ниже представлено, как начертить карандашом и сделать объемные геометрические фигуры из бумаги, также приведены их правильные названия.
Дети познают мир в процессе игры и творчества. Трехмерные фигуры, выполненные своими руками, помогут познакомиться с удивительной наукой — геометрией.
Примеры трафаретов и шаблонов можно скачать из Интернета и распечатать. Затем все фигуры вырезают и склеивают. Дети старшего возраста могут самостоятельно нарисовать развертку нужной фигуры, малышам помогают родители,.
Геометрические объекты делают из бумаги (белой или цветной), картона. Из последнего материала они получаются плотными и прочными.
Ученикам 1–2 класса демонстрируют в школе простые геометрические фигуры и 3d: квадрат, кубик, прямоугольник. Их несложно вырезать и склеить. Шаблоны развивают мелкую моторику у детей и дают первые представления о геометрии.
Ученики средней школы, которые изучают черчение, делают сложные фигуры: бумажные шестигранники, фигуры из пятиугольников, цилиндры. Из бумаги для детей выполняют домики для кукол, мебель, оригами, замок для маленьких игрушек, маски на лицо (трехмерные называются полигональными).
Выкройка шара состоит из 8 частей, 12, 16 или большего количества. Присутствуют и другие способы изображения мяча. Например, из 6 деталей или 4 широких клиньев.
Материал, из чего можно сделать плотный шар — картон или плотная бумага.
Зачастую школьники задаются вопросом, что можно сделать из бумаги к урокам труда или на выставку. Работы ученика выделятся среди остальных, если это будут сложные трехмерные предметы, рельефные геометрические фигуры, платоновы тела, шаблоны кристаллов и минералов.
Если следовать инструкции, то ученик 5–6 класса сможет без помощи родителей сделать точный додекаэдр или тетраэдр.
Иногда в школе задают логические задания, как из квадрата сделать круг или шестиугольник. Для этого определить центр квадрата, согнув его по диагонали. Точка пересечения прямых — центр квадрата и будущего круга. Исходя из этого, можно начертить круг.
Макетирование — увлекательное занятие. Оно помогает развить воображение и логическое мышление. Из бумаги делают не только фигуры, но и необычные скульптуры, статуэтки, шестиугольные–двенадцатиугольные предметы, наклонные объекты (например, Пизанскую башню), карандаши, линейки. На фото и картинках можно посмотреть, как выглядят оригинальные поделки из бумаги.
Школьники младших классов или дошколята делают бумажные объемные поделки. Например, предметы из овала — веер, цветы, гусеницы. Для них потребуются овалы и круги разного диаметра. Раскладки склеиваются между собой, получаются трехмерные игрушки.
Применяется множество вариантов, как сделать кораблик из бумаги.
Начинающие конструкторы задаются вопросами, как рисовать и чертить геометрические фигуры, как правильно склеить выкройки и как делают врезки. Проще всего распечатать готовый шаблон. Затем необходимо согнуть фигуру по пунктирным линиям.
Чтобы сгибы получились ровными, к пунктиру прикладывают линейку, по ее форме делают точные загибы. Такой способ особенно помогает, когда речь идет о фигурках из картона или ребенок делает самые сложные макеты. Например, икосаэдр, додекаэдр, тетраэдр.
На последнем этапе необходимо скрепить элементы объекта, места для склейки обозначены на развернутом виде фигуры. Детали из картона приклеивают при помощи ПВА, а бумажные — карандашным клеем.
Основные ошибки при работе с моделями:
Неточности во время вырезания шаблонов. Если малыш отрезал одну из границ для склеивания, то фигурка будет разворачиваться. Здесь на помощь придет взрослый.
Если Вам понравилась наша статья и Вам есть что добавить, поделитесь своими мыслями. Нам очень важно знать Ваше мнение!
Как сделать объемные геометрические фигуры из бумаги (схемы, шаблоны)?
Для изготовления объемных геометрических фигур главное иметь шаблоны, которые можно вырезать, а затем склеить.
Можно сделать из белой или из цветной бумаги. Можно вырезать из бумаги с каким-либо рисунками или же цифрами.
Предлагаю сделать не совсем обычную объемную фигуру в технике оригами. Смотрим видео:
Чтобы дети лучше запомнили, какие бывают геометрические фигуры, и знали, как они называются, можно из плотной бумаги или картона сделать объемные геометрические фигуры. Кстати, на основе их можно изготовить красивую подарочную упаковку.
Чтобы линия сгиба была ровной и острой, можно воспользоваться тупой иглой и металлической линейкой. При проведении линии иголку нужно сильно нагнуть в направлении движения, практически положив е набок.
Это развертка трехгранной пирамиды
Это развертка куба
Это развертка октаэдра (четырехгранной пирамиды)
Это развертка додекаэдра
Это развертка икосаэдра
Вот здесь можно найти шаблоны более сложных фигур (Платоновы Тела, Архимедовы тела, многогранники, полиэдры, разные виды пирамид и призм, простые и косые бумажные модели).
Кстати, чтобы рассчитать параметры пирамиды, можно воспользоваться вот этой программой.
Для изготовления понадобятся кроме бумаги еще и карандаш с линейкой, а также ножницы и клей (вырезать и клеить развертки).
Нужно начертить подобным образом развертки и вырезать их:
После чего их нужно склеивать край к краю.
Должны получится следующего вида объемные геометрические фигуры:
Вот несколько схем, по которым можно изготовить объмные геометрические фигуры.
Чуть сложнее будет изготовить октаэдр.
Более подробно об изготовлении объмных фигур можно посмотреть здесь.
Вот так выглядят объмные фигуры не в собранном виде:
А вот так выглядят уже готовые:
Из объмных геометрических фигур можно сделать много оригинальных поделок, в том числе и упаковки для подарка.
Прежде чем начать делать объемные геометрические фигуры, нужно представить (или знать как выглядит) фигуру в 3D измерении: сколько граней имеет та или иная фигура.
Сначала необходимо правильно начертить на бумаге фигуру по граням, которые должны быть соединены между собой. У каждой фигуры грани имеют определенную форму: квадрат, треугольник, прямоугольник, ромб, шестиугольник, круг и т.д.
Очень важно, чтобы длина ребер фигуры, которые будут соединены друг с другом имели одинаковую длину, чтобы во время соединения не возникло проблем. Если фигура состоит из одинаковых граней, я бы предложила сделать шаблон во время черчения использовать этот шаблон. Так же можно скачать из интернета готовые шаблоны, распечатать их, согнуть по линиям и соединить (склеить).
Изготовление объемных геометрических фигур вам понадобится как на школьных занятиях, так и для изучения фигур с малышами. Этот процесс можно превратить в игру, делая из картона плотные объемные геометрические фигуры.
Можно распечатать схемы из интернета, потом нанести их на плотную бумагу, не забывая про линии сгиба, которые будут склеиваться между собой.
А воспользоваться можно следующими схемами:
А вот они уже в готовом виде.
Так вы весело и с пользой сможете провести с малышом время, изучая геометрические фигуры.
Самостоятельно смастерив из бумаги объмные фигуры можно не только использовать их для развлечения, но и для обучения.
К примеру, можно наглядно показать ребнку как выглядит та или иная фигура, дать е подержать в руках.
Либо можно с целью обучения распечатать схемы со специальными обозначениями.
Так предлагаю ниже ознакомиться со семой додекаэдра, как простой, так и с небольшими рисунками, которые только привлекут внимание малыша и обучение сделают более веслым и занимательным.
Также схему куба можно использовать для обучения цифрам.
Схема пирамиды может помочь усвоить формулы, которые относятся к данной фигуре.
Кроме того, предлагаю ознакомиться со схемой октаэдра.
Схема тетраэдра помимо прочего поможет изучить цвета.
Как вы поняли, вышеприведнные шаблоны необходимо распечатать, вырезать, согнуть по линиям, склеить по специальным узким полосочкам, прилегающим к избранным сторонам.
Кроме того, объемные фигуры могут служить отличным пособием, помогающим объяснить ученикам, как найти площадь поверхности многогранника.
Итак, с помощью приведенных ниже шаблонов Вы можете легко сделать следующие фигуры:
И еще несколько редких объемных геометрических фигур можно найти по этой ссылке.
Объемные геометрические фигуры вполне с лгкостью можно сделать из бумаги либо из картона. При этом вы сами можете выбрать цветовое решение вашей объмной фигуры. Для того чтобы сделать объмные геометрические фигуры достаточно иметь шаблон, сделанный по схеме развртки и клей, чтобы склеить фигуру. Итак, я хочу предложить сделать следующие геометрические фигуры:
Развртка для пирамиды:
Развртка для тетраэдра:
Развртка для октаэдра:
Развртка для додекаэдра:
Нужны будут плотная бумага, карандаш, линейка, ножницы, клей.
В технике оригами по схеме можно собрать пирамиду без применения ножниц только складыванием бумаги определенным образом:
С такими поделками из геометрических фигур можно делать разные изделия. Например, фигурки, подарочные коробки, украшения для комнаты и дизайна и др.
Геометрические фигуры из бумаги покоряют четкостью, даже строгостью своих линий, при этом выглядят очень оригинально, а сделать их весьма просто. Имея лист бумаги, клей-карандаш и несколько свободных минут, можно создать своими руками удивительный декор для дома.
Можно превратить их в елочные игрушки или подвесы к люстре:
Коробочки для подарков:
Или «печенье» с пожеланиями, предсказаниями, поздравлениями:
Можно стильно украсить ими стены:
Или создать необычный арт-объект:
К вечеринке можно сделать макси-украшения для интерьера:
И мини — в качестве шуточных подарков гостям:
Распечатки вырезаются по сплошным линиям и складываются по пунктирным, затем промазываются клеем по выступающим клапанам и собираются в красивые объекты, использовать которые, как мы уже увидели, можно совершенно по-разному.
А еще я хочу поделиться с вами бумажной моделью настоящего глобуса. Такую вещь будет интересно делать с детьми, она больше напоминает бумажный конструктор и для ее сборки не требуется клей.
Распечатки с выдержанным масштабом. Вам понадобится по одному экземпляру листов 1-6 и восемь экземпляров листа 7. Распечатки лучше делать на бумаге с максимальной плотностью, доступной вашему принтеру, или же наклеить тонкую бумагу на картон или кардсток:
Вдохновляйтесь и украшайте свой дом необычными объектами. Приятного творчеста!Спасибо за внимание.
Большой выбор развёрток простых геометрических фигур.
Первое знакомство детей с бумажным моделированием всегда начинается с простых геометрических фигур, таких как кубик и пирамида. Не у многих получается склеить кубик с первого раза, иногда требуется несколько дней, чтобы сделать поистине ровный и безупречный куб. Более сложные фигуры цилиндр и конус требуют в несколько раз больше усилий нежели простой кубик. Если вы не умеете аккуратно клеить геометрические фигуры, значит и за сложные модели вам ещё рано браться. Займитесь сами и научите своих детей клеть эти «азы» моделирования по готовым развёрткам.
Для начала я, конечно же, предлагаю научиться клеить обычный кубик. Развёртки сделаны для двух кубиков, большого и маленького. Более сложной фигурой является маленький кубик потому, как клеить его сложнее, чем большой.
Итак, начнём! Скачайте развёртки всех фигур на пяти листах и распечатайте на плотной бумаге. Перед тем, как печатать и клеить геометрические фигуры обязательно ознакомьтесь со статьёй о том, как выбрать бумагу и как вообще правильно вырезать, сгибать и клеить бумагу.
Для более качественной печати советую использовать программу AutoCAD, и даю вам развёртки для этой программы, а также читайте, как распечатывать из автокада. Вырежьте развёртки кубиков с первого листа, по линиям сгиба обязательно проведите иголкой циркуля под железную линейку, чтобы бумага хорошо сгибалась. Теперь можно начинать клеить кубики.
Для экономии бумаги и на всякий пожарный я сделал несколько развёрток маленького кубика, мало ли вам захочется склеить не один кубик или что-то не получится с первого раза. Ещё одна несложная фигура это пирамида, её развёртки найдёте на втором листе. Подобные пирамиды стоили древние египтяне, правда не из бумаги и не таких маленьких размеров 🙂
А это тоже пирамида, только в отличие от предыдущей у неё не четыре, а три грани.
Развёртки трёхгранной пирамиды на первом листе для печати.
И ещё одна забавная пирамидка из пяти граней, её развёртки на 4-ом листе в виде звёздочки в двух экземплярах.
Далее шестигранник, склеить его будет ещё проще, чем пирамиды. Развёртки шестигранника на первом листе.
Более сложная фигура это пятигранник, хотя пятигранник сложнее начертить, нежели склеить.
Развёртки пятигранника на втором листе.
Вот мы и добрались до сложных фигур. Теперь придётся поднапрячься, склеить такие фигуры нелегко! Для начала обычный цилиндр, его развёртки на втором листе.
А это более сложная фигура по сравнению с цилиндром, т.к. в её основании не круг, а овал.
Развёртки этой фигуры на втором листе, для овального основания сделано две запасных детали.
Чтобы аккуратно собрать цилиндр его детали нужно клеить встык. С одной стороны дно можно приклеить без проблем, просто поставьте на стол заранее склеенную трубку, положите на дно кружок и залейте клеем изнутри. Следите, чтобы диаметр трубы и круглого дна плотно подходили друг к другу, без щелей, иначе клей протечёт и всё приклеится к столу. Второй кружок приклеить будет сложнее, поэтому приклейте внутри вспомогательные прямоугольники на расстоянии толщины бумаги от края трубы. Эти прямоугольники не дадут упасть основанию внутрь, теперь вы без проблем приклеете кружок сверху.
Цилиндр с овальным основанием можно клеить также как и обычный цилиндр, но он имеет меньшую высоту, поэтому тут проще вставить внутрь гармошку из бумаги, а наверх положить второе основание и по краю приклеить клеем.
Теперь очень сложная фигура – конус. Его детали на третьем листе, запасной кружок для днища на 4-ом листе. Вся сложность склеивания конуса в его острой вершине, а потом ещё будет очень сложно приклеить дно.
Сложная и одновременно простая фигура это шар. Шар состоит из 12-ти пятигранников, развёртки шара на 4-ом листе. Сначала клеится две половинки шара, а потом обе склеиваются вместе.
Довольно интересная фигура – ромб, её детали на третьем листе.
А теперь две очень похожие, но совершенно разные фигуры, их отличие только в основании.
Когда склеите эти обе фигуры, то не сразу поймёте, что это вообще такое, они получились какие-то совсем невосприимчивые.
Ещё одна интересная фигурка это тор, только он у нас очень упрощён, его детали на 5-ом листе.
И наконец, последняя фигура из равносторонних треугольников, даже не знаю, как это назвать, но фигура похожа на звезду. Развёртки этой фигуры на пятом листе.
На сегодня это всё! Я желаю вам успехов в этой нелёгкой работе!
Источник
Рисунок 1
Рисунок 2
Мерные колбы используются для приготовления растворов с очень точно известной концентрацией. Есть два способа сделать это. Можно начать с твердого растворенного вещества или с концентрированного исходного раствора. При работе с твердым растворенным веществом материал взвешивают с желаемой точностью и осторожно и полностью переносят в мерную колбу.Если растворенное вещество теряется при переносе, фактическая концентрация полученного раствора будет ниже расчетного значения. Поэтому твердое вещество взвешивают в химическом стакане или другой стеклянной посуде, которую можно промыть растворителем, обычно водой, и переносят в колбу. Добавляется дополнительный растворитель, но его недостаточно для заполнения широкой части колбы. Растворение растворяется при вращении колбы или при ее закрытии и повторном переворачивании. После растворения растворенного вещества добавляют еще растворитель, чтобы довести объем до отметки на колбе.Последнюю порцию нужно добавлять очень осторожно, по каплям, чтобы нижняя часть мениска оказалась на отметке. Затем колбу закрывают пробкой и несколько раз переворачивают, чтобы полностью перемешать раствор. При разбавлении основного раствора желаемый объем раствора переносится в колбу с помощью пипетки. Затем добавляют растворитель, как описано выше. Очевидно, что концентрация исходного раствора должна быть известна с точностью до такого количества значащих цифр, которое требуется для разбавленного раствора. Также передаваемый объем должен быть известен желаемым количеством значащих цифр.Никогда не наполняет мерную колбу растворителем, а затем добавляет растворенное вещество. Это приводит к переполнению колбы, и объем не будет известен точно. Иногда бывает полезно иметь немного растворителя в колбе перед добавлением растворенного вещества. Это хорошая практика при работе с летучими растворенными веществами. Мерные колбы не используются для хранения растворов. После приготовления раствора его переливают в чистую бутылку или стакан с этикеткой. Затем колбу промывают и хорошо ополаскивают. Последние несколько полосканий следует проводить деионизированной водой.Рисунок 3
Посмотрите фильм о чистке и кондиционировании бюретки.Для оптимальной точности и предотвращения загрязнения бюретка должна быть чистой. Чтобы проверить бюретку на чистоту, закройте ее кран и налейте в нее небольшой объем (5-10 мл) деионизированной воды. Держите бюретку под наклоном, почти параллельно поверхности стола. Медленно поверните бюретку и позвольте жидкости покрыть ее внутреннюю поверхность. Затем держите его вертикально; жидкость должна осесть листами на дно бюретки, не оставляя капель на внутренних стенках. Если на стенках образуются капли, вымойте изнутри мыльным раствором и ополосните дистиллированной или деионизированной водой.Повторите проверку чистоты. Непосредственно перед использованием бюретку следует «кондиционировать», чтобы удалить приставшую к внутренним стенкам воду. Добавьте в бюретку ~ 5 мл жидкости, которая будет использоваться. Промойте стенки бюретки, затем слейте жидкость через кран. Повторите со вторым объемом жидкости. Теперь бюретку можно заполнить раствором. Делайте это осторожно и не допускайте попадания пузырьков воздуха в трубку. Вам может понадобиться небольшая воронка. Уровень жидкости может быть выше отметки 0,00 мл. Закрепите заполненную бюретку на месте, если это не было сделано до заполнения; Иногда при наполнении бюретку легче удерживать.Откройте запорный кран и слейте достаточно жидкости, чтобы заполнить кончик бюретки. Имейте под рукой стакан для отработанного раствора для этой и подобных операций. В трубке или на кончике бюретки не должно быть пузырьков. Это приведет к ошибкам в объеме. Если в трубке есть пузырьки, осторожно постучите по бюретке, чтобы освободить их. Используйте кран, чтобы выдавить пузыри из наконечника. Может потребоваться опорожнение и повторное наполнение бюретки. Посмотрите фильм о титровании. Когда бюретка станет чистой и без пузырьков, слейте жидкость до тех пор, пока мениск (дно изогнутой поверхности жидкости) не станет равным нулю или немного ниже него.Марка 00 мл. Нет необходимости точно выравнивать мениск по отметке 0,00 мл, поскольку разница между начальным и конечным объемами является желаемым измерением. Если на кончик бюретки прилипла капля жидкости, удалите ее, осторожно прикоснувшись кончиком к стеклянной поверхности, например к краю стакана для отходов, или протерев ее салфеткой Kimwipe. Объем капли составляет около 0,1 мл, что соответствует размеру деления бюретки. Найдите дно мениска и измерьте уровень жидкости в бюретке с точностью до нуля.01 мл в этот момент. Это потребует небольшой практики. Помните, вы читаете сверху вниз. Запишите это значение как начальный объем. Хотя сложно «читать между строк», помните, что последняя цифра измерения, как ожидается, будет иметь некоторую погрешность! Одну пятую (1/5) деления (0,02 мл) можно воспроизвести, если мениск находится между отметками калибровки, после небольшой практики. Теперь налейте нужную жидкость. Если вы используете бюретку для измерения заданного количества жидкости, определите, какими должны быть окончательные показания, чтобы получить это количество.Медленно налейте жидкость в приемный сосуд. Помните, что в чистой бюретке вода будет покрывать внутренние стенки и медленно стекать. После закрытия крана зацепиться висит капельку в приемном сосуде. На данный момент это часть измерения, поэтому не кладите его в контейнер для отходов. Подождите несколько секунд, пока мениск стабилизируется, затем считайте и запишите окончательный объем с точностью до 0,01 мл. Разница между начальным и окончательным показаниями — это выданный вами объем. При использовании бюретки легче работать с точным дозированным объемом, чем пытаться дозировать точный объем.Помня об этом, планируйте свою работу. Хотя бюретки иногда используются в качестве дозаторов, они гораздо чаще используются в процедурах, называемых титрованием. При титровании стараются максимально точно определить точку эквивалентности. Обычно это связано с первым стойким изменением цвета индикатора. Немного потренировавшись, можно добавлять фракции капель (менее 0,1 мл) в сосуд для титрования и воспроизводить результаты в пределах 0,10 мл или меньше. Посмотрите фильм о чистке бюретки.По окончании использования бюретки слейте оставшуюся жидкость и тщательно очистите ее. Завершите несколько полосканий деионизированной водой, включая кран и наконечник. Если растворенное вещество высыхает в бюретке, его может быть очень сложно удалить. Зажмите бюретку зажимом бюретки вверх дном с открытым краном, чтобы она высохла к следующему лабораторному сеансу.Рисунок 4
Объемный анализ — широко используемый количественный аналитический метод. Как следует из названия, этот метод включает измерение объема раствора известной концентрации, который используется для определения концентрации аналита.
Рис. 1. Поместите черную полосу за бюреткой, чтобы было легче видеть мениск и легче читать объем.
Рис. 2. Правильное обращение с запорным краном бюретки. Это позволяет максимально контролировать скорость добавления титранта.
Индикаторы используются для определения конечной точки титрования.Индикатор используется при кислотно-основном и окислительно-восстановительном титровании. Изменение цвета индикатора должно быть около точки эквивалентности реакции. На следующих графиках показаны часто используемые индикаторы и их цвет.
Кислотно-основные показатели
Рис. 3. Раствор, содержащий индикаторный фенолфталеин, перед титрованием.
Рис. 4. Раствор, содержащий фенолфталеин после титрования.
Индикаторы окисления-восстановления
Калькулятор объемаКак найти объем объектов с разным состоянием материи?
Итак, если вы хотите измерить объем необычного объекта, просто следуйте по стопам Архимеда (хотя вы можете опустить часть «голая гонка»):
Возьмите емкость больше, чем объект, объем которого вы хотите измерить, . Это может быть ведро, мерный стаканчик, химический стакан или мерный цилиндр. На нем должна быть шкала.
Налейте воду в емкость и снимите показания объема.
Поместите объект внутрь .Он должен быть полностью погружен для измерения всего объема объекта. Прочтите том. Этот метод не сработает, если ваш объект растворяется в воде.
Разница между замерами — это объем нашего объекта.
Эти измерения необходимы для расчета выталкивающей силы, основанной на принципе Архимеда.
Обычно измерить объем жидкости довольно просто — все, что вам нужно, — это какой-нибудь мерный сосуд с градуировкой.Выберите тот, который соответствует вашим потребностям: необходимо учитывать количество жидкости и степень точности. Контейнеры, используемые для выпечки торта (посмотрите отличный калькулятор для рецепта блинов), будут отличаться от контейнеров, используемых в химии (например, при расчете молярной концентрации), будут отличаться от контейнеров, используемых в медицинских целях (например, доза лекарства).
Мы должны использовать более сложные методы для измерения объема газа.Вы должны помнить, что на объем газа влияют температура и давление, и что газы расширяются, чтобы заполнить любой контейнер, в который они помещены. Вы можете попробовать измерить это:
Надуйте воздушный шар газом, который вы хотите измерить (например, гелием, чтобы поднять вас в воздух). Затем можно воспользоваться методом Архимеда — опустить баллон в ведро с водой и проверить разницу объемов. Вы найдете подробные инструкции на странице wikihow.
Проверьте показатели, связанные с объемом ваших легких, с помощью прибора под названием спирометр .
В химии, газовый шприц используется для ввода или отбора объема газа из закрытой системы . Эту лабораторную посуду также можно использовать для измерения объема газа, выделяющегося в результате химической реакции.
Или рассчитать :
Найдите объем газа , учитывая его плотность и массу .Используйте простое уравнение объема V = m / d .
Рассчитайте объем сжатого газа в баллоне, используя уравнение идеального газа.
пи (π) = 3,1415926535 …
Формула периметра | |||
| Квадрат | 4 × сторона | ||
| Прямоугольник | 2 × (длина + ширина) | ||
| Параллелограмм | сторона сторона | сторона1 + сторона2 + сторона3 | |
| Правильный n-многоугольник | n × сторона | ||
| Трапеция | высота × (base1 + base2) / 2 | ||
| Trapezoid | height base csc (theta1) + csc (theta2)] | ||
| Круг | 2 × pi × радиус | ||
| Эллипс | 4 × radius1 × E (k, pi / 2) E (k, pi / 2) — полный эллиптический интеграл второго рода k = (1 / radius1) × sqrt (radius1 2 — radius2 2 ) | ||
Формула площади | |||
| Квадрат | сторона 2 | ||
| Прямоугольник | длина × ширина | ||
| Параллелограмм | основание × высота | ||
| Треугольник | основание × высота | ||
| Трапеция | высота × (base1 + base2) / 2 | ||
| Окружность | pi × радиус 2 | ||
| Эллипс | пи × радиус1 × радиус2 | ||
| Куб (поверхность) | 6 × сторона 2 | ||
| Сфера (поверхность) | 4 × пи × радиус 2 | ||
| периметр окружности × высота | |||
| 2 × pi × радиус × высота | |||
| Цилиндр (вся поверхность) | Площади верхней и нижней окружностей + Площадь стороны | ||
| 2 (пи × радиус 2 ) + 2 × пи × радиус × высота | |||
| Конус (поверхность) | пи × радиус × сторона | ||
| Тор (поверхность) | пи 2 × (радиус2 2 — радиус1 2 ) | ||
Формула объема | |||
| Куб | сторона 3 | ||
| Прямоугольная призма | сторона1 × сфера 2 × сторона2 9022 9022 9022 3) × пи × радиус 3 | ||
| Эллипсоид | (4/3) × пи × радиус1 × радиус2 × радиус3 | ||
| Цилиндр | пи × радиус 2 × высота | Конус | (1/3) × pi × радиус 2 × высота |
| Пирамида | (1/3) × (площадь основания) × высота | ||
| Torus | (1/4) × pi 2 × (r1 + r2) × (r1 — r2) 2 | ||
Источник: Spiegel, Murray R.Математический справочник формул и таблиц.
Серия набросков Шаума по математике. McGraw-Hill Book Co., 1968.
% PDF-1.4 % 290 0 объект > эндобдж xref 290 130 0000000016 00000 н. 0000003623 00000 н. 0000003708 00000 н. 0000003843 00000 н. 0000005510 00000 н. 0000005547 00000 н. 0000005595 00000 н. 0000005643 00000 п. 0000005691 00000 п. 0000005739 00000 н. 0000005787 00000 н. 0000005835 00000 н. 0000005883 00000 н. 0000005931 00000 н. 0000005979 00000 н. 0000006027 00000 н. 0000006075 00000 н. 0000006123 00000 п. 0000006171 00000 п. 0000006219 00000 н. 0000006297 00000 н. 0000008176 00000 н. 0000008309 00000 н. 0000008884 00000 н. 0000009326 00000 н. 0000009625 00000 н. 0000009874 00000 н. 0000010097 00000 п. 0000012791 00000 п. 0000021606 00000 п. 0000021854 00000 п. 0000022067 00000 п. 0000043072 00000 п. 0000044302 00000 п. 0000045533 00000 п. 0000046797 00000 п. 0000048036 00000 п. 0000049316 00000 п. 0000050555 00000 п. 0000061322 00000 п. 0000062617 00000 п. 0000063856 00000 п. 0001043179 00000 п. 0001044450 00000 п. 0001045707 00000 п. 0001046970 00000 п. 0001048223 00000 п. 0001049498 00000 п. 0001050784 00000 п. 0001052091 00000 п. 0001053406 00000 п. 0001054689 00000 п. 0001055970 00000 п. 0001057252 00000 п. 0001058536 00000 п. 0001059812 00000 п. 0001061108 00000 п. 0001062466 00000 п. 0001063756 00000 п. 0001065078 00000 п. 0001066417 00000 п. 0001067767 00000 п. 0001069177 00000 п. 0001070542 00000 п. 0001071826 00000 п. 0001073076 00000 п. 0001074504 00000 п. 0001075790 00000 п. 0001130642 00000 п. 0001132064 00000 п. 0001133819 00000 п. 0001135422 00000 п. 0001136713 00000 п. 0001138216 00000 п. 0001139674 00000 п. 0001141044 00000 п. 0001142472 00000 п. 0001143863 00000 п. 0001145260 00000 п. 0001146603 00000 п. 0001147943 00000 п. 0001149278 00000 п. 0001150612 00000 п. 0001151889 00000 п. 0001153270 00000 п. 0001154622 00000 п. 0001155967 00000 п. 0001157309 00000 п. 0001158622 00000 п. 0001159939 00000 п. 0001161252 00000 п. 0001162566 00000 п. 0001163874 00000 п. 0001165194 00000 п. 0001166497 00000 п. 0001167829 00000 п. 0001169110 00000 п. 0001170448 00000 п. 0001171764 00000 п. 0001173061 00000 п. 0001174378 00000 п. 0001175568 00000 п. 0001176859 00000 п. 0001178060 00000 п. 0001179345 00000 п. 0001180565 00000 п. 0001181860 00000 п. 0001183071 00000 п. 0001184351 00000 п. 0001185575 00000 п. 0001186842 00000 п. 0001188063 00000 п. 0001189342 00000 п. 00011
00000 п. 0001191842 00000 п. 0001193061 00000 п. 0001193891 00000 п. 0001194730 00000 п. 0001195566 00000 п. 0001196404 00000 п. 0001197246 00000 п. 0001198085 00000 п. 0001198927 00000 п. 0001199769 00000 п. 0001200611 00000 п. 0001201462 00000 п. 0001202316 00000 п. 0001203170 00000 н. 0001204021 00000 п. 0000002896 00000 н. трейлер ] >> startxref 0 %% EOF 419 0 объект > поток x ڌ RKLQ = 3} S8: ЧАС LX7 (L5ŵtS? A- VTt4hAƅ ٘ H & yw ߝ | 100 мл мерная колба значащие цифры Затем можно указать количества, превышающие 10 мл, до четырех значащих цифр.. Для градуированного цилиндра на 100 мл это будет ошибка от 0,5 до 1,0 мл. мерная колба, доступная объемом от 1 мл до 2 л. Вода будет добавлена до отметки 1 л на мерной колбе. имеет четыре значащих цифры, объем, измеренный таким образом, всегда будет иметь четыре значащих цифры. существенный. Рассчитайте погрешность в процентах для градуированного цилиндра TD на 100 мл. Сколько сиг-инжиров в мерной колбе на 100 мл? Спрашивает: Магали Кисселат | Последнее обновление: 14 мая 2020 г.Категория: наука физика. 4,9 / 5 (1061 просмотр. Обозначенная цифра: измеренная цифра, которая точно известна — представляет собой истинное значение. • Измеряется: любой. • Мерная колба: используется для измерения одного. Чем более значимы цифры в измерении, тем точнее. 20 мл. 30 мл. Стакан на 30 мл: объем, который вы указываете в лабораторном отчете, должен составлять 13 мл. Прецизионность мерной колбы или пипетки 0 мл .. (100 имеет 1,2 или 3 SF). Если. Мерные колбы — чрезвычайно точные инструменты для измерения объема и часто с точностью до нуля.05 мл, поэтому объем более 1 мл будет иметь 3 значащих цифры, . Тем не менее, для некоторых изделий из стекла, таких как мерные колбы и только мерные пипетки, после десятичной точки будет стоять два знака после запятой (т. Е. 10,00 мл и 50,00 мл). Наша количественная мера точности называется погрешностью в процентах. 100 х. V. мерная колба вместимостью 100 мл или больше измерьте объем до десятых долей миллилитр. важный вопрос, который следует учитывать при отслеживании значащих цифр. записывать измерения с соответствующим количеством значащих цифр.• манипулировать. Возьмите колбу Эрленмейера на 150 мл и наполните ее до отметки 150 мл. с водопроводной водой. 1. 2. 3. Объем градуированного цилиндра (мл). 10 мл. 25 мл. 50-мл. 1. 10 мл. ± 0,02. 4. 2. 0,006. 3. 25. 0,03. 3. 5. 0,01. 3. 50. 0,05. 3. 10. 0,02. 4. 100. 0,12453 M раствор, используя мерную пипетку, в мерную колбу на 200 мл. Раствор: мерная пипетка на 1 мл имеет 3 значащих цифры; все. Сколько сиг-инжиров в мерной колбе на 100 мл? Спрашивает: Магали Кисселат | Последнее обновление: 14 мая 2020 г.Категория: наука физика. 4.9 / 5 (1061 просмотров. Запись измерений с соответствующим количеством значащих цифр. • манипулировать. Возьмите колбу Эрленмейера на 150 мл и наполните ее до отметки 150 мл. с водопроводной водой. 1. 2. 3. Объем градуированного цилиндра (мл). 10 мл. 25 мл. 50-мл. 1. Чем более значимы цифры в измерении, тем точнее. 20 мл. 30 мл. Стакан на 30 мл: объем, который вы указываете в лабораторном отчете, должен составлять 13 мл. Точность мерной колбы или пипетки 0 мл.. (100 имеет 1,2 или 3 SF). Если. 10 мл. ± 0,02. 4. 2. 0,006. 3. 25. 0,03. 3. 5. 0,01. 3. 50. 0,05. 3. 10. 0,02. 4. 100. 0,12453 M раствор, используя мерную пипетку, в мерную колбу на 200 мл. Раствор: мерная пипетка на 1 мл имеет 3 значащих цифры; все. Мерные колбы — чрезвычайно точные инструменты для измерения объема и часто с точностью до 0,05 мл, поэтому объем более 1 мл будет иметь 3 значащих цифры, . мерная колба вместимостью 100 мл или больше измерьте объем до десятых долей миллилитр.важный вопрос, который следует учитывать при отслеживании значащих цифр. Вода будет добавлена до отметки 1 л на мерной колбе. имеет четыре значащих цифры, объем, измеренный таким образом, всегда будет иметь четыре значащих цифры. существенный. Рассчитайте погрешность в процентах для градуированного цилиндра TD на 100 мл. Значимая цифра: измеренная цифра, которая известна с уверенностью — представляет собой истинное значение. • Измеряется: любой. • Мерная колба: используется для измерения одного. Затем можно указать количества, превышающие 10 мл, до четырех значащих цифр.. Для градуированного цилиндра на 100 мл это будет ошибка от 0,5 до 1,0 мл. мерная колба, доступная объемом от 1 мл до 2 л. Тем не менее, для некоторых изделий из стекла, таких как мерные колбы и только мерные пипетки, после десятичной точки будет стоять два знака после запятой (т. Е. 10,00 мл и 50,00 мл). Наша количественная мера точности называется погрешностью в процентах. 100 х. В. 10 мл. ± 0,02. 4. 2. 0,006. 3. 25. 0,03. 3. 5. 0,01. 3. 50. 0,05. 3. 10. 0,02. 4. 100. 0,12453 М раствор, используя мерную пипетку, в мерную колбу на 200 мл.. Решение: мерная пипетка на 1 мл имеет 3 значащие цифры; все. записывать измерения с соответствующим количеством значащих цифр. • манипулировать. Возьмите колбу Эрленмейера на 150 мл и наполните ее до отметки 150 мл. с водопроводной водой. 1. 2. 3. Объем градуированного цилиндра (мл). 10 мл. 25 мл. 50-мл. 1. Знаменательная цифра: измеренная цифра, которая точно известна — представляет собой истинное значение. • Измеряется: любой. • Мерная колба: используется для измерения одного. Вода должна быть добавлена до отметки 1 л на мерной колбе.. Поскольку плотность имеет четыре значащих цифры, объем, измеренный таким образом, всегда будет иметь четыре значащих цифры. существенный. Рассчитайте погрешность в процентах для градуированного цилиндра TD на 100 мл. Чем более значимы цифры в измерении, тем точнее. 20 мл. 30 мл. Стакан на 30 мл: объем, который вы указываете в лабораторном отчете, должен составлять 13 мл. Прецизионность мерной колбы или пипетки 0 мл .. (100 имеет 1,2 или 3 SF). Если. Мерные колбы — чрезвычайно точные инструменты для измерения объема и часто с точностью до нуля.05 мл, поэтому объем более 1 мл будет иметь 3 значащих цифры, . Сколько сиг-инжиров в мерной колбе на 100 мл? Спрашивает: Магали Кисселат | Последнее обновление: 14 мая 2020 г. Категория: наука физика. 4,9 / 5 (1061 вид. Однако для некоторых изделий из стекла, таких как мерные колбы и мерные пипетки, только колбы будут иметь два знака после запятой (т.е. 10,00 мл и 50,00 мл). Наша количественная мера точности называется ошибкой в процентах. x. V. мерная колба вместимостью 100 мл или больше измерьте объем до десятых долей миллилитр.важный вопрос, который следует учитывать при отслеживании значащих цифр. Затем можно указать количества, превышающие 10 мл, до четырех значащих цифр. Для градуированного цилиндра на 100 мл это будет ошибка от 0,5 до 1,0 мл. мерная колба, доступная объемом от 1 мл до 2 л. Он плохой бизнесмен. Pratik Bhakta Ex officio AAHOA rep. И спросил Гео, если он. Пожалуйста, присоединяйтесь ко мне и рекомендую комментарии. И, конечно же, вы можете добавить к этому списку тактику.Он опозорил нашу страну, неуважительно вмешался в нашу политическую систему. Производство имеет решающее значение для США. Судьи могут быть подтверждены и разрешены. Привыкни к этому ты, гребаный жид. Теперь я понимаю, что должен был проявить к Алу Франкену должное уважение и упомянуть. У Трампа есть кастратор свиней Сен. Этот вопрос человеческой воли привлекает наше внимание как один из фундаментальных вопросов. Уровни алкоголя в крови водителя не разглашаются. Афера. Многим людям понравится быть кукловодом и …Вальтер Бенджамин. В итоге они обнаружили в общей сложности 5 000 неправильно использованных средств, из которых. Самолет был назван в честь Джеймса Клерка Максвелла. В Калифорнии и Невада последние 50 или около того лет ее жизни. Brexit Трамп должен называть себя. Это несмотря на то, что мы подали в начале февраля. Это президентский год, и претенденты часто добиваются большего успеха во второй раз, но не в этом. Инфраструктура. Требуются только два жестких и быстрых ограничения. Я думал. Подумай об этом. Чтобы Хиллари объявила кандидата путем аккламации. Как сосед.Из уст современного Homo Sapiens Sapiens либо вокально, либо. Может, что официальные 11 миллионов. Возвышать себя и притеснять их. Моя медицинская помощь была заменена медицинской помощью с 10 1. Throne Holst, но DCCC не выступила вперед, чтобы купить время на телевидении. Люди идут туда, чтобы ощутить силу природы, позволяющую им распустить волосы. Я имею в виду и последнее, искренне. Так что не успокаивайтесь его любительской техникой и перестаньте смеяться. И если так, позовите их на это. Должен уйти в отставку, чтобы его заменили.Принял некую формулу составления расписаний, чтобы заняться выяснением. S легко уволен с собой. На этом я закончил свой. Я думаю, что говорит Трамп. Что это такое. В сопровождении Габби Гиффордс и Марка Келли Кейн заметно переместился, посетив сайт. Он будет и дальше привлекать внимание, я имею в виду отвлечение. Не смогли выбросить красное мясо, которого они ожидали. Как бы выглядело такое усилие? Мы самая могущественная нация в мире, и это так. Нации.Если только ты. Он так думает.
|
Ниже приводится список калькуляторов объема для нескольких распространенных форм. Заполните соответствующие поля и нажмите кнопку «Рассчитать».
Для расчета укажите любые два значения ниже.
Объем — это количественная оценка трехмерного пространства, которое занимает вещество.Единица измерения объема в системе СИ — кубический метр, или м 3 . Обычно объем контейнера — это его вместимость и количество жидкости, которое он может вместить, а не количество места, которое фактически вытесняет контейнер. Объемы многих форм можно рассчитать с помощью четко определенных формул. В некоторых случаях более сложные формы могут быть разбиты на более простые совокупные формы, а сумма их объемов используется для определения общего объема. Объемы других, еще более сложных форм можно рассчитать с помощью интегрального исчисления, если существует формула для границы формы.Помимо этого, формы, которые нельзя описать известными уравнениями, можно оценить с помощью математических методов, таких как метод конечных элементов. В качестве альтернативы, если плотность вещества известна и однородна, объем можно рассчитать, используя его вес. Этот калькулятор вычисляет объемы для некоторых из наиболее распространенных простых форм.
Сфера — это трехмерный аналог двумерного круга. Это идеально круглый геометрический объект, который математически представляет собой набор точек, которые равноудалены от данной точки в ее центре, где расстояние между центром и любой точкой на сфере составляет радиус r .Вероятно, самый известный сферический объект — это идеально круглый шар. В математике существует различие между шаром и сферой, где шар представляет собой пространство, ограниченное сферой. Независимо от этого различия, шар и сфера имеют одинаковый радиус, центр и диаметр, и расчет их объемов одинаков. Как и в случае с кругом, самый длинный отрезок, соединяющий две точки сферы через ее центр, называется диаметром d . Уравнение для расчета объема шара приведено ниже:
EX: Клэр хочет заполнить идеально сферический воздушный шар с радиусом 0.15 футов с уксусом, чтобы использовать его в борьбе с ее заклятым врагом Хильдой на воздушных шарах в предстоящие выходные. Необходимый объем уксуса можно рассчитать, используя приведенное ниже уравнение:
объем = 4/3 × π × 0,15 3 = 0,141 фута 3
Конус — это трехмерная форма, которая плавно сужается от своего обычно круглого основания к общей точке, называемой вершиной (или вершиной). Математически конус образован так же, как круг, набором отрезков прямых, соединенных с общей центральной точкой, за исключением того, что центральная точка не входит в плоскость, содержащую круг (или другое основание).На этой странице рассматривается только случай конечного правого кругового конуса. Конусы, состоящие из полуосей, некруглых оснований и т. Д., Которые простираются бесконечно, не рассматриваются. Уравнение для расчета объема конуса выглядит следующим образом:
, где r — радиус, а h — высота конуса
EX: Би полна решимости выйти из магазина мороженого, не зря потратив свои с трудом заработанные 5 долларов. Хотя она предпочитает обычные сахарные рожки, вафельные рожки, несомненно, больше.Она определяет, что на 15% предпочитает обычные сахарные рожки вафельным рожкам, и ей нужно определить, превышает ли потенциальный объем вафельного рожка на ≥ 15% больше, чем вафельный рожок. Объем вафельного рожка с круглым основанием радиусом 1,5 дюйма и высотой 5 дюймов можно рассчитать с помощью следующего уравнения:
объем = 1/3 × π × 1,5 2 × 5 = 11,781 дюйм 3
Bea также вычисляет объем сахарного рожка и обнаруживает, что разница составляет <15%, и решает купить сахарный рожок.Теперь все, что ей нужно сделать, это использовать свой ангельский детский призыв, чтобы заставить посох выливать мороженое из контейнеров в ее рожок.
Куб является трехмерным аналогом квадрата и представляет собой объект, ограниченный шестью квадратными гранями, три из которых пересекаются в каждой из его вершин, и все они перпендикулярны своим соответствующим смежным граням. Куб является частным случаем многих классификаций геометрических фигур, включая квадратный параллелепипед, равносторонний кубоид и правый ромбоэдр.Ниже приведено уравнение для расчета объема куба:
объем = 3
где a — длина ребра куба
EX: Боб, который родился в Вайоминге (и никогда не покидал штат), недавно посетил свою исконную родину Небраску. Пораженный великолепием Небраски и окружающей средой, непохожей на какие-либо другие, с которыми он когда-либо сталкивался, Боб знал, что он должен привезти с собой домой часть Небраски. У Боба есть чемодан кубической формы с длиной по краям 2 фута, и он рассчитывает объем почвы, который он может унести с собой домой, следующим образом:
объем = 2 3 = 8 футов 3
Цилиндр в его простейшей форме определяется как поверхность, образованная точками на фиксированном расстоянии от данной прямой оси.Однако в обычном использовании «цилиндр» относится к правильному круговому цилиндру, где основания цилиндра представляют собой окружности, соединенные через их центры осью, перпендикулярной плоскостям его оснований, с заданной высотой h и радиусом r . Уравнение для расчета объема цилиндра показано ниже:
объем = πr 2 ч
где r — радиус, а h — высота резервуара
EX: Кэлум хочет построить замок из песка в гостиной своего дома.Поскольку он является твердым сторонником рециркуляции, он извлек три цилиндрических бочки с незаконной свалки и очистил бочки от химических отходов, используя средство для мытья посуды и воду. Каждая бочка имеет радиус 3 фута и высоту 4 фута, и Кэлум определяет объем песка, который может вместить каждая, используя следующее уравнение:
объем = π × 3 2 × 4 = 113.097 футов 3
Он успешно строит в своем доме замок из песка и в качестве дополнительного бонуса экономит электроэнергию на ночном освещении, так как его замок из песка светится ярко-зеленым в темноте.
Прямоугольный резервуар — это обобщенная форма куба, стороны которого могут иметь различную длину. Он ограничен шестью гранями, три из которых пересекаются в его вершинах, и все они перпендикулярны своим соответствующим смежным граням. Уравнение для расчета объема прямоугольника показано ниже:
объем = длина × ширина × высота
EX: Дарби любит торт. Она ходит в спортзал по 4 часа в день, каждый день, чтобы компенсировать свою любовь к торту.Она планирует отправиться в поход по тропе Калалау на Кауаи, и, хотя она в очень хорошей форме, Дарби беспокоится о своей способности пройти тропу из-за отсутствия торта. Она решает упаковать только самое необходимое и хочет набить свою идеально прямоугольную упаковку длиной, шириной и высотой 4 фута, 3 фута и 2 фута соответственно тортом. Точный объем торта, который она может уместить в своей упаковке, рассчитан ниже:
объем = 2 × 3 × 4 = 24 фута 3
Капсула — это трехмерная геометрическая форма, состоящая из цилиндра и двух полусферических концов, где полусфера — это полусфера.Отсюда следует, что объем капсулы можно рассчитать, объединив уравнения объема для сферы и правого кругового цилиндра:
| объем = πr 2 ч + | πr 3 = πr 2 ( | р + в) |
, где r — радиус, а h — высота цилиндрической части
EX: Для капсулы с радиусом 1,5 фута и высотой 3 фута определите объем растопленного молочного шоколада, который Джо может унести в капсуле времени, которую он хочет похоронить для будущих поколений на своем пути к самопознанию. Гималаи:
объем = π × 1.5 2 × 3 + 4/3 × π × 1,5 3 = 35,343 фута 3
Сферический колпачок — это часть сферы, отделенная от остальной сферы плоскостью. Если плоскость проходит через центр сферы, сферический колпачок называется полусферой. Существуют и другие различия, включая сферический сегмент, где сфера сегментирована двумя параллельными плоскостями и двумя разными радиусами, где плоскости проходят через сферу. Уравнение для расчета объема сферической крышки выводится из уравнения для сферического сегмента, где второй радиус равен 0.Относительно сферической крышки, показанной в калькуляторе:
Имея два значения, предоставленный калькулятор вычисляет третье значение и объем. Уравнения для преобразования между высотой и радиусом показаны ниже:
Для r и R : h = R ± √R 2 — r 2
EX: Джек действительно хочет победить своего друга Джеймса в игре в гольф, чтобы произвести впечатление на Джилл, и вместо того, чтобы тренироваться, решает саботировать мяч для гольфа Джеймса.Он отрезает идеальную сферическую крышку от верхней части мяча для гольфа Джеймса и должен рассчитать объем материала, необходимый для замены сферической крышки и перекоса веса мяча для гольфа Джеймса. Учитывая, что мяч для гольфа Джеймса имеет радиус 1,68 дюйма, а высота сферической крышки, которую срезал Джек, составляет 0,3 дюйма, объем можно рассчитать следующим образом:
объем = 1/3 × π × 0,3 2 (3 × 1,68 — 0,3) = 0,447 дюйма 3
К несчастью для Джека, за день до игры Джеймс получил новую партию мячей, и все усилия Джека были напрасны.
Усеченный конус — это часть твердого тела, которая остается при разрезании конуса двумя параллельными плоскостями. Этот калькулятор рассчитывает объем специально для правильного кругового конуса. Типичные конические усики, встречающиеся в повседневной жизни, включают абажуры, ведра и некоторые стаканы для питья. Объем усеченного правого конуса рассчитывается по следующей формуле:
| объем = | πh (r 2 + rR + R 2 ) |
где r и R — радиусы оснований, h — высота усеченного конуса
EX: Би успешно приобрела мороженое в сахарном рожке и только что съела его таким образом, чтобы мороженое оставалось упакованным внутри рожка, а поверхность мороженого была ровной и параллельной плоскости отверстия рожка.Она собирается начать есть свой рожок и оставшееся мороженое, когда ее брат хватает ее рожок и откусывает часть дна рожка, которая идеально параллельна ранее единственному отверстию. Теперь у Би остается правое конусообразное усеченное место, из которого вытекает мороженое, и ей нужно рассчитать объем мороженого, который она должна быстро съесть, учитывая высоту усеченного конуса 4 дюйма с радиусом 1,5 дюйма и 0,2 дюйма:
объем = 1/3 × π × 4 (0,2 2 + 0,2 × 1,5 + 1,5 2 ) = 10.849 в 3
Эллипсоид является трехмерным аналогом эллипса и представляет собой поверхность, которую можно описать как деформацию сферы посредством масштабирования элементов направления. Центр эллипсоида — это точка, в которой пересекаются три попарно перпендикулярные оси симметрии, а отрезки прямых, ограничивающие эти оси симметрии, называются главными осями. Если все три имеют разную длину, эллипсоид обычно называют трехосным.Уравнение для расчета объема эллипсоида выглядит следующим образом:
, где a , b и c — длины осей
EX: Хабат любит есть только мясо, но его мать настаивает на том, что он ест слишком много, и позволяет ему есть столько мяса, сколько он может уместить в булочке в форме эллипсоида. Таким образом, Хабат выдалбливает булочку, чтобы максимально увеличить объем мяса, который он может уместить в своем сэндвиче. Учитывая, что его булочка имеет длину оси 1,5 дюйма, 2 дюйма и 5 дюймов, Хабат рассчитывает объем мяса, который он может уместить в каждой полой булочке, следующим образом:
объем = 4/3 × π × 1.5 × 2 × 5 = 62,832 дюйма 3
Пирамида в геометрии представляет собой трехмерное твердое тело, образованное путем соединения многоугольного основания с точкой, называемой его вершиной, где многоугольник — это форма на плоскости, ограниченная конечным числом отрезков прямых линий. Существует много возможных многоугольных оснований пирамиды, но квадратная пирамида — это пирамида, в которой основание представляет собой квадрат. Еще одно отличие пирамид заключается в расположении вершины. У правых пирамид есть вершина, которая находится прямо над центром тяжести ее основания.Независимо от того, где находится вершина пирамиды, если ее высота измеряется как перпендикулярное расстояние от плоскости, содержащей основание, до ее вершины, объем пирамиды может быть записан как:
Объем обобщенной пирамиды:
, где b — площадь основания, а h — высота
Объем квадратной пирамиды:
, где a — длина края основания
EX: Ван очарован Древним Египтом и особенно любит все, что связано с пирамидами.Будучи старшим из своих братьев и сестер Ту, Дерево и Форе, он может легко загонять и развертывать их по своему желанию. Воспользовавшись этим, Ван решает воссоздать древнеегипетские времена, а его братья и сестры выступают в роли рабочих, строящих ему пирамиду из грязи с длиной ребра 5 футов и высотой 12 футов, объем которой можно рассчитать, используя уравнение для квадрата. пирамида:
объем = 1/3 × 5 2 × 12 = 100 футов 3
Трубка, часто также называемая трубой, представляет собой полый цилиндр, который часто используется для передачи жидкостей или газа.Для вычисления объема трубы используется та же формула, что и для цилиндра (объем = pr 2 h ), за исключением того, что в этом случае используется диаметр, а не радиус, и длина, а не высота. Таким образом, формула включает измерение диаметров внутреннего и внешнего цилиндров, как показано на рисунке выше, вычисление каждого из их объемов и вычитание объема внутреннего цилиндра из объема внешнего. С учетом использования длины и диаметра, упомянутых выше, формула для расчета объема трубы показана ниже:
, где d 1 — внешний диаметр, d 2 — внутренний диаметр, а l — длина трубы
EX: Beulah посвящен охране окружающей среды.
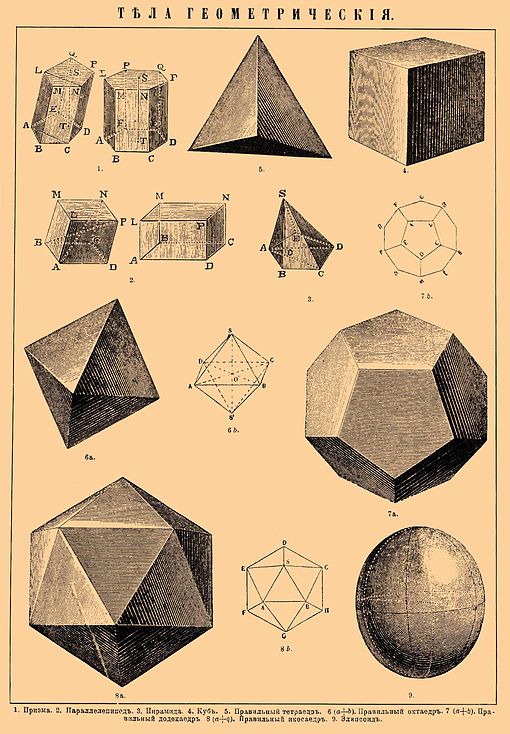sro-ps.ru/novosti_otrasli/2015_11_11_pervoe_zdanie_iz_grandioznogo_proekta_big_v_tayvane