Главная » Детские рисунки » Школа » Математика » Цифры
ЦифрыВремя чтения 2 мин.Просмотры 1.2к.
В народном фольклоре часто можно встретить прямые и косвенные упоминания цифры 3. Где-то в анекдотах будет три персонажа, в какой то сказке будет у героя 3 попытки и даже в религии это число не обошли стороной. Предлагаем Вашему вниманию самые разнообразные варианты написания тройки в картинках и рисунках.
Со штриховкой.
В очках.
Картинка с огоньком.
Шаблон-трафарет.
В осенней стилистике.
Фотография.
Металлическая цифра.
В радужной расцветке.
С красивым узором.
Чёрно-белая иллюстрация.
Из роз.
Живая цифра.
Цифра 3.
Яркая картинка.
Срисовка.
Картинка для оформления.
В виде животного.
Тройка с большими глазками.
Желтый рисунок.
Для раскрашивания.
С цветочками.
Рисуем синей ручкой.
Красивые цвета.
Со звёздами.
В виде граффити.
В виде монстра.
3 в шляпе.
Объёмная цифра.
Контурный рисунок.
Крупная картинка.
В кружочке.
В виде зелёного шарика.
Из дерева.
Современный арт.
Значок.
Рисуем число.
Весёлая 3.
С короной.
Без фона.
С заданием для дошкольников.
Срисовка для юных художников.
На урок в школу.
В детский садик.
Макет для вырезания.
Классный арт.
Трафарет для ребёнка.
Учимся писать по точкам.
Под старину.
Крутой арт.
Для социальных сетей.
Змея изобразила цифру 3.
Со стихами.
Мелкая иллюстрация.
Лежит на красном фоне.
С тенью.
Черная тройка на белом фоне.
В виде крабика.
Картинка с наклоном.
Удовлетворительная оценка.
Картинка в хорошем качестве.
Можно нарисовать синей ручкой.
Под золотое оформление.
С сердечками.
Срисовка для цветных карандашей.
Маленький рисунок.
Для юных художников.
По клеточкам.
С ручками и ножками.
С бликами.
Живая 3.
Для стены.
Картинка с приколом.
Рисуем цифру вместе с мальчиками.
Срисовка для девочек.
На урок в школу.
В виде кнопки.
Арт для девушек.
Рисуем по штрихам.
Цветная картинка с цифрой.
Сиреневый шарик.
На рабочий стол.
Рисунок для детей.
Срисовка для начинающих художников.
Картинка с тройкой.
На прозрачном фоне.
Можно повторить кисточкой и красками.
3 в огне.
Под новый год.
Красное и чёрное.
С весёлым личиком.
В интересном оформлении.
С крючками.
Необычный зверь.
В необычном свете.
Для оформления социальных сетей.
Спреем.
В неоновом свете.
На сером фоне.
Рисуем вместе с ребёнком.
17100 ₽
Купить
17100 ₽
Купить
17100 ₽
Купить
17100 ₽
Купить
17100 ₽
Купить
17100 ₽
Купить
17100 ₽
Купить
17100 ₽
Купить
17100 ₽
Купить
17100 ₽
Купить
17100 ₽
Купить
17100 ₽
Купить
17100 ₽
Купить
17100 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
6000 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
499 ₽
Купить
6000 ₽ 4500 ₽
Купить
700 ₽ 540 ₽
Купить
700 ₽ 540 ₽
Купить
700 ₽ 540 ₽
Купить
700 ₽ 540 ₽
Купить
700 ₽ 540 ₽
Купить
700 ₽ 540 ₽
Купить
700 ₽ 540 ₽
Купить
700 ₽ 540 ₽
Купить
700 ₽ 540 ₽
Купить
700 ₽ 540 ₽
Купить
700 ₽ 540 ₽
Купить
700 ₽ 540 ₽
Купить
700 ₽ 540 ₽
Купить
700 ₽ 540 ₽
Купить
700 ₽ 540 ₽
Купить
700 ₽ 540 ₽
Купить
700 ₽ 540 ₽
Купить
700 ₽ 540 ₽
Купить
700 ₽ 540 ₽
Купить
700 ₽ 540 ₽
Купить
700 ₽ 540 ₽
Купить
700 ₽ 540 ₽
Купить
700 ₽ 540 ₽
Купить
700 ₽ 540 ₽
Купить
700 ₽ 540 ₽
Купить
700 ₽ 540 ₽
Купить
700 ₽ 540 ₽
Купить
700 ₽ 540 ₽
Купить
700 ₽ 450 ₽
Купить
1800 ₽ 800 ₽
Купить
1800 ₽ 800 ₽
Купить
1800 ₽ 800 ₽
Купить
1800 ₽ 800 ₽
Купить
1800 ₽ 800 ₽
Купить
1800 ₽ 800 ₽
Купить
1800 ₽ 800 ₽
Купить
1800 ₽ 800 ₽
Купить
1800 ₽ 800 ₽
Купить
1800 ₽ 800 ₽
Купить
1800 ₽ 800 ₽
Купить
1800 ₽ 800 ₽
Купить
1800 ₽ 800 ₽
Купить
1800 ₽ 800 ₽
Купить
1800 ₽ 800 ₽
Купить
1800 ₽ 800 ₽
Купить
1800 ₽ 800 ₽
Купить
1800 ₽ 800 ₽
Купить
1800 ₽ 800 ₽
Купить
1800 ₽ 800 ₽
Купить
1800 ₽ 800 ₽
Купить
50000 ₽ 45000 ₽
Купить
1800 ₽ 800 ₽
Купить
1800 ₽ 800 ₽
Купить
1800 ₽ 800 ₽
Купить
1800 ₽ 800 ₽
Купить
1800 ₽ 800 ₽
Купить
1800 ₽ 800 ₽
Купить
1800 ₽ 800 ₽
Купить
1800 ₽ 800 ₽
Купить
1800 ₽ 800 ₽
Купить
1800 ₽ 800 ₽
Купить
1800 ₽ 800 ₽
Купить
1800 ₽ 800 ₽
Купить
1800 ₽ 800 ₽
Купить
1800 ₽ 800 ₽
Купить
1800 ₽ 800 ₽
Купить
1800 ₽ 800 ₽
Купить
1800 ₽ 800 ₽
Купить
1800 ₽ 800 ₽
Купить
1800 ₽ 800 ₽
Купить
1800 ₽ 800 ₽
Купить
1800 ₽ 800 ₽
Купить
700 ₽ 450 ₽
Купить
Показать все красивые номера
Золотое сечение.
Божественная пропорция. Число 1,618… имеет много разных имен. Однако математики чаще всего называют его фи . Повсюду вокруг нас мы видим это красивое число. Не само число особенное, а все другие красивые объекты, которые вращаются вокруг него. Математически это число можно выразить в виде:
Символ слева — это греческая буква, обозначающая фи . Если вы заметили, это также положительный корень уравнения x²-x-1. Одно очень интересное свойство этого числа можно найти в последовательности Фибоначчи. Последовательность Фибоначчи в основном начинается с 2 единиц, а затем следующие числа могут быть выражены как сумма предыдущих 2 чисел. Рекурсивно это может быть выражено как:
Численно это может быть выражено как:
В этой последовательности, если вы разделите каждый член на член, который ему предшествует, вы заметите, что частное начинает медленно приближаться к фи . Мы можем построить график, чтобы визуализировать это.
Вместо того, чтобы вручную вычислять частные, я сделал простой код Python для расчета частных:
Код:
num_1 = 1
num_2 = 1
fib_no = [1, 1]
update = 0
flag = 0
while update < 14:
if flag == 0:
num_1 += num_2
fib_no.append(num_1)
flag = 1
elif flag ==1:
num_2 += num_1
fib_no.append(num_2)
флаг = 0
обновление += 1
print(fib_no)
quo_list = []
for ind in range(0, len(fib_no)-1):
quo = fib_no[ind+1]/fib_no[ind]
quo_list.append(quo)
print( quo_list)
Вывод:
[1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987] [1.0, 2.0, 1.5, 1.6666666666,666667 1.6, 1.625, 1.6153846153846154, 1.61119, 1.6176470588235294, 1.6181818181818182, 1.6179775280898876, 1.6180555555555556, 1.6180257510729614, 1.6180371352785146, 1.618032786885246]
Using this data, we will construct a graph with the index of the dividend on the x-axis and the quotient, up to 3 десятичных знака по оси Y:
График частных и индексов, нарисованный автором с использованием GeoGebra Как вы можете ясно видеть на этом графике, все частные приближаются к y = 1,618. Это традиционное математическое происхождение фи .
Несмотря на это блестящее происхождение числа фи , это число чаще встречается в природе. Из-за того, что число фи присутствует почти во всех красивых или элегантных вещах на Земле, оно получило название «Божественная пропорция», поскольку считалось, что только Бог мог поместить такое число в каждую красивую вещь. Phi также считается одним из фундаментальных строительных блоков природы. Давайте посмотрим на несколько примеров, где фи заметно видны.
Один из наиболее распространенных примеров, который люди приводят, когда говорят о фи , находится в центре подсолнуха.
Photo by Laura Gilchrist on Unsplash Как вы можете видеть на этом изображении, семена подсолнуха растут по противоположным спиралям. Теперь, если вы посчитаете диаметры последовательных спиралей и разделите их, у вас останется фи ! Довольно блестяще, не так ли? Поскольку мы сейчас говорим о спиралях, давайте посмотрим на это морское животное, называемое наутилусом.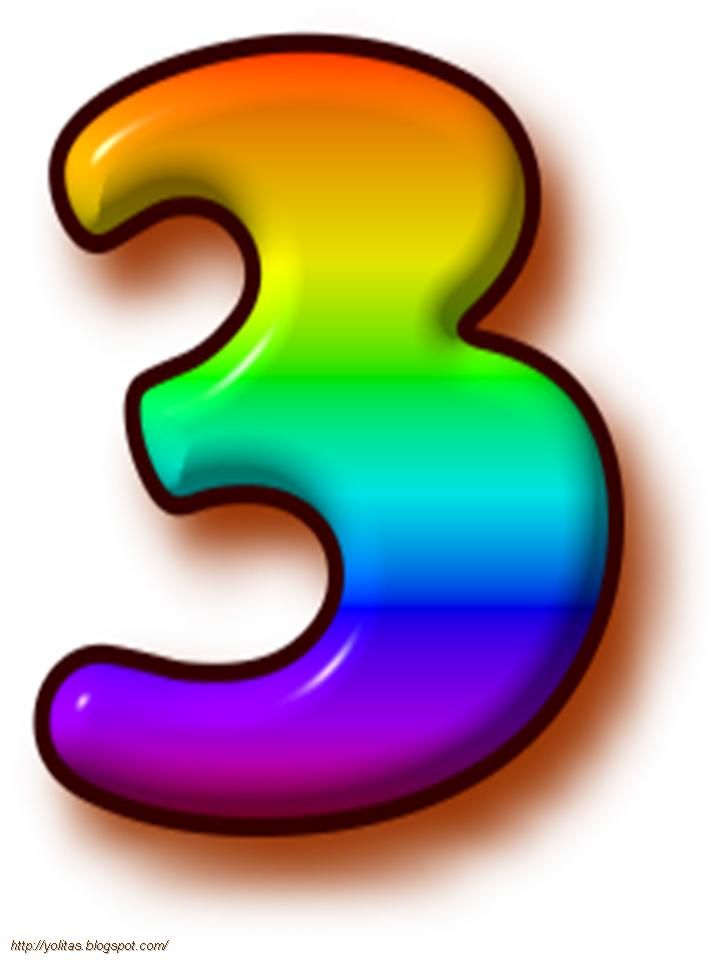
У наутилуса очень интересная раковина, и если вы посмотрите на следующие две фотографии, вы поймете, что я имею в виду:
Как вы можете ясно видеть на этом изображении, если вы разделите длину большего квадрата на длину предшествующего меньшего квадрата, у вас останется с фи снова . Очень часто вы будете видеть эту кривую наложенной на изображения подсолнуха и наутилуса, которые мы видели выше.
Галактика Млечный Путь действительно очень красива. Лучистые рукава галактики не перестают привлекать внимание.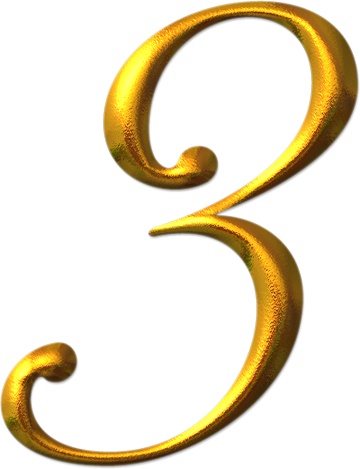
Однако, поскольку это спираль, как и в других примерах, думаете ли вы, что деление диаметров даст фи ? Если вы так подумали, то вы правы! Действительно, частное, которое получается при делении последовательных диаметров спиралей в галактике, и есть золотое сечение. Несомненно, наши предки были бы поражены, увидев повсюду это число, и поверили бы, что оно было введено самим Богом.
Ураганы — одно из самых смертоносных стихийных бедствий в мире. Но видели ли вы когда-нибудь их спутниковое изображение сверху? Если да, то вы бы знали, что ураган выглядит как спираль. И, без сомнения, на этот раз, если вы разделите диаметры каждой спирали, у вас останется фи снова. Многократное наблюдение этого числа в природе действительно показывает, что это число чрезвычайно красиво и элегантно.
Photo by NASA on Unsplash Известно, что в улье самок всегда больше, чем самцов. Однако что действительно особенного, так это то, что если вы разделите количество пчел-самок на количество пчел-самцов, вы получите , всегда останется с фи ! Разве это не удивительно? Божественную Пропорцию можно увидеть и вне природы, внутри наших собственных тел! «Где?», — спросите вы.
Что ж, посмотрим!
Если вы разделите длину вашего плеча до пальцев на длину вашего локтя до ваших пальцев, вы снова получите фи ! Точно так же, разделив расстояние от бедра до пальцев ног на расстояние от колена до пальцев ног, неудивительно, что вы снова получите фи . Есть еще несколько примеров золотого сечения, которые можно увидеть в человеческом теле. Как сказал Роберт Лэнгдон в международном бестселлере Дэна Брауна Код да Винчи :
Друзья мои, каждый из вас — ходячая дань уважения Божественной Пропорции.
Неудивительно, что, увидев красоту этого числа, многие художники, архитекторы и музыканты стали использовать это число в своих работах. От Да Винчи до Микеланджело, от Бетховена до Моцарта, все эти люди строго следовали Божественной Пропорции. Это число встречается во многих памятниках, таких как Великие пирамиды в Египте, Парфенон в Греции и даже в современных зданиях, таких как штаб-квартира Организации Объединенных Наций в Нью-Йорке.
Легенда гласит, что знаменитая семья скрипичных мастеров Страдивари использовала фи как основа для маркировки эфов на их скрипках! С такими легендами, использующими в своих работах золотое сечение, можно не сомневаться, что фи действительно самое красивое число в математике.
Все эти примеры показывают, что золотое сечение проявляется повсюду, куда бы мы ни пошли. Имея изящные корни в математике, число фи преодолевает все границы и распространяется на самые разные области нашей жизни. Он показывает нам, как просто строго соблюдая золотое сечение, можно действительно создавать прекрасные объекты.
Фото Wikimedia Commons Иногда числа находятся с помощью красивых уравнений и формул. Они также могут иметь математическую красоту, поскольку их свойства предлагают предсказуемый результат, привлекательный визуально и интеллектуально.
Aleph Null — красивая концепция. Это наименьшее бесконечное число. Я знаю, о чем вы думаете, бесконечность должна быть всего лишь одним понятием, а не множеством бесконечных чисел. Ведь если есть бесконечность больше другой бесконечности, то первая точно не бесконечность .
Предположим, что у нас есть базовое представление о том, что такое бесконечность (обсуждается ниже, 12 в списке). Алеф нуль — это количество натуральных чисел (0, 1, 2, 3 и т. д.). Это понятие или число огромно по размеру и бесконечно.
Что, если мы посчитаем все натуральные числа два или три раза? После завершения первого набора у нас будут числа, выходящие за пределы натуральных чисел в 9.0085 заказ
Приведенный ниже график является упрощенным представлением. Каждый набор может представлять существующий набор натуральных чисел, и каждый набор имеет мощность ℵ0. Добавление одного после первого набора не меняет кардинальность (вы можете просто изменить порядок, и вы все равно останетесь с кардинальностью Алеф Нуль).Полезно думать о них как о ординалах (порядке). Следовательно, первое порядковое трансфинитное число после набора — это то, что мы обсуждали выше. «ω»
Представление спички. Источник изображения: Википедия.У вас нет омега-яблок, но вы можете финишировать омега в гонке (если вы действительно плохи)
Интересно, что ω + 1 не обязательно больше, чем ω, оно просто идет после него. Это все слишком много, чтобы принять во внимание, поэтому рассмотрение вещей в перспективе должно помочь. Вот что мы должны знать:
Алеф Нуль — это только первый из огромного набора других «Алефов». Vsauce сделал потрясающее видео, в котором обсуждается эта концепция, и я очень рекомендую его.
Итак, это скорее идея или концепция , чем число. Символ часто называют лемнискатой ∞ . Прежде чем обсуждать характеристики и забавные факты о бесконечности, важно отметить, что число пи (обсуждаемое ниже в списке) считается формой бесконечности. Разумеется, под этим мы подразумеваем диапазон чисел после точки 3,14159.… Вот почему бесконечность — это концепция, а не то, что мы можем измерить количественно.
Другой пример исходит из прекрасного поля фракталов. Возьмем, к примеру, простую снежинку Коха, которую можно разделить на бесконечно малые снежинки одинаковой формы.
Интересно, что когда мы думаем о бесконечности, мы представляем себе постоянно растущую меру, но она не расширяется или становится больше. Это уже то, что есть.
Давайте обсудим две простые темы, связанные с бесконечностью (те, которые не требуют мозговой активности, потому что моему на данном этапе нужно вздремнуть после разговоров о Алеф Нуль и Бесконечности). Интересно, Георг Кантор отец теории множеств и исследований бесконечности был институционализирован во многих моментах своей жизни):
Естественно, 0,99999 имеет девятки, стремящиеся к бесконечности, так что мы приблизительно знаем, что оно равно 1 . Proving it algebraically is also possible:
If we have X = 0.9999 then
10X = 9.
If we subtract X from each side, we’d have
9X = 9.9999 -0.9999
9X = 9
Деление на 9
X = 1
Странно, да?
Любое число, вычтенное из самого себя, даст ноль. Но бесконечность — это не число. Следовательно, давайте проверим тест:
∞ — ∞ = 0
∞ — ∞ + 1= 0 + 1 # Добавляем 1 к обеим сторонам
∞ + 1 — ∞, зная, что = 1 # = ∞, мы можем упростить уравнение
Мы получили совершенно другой результат. С помощью этого метода мы можем получить бесконечность минус бесконечность, чтобы получить любое число, которое мы хотим. Таким образом, ответ на ∞ — ∞ не определено.
Наконец, нас также учат, что мы не можем делить на 0. Нас учат, что 1 / 0 = Undefined, однако это не ложно, но не раскрывает всей истории. Подумайте об этом интуитивно, если вы разделите 1 яблоко на 0 человек, сколько человек вам понадобится, чтобы покрыть все яблоко? Естественно, это форма бесконечности, которая никогда не схлопывается .
Итак, изначально 1/0 = ∞ . Почему нас учат, что результат не определен? Просто, когда у нас есть 1/маленькие положительные числа, стремящиеся к нулю, просто предположить, что 1/0 = ∞ . Дело в том, что здесь бесконечность — это положительная бесконечность. А если мы делаем 1/маленькими отрицательными числами, стремящимися к нулю, то можно также считать, что 1/0 = — ∞ . Итак, что это? 1/0 = ∞ или 1/0 = — ∞ ? Что ж, ответ undefined .
Итоговая таблица операций на бесконечности:
∞ + ∞ = ∞ Буква i обозначает мнимое число. Определение мнимого числа состоит в том, что когда мы возводим его в квадрат, это дает нам отрицательный результат. Это не то, о чем мы обычно думаем, возводя числа в квадрат, потому что мы знаем, что умножение двух одинаковых символов всегда даст положительный результат. Концепция мнимых чисел проста. Мы можем предположить (или вообразить), что они существуют. Чем они полезны? Ну, мы можем решать уравнения, которым нужен квадратный корень из отрицательного числа. Вот пример: Мы добавляем i для представления мнимого числа, чтобы 2, возведенное в степень 2, равнялось -4. Давайте проверим очень простое уравнение, которое обычно не имеет решения, и посмотрим, как оно решается с помощью мнимых чисел: Очевидно, что x, возведенный в степень 2, никогда не может дать отрицательное число (-1 в нашем случае), поэтому мы просто предполагаем, что ответ (как мы сделали выше) умножается на i. Вы можете представить себе квадратный корень из -1 (√-1) как исходное мнимое число. Как и в числе 1 для действительных чисел. Другое использование мнимых чисел заключается в их объединении с натуральными числами для получения комплексных чисел (например, 7i + 12) и в электричестве через соответствующие токи. Гугол равен 10, за которым следуют 100 нулей, поэтому, чтобы представить ситуацию в перспективе, подумайте о следующем числе: 10,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000 ,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000, 000, или вы можете просто быть нормальным и думать об этом так: Это примерно 70! (Факториал). что составляет 70 х 69 х 68 х 67 х 66 х 65 х 64 х 63 х 62 х 61 х 60 х 59 …. x 1 Чтобы еще больше усложнить нам ум, существует число, называемое Googol plex, которое просто равно 10 в степени Googol и записывается как: Интересно отметить, что компания Google — это неправильное написание названия Googol. Это мое любимое число, и, вероятно, оно предназначено для торговли, но я также нахожу его визуально и математически красивым. В геометрии мы склонны находить его скрытым во многих местах, например:
∞ × ∞ = ∞
-∞ × -∞ = ∞
-∞ × -∞ = ∞
-∞ × ∞ = ∞
-∞ × ∞
Но это не мешает нам создать аксиому, запрещающую существование таких чисел. Мы называем их воображаемыми, потому что они не должны существовать. Чему равен квадратный корень из -6? Мы не знаем. Калькулятор выдаст вам недопустимую ошибку ввода, потому что какие два числа нужно перемножить, чтобы получить отрицательное число? Но прелесть математики в том, что, в отличие от других научных инструментов, вы можете предположить, что вещи существуют, и настроить их так, чтобы они существовали, если они вам не подходят.
Это действительно умный способ назвать вашу поисковую систему. Это число в основном используется в астрономических исследованиях, таких как большое замораживание Вселенной.
)
Каждый угол равен 60 x 3 (180 = 1 + 8 = 9 )Следующие фигуры и их углы.
Источник: wikipedia.orgСлева направо: Пентагон, Восьмиугольник, Декагон.
Кроме того, если мы добавим цифры, которые стоят перед числом 9 (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 36). Тогда у нас будет, как обычно, 3 + 6 = 9
Умножение цифр, стоящих перед 9 , и суммирование их элементов всегда даст нам 9 , примеры:
, примеры:
Я слышал, как доктор Шелдон Купер утверждал, что 73 — идеальное число, вот цитата:“ Лучшее число 73. Почему? 73 — 21-е простое число. Его зеркало 37 является 12-м, а его зеркало 21 является произведением 7 и 3 . ”’”
“ В двоичном коде 73 есть палиндром, 1001001, который в обратном порядке равен 1001001 . »’
Цитаты взяты из сериала из 10 серии 4 сезона, которая по совпадению является 73 -й серией шоу (и годом рождения Джима Парсонса, актера, изображающего Шелдона).
Назван в честь Леонарда Эйлера, e — иррациональное число и основание натуральных логарифмов. Интересно, что число Эйлера известно с точностью до 1 триллиона знаков [источник: mathisfun.com]. Оно находится по следующей формуле:
Когда n приближается к бесконечности, мы получаем более четкое представление о значении e .
Когда n = 100 000, e = 2,71827. Интересное свойство e состоит в том, что его 9Наклон 0085 равен его значению . Он также используется в финансах для расчета сложных процентов. Я полагаю, что те из вас, кто уже прошел тест CFA, знакомы с этой информацией.
Леонардо Боначчи, также известный как Леонардо Фибоначчи (это прозвище означает «сын Боначчи»), создал одну из самых захватывающих серий в нашей вселенной, используя простые методы сложения и наблюдая за популяциями кроликов. Теперь, чтобы быть справедливым, есть некоторые свидетельства того, что индийские математики знали эту последовательность заранее, мы будем придерживаться общепризнанного факта, что Фибоначчи придумал эту последовательность (хотя, зная яркую научную и математическую историю индийских исследователей, я бы не удивлюсь, узнав, что они были первыми, кто обнаружил это).
Числа Фибоначчи получаются с помощью следующей простой формулы для n > 2:
Это дает нам следующую последовательность, уходящую в бесконечность:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ….
Прелесть этой последовательности в том, что она связана с природой. Например, появляется цветение артишока, лепестки некоторых цветов, таких как ромашки, медоносные пчелы и т. д. Встречается ли это даже в спиралях галактики?
Существует даже очень интересное наблюдение, основанное на фактах, которое предполагает, что размеры Земли и Луны находятся в соотношении Фи, образуя Треугольник, основанный на 1,618, Гэри Мейснера. Но что такое Phi и что такое 1,618?
Если мы возьмем любые два последовательных числа в последовательности, их отношение (Xn / Xn-1) приблизится к 1,618, что мы называем золотым сечением:
3 / 2 = 1 .5
13 / 8 = 1,6 66
55 /34 = 1,61 764
233 /144 = 1,6180 5
…
317,811 / 196,418 = 1,6180 3
Многие из нас видели фильм «Число 23 », в котором Джим Керри изображает Уолтера Воробья как человека, который становится одержимым числом 23 , прочитав об этом в книге. Считается, что это число таинственным образом совпадает со многими событиями по всему миру и , хотя это может быть прекрасным примером Апофения , , все же интересно перечислить некоторые события, которые имеют 23 9В них встроено число 0086:
% шанс.
Сообщение Аресибо — это сообщение, отправленное с Земли в космос в поисках разумной жизни. Подводит итог нашей жизни.
В этом списке есть много других чисел с гораздо более интересными характеристиками.Знаменитое иррациональное число, представляющее отношение длины окружности к ее радиусу. Кто из нас не встречал этот номер?
Если начертить круг диаметром 1, то длина окружности будет равна 3,14159 … что просто обозначается буквой π . Это просто окружность на диаметр. Теперь нам не нужно возвращаться к понятиям геометрии средней школы, поэтому я просто перечислю два интересных свойства числа π :
Почему я включил Тау? Некоторые математики спорят о полезности π и вместо этого предлагают Тау, который равен просто τ = 2π . Многие математики утверждают, что Тау больше подходит для вычисления окружностей.
Их интуиция верна, когда мы хотим углубиться в детали, но кто не любит Pi(e) ?
Интересно отметить, что существует день числа Пи, который отмечается каждый год 14 марта (дата в США отображается в формате ММ/ДД, что дает нам 3/14).
Вот почему я включил в название слово «красота». Сочетание некоторых из самых красивых концепций в математике может дать нам такие простые результаты. Давайте вернемся на первое место, о чем мы говорим, и как мы собираемся их объединить:
Как мы получили -1 от трех мушкетеров?
Как мы уже вместе видели, я возвел в степень 2 = -1. Леонард Эйлер применил ряд Тейлора, дав ему следующее уравнение (опуская детали, поскольку они выходят за рамки этой статьи): круг. Включив радиус r, мы можем преобразовать точки в другую форму, такую как re в степени ix .
Если принять x = π , то мы будем иметь следующее:
Зная, что cos π = -1 и sin π = 0, то i справа исчезнет:
Итак, мы также можем изменить это уравнение, чтобы сделать его более красивым, и добавить еще одно простое число:
Также известное как константа Капрекара, это число имеет особую особенность, если вы выполните следующие шаги (взято из разных источников, но скажем, из Википедии):
Если вы сделаете это для нескольких шагов, вы всегда получите 6174 , и это загадочная вещь. Почему мы всегда заканчиваем этим числом, независимо от того, с каких чисел вы начинаете. Возьмем пример 2714:
Другой пример 3687:
Теперь, если у нас есть 6174 , мы всегда будем оставаться на 6174 , потому что 7641 -1467 = 0874 6174.
Это также число Харшада, означающее, что оно делится на сумму своих составляющих: 6174 / (6 + 1 + 7 + 4) = 6174 / 18 = 343. Так что это добавляет ему крутости.
Мы уже обсуждали это соотношение, но это, вероятно, самое важное соотношение в мире (Его назвали греки). Вот список его характеристик:
Например, лицо. Следующее, вероятно, не является самым точным исследованием, но доктор Шмид имеет 10-кратное соотношение по шкале, где 10 является самым высоким (самый красивый человек), а большинство людей получают от 4 до 6. Метрика красоты сначала измеряется длиной и ширина лица затем делится на ширину. Оптимальный результат 1,618. Это означает, что лицо красивого человека в 1,618 раза длиннее его ширины. Позже рассчитываются другие отношения, такие как нижняя часть носа к нижней части подбородка. Наконец, выполняются тесты на симметрию, чтобы проверить больше показателей красоты. Доктор Шмид говорит, что длина уха должна быть равна длине носа на идеальном лице, среди прочих характеристик.
Недавно я начал собирать NFT для поддержки различных гуманитарных и медицинских целей. Общество Света — это набор ограниченных предметов коллекционирования, которые помогут сделать мир немного лучше, так как процент от каждой продажи будет отправлен непосредственно на благотворительность, связанную с аватаром. Как я всегда говорю, нет ничего лучше, чем маркированный список, чтобы обозначить преимущества покупки этих NFT:
append(num_1)