Оригами геометрические фигуры схемы: Объемные фигуры из бумаги, схемы. Как сделать объемные геометрические фигуры
Математические фигуры из бумаги
Автор На чтение 4 мин. Опубликовано
В основе самых сложных и необычные формы сооружений, устройств, механизмов лежат элементарные геометрические фигуры: куб, призма, пирамида, шар и другие. Для начала научитесь создавать самые простые фигуры, а после вы легко освоите более сложные формы.
Многие моделисты начинают свой путь с бумажных моделей. Это обусловлено доступностью материала (найти бумагу и картон не составляет трудности) и легкостью в его обработки (не требуются специальные инструменты).
Однако, бумага имеет и ряд характерных особенностей:
- капризный, хрупкий материал
- требует высокой аккуратности, внимательности, усидчивости при работе
По этим причинам бумага является материалом, как для начинающих, так и для настоящих мастеров и из нее создаются модели самой разной сложности.
В этот статье мы изучим простейшие геометрические фигуры, которые можно сделать из бумаги.
Вам понадобятся следующие материалы:
- лист бумаги
- карандаш
- линейка
- ластик
- ножницы
- клей ПВА либо клеящий карандаш
- кисточка для клея, лучше из жесткой щетины
- циркуль (для некоторых фигур)
Как сделать куб из бумаги?
Куб – правильный многогранник, каждая грань которого представляет собой квадрат
Создание куба состоит из двух этапов: создание развертки и склеивание. фигуры. Для создания схемы вы можете воспользоваться принтером, просто распечатав готовую схему. Либо вы можете самостоятельно с помощью чертежных инструментов нарисовать развертку.
- Выбираем размеры квадрата – одной стороны нашего куба. Лист бумаги должен быть шириной не менее 3 сторон этого квадрата и длиной немного более 4 сторон.
- Чертим в длину нашего листа четыре квадрата, которые станут боковыми сторонами куба.
 Рисуем их строго на одной линии, вплотную друг к другу.
Рисуем их строго на одной линии, вплотную друг к другу. - Над и под любыми из квадратов рисуем по одному такому же квадрату.
- Дорисовываем полоски для склеивания, с помощью которых грани будут соединяться между собой. Каждые две грани должны соединяться одной полоской.
- Куб готов!
После рисования развертка вырезается ножницами и склеивайте ПВА. Клей очень тонким слоем равномерно размазываем кистью по поверхности склеивания. Соединяем поверхности и закрепляем в нужном положении на некоторое время, с помощью скрепки или небольшого груза. Срок схватывания клея где-то 30-40 минут. Ускорить высыхание можно методом нагрева, например, на батарее. После склеиваем следующие грани, закрепляем в нужном положении. И так далее. Так постепенно вы проклеите все грани куба. Используйте небольшие порции клея!
Как сделать конус из бумаги?
Конус – тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность.
- Рисуем циркулем окружность
- Вырезаем сектор (часть круга, ограниченная дугой окружности и двумя радиусами, проведенными к концам этой дуги) из этой окружности. Чем больший сектор вы вырежете, тем острее будет конец конуса.
- Склеиваем боковую поверхность конуса.
- Измеряем диаметр основания конуса. С помощью циркуля рисуем окружность на листе бумаге требуемого диаметра. Дорисовываем треугольнички для склеивания основания с боковой поверхностью. Вырезаем.
- Приклеиваем основание к боковой поверхности.
- Конус готов!
Как сделать цилиндр из бумаги?
Цилиндр – геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.
- Рисуем прямоугольник на бумаги, в котором ширина – это высота цилиндра, а длина определит диаметр будущей фигуры. Отношение длины прямоугольника к диаметру определяется выражением: L=πD, где L- длина прямоугольника, а D – диаметр будущего цилиндра.
 Подставив в формулу требуемый диаметр, найдем длину прямоугольника, который будем рисовать на бумаге. Дорисовываем небольшие дополнительные треугольнички, которые необходимы для склеивания деталей.
Подставив в формулу требуемый диаметр, найдем длину прямоугольника, который будем рисовать на бумаге. Дорисовываем небольшие дополнительные треугольнички, которые необходимы для склеивания деталей. - Рисуем на бумаге два круга, диаметром цилиндра. Это будет верхнее и нижнее основания цилиндра.
- Вырезаем все детали будущего бумажного цилиндра.
- Склеиваем боковую поверхность цилиндра из прямоугольника. Даем детали высохнуть. Приклеиваем нижнее основание. Ждем высыхания. Приклеиваем верхнее основание.
- Цилиндр готов!
Как сделать параллелепипед из бумаги?
Параллелепипед – многогранник, у которого шесть граней и каждая из них параллелограмм.
- Выбираем размеры параллелепипеда и величины углов.
- Чертим параллелограмм – основание. С каждой стороне дорисовываем боковые стороны – параллелограммы. От любой из боковой стороны дорисовываем второе основание. Добавляем полоски для склеивания. Параллелепипед может быть прямоугольным, если стороны прямоугольники. Если параллелепипед не прямоугольный, то создать развертку немного сложнее. Для каждого параллелограмма нужно выдержать требуемые углы.
- Вырезаем развертку и склеиваем.
- Параллелепипед готов!
Как сделать пирамиду из бумаги?
Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину.
- Выбираем размеры пирамиды и количество ее граней.
- Рисуем основание – многогранник. В зависимости от количества граней это может быть треугольник, квадрат, пятиугольник или другой многогранник.
- От одной из сторон основания рисуем треугольник, который будет боковой стороной. Следующий треугольник рисуем так, чтобы одна сторона у него с предыдущим была общая и так далее. Так рисуем столько треугольников, сколько сторон в пирамиде. Дорисовываем полоски для склеивания в нужных местах.
- Вырезаем и склеиваем фигуру.
- Пирамида готова!
- Видео уроки
- Геометрические фигуры
- Подарки и праздничные
Дек 3, 2016
Наряду со сложными моделями оригами, на сборку которых порой может уйти целый день, хотим предложить вам сборку достаточно простой, но очень симпатичной ёлки. Такую небольшую модель смогут сложить даже дети. Надеемся, наше новогоднее настроение передастся и вам.
Такую небольшую модель смогут сложить даже дети. Надеемся, наше новогоднее настроение передастся и вам.
- Видео уроки
- Геометрические фигуры
- Объемные фигуры
Сен 30, 2016
Джереми Шейфер (Jeremy Shafer) – известный мастер оригами, который славится своими необычными моделями, состоящими из многочисленных деталей, но сложенными зачастую из цельных листов бумаги. Наша сегодняшняя модель под названием Cube Dude Wearing Headphones – Кубик в очках и наушниках как раз относится к таким интересным и сложным моделям. Надеемся, вы сможете без проблем ее сложить по подробному видео-уроку от автора. Удачи!
- Видео уроки
- Геометрические фигуры
Мар 14, 2016
Бумажные оригами модели могут представлять собой не только симпатичных животных и птиц, но и совершенно обыденные вещи, которые имеют практическое значение. Сегодня мы предлагаем вам сложить простой кард-холдер в виде сюрикера или японского метательного ножа.
- Видео уроки
- Геометрические фигуры
- Объемные фигуры
- Оригами в движении
Июл 19, 2015
Сегодня мы предлагаем вашему вниманию очень интересную модель в технике подвижного оригами. Это замечательная бумажная игрушка-тетраэдр от мастера оригами Tomoko Fuse. Данная модель по своему типу очень похожа на оригами фейерверк по схеме Ями Ямаучи, но складывается гораздо проще и из меньшего количества модулей.
- Видео уроки
- Геометрические фигуры
- Оригами для детей
Июл 11, 2015
Как часто вы устраиваете вечеринки? А как часто вам приходится придумывать различные декорации и антураж, чтобы создать соответствующую обстановку? Сегодня мы немного поможем вам в этом. Предлагаем простой способ украсить любой праздник – шутиха из бумаги или симпатичная вертушка на палочке! Такими яркими аксессуарами можно украсить не только праздник, но и, например, детскую комнату, или же сделать их несколько штук в качестве подарков детям.
- Видео уроки
- Геометрические фигуры
Июн 14, 2015
Сегодня на нашем сайте очень интересная и трудоемкая в сборке модель от мастера оригами по имени Robin Scholz. Представляем вашему вниманию модель “Кельтский круг” в технике тесселяция. Это довольно непростая техника, к которой нужно приловчиться. Надеемся, у вас все получится.
- Видео уроки
- Геометрические фигуры
- Модульное оригами схемы
Май 24, 2015
Сборка различных геометрических фигур занимает особую нишу в технике оригами. Сегодня мы предлагаем вам сложить так называемый Burr Puzzle по схеме Barlaham Benítez Vargas (Froy). Это не совсем обычная бумажная поделка – а целая головоломка, которая собирается из шести модулей интересной формы.
- Видео уроки
- Геометрические фигуры
Май 2, 2015
Складывать различные оригами звезды можно несколькими способами. Первый из них – из модулей, но не из обычных треугольных для объемных моделей, а своеобразных одинаковых модулей для каждой звезды отдельно. Второй, более интересный, – из цельного квадратного листа бумаги, так сказать, в лучших традициях оригами искусства. Именно такую шестиконечную звезду мы сложим с вами сегодня по схеме Stephan Weber.
- Геометрические фигуры
Апр 18, 2015
Сборка различных оригами животных, птиц и других моделей живых существ, несомненно, интересна. Однако в мире оригами существуют и другие не менее замечательные модели. Например, всевозможные геометрические преобразования, которые при детальном рассмотрении напоминают небесные тела, звезды, снежинки и многие другие не менее прекрасные формы.
Здесь мы подготовили для вас объемные геометрические фигуры из бумаги, которые нужно вырезать и склеить. Также на этой странице вы найдете плоские фигуры для вырезания, из которых нужно сложить замок. Этот учебный материал поможет ребенку наглядно изучить объемные геометрические фигуры: куб, пирамиду, ромб, шестигранник, цилинд и конус. Задание развивает наглядно-образное мышление.
Задание развивает наглядно-образное мышление.
Объемные геометрические фигуры из бумаги – Вырезаем и клеим:
Здесь вы можете скачать объемные геометрические фигуры из бумаги в виде разверток, которые необходимо распечатать на принтере, вырезать и склеить по указанным местам. В результате у вас получатся объемные фигуры: куб, пирамида (трехгранная и четырехгранная), ромб, шестиугольник, конус и цилиндр. На каждой развертке написано название фигуры, чтобы ребенок во время работы всегда мог видеть, какую фигуру он делает. Это очень удобно для обучения, так как дети обычно не любят, когда взрослые по несколько раз повторяют одно и то же. А в этом случае у родителей нет необходимости проговаривать вслух названия фигур.
- Итак, в первом листе мы выложили следующие геометрические фигуры: куб (фигура, поверхность которого состоит из 6 квадратов), трехгранная пирамида (основание пирамиды и 3 грани), четырехгранная пирамида (основание и 4 грани), ромб (фигура, визуально состоящая из двух пирамид, имеющих общее основание).
- Во втором листе вы найдете развертки таких геометрических фигур из бумаги: шестигранник (фигура, состоящая из шести граней), цилиндр (состоящий из свернутого прямоугольника и двух окружностей-оснований) и конус.
Скачать геометрические фигуры из бумаги – развертки для вырезания вы можете во вложениях внизу страницы
Скачайте и распечатайте 2 листа с фигурами, вырежьте их аккуратно ножницами и склейте в нужных местах. Учтите, что у бумажных фигур есть дополнительные места для сгиба и склеивания (у нас они выделены оранжевым цветом). Все оранжевые места вам необходимо согнуть и намазав их клеем вклеить с внутренней стороны фигуры.
После того, как дети, при помощи взрослых, склеят все геометрические фигуры из бумаги, можно продолжить занятие, задавая детям вопросы. Например: “Покажи мне пирамиду. Сколько у нее сторон? Где ее основание? Чем эта пирамида (показываете трехранную) отличается от этой (четырехранной)? Покажи мне цилиндр. Какие предметы он тебе напоминает? Покажи конус. На что он похож? Покажи куб. Сколько у него сторон? Из какой геометрической фигуры состоят его стороны?” – и так далее.
Какие предметы он тебе напоминает? Покажи конус. На что он похож? Покажи куб. Сколько у него сторон? Из какой геометрической фигуры состоят его стороны?” – и так далее.
В зависимости от возраста ребенка, можно использовать в занятии различные обучающие материалы. Например, что такое пирамида:
Какие бывают пирамиды. (Пусть ребенок покажет из них те, которые он склеил)
Что такое конус и цилиндр. На что они похожи:
Можете также скачать эти обучающие картинки во вложениях.
Плоские геометрические фигуры из бумаги – Строим замок
В этом упражнении вы можете скачать плоские геометрические фигуры из бумаги и построить из них замок, то есть выложить их на столе таким образом, чтобы получился заданный силуэт замка. Для начала скачайте во вложениях бланки с заданием и распечатайте на принтере. Затем вырежьте геометрические фигуры (квадрат, трапеция, полукруг и треугольник), которые даны к этому заданию. Все карточки с заданиями даны с увеличением уровня сложности (от 1 до 6 задания).
Все карточки с замками можно распечатывать на обычной офисной белой бумаге. А геометрические фигуры нужно распечатать на цветном картоне. Если нет цветного картона, можно использовать для распечатки цветную бумагу, а затем наклеить бумагу на лист картона и вырезать фигуры.
После этого подробно объесните ребенку инструкцию к выполнению упражнения.
“Строители, прежде чем строить какое-либо здание, смотрят сначала на его чертеж или схему, в которых показано каким оно должно быть. Такие чертежи бывают разными. Вот например, один из них”, – взрослый показывает одну или две игровых схемы замка с нашего задания. – “Тебе нужно мысленно представить из каких частей состоит каждый замок, руководствуясь теми фигурами, которые можно использовать для строительства.” – взрослый показывает все геометрические фигуры, которые заранее вырезаны из цветного картона.
Очень важно начинать занятие, не используя подсказки, то есть нужно закрывать от ребенка геометрические фигуры, которые нарисованы рядом с силуэтом каждого замка. Пусть ребенок сам подумает, какие фигуры и какого размера ему понадобятся для строительства данного замка. И только если он испытвает трудности, можно приоткрыть для него подсказку.
Пусть ребенок сам подумает, какие фигуры и какого размера ему понадобятся для строительства данного замка. И только если он испытвает трудности, можно приоткрыть для него подсказку.
Также не нужно допускать, чтобы ребенок накладывал вырезанные геометрические фигуры из бумаги на силуэт замка, так как при этом он не будет развивать наглядно-образное мышление. Старайтесь, чтобы всю основную работу ребенок проводил в уме, а не методом подбора.
Скачать карточки с плоскими геометрическими фигурами для строительства замка вы можете во вложениях внизу страницы.
Геометрические фигуры для вырезания:
Также вам будут полезны и другие материалы по изучению геометрических фигур:
Веселые и красочные задания для детей “Рисунки из геометрических фигур” являются очень удобным обучающим материалом для детей дошкольного и младшего школьного возраста по изучению и запоминанию основных геометрических формю
Здесь вы с ребенком можете изучить геометрические фигуры и их названия с помощью веселых заданий в картинках.
Задания ознакомят ребенка с основными фигурами геометрии – кругом, овалом, квадратом, прямоугольником и треугольником. Только здесь не занудное зазубривание названий фигур, а своеобразная игра-раскраска.
Как правило, геометрию начинают изучать, рисуя плоские геометрические фигуры. Восприятие правильной геометрической формы невозможно без выведения ее своими руками на листе бумаги.
Это занятие изрядно позабавит ваших юных математиков. Ведь теперь им придется находить знакомые формы геометрических фигур среди множества картинок.
Наложение фигур друг на друга – это занятие по геометрии для дошкольников и младших школьников. Смысл упражнения состоит в решении примеров на сложение. Только это необычные примеры. Вместо цифр здесь нужно складывать геометрические фигуры.
Это задание составлено в виде игры, в которой ребенку предстоит менять свойства геометрических фигур: форму, цвет или размер.
Здесь вы можете скачать задания в картинках, в которых представлен счет геометрических фигур для занятий по математике.
В этом задании ребенок познакомится с таким понятием, как чертежи геометрических тел. По сути, это занятие представляет собой мини-урок по начертательной геометрии
Дети любят раскрашивать и обводить, поэтому данные задания сделают ваши занятия по обучению счету максимально эффективными.
И еще можете поиграть в математические игры онлайн от лисенка Бибуши:
В этой развивающей онлайн игре ребенку предстоит определить, что является лишним среди 4 картинок. При этом необходимо руководствоваться признаками геометрических форм.
“>
Необычные фигуры из бумаги
Большой выбор развёрток простых геометрических фигур.
Первое знакомство детей с бумажным моделированием всегда начинается с простых геометрических фигур, таких как кубик и пирамида. Не у многих получается склеить кубик с первого раза, иногда требуется несколько дней, чтобы сделать поистине ровный и безупречный куб. Более сложные фигуры цилиндр и конус требуют в несколько раз больше усилий нежели простой кубик. Если вы не умеете аккуратно клеить геометрические фигуры, значит и за сложные модели вам ещё рано браться. Займитесь сами и научите своих детей клеть эти «азы» моделирования по готовым развёрткам.
Для начала я, конечно же, предлагаю научиться клеить обычный кубик. Развёртки сделаны для двух кубиков, большого и маленького. Более сложной фигурой является маленький кубик потому, как клеить его сложнее, чем большой.
Итак, начнём! Скачайте развёртки всех фигур на пяти листах и распечатайте на плотной бумаге. Перед тем, как печатать и клеить геометрические фигуры обязательно ознакомьтесь со статьёй о том, как выбрать бумагу и как вообще правильно вырезать, сгибать и клеить бумагу.
Для более качественной печати советую использовать программу AutoCAD, и даю вам развёртки для этой программы, а также читайте, как распечатывать из автокада. Вырежьте развёртки кубиков с первого листа, по линиям сгиба обязательно проведите иголкой циркуля под железную линейку, чтобы бумага хорошо сгибалась. Теперь можно начинать клеить кубики.
Вырежьте развёртки кубиков с первого листа, по линиям сгиба обязательно проведите иголкой циркуля под железную линейку, чтобы бумага хорошо сгибалась. Теперь можно начинать клеить кубики.
Для экономии бумаги и на всякий пожарный я сделал несколько развёрток маленького кубика, мало ли вам захочется склеить не один кубик или что-то не получится с первого раза. Ещё одна несложная фигура это пирамида, её развёртки найдёте на втором листе. Подобные пирамиды стоили древние египтяне, правда не из бумаги и не таких маленьких размеров 🙂
А это тоже пирамида, только в отличие от предыдущей у неё не четыре, а три грани.
Развёртки трёхгранной пирамиды на первом листе для печати.
И ещё одна забавная пирамидка из пяти граней, её развёртки на 4-ом листе в виде звёздочки в двух экземплярах.
Далее шестигранник, склеить его будет ещё проще, чем пирамиды. Развёртки шестигранника на первом листе.
Более сложная фигура это пятигранник, хотя пятигранник сложнее начертить, нежели склеить.
Развёртки пятигранника на втором листе.
Вот мы и добрались до сложных фигур. Теперь придётся поднапрячься, склеить такие фигуры нелегко! Для начала обычный цилиндр, его развёртки на втором листе.
А это более сложная фигура по сравнению с цилиндром, т.к. в её основании не круг, а овал.
Развёртки этой фигуры на втором листе, для овального основания сделано две запасных детали.
Чтобы аккуратно собрать цилиндр его детали нужно клеить встык. С одной стороны дно можно приклеить без проблем, просто поставьте на стол заранее склеенную трубку, положите на дно кружок и залейте клеем изнутри. Следите, чтобы диаметр трубы и круглого дна плотно подходили друг к другу, без щелей, иначе клей протечёт и всё приклеится к столу. Второй кружок приклеить будет сложнее, поэтому приклейте внутри вспомогательные прямоугольники на расстоянии толщины бумаги от края трубы. Эти прямоугольники не дадут упасть основанию внутрь, теперь вы без проблем приклеете кружок сверху.
Эти прямоугольники не дадут упасть основанию внутрь, теперь вы без проблем приклеете кружок сверху.
Цилиндр с овальным основанием можно клеить также как и обычный цилиндр, но он имеет меньшую высоту, поэтому тут проще вставить внутрь гармошку из бумаги, а наверх положить второе основание и по краю приклеить клеем.
Теперь очень сложная фигура – конус. Его детали на третьем листе, запасной кружок для днища на 4-ом листе. Вся сложность склеивания конуса в его острой вершине, а потом ещё будет очень сложно приклеить дно.
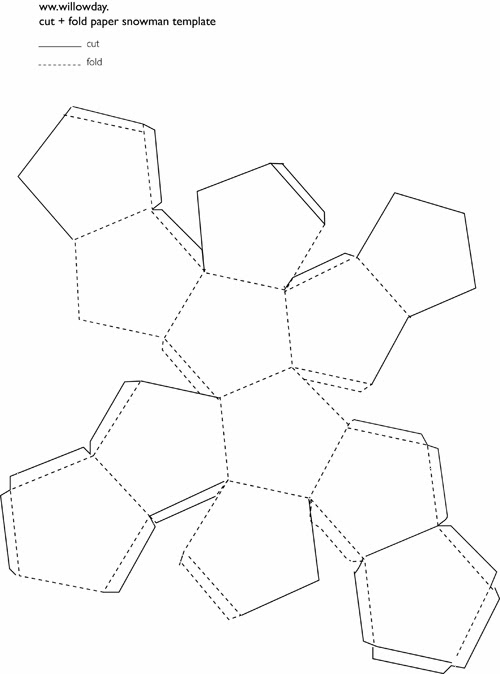
Сложная и одновременно простая фигура это шар. Шар состоит из 12-ти пятигранников, развёртки шара на 4-ом листе. Сначала клеится две половинки шара, а потом обе склеиваются вместе.
Довольно интересная фигура – ромб, её детали на третьем листе.
А теперь две очень похожие, но совершенно разные фигуры, их отличие только в основании.
Когда склеите эти обе фигуры, то не сразу поймёте, что это вообще такое, они получились какие-то совсем невосприимчивые.
Ещё одна интересная фигурка это тор, только он у нас очень упрощён, его детали на 5-ом листе.
И наконец, последняя фигура из равносторонних треугольников, даже не знаю, как это назвать, но фигура похожа на звезду. Развёртки этой фигуры на пятом листе.
На сегодня это всё! Я желаю вам успехов в этой нелёгкой работе!
КОММЕНТАРИИ
Задали по геометрии: тетраэдр, куб, октаэдр, додекаэдр, икосаэдр. Тетраэдр, куб и додекаэдр сделала, а вот оставшиеся две никак(((
Еще возникли трудности с склеиванием..
спасибо, хз че бы делал еслиб не этот сайт =)
Спасибо большое!)))) очень выручили!
Я бы и так не смогла, полезно было ознакомиться.
помогите, как сделать развертку Четырёхугольной пирамиды с основанием – ромб
Как сделать развёртку тора (то есть кольца, вернее, его поверхности)?
Вопрос задан с практической целью, хочу самостоятельно обшить руль машины кожей, но для этого необходимо начертить выкройку, вот тут и возникла трудность – не хватает воображения всё это нарисовать, ведь поверхность тора – это т. н. неразвёртываемая поверхность (вернее, условно-развёртываемая).
н. неразвёртываемая поверхность (вернее, условно-развёртываемая).
Люди, помогите советом или ссылкой, плиз!
Я бы вам посоветовал сходить в магазин и посмотреть как сшиты подобные чехлы для автомобильного руля. Вообще кожа специфический материал, с ней можно делать практически всё, из бумаги такого не сделаешь, поэтому и выкройти тут трудно посоветовать, лучше посмотреть как это уже сделано и дома подумать как сделать своё.
как сделать усечённую пирамиду
Спасибо за информацию,но не все фигуры изображены.Пошли в 9 класс ,но не в РОссии.Необходима помощь. С уважением,Тамара.
Может глупый вопрос, но как сделать из бумаги шар? т.е. не просто круг, а именно объемный шар? есть ли вообще в природе такая развертка?
Развёртка шара из бумаги представляет собой дольки, полоски бумаги сужающиеся по краям. Развёртка шара похожа на рисунок из полосок на арбузе.
Дмитрий, это я тоже помню из курса школьной географии 🙂
А вот как сделать из атласа в электронном виде шар в электронном виде, чтобы потом распечатать и наклеить?
Почему не указаны параметры? Длина, ширина и т.д.?
как сделать цилиндр из бумаги помамогите плиз
Большое человеческое СПАСИБО.
Спасибо вам огромное! Очень нужен был конус. Теперь, благодаря вам, я знаю, как его сделать))
фу
дану это проче простого ещебы квадраты делать учили
мне по технологие задали это
спасибо большое. по геометрии 3 выходит а так 4 :DDD
плохо не чё не пойму
развертка паллалеллограмма неправильная 5 лист
можно было бы еще акуратнее , как-то грубо
шар не получился там не правильный чертеж
Спасибо большое)))) Ну очень помогли)))
Велике спасибі.Розгортки допомогли мені при виготовленні геометричних фігур на технологіях.
Спасибо большое, хорошие и удобные развёртки)
Проблема с параллелепипедом на пятом листе решается отрезанием косячной грани и её разворотом в правильную сторону)
Развертка фигур. Может развертка геометрических тел?
Может развертка геометрических тел?
красиво можно научиться
thank you very much
Спасибо большое! Ребенку во втором класе уже задали эти фигуры. Спасибо Вам за модели, очень удобно, распечатали, сидит, клеит )
Модели конечно интересные, но люди парятся выполняя их, хотя особо труда не составило мне сделать даже сферу. Сыновьям моим (близнецам) задали сделать фигурки из картона, но я то заканчил политех и по начерталке и проходили развертки этих фигур. А у кого гуманитарное образование? Вот у них то и проблемма.
Полезно для изо в 6 классе
Мне кажется, что у Вашего шестигранника восемь граней, а у пятигранника – семь. И называются эти тела либо призмами, либо усеченными пирамидами( в зависимости от соотношения оснований)
- Видео уроки
- Геометрические фигуры
- Подарки и праздничные
Дек 3, 2016
Наряду со сложными моделями оригами, на сборку которых порой может уйти целый день, хотим предложить вам сборку достаточно простой, но очень симпатичной ёлки. Такую небольшую модель смогут сложить даже дети. Надеемся, наше новогоднее настроение передастся и вам.
- Видео уроки
- Геометрические фигуры
- Объемные фигуры
Сен 30, 2016
Джереми Шейфер (Jeremy Shafer) – известный мастер оригами, который славится своими необычными моделями, состоящими из многочисленных деталей, но сложенными зачастую из цельных листов бумаги. Наша сегодняшняя модель под названием Cube Dude Wearing Headphones – Кубик в очках и наушниках как раз относится к таким интересным и сложным моделям. Надеемся, вы сможете без проблем ее сложить по подробному видео-уроку от автора. Удачи!
- Видео уроки
- Геометрические фигуры
Мар 14, 2016
Бумажные оригами модели могут представлять собой не только симпатичных животных и птиц, но и совершенно обыденные вещи, которые имеют практическое значение. Сегодня мы предлагаем вам сложить простой кард-холдер в виде сюрикера или японского метательного ножа.
Сегодня мы предлагаем вам сложить простой кард-холдер в виде сюрикера или японского метательного ножа.
- Видео уроки
- Геометрические фигуры
- Объемные фигуры
- Оригами в движении
Июл 19, 2015
Сегодня мы предлагаем вашему вниманию очень интересную модель в технике подвижного оригами. Это замечательная бумажная игрушка-тетраэдр от мастера оригами Tomoko Fuse. Данная модель по своему типу очень похожа на оригами фейерверк по схеме Ями Ямаучи, но складывается гораздо проще и из меньшего количества модулей.
- Видео уроки
- Геометрические фигуры
- Оригами для детей
Июл 11, 2015
Как часто вы устраиваете вечеринки? А как часто вам приходится придумывать различные декорации и антураж, чтобы создать соответствующую обстановку? Сегодня мы немного поможем вам в этом. Предлагаем простой способ украсить любой праздник – шутиха из бумаги или симпатичная вертушка на палочке! Такими яркими аксессуарами можно украсить не только праздник, но и, например, детскую комнату, или же сделать их несколько штук в качестве подарков детям.
- Видео уроки
- Геометрические фигуры
Июн 14, 2015
Сегодня на нашем сайте очень интересная и трудоемкая в сборке модель от мастера оригами по имени Robin Scholz. Представляем вашему вниманию модель «Кельтский круг» в технике тесселяция. Это довольно непростая техника, к которой нужно приловчиться. Надеемся, у вас все получится.
- Видео уроки
- Геометрические фигуры
- Модульное оригами схемы
Май 24, 2015
Сборка различных геометрических фигур занимает особую нишу в технике оригами. Сегодня мы предлагаем вам сложить так называемый Burr Puzzle по схеме Barlaham Benítez Vargas (Froy). Это не совсем обычная бумажная поделка – а целая головоломка, которая собирается из шести модулей интересной формы.
- Видео уроки
- Геометрические фигуры
Май 2, 2015
Складывать различные оригами звезды можно несколькими способами. Первый из них – из модулей, но не из обычных треугольных для объемных моделей, а своеобразных одинаковых модулей для каждой звезды отдельно. Второй, более интересный, – из цельного квадратного листа бумаги, так сказать, в лучших традициях оригами искусства. Именно такую шестиконечную звезду мы сложим с вами сегодня по схеме Stephan Weber.
Первый из них – из модулей, но не из обычных треугольных для объемных моделей, а своеобразных одинаковых модулей для каждой звезды отдельно. Второй, более интересный, – из цельного квадратного листа бумаги, так сказать, в лучших традициях оригами искусства. Именно такую шестиконечную звезду мы сложим с вами сегодня по схеме Stephan Weber.
- Геометрические фигуры
Апр 18, 2015
Сборка различных оригами животных, птиц и других моделей живых существ, несомненно, интересна. Однако в мире оригами существуют и другие не менее замечательные модели. Например, всевозможные геометрические преобразования, которые при детальном рассмотрении напоминают небесные тела, звезды, снежинки и многие другие не менее прекрасные формы.
Во все времена бумажные изделия пользовались особой популярностью, так как сам материал не является затратным, а изделия выглядят достойно. Все мы знакомы с техникой оригами, но человечество шагнуло дальше и возник новый вид искусства. В переводе с английского обозначает крафтовая бумага и подразумевает собой геометрическое моделирование из картона или бумаги, живых и неживых предметов.
Пингвин и детёныш
Развёртки разных покорили все возрасты и сейчас являются одним из самых популярных видов для проведения семейного досуга.Некоторые творения требуют особой щепетильности и временных затрат. Если вы впервые сталкиваетесь с этой техникой, то поэтапный мастер класс по бумажному моделированию поможет вам разобраться в теме
Это могут быть живые предметы или существа, вымышленные любимые персонажи детей и всё то, что пожелает ваша фантазия. Эту деятельность принято воспринимать как отдых, который собирает вместе всю семью. Согласитесь, нечасто удаётся проводить семейный досуг с пользой.
Набор полигональных фигур из бумаги
Для того чтобы иметь представление о том, как выглядят заготовки будущего изделия, предлагаем вашему вниманию доступные полигональные фигуры из бумаги и их шаблоны для вырезания. Огромным спросом в изготовлении пользуются животные.
Огромным спросом в изготовлении пользуются животные.
3d акула в декоре
Моделирование из картона или бумаги – тонкий процесс изготовления разнообразных геометрических фигур и изделий.
ночник в виде кита
Это общая инструкция, где описаны основные принципы работы. К каждому набору предлагается отдельная в напечатанном виде.
Создание и редактирование разверток
Для полноценной работы вам необходимо скачать соответствующие рабочие программы. Pepakura бывает двух видов: «Viewer» и «Designer». «Viewer» позволяет просматривать доступные развёртки, в интернет-ресурсах их найти просто. «Designer» предоставляет возможность редактировать готовые развертки, часто это нужно для упрощения. Так же можно в любой из этих программ вертеть для лучшего рассмотрения, выбирать детали на 2D развертке, чтобы смотреть линии склейки и сгибов.
Можно ограничиться Viewer для начала. Файлы имеют формат pdo. Выбираем по уровню сложности. Чаще всего о ней пишется в описании, зависит от количества станиц и мелких деталей. Выбираем, скачиваем, открываем через Viewer и печатаем. Мой личный совет – начинать лучше с полностью белых заготовок. Но если вы скачали уже со встроенными текстурами, то их легко убрать – нажмите на кубик и они пропадут.
Мастер класс по объемному моделированию и конструированию из бумаги
Модели собираются из предварительно подготовленных и согнутых деталей. Развертки необходимо распечатывать на бумаге плотностью 170—200 г/м². Это будет гарантировать прочность и долговечность конструкции.
Для сборки потребуется:
- развертки или схемы
- клей (не используйте ПВА, после высыхания он деформирует бумагу) или тонкий двухсторонний скотч
- кисть
- иголка для нанесения клея в труднодоступных местах
- металлическая линейка
- острые ножницы, подойдут практически любые прямые или канцелярский нож, который часто поставляется в приобретенном наборе
- дотс для продавливания сгибов
- любая ровная поверхность для резки
- Чтобы не испортить рабочий стол, на поверхность необходимо положить кусок линолеума, фанеры или стекла
Бумажное моделирование и рекомендации
Главным материалом для изготовления служит бумага. В принципе можно использовать обычные листы формата А4 плотностью 65-80 г/м3, но если творение большое, то лучше использовать ватман либо чертёжную бумагу (160-180 г/м3), для самых маленьких деталей можно попробовать (если конечно найдете, я не смог) папиросную. При построении бумажных многогранников рекомендую работать следующим образом: После того, как необходимая развёртка скачана и все инструменты под рукой, приступайте к вырезанию и склейке.
В принципе можно использовать обычные листы формата А4 плотностью 65-80 г/м3, но если творение большое, то лучше использовать ватман либо чертёжную бумагу (160-180 г/м3), для самых маленьких деталей можно попробовать (если конечно найдете, я не смог) папиросную. При построении бумажных многогранников рекомендую работать следующим образом: После того, как необходимая развёртка скачана и все инструменты под рукой, приступайте к вырезанию и склейке.
Вырезание фигуры из бумаги по схеме
Прежде чем приступить к сборке, необходимо подготовить рабочее место. Затем, распечатайте заготовки. Следите за тем, чтобы детали были пронумерованы. В случае отсутствия номерков, собственноручно напишите их на полях. Это сэкономит время при склеивании крупных поделок. Существует три вида линий, согласно которым появляются заготовки. Сплошная линия — отрезать часть бумаги с помощью ножниц. Пунктирная линия — на моделях без текстур сгибается внутрь, с текстурами — наружу. Шрих-пунктирная — без текстур наружу, с текстурами – внутрь.
Заготовки вырезайте осторожно, не забывайте оставлять «клейкие поля». Благодаря им, различные части изделия будут соединяться друг с другом. Всё сгибайте по линиям сгиба. Если он очень длинный (более 8 см) то, пользуйтесь линейкой.
Сгибание и сборка паперкрафта из бумаги
Подготовка сгибов. Чтобы деталь загнулась в правильном положении, необходимо пошагово пройтись по всем линиям. В этом вам поможет непишущая ручка. Сгибайте элемент по пунктиру. Старайтесь складывать максимально ровно и не бойтесь прикладывать силу, при сборке всё будет на своих местах. Согнутый край с внешней стороны обильно промазывается клеем, либо можете использовать узкий двухсторонний скотч, кому как удобно. Ищите идентичные цифры и их соединяйте. Процесс несложный. Хорошо развивает внимательность. Склейка прячется внутрь поделки, чтобы не выставлять на всеобщее обозрение неровности.
Не торопитесь соединить всё и сразу, если ваш метод скрепления – клеем, то стоит подождать полного высыхания, а затем приступать к оставшимся деталям. Из личного опыта советуем пользоваться двухсторонним скотчем. Возьмите на вооружение, как вариант. Его использование сэкономит ваше время и нервную систему. Помимо привычного нам, толстого скотча существует и узкий. Зачастую, он оказывается лучше и служит дольше обычного клея. Правда, трудиться с ним – достаточно кропотливое занятие, поэтому сразу приготовьте пинцет, дабы с лёгкостью снимать защитную бумагу. Но будьте осторожны, включайте логику и просчитывайте порядок скрепления деталей, дабы не возникало неудобных моментов в конце процесса.
Из личного опыта советуем пользоваться двухсторонним скотчем. Возьмите на вооружение, как вариант. Его использование сэкономит ваше время и нервную систему. Помимо привычного нам, толстого скотча существует и узкий. Зачастую, он оказывается лучше и служит дольше обычного клея. Правда, трудиться с ним – достаточно кропотливое занятие, поэтому сразу приготовьте пинцет, дабы с лёгкостью снимать защитную бумагу. Но будьте осторожны, включайте логику и просчитывайте порядок скрепления деталей, дабы не возникало неудобных моментов в конце процесса.
Процедура склейки является очень ответственным делом, поскольку требует усидчивости и максимальной внимательности. Все стыки должны совпадать – это главный секрет успеха при процессе соединения. Наносите тонкий равномерный слой клея на две стороны. Следует чуть-чуть подвигать детали, чтобы происходило равномерное распределение. После того, как части приведены в правильное положение, их следует плотно сжать и дождаться, пока клей не подсохнет.
Время от времени надо пользоваться пинцетами. Эти инструменты особенно полезны на завершающих стадиях, когда приходится работать внутри через небольшое отверстие. Следует чуть-чуть подвигать детали, чтобы произошло равномерное распределение. После того, как части приведены в правильное положение, их следует плотно сжать и дождаться, пока клей не подсохнет. Время от времени надо пользоваться пинцетами или, еще лучше, хирургическими зажимами. Эти инструменты особенно полезны на завершающих стадиях, когда приходится работать с внутренней частью через небольшое отверстие. Супер-клей используем для приклеивания мелких деталей или если нужно быстро соединить что-либо.
Но если всё же клей, то стоит понимать, какой фирме отдавать предпочтение. Проверьте его на клейкость. Нужно, чтобы после полного высыхания он не съёживал творение и не оставлял следов. Помимо этого, склейка должна произойти за 15-25 секунд, этот момент покажет вам качество. Следует помнить и о технике безопасности. Он не должен быть токсичным.Кроме того, он должен схватываться достаточно быстро, но не мгновенно. Последнее, но очень важное требование – клей не должен быть токсичным. Часто поделки украшают гирляндами или лампочками, превращая их в ночники.
Он не должен быть токсичным.Кроме того, он должен схватываться достаточно быстро, но не мгновенно. Последнее, но очень важное требование – клей не должен быть токсичным. Часто поделки украшают гирляндами или лампочками, превращая их в ночники.
Обработка разверток для бумажного моделирования
Если изделие бесцветно или вы решили его перекрасить, то лучше всего подходят специальные краски. Они на нитрооснове, быстро сохнут, бумага от них не размокает, единственное, они дорогостоящие, несколько цветов обойдутся как целая пластиковое изделие. Поэтому попробуйте аккуратно покрыть поверхность густой гуашью, следя за тем чтобы не размокла
Укрепление бумажной модели в паперкрафте
Техника безопасности
- Сухое место обезопасит от попадания ненужной влаги.
- Процесс склейки проводите за столом, а не где нибудь на диване или полу.
- Готовое изделия на краю стола, стеллажа, шкафа, обязательно упадет.
- Пыль с готового изделия вытирайте сухой тряпкой.
- Содержите рабочее место в порядке, так как труд очень кропотливый и лишний хаос в заготовках вам точно не нужен.
Простая модель из бумаги для детей
Для развития у малыша логики и мелкой моторики, специалисты решили создавать фигуры, но с меньшим уровнем сложности. Ребёнок будет доволен, если вы предложите ему сборку забавных фигурок.
Картонное моделирование в примерах.
Схемы животных, птиц
Они занимают особое место в жизни человека. Да и природа без зверей была бы неполноценной. Почему бы нам не окунуться в этот прекрасный мир. Вы только посмотрите на птиц, сделав их в технике, вы сумеете привнести кусочек живого и прекрасного в ваш интерьер. А если птица послужит подарком, то для хозяина она принесёт свободу в затруднённые сферы.
Полигональный ворон сложная конструкция требующая навыков.
Лёгкие фигуры из бумаги для детей и их развертки вы можете скачать на сайте ru. dreamstime.com вставив наш реферальный номер res25459430 чтобы получить скидку на платные подписки и получить доступ к бесплатным.
dreamstime.com вставив наш реферальный номер res25459430 чтобы получить скидку на платные подписки и получить доступ к бесплатным.
Голуби мира украсят любой детсад и станут развивающей поделкой для ребёнка.
Развертки этих чудных черных птиц для декора птиц вы можете скачать на Etsy.
Мудрая сова готова вдохновлять на принятие разумных решений.
Только посмотрите на эту красоту! Настенный попугай станет любимчиком и детей, и взрослых.
Низкополигональный 3д белый голубь.
Панда – отличная деталь минималистичного однотонного интерьера.
Хитрая лиса привнесёт лесной атмосферы в ваше жилище.
Хищная пантера и черная кошка символ грации в вашем дизайне
Креативный дизайн кошачий релакс
А также, замечательный сувенир – сердце. Может быть картонным, железным или пластиковым, какой материал выбрать решать вам.
Простые фигуры из бумаги
Красочные творения станут украшением для любого интерьера и станут приятным презентом. Выбирайте макеты, которые понравились вам. Проводите время вместе, собирая чудесные фигуры.
творческий фото шедевр головы лошади
Единорог – мифическое существо, которое так любят девчонки. Отличным дополнением для маленькой принцессы станет объёмная фигурка.
Трофей – горный олень в чёрно-красной расцветке.
Розовый слон может быть украшением для любого ютуб блогера, который снимает репортажи про животный мир Азии.
Бумажная пластика в схемах и шаблонах для начинающих
Этот вид творчества заключается в том, что объём – ключевая характеристика изделия, детали же – реалистичные и пластичные.
Мальчишкам посоветуем на просторах интернета искать модели, которые им по душе: военный корабль, машина, самолёт, танк.
Советы по креплению скульптурных фигур и трофеев
Не все бумажные изделия требуют укрепления. К примеру, предметам интерьера (головам зверьков) достаточно жесткости картона. Если изготавливается маскарадный костюм или супергеройская маска (которая будет активно использоваться), ее обязательно нужно укрепить. Укрепление эпоксидной смолой. Сначала необходимо подготовить клеящую смесь: смешайте смолу с отвердителем, затем разбавьте ее спиртом до жидкого, но тягучего состояния. Нанесите состав на внутреннюю сторону изделия в один слой, дождитесь полного высыхания. Покрасьте смолой внешнюю часть изделия, затем положите тонкий слой стекловаты (можно заменить бинтом) и повторно нанесите эпоксидку. Во время высыхания смола может течь, поэтому изделие необходимо поместить на болванку и вынести на улицу, либо постелить на пол большое количество газет. Волны и подтеки сгоняются с помощью фена. В завершении необходимо обработать изделие наждачной бумагой и повторно покрыть тонким слоем эпоксидки.
К примеру, предметам интерьера (головам зверьков) достаточно жесткости картона. Если изготавливается маскарадный костюм или супергеройская маска (которая будет активно использоваться), ее обязательно нужно укрепить. Укрепление эпоксидной смолой. Сначала необходимо подготовить клеящую смесь: смешайте смолу с отвердителем, затем разбавьте ее спиртом до жидкого, но тягучего состояния. Нанесите состав на внутреннюю сторону изделия в один слой, дождитесь полного высыхания. Покрасьте смолой внешнюю часть изделия, затем положите тонкий слой стекловаты (можно заменить бинтом) и повторно нанесите эпоксидку. Во время высыхания смола может течь, поэтому изделие необходимо поместить на болванку и вынести на улицу, либо постелить на пол большое количество газет. Волны и подтеки сгоняются с помощью фена. В завершении необходимо обработать изделие наждачной бумагой и повторно покрыть тонким слоем эпоксидки.
Бумажные скульптуры своими руками в примерах
- Статуя железного Арни достойная руки скульптора.
Железный человек собственной персоной
могучий и невозмутимый Халк
Паперкрафт для начинающих в видеоуроке
Поделки из геометрических фигур — 70 фото идей необычных поделок
Творческий процесс создания поделок из геометрических фигур напоминает конструирование. Занятия в этом направлении очень полезны для развития ребенка. Помимо активации мелкой моторики они помогают ребенку запомнить геометрические фигуры и цвета, формируют понимание частей и целого, что в свою очередь способствует освоению математики.
Ребенок учится складывать из элементов целые конструкции, развивается пространственное и творческое мышление.
Особенности работы с геометрическими фигурами в разном возрасте
Поделки из фигур доступны для занятий с детьми с самого младшего возраста.
- Для малышей 2-4 лет задание не должно включать в себя больше 5 деталей.
 В противном случае ребенок быстро устает, путается, а внимание его рассеивается. Для изготовления поделки малышу необходимо приготовить готовые элементы поделки из цветной бумаги и предложить основу с готовым контуром. Или показать, последовательность выполнения работы.
В противном случае ребенок быстро устает, путается, а внимание его рассеивается. Для изготовления поделки малышу необходимо приготовить готовые элементы поделки из цветной бумаги и предложить основу с готовым контуром. Или показать, последовательность выполнения работы. - Дети в возрасте 4-5 лет могут вырезать из бумаги простые детали самостоятельно, но под присмотром взрослых. Для работы ребенку необходимы ножницы с закругленными концами. Дети такого возраста способны сами выполнить поделки средней сложности.
- Учащиеся младших классов справляются самостоятельно с достаточно сложными заданиями.
Для того, чтобы заинтересовать ребенка изготовлением поделки из геометрических фигур, можно предложить ему интерактивную игру на основе сказки «Мышонок и карандаш». Затею эту можно осуществить в домашних условиях на занятиях в детском саду. Необходимо заранее приготовить элементы, из которых состоит кошка: круги, овалы и треугольники.
Увлекательная игра поможет сделать творческий процесс интереснее для очень активных детей.
Аппликации из геометрических фигур
Простые аппликации
Самым распространенным видом творчества из геометрических фигур являются аппликации из бумажных элементов.
Малышам можно предложить сделать простейшие работы из нескольких деталей.
Например:
- елка из треугольников с основанием-квадратом,
- снеговик из кругов,
- кораблик из треугольников,
- простой домик,
- дерево из прямоугольного ствола и круглой кроны.
Вариантов простых поделок очень много.
Из готовых деталей на основу с нарисованным на ней шаблоном малыши могут самостоятельно наклеить детали простого грузовика.
Несложно сделать схематичного цыпленка из двух желтых кругов и треугольного клювика.
Простая поделка «Кошка»
Для работы понадобятся:
- круглая деталь диаметром 5-6 см,
- 2 маленьких равносторонних треугольника,
- большой прямоугольный треугольник,
- квадрат для обозначения лапок,
- овальный хвост.
Последовательность работы.
- Изготовление аппликации начинаю с наклеивания треугольника вертикально. Его основой служит маленький катет, а гипотенуза будет выполнять роль спинки кошки.
- Наклеивают голову, к ней крепят уши.
- Затем на место приклеивают квадрат-лапки и хвост.
С возрастом количество элементов поделки увеличивается, задача по конструированию усложняется. Ребенок должен понимать важность соблюдения определенной последовательности действий. Анализировать, с каких элементов начинать работу.
Для детей среднего возраста поделки из фигур являются полезным видом деятельности. Они развивают усидчивость, аккуратность и трудолюбие.
Для примера таких поделок можно привести вазу с фруктами. Потребуются дополнительные мелкие элементы для веточек, знания о фруктах, их форме и цветах.
Сложные аппликации из геометрических фигур
Сложность творческой задачи заключается в количестве деталей поделки, необходимости соблюдать определённую последовательность при выполнении работы.
Дети этого возраста должны уметь самостоятельно подбирать форму и цвет нужных деталей, анализировать порядок решения задачи.
Хорошими вариантами поделок является декор крупных деталей более мелкими.
Например, украшение пуловера узором из геометрических фигур, оформление деревенского пейзажа, обозначение фруктовых деревьев в тематической поделке «Сад».
Другим примером сложных работ из фигур может послужить конструирование аппликации машина из треугольных элементов.
В этом случае кузов автомобиля предполагает сборку крупных элементов из небольших деталей. Это увлекательный процесс создания интересной аппликации своими руками. Он требует внимания и аккуратности, развивает пространственное мышление, дает представление о частях целого.
Поделка «Рыбка»
Оригинальная идея поделки заключается в использовании большого количества кругов.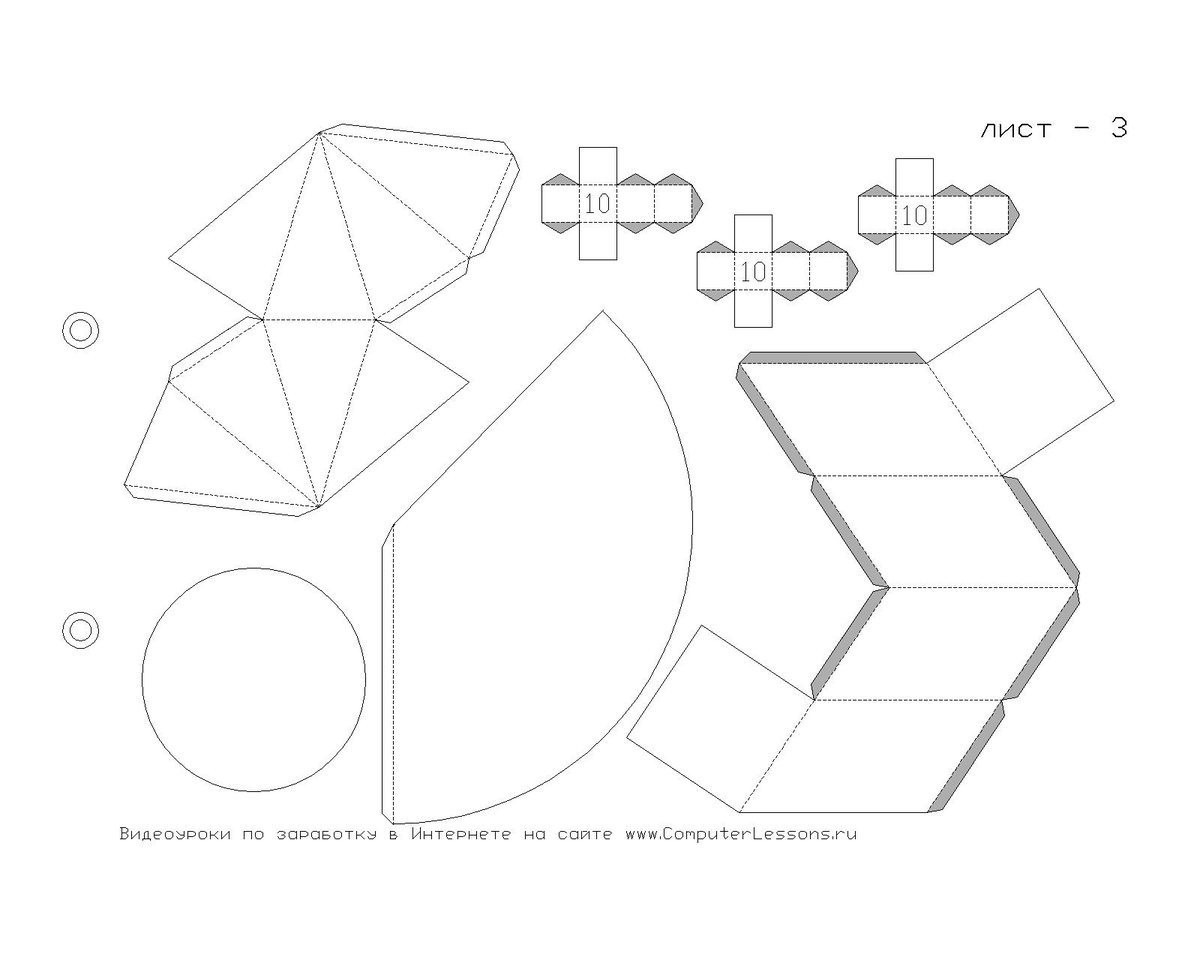
- Для основы понадобится лист картона синего цвета.
- Большой круг выполняет роль головы рыбки. Его надо условно поделить вертикальной полосой на две равные части.
- Чешуя рыбки выполняется из сложенных пополам кругов.
- Нижние половинки «чешуек» наклеивают на основу от середины головы ровными рядами.
- Хвост оформляют при помощи двух половинок круга.
- Дополнительные элементы поделки необходимы для оформления фона. Небольшие кружочки обозначают пузырьки воздуха и камешки на дне.
Проявив терпение и усидчивость, ребенок своим руками может изготовить удивительные поделки. Идеи для творчества можно почерпнуть из видео уроков и фотографий тематических поделок в сети.
Поделки из ватных дисков
Для поделок из геометрических фигур удобно использовать готовые ватные диски. Они хорошо приклеиваются на бумажную основу. Работать с ними просто. Есть возможность покрасить их в разные цвета.
Самой простой поделкой из таких дисков будет снеговик. Фактура материала удивительно подходит для осуществления задумки. С такой простой поделкой справится и ребенок младшего возраста под присмотром взрослых.
Оригинально выглядит аппликация «Солнышко в облаках». Фактура материала хорошо передает фактуру облаков. Солнышко красят желтой акварельной краской.
Немного сложнее выполнить из ватных дисков гусеницу. Диски надо покрасить в зеленый цвет, просушить и наклеить на основу. Из пластилина выполнить детали оформления: мордочку, усики, пятнышки на спинке.
Поделки из подручных материалов
Поделки из геометрических фигур могут быть и объемными изделиями. В качестве основы можно использовать подручные материалы.
Бинокль из втулок от туалетной бумаги
Втулка представляет собой готовый цилиндр, форму которого можно обыграть при творческом подходе.
- Бинокль изготавливается из двух втулок путем их склеивания.
- Поделку можно покрасить или обклеить цветной бумагой для придания сходства с настоящим биноклем.
- Можно дополнить изделие тесьмой или шнурком для удобства использования.
Творческих идей может быть очень много. А поделки отлично послужат для интересных игр.
Из втулок можно смастерить ракету, подзорную трубу, смастерить оригинальную подставку для карандашей.
Игровой домик из коробки
Упаковочные коробки прямоугольной и квадратной формы тоже пригодный материал для поделок из геометрических фигур.
Поделка может быть разной степени сложности. Самые простые требуют декоративного дополнения в виде двери, окон и крыши. Вся работа строится на применении геометрических фигур.
Поделки в технике оригами
Умение делать объемные геометрические фигуры пригодится малышу в жизни. Техника оригами сегодня пользуется большой популярностью, она дает возможность создавать оригинальные вещи. Но к выполнению сложных изделий не стоит приступать сразу, необходимо начинать с простых фигур.
Существует много мастер-классов, которые облегчат любую задачу. Необходимо только найти подходящий вариант, чтобы приступить к реализации задуманного. Занятия оригами позволят лучше представить фигуры младшим школьникам.
Куб
Простой многогранник состоит из квадратов. Для развертки понадобится схема, которую лучше сделать самостоятельно. На ней обязательно предусматривают места для склеивания фигуры. Готовый куб может использоваться для различных игр, он станет великолепным украшением дома.
Конус
Сделать такую фигуру сложнее. Циркулем рисуют окружность, вырезают сектор. Затем фигуру склеивают. После измеряют диаметр основания, рисуют по полученным меркам круг. Боковая часть и основания соединяются. Полученный конус можно использовать в качестве каркаса для других поделок. Из него получится замечательная елочка, колпак для чародея или гнома.
Пирамида
В основе этой фигуры лежит многогранник. Все боковые стороны являются треугольниками. Заранее подготавливается шаблон, с помощью которого получают развертку. Ее аккуратно склеивают, чтобы получить готовую фигуру.
Ее аккуратно склеивают, чтобы получить готовую фигуру.
Украшения для дома
Если вырезать и склеить много фигур разных цветов и размеров, то их можно использовать для декора помещения. Они станут отличными игрушками на новогоднюю елку. Их вешают на нитки или леску, чтобы прикрепить к потолку. Такие цветные фигуры предварительно украшают блестками, тесьмой, бусинами, чтобы они сверкали. Из них создают великолепные гирлянды.
Занятия с ребенком обязательно будут способствовать его всестороннему развитию. Вырезая цветные фигурки или склеивая объемный предмет, он научится правильно воспринимать оттенки. Создание аппликаций полезно для мелкой моторики рук, развития мышления и фантазии.
Проявив фантазию, можно смастерить с использованием фигур из геометрии интересные поделки и аппликации. Работа с фигурами полезна для развития ребенка. Она подготавливает его к обучению математики, облегчает понимание основ конструирования. Учит аккуратности, усидчивости. Развивает аналитические способности и пространственное мышление.
Фото идеи поделок из геометрических фигур
Семейный очаг. Домоводство. Дети. Рецепты. Психология. Отношения
Любому ребенку нравится делать яркие и объемные поделки. Творчество можно объединить с изучением математики и склеить вместе с детьми геометрические фигуры. Ребенок с интересом проведет время, а дополнительно постигнет основы точной науки. Ниже представлено, как начертить карандашом и сделать объемные геометрические фигуры из бумаги, также приведены их правильные названия.
Как сделать объемные геометрические фигуры
Дети познают мир в процессе игры и творчества. Трехмерные фигуры, выполненные своими руками, помогут познакомиться с удивительной наукой — геометрией.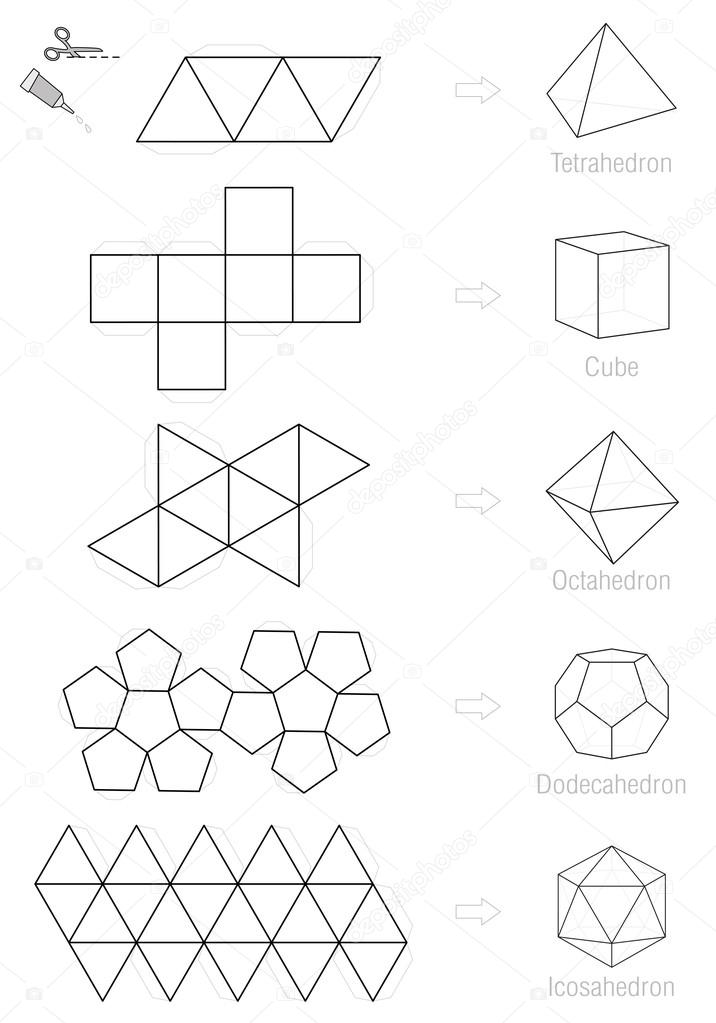
Примеры трафаретов и шаблонов можно скачать из Интернета и распечатать. Затем все фигуры вырезают и склеивают. Дети старшего возраста могут самостоятельно нарисовать развертку нужной фигуры, малышам помогают родители,.
Геометрические объекты делают из бумаги (белой или цветной), картона. Из последнего материала они получаются плотными и прочными.
Из бумаги
Из картона
Развертки куба
Треугольника
Прямоугольника
Цилиндра
Ромба
Призмы
Схемы для вырезания
Ученикам 1–2 класса демонстрируют в школе простые геометрические фигуры и 3d: квадрат, кубик, прямоугольник. Их несложно вырезать и склеить. Шаблоны развивают мелкую моторику у детей и дают первые представления о геометрии.
Ученики средней школы, которые изучают черчение, делают сложные фигуры: бумажные шестигранники, фигуры из пятиугольников, цилиндры. Из бумаги для детей выполняют домики для кукол, мебель, оригами, замок для маленьких игрушек, маски на лицо (трехмерные называются полигональными).
Конуса
Пирамиды
Шестигранника
Макета с припусками
Параллелепипеда
Трапеции
Овала
Шара
Выкройка шара состоит из 8 частей, 12, 16 или большего количества. Присутствуют и другие способы изображения мяча. Например, из 6 деталей или 4 широких клиньев.
Материал, из чего можно сделать плотный шар — картон или плотная бумага.
Многогранника
Параллелограмма
Шаблоны для склеивания
Зачастую школьники задаются вопросом, что можно сделать из бумаги к урокам труда или на выставку.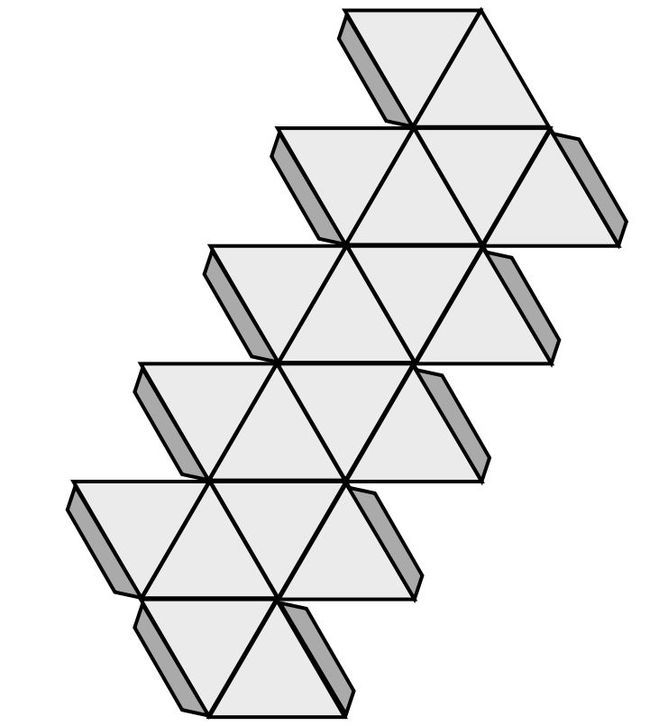 Работы ученика выделятся среди остальных, если это будут сложные трехмерные предметы, рельефные геометрические фигуры, платоновы тела, шаблоны кристаллов и минералов.
Работы ученика выделятся среди остальных, если это будут сложные трехмерные предметы, рельефные геометрические фигуры, платоновы тела, шаблоны кристаллов и минералов.
Если следовать инструкции, то ученик 5–6 класса сможет без помощи родителей сделать точный додекаэдр или тетраэдр.
Иногда в школе задают логические задания, как из квадрата сделать круг или шестиугольник. Для этого определить центр квадрата, согнув его по диагонали. Точка пересечения прямых — центр квадрата и будущего круга. Исходя из этого, можно начертить круг.
Сложных фигур
3d
Октаэдра
Тетраэдра
Икосаэдра
Додекаэдра
Гексаэдра
Фигурок из треугольников
Макетирование — увлекательное занятие. Оно помогает развить воображение и логическое мышление. Из бумаги делают не только фигуры, но и необычные скульптуры, статуэтки, шестиугольные–двенадцатиугольные предметы, наклонные объекты (например, Пизанскую башню), карандаши, линейки. На фото и картинках можно посмотреть, как выглядят оригинальные поделки из бумаги.
Школьники младших классов или дошколята делают бумажные объемные поделки. Например, предметы из овала — веер, цветы, гусеницы. Для них потребуются овалы и круги разного диаметра. Раскладки склеиваются между собой, получаются трехмерные игрушки.
Начинающие конструкторы задаются вопросами, как рисовать и чертить геометрические фигуры, как правильно склеить выкройки и как делают врезки. Проще всего распечатать готовый шаблон. Затем необходимо согнуть фигуру по пунктирным линиям.
Чтобы сгибы получились ровными, к пунктиру прикладывают линейку, по ее форме делают точные загибы. Такой способ особенно помогает, когда речь идет о фигурках из картона или ребенок делает самые сложные макеты.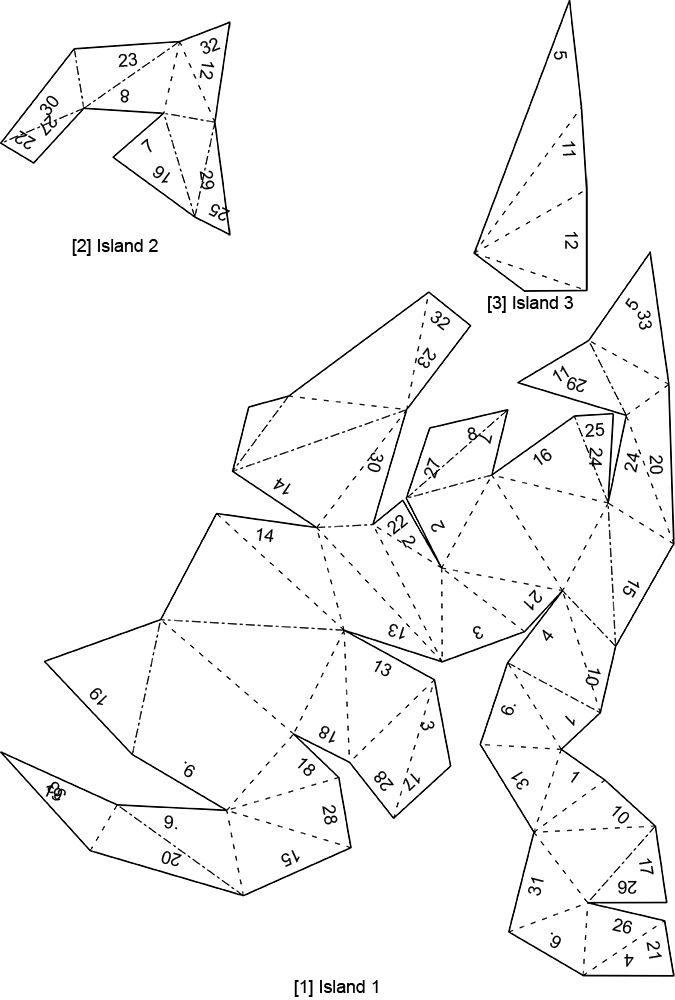 Например, икосаэдр, додекаэдр, тетраэдр.
Например, икосаэдр, додекаэдр, тетраэдр.
На последнем этапе необходимо скрепить элементы объекта, места для склейки обозначены на развернутом виде фигуры. Детали из картона приклеивают при помощи ПВА, а бумажные — карандашным клеем.
Основные ошибки при работе с моделями:
- Ребенок делает неправильные сгибы — например, изгиб отклоняется в сторону от пунктира на несколько градусов. В результате модель получится неточной.
Неточности во время вырезания шаблонов. Если малыш отрезал одну из границ для склеивания, то фигурка будет разворачиваться. Здесь на помощь придет взрослый.
Оригами – бумажные фигурки, которые относятся к японскому искусству и существуют в нём уже не одно столетие. Монахи ещё в древние времена, использовали фигурки из бумаги для декорации храмов и его залов, а также для применения их в религиозных целях (осуществление обрядов).
Сделать оригами из бумаги своими руками в состоянии каждый малоопытный мастер, но главным критерием есть имение усидчивости и точности движений. Сегодня вы поймёте, что не нужно быть асом, чтобы красиво сделать эти изделия.
Инструменты для оригами
Основное внимание стоит уделить выбору бумаги для поделок. Для оригами подойдёт офисная, твёрдая бумага разной цветовой гаммы. Она подойдёт для любых схем, как простых, так и сложных.
Для закрепления бумаги нужно приобрести клей-карандаш или клей ПВА. Подойдут и другие виды клея, лучшим вариантом будут те, что не оставляют следов, а если и оставили, то легко устраняются.
Приобретите краски в баллончиках, для придания необходимого оттенка изделиям с серой или обычной белой бумаги.
Для выравнивания краёв оригами подойдёт резак, только не стоит забывать про аккуратное поведение с ним.
Также для создания игрушек надо линейки, карандаши для черчения схем. Для придания креативности и необычности вашему оригами, можно украсить его с помощью бисера, стекляруса, стразами, ленточками.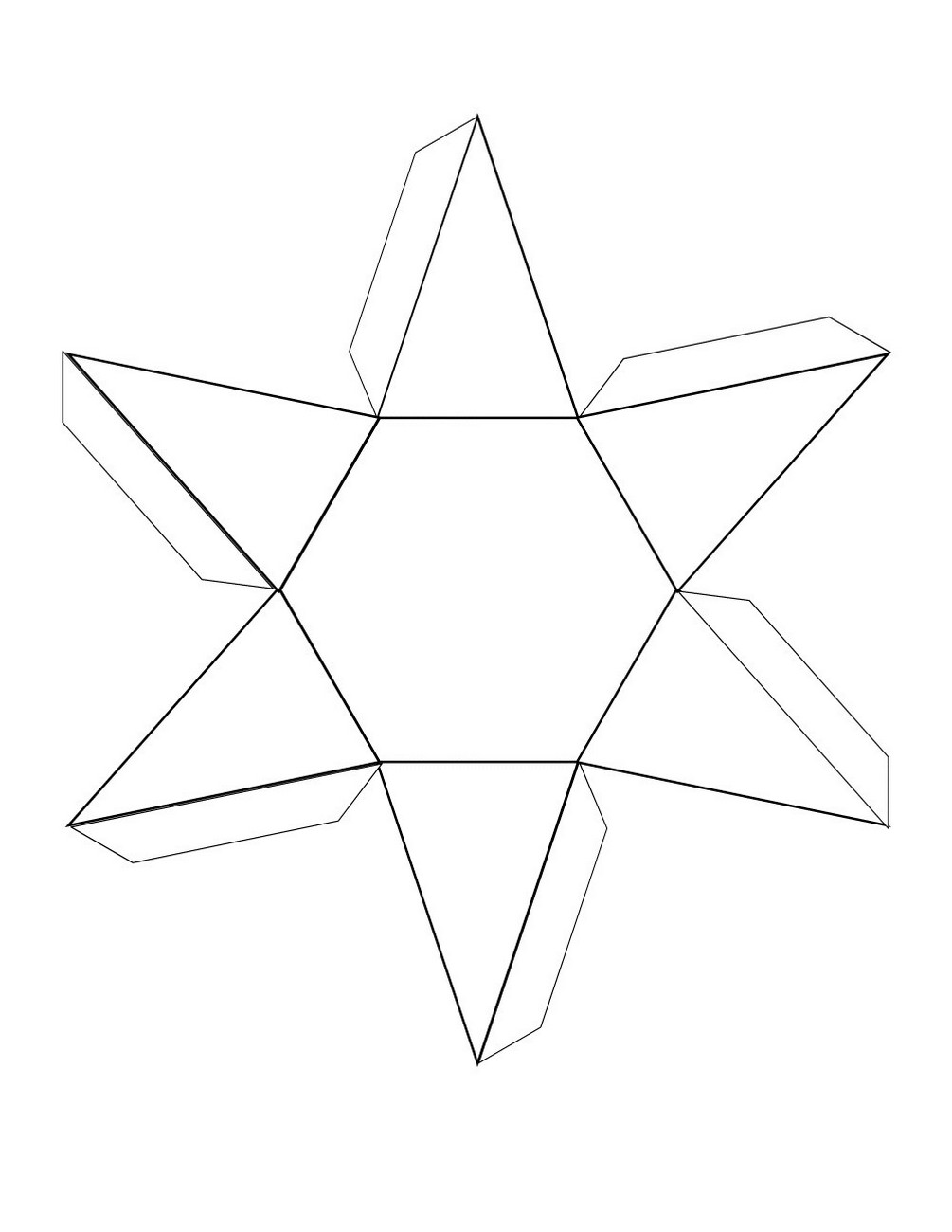
Разновидности бумажных фигурок
Не считая классического вида, есть ещё много разных альтернативных видов:
- Классическое простое оригами – с него стоит начинать тем, кто впервые решил заняться бумажными фигурками. Примером данного стиля есть фигурка журавлика.
- Оригами из модулей – сложнее чем первый вид. Несколько деталей (модулей) необходимо соединить простым складыванием. Изделие держится достаточно долго.
- Аэрогами – фигурки самолётов из бумаги.
- Киригами – создание фигурок происходит с использованием ножниц. Например, открытки.
- Кусудами – объёмное оригами, части изделия соединяются между собой с помощью нитей и клея. Форма фигурки часто напоминает большой шар. Данный вид часто использовался для украшений входа в храм.
Бумажный журавлик
Является классическим видом оригами. В народе ходит легенда, что если сделать тысячу журавликов, то сбудется то, что сердце хочет.
Подробно рассмотрим, как делать сделать эту чудесную фигурку.
- Согнув лист по диагонали, отрезаем ненужную бумагу, так чтобы остался лист напоминающий треугольник.
- Ещё раз сгибаем. Должно быть 2 треугольника. Из образовавшегося треугольника, расправляя делаем квадрат. Такую же процедуру проделываем и, с другой стороны.
- Держим так, чтобы края были сверху, и загибаем их строго к центру.
- Верхний треугольник тоже сгибаем. И сразу расправляем сгиб, у нас получается контур.
- Уголок тот, что ниже остальных, загибаем горизонтально.
- Делаем ромб (слаживаем краешки к центру стороны). Проделываем те же маневры с другой стороной.
- Для формирования шеи, берёмся за нижнюю часть и начинаем загибать там, где внутренний контур. Таким же методом делаем журавлику хвост.
- Там, где находится шея, начало изгибаем, таким образом у нас получится клюв.
- Складываем ему крылья, воспользовавшись сгибанием на маленький угол.
При желании, журавля можно покрасить или сразу взять цветную бумагу.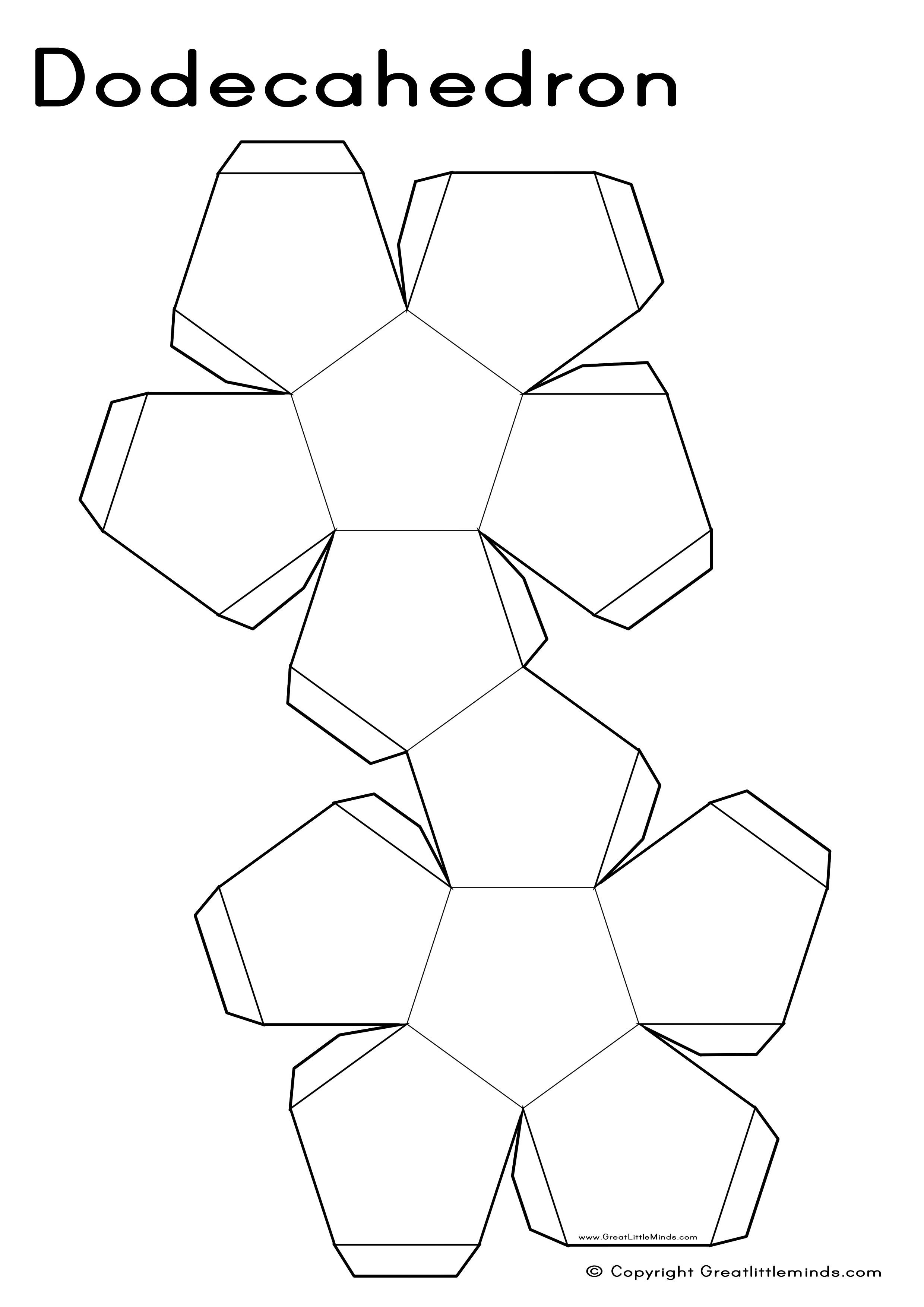 Оригами журавель готов.
Оригами журавель готов.
Роза техникой оригами
Более привлекательными и легкими для большинства новичков, так и для мастеров оригами, являются цветы из оригами. Распространённой фигуркой является бумажная роза.
Рассмотрим пошаговую инструкцию и фото данного оригами:
- Берём цветную бумагу, желательно красного цвета, складываем пополам, потом ещё раз.
- Слой бумаги, что находится вверху, немного раскрываем так, чтобы у нас получился раздутый верх.
- Переворачиваем на другую сторону, и повторяем действие, что описаны в предыдущем пункте.
- Берём углы и загибаем их к верхнему уголку.
- Треугольник, что вскоре получился, сгибаем пополам, до появления контура.
- Раскрываем треугольник, потянув за оба угла вниз.
- Держа кармашки за верхнюю часть, загибаем вниз.
- Пункты с 4 по 7 проделываем и на другой стороне.
- Делаем загиб верхнего угла.
- Нижнюю часть разворачиваем как книгу.
- Выпучиваем так, чтобы получились 2 треугольника.
- Переворачиваем изделие.
- Правый нижний квадрат аккуратно сгибаем с верхнего в нижний край (строго по диагонали).
- Повернув на 180̊ и проделываем 13 пункт.
- Берёмся пальцами за стенки оригами, и не боясь крутим на 360̊, пока не увидим получившееся лепестки.
Бумажный лебедь
Данная техника более сложная, чем остальные так как здесь используется метод модульного оригами. Для того, чтобы сделать объёмного лебедя, нужно:
- Сделать приблизительно 460 треугольников с белой бумаги и 1 красный для клюва.
- Уголки двух треугольников вставляем в карманчик третьего.
- Прибавляем ещё два. Все уголки вкладываем в карман.
- Делаем три таких ряда. Необходимо взять около 30 модулей для каждого ряда. Закрываем круг.
- Вставляем заготовки для следующих двух рядов.
- Вдавливаем центр так, чтобы он потихоньку выворачивался.
- При всём этом края заворачиваем вверх.
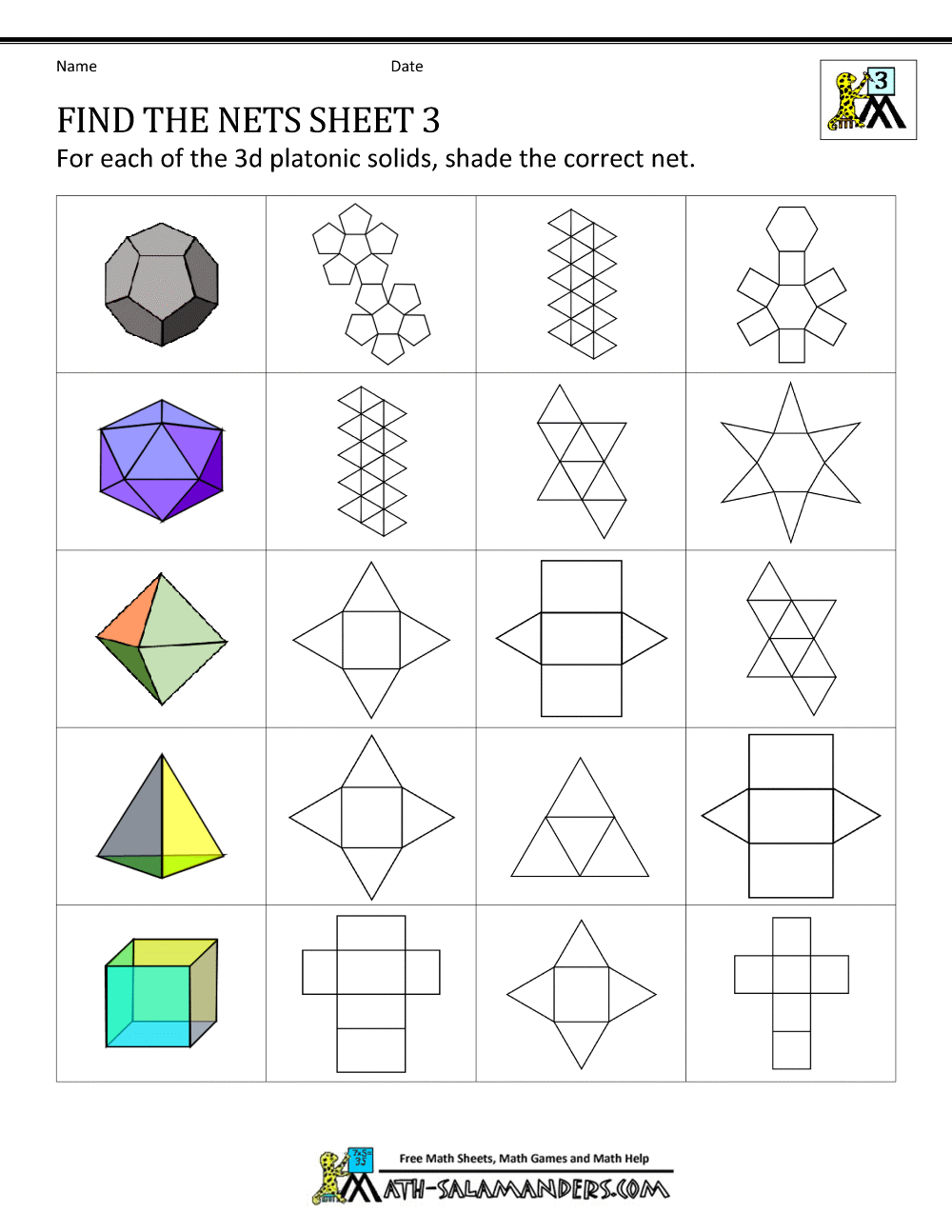
- Делаем ряды дальше, но не забываем про шахматный порядок модулей.
- В 7 ряду делаем модули под крылья. Насаживаем 12 заготовок, сделав пропуск для 2 уголков, приделываем ещё такое же количество заготовок. На оставленных местах делаем лебедю хвост и шею.
- В 8 ряде для крыльев количество заготовок становится на 1 меньше.
- Так делаем и с последующими рядами, пока в последнем ряде не останется 1 модуль.
- Хвост делаем методом уменьшения на одну заготовок в каждом ряде.
- Шею собираем из 10-12 модулей, а голову из одной красной заготовки. Создаём шею, постепенно выгибая её.
- Когда шея готова, собираем её вместе с телом воедино.
Фото оригами своими руками
Обратите внимание!
Обратите внимание!
Создавать поделки своими руками интересно не только детям, но и взрослым. Однако для взрослых придумано достаточное количество моделей, которые отличаются сложностью выполнения и временем, затраченным на их создание. В последнее время у взрослых и детей появился интерес к созданию сложных геометрических фигур. К такому виду фигур относится икосаэдр, который представляет собой правильный многоугольник и является одним из платоновых тел – правильных многогранников. Эта фигура имеет 20 треугольных граней (равносторонних треугольников), 30 ребер и 12 вершин, которые являются местом стыка 5 ребер. Правильный икосаэдр из бумаги собрать достаточно сложно, но интересно. Если вы увлечены оригами, то сделать икосаэдр бумажный своими руками вам не составит труда. Его сделать из цветной, гофрированной бумаги, фольги, упаковочной бумаги для цветов. Используя разнообразные материалы, можно придать еще большую красоту и эффектность своему икосаэдру. Все зависит только от фантазии его создателя и подручного материала, имеющегося на столе.
Предлагаем вам несколько вариантов разверток икосаэдра, которые можно распечатать, перенести на плотную бумагу и картон, согнуть по линиям и склеить.
Как сделать икосаэдр из бумаги: схема
Для того чтобы собрать икосаэдр из листа бумаги или картона, необходимо предварительно подготовить следующие материалы:
- макет икосаэдра;
- клей ПВА;
- ножницы;
- линейка.
Во время создания икосаэдра важно обратить особое внимание на процесс сгиба всех деталей: для того, чтобы ровно согнуть бумагу, можно использовать обычную линейку.
Примечательно, что икосаэдр можно встретить и в повседневной жизни. Например, в форме усеченного икосаэдра (многогранник, состоящий из 12 пятиугольников и 20 шестиугольников правильной формы) выполнен футбольный мяч. Это особенно видно, если раскрасить получившийся икосаэдр в черно-белый цвет, как и сам мяч.
Такой футбольный мяч можно сделать самостоятельно, распечатав предварительно развертку усеченного икосаэдра в 2 экземплярах:
Создание икосаэдра своими руками представляет интересный процесс, который требует вдумчивости, терпения и большого количества бумаги. Однако результат, полученный в итоге, будет радовать глаз еще долгое время. Икосаэдр можно дать поиграть ребенку, если он достиг уже трехлетнего возраста. Играя с такой сложной геометрической фигурой, он будет развивать не только образное мышление, пространственные навыки, но и знакомиться с миром геометрии. Если же взрослый решил создать икосаэдр самостоятельно, то такой творческий процесс по конструированию икосаэдра позволит скоротать время, а также похвастаться перед близкими своим умением создавать сложные фигуры.
В основе самых сложных и необычные формы сооружений, устройств, механизмов лежат элементарные геометрические фигуры: куб, призма, пирамида, шар и другие. Для начала научитесь создавать самые простые фигуры, а после вы легко освоите более сложные формы.
Многие моделисты начинают свой путь с бумажных моделей. Это обусловлено доступностью материала (найти бумагу и картон не составляет трудности) и легкостью в его обработки (не требуются специальные инструменты).
Однако, бумага имеет и ряд характерных особенностей:
- капризный, хрупкий материал
- требует высокой аккуратности, внимательности, усидчивости при работе
По этим причинам бумага является материалом, как для начинающих, так и для настоящих мастеров и из нее создаются модели самой разной сложности.
В этот статье мы изучим простейшие геометрические фигуры, которые можно сделать из бумаги.
Вам понадобятся следующие материалы:
- лист бумаги
- карандаш
- линейка
- ластик
- ножницы
- клей ПВА либо клеящий карандаш
- кисточка для клея, лучше из жесткой щетины
- циркуль (для некоторых фигур)
Как сделать куб из бумаги?
Куб – правильный многогранник, каждая грань которого представляет собой квадрат
Создание куба состоит из двух этапов: создание развертки и склеивание. фигуры. Для создания схемы вы можете воспользоваться принтером, просто распечатав готовую схему. Либо вы можете самостоятельно с помощью чертежных инструментов нарисовать развертку.
Рисование развертки:
- Выбираем размеры квадрата — одной стороны нашего куба. Лист бумаги должен быть шириной не менее 3 сторон этого квадрата и длиной немного более 4 сторон.
- Чертим в длину нашего листа четыре квадрата, которые станут боковыми сторонами куба. Рисуем их строго на одной линии, вплотную друг к другу.
- Над и под любыми из квадратов рисуем по одному такому же квадрату.
- Дорисовываем полоски для склеивания, с помощью которых грани будут соединяться между собой. Каждые две грани должны соединяться одной полоской.
- Куб готов!
После рисования развертка вырезается ножницами и склеивайте ПВА. Клей очень тонким слоем равномерно размазываем кистью по поверхности склеивания. Соединяем поверхности и закрепляем в нужном положении на некоторое время, с помощью скрепки или небольшого груза. Срок схватывания клея где-то 30-40 минут. Ускорить высыхание можно методом нагрева, например, на батарее. После склеиваем следующие грани, закрепляем в нужном положении. И так далее. Так постепенно вы проклеите все грани куба. Используйте небольшие порции клея!
Ускорить высыхание можно методом нагрева, например, на батарее. После склеиваем следующие грани, закрепляем в нужном положении. И так далее. Так постепенно вы проклеите все грани куба. Используйте небольшие порции клея!
Как сделать конус из бумаги?
Конус – тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность.
Рисование развертки:
- Рисуем циркулем окружность
- Вырезаем сектор (часть круга, ограниченная дугой окружности и двумя радиусами, проведенными к концам этой дуги) из этой окружности. Чем больший сектор вы вырежете, тем острее будет конец конуса.
- Склеиваем боковую поверхность конуса.
- Измеряем диаметр основания конуса. С помощью циркуля рисуем окружность на листе бумаге требуемого диаметра. Дорисовываем треугольнички для склеивания основания с боковой поверхностью. Вырезаем.
- Приклеиваем основание к боковой поверхности.
- Конус готов!
Как сделать цилиндр из бумаги?
Цилиндр – геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.
Рисование развертки:
- Рисуем прямоугольник на бумаги, в котором ширина — это высота цилиндра, а длина определит диаметр будущей фигуры. Отношение длины прямоугольника к диаметру определяется выражением: L=πD, где L- длина прямоугольника, а D — диаметр будущего цилиндра. Подставив в формулу требуемый диаметр, найдем длину прямоугольника, который будем рисовать на бумаге. Дорисовываем небольшие дополнительные треугольнички, которые необходимы для склеивания деталей.
- Рисуем на бумаге два круга, диаметром цилиндра. Это будет верхнее и нижнее основания цилиндра.
- Вырезаем все детали будущего бумажного цилиндра.
- Склеиваем боковую поверхность цилиндра из прямоугольника. Даем детали высохнуть. Приклеиваем нижнее основание. Ждем высыхания. Приклеиваем верхнее основание.
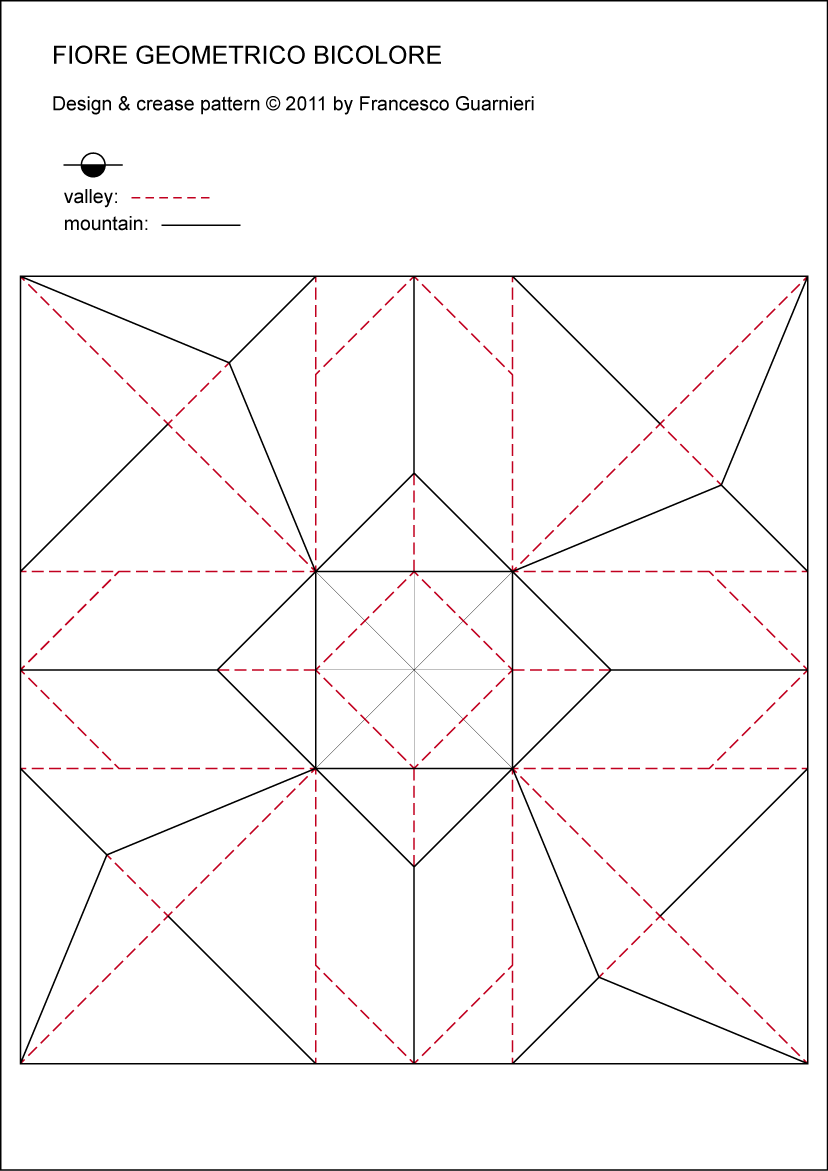
- Цилиндр готов!
Как сделать параллелепипед из бумаги?
Параллелепипед – многогранник, у которого шесть граней и каждая из них параллелограмм.
Рисование развертки:
- Выбираем размеры параллелепипеда и величины углов.
- Чертим параллелограмм — основание. С каждой стороне дорисовываем боковые стороны — параллелограммы. От любой из боковой стороны дорисовываем второе основание. Добавляем полоски для склеивания. Параллелепипед может быть прямоугольным, если стороны прямоугольники. Если параллелепипед не прямоугольный, то создать развертку немного сложнее. Для каждого параллелограмма нужно выдержать требуемые углы.
- Вырезаем развертку и склеиваем.
- Параллелепипед готов!
Как сделать пирамиду из бумаги?
Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину.
Рисование развертки:
- Выбираем размеры пирамиды и количество ее граней.
- Рисуем основание — многогранник. В зависимости от количества граней это может быть треугольник, квадрат, пятиугольник или другой многогранник.
- От одной из сторон основания рисуем треугольник, который будет боковой стороной. Следующий треугольник рисуем так, чтобы одна сторона у него с предыдущим была общая и так далее. Так рисуем столько треугольников, сколько сторон в пирамиде. Дорисовываем полоски для склеивания в нужных местах.
- Вырезаем и склеиваем фигуру.
- Пирамида готова!
Геометрические фигуры из бумаги должен научиться делать каждый! Ведь никогда не знаешь, какие знания тебе могут пригодиться в жизни. В последнее время техника оригами набирает широкую популярность среди детей и взрослых. Но перед тем как делать разнообразные поделки (животных, птиц, растений, маленьких домиков), нужно начать с простых геометрических фигур. Такие изделия подойдут для школьников для хорошего визуального представления разных фигур.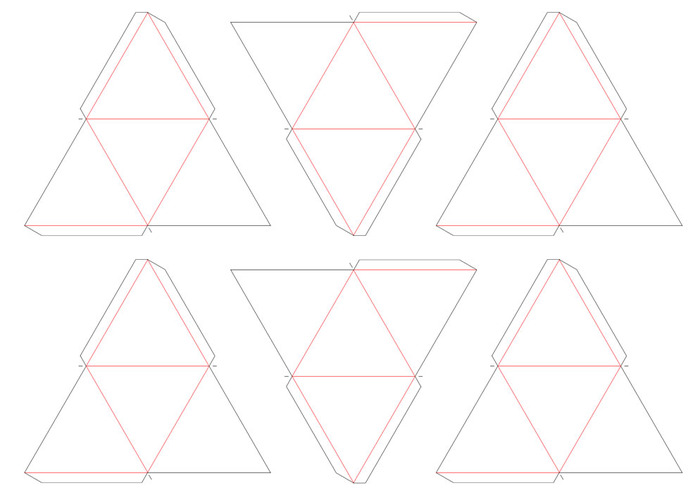
Мастерим куб
Итак, для сегодняшнего мастер-класса нам пригодится бумага, схемы, клей, ножницы, линейки и немножечко терпения.
Куб — самая простая фигура для оригами, простой многогранник, в котором каждая грань является квадратом. Схему для создания развертки можно распечатать на принтере, либо начертить самим. Для этого выбрать размеры граней. Ширина листа бумаги должна быть не менее 3 сторон одного квадрата, а длина не более 5 сторон. Начертить в длину листа четыре квадрата, которые станут боковыми сторонами куба. Рисовать строго на одной линии, вплотную. Над и под одним квадратом нарисовать по одному квадрату. Дорисовать полоски для склеивания, благодаря которым грани будут соединяться между собой. Наш куб уже практически готов!
Далее тонким слоем клея равномерно размазать по местам соединения. Склеить эти поверхности и закрепить на некоторое время с помощью скрепки. Клей будет схватываться около 30-40 минут. Таким образом склеить все грани.
Поделка посложнее
Конус делается немного сложнее. Для начала нарисовать циркулем окружность. Вырезать сектор (часть кружка, ограниченная дугой окружности и двумя радиусами) из этой окружности. Острота конца конуса зависит от вырезанной части большого сектора.
Склеить боковую поверхность конуса. Далее измерить диаметр основания конуса. Циркулем нарисовать окружность на листе бумаги. Затем дорисовать треугольнички для склеивания основы с боковой поверхности. Вырезать. После приклеить основание к боковой поверхности. Поделка готова!
Сложный параллелепипед
Параллелепипед — сложная фигура многогранник, у которого 6 граней и каждая из них параллелограмм.
Чтобы сделать параллелепипед техникой оригами, нужно начертить основание — параллелограмм любого размера. С каждой его стороны нарисовать боковые стороны — тоже параллелограммы. Далее от любой из боковых сторон дорисовать второе основание.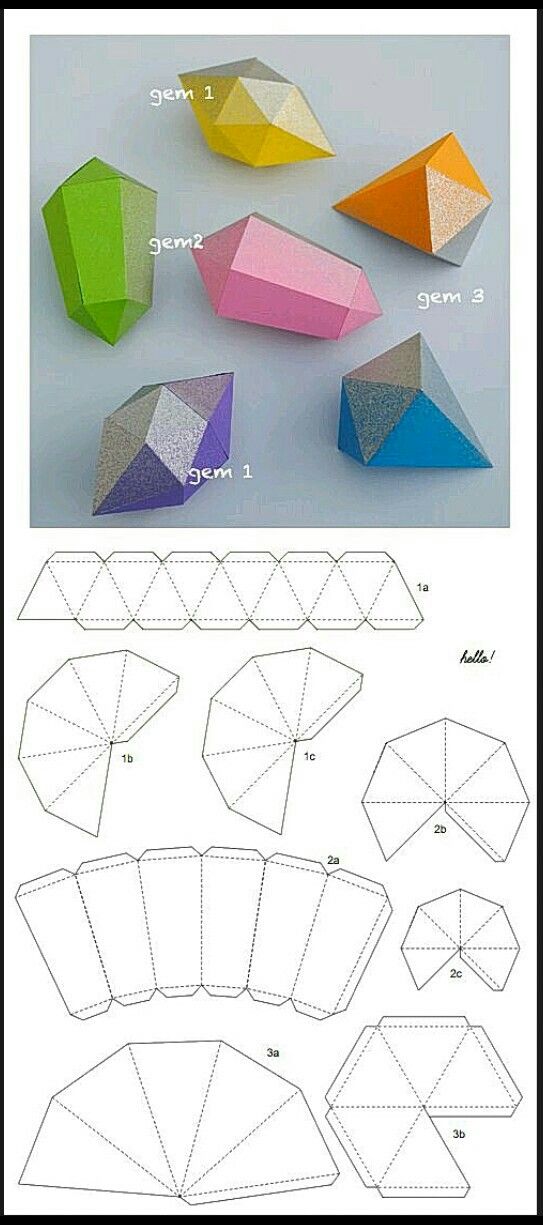 Добавить места для склеивания. Параллелепипед может быть прямоугольным, если все стороны имеют прямые углы. Затем вырезать развертку и склеить. Готово!
Добавить места для склеивания. Параллелепипед может быть прямоугольным, если все стороны имеют прямые углы. Затем вырезать развертку и склеить. Готово!
Пирамида-оригами
Пришло время сделать пирамиду из бумаги. Это многогранник, основание которого — многоугольник, а другие грани — треугольники с общей вершиной.
Для начала нужно выбрать размеры пирамиды и количество граней. Далее нарисовать многогранник — он будет основанием. Смотря на количество граней, это может быть также треугольник, квадрат, пятиугольник.
От одной из сторон нашего многогранника нарисовать треугольник, который будет боковой стороной. Затем нарисовать еще треугольник, чтобы одна его сторона была общей с первым треугольником. Нарисовать их столько, сколько сторон в пирамиде. Далее дорисовать полоски для склеивания в необходимых местах. Вырезать и склеить фигуру. Пирамида готова!
Бумажный цилиндр
Цилиндр — это геометрическая фигура, ограниченная цилиндрической поверхностью и двумя параллельными плоскостями, которые ее пересекают.
Нарисовать прямоугольник на бумаге, в которой ширина — высота цилиндра, а длина — диаметр. Любители геометрии знают, что отношение длины прямоугольника к диаметру определяется формулой: L=nD, где L — длина прямоугольника, а D — диаметр цилиндра. С помощью этого вычисления узнать длину прямоугольника, которого будем рисовать на бумаге. Дорисовать маленькие треугольнички для склеивания деталей.
Затем нарисовать на бумаге два круга, диаметром как цилиндр. Это будет верхнее и нижнее основания цилиндра. Далее вырезать все детали. Склеить боковую поверхность цилиндра из прямоугольника. Дать детали высохнуть и приклеить к нему нижнее основание. Снова подождать, пока высохнет, и приклеить верхнюю основу. Готово!
Видео по теме статьи
Оригами как средство формирования представлений о геометрических фигурах
В настоящее
время проблема качества обучения и
воспитания, развития и
формирования представлений о геометрических
фигурах приобретает
еще большую
остроту и актуальность. Развитие
представлений о геометрических
фигурах, это одна из сложных задач в
интеллектуальном развитии ребенка.
Ведь именно в дошкольный период
дети
накапливают
первые
представления о форме, размерах и
взаимном положении предметов в
пространстве.
Развитие
представлений о геометрических
фигурах, это одна из сложных задач в
интеллектуальном развитии ребенка.
Ведь именно в дошкольный период
дети
накапливают
первые
представления о форме, размерах и
взаимном положении предметов в
пространстве.
Актуальность заключается в том, что применение оригами в развитии дошкольников, является эффективным средством формирования представлений о геометрических фигурах. Геометрические истоки прослеживаются в оригами из бумаги и отображаются в складывании квадратных форм с наибольшей аккуратностью и точностью. Известный преподаватель из Германии и учредитель системы дошкольного обучения Фребель Фридрих (1782-1852) признал достоинства оригами для детей как метод ознакомления с основами геометрии. Ведь «геометрия и оригами» являются всесторонним развитием геометрического мышления. Формирование геометрических знаний средствами оригами, которые помогают преодолеть указанные трудности, и позволяют дошкольникам «войти в пространство». Главная особенность представляемого курса заключается в том, чтобы представить это у дошкольников, складывающих бумагу, достигается наглядное представление геометрических фигур и их свойств. В игровой и занимательной форме в практической деятельности они каждый раз находят самое приблизительное сходство предметов, фигурки. Он начинает видеть самое характерное, доделывает, додумывает, досоздает образ в своем воображении. Стремление разобрать во всем самостоятельно и освоить всю предоставляемую информацию по геометрии помогает преодолеть препятствия, которые стоят на пути к этому освоению.
Оригами при изучении
поможет детям окунуться
в мир геометрических фигур, разглядеть
возможности складывания бумаги, при
этом получая интересные образы и фигуры.
Складывая фигурки, ребенок познает
окружающий мир. А также оригами служит
главным средством формирования
положительной мотивации к изучению
геометрических фигур. Характер
геометрии и сложность
материала приводит к тому, что решение
геометрических задач уже на самом первом
этапе часто вызывает трудности. Нужно
обладать хорошо развитым геометрическим
воображением, чтобы представить себе
соответствующую пространственную
картину. Активное использование оригами
позволяет разнообразить учебную
деятельность, что способствует развитию
у детей не только памяти, но и внимания,
восприятия, воображения и разных форм
мышления.
Нужно
обладать хорошо развитым геометрическим
воображением, чтобы представить себе
соответствующую пространственную
картину. Активное использование оригами
позволяет разнообразить учебную
деятельность, что способствует развитию
у детей не только памяти, но и внимания,
восприятия, воображения и разных форм
мышления.
В настоящее время можно с уверенностью сказать, что развитие представлений о геометрических фигурах у дошкольников уделяют большое внимание а также уделяется к поиску новых методик обучения о геометрических фигурах.
«Геометрия через оригами» — математика, прочее
Муниципальное бюджетное общеобразовательное учреждение
«Средняя школа № 47» (г. Тверь)
«Геометрия глазами оригами».
Разработала: Шишова А.А.,
учитель математики
МБОУ СШ № 47
Тверь, 2019
Содержание
Введение…………………………………………………………………………………..
Глава 1. Понятие об оригами…………………………………………………………….
1.1. История оригами…………………………………………………………………….
1.2. Виды и техники оригами……………………………………………………………
1.3. Базовые формы оригами…………………………………………………………….
1.4. Этапы развития оригами…………………………………………………………….
Глава 2. Азбука оригами………………………………………………………………….
1. Бумага, материалы, формы бумаги……………………………………….
Глава 3. Оригами -это математика…………………………………………………………
Некоторые примеры связи математики и оригами………………………………………
Заключение …………………………………………………………………………………
Использованная литература ………………………………………………………………
Японская мудрость издревле гласит:
«Великий квадрат не имеет пределов».
Попробуй простую фигурку сложить,
И вмиг увлечет интересное дело.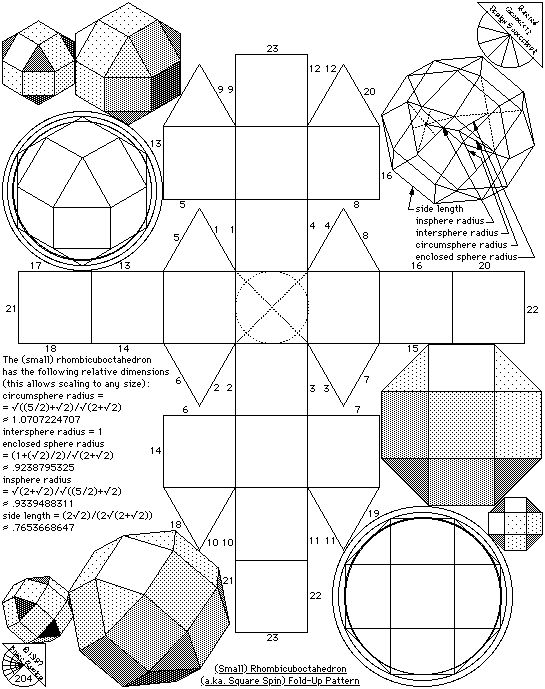
А.Е. Гайдаенко
Введение
Оригами — удивительное искусство бумажной пластики. Сегодня множество людей во всем мире увлекаются искусством «оригами». Бумажные фигурки делают дети и взрослые, художники и конструкторы. Его даже преподают в школах, о нем пишут книги и выпускают журналы с интересными статьями и описанием различных моделей. Я заметил, что, складывая фигурки оригами, сталкиваюсь с математическими понятиями. Мне стало интересно, как связаны таинственное искусство складывания фигурок из бумаги и давно интересующая меня математика.
Цели работы:
— изучить научно-популярную литературу
— Изучить происхождение оригами
— связь этого искусства с математикой
— исследовать применение математики в создании и построении оригами.
Задачи:
Определить, что называют оригами
Рассмотреть базовые формы и приемы оригами
Изучить понятие, виды, историю происхождения оригами.
Проанализировать связь оригами и математики на примере основных элементов азбуки оригами.
Методы исследования:
Изучение литературы.
Построение оригами.
Анализ проведённой работы.
Предмет: оригами
Гипотеза: Искусство оригами тесно связано с математикой и может стать хорошей основой для ее изучения.
Актуальность:
Оригами- метод развития творческих способностей.
В книге Н. Г. Юрина «По книге «Я познаю мир»» я узнал о понятии оригами. В книге «Соколова «Оригами» Большая настольная книга для всей семьи 240 лучших проектов для совместного творчества» я нашел азбуку оригами, основные приемы создания оригами и много схем. На сайтах интернета я познакомился с техникой и видами данного искусства, узнал о бумаге, которая предназначена для складывания фигур, узнал о первых фигурках и где их используют.
Глава 1. Понятие об оригами
Многие удивляются, услышав слово «оригами». «А что это такое?» — спрашивают они. Между тем каждый человек наверняка хоть раз в жизни создавал самое простенькое изделие из квадратного листа бумаги— кораблик или самолетик. А в те времена, когда в магазинах не было такого выбора соломенных шляп и панам, люди летом нередко сооружали себе «пилотку» из газеты. И бумажные кораблики, и пилотка сделаны по принципу «оригами».
Это искусство родилось в Японии. В «Японских хрониках» говорится, что его начало восходит к 610-му году. Кто бы подумал, глядя на простенький кораблик, что первоначально в изделия из бумажного квадрата вкладывался большой смысл! На востоке к квадрату относились с большим уважением. В буддизме он считался отражением Космоса, той великой Пустоты, из которой происходят все вещи. К бумаге японцы тоже относились с почтением, как ко всему недолговечному, непрочному, живущему один миг
Сегодня множество людей во всем мире увлекаются искусством «оригами». Бумажные фигурки делают дети и взрослые, художники и конструкторы. Его даже преподают в школах, о нем пишут книги и выпускают журналы с интересными статьями и описанием различных моделей.
В наше время оригами перестало быть только игрушкой. Этим искусством заинтересовались ученые и конструкторы. Проходят научные симпозиумы по оригами. Уже создаются сложнейшие технические конструкции — бумажные модели…
Но детей, конечно, больше всего интересует оригами как возможность создать новую игрушку. А можно создать новые, свои собственные объемные фигурки из бумаги.
Итак, оригами – это искусство складывания из бумаги.
1.1. История оригами
Оригами в переводе с японского означает «сложенная бумага». «Ori» — это складывать, a «kami» — бумага. Таким образом, оригами — это древнее искусство складывания фигурок из бумаги, бумажной пластики. Несмотря на традиционно приписываемые японские корни, искусство оригами своими корнями уходит к древнему Китаю, где и была открыта бумага.
Несмотря на традиционно приписываемые японские корни, искусство оригами своими корнями уходит к древнему Китаю, где и была открыта бумага.
Первоначально оригами использовалось в религиозных обрядах. Долгое время этот вид искусства был доступен лишь представителям высших сословий, где признаком хорошего тона было владение техникой складывания из бумаги. Лишь после второй мировой войны оригами вышло за пределы Востока и попало в Америку и Европу, где сразу обрело своих поклонников.
Для оригами требуется лишь листок бумаги, что делает его одним из наиболее доступных искусств. Для оригами может использоваться любая бумага, но существует определенный стандарт для складывания
Законченная фигура оригами называется моделью, метод складывания модели называется проектом, а нарисованные инструкции для модели называются набором схем.
Оригамисты любят складывать модели животных, а также все объекты живой природы. Кроме моделей животных, созданы модели почти всех физических объектов, включая людей, лица, растения, транспортные средства, здания и др. Некоторые оригамисты складывают абстрактные или математические формы, другие специализируются в модульном оригами, где из множества сложенных простых частей собирают большие сложные структуры.
1.2. Виды и техники оригами
Модульное оригами
Одной из популярных разновидностей оригами является модульное оригами, в котором целая фигура собирается из многих одинаковых частей (модулей). Каждый модуль складывается по правилам классического оригами из одного листа бумаги, а затем модули соединяются путем вкладывания их друг в друга, появляющаяся при этом сила трения не дает конструкции распасться. Одним из наиболее часто встречающихся объектов модульного оригами является кусудама, объемное тело шарообразной формы. (Приложение № 1)
Простое оригами
Простое оригами — стиль оригами, придуманный британским оригамистом Джоном Смитом, и который ограничен использованием только складок горой и долиной.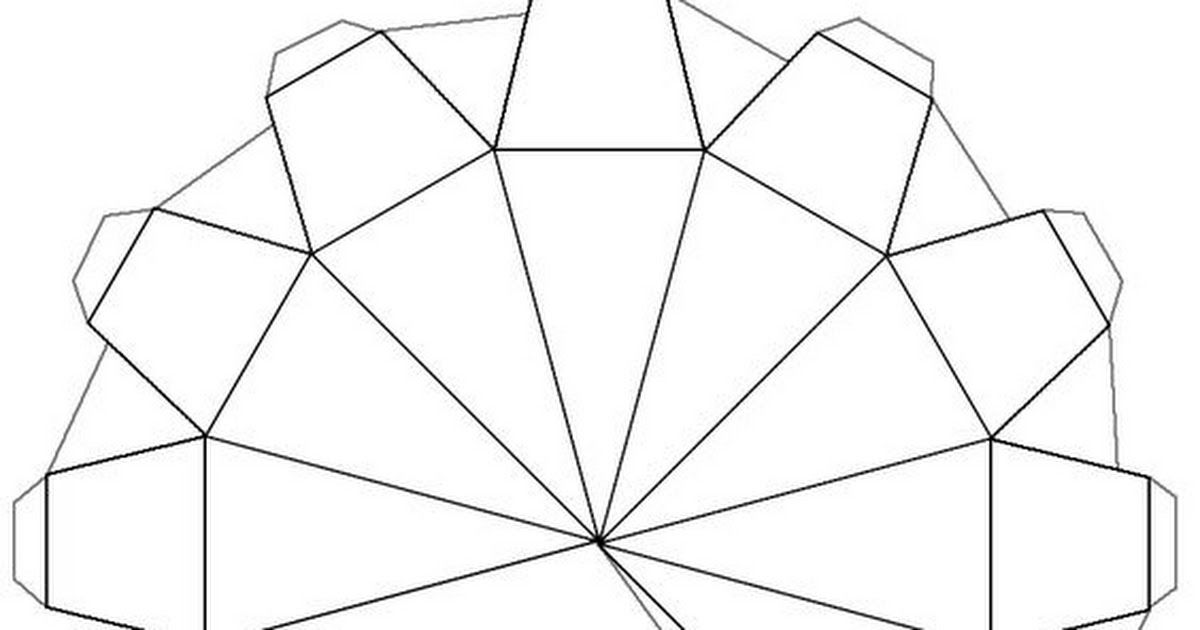 Целью оригами является облегчение занятий неопытным оригамистам, а также людям с ограниченными двигательными навыками. Данное выше ограничение означает невозможность многих (но не всех) сложных приемов, привычных для обычного оригами, что вынуждает к разработке новых методов, дающих сходные эффекты.
Целью оригами является облегчение занятий неопытным оригамистам, а также людям с ограниченными двигательными навыками. Данное выше ограничение означает невозможность многих (но не всех) сложных приемов, привычных для обычного оригами, что вынуждает к разработке новых методов, дающих сходные эффекты.
Складывание по развертке
Развертка (англ. crease pattern; паттерн складок) — один из видов диаграмм оригами, представляющий собой чертеж, на котором изображены все складки готовой модели. Складывание по развертке сложнее складывания по традиционной схеме, однако, данный метод дает не просто информацию, как сложить модель, но и как она была придумана — дело в том, что развертки используются при разработке новых моделей оригами. Последнее также делает очевидным факт отсутствия для некоторых моделей иных диаграмм, кроме развертки.
Мокрое складывание
Мокрое складывание — техника складывания, разработанная Акирой Ёсидзавой и использующая смоченную водой бумагу для придания фигуркам плавности линий, выразительности, а также жесткости. Особенно актуален данный метод для таких негеометричных объектов, как фигурки животных и цветов — в этом случае они выглядят намного естественней и ближе к оригиналу.
Не всякая бумага подходит для мокрого складывания, а лишь та, в которую при производстве добавляют водорастворимый клей для скрепления волокон. Как правило, данным свойством обладают плотные сорта бумаги.
1.3. Базовые формы оригами.
С древних времен в японском оригами существуют некоторые формы, которые принято считать базовыми. Это стандартные, легко распознаваемые заготовки, из которых впоследствии можно получить сотни вариаций. Все эти базовые модели должны стать хорошо вам знакомыми, и делать каждую базовую заготовку вы должны автоматически, зная каждую её складку и последовательность операций. Освоив базовые формы, вы с успехом сможете складывать не только классические модели, но и свои собственные.
На самых первых этапах работы квадратный лист можно сложить несколькими способами. Их немного — одиннадцать, и у каждой свое имя. (Приложение № 2)
1.4. Этапы развития оригами
Со временем оригами (а этот термин возник только в 1880 года) становится обязательным занятием во многих японских семьях. Мамы обучали дочерей складывать бумажные фигурки. И девочка, если она желала стать хорошей хозяйкой, должна была владеть этим искусством в достаточной мере.
Искусство оригами много веков существовало исключительно как храмовое, чрезвычайно регламентированное по технике исполнения. Количество фигурок было невелико, но приемы работы с бумагой как с материалом, на котором можно не только рисовать, но и особым образом сворачивать, тщательно шлифовались.
Расцвет оригами приходится на середину XX века, когда рабочий-металлист Акира Ёсидзава решил посвятить себя оригами и его развитию. Основная заслуга его в создании «азбуки оригами». Условные обозначения, символы, графические знаки, придуманные Акирой, позволили зафиксировать на бумаге процесс складывания фигурок. Это дало возможность оригами стать универсальным международным языком.
В сороковых годах нашего столетия в Америке и Европе появилось множество энтузиастов, для которых древнее, японское занятие становится способом реализации собственных творческих возможностей, создаются первые центры и школы оригами.
Сегодня оригами переживает очередную волну интереса. Практически во всем мире это искусство развивается в соответствии с традициями народа. Появились новые направления оригами и области его применения. Например, математики благодаря оригами открыли множество возможностей для решения геометрических и топологических задач. Архитекторы и строители увидели в конструировании оригами возможности для создания многогранных структур из плоского листа. Даже возник новый термин — оригамика. Для педагогов оригами — это уникальная возможность развития тонкой моторики ребенка, что напрямую связано с развитием интеллекта.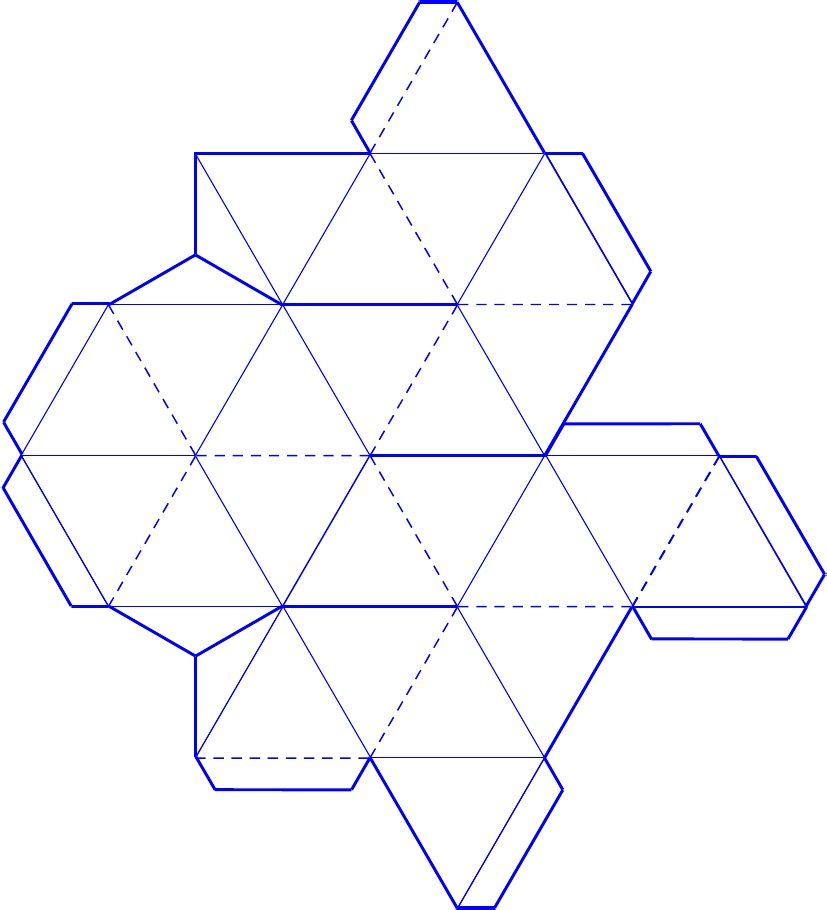 Для психологов оригами — это одно из направлений арт-терапии, возможность оказать больному психологическую помощь посредством искусства.
Для психологов оригами — это одно из направлений арт-терапии, возможность оказать больному психологическую помощь посредством искусства.
В России оригами попало на благодатную почву, стало серьезным занятием для множества педагогов, художников, конструкторов. Сегодня в России тысячи людей занимаются этим искусством. Во многих городах возникли клубы и центры оригами, ежегодно проходят встречи и конференции, посвященные проблеме использования оригами в педагогике, математике, архитектуре.
Глава 2. Азбука оригами.
Важнейшее событие в культуре оригами произошло в середине прошлого века. Рабочий-металлург Акирой Ёсидзавой, посвятивший себя развитию оригами, создал оригамную азбуку. В ней содержатся специальные символы для обозначения сгибов «горкой» (выпуклых) и «долиной» (вогнутых), различных приемов сгибания и разгибания бумаги, точек соприкосновения, манипуляций с фигурой (повернуть, перевернуть). Благодаря азбуке Иошидзавы оригамисты (и авиамоделисты) всего мира получили возможность делиться схемами своих конструкций, учиться на чужом опыте. Даже моделист, ни сном, ни духом не слыхавший об оригами, наверняка не раз пользовался общепринятыми схематическими символами.
Отрабатывая технику складывания различных элементов изделий оригами, следует обратить особое внимание на правильное выполнение сгибов. Они должны быть практически «острыми» и слои бумаги в них должны плотно прилегать друг к другу. В противном случае при наложении сгибов друг на друга в последующих операциях происходит смещение элементов и невозможно создать красивое, аккуратное изделие. Поэтому после выполнения каждого отдельного этапа работы нужно проверять «остроту» всех сгибов.
При отработке сгибов для получения головы, клюва, лапы, хвоста следует обратить внимание, на часть какого животного или птицы похоже то, что получилось во время складывания. Важно знать особенности их строения в жизни, понять возможности стилизации. Это поможет выполнять изделия по схемам, а также совершенствовать их и разрабатывать собственные модели. (Приложение № 2)
(Приложение № 2)
Условные обозначения
Чтобы свободно владеть техникой оригами, самостоятельно конструировать поделки, решать оригамные задачи, необходимо познакомиться с основными условными обозначениями. Для удобства все условные обозначения свел в таблицу. (Приложение № 2) При этом использовал такие подходы как:
метод аппликации;
метод обрисовки;
с помощью чертежных инструментов.
2.1. Бумага
Новички, которые впервые сталкиваются с этим искусством, обычно придают больше значения первой составляющей этого слова.
Увлекаясь самим процессом складывания, они забывают о том, что для достижения художественного эффекта необходимо для каждой работы подобрать наиболее подходящую для нее бумагу. Это может быть и полупрозрачная калька, и толстый картон. Все зависит от поставленных задач. В Японии существуют десятки разновидностей бумаги, каждая из которых имеет свое название. Примеры видов бумаги в приложении № 3.
Хотя для складывания подходит практически любой листовой материал, выбор последнего очень сильно влияет как на процесс складывания, так и на окончательный вид модели.
- Формат бумаги.
Чаще всего для оригами используют квадратные листы бумаги, но допускается и применение других форматов. Например, прямоугольные листы (формата А или половинки квадратов), треугольники, пятиугольники, шести- и восьмиугольники. Существуют даже модели, складываемые из круга.
Глава 3. Оригами – это математика!
Как связано искусство оригами и точная наука математика. Этот вопрос я решила изучить.
Я проанализировала базовые формы оригами и заметила, что уже при первом знакомстве с этим искусством мы узнаем о таких простых формах, как прямоугольник и треугольник. Когда складываем простую форму, то знакомимся с квадратом, согнув углы которого к центру можно увидеть, что квадрат может состоять из четырёх одинаковых треугольников. Складывая форму «Воздушный змей», знакомимся с ромбом. Азбука оригами включает в себя такие геометрические понятия, как точка и линия.
Когда складываем простую форму, то знакомимся с квадратом, согнув углы которого к центру можно увидеть, что квадрат может состоять из четырёх одинаковых треугольников. Складывая форму «Воздушный змей», знакомимся с ромбом. Азбука оригами включает в себя такие геометрические понятия, как точка и линия.
Таким образом, оригами и математика (а именно геометрия) неразрывно связаны. Множество понятий из математики (такие как точка, линия, квадрат, прямоугольник, треугольник) используем мы при изготовлении оригами.
К сожалению, складывание из бумаги, пока еще редко воспринимается как настоящее искусство. Чудесные превращения бумажного листа в шляпу или кораблик восхищают людей, но мало кто из них догадывается о том, что большинство упаковочных коробок для современных товаров и даже целые конструкции зданий сделаны по тем же правилам, что и бумажные кораблики.
Не будучи инженером, математиком и художником, одновременно, нельзя понять всей гениальной простоты метода, благодаря которому плоская поверхность в руках мастера оригами может превратиться в сложнейшую пространственную конструкцию. Учитывая превосходные свойства бумаги, позволяющие легко складывать, резать и склеивать этот материал, его издавна использовали для архитектурного макетирования и декоративного моделирования. В самом деле, прежде чем изготавливать даже опытный образец изделия или сооружения, гораздо легче сначала сделать его макет из бумаги. По этой же причине бумагу применяют при изготовлении шаблонов, выкроек и трафаретов. И тем более трудно себе представить без этого материала вырезание силуэтов, составление коллажей и аппликаций.
Искусство оригами, напротив, полностью исключает вырезание, склеивание и, уж тем более, вытягивание поверхности. Из всех возможных способов в классическом оригами допускается только изгибание и складывание. Это ограничение бесконечно усложняет задачу моделирования формы, но, с другой стороны, заставляет мастера неожиданно для самого себя раскрывать такие возможности материала, которые во всех иных способах работы с ним оставались невостребованными.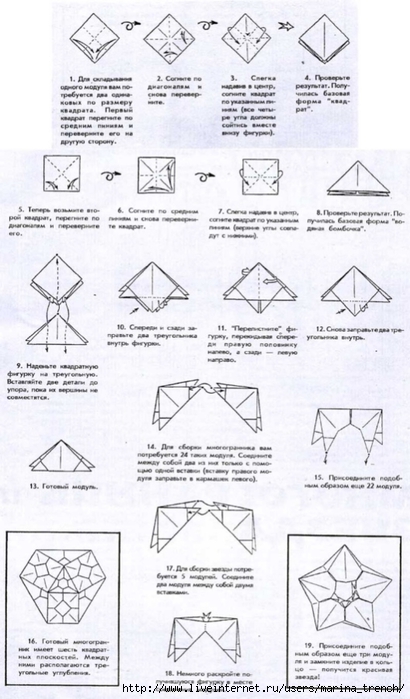
Но, к сожалению, даже знатоки оригами не всегда задумываются над этим. Обычно, складывание рассматривается, прежде всего, как тонкое рукоделие, повторение по схемам уже известных конструкций фигурок или придумывание новых.
Стало очевидным, что математическое понимание оригами допускает абстрагирование поверхности от материала, а топологические складчатые трансформации листа могут быть дополнены введением конструкционно-оправданных сечений поверхности и расширением ее понимания из плоской, в криволинейную, в оболочку замкнутого объема, в трехмерную конструкцию и т.д.
В России Михаил Максимович Литвинов первым не только сформулировал понятие «оригамики», но и показал, научил и создал в России новое движение единомышленников, объединив их вокруг учебно-художественного Центра Оригами, впоследствии преобразованного в Московский Клуб Оригами.
Таким образом, оригами из невинной игры и ремесла превратилось в интеллектуальное занятие, чья энергия массового увлечения направилась в сторону научного и художественного творчества. Оригами стало постепенно сливаться с современной культурой и технологиями третьего тысячелетия.
Некоторые примеры связи математики и оригами.
Согласно классическому оригами, объектом складывания является не размеченный квадратный лист бумаги, без разрезов.
С точки зрения математики, целью оригамиста является точное определение местоположения одной или более точек листа, задающих складки, необходимые для формирования окончательного объекта. Процесс складывания подразумевает выполнение последовательности точно определенных действий по следующим правилам:
Линия определяется либо краем листа, либо линией сгиба бумаги.
Точки определяются пересечениями линий.
Все складки определяются единственным образом путем совмещения
различных элементов листа — линий или точек.
Сгиб формируется единственной складкой, причем в результате
складывания фигура остается плоской.
Последний пункт сильно ограничивает возможности складывания, разрешая только одну складку за раз. На практике даже простейшие модели оригами подразумевают создание нескольких складок за одно действие.
В процессе складывания фигур оригами мы знакомимся с различными геометрическими фигурами: треугольником, квадратом, трапецией и т.д., учимся легко ориентироваться в пространстве и на листе бумаги, делить целое на части, находить вертикаль, горизонталь, диагональ, узнаём многое другое, что относится к геометрии и математике. Американский педагог Ф. Фребель уже в середине XIX века заметил геометрическую особенность оригами и ввел его как учебный предмет в школе.
Например, основы геометрии он предлагал изучать не с помощью циркуля, линейки и некоторых понятий, а на примере фигур складывающейся бумаги. Он активно внедрял оригами в педагогический процесс. К сожалению тогда Фребель не владел такой, как в настоящее время, техникой складывания фигур.
Но система его детских садов выжила, уже в 1892 году в Англии был основан специальный Фребелевский колледж, были они и в Америке, Японии, во многих странах Азии.
Идеи Фребеля и сегодня очень интересны. Не удивительно поэтому, что в наши дни оригами продолжает играть определённую роль в развитии и воспитании. Оригами способствует активности, как левого, так и правого полушарий мозга, так как требует одновременного контроля за движениями обеих рук
В теории оригами существуют правила, закономерности, которые доказываются с помощью математики, а общие свойства объёмных тел изучает специальная математическая наука — топология.
Заключение
Таинственный мир превращенья бумаги…
Здесь все чародеи, волшебники, маги.
Творят они сказки своими руками.
И мир тот чудесный зовут ОРИГАМИ
Марданова Е.У.
Так для чего же нужно оригами???
Оригами, прежде всего, – искусство, призванное дарить людям радость.
Некоторые люди сделали изготовление бумажных фигурок своей профессией. Бумажные птицы и рыбы, звери и многогранники украшают витрины магазинов. Красивые и выразительные маски широко продаются как настенные украшения. Многие предприниматели заказывают мастерам бумажные фигурки для использования в качестве символа фирмы. Муниципалитеты платят за оформление городских праздников, шоу и карнавалов. Бумажные фигурки используются при создании рекламных роликов и плакатов.
Оригами – и детская забава, и элемент дизайна, и неотъемлемый атрибут народных праздников во многих странах мира. Существуют театры, где персонажами и декорациями являются бумажные фигурки.
Занятие оригами оказывает положительное влияние на развитие детей. Я провел мастер-классы по изготовлению оригами в начальных классах. Мне было очень приятно поделиться знаниями, полученными в результате исследования.(приложение № 4)
Специалисты-медики считают, что оно позволяет полнее использовать ресурсы психики, гармонично развивая оба полушария головного мозга. У ребят совершенствуются мелкая моторика рук, движения пальцев становятся более точными (что немаловажно для школьников начальных классов, овладевающих письмом), вырабатывается усидчивость. Ведь чтобы получилась красивая фигурка, нужна аккуратность, внимание, сосредоточенность. Кроме того, оригами развивает память, мышление, пространственное воображение, сообразительность. Неспроста это занятие применяют в своей практике врачи-логопеды. Помогает оно и людям с нарушениями опорно-двигательного аппарата, с психическими расстройствами.
Лично для меня оригами стало новым увлечением, которое поглотило меня с головой!!! Сейчас я уже освоила азбуку оригами и теперь перешла к более сложным композициям… В дальнейшем хочу разработать проект, с помощью которого можно будет применять оригами на уроках в школе.
Один из выдающихся людей писал: «Глядя на мир, нельзя не удивляться!» и я думаю, что он был абсолютно прав!
Вывод: искусство оригами тесно связано с математикой и может стать хорошей
основой для ее изучения. Занимаясь оригами, я вышла за границы стандартной программы по математике и познакомилась на практике с элементами геометрии на плоскости и в пространстве.
Я думаю, что результаты моей работы могут быть интересны другим людям и детям.
Рекомендации:
Результаты моей исследовательской работы можно использовать:
На уроках труда в начальных классах
В детском саду для развития дошкольников
На уроках геометрии в 7-11 классах
На факультативе по математики в 4-6 классах
В ресторанах (для оформления столов салфетками)
А архитектуре для создания макетов и т.д.
Литература
Соколова Г.А. Ориентиры для конструирования, содержания подготовительного курса геометрии средствами оригами: Научно–методическое пособие. / Новосибирск: Издательство НИПКиПРО, 2004, – 60с.
Шеремет Г. Оригами помогает изучать математику. / Математика. – 2007. № 19. с.16–18.
Ткачева М.В. Домашняя математика. М.: Просвещение, 1994. – 190 с.
Белим С.Н. Задачи по геометрии, решаемые методом оригами. – М.: Аким, 1997.– 60 с.
Восканян К.В. Построение геометрических фигур как средство развития мышления школьников. / Вопросы психологии. 1989.–№6.– с.56–61.
Н. Г. Юрина. По книге “Я познаю мир”
© 2007 Кальчева Анастасия http://jp5.ru
Ресурсы интернета
http://origamis.ru
http://www.vlasta-idea.ru
http://bebi.lv
http://www.origami.kulichki.ru/modules.php?name=Pages&go=page&pid=2
http://www.origami.ru
Приложение № 1
Кусудама (яп. «лекарственный шар») – бумажная модель, которая обычно (но не всегда) формируется сшиванием вместе концов множества одинаковых пирамидальных модулей (обычно это стилизованные цветы, сложенные из квадратного листа бумаги), так что получается тело шарообразной формы. Как вариант, отдельные компоненты могут быть склеены вместе. Иногда, как украшение, снизу прикрепляется кисточка.
Искусство кусудамы происходит от древней японской традиции, когда кусудамы использовались для фимиама и смеси сухих лепестков; возможно, это были первые настоящие букеты цветов или трав. Само слово представляет комбинацию двух японских слов кусури (лекарство) и тама (шар). В настоящее время кусудамы обычно используют для украшения или в качестве подарков.
Приложение № 2
Все обозначения в оригами можно разделить на линии, стрелки и знаки.
Линии
линия сгиба «долина» (на себя)
линия сгиба «гора» (от себя)
линия после перегиба
невидимая или воображаемая линия
Стрелки
Согнуть на себя — сделать складку «долина».
Согнуть от себя — сделать складку «гора».
Перегнуть на себя — согнуть и разогнуть, сделав складку «долину».
Перегнуть от себя — согнуть и разогнуть, сделав складку «гору».
Складка-молния — сочетание складок «долиной» и «горой».
Двойная складка-молния — сочетание складок «долиной» и «горой», которые выполняются с двумя слоями бумаги.
Тащить, тянуть.
Раскрыть (обычно «карман»).
Повернуть (в одной плоскости).
Перевернуть на другую сторону.
Завернуть (сделать подряд несколько линий «долин»).
Сделать подряд несколько складок-молний.
Знаки
Повторить действие (обычно сзади или на соседней стороне).
Нажать, надавить, вогнуть.
Держать здесь.
Точка, отмечающая угол, край, линию или пересечение линий.
Прямой угол.
Равные углы.
Следующая картинка — вид отсюда.
Увеличение изображения.
Равные части или стороны.
Базовые формы:
1.Треугольник и прямоугольник:
2. Блин или блинчик:
Схема:
3. Водяная бомбочка :
Схема:
4, 5. Бумажный змей (воздушный змей), плавно переходящий в ромб
Змей: Ромб:
А вот схема для них. На четвёртом этапе получаем змея, на пятом змей трансформируется в ромб:
6,7. Рыбное ассорти: рыба-1 и рыба-2:
Рыба-1: Рыба-2:
И рыбная схема. На четвёртом этапе рыба в первой инкарнации, на пятом — во второй:
8. Квадрат, он же двойной квадрат:
Схема:
9, 10. Птица-1 и птица-2:
Птица-1: Птица-2:
Обе птицы берут начало из базовой формы квадрат (двойной квадрат). Такая вот рекурсия получается, базовая форма, базирующаяся на более базовой форме. На третьем этапе схемы получается первая птица, на четвертом — вторая. Схема:
11, 12. Лягушка-1 и лягушка-2:
Лягушка-1: Лягушка-2:
Отцом обеих лягушек снова-таки служит базовая форма “квадрат”. Такая вот популярная фигура: хочешь — лягушки, хочешь — птицы. То ли еще будет! На пятом этапе схемы первый вариант лягушки, на шестом — второй:
13. Дверь:
Схема:
14, 15. Катамаран, вертушка:
Катамаран: Вертушка:
В основе обеих фигур лежит базовая складка “дверь”. Схема начинается именно с неё. На четвёртой итерации получается катамаран, на шестой же он превращается в вертушку:
16, 17. Узор и стол:
Узор: Стол:
И узор, и стол мы получаем из катамарана, такое вот это универсальное средство. Схема начинается именно с этой базовой схемы, на втором этапе катамаран чудесным образом становится узором, а на последнем трансформируется в стол:
Вот такие вот базовые фигуры в искусстве оригами. Разумеется, от трактовки к трактовке могут варьироваться названия, этапы получения, но суть остаётся нерушимой: это основные складки, на которых базируются все сложные фигуры.
Приложение № 3
Данси — так называемая “песчано-древесная” бумага, которую начали производить еще в период Нара (710-794) и производят до сих пор для упаковки ценных подарков.
Козо — толстая белая бумага, на которой придворные дамы периода Хейан (794-1192) предпочитали записывать стихи.
Фудагами — не смачиваемая водой бумага с добавлением танинов для изготовления этикеток, прикрепляемых к ткани
Фусумагами — бумага для изготовления раздвижных панелей “фусума”
Газенси — бумага для каллиграфии и рисунков тушью, которую импортировали из Китая в период Эдо (1603-1867).
Хакуаиси — бумага для упаковки с золотой и серебряной фольгой.
Хакуучиси — бумага с добавлением крошечных кусочков серебряной и золотой фольги.
Ханси — тонкая легкая и недорогая бумага для различных целей
Ходомураси — бумага, производящаяся в провинции Точиги.
Хососи — бумага, на которой в период Эдо (1603-1867) чиновники записывали устные приказания сёгунов, придавая им статус законов.
Хосокаваси — производимая в провинции Огава прочная бумага для счетов, записей и т.п.
Каиси — бумага, которую используют в чайной церемонии для вытирания пальцев. Обычно ее засовывают под пояс кимоно
Караками — буквально “китайская бумага” — импортировавшаяся из Китая
Камико — “бумажная одежда” — бумага для изготовления одежды
Кинси Гинси Йоси — бумага, которую режут на ленты, затем сворачивают в веревки, золотят и серебрят (кин — “золото”, гин — “серебро”).
Кумогами — бумага с “облачным” рисунком Мичинокугами — буквально “бумага с севера Японии”, использовалась во время периода Хейан (794-1192) в церемониальных целях Минатогами — вид обоев, использующихся исключительно в чайных домиках Миногами — один из наиболее древних видов бумаги, происхождение которого датируется 702 годом.
Рамонси — бумага с добавлением шелковых волокон, расположение которых делает ее похожей на ткань “рамон”.
Сенси — рисовая бумага для рисования.
Соджигами — бумага для изготовления ширм и раздвижных дверей.
Сугихараси — бумага, которую в средние века самураи и священники использовали в качестве подарков.
Сукуси — бумага, которую производят из макулатуры.
Тенгуджоси — бумага для литографий.
Ториноко — буквально “цыпленок” — неотбеленная бумага с желтоватым оттенком.
Удагами — бумага с добавлением глины.
Йосиногами — бумага для фильтрования лака.
▶▷▶▷ модульное оригами схемы корзина для начинающих
▶▷▶▷ модульное оригами схемы корзина для начинающих| Интерфейс | Русский/Английский |
| Тип лицензия | Free |
| Кол-во просмотров | 257 |
| Кол-во загрузок | 132 раз |
| Обновление: | 26-05-2019 |
модульное оригами схемы корзина для начинающих — Модульное оригами для начинающих alegrirurukodelieorigamimodulnoe-origami Cached Модульное оригами собирается из одинаковых частей (модулей), которые складываются по определённому правилу Детали при этом между собой не склеиваются, а вставляются одна в другую Модульное оригами для начинающих: схемы, пошаговая инструкция 1igolkacomrukodeliemodulnoe-origami Cached Модульное оригами для начинающих это очень интересное занятие Человек может научиться создавать маленькие фигурки из модулей довольно быстро, это легко Модульное Оригами Схемы Корзина Для Начинающих — Image Results More Модульное Оригами Схемы Корзина Для Начинающих images Схемы модульного оригами для начинающих бабочка csb-polimerruprimery-origamishemy-modulnogo-origami Cached Выбирая занятия для детей, многие интересуются творчеством и ищут интересные идеи, в том числе схемы модульного оригами из бумаги для начинающих МОДУЛЬНОЕ ОРИГАМИ ДЛЯ НАЧИНАЮЩИХ Советы мастеров,схемы и bebilvorigami-podelki-shemi-i-urokimodulnoe Cached Модульное оригами для начинающих Разновидностью прикладного искусства по изготовлению поделок из бумаги является модульное оригами , отличающееся тем, что в исполнении мастеров оригамистов для создания объекта Презентация на тему Модульное оригами для начинающих prezentaciiorgprezentaciiprezentacii-po Cached Презентация на тему Модульное оригами для начинающих Презентацию на тему Модульное оригами для начинающих можно скачать абсолютно бесплатно на нашем сайте Пошаговая инструкция, схемы для начинающих в модульном hendmeidgurupodelkiinstruktsiya-modulnogo-origami Cached Дети всегда требуют к себе внимания Выбирая занятия для детей, многие интересуются творчеством и ищут интересные идеи, в том числе схемы модульного оригами из бумаги для начинающих Модульное оригами для начинающих masterclassyruorigamimodulnoe-origami332 Cached Теги: оригами модульное оригами Электронная книга Лучшие мастер классы по рукоделию Для того, чтобы получить книгу, вам нужно просто ввести ваш EMAIL и ИМЯ в форму ниже Оригами для начинающих — Master classy masterclassyruorigamiorigami-dlya-nachinayuschih Cached Оригами для начинающих лучше начинать с изготовления простых поделок Немного практики и вы с легкостью сможете сделать оригами из модулей Модульное оригами Мастер классы alegrirurukodelieorigamimodulnoe-origami Cached Модульное оригами для начинающих Как собрать из бумажных модулей лукошко Лукошко из бумажных модулей Мастер класс Мы расскажем вам как изготовить из бумажных модулей лукошко Поэтапные схемы модульного оригами Как сделать из бумаги svoimi-rukami-clubru модульное — оригами Cached Научитесь создавать из бумаги интересные и необычные модульные оригами Наши подробные схемы с фото и описаниями помогут вам с легкостью овладеть техникой создания великолепных поделок Promotional Results For You Free Download Mozilla Firefox Web Browser wwwmozillaorg Download Firefox — the faster, smarter, easier way to browse the web and all of 1 2 3 4 5 Next 31,200
- Как плести фенечки из ниток мулине: схемы и уроки плетения. Модульное оригами схемы сборки тюльпанов
- . Cхемы вязания спицами для начинающих: основные узоры и схемы. Поэтому и в книге ожидала увидеть схемы. Модульное оригами 1 рец. Плетение из резиночек для начинающих 1 рец. Корзина пуста. Схемы п
- хемы. Модульное оригами 1 рец. Плетение из резиночек для начинающих 1 рец. Корзина пуста. Схемы поделок в технике оригами. Целевая аудитория: учителя и воспитатели школ, педагоги дополнительного образования, родители, учащиеся 2-4 классов. Модульное оригами для начинающих. Спасибо за схемы!!! А какое из ваших творений модульных самое маленькое? Я на сайте совсем недавно, но меня очень заинтересовало модульное оригами. Модульное оригами для детей. Модульное оригами — модное направление древнего искусства создания фигурок из бумаги. Книга содержит схемы складывания более 170 фигурок из бумаги, которые можно использовать для различных фокусов, игр и забав. quot;Педсоветquot; — открытое образовательное сообщество. Фестиваль сетевых сообществ; форумы, доклады, консультационные линии. Изготовление вазы (модульное оригами) Сборка вазы очень хороша для начинающих. Схемы снежинок из бумаги. Часть 8 — Снежинки из бусин и бисера своими руками Часть 9 — Новогодние линии-разделители с кодом Часть 10 — СНЕЖИНКИ — модульное оригами Часть 11 — СМС поздравления на Новый Год! Весь спорт Ярославля. Локомотив, Шинник, Ярославич. Футбол, Хоккей, Волейбол. Внимание, обнаружена ошибка У вас недостаточно прав для просмотра выбранной страницы. Занятия оригами одна из форм пропедевтики изучения геометрии, позволяют детям удовлетворить познавательные интересы, действовать в соответствии с простейшими алгоритмами, работать со схемами, распознавать простейшие геометрические фигуры, обогатить навыки общения и действовать сообща при изучении программы. Работать с простейшими … Схема вложения: Модульная мягкая мебель (97) Оригами кусудама шар,Хризантема,АБ 11-452. Товары Товары Товары Наборы Наборы для оригами.
педагоги дополнительного образования
распознавать простейшие геометрические фигуры
- вам нужно просто ввести ваш EMAIL и ИМЯ в форму ниже Оригами для начинающих — Master classy masterclassyruorigamiorigami-dlya-nachinayuschih Cached Оригами для начинающих лучше начинать с изготовления простых поделок Немного практики и вы с легкостью сможете сделать оригами из модулей Модульное оригами Мастер классы alegrirurukodelieorigamimodulnoe-origami Cached Модульное оригами для начинающих Как собрать из бумажных модулей лукошко Лукошко из бумажных модулей Мастер класс Мы расскажем вам как изготовить из бумажных модулей лукошко Поэтапные схемы модульного оригами Как сделать из бумаги svoimi-rukami-clubru модульное — оригами Cached Научитесь создавать из бумаги интересные и необычные модульные оригами Наши подробные схемы с фото и описаниями помогут вам с легкостью овладеть техникой создания великолепных поделок Promotional Results For You Free Download Mozilla Firefox Web Browser wwwmozillaorg Download Firefox — the faster
- отличающееся тем
- пошаговая инструкция 1igolkacomrukodeliemodulnoe-origami Cached Модульное оригами для начинающих это очень интересное занятие Человек может научиться создавать маленькие фигурки из модулей довольно быстро
Request limit reached by ad vlaXML
Как плести фенечки из ниток мулине: схемы и уроки плетения. Модульное оригами схемы сборки тюльпанов. Cхемы вязания спицами для начинающих: основные узоры и схемы. Поэтому и в книге ожидала увидеть схемы. Модульное оригами 1 рец. Плетение из резиночек для начинающих 1 рец. Корзина пуста. Схемы поделок в технике оригами. Целевая аудитория: учителя и воспитатели школ, педагоги дополнительного образования, родители, учащиеся 2-4 классов. Модульное оригами для начинающих. Спасибо за схемы!!! А какое из ваших творений модульных самое маленькое? Я на сайте совсем недавно, но меня очень заинтересовало модульное оригами. Модульное оригами для детей. Модульное оригами — модное направление древнего искусства создания фигурок из бумаги. Книга содержит схемы складывания более 170 фигурок из бумаги, которые можно использовать для различных фокусов, игр и забав. quot;Педсоветquot; — открытое образовательное сообщество. Фестиваль сетевых сообществ; форумы, доклады, консультационные линии. Изготовление вазы (модульное оригами) Сборка вазы очень хороша для начинающих. Схемы снежинок из бумаги. Часть 8 — Снежинки из бусин и бисера своими руками Часть 9 — Новогодние линии-разделители с кодом Часть 10 — СНЕЖИНКИ — модульное оригами Часть 11 — СМС поздравления на Новый Год! Весь спорт Ярославля. Локомотив, Шинник, Ярославич. Футбол, Хоккей, Волейбол. Внимание, обнаружена ошибка У вас недостаточно прав для просмотра выбранной страницы. Занятия оригами одна из форм пропедевтики изучения геометрии, позволяют детям удовлетворить познавательные интересы, действовать в соответствии с простейшими алгоритмами, работать со схемами, распознавать простейшие геометрические фигуры, обогатить навыки общения и действовать сообща при изучении программы. Работать с простейшими … Схема вложения: Модульная мягкая мебель (97) Оригами кусудама шар,Хризантема,АБ 11-452. Товары Товары Товары Наборы Наборы для оригами.
Математика и искусство в оригами — Как создавать геометрические каркасы: 6 шагов (с изображениями)
Как можно изменять эти углы для создания любого многоугольника?
Анализ того, как был получен внутренний угол 60 °, позволяет выполнить складывание на любой угол примерно до 140 °, прежде чем блоки перестанут фиксироваться вместе. Для обратного сгиба кармана использовались контрольные точки центральной линии и самой левой четвертичной линии. Эти контрольные линии использовались для складывания треугольника с пропорциями основания 1 и гипотенузы 2.-1 (1/2) = 30 °
Это показано на первом изображении.
Затем следуйте моим синим стрелкам мыслительного процесса. Угол 30 ° можно геометрически перенести на угол между центральной линией и краем заслонки. Поскольку это угол в прямоугольном треугольнике, мы можем найти угол по часовой стрелке, потому что мы знаем два из трех углов, а также сумму углов:
180 ° — 90 ° — 30 ° = 60 °
Его можно перенести на угол между центральной линией и обратным сгибом, который образует дно кармана.
На третьем изображении два блока, которые мы собираем, перевернуты с предыдущего шага, так что карман все еще находится на правой стороне блока. Видно, что край правого блока лежит по обратному сгибу в кармане левого блока. Таким образом, красный угол, который мы уже нашли, можно перенести на угол между единицами. Следовательно, единицы имеют угол 60 °, или внутренний угол угла равностороннего треугольника, между собой.
Аналогичные рассуждения, сделанные в обратном порядке, можно использовать, чтобы найти достаточно точные опорные сгибы для других углов, если это необходимо.Понимание того, что угол кармана определяет угол между элементами, необходимо для элементов складывания, которые являются общей кромкой между двумя многоугольниками разной формы, как, например, в архимедовых твердых телах. Немного тригонометрии, геометрических манипуляций, места для записи и практики позволят вам легко создавать множество многоугольников, правильных и неправильных, из которых можно делать многогранники.
При создании соединений многогранников важна точная длина элементов, чтобы окончательная модель плотно прилегала.При расчете размеров прямоугольника бумаги, необходимого для получения края заданной длины, имейте в виду следующий артефакт механизма блокировки. Любая бумага за пределами того места, где угловой сгиб пересекает центральную линию (как показано на последнем рисунке), не будет влиять на длину края (это интуитивно очевидно после того, как вы немного сгибаете). Следовательно, для точной длины кромки необходимо определить, сколько будет обрезано на концах единиц, и добавить это к исходным размерам бумаги.
Оригами и математика
Оригами и математика
Итак, вы интересуетесь оригами и математикой … возможно, вы учитель математики средней школы или K-8, или ученик математики делает отчет по предметом, или, может быть, вы всегда интересовались обоими и никогда не делали связь, или, может быть, вам просто любопытно. Оригами действительно есть много образовательных выгоды. Если вы студент, учитель или просто случайный серфер, я изо всех сил старался ответить на ваши вопросы, поэтому, пожалуйста, прочтите на.
CheapWritingHelp.com — письменный сервис по доступным ценам — это доступны 24/7 онлайн, чтобы предоставить студентам индивидуальные эссе, научно-исследовательские работы и диссертации по математике.
Так как же именно оригами и математика связаны друг с другом? В связь с геометрией ясна и вместе с тем многогранна; сложенная модель одновременно и произведение искусства, и геометрическая фигура.Просто разверните его и возьмите Смотри! Вы увидите сложный геометрический узор, даже если модель вам в сложенном виде был простой. Начинающий изучающий геометрию может захотеть выяснить типы треугольников на бумаге. Какие углы можно увидеть? Какие формы? Как эти углы и формы попали туда? Вы знали что вы складывали эти углы или формы во время самого складывания?
Например, когда вы складываете традиционную основу водяной бомбы, вы создали узор сгиба из восьми совпадающих прямоугольных треугольников.В традиционная основа для птиц создает рисунок складок с множеством других треугольников и все перевернутые сгибы (например, та, что создает птичий шея или хвост) создает еще четыре! Любая основная складка имеет связанный геометрический узор. Возьмите складку для сквоша — когда вы сделаете эту складку и посмотрите на шаблоне складки вы увидите, что вы разделили угол пополам, дважды! Можете ли вы придумать похожие отношения между складкой и что-то знаешь по геометрии? Вы можете почерпнуть еще больше идей из этого презентация по Оригами: В создании геометрии в классе.
С другой стороны, если вы любитель головоломок, то здесь несколько отличных оригами проблемы, которые вы могли бы нравится пытаться решить. В этих головоломках нужно сложить лист бумаги так, чтобы возникают определенные цветовые узоры или форма определенной области полученные результаты. Но продолжим с узорами складок …
Оригами, геометрия и теорема Кавасаки
Более продвинутый студент или учитель геометрии может захотеть более подробно изучить взаимосвязь между математикой и оригами.Ты можете взглянуть на эту геометрию упражнения, чтобы получить вас началось. Например, традиционный кран (или другой комплект диаграмм) в разложенном виде дает узор складок, по которому мы можем многому научиться. Укажите точку (вершину) на шаблоне складки. Сколько складки берут начало в этой вершине? Возможно ли плоское оригами модель должна иметь нечетное количество складок, выходящих из вершины на ней узор складки? Как насчет отношений между горой и долиной? складки? У вас может быть вершина только со складками долины или только гора? складки?
Как насчет углов вокруг этой точки? Вы действительно можете произвести впечатление ваш учитель (или ваши ученики) с этим… конечно, вам нужно будет понять это первый! Существует Теорема называется КАВАСАКИ ТЕОРЕМА , которая гласит, что если углы, окружающие единственная вершина в плоском шаблоне складки оригами — это 1 , а 2 , а 3 , …, а 2n , затем:
а1 + а 3 + а 5 + … + a 2n-1 = 180 иа2 + а 4 + а 6 + … + a 2n = 180 |
Другими словами, если вы сложите угловые измерения каждого другого угол вокруг точки, сумма будет 180. Попробуйте и убедитесь!
Вы видите, что это правда, или, что еще лучше, можете это доказать?
Прямой край и компас против оригами и аксиом Хузиты
Хотя о шаблонах складок нужно многое понять, оригами — это процесс складывания бумаги, который математически может следует понимать с точки зрения геометрической конструкции.Самый известный конструкция представляет собой конструкцию «прямой край и компас», которая относится к геометрическим операциям, которые могут быть образованы только этими двумя инструменты (обратите внимание, что линейка — это , а не a линейка с разметкой длины). Как известно, конструкции SE&C могут быть охвачены (без каламбура) четырьмя основными аксиомами, впервые определенными Евклидом, более 2000 лет назад. Также хорошо известно, что есть определенные операции, которые невозможны при наличии только линейки и компас.Две такие операции — это деление угла на три части и удвоение куба. (нахождение кубического корня из 2).
Но вернемся к конструкции оригами … конструкция оригами определяется как те геометрические операции, которые можно образовать, сложив кусок бумагу, используя необработанные края и концы бумаги, а также любые последующие линии и точки сгиба, созданные при складывании. Что такое завораживает то, что конструкция оригами, хотя на первый взгляд может показаться менее мощный, чем SE&C, на самом деле более мощный, что позволяет трисекция угла, а также удвоение куба.В математик Хумиаки Хузита разработал шесть аксиом (а позже и седьмую) на основе конструкции оригами. Я не буду здесь вдаваться в подробности, так как ниже приведены ссылки на несколько сайтов, которые очень тщательно описания Аксиом Хузиты:
- Аксиомы Хузиты, любезно предоставлено Википедией
- Обзор Оригами Тома Халла и геометрическое построение, которое дает отличные описания и упражнения для 5-й и 6-й аксиом, а также описания как разрезать угол пополам и удвоить куб с помощью складывания
- Страница Коширо Хатори о строительстве оригами описывает Шесть аксиом Хузиты, а также седьмая аксиома, которую Хатори-сан обнаруженный!
- Кристиан Лавуа разработал вычислительную модель оригами для курс вычислительной геометрии в Университете Макгилла в 2002 году.Как фон для этого проекта она предоставляет аксиомы оригами вместе с графики и уравнения.
Что особенно замечательно во всем этом, так это то, что эти аксиомы не только теоретические — они были реализованы на практике! Роберта Лэнга программа оригами, ReferenceFinder, использует все семь аксиом. ReferenceFinder — это программа, которая находит последовательности складывания, чтобы приблизительно найти любую точку на квадрате с помощью небольшое количество складок.
Оригами и топология
Изучение оригами и математики можно отнести к разряду топология, хотя некоторые считают, что она более тесно связана с комбинаторика, а точнее теория графов. Я дам пример теоремы оригами, которую можно увидеть с обеих точек зрения посмотрим, но сначала немного о топологии.
Связь с топологией менее ясна, чем связь с геометрией, вероятно потому, что большинство людей гораздо менее знакомы с это поле.Если вы студент и делаете доклад по оригами и математике, вы может снова произвести впечатление на вашего учителя, показав, что вы знаете, какая топология есть, и как это связано с оригами.
Итак, что такое топология? Вот короткое и своеобразный ответ, но вы действительно должны прочитать Нила Подробный ответ Стрикленда с картинками. Важно, чтобы вы поймите, что геометрия и топология очень разные. Топология иногда называют «геометрией резинового листа», что означает, что в топологии растяжение объекта или изменение его формы не повлияет на него (пока так как вы не делаете дыр и не заделываете дыры).Топологу, чашка кофе и пончик — это одно и то же, а геометр видит их как полностью отличается.
Если вы прочитали ответ Нила, то заметили, что он упомянул метро. карта, которая представляет собой просто сеть точек, соединенных линиями, как оригами складки! Нам может помочь изучение выкройки складок оригами узнать о сетях, таких как метро и телефонные сети, и о том, как сделать их быстрее и эффективнее. Но не верьте мне на слово.Томас Халл, доцент математики в колледже Мерримак в г. Северный Андовер, Массачусетс, является экспертом в области оригами и топология. Том в настоящее время преподает курс комбинаторной геометрии, и вы можете просмотреть программу курса и задания. Если вы хотите провести более глубокое исследование в это поле, первым делом вам нужно связаться с Томом. Его Веб-сайт был даже упомянутый в рассказ на ABCnews.com!
Теперь вернемся к теореме оригами, о которой я упоминал ранее. можно увидеть с двух точек зрения.
Теорема: Каждый плоский складной узор сгиба можно раскрасить в 2 цвета. |
Другими словами, предположим, что вы сложили модель оригами, которая лежит плоский. Если полностью развернуть модель, то рисунок складки, который вы увидит, имеет особое свойство. Если вы хотите раскрасить регионы ваш шаблон складки с разными цветами, чтобы не было двух граничащих областей того же цвета, только у вас нужно два цвета .Это может напомнить вам о знаменитом картографе проблема: какое наименьшее количество цветов нужно для раскраски стран на карте (опять же, чтобы две соседние страны не совпадали цвет)? Это известно как Четыре Теорема о цвете, поскольку ответ — четыре цвета. Как интересный Кроме того, эта теорема была доказана в 1976 году американскими математиками Аппелем. и Хакен с помощью компьютера проверил тысячи различных случаев вовлеченный. Ты можешь выучить подробнее об этом доказательстве, если хотите.
Но вернемся к нашей теореме . Вы видите, что вам нужно всего два цвета, чтобы раскрасить складку? Пытаться это сами! Вы увидите, что все, что вы сбрасываете (пока оно лежит плоский) потребуется всего два цвета для раскраски областей на его складке шаблон.
Вот простой способ увидеть это: сложите что-нибудь плоское. Теперь покрасьте все области, обращенные к вам, красным, а те, которые обращены к стол синий (не забудьте раскрасить только одну сторону листа).Когда ты разверните, вы увидите, что у вас правильная 2-раскраска!
Предупреждение … этот раздел становится еще сложнее! Более строгий Доказательство выглядит следующим образом: сначала покажите, что каждая вершина в вашей складке узор имеет четную степень (степень — это количество выходящих складок каждой вершины — мы обсуждали это ранее!). Тогда вы знаете складку pattern — это эйлеров граф, то есть граф, содержащий путь, который начинается и заканчивается в одной и той же точке и проходит вдоль каждого края (например, путь называется эйлеровым циклом). Не попробуйте доказать это, если вы не опытный математик! Наконец, хорошо известно, что эйлеровы графы 2-раскрашиваемы.
Хммм … Я начал с обещания результата, который можно рассматривать как как комбинаторные, так и топологические. Мы поняли? Что ж, результат очевидно комбинаторный, поскольку это теория графов. Как результат топологический? Что ж, 2-раскраска дает нам простой способ определение ориентации каждой области, которую мы раскрашиваем.Все регионы окрашенные в синий цвет будут направлены вверх (или вниз), в то время как все области, окрашенные в красный цвет будет смотреть в противоположную сторону. Попробуй это! На этот раз сложите модель, разверните и раскрасьте области сгиба красным и синим. А теперь сложите заново модель и убедитесь сами!
Другие ресурсы
Большинство людей не понимают, сколько информации по этому поводу. математики и оригами.На сайте опубликованы книги и статьи. тема, презентации, а также международная конференция под названием «Международная встреча по науке и технике оригами». В Фактически, многие создатели и авторы оригами здесь, в США и за рубежом математики, физики и другие ученые. Я думаю о такие люди, как Роберт Ланг, Дзюн Маэкава, Тошиказу Кавасаки и Томас Корпус. Еще одна математическая фигура оригами без формальной математики обучение Крис Палмер (также см. статья про Криса), создателя цветка башня (см. рисунок).
Что касается книг, то первое, что приходит в голову — это набор книг. Рона Гуркевиц и Беннет Арнштейн: 3D Геометрическое оригами: Модульные многогранники , Модульные Оригами Многогранник , и только что опубликованный в 2003 году, Multimodular Оригами Многогранники: архимеды, баккиболы и двойственность. Ты можешь выучить больше о работе профессора Гуркевица, а также просмотреть галереи, ссылки и многое другое.
Несколько других книг по оригами, в которых обсуждается связь с математика Оригами Омнибус от Кунихико Касахара (ISBN 0-87040-699-x), Оригами от Angelfish до Zen — автор Питер Энгель (ISBN 0-486-28138-8), Easy Оригами , авторы Гей Меррилл Гросс и Тина Вайнтрауб, и математика in Motion: Origami in the Classroom K-8 Автор: Барбара Перл (ISBN 0-9647924-3-5).Веб-сайт по математике in Motion даже включает образец плана урока для педагогов. Если учить классы К-8, то это книга может быть тем, что вы искали.
Первая книга, которую я упомянул, Оригами. Омнибус обсуждает темы такие как складывание изоплощади, золотой прямоугольник, складывание обычного пятиугольник из квадрата и теорема Кавасаки. Книга закончилась распечатать, но вы, вероятно, можете получить его в местной библиотеке или через межбиблиотечный абонемент.
В следующем «Оригами от рыбы-ангела до дзен» замечательный введение под названием «Преодоление пропасти», в котором обсуждаются взаимосвязь между оригами и такими темами, как М.С. Эшер, философия дзен, фракталы и хаос, музыка и искусство. Отличное введение в оригами и математика. Эта книга должна быть доступна на таких сайтах, как Amazon.com, Sasuga. Книжный магазин и увлекательный Складки.
Легкое оригами , автор Гей Меррилл Гросс и Тина Вайнтрауб (ISBN 0-590-53549-8), рабочая тетрадь проектов для учителей K-6, многие из которых имеют базовое содержание математики.
Я также много слышал о Paperfolding, Веселый и эффективный метод изучения математики . У него приятный Интернет сайт, который стоит проверить.
Еще одна недавняя книга — Математическая. Оригами Дэвида Митчелла (ISBN 1-899618-18-X). Известен своим модульные конструкции и скульптуры, Дэвид дает в этой книге инструкции для платоновых тел и их вариантов, а также других геометрических формы, такие как кольца, звезды, ромбические формы, а также скелет и контур твердые тела.
Вы можете найти список других книг по оригами по математике на сайте Tom Библиография оригами Халла
В Интернете также есть множество отличных мест, с которых можно начать Ищу. Том Сайт Hull’s Origami Math, о котором я уже упоминал раз, это исчерпывающий ресурс в Интернете по оригами и математика. Том Халл проделал довольно продвинутую работу в этой области. Его работы по оригами-математике появились в MAA. (Математическая ассоциация Америки) журналы.Он писал на такие темы, как конструктивность оригами против линейки / компаса. конструктивность и оригами и топология.
Я также могу рассказать вам о Елене Страница оригами Веррилла, на которой есть информация о модульном оригами, мозаики оригами и задачи мозаики оригами-математики, а также другие задачи оригами-математики, такие как трисекция угла и периметр проблема. Отличный материал для школьного проекта!
Еще одна интересная страница (особенно если вам нравятся фракталы) — это Jeannine Визитная карточка Мозли — проект Menger Sponge, цель которого построить модульную губку Менгера для оригами глубины 3 из 66048 визитки.
Недавнее добавление в Интернет — Кристина. Галерея оригами Бурчика, в которой представлены модульные элементы, обычные многогранники и полуправильные многогранники. Здесь можно многому научиться; как может ли школьный отчет со словом «ромбикосадодекаэдр» получить плохую оценку оценка?
У Wolfram Research есть страница об оригами и математике, которые содержит изображения, перечисляет аксиомы Хузиты и предлагает много дополнительных использованная литература.
Еще один отличный сайт — Geometry Свалка, которая содержит ряд ссылок на различные темы в оригами и математика.
Наконец, если вы все еще жаждете большего, проверьте Тома Ссылки Hull’s Origami Math. Когда вы закончите работу с этими сайтами, у вас должно быть много отличных идей для этого отчета, проекта или урока строить планы!
Надеюсь, это дает вам хороший общий обзор темы оригами и математики.Я буду продолжать обновлять это по мере появления новых веб-сайтов по этой теме. Если у вас есть комментарии или предложения для меня, пожалуйста, напишите мне.
Оригами Математика Страница
Оригами Математика Страница Эти страницы представляют собой попытку начать сбор информации о математика складывания бумаги. Любой, кто занимается оригами, имеет наверное, в тот или иной момент развернул модель оригами и дивился в замысловатом узоре складок, образующем «чертеж» складки.Очевидно, что в этой коллекции складок действуют некоторые правила. Ясно, что при складывании бумаги действует геометрия оригами .Такая геометрия, эта математика оригами, широко изучалась. оригамистов, математиков, ученых и художников. В Итало-японский математик Хумьяки Хузита составил список аксиомы для геометрического определения оригами. Физик Джун Маэкава имеет открыл некоторые фундаментальные теоремы об оригами и использовал их для создавать модели оригами удивительной элегантности.Математик Тошиказу Кавасаки написал несколько теорем оригами и даже обобщил некоторые из них для описания складывания бумаги в более высоких измерениях. (Оригами в четвертом измерении!) Роберт Лэнг из Калифорнии разработал гениальный способ алгоритмизации процесса проектирования оригами, используя компьютер, чтобы помочь ему изобретать модели удивительной сложности. Педагог Сюдзо Фудзимото и художник Крис Палмер открыли для себя удивительные параллели между оригами и мозаикой.И огромное количество учителя разрабатывают способы использования оригами для обучения концепциям в математика, химия, физика и архитектура.
К сожалению, большая часть вышеупомянутых работ является новой и в то время на данный момент есть несколько хороших ссылок на этот тип Информация. На этих страницах будет предпринята попытка решить эту проблему путем предоставление обширная библиография по оригами-математике, список предстоящих лекций и событиях, а также предлагают инструкции и учебные пособия по избранным темам.
Однако этот проект продолжается! Эти страницы все еще находятся на своих младенчество, и любые комментарии или предложения (или предложения о помощи!) будут очень признателен!
Математическое меню оригами:
- Просмотрите нашу математику оригами Библиография, которая включает ссылки на несколько недавних книг по оригами-математике.
- Научная ярмарка и консультации по проектам
Ищете идеи для научной выставки или классного проекта по математике оригами? Посмотри сюда, прежде чем писать мне. - Мой канал на YouTube
Здесь (пока) не так много математики, но я разместил там несколько видеороликов, которые преподают некоторые из моих последних геометрических модульных моделей. - Учебник: Оригами геометрическое
Конструкции
Мы представляем список аксиом оригами Хумьяки Хузиты и сравниваем его с традиционные конструкции с прямым краем и компасом. Инструкции для Также включены тройные углы и удваивающие кубы. Примечание: Этот раздел сильно устарел.Мне нужно его обновить. - Жесткое оригами
Если бы лист бумаги был сделан из листового металла с петлями вместо складок, он все равно сложился бы? Это очень краткое обсуждение этой проблемы. - Жесткое складывание тетраэдра
Вы не можете жестко сложить тетраэдр (так как это нарушит теорему о мехах). Но что, если сделать в тетраэдре небольшую прорезь? Тогда ты сможешь это сделать! - Треугольная жесткая складка в заблокированном состоянии
Некоторые люди думали, что если у вас есть модель оригами, которая не складывается жестко, то вы можете сделать ее жестко складываемой, добавив складки, чтобы каждая сторона образца складки была треугольником.Обычно это работает, но не всегда! Пример, который мы здесь показываем, представляет собой шаблон сгиба со всеми треугольными гранями, который находится в «заблокированном сложенном состоянии», из которого его нельзя жестко развернуть! - Жесткое складывание усиленной квадратной скрутки
Это работа с моим студентом Майклом Урбански из Университета Западной Новой Англии (выполненная в 2017-2018 годах). В нем рассматривается способ сделать классический квадратный поворот жестко складывающимся! Модель - : пять пересекающихся
Тетраэдры
- / Учебное пособие:
Пентагон-Шестиугольник Зиг-Заг (PHiZZ) Единицы
- Галерея моделей оригами Модель
- : соединение трех Октаэдра в стадии строительства!
- Заметки для курса оригами / комбинаторной геометрии
Это заметки и задания для курса в Merrimack College на комбинаторная геометрия.Основное приложение, рассматриваемое в этом курсе математика складывания бумаги. - Есть отличная статья (формат PDF) Барри Сипра в выпуске SIAM News за октябрь 2001 г. Барри сообщает о 3OSME конференции, но статья резюмирует много оригами математики, дизайна и приложения очень хорошо. Проверьте это!
- Другая математика оригами Страницы
Авторские права на эти страницы принадлежат Томасу Халлу, 1997-2015 гг. Последнее изменение 14.03.15.Столбец с характеристиками
из AMS
Математика и искусство
6. Оригами
Традиционное оригами было связано с тем, что из одного листа бумаги складывались сложные формы, как правило, в виде животных или чего-то другого. Однако Томоко Фузе произвел революцию в мире оригами с математической точки зрения, популяризировав «модульное» оригами. В модульном оригами обычно начинают с одинаковых кусочков бумаги (обычно квадратов) и складывают каждый из них в одинаковые «блоки».«Эти элементы затем« сплетаются »вместе, образуя высокосимметричные объекты, такие как многогранники, мозаики или коробки. Используя соответствующие цвета, часто можно построить очень привлекательные бумажные модели из самых разнообразных многогранников и мозаик с привлекательными свойствами симметрии. Творчество, связанное с единичным оригами, заключается в изобретательных панелях, которые были разработаны, и способах их сборки. Книги Фузе появляются в «художественных отделах» книжных магазинов. Интересно, что для людей с некоторым опытом оригами книги Фузе книги, которые не были переведены на английский язык, все еще можно использовать из-за универсальности системы инструкций по складыванию оригами (например,грамм. символы складок гор, складок долин и т. д.).
Параллельно с художественными аспектами конструкций оригами шла разработка математической теории оригами. Для этого потребовалось множество подходов. Сложная математическая теория того, какие плоские фигуры могут быть нарисованы с использованием традиционных евклидовых инструментов построения прямой кромки (немаркированной линейки) и компаса, имеет спутника оригами. Какие формы можно построить, используя различные правила (аксиомы) складывания бумаги? Томас Халл, Эрик Демейн и другие также изучали вопросы, связанные со складыванием и оригами.Основной интерес представляет изучение складок (системы линий на бумаге), которые можно складывать «плоско». Необходимая математика включает идеи и методы, несколько отличные от того, что делалось в прошлом, когда пытались понять, как кусок плоскости (квадрат бумаги оригами) может быть преобразован геометрическим преобразованием, потому что в конце преобразования части бумага оригами соприкасается друг с другом, но не проникает в другие части бумаги.
Вот пример впечатляющего проверенного результата в этой области. Предположим, что, сложив лист бумаги, можно сделать один разрез по прямой с целью взять отрезанные куски и раскрыть их. Какие фигурные детали возможны таким образом? Удивительный ответ: возможен любой граф, состоящий из вершин и отрезков прямых, который можно нарисовать на плоскости! Например, можно вырезать форму чего-нибудь прозаического, например буквы «Я» или очертания бабочки.Этот результат был первоначально разработан Эриком Демейном, Мартином Демейном и Анной Любив. Впоследствии Маршалл Берн, Эрик Демейн, Дэвид Эппштейн и Барри Хейс разработали другой подход к результату.
С помощью модульного оригами можно сделать много разных многогранных объектов. Вот образец оригами модели Хелены Веррилл:
(Модели использованы с разрешения Хелены Веррилл)
В моделях многогранников оригами используются подходы, при которых панели становятся гранями многогранников, поэтому проблема заключается в создании панелей с разным количеством сторон с одинаковой длиной кромки.Можно также создавать многогранники «пирамидальной формы». Под этим я подразумеваю, что твердые тела представляют собой выпуклые многогранники с пирамидами, построенными на каждой грани. (Это не звездочки в том смысле, в котором этот термин используется в геометрии.) Другие многогранники, подобные этим, подчеркивают края многогранника и, по сути, служат моделями жестких стержней для многогранников. Они напоминают рисунки Леонардо да Винчи, демонстрирующие новые методы рисования многогранников в перспективе.
Многие многогранники, которые можно создать из бумаги для оригами, не только красивы, но и предполагают интересующие математические вопросы.Вот простой пример: из шести частей оригами можно сделать куб. Если все эти шесть частей одного цвета, то можно сделать только один «тип» цветного куба. Предположим, что у одного есть три панели одного цвета и три панели другого цвета. Сколько неэквивалентных кубиков можно сделать?
На схеме ниже показана конструкция оригами, основанная на идеях Томаса Халла и сложенная Джо Джиларди. На математическом уровне это вложенный набор тетраэдров, сложенных из долларовых купюр.Многие тоже видят произведение искусства!
(используется с разрешения Джо Джиларди)
В приведенных выше обсуждениях я обозначил верхушку айсберга связи между математикой и искусством. Эти связи хороши как для математики, так и для искусства. Ясно, что интерес к связи между математикой и искусством будет продолжать расти и процветать.
- Введение
- Математические инструменты для художников
- Симметрия
- Художники-математики и художники-математики
- Многогранники, мозаики и разрезы
- Оригами
- Список литературы
Удерживать и складывать | Математические решения
Урок для первоклассников и второклассников
Крис Конфер
Этот урок для всего класса адаптирован из раздела «Математика всеми средствами» «Геометрия» для 1–2 классов, написанного Крисом Конфером.Сложив квадрат бумаги несколькими заранее определенными способами, дети исследуют и записывают различные формы, которые они могут сделать. Это задание дает детям ценный опыт в изучении того, как формы соотносятся друг с другом.
Чтобы подготовиться к уроку, Крис вырезал для детей квадраты из копировальной бумаги. (Квадраты были около 4 дюймов со стороны.) Крис также приготовил по одному листу газетной бумаги размером 12 на 18 дюймов для каждой пары детей и большой лист диаграммной бумаги, чтобы использовать его для начертания фигур для записи в классе.
Дав каждому ребенку по квадрату, Крис сказал: «Смотри внимательно и складывай свою бумагу, как я складываю свою».
Крис сложила свой квадрат пополам, чтобы получился прямоугольник. Когда дети сложили свои листы, она попросила их пересчитать, чтобы убедиться в наличии четырех сторон и четырех углов. «Какой оно формы?» она спросила. (См. Рисунок 1.)
Рисунок 1.
Большинство детей ответили: «Прямоугольник».
Крис развернул прямоугольник, сложил его в другом направлении и попросил детей сделать то же самое.
«Мы хотим иметь возможность легко складывать бумагу вперед и назад, вперед и назад», — объяснила она, поворачивая складку, чтобы соответствовать ее словам. Дети поступили так же. Затем Крис попросил детей развернуть лист до полной квадратной формы.
«Сначала посмотрите, как я складываю два угла вниз, как мы делаем бумажный самолетик», — сказал Крис. (См. Рисунок 2.)
Рисунок 2.
После того, как класс сложил свои листы и сосчитал стороны и углы, Крис объяснил: «Когда фигура имеет пять сторон и пять углов, она называется пятиугольником.Она попросила детей негромко произнести «пятиугольник». Затем она сказала им несколько раз покачивать новые складки вперед и назад.
Рисунок 3.
Крис затем показал, как сложить оставшиеся два угла, чтобы получился квадрат меньше исходного, но у детей были свои идеи. «Это воздушный змей!» «Это алмаз». (См. Рисунок 3.)
Крис повернула сложенный квадрат так, чтобы одна сторона была параллельна полу. «Что это за форма?» она спросила.
«Это квадрат», — ответили студенты.«Но я знаю, что это бриллиант», — настаивал Стив.
«Эта форма может выглядеть как воздушный змей или алмаз, когда я держу ее вот так», — объяснил Крис, поворачивая фигуру так, чтобы угол был направлен вверх. «Но это все равно квадрат, как бы он ни повернулся».
Затем Крис представил исследование. «Сегодня мы собираемся исследовать формы, которые можно сделать, складывая бумагу разными способами. Правило таково: вы можете сложить бумагу на один, два или несколько сгибов, но только на уже сделанных сгибах. Вы не можете делать новые складки.Проследите различные формы, которые вы найдете. Вы будете работать с партнером, обрисовывая свои формы на одном листе газетной бумаги ».
Когда Крис раздавала каждой паре студентов по листу газетной бумаги размером 12 на 18 дюймов, она спросила: «Как вы думаете, сколько форм вы найдете?»
По оценке детей, от двух до десяти. (На самом деле существует девять различных форм, если считать исходный квадрат; см. Диаграмму ниже, рисунок 4.)
Рисунок 4.
Наблюдая за детьми
Крис распространил, когда дети начали складывать свои листы и обводить найденные формы.
Дэнни спросил: «Можем ли мы написать что-нибудь посередине?» Он указал на начертанный им пятиугольник.
«Как что?» — поинтересовался Крис.
«Супермен», — ответил он. Форма напомнила Дэнни символ на рубашке Супермена.
Другие дети решили украсить свои фигуры. Из пятиугольников выросли дымоходы и кирпичи, а из трапеций выросли колеса и выхлопные трубы, пока дети связывали формы со знакомыми объектами.
Габриэль и Стейси усердно работали и уже нарисовали шесть различных форм.»Смотреть! Я сделала пятиугольник, — сказала Стейси, пробуя новое слово. «И в перевернутом виде это похоже на кошку», — добавила она.
Адриан также усердно работал, отслеживая свою первую форму. Хотя способности детей сильно различаются, каждый ребенок может добиться успеха в этом исследовании формы.
«Могу я сделать это?» — спросил Дэнни, показывая Крису тощий пятиугольник.
«Он отличается от форм, которые вы уже нашли?» она спросила. Крис и Дэнни посмотрели на очертания, которые он нарисовал.
«Да», — ответил Дэнни, демонстрируя, как он создал два разных пятиугольника, сложив свой квадрат по-разному.
Джози и Франциска нарисовали на своей бумаге два одинаковых квадрата. Крис сказал им: «Мне кажется, вы дважды нарисовали одну и ту же фигуру на своей бумаге».
«Но мы сделали один квадрат, а другой ромб», — сказала Франциска.
«Мне они кажутся одинаковыми, — сказал Крис. «Они кажутся одинаковыми по размеру и форме, но этот перевернут», — указал Крис на бриллиант. Девочки кивнули и начали стирать одну из фигур.
Стив и Хавьер, казалось, закончили.«Сколько разных форм вы нашли?» — спросил Крис.
«Шесть», — ответил Стив. «Вот сколько их». Стив изначально предсказывал, что будет шесть различных форм.
«Откуда вы знаете, что их всего шесть?» — спросил Крис.
Стив пожал плечами. «Мы смотрели и смотрели, и вот сколько мы нашли», — сказал он. Но затем Хавьер обрел новую форму. Он показал Стиву, как складывать все створки, кроме одного, чтобы получить пятиугольник. (См. Рисунок 5.)
Рис. 5. Стив и Хавьер обрисовали и пометили все девять фигур.
Обсуждение класса A
Когда у детей было время поработать над заданием, Крис начал обсуждение в классе. «Кто бы хотел подойти и нарисовать фигуру?» — спросила она, раскладывая диаграмму. Многие дети подняли руку, желая поучаствовать.
Хавьер поднес свой свернутый шестиугольник к таблице и аккуратно обвел его маркером. Крис и дети вместе сосчитали стороны и углы. «Это бриллиант!» «Это шестиугольник!» «Это трапеция!» — кричали дети.
«Фигура с шестью сторонами и шестью углами называется шестиугольником», — сказал Крис и обозначил фигуру. Крис поднял для сравнения один из желтых шестиугольников из блоков шаблона. Дети заметили, что хотя их шестиугольник также имел шесть сторон, он был длиннее, тоньше и больше походил на алмаз. Некоторые говорили, что шестиугольник Pattern Block был толще и больше напоминал круг.
Адриан затем показал классу пятиугольник. Никто не запомнил это слово. Франциска подошла вплотную. «Ручка . . . ручка .. . »
«Это пятиугольник», — сказал Крис. Детям требуется много опыта, чтобы выучить новую терминологию и научиться ее использовать.
Класс продолжил рисовать фигуры, маркировать их и считать стороны и углы. Габриэль указал на пятиугольник и сказал: «Это похоже на лицо клоуна! Вот волосы. Адриан назвал трапецию ботинком. Маркосу показалось, что его сложенный квадрат раскрывается, как конверт. «Послушайте, это письмо, — сказал он.
Затем Крис сказал детям, что для выполнения домашних заданий они должны забрать домой свои квадраты и поработать вместе со своими семьями, чтобы найти все формы.Крис знал, что детям будет полезно снова заняться этим заданием, и им это понравится. Кроме того, это была возможность показать родителям геометрию, которую они изучали в школе.
Из выпуска 22 печатного информационного бюллетеня, осень 1997 г.
шаблонов складок для папок
В последние годы в современном искусстве оригами стала распространена новая форма письменных инструкций: узор сгиба (часто обозначаемый сокращением CP).В обычных схемах оригами фигура описывается последовательностью складывания — линейной пошаговой схемой развития. Шаблоны складок, напротив, обеспечивают одноэтапное соединение развернутого квадрата со сложенной формой, сжимая сотни складок, а иногда и часы складывания в единую диаграмму! Поэтому неудивительно, что для многих концепция шаблона складок оригами как формы инструкций по оригами более чем немного напоминает знаменитую карикатуру Сидни Харриса, в которой научное происхождение описывается фразой «тогда происходит чудо. … »
По мере того, как сложность оригами возросла, рисунки складок стали гораздо более популярными как средство передачи оригами.Отчасти причина в том, что нарисовать единичный узор сгиба намного проще, чем нарисовать подробную пошаговую последовательность сгиба. Отчасти причина в том, что многие составители оригами (включая меня) создают шаблоны складок как часть своего процесса проектирования, поэтому готовый узор складок предоставляется «бесплатно». И отчасти причина в том, что с общим ростом возможностей складывания во всем мире, разумное количество людей теперь имеет навык «читать» шаблон складки и складывать закодированную форму.
Профиль CP был повышен в последние годы с помощью функции «Crease Pattern Challenge» в журнале Origami Tanteidan Magazine , и в настоящее время почти de rigueur добавляет миниатюру шаблона складки на этикетку фигурки оригами на выставки оригами.Следует, однако, отметить, что, хотя повсеместное распространение узоров складок возникло недавно, самой концепции уже несколько десятилетий: многие пионеры современного искусства 1960-х и 1970-х годов, в частности Нил Элиас, часто записывали свои композиции в виде узоров складок. по крайней мере в их личных записных книжках.
Человеку, не относящемуся к оригами, последовательность превращения листа бумаги в красивый сложенный объект может показаться чудом. Однако даже любителям оригами идея о том, что один рисунок складок передает полную последовательность складывания, может показаться столь же чудесной.Но на самом деле узор сгиба иногда может быть более ярким, чем подробный порядок складывания, передавая не только «как складывать», но и то, как изначально была спроектирована фигура. И, таким образом, он может дать папке представление о мыслительных процессах композитора оригами так, как это не может сделать пошаговая последовательность складывания.
Таким образом, ценность шаблонов складок выходит за рамки экономии времени для ленивых составителей диаграмм. Но на самом деле есть еще одна причина, по которой некоторые композиции публикуются как CP; Дело не только в том, что композитор не хочет тратить время на составление пошаговой последовательности складывания.Может быть, композитор даже не знает пошаговой последовательности. Фактически, его может и не быть! Многие современные дизайны оригами, особенно если они были разработаны с использованием теории деревьев, упаковки кругов, складывания коробок или любого другого инструмента современного дизайна, созданы по принципу «все или ничего». Все складки работают вместе, когда они полностью сложены, но часто бывает, что нет промежуточных состояний — никаких подмножеств складок, — которые можно было бы сложить вместе, чтобы сформировать отдельные ступени.Для такой модели единственный способ собрать модель — это предварительно уменьшить все складки, а затем аккуратно заставить их все сойтись одновременно с минимумом бодинга. Этот метод сборки, как оказалось, почти всегда используется для складывания модели из КП.
Итак, хотя часто можно сложить целую модель из КП и фотографии, в этом упражнении есть небольшая загадка.
Первое, что нужно понять о шаблоне складки: он может не отображать все складки, в зависимости от жанра складывания.Математические и геометрические модели складок обычно показывают все складки, но репрезентативное оригами редко показывает каждую складку в законченной форме, так как это сделало бы узор складок невозможным. Вместо этого рисунок складок дает складки, необходимые для складывания «основы», то есть геометрической формы, которая имеет правильное количество и расположение клапанов. По крайней мере, это все еще оставлено на усмотрение папки, чтобы добавить утончение и придание формы складкам; но также могут быть довольно существенные манипуляции с основанием, которые не отражаются в шаблоне складок, и они, как и формирование складок, оставляются на усмотрение папки.
Одно различие между CP и диаграммами состоит в том, что CP редко используют как стандартные горные (штрих-точка-точка), так и долинные (пунктирные) линии. В то время как стандартные узорчатые линии хорошо подходят для пошаговых диаграмм, в которых каждая диаграмма содержит только несколько линий действий, в образцах складок, которые могут содержать десятки или сотни складок гор и долин, стандартные образцы линий очень трудно различить. Один из ключей к умению читать CP — это способность идентифицировать крупномасштабные особенности паттерна с некоторого расстояния.Это означает, что нам нужно уметь четко различать линии изгибов гор и долин издалека, а стандартные образцы линий просто не работают: они растворяются в болоте суеты.
Таким образом, разработчики шаблонов складок используют разные стили линий, чем составители пошаговых диаграмм, но пока нет единого установленного стиля. Со временем я экспериментировал с несколькими разными стилями, и вы увидите, что эти эксперименты отражены в рисунках справа. Совсем недавно для максимальной читаемости я использовал сплошные черные линии для складок гор и цветные пунктирные линии для складок долин.Этот стиль сохраняет линии впадин в соответствии с пошаговыми стилями и обеспечивает четкое различие между стилями линий как при цветной, так и при черно-белой печати.
Шаблоны складок также могут отображать дополнительную информацию, которая освещает дизайн или полезна для фактического складывания. Иногда полезно показать складки, которые на самом деле не сложены, потому что они помогают передать информацию о структуре или могут показать, как построить ключевые ориентиры. Для зеркально-симметричных моделей я часто показываю предварительные сгибы или основную геометрию на одной стороне узора, а полный узор — на другой.Иногда также полезно выделить складки на петлях и / или показать набивку в виде круга / реки; вы найдете несколько примеров того и другого в опубликованных мной CP.
Галерея шаблонов складок
Щелкните здесь, чтобы просмотреть список шаблонов складок для многих моих дизайнов. У меня нет КП для каждой композиции, только эти. Если для проекта нет опубликованных диаграмм, это лучшее, что вы можете сделать для получения инструкций.
Разгадывать складки может быть весело; если вас зацепят, в Интернете разбросано много других.Даже если вы не пытаетесь складывать их, узоры складок красивы, интригуют и вдохновляют сами по себе. Наслаждаться!
звенья с рисунком складки
В Интернете есть несколько хороших источников шаблонов складок. Вот несколько ссылок на интересующие страницы.
Руководство Гервина Штурма по складке коробки
Очень хорошее руководство по интерпретации и складыванию складок коробки. Прокрутите вниз, чтобы найти ссылки.
Сатоши Камия
Сатоши создал, вероятно, самые сложные модели в мире оригами, многие из которых описываются одними из самых ярких рисунков складок.
Брайан Чан
Заслуженная звезда американского оригами, Брайан создал множество новых дизайнов, используя теорию деревьев и другие техники.
Grupo Origami Patrones
Испаноязычная группа Yahoo, занимающаяся изучением узоров складок.
Diego Quevedo
Блог на испанском языке о шаблонах складок и их интерпретации.
Оригами: смесь скульптуры и математики | Наука
Для сборки этой оригами-конструкции, названной «Зеленые циклы» Эрика Демейна и его отца Мартина, потребовалась неделя импровизации.Предоставлено: Renwick Gallery
.Форма Прингла, математически говоря, называется гиперболическим параболоидом. Художники складывали бумагу в такую форму в течение многих лет. Поворот? Гиперболические параболоиды не должны существовать в оригами — невозможно создать такую трехмерную форму, используя только складки, вдавленные в бумагу вручную.
По этой логике, некоторые работы Эрика Демейна тоже не должны существовать.
Демейн, ведущий теоретик вычислительного оригами в мире, создал серию скульптур, складывая концентрические квадраты в квадратные листы бумаги, чередуя горы и долины и складывая диагонали.С каждой скульптурой бумага превращается в седло, называемое гиперболическим параболоидом, и остается там. На его складки, похожие на гармошку, приятно смотреть, но Демейн, профессор информатики Массачусетского технологического института, не понимает, как это работает.
Бумажная структура с несколькими гиперболическими параболоидами. Предоставлено: Эрик Демейн
.После того, как бумага сложена, вся структура принимает естественную форму. «Физика находит этот баланс», — говорит Демейн. Но механизмы формы Прингла все еще плохо изучены.Демейн утверждает, что на бумаге должны быть небольшие складки, невидимые невооруженным глазом, поскольку складки вручную сами по себе не могут объяснить конечную форму.
Пытаться разгадать эту загадку — значит объединить скульптуру и математику.
«Мы придумали математическую задачу, которая вдохновляет на новое искусство, и художественную задачу, которая вдохновляет на новую математику», — говорит Демейн. 31-летний художник создает свои скульптуры оригами вместе со своим отцом Мартином.
Конечный продукт, «Зеленые циклы» (на фото вверху), был создан с использованием двух листов акварельной бумаги Mi-Teintes французского производства, скрепленных вместе.Используя шариковый полировщик, который по сути представляет собой шариковую ручку без чернил, Демейн вдавил двухслойный лист в кольца концентрических кругов, вырезанных на деревянном шаблоне. На бумаге надрезают круговые складки и нарезают в форме пончика, прежде чем она приобретет трехмерную форму. Художник создает несколько таких моделей и соединяет их вместе в переплетенную бумажную скульптуру. Младший Демейн говорит, что самая сложная часть — это сборка, на которую уходит до недели, потому что они не могут предсказать, будут ли полученные формы закручиваться друг вокруг друга, чтобы создать прочную, эстетически приятную деталь.
«Мы заставляем их блокироваться, отпускать и позволять им расслабиться, иногда на ночь, если мы думаем, что у нас есть скульптура кандидата», — говорит он. Если конструкция обвалится или развалится, пара попытается снова.
«Естественные циклы» Эрика и Мартина Демейнов
Письменные инструкции по складыванию бумаги впервые появились в 1797 году в Японии. Акисато Рито опубликовал книгу Sembazuru Orikata с уроками для 1000 бумажных журавликов. Адачи Казуюки опубликовал более подробный сборник практических рекомендаций в 1845 году.К концу 1800-х годов детские сады по всей Европе начали складывать цветные квадраты в классе.
Идея была проста: без ножниц, без клея, без скотча — просто ловкие пальцы сгибали и скручивали бумагу в новые формы. Оригами стало современным видом искусства в 1950-х годах, когда японский художник Акира Йошизава соединил механику ремесла с эстетикой скульптуры. Он создал более 50 000 бумажных моделей, но так и не продал ни одной. С тех пор сморщенные, похожие на живые фигуры животных и людей художника Эрика Джойзеля экспонировались в Лувре, а подробные композиции художника-физика Роберта Ланга выставлялись в Музее современного искусства.
Но складывание бумаги — это не просто то, что мы можем охарактеризовать. Он также играет роль в ответах на давние вопросы по математике, такие как задача «сложить и вырезать».
Первое известное упоминание об этой проблеме появилось в 1721 году в японской книге головоломок, в одной из которых читателю предлагалось сложить прямоугольный лист бумаги и сделать только один прямой разрез, чтобы получить японский герб под названием сангайбиси , который переводится как «тройные ромбики».Автор предложил решение в виде диаграммы, но проблема оставалась открытым на протяжении столетий — сколько форм возможно? — пока Демейн не решил ее.
Оказывается, возможна любая форма — лебеди, кони, пятиконечные звезды. Все, что нужно, — это геометрическая схема, руководство по складыванию здесь и изгибу там.
«Обнимающие круги» Эрика и Мартина Демейнов
Использование таких чертежей добавило сложности оригами. В 1960-х годах складные диаграммы включали от 20 до 30 шагов.Теперь для модели может потребоваться от 200 до 300 шагов от начала до конца. Это много для одного листка бумаги. Но хитрость заключается в использовании сверхтонкой бумаги с длинными волокнами, которые придают ей прочность, чтобы выдерживать все тяги и тяги.
Компьютерные программы только добавили удовольствия. TreeMaker, бесплатная программа, созданная художником Робертом Лэнгом, берет созданный пользователем линейный рисунок и выдает узоры, которые можно распечатать и сложить для создания фигур. Origamizer позволяет пользователям создавать 3D-модели и изменять их складки на экране, исследуя различные формы и формы.
С помощью компьютерного программного обеспечения оригами вышло за пределы мира искусства. Ученые и инженеры нашли практическое применение складыванию бумаги. Производители автомобилей, например, используют математику оригами для расчета схемы складок для складывания подушек безопасности в сплющенные формы.
