Модели фигур геометрических фигур: Модели геометрических фигур и тел для дошкольников
Модели геометрических фигур и тел для дошкольников
МОдели геометрических фигур и тел.
Геометрия очень интересная и познавательная наука. «Геометрия – раздел математики, в котором изучаются пространственные отношения (например, взаимное расположение) и формы (например, геометрические тела) и их обобщение».
Но если для школьников геометрия – это наука, которую они изучают не один год, то маленькому дошкольнику очень тяжело понять некоторые ее аксиомы и теоремы. Нельзя объяснить некоторые понятия одинаково детям 10 и 5 лет. Чтобы ознакомить маленького дошкольника с элементарными геометрическими понятиями приходится придумывать разнообразные игры, развлечения. При ознакомлении дошкольников с геометрическими понятиями, а позднее с геометрическими телами у меня возникли трудности. Сначала детям тяжело было запомнить названия фигур: треугольник, прямоугольник, квадрат, тяжело было их различать.
Позже, когда мы перешли к изучению геометрических тел, началась путаница. Дошкольники не видели разницы между кругом и шаром, между кубом и квадратом. Детям было тяжело усвоить эти понятия. Тогда мною была разработана система моделей – основных геометрических фигур и тел. Сначала детям показывались кодовые карточки, на которых были изображены структурные элементы фигур и тел: угол, вершина, сторона, ребро, грань, основание. Дети рассматривали карточки и соотносили изображение с реальными предметами. Они четко научились показывать, где угол, а где вершина. Кодовые карточки показывали: сколько сторон у фигуры и равны ли они.
Работая с моделями, дети очень четко и правильно называли структурные элементы и признаки фигур. Когда дети хорошо усвоили геометрические фигуры, их структурные элементы, мы перешли к изучению геометрических тел. Как объяснить детям разницу между геометрическими телами и геометрическими фигурами? Я решила отобразить это в цвете: модели геометрических фигур – одного цвета, модели геометрических тел – другого цвета.
Дети быстро освоили разницу между телами и фигурами и активировали в речи слова: плоскостные и объемные. Модели заставляют детей думать, логически рассуждать, мыслить, развивают речь, активизируют в речи слова: ребро, основание, грань, угол, вершина. Дети учатся словесно описывать фигуру и тела, подбирать модель к заданной фигуре и телу. Дошкольники научились сравнивать 2 фигуры – находить, чем они похожи, чем различаются?
В старшем дошкольном возрасте я предлагаю ввести усложнение в модели, новые кодовые карточки с изображением видов углов: прямой, тупой, острый. Теперь при описании фигуры – ребенок не просто говорит, что у нее 4 угла, а уточняет, какие именно. Речь ребенка развивается. Пополняется его словарный запас. Создавая модели я ставила перед собой следующие цели:
-модель должна быт доступной для детей;
-модель должны четко отражать основные свойства обследуемого предмета;
модель должна помочь ребенку в ознакомлении с данным предметом.
Геометрическая пропедевтика – одно из самых интересных направлений в дошкольной математике. Анализируя содержание обучения в дошкольных учреждениях и в начальных классах, с сожалением приходится констатировать, что его доля очень мала. Например, понятие «треугольник» и «четырехугольник» начинают раскрываться только с первого класса, а «квадрат» и «прямоугольник» впервые вводится во втором классе (через выделение существенных признаков этих понятий). Между тем дети 3-4 летнего возраста подготовлены к восприятию формы. Опробовав модели в работе с детьми младшего и среднего дошкольного возраста, я увидела положительную динамику: дети быстрее и легче воспринимали материал, лучше развивалась речь детей, дошкольники правильно строили предложения, правильно называли структурные элементы фигур, сравнивали фигуры, различали фигуры и тела.
Я рекомендую к использованию модели геометрических фигур и геометрических тел к работе с дошкольниками, начиная со 2 младшей группы.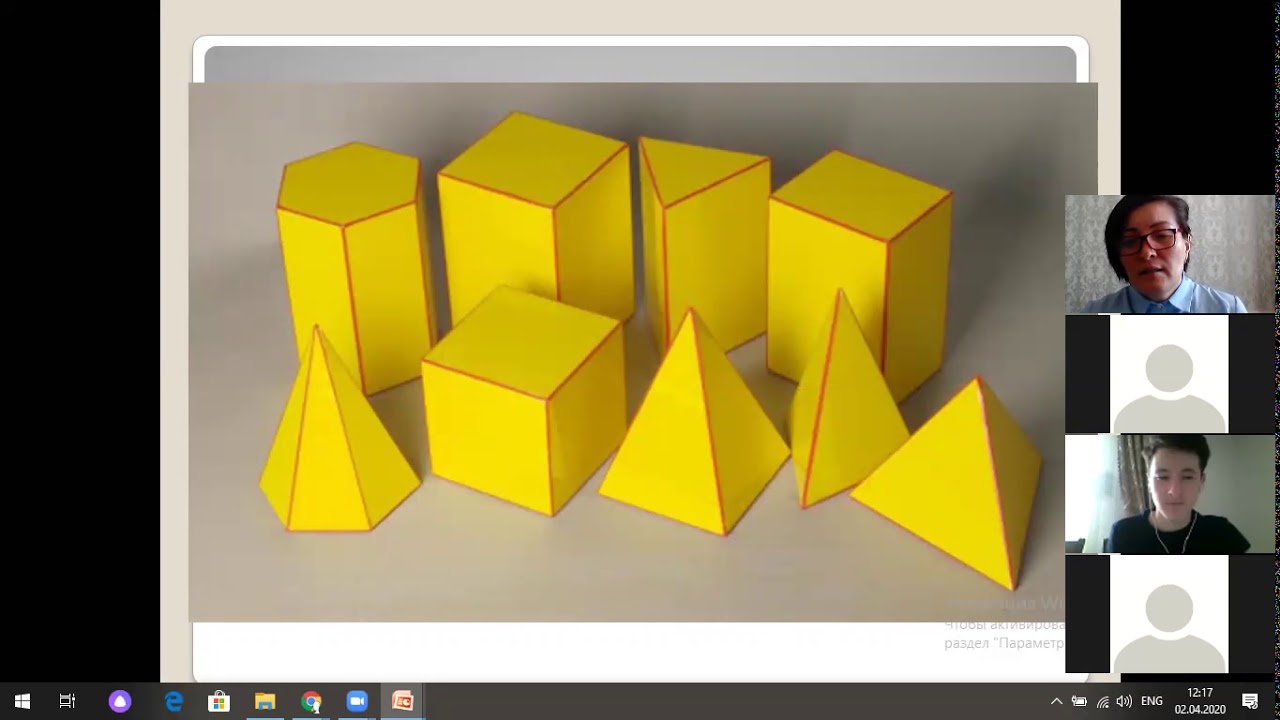
модели геометрических фигур
«Модель квадрата»
4 угла
4 вершины
4 стороны
все стороны равныМодель прямоугольника
4 угла
4 вершины
4 стороны
стороны не равны: две длинные,две короткие
Модель треугольника
3 угла
3 стороны
3 вершины
Модель трапеции
4 вершины
4 стороны
боковые стороны равны
верхняя и нижняя стороны не равны
4 угла
2 тупых угла
2 острых угла
модель ромба
4 вершины
4 сторонывсе стороны равны
4 угла
2 тупых угла
2 острых угла
Модель круга
нет углов
нет вершин
нет сторон
Модели геометрических тел
модель пирамиды
квадратное основание
4 трёхугольные грани
есть углы
есть вершины
4 ребра
модель куба
6 квадратных оснований
есть углы
6 квадратных граней
8 вершин
12 рёбер
модель конуса
одно круглое основание
одна вершина
нет углов
нет граней
нет рёбер
модель цилиндра
два круглых основания
нет углов
нет вершин
нет граней
модель шара
нет углов
нет вершин
нет граней
нет рёбер
Источник высокого качества Модель Геометрические Фигуры производителя и Модель Геометрические Фигуры на Alibaba.
 com
comДайте ребенку фору при покупке. модель геометрические фигуры из большого разнообразия, предлагаемого на Alibaba.com. Эти предметы - веселый и увлекательный способ заинтересовать малышей и маленьких детей математикой и развить их навыки в неформальной обстановке. Эти. модель геометрические фигуры надежных производителей, которые используют безопасные и совершенно нетоксичные материалы, что делает их безопасными даже для очень маленьких детей. Файл. модель геометрические фигуры на сайте тщательно продуманы, чтобы соответствовать уровню целевой возрастной группы и поддерживать их интерес.The. модель геометрические фигуры на Alibaba.com представлены в виде пластиковых и деревянных блоков, открыток и даже мягких игрушек. Их может использовать ребенок самостоятельно или под руководством опекуна для еще лучших результатов. Эти. модель геометрические фигуры предлагаются в ярких и привлекательных цветах и дизайне, чтобы понравиться более молодой аудитории и заставить их поиграть с ними.
Файл. модель геометрические фигуры ориентированы на ряд навыков, таких как распознавание чисел, понимание сложения и вычитания, а также на более сложные концепции, такие как трехзначные суммы, умножение и деление, для детей старшего возраста.
The. Предлагаемое модель геометрические фигуры может содержать изображения героев мультфильмов, животных и другие привлекательные мотивы для поддержания интереса. Эти. модель геометрические фигуры бывают больших размеров, подходящие для дома, или в портативных рюкзаках, которые можно брать с собой в поездку, чтобы привлечь ребенка и помочь ему учиться. Файл. Предлагаемые модель геометрические фигуры также отлично подходят для подарков маленьким детям на дни рождения.
Выберите из блестящего ассортимента. модель геометрические фигуры на Alibaba.com и покупайте наиболее подходящие. Это идеальный вариант для. модель геометрические фигуры поставщики, желающие закупать в больших количествах по экономичным ценам.
Они обязательно понравятся детям и родителям.
Середина урока | Сообщите о том, что на уроке первоклассники научатся создавать модели плоских фигур. Спросите, какой способ получения плоских фигур им знаком. Выслушайте ответы. Вероятнее всего, дети предложат обвести пространственную фигуру, которую они выберут из набора, и вырезать ее. Подтвердите, что плоские фигуры помогают обозначать окружающие нас предметы, имеющие объемные формы, например, на плане, карте или рисунке. Предложите каждому человеку самостоятельно сделать из картона любую плоскую фигуру при помощи пространственной фигуры. Пусть они выполнят это задание самостоятельно, по своему выбору. Таким образом вы закрепите у них осознание того, что они способны самостоятельно принимать решения и имеют право выбора на уроке. Ваша задача будет заключаться в осуществлении контроля за этим процессом, в оказании индивидуальной помощи и поддержке детей, нуждающихся в этом. Что это за фигура? Сколько у нее сторон? Продемонстрируйте модель плоской фигуры, например, треугольника, выполненную из счетных палочек или трубочек для коктейля. Задайте вопросы: Что это за фигура? Эта фигура пространственная или плоская? Каким способом она получена? Выслушайте ответы ребят. Сообщите учащимся, что это модель треугольника. Спросите, хотят ли они научиться создавать фигуры таким способом. Как создать модель треугольника? Рассмотрите с учащимися в учебнике этапы создания треугольника из трубочек для коктейля. Перед началом работы предложите первоклассникам обсудить, какие материалы и в каком количестве потребуются для создания треугольника. Для учащихся-кинестетиков будет полезно, если вы проведете связь между моделированием из соломинок и пластилина и изучением темы «Отрезок. Ломаная». Обсудите с ними, на что похожи соломинки и кусочки пластилина. Ребята должны соединять соломинки-отрезки при помощи точек из пластилина. Создай модель квадрата. Организуйте работу по созданию квадрата. Предложите учащимся рассмотреть алгоритм действий в учебнике. Обсудите с ними, какие ресурсы потребуются для создания квадрата. Обратите внимание на то, что для создания квадрата потребуются четыре соломинки одинаковой длины и четыре кусочка пластилина, так как у квадрата четыре стороны и четыре вершины. Сделай прямоугольник сам. Первоклассники к этому моменту хорошо освоят технологию изготовления модели, поэтому предложите им самостоятельно рассмотреть алгоритм в учебнике. Реши. Предложите школьникам подумать и решить, какую фигуру можно получить из пяти соломинок и пяти кусочков пластилина. Если они не смогут выполнить задание, предложите поэкспериментировать на практике и найти ответ. Ответ Пятиугольник, так как у него 5 сторон и 5 вершин. Попробуй. Предложите ребятам обсудить и решить проблемную ситуацию, опираясь на полученные знания по созданию моделей плоских фигур. Если они будут испытывать затруднения, предложите им попробовать на практике решить поставленную задачу и определить нужную фигуру. Ответ Цилиндр. Развитие языковых компетенций Используйте для закрепления ключевого слова модели плоских фигур, изготовленные первоклассниками. В ходе игры ведущий демонстрирует детям реальные предметы, а те в свою очередь с места показывают модель фигуры, форму которой имеет данный предмет. Ведущий отдает команды, произнося слово «модель». Ребята при демонстрации модели могут составить словосочетания: «модель треугольника», «модель квадрата», «модель треугольника», используя ключевые слова из предыдущего урока. Паровозик. Задание направлено на развитие умения определять вид плоской фигуры. Предложите учащимся рассмотреть изображение паровозика из плоских геометрических фигур — посчитать количество фигур каждого вида и внести результаты счета в таблицу. | Учебник: Модели плоских фигур (1), с. Рабочий лист 53 «Модели плоских фигур (1)», с. 55. Рабочий лист 54 «Картина из фигур», с. 56. Ресурсы: мешочек из плотной ткани для игры «Таинственный мешок»; наборы геометрических пространственных и плоских фигур; листы цветного картона; ножницы; пластилин; трубочки для коктейля или счетные палочки для каждого человека. | Конец урока | Нарисуй свой паровозик. Предложите воспитанникам нарисовать свой паровозик, используя определенное количество плоских фигур. Задание развивает их творческие способности и направлено на формирование умения изображать плоские геометрические фигуры, создавая собственные композиции. Создай необычную картину. Первоклассники смогут создать картину из плоских фигур. Организуйте в классе выставку работ своих подопечных. Для этого попросите прикрепить фигуры на лист картона и подписать их названия. Работы могут висеть в классе, чтобы учащиеся имели возможность подходить к ним, рассматривать, обсуждать, показывать родителям. Вставь пропущенные слагаемые. Задание на повторение и закрепление. Вставь пропущенные уменьшаемые. Задание на повторение и закрепление. Вставь пропущенные слагаемые. Задание на повторение и закрепление. | Дифференциация Каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися? | Оценивание Как Вы планируете проверить уровень усвоения материала учащимися? Используйте данный раздел для записи методов, которые Вы будете использовать для оценивания того, чему учащиеся научились во время урока. | Здоровье и соблюдение техники безопасности Здоровьесберегающие технологии. Используемые физминутки и активные виды деятельности. | К концу урока учащиеся научатся: создавать модели плоских фигур; строить композиции из плоских фигур. Задайте им вопросы, чтобы выявить уровень усвоения учебного материала: Как можно создать модели плоских фигур? Перечислите модели плоских фигур, которые вы научились делать на уроке. Организуйте самооценивание первоклассников с помощью «Лестницы успеха» в рабочей тетради. | Одолела вас дремота… Шевельнуться неохота? Ну-ка, делайте со мною упражнение такое: Вверх, вниз потянись, окончательно проснись. Руки вытянуть пошире – раз, два, три, четыре, пять. Наклониться – три, четыре – и на месте поскакать. На носок, потом на пятку, все мы делаем зарядку. №2 Мы считали – и устали, Дружно все мы тихо встали. Ручками похлопали, раз, два, три. Ножками потопали, раз, два, три. Сели, встали, встали, сели И друг друга не задели. Мы немножко отдохнем И опять считать начнем. Выше руки! Шире плечи! Раз, два, три! Дыши ровней! От зарядки станешь крепче, Станешь крепче и сильней. |
Конспект урока по математике » Модели плоских геометрических фигур «
Организационный момент:
Прозвенел звонок на урок. — Добрый день, ребята! Мне приятно вас всех видеть. Давайте подарим друг другу хорошее настроение:
Давайте подарим друг другу хорошее настроение:
На части не делится солнце лучистое
И вечную землю нельзя поделить,
Но искорку счастья луча золотистого
Ты можешь, ты в силах друзьям подарить.
— Ребята, я улыбаюсь вам, вы улыбнитесь мне. Улыбка может согреть других своим теплом, показать ваше дружелюбие и улучшить всем настроение. Хорошее настроение всегда помогает справиться с любой задачей и добиться хороших результатов.
Мотивация Стартер
Дети встают в круг. Учитель даёт задание: образуйте прямую, ломанную кривую, точку. Покажите орган человека, который похож на точку, покажите отрезок с помощью рук, луч, как можно показать кривую? Квадрат? Треугольник? Прямоугольник?
— Сегодня мы вновь отправимся в страну Геометрию,
Постановка проблемного вопроса и создание проблемной ситуации
— Расположите числа в порядке возрастания и прочитайте получившееся слово.
6 | 1 | 4 | 3 | 5 | 8 |
р | ф | г | и | у | ы |
—– Что вы знаете о значении этого слова? Что называют фигурой? Показываю шахматные фигуры, геометрические.
Не случайно появилось это слово на доске.
Можно предположить, что тема урока связана с фигурами?
– Как вы думаете, о каких фигурах мы будем говорить?
Открываю на доске закрытое полосой бумаги задание.
– Посмотрите на доску. Догадайтесь, что за задание я приготовила.
На клетчатом фоне доски в ряд изображены фигуры – треугольник, круг, квадрат, треугольник, круг.
– Определим закономерность (проговариваем хором).
– Начертите фигуры карандашом в тетрадях, продолжите ряд до конца строки. – Какие еще геометрические фигуры вам известны? (Ромб, прямоугольник, овал…)
Повторение о геометрических фигурах
Постановка цели урока У: Можете ли вы самостоятельно изготовить геометрические фигуры? Из чего? Поставим цель себе на урок (чему мы хотим научиться).
(изготавливать модели плоских фигур и составлять из них композиции) ;
— Чему мы должны научиться, чтобы достичь цели урока? (достигнем цели, если научимся изготавливать плоские фигуры)
Середина урока1) Работа с учебником.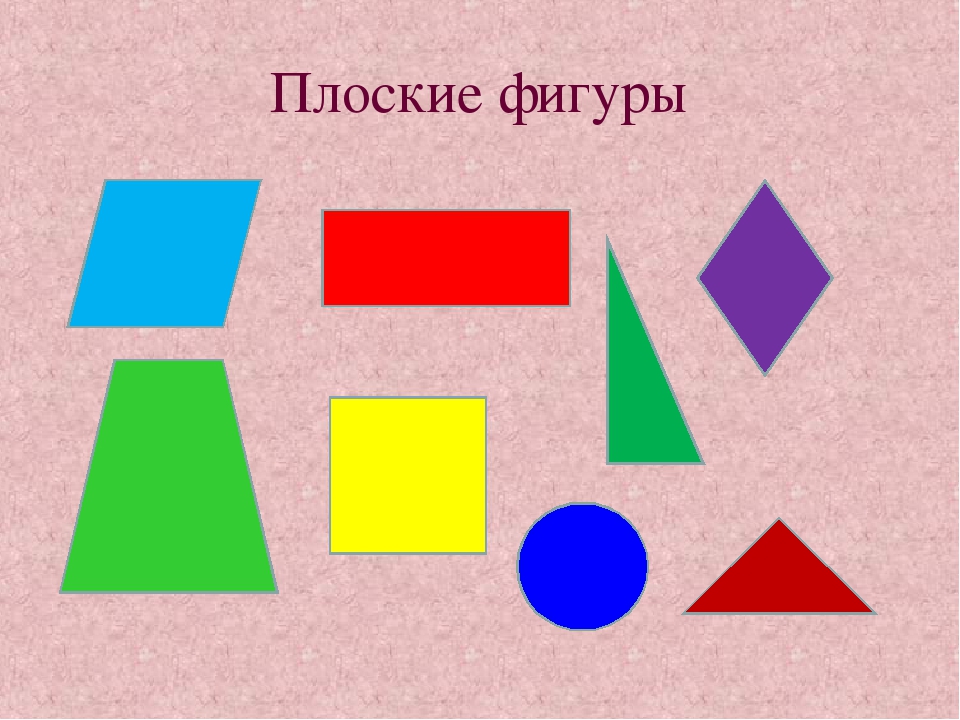 Рассматривание иллюстраций.
Рассматривание иллюстраций.
— Объясните, из чего изготовлены геометрические фигуры?
2)Практическая работа в группах. -У вас на партах лежат геометрические фигуры . (квадрат, круг, треугольник, прямоугольник.) Учитель: Обсудите в группе, как можно изготовить эти фигуры из трубочек или проволоки.
Прежде, давайте, вспомним какие правила надо соблюдать при работе в группе. В группе есть ответственный. Каждый работает на общий результат.
Один говорит, а все слушают.
Свое несогласие высказывай вежливо. Переспроси тихо, если что не понял
5. Итог урока. Рефлексия деятельности. — В какой стране мы сегодня побывали? Чему научились?
Рефлексия. Получение обратной связи.
С какими геометрическими фигурами работали?
Учитель просит поднять зелёный кружок, если на уроке чувствовали себя уверенно, не испытывали затруднения, жёлтый кружок – если были затруднения, красный – пока ничего не понятно.
Урок на тему «Моделирование геометрических операций и фигур». 9-й класс
Цель: Познакомить с алгоритмами построения основных геометрических операций. Сформировать навыки построения геометрических моделей в графическом редакторе Paint.
Задачи:
Образовательные
- формирование навыков работы с программным обеспечением;
- выбор определённого программного средства для реализации, поставленной задачи;
- выработка умений и навыков решения практических задач в соответствующих программах.
Развивающие
- развитие внимания, способности к анализу;
- развитие логического мышления;
- развитие способностей к определённым видам деятельности (дизайн, инженерная графика, программирование и т.д.)
Воспитательные
- формирование самостоятельности мышления, чёткости и организованности в работе, умения контролировать свою деятельность;
- работать эффективно в соответствии с располагаемым временем,
- работать в группе.
Тип урока: комбинированный
Используемые образовательные технологии: компетентностно-ориентированное обучение, здоровьесберегающая технология, исследование в обучении, информационно-коммуникационные технологии.
Необходимое оборудование: компьютеры, интерактивная доска с программным обеспечением, проектор, рабочий лист группы.
Ход урока
1. Организационный момент.
Учитель: Тему “Моделирование” мы изучаем уже не первый урок. Мы моделировали различные ситуации, биологические процессы, решали задачи, связанные с математическими расчетами. Модели применяются людьми ещё с глубокой древности, однако лишь в эпоху новых информационных технологий и компьютеризации этот метод исследования приобрел столько разнообразных форм и средств реализации.
2. Актуализация знаний.
Учитель: Для работы на уроке нам
необходимо вспомнить схему этапов
моделирования.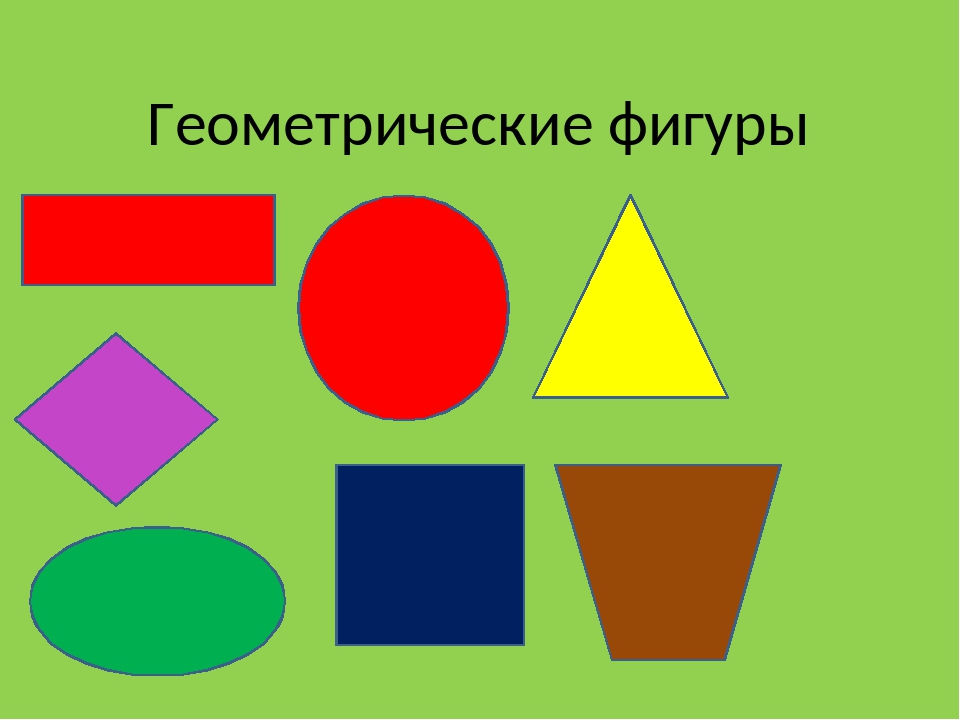
3. Постановка целей и задач урока
Учитель: Я предлагаю послушать несколько выступлений ваших одноклассников, которые поделятся своими наблюдениями
Наблюдение 1. (Ученик 1)
В информатике много терминов, которые пришли в нее из геометрии. Например,
Наблюдение 2. (Ученик 2)
Задачи на построение возникли в глубокой
древности и были связаны с практическими
потребностями. Примеры из истории развития
геометрии свидетельствуют, что можно добиться
точности даже если под рукой нет специальных
измерительных инструментов, а есть подсобные
предметы: кусок верёвки, ровная палка и т.д.
Поэтому необходимо научиться строить модели
геометрических фигур с заданными свойствами:
равносторонний треугольник, шестиугольник,
равнобедренный треугольник и пр. Это можно
сделать, используя законы геометрии
Это можно
сделать, используя законы геометрии
Учитель: Спасибо. А теперь объедините все, что увидели и услышали с момента начала урока и попробуйте сформулировать тему нашего урока. (Моделирование геометрических фигур)
Какие цели мы поставим перед собой? (научиться моделировать геометрические фигуры в графическом редакторе)
В каких ситуациях вам может пригодиться такой навык? (для оформления презентаций, вставить в текстовый файл, для подготовки исследовательских работ)
И действительно, в курсе геометрии вы знакомились с темой “Построение геометрических фигур при помощи циркуля и линейки”, однако наше время диктует нам использовать все свои знания в цифровом пространстве, поэтому сегодня мы будем создавать модели геометрических фигур в графическом редакторе и строго соблюдать все этапы создания моделей.
Вся история геометрии связана с практикой
построения при помощи подручных средств для
измерения недоступного. И мы сегодня будем
создавать модели в простейшем графическом
редакторе, который не требует дополнительной
установке, он является стандартным для
операционной системы Windows.
4. Получение новых знаний
Моделирование объектов с заданными геометрическими свойствами.
I этап. Постановка задачи.
Постановка задачи.
Учитель: геометрических фигур существует очень много и построить модели всех на одном уроке невозможно. Посмотрите внимательно на слайд (слайд 4) и скажите, как можно назвать такие фигуры? (правильные многоугольники)
Давайте вспомним особенности правильных многоугольников и подумаем, на каких этапах моделирования они нам могут понадобиться. (слайд 5)
Цель моделирования
В среде графического редактора научиться моделировать геометрические объекты с заданными свойствами.
Формализация задачи.
Геометрическая фигура характеризуется длинной сторон и углами, которые необходимо задать в виде отрезков и углов на рабочем поле графического редактора перед началом построения.
II этап. Разработка алгоритмов для решения задач
Разработка алгоритмов для решения задач
Учитель: Перед тем как вы приступите к выполнению построения правильных многоугольников, мы рассмотрим простые построения, которые могут понадобиться вам в процессе работы над заданием.
Модель 1. Деление отрезков (моделирование функций линейки) покажет Ученик 3.
Алгоритм деления отрезка пополам приведён на <Рисунке 1.>
Рис. 1
Порядок построения.
1. Копируем данный отрезок.
2. Из концов данного отрезка проводим линии под углом 45 (с помощью клавиши Shift)
3. Из точки их пересечения проводим строго вертикальную линию (с помощью клавиши Shift) до пересечения с данным отрезком.
4. Точка пересечения и есть искомая середина.
Построение основано на том, что высота в равнобедренном треугольнике является одновременно биссектрисой и медианой. Для построения достаточно инструмента Линия и клавиша Shift.
Сохрани построение в Сетевой папке, чтобы им
могли пользоваться ребята.
Модель 2. Построение окружности заданного радиуса и определение её центра (моделирование функции циркуля) покажет Ученик 4. Окружность в графическом редакторе вписывается в квадрат со стороной, равной удвоенному радиусу. Алгоритм построение окружности изображен на рис.
Порядок построения.
1. Копируем данный отрезок а два раза.
2. С помощью стандартной операции (квадрат) строим квадрат со стороной 2а
3. В полученный квадрат, с помощью стандартной операции (окружность) вписываем окружность с радиусом а.
Учитель: Можно убрать дополнительные построения, чтобы такой окружностью можно было бы воспользоваться в процессе работы.
5. Решение практических задач.
Приступаем к работе в группах. У каждой будет свой модератор. Эти ребята уже предложили свой способ построения, и теперь будут координировать ваши действия. На выполнение задания 10 минут.
РОБОТА в ГРУППАХ
Группа 1. Модератор группы Ученик 5
Модератор группы Ученик 5
1. Разработка моделей
Модель А. Построение равностороннего треугольника с заданной стороной. Данный алгоритм предложил Евклид в IV веке до н.э. Построить треугольник по алгоритму, приведенному на рисунке, и доказать, что полученный треугольник действительно правильный. Рисунок
Порядок построения.
1. С помощью стандартной операции (квадрат) строим квадрат со стороной а.
2. Для того чтобы вписать две окружности, проходящие через центр друг друга строи шесть квадратов, вписываем в них две окружности с радиусом а.
3. Точки пересечения окружностей является вершинами треугольника.
Модель В. Построить правильный шестиугольник.
Рис. 4
Построение правильного шестиугольника с
заданной стороной. Используя свойство
правильных фигур, вписываются в окружность и то,
что сторона равностороннего шестиугольника
равна радиусу описанной окружности, выполнить
построение по алгоритму на <Рисунке 4. >. Начать
построение окружности с радиусом, равным
заданной стороне шестиугольника.
>. Начать
построение окружности с радиусом, равным
заданной стороне шестиугольника.
Компьютерный эксперимент
Группа 2. Модератор группы Ученик 6.
Разработка моделей
Модель А.
Построение квадрата. Пусть w-данная окружность с центром в точки О и радиусом R. Через точку О проведем диаметр АС и к этому диаметру проведем серединный перпендикуляр, который пересечет окружность w в двух точках В и D.Теперь последовательно соединим точки A,B,C и D. ABCD-искомый квадрат. <Рисунок 5.>
Рис. 5
Модель В.
Построение правильного восьмиугольника. Для
того, чтобы построить правильный восьмиугольник
нужно сначала построить правильный
четырехугольник, например, А1А3А5А7-квадрат, потом
построить биссектрисы углов А1OА3, А3OА5, А5OА7, А7OА1,
которые прересекут окружность в точках А2, А4, А6,
А8 соответственно, затем последовательно
соединить точки А1,А2,А3,А4,А5,А6,А7,А8. А1А2…А8-искомый
восьмиугольник. <Рисунок 6.>
А1А2…А8-искомый
восьмиугольник. <Рисунок 6.>
Рис. 6
Компьютерный эксперимент
Группа 3. Модератор группы Ученик 7.
Разработка моделей
Построение правильного пятиугольника с заданной стороной
Альбрехт Дюрер (1471-1527 гг.), ставший олицетворением Возрождения в Германии приводит теоретически точный способ построения правильного пятиугольника, заимствованный из великого сочинения Птолемея «Альмагест». Интерес Дюрера к построению правильных многоугольников отражает использование их в Средние века в арабских и готических орнаментах, а после изобретения огнестрельного оружия — в планировке крепостей
Альбрехт Дюрер не только в рукописях, но также в
картинах и книгах оставил многочисленные следы
своего математического таланта и увлечение
математикой. Об этом свидетельствует знаменитый
дюреровский магический квадрат, являющийся
одним из самых старых магических квадратов в
Европе.
Рассмотрим одно небольшое произведение Дюрера, в котором гениальный художник проводит очень хороший и легкий способ построение правильного пятиугольника с помощью окружности, если известна только длина стороны. <Рисунок 7.>
Рис. 7
Порядок построения.
Приближенное построение правильного
пятиугольника представляет собой интерес.
А.Дюрером оно проводится при условии
неизменности раствора циркуля, что повышает
точность построения. Способ построения описан
Дюрером так:»Однако пятиугольник, построенный
неизменным раствором циркуля, делай так. Проведи
две окружности так, чтобы каждая из них проходила
через центр другой. Два центра А и В соедини
прямой линией. Это и будет стороной
пятиугольника. Точки пересечения окружностей
обозначь сверху С, снизу D и проведи прямую линию
CD. После этого возьми циркуль с неизменным
раствором и, установив одну его ножку в точку D,
другой проведи через оба центра А и В дугу до
пересечения её с обеими окружностями. Точки
пересечения обозначь через E и F, а точку
пересечения с прямой CD обозначь буквой G. Теперь
проведи прямую линию через Е и G до пересечения с
линией окружности. Эту точку обозначь Н. Затем
проведи другую линию через F и G до пересечения с
линией окружности и поставь здесь J. Соединив J,A и
H,B прямыми, получим три стороны пятиугольника.
Дав возможность двум сторонам такой длины
достигнуть совпадения в точке K из точек J и H,
получим некоторый пятиугольник.»
Точки
пересечения обозначь через E и F, а точку
пересечения с прямой CD обозначь буквой G. Теперь
проведи прямую линию через Е и G до пересечения с
линией окружности. Эту точку обозначь Н. Затем
проведи другую линию через F и G до пересечения с
линией окружности и поставь здесь J. Соединив J,A и
H,B прямыми, получим три стороны пятиугольника.
Дав возможность двум сторонам такой длины
достигнуть совпадения в точке K из точек J и H,
получим некоторый пятиугольник.»
Компьютерный эксперимент
6. Подведение итогов.
Учитель: Молодцы. Все работы групп сохраните в Сетевой папке. Они вам понадобятся для работы.
7. Выставление оценок в журнал.
Практическое применения построения правильных многоугольников. Сообщение ученика 8. <Рисунок 8.>
Рис. 8
8. Постановка домашнего задания.
Повторить материал по теме “Моделирование”. Найти 3-4 примера правильных многоугольников в
природе.
Найти 3-4 примера правильных многоугольников в
природе.
9. Рефлексия. Ответьте в группах на вопросы рефлексии
| Все ли получилось? Почему? | ___________________ |
| Как менялись чувства и настроение во время урока? | ___________________ |
| Лучше всего у нас получилось | ___________________ |
| Этого мы достигли благодаря | ___________________ |
| Труднее всего было | ___________________ |
| Эти трудности мы преодолели так: | ___________________ |
| Выполнили поставленные цель и задачи? | ___________________ |
Кто хочет озвучит то, что получилось? (желающие от групп отвечают на вопросы)
Источники информации.
- Макарова Н.В. Программа по информатике и ИКТ (системно-информационная концепция). – СПб.: Питер, 2007. – 128 с.: ил.
- Информатика. 7-9 класс. Базовый курс. Практикум-задачник по моделированию / Под ред. Н.В. Макаровой. – СПб.: Питер, 2007. – 176 с.: ил.
- Практическая работа №1 по теме “Моделирование геометрических операций и фигур”. https://videouroki.net/razrabotki/praktichieskaia-rabota-po-tiemie-modielirovaniie-ghieomietrichieskikh-opieratsii.html
- http://ppt4web.ru/informatika/modelirovanie-geometricheskikh-operacijj-i-figur.html
- Представление о моделировании в среде графического редактора. http://xn—-7sbbfb7a7aej.xn--p1ai/informatika_09/informatika_materialy_zanytii_09_03.html
Программа «Начальное техническое моделирование»
Проблема развития познавательной активности и интеллектуальных способностей обучающихся является одной из важнейших задач в педагогике на современном этапе. Большим потенциалом развития обучающихся обладает начальное техническое моделирование, которое является одним из способов воспитания будущих изобретателей, ученых, дизайнеров, творческих и креативно мыслящих людей.
На занятиях НТМ обучающиеся не только познают свойства, осваивают приемы обработки различных материалов (картона, бумаги, пенопласта), но и используют различные инструменты, изготавливают различные технические конструкции и модели. Оформление изделий позволяет развивать свою творческую фантазию, дизайнерские способности, аккуратность. Занятия по графической подготовке способствуют освоению чертежных инструментов, у обучающихся развивается мелкая моторика рук, пространственное воображение, образное и логическое мышление; зрительная память. Они читают условные обозначения на чертежах, чертят геометрические фигуры, выполняют разметку несложных объектов, работают с шаблонами, конструируют на плоскости, изготавливают объемные модели на основе геометрических фигур, вносят изменения в конструкцию модели, используют техническую терминологию.
Для учащихся дошкольного и младшего школьного возраста характерно несовершенство мелкой моторики рук, гиперактивность, стремление узнавать новое, мастерить своими руками. Овладевая приемами работы с бумагой, картоном и природными и бросовыми материалами, дети развивают руки, глазомер, усидчивость, пространственное воображение, снимают эмоциональное напряжение.
Овладевая приемами работы с бумагой, картоном и природными и бросовыми материалами, дети развивают руки, глазомер, усидчивость, пространственное воображение, снимают эмоциональное напряжение.
В этом возрасте для ребят важно быть интересным для своих сверстников, иметь возможность творческого самовыражения, и занятия начальным техническим моделированием помогают в этом.
В процессе совместной деятельности детей, прививаются навыки общения, поведения в коллективе уважительное отношение к сверстникам, к труду, как своему собственному, так и чужому, устойчивые морально-нравственные ориентиры, что соответствует Концепции модернизации российского образования, где воспитание подрастающего поколения объявлено приоритетным направлением.
Геометрические фигурки и их названия. Удивительные фигуры в геометрии. Линейные геометрические фигуры
Геометрические фигуры представляют собой комплекс точек, линий, тел или поверхностей. Эти элементы могут располагаться как на плоскости, так и в пространстве, формируя конечное количество прямых.
Термин «фигура» подразумевает под собой несколько множеств точек. Они должны располагаться на одной или нескольких плоскостях и одновременно ограничиваться конкретным числом оконченных линий.
Основными геометрическими фигурами считаются точка и прямая. Они располагаются на плоскости. Кроме них, среди простых фигур выделяют луч, ломаную линию и отрезок.
Точка
Это одна из главных фигур геометрии. Она очень маленькая, но ее всегда используют для построения различных форм на плоскости. Точка — это основная фигура для абсолютно всех построений, даже самой высокой сложности. В геометрии ее принято обозначать буквой латинской алфавита, к примеру, A, B, K, L.
С точки зрения математики точка — это абстрактный пространственный объект, не обладающий такими характеристиками, как площадь, объем, но при этом остающийся фундаментальным понятием в геометрии. Этот нульмерный объект просто не имеет определения.
Прямая
Это фигура полностью размещается в одной плоскости. У прямой нет конкретного математического определения, так как она состоит из огромного количества точек, располагающихся на одной бесконечной линии, у которой нет предела и границ.
У прямой нет конкретного математического определения, так как она состоит из огромного количества точек, располагающихся на одной бесконечной линии, у которой нет предела и границ.
Существует еще и отрезок. Это тоже прямая, но она начинается и заканчивается с точки, а значит, имеет геометрические ограничения.
Также линия может превратиться в направленный луч. Такое происходит, когда прямая начинается с точки, но четкого окончания не имеет. Если же поставить точку посредине линии, то она разобьется на два луча (дополнительных), причем противоположно направленных друг к другу.
Несколько отрезков, которые последовательно соединяются друг с другом концами в общей точке и располагаются не на одной прямой, принято называть ломаной линией.
Угол
Геометрические фигуры, названия которых мы рассмотрели выше, считают ключевыми элементами, использующимися при построении более сложных моделей.
Угол — это конструкция, состоящая из вершины и двух лучей, которые выходят из нее. То есть стороны этой фигуры соединяются в одной точке.
То есть стороны этой фигуры соединяются в одной точке.
Плоскость
Рассмотрим еще одно первичное понятие. Плоскость — это фигура, у которой нет ни конца, ни начала, равно как и прямой, и точки. Во время рассмотрения этого геометрического элемента во внимание берется лишь его часть, ограниченная контурами ломаной замкнутой линии.
Любую гладкую ограниченную поверхность можно считать плоскостью. Это может быть гладильная доска, лист бумаги или даже дверь.
Четырехугольники
Параллелограмм — это геометрическая фигура, противоположные стороны которой параллельны друг другу попарно. Среди частных видов этой конструкции выделяют ромб, прямоугольник и квадрат.
Прямоугольник — это параллелограмм, у которого все стороны соприкасаются под прямым углом.
Квадрат — это четырехугольник с равными сторонами и углами.
Ромб — это фигура, у которой все грани равны. При этом углы могут быть совершенно разными, но попарно. Каждый квадрат считается ромбом. Но в противоположном направлении это правило действует не всегда. Далеко не каждый ромб является квадратом.
Но в противоположном направлении это правило действует не всегда. Далеко не каждый ромб является квадратом.
Трапеция
Геометрические фигуры бывают совершенно разными и причудливыми. Каждая из них имеет своеобразную форму и свойства.
Трапеция — это фигура, которая чем-то схожа с четырехугольником. Она имеет две параллельные противоположные стороны и при этом считается криволинейной.
Круг
Эта геометрическая фигура подразумевает расположение на одной плоскости точек, равноудаленных от ее центра. При этом заданный ненулевой отрезок принято называть радиусом.
Треугольник
Это простая геометрическая фигура, которая очень часто встречается и изучается.
Треугольник считается подвидом многоугольника, расположенным на одной плоскости и ограниченным тремя гранями и тремя точками соприкосновения. Эти элементы попарно соединены между собой.
Многоугольник
Вершинами многоугольников называют точки, соединяющие отрезки. А последние, в свою очередь, принято считать сторонами.
Объемные геометрические фигуры
- призма;
- сфера;
- конус;
- цилиндр;
- пирамида;
Эти тела имеют нечто общее. Все они ограничиваются замкнутой поверхностью, внутри которой находится множество точек.
Объемные тела изучают не только в геометрии, но и в кристаллографии.
Любопытные факты
Наверняка вам будет интересно ознакомиться с информацией, предоставленной ниже.
- Геометрия сформировалась как наука еще в давние века. Это явление принято связывать с развитием искусства и разнообразных ремесел. А названия геометрических фигур свидетельствуют об использовании принципов определения подобия и схожести.
- В переводе с древнегреческого термин «трапеция» обозначает столик для трапезы.
- Если вы возьмете различные фигуры, периметр которых будет одинаковым, то наибольшая площадь гарантированно будет у круга.
- В переводе с греческого языка термин «конус» обозначает сосновую шишку.
- Существует известная картина Каземира Малевича, которая начиная с прошлого века притягивает к себе взгляды многих живописцев.
 Работа «Черный квадрат» всегда была мистической и загадочной. Геометрическая фигура на белом полотне восхищает и поражает одновременно.
Работа «Черный квадрат» всегда была мистической и загадочной. Геометрическая фигура на белом полотне восхищает и поражает одновременно.
Существует большое количество геометрических фигур. Все они отличаются параметрами, а порой даже удивляют формами.
Цели урока :
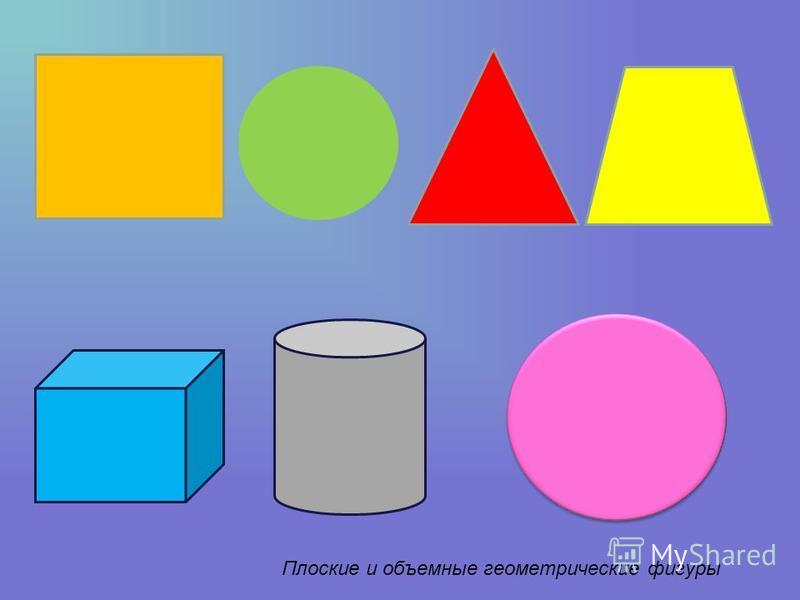
- Познавательная : создать условия для ознакомления с понятиями плоские и объёмные геометрические фигуры, расширить представление о видах объёмных фигур, научить определять вид фигуры, сравнивать фигуры.
- Коммуникативная : создать условия для формирования умения работать в парах, группах; воспитание доброжелательного отношения друг к другу; воспитывать у учащихся взаимопомощь, взаимовыручку.
- Регулятивная : создать условия для формирования планировать учебную задачу, выстраивать последовательность необходимых операций, корректировать свою деятельность.
- Личностная : создать условия для развития вычислительных навыков, логического мышления, интереса к математике, формирования познавательных интересов, интеллектуальных способностей учащихся, самостоятельность в приобретении новых знаний и практических умений.

Планируемые результаты:
личностные:
- формирование познавательных интересов, интеллектуальных способностей учащихся; формирование ценностных отношений друг к другу;
самостоятельность в приобретении новых знаний и практических умений; - формирование умений воспринимать, перерабатывать полученную информацию, выделять основное содержание.
метапредметные:
- овладение навыками самостоятельного приобретения новых знаний;
- организация учебной деятельности, планирования;
- развитие теоретического мышления на основе формирования умений устанавливать факты.
предметные:
- усвоить понятия плоские и объёмные фигуры, научиться сравнивать фигуры, находить плоские и объёмные фигуры в окружающей действительности, научиться работать с развёрткой.
УУД общенаучные :
- поиск и выделение необходимой информации;
- применение методов информационного поиска, осознанное и произвольное построение речевого высказывания в устной форме.
УУД личностные :
- оценивать свои и чужие поступки;
- проявление доверия, внимательности, доброжелательности;
- умение работать в паре;
- выражать положительное отношение к процессу познания.
Оборудование : учебник, интерактивная доска, смайлики, модели фигур, развёртки фигур, светофоры индивидуальные, прямоугольники -средства обратной связи, Толковый словарь.
Тип урока : изучение нового материала.
Методы : словесные, исследовательские, наглядные, практические.
Формы работы : фронтальная, групповая, парная, индивидуальная.
1. Организация начала урока.
Утром солнышко взошло.
Новый день нам принесло.
Сильными и добрыми
Новый день встречаем мы.
Вот мои руки, я раскрываю
Их навстречу солнцу.
Вот мои ноги, они твердо
Стоят на земле и ведут
Меня верной дорогой.
Вот моя душа, я раскрываю
Её навстречу людям.
Наступи, новый день!
Здравствуй, новый день!
2. Актуализация знаний.
Создадим хорошее настроение. Улыбнитесь мне и друг другу, садитесь!
Чтобы дойти до цели, надо прежде всего идти.
Перед вами высказывание, прочитайте. Что означает это высказывание?
(Чтобы чего-то добиться, нужно что-то делать)
И действительно, ребята, попадающим в цель может стать только тот, кто настраивает себя на собранность и организованность своих действий. И вот я надеюсь, что мы с вами на уроке достигнем своей цели.
Начнем наш путь к достижению цели сегодняшнего урока.
3. Подготовительная работа.
Посмотрите на экран. Что вы видите? (Геометрические фигуры)
Назовите эти фигуры.
Какое задание, вы можете предложить своим одноклассникам? (разделите фигуры на группы)
У вас на партах лежат карточки с этими фигурами. Выполните это задание в парах.
По какому признаку вы разделили эти фигуры?
- Плоские и объемные фигуры
- По основаниям объемных фигур
С какими фигурами мы уже работали? Что учились находить у них? Какие фигуры встречаются нам на геометрии впервые?
Какая же тема нашего урока? (Учитель добавляет слова на доске: объёмные, на доске появляется тема урока: Объёмные геометрические фигуры. )
Чему мы должны научиться на уроке?
4. «Открытие» нового знания в практической исследовательской работе.
(Учитель показывает куб и квадрат.)
Чем они похожи?
Можно ли сказать, что это одно и тоже?
Чем же отличается куб от квадрата?
Давайте проведём опыт. (Ученики получают индивидуальные фигуры – куб и квадрат.)
Попробуем приложить квадрат к плоской поверхности порты. Что видим? Он весь (целиком) лёг на поверхность парты? Вплотную?
! Как назовём фигуру, которую можно целиком расположить на одной плоской поверхности? (Плоской фигурой.)
Можно ли куб полностью (весь) прижать к парте? Проверим.
Можно ли назвать куб плоской фигурой? Почему? Есть ли пространство между рукой и партой?
! Значит, что мы можем сказать о кубе? (Занимает определённое пространство, является объёмной фигурой.)
ВЫВОДЫ: Чем же отличаются плоские и объёмные фигуры? (Учитель вывешивает на доске выводы. )
)
- Можно целиком расположить на одной плоской поверхности.
ОБЪЁМНЫЕ
- занимают определённое пространство,
- возвышаются над плоской поверхностью.
Объёмные фигуры: пирамида, куб, цилиндр, конус, шар, параллелепипед.
4. Открытие новых знаний.
1. Назовите фигуры, изображенные на рисунке.
Какую форму имеют основания этих фигур?
Какие еще формы можно увидеть на поверхности куба и призмы?
2. Фигуры и линии на поверхности объемных фигур имеют свои названия.
Предложите свои названия.
Боковые стороны, образующие плоскую фигуру называются гранями. А боковые линии – рёбра. Углы многоугольников – вершины. Это элементы объемных фигур.
Ребята, а как вы думаете, как называются такие объемные фигуры, у которых много граней? Многогранники.
Работа с тетрадями: чтение нового материала
Соотнесение реальных объектов и объёмных тел.
А теперь подберите для каждого предмета ту объёмную фигуру, на которую он похож.
Коробка – параллелепипед.
- Яблоко – шар.
- Пирамидка – пирамида.
- Банка – цилиндр.
- Горшок из-под цветка — конус.
- Колпачок – конус.
- Ваза – цилиндр.
- Мяч – шар.
5. Физминутка.
1. Представьте себе большой шар, погладьте его со всех сторон. Он большой, гладкий.
(Ученики «обхватывают» руками и гладят воображаемый шар.)
А теперь представьте себе конус, дотроньтесь до его вершины. Конус растёт вверх, вот он уже выше вас. Допрыгните до его вершины.
Представьте, что вы внутри цилиндра, похлопайте по его верхнему основанию, потопайте по нижнему, а теперь руками по боковой поверхности.
Цилиндр стал маленькой подарочной коробочкой. Представьте, что вы сюрприз, который находится в этой коробочке. Я нажимаю кнопку и… сюрприз выскакивает из коробочки!
6. Групповая работа :
(Каждая группа получает одну из фигур: куб, пирамиду, параллелепипед. Полученную фигуру дети изучают, выводы записывают в подготовленную учителем карточку .)
Полученную фигуру дети изучают, выводы записывают в подготовленную учителем карточку .)
Группа 1. (Для изучения параллелепипеда)
Группа 2. (Для изучения пирамиды)
Группа 3. (Для изучения куба)
7. Решение кроссворда
8. Итог урока. Рефлексия деятельности.
Решение кроссворда в презентации
Что нового вы для себя сегодня открыли?
Все геометрические фигуры можно разделить на объёмные и плоские.
А я узнал названия объёмных фигур
Геометрия — это раздел математики, в котором изучаются формы и их свойства.
Геометрия, которая изучается в школе, называется евклидовой, по имени древнегреческого учёного Евклида (III век до н. э.).
Изучение геометрии начинается с планиметрии. Планиметрия — это раздел геометрии, в котором изучаются фигуры, все части которых находятся в одной плоскости.
Геометрические фигуры
В окружающем нас мире существует множество материальных предметов разных форм и размеров: жилые дома, детали машин, книги, украшения, игрушки и т. д.
д.
В геометрии вместо слова предмет говорят геометрическая фигура. Геометрическая фигура (или кратко: фигура ) — это мысленный образ реального предмета, в котором сохраняются только форма и размеры, и только они принимаются во внимание.
Геометрические фигуры разделяют на плоские и пространственные . В планиметрии рассматриваются только плоские фигуры. Плоской геометрической фигурой называется такая, все точки которой лежат на одной плоскости. Представление о такой фигуре даёт любой рисунок, сделанный на листе бумаги.
Геометрические фигуры бывают весьма разнообразны, например, треугольник, квадрат, окружность и др.:
Часть любой геометрической фигуры (кроме точки), также является геометрической фигурой. Объединение нескольких геометрических фигур, тоже будет являться геометрической фигурой. На рисунке ниже левая фигура состоит из квадрата и четырёх треугольников, а правая фигура состоит из окружности и частей окружности.
Раиса Баландина
«Объемные геометрические фигуры»
Конспект НОД в подготовительной группе на тему :
«Объемные геометрические фигуры » .
Задачи :
Упражнять в счёте в пределах 20 в прямом и обратном порядке
Закрепить знания о последовательности дней недели, времён года
Закрепить представления детей о геометрических фигурах
НОД занятия.
Ребята, посмотрите, сегодня утром я шла в детский сад и встретила почтальона. Он мне дал вот такое интересное письмо. Его прислал Буратино. Он уже ходит в школу. Вот,что он пишет :
«Дорогие ребята! Для того чтобы хорошо учиться в школе, надо много знать, уметь, думать, догадываться. А также решать необычные задачи, выполнять задания на смекалку и сообразительность. Вот мне и задали такие задания, а я затрудняюсь их выполнить. Помогите мне, пожалуйста».
Ребята, давайте поможем Буратино.
1 задание.Ответьте на вопросы :
Какое время года сейчас? (Весна)
Назовите весенние месяцы
Какой месяц сейчас идёт? (март)
Сколько дней в недели? (семь)
Назови их;
Какой сегодня день недели? (вторник)
Какой четверг по счету? (четвертый)
Вчера какой был день недели?
Завтра какой будет день недели?
2 задание.
Ребята, Буратино, не может выполнить следующее задание.Давайте ему поможем :
Какой бывает счет? (прямой и обратный)
Считай от 10 до 20;
Считай от 20 обратно;
Назови число меньше пятнадцати;
Назови соседа 11 и 14;
Сравни числа 16 и 18;
Сравни числа 15 и 15;
3 задание.
Воспитатель : А сейчас мы будем работать с карточкой, которую прислал Буратино. Вы должны рассказать, где и как расположены фигуры .
Воспитатель : — Где находиться прямоугольник?
Ребенок : — Прямоугольник находится посередине.
Воспитатель : — Где находится овал?
Ребенок : — Овал находится справа от прямоугольника
Воспитатель : — Где находится круг?
Ребенок : — Круг находится внизу, под прямоугольником
Воспитатель : — Где находится квадрат?
Ребенок : — Квадрат находится слева от прямоугольника
Воспитатель : — Где находится треугольник?
Ребенок : — Треугольник находится сверху, над прямоугольником.
Физминутка.
Поработали, ребятки,
А теперь все на зарядку!
Столько раз ногою топнем (показываю цифру 6)
Столько раз руками хлопнем (показываю цифру 10)
Мы присядем столько раз (показываю цифру 7)
Мы наклонимся сейчас (показываю цифру 4)
Мы подпрыгнем ровно столько (показываю цифру 8)
Ай да счёт! Игра и только.
4 задание.
На столе перед детьми расположены объёмные геометрические фигуры (шар, куб, цилиндр, конус)
— Следующее задание : Дети что это? Какие фигуры ? Сколько их? Какая фигура стоит первой ? Второй? Третьей? Какая стоит последней?
Воспитатель : Ребята, а вы знаете, что геометрические фигуры можно нарисовать , начертить в тетради, вырезать из цветной бумаги. А еще их можно выложить из счетных палочек. И не одну, а сразу несколько. Давайте попробуем.
А)- отсчитайте три палочки и сделайте треугольник
Отсчитайте еще две палочки и сделайте еще один треугольник
Сколько треугольников получилось? (два)
Сколько палочек вы отсчитали?
Б)- отсчитайте четыре палочки и сделайте квадрат.
Отсчитайте еще три палочки и сделайте еще один квадрат
Какая фигура у вас получилась ? (прямоугольник)
Сколько четырехугольников получилось? (три)
А сколько многоугольников получилось? (три)
Назовите их (два квадрата и один многоугольник)
На какие делятся геометрические фигуры ? (объёмные и плоские)
Чем они отличаются друг от друга? (плоские можно расположить на плоскости, а объёмные нет) .
Мы сейчас с вами выкладывали на столе объемные или плоские фигуры ?
А сейчас мы с вами сделаем из палочек и пластилина фигуру , которая состоит из нескольких… а чего? Вы узнаете,отгадав загадку :
Три вершины в нем видны,
Три угла, три стороны,
С ним знаком даже дошкольник
Ведь фигура – (треугольник) .
Ребята, как называется фигура , которая состоит из нескольких треугольников? (пирамида)
Давайте, сделаем из пластилина и счетных палочек пирамиду.
5 задание.
Ребята, Буратино говорит, что вы уже устали — давайте поиграем. Эта игра — испытание «Верно-неверно» — поможем исправить ошибки, которые Буратино специально кое-где оставил.
Если вы услышите то, что считаете правильным, хлопайте в ладоши, если же то, что не правильно – покачайте головой
Утром солнышко встает; (верно)
По утрам нужно делать зарядку; (верно)
Нельзя умываться по утрам; (неверно)
Днем ярко светит луна; (неверно)
Утром дети идут в детский сад; (верно)
Ночью люди обедают; (неверно)
Вечером вся семья собирается дома; (верно)
В неделе 7 дней; (верно)
За понедельником следует среда; (неверно)
После субботы идет воскресение; (верно)
Перед пятницей стоит четверг; (верно)
Всего 5 времен года; (неверно)
Весна наступает после лета; (неверно) .
8 задание. А теперь Буратино приготовил вам графический диктант. Вы должны нарисовать один из признаков (явлений весны) .
А теперь Буратино приготовил вам графический диктант. Вы должны нарисовать один из признаков (явлений весны) .
Дети, поставьте карандаш на выделенную точку и рисуйте по клеткам.
Посмотрите и сравните получившийся у вас рисунок с образцом.
Молодцы, ребята!
Итог занятия.
Вот и выполнили вы все задания Буратино. Что же мы сегодня нового узнали? Какие задания с вами выполняли? Какие задания были трудными?
Буратино благодарит вас за помощь.
Тема урока
Геометрические фигуры
Что такое геометрическая фигура
Геометрические фигуры – это совокупность множества точек, линий, поверхностей или тел, которые расположены на поверхности, плоскости или пространстве и формирует конечное количество линий.
Термин «фигура» в какой-то степени формально применяется к множеству точек, но как правило фигурой принято называть такие множества, которые расположенные на плоскости и ограничиваются конечным числом линий.
Точка и прямая — это основные геометрические фигуры, расположенные на плоскости.
К самым простым геометрическим фигурам на плоскости принадлежат — отрезок, луч и ломаная линия.
Что такое геометрия
Геометрия – это такая математическая наука, которая занимается изучением свойств геометрических фигур. Если дословно перевести на русский язык термин «геометрия», то он обозначает «землемерие», так как в стародавние времена основной задачей геометрии, как науки, стало измерение расстояний и площадей на поверхности земли.
Практическое применение геометрии бесценно во все времена и независимо от профессии. Без знаний геометрии не может обойтись ни рабочий, ни инженер, ни архитектор и даже художник.
В геометрии есть такой раздел, который занимается изучением различных фигур на плоскости и называется планиметрия.
Вам уже известно, что фигурой называют произвольное множество точек, находящиеся на плоскости.
К геометрическим фигурам принадлежат: точка, прямая, отрезок, луч, треугольник, квадрат, круг и другие фигуры, которые изучает планиметрия.
Точка
Из выше изученного материала вам уже известно, что точка относится к главным геометрическим фигурам. И хотя это самая малая геометрическая фигура, но она необходима для построения других фигур на плоскости, чертеже или изображении и является основой для всех остальных построений. Ведь построение более сложноватых геометрических фигур складывается из множества точек, характерных для данной фигуры.
В геометрии точки обозначают прописными буквами латинского алфавита, например, такими, как: А, В, С, D ….
А теперь подведем итог, и так, с математической точки зрения, точка является таким абстрактным объектом в пространстве, который не имеет объема, площади, длины и других характеристик, но остается одним из фундаментальных понятий в математике. Точка – это такой нульмерный объект, которые не имеет определения. По определению Евклида, точкой называют то, что невозможно определить.
Прямая
Как и точка, прямая относится к фигурам на плоскости, которая не имеет определения, так как состоит из бесконечного множества точек, находящихся на одной линии, которая не имеет ни начала ни конца. Можно утверждать, что прямая линия бесконечна и не имеет предела.
Можно утверждать, что прямая линия бесконечна и не имеет предела.
Если же прямая начинается и заканчивается точкой, то она уже не является прямой и называется отрезком.
Но иногда прямая, с одной стороны имеет точку, а с другой нет. В таком случае прямая превращается в луч.
Если же взять прямую и на ее средине поставить точку, то она разобьет прямую на два противоположно направленных луча. Данные лучи являются дополнительными.
Если же перед вами несколько отрезков, соединенных между собой так, что конец первого отрезка становиться началом второго, а конец второго отрезка — началом третьего и т. д., и эти отрезки находятся не на одной прямой и при соединении имеют общую точку, то такая цепочка является ломаной линией.
Задание
Какая ломаная линия называется незамкнутой?
Как обозначается прямая?
Как называется ломаная линия, у которой четыре замкнутых звена?
Какое название имеет ломаная линия с тремя замкнутыми звеньями?
Когда конец последнего отрезка ломаной совпадает с началом 1-го отрезка, то такую ломаную линию называют замкнутой.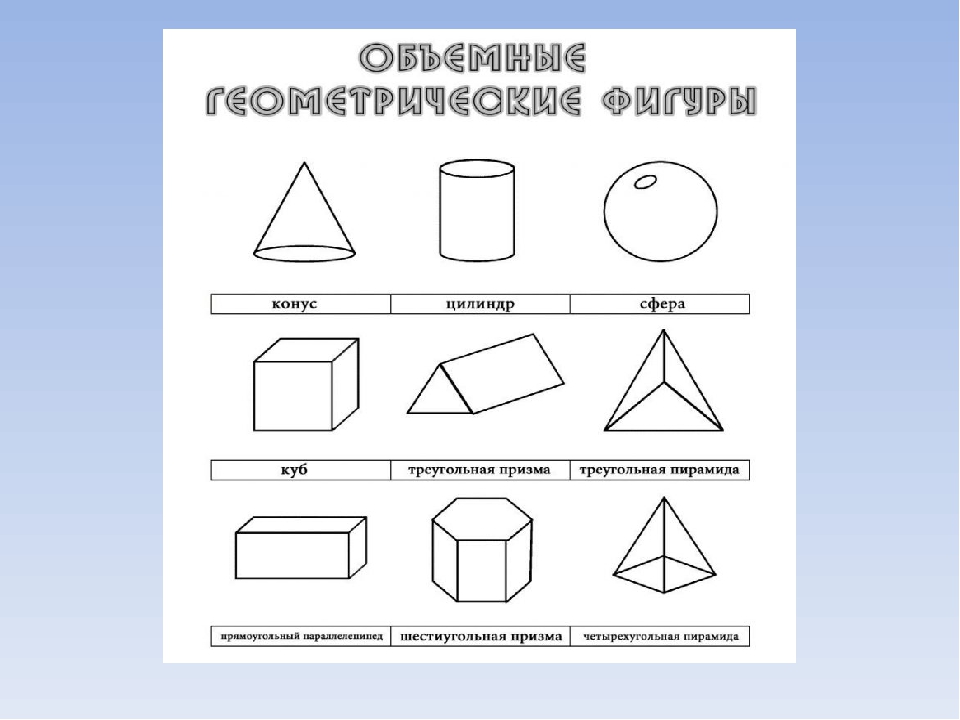 Примером замкнутой ломаной является любой многоугольник.
Примером замкнутой ломаной является любой многоугольник.
Плоскость
Как точка и прямая, так и плоскость является первичным понятием, не имеет определения и у нее нельзя увидеть ни начала, ни конца. Поэтому, при рассмотрении плоскости, мы рассматриваем только ту ее часть, которая ограничивается замкнутой ломаной линией. Таким образом, плоскостью можно считать любую гладкую поверхность. Этой поверхностью может быть лист бумаги или стола.
Угол
Фигура, которая имеет два луча и вершину, называется углом. Место соединения лучей, является вершиной этого угла, а его сторонами считаются лучи, которые этот угол образуют.
Задание:
1. Как в тексте обозначают угол?
2. Какими единицами можно измерить угол?
3. Какие бывают углы?
Параллелограмм
Параллелограмм — это четырехугольник, противолежащие стороны которого попарно параллельны.
Прямоугольник, квадрат и ромб являются частными случаями параллелограмма.
Параллелограмм, имеющий прямые углы равные 90 градусам, является прямоугольником.
Квадрат — это тот же параллелограмм, у него и углы и стороны равны.
Что до определения ромба, то это такая геометрическая фигура, все стороны которого равны.
Кроме того, следует знать, что любой квадрат является ромбом, но не каждый ромб может быть квадратом.
Трапеция
При рассмотрении такой геометрической фигуры, как трапеция, можно сказать, что в частности она, как и четырехугольник имеет одну пару параллельных противолежащих сторон и является криволинейной.
Окружность и круг
Окружность — геометрическое место точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное ненулевое расстояние, называемое её радиусом.
Треугольник
Также к простым геометрическим фигурам принадлежит и уже изучаемый вами треугольник. Это один из видов многоугольников, у которого часть плоскости ограничена тремя точками и тремя отрезками, которые соединяют эти точки попарно.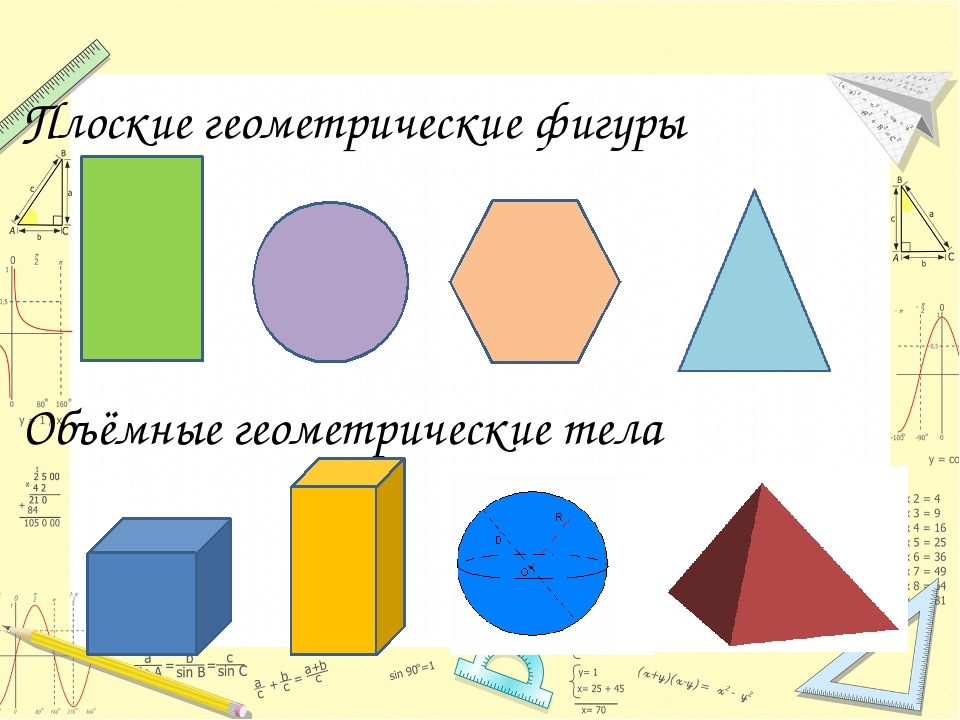 Любой треугольник имеет три вершины и три стороны.
Любой треугольник имеет три вершины и три стороны.
Задание: Какой треугольник называют вырожденным?
Многоугольник
К многоугольникам относятся геометрические фигуры разных форм, у которых замкнутая ломаная линия.
В многоугольнике все точки, которые соединяют отрезки, являются его вершинами. А отрезки, из которых состоит многоугольник, являются его сторонами.
А известно ли вам, что возникновение геометрии уходит в глубину веков и связано с развитием различных ремесел, культуры, искусства и наблюдением за окружающим миром. Да и название геометрических фигур является тому подтверждением, так как их термины, возникли не просто так, а благодаря своей схожести и подобию.
Ведь термин «трапеция» в переводе с древнегреческого языка от слова «трапезион» обозначает столик, трапеза и другие производные слова.
«Конус» произошел от греческого слова «конос», что в переводе звучит, как сосновая шишка.
«Линия» имеет латинские корни и происходит от слова «линум», в переводе это звучит, как льняная нить.
А знаете ли вы, что если взять геометрические фигуры с одинаковым периметром, то среди них обладателем самой большой площади оказался круг.
Что такое формы? [Определение, факты и пример]
Учитесь с помощью полной программы обучения математике K-5
Что такое фигуры?В геометрии форма может быть определена как форма объекта или его контур, внешняя граница или внешняя поверхность.
Все, что мы видим в окружающем мире, имеет форму. Мы можем найти различные основные формы, такие как двумерный квадрат, прямоугольник и овал или трехмерную прямоугольную призму, цилиндр и сферу в объектах, которые мы видим вокруг.Эти геометрические формы появляются в объектах, которые мы видим как кредитные карты, банкноты и монеты, кольца на пальцах, фоторамки, доски для дартса, хижины, окна, волшебные палочки, высокие здания, цветочные горшки, игрушечные поезда и воздушные шары.
Различные типы фигур
Формы можно разделить на открытые и закрытые.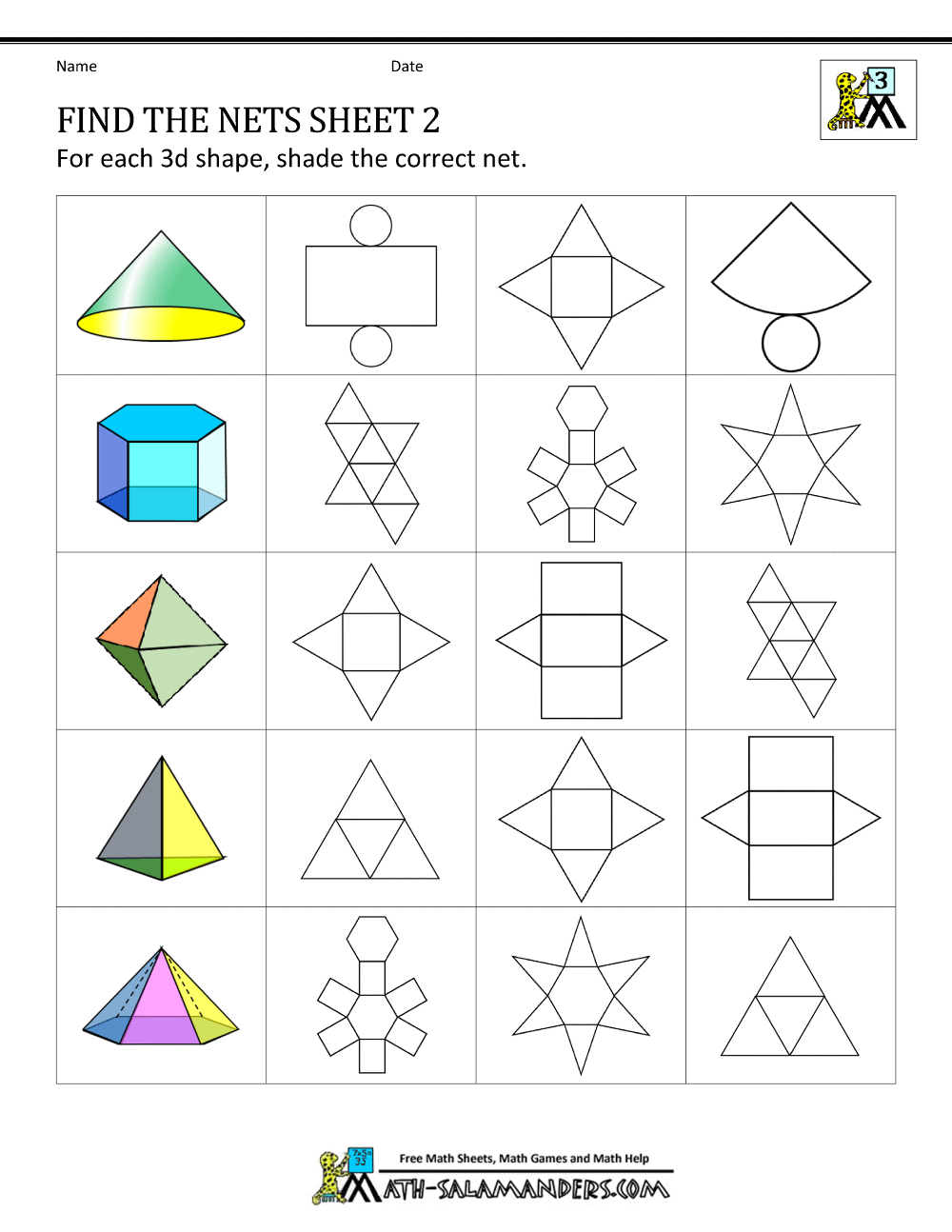
Замкнутые геометрические фигуры можно разделить на две большие категории, а именно двухмерные и трехмерные формы.
Вот список двумерных или двумерных фигур с их названиями и изображениями:
| Двумерные геометрические формы |
Вот список трехмерных или трехмерных фигур с их названиями и изображениями:
| Трехмерные геометрические фигуры |
Цвет, общий размер и ориентация, называемые не определяющими атрибутами двухмерной или трехмерной формы, никоим образом не определяют и не влияют на форму.Эти атрибуты могут изменяться без какого-либо влияния на форму.
С другой стороны, определение таких атрибутов, как количество сторон (параллельных или непараллельных, прямых или изогнутых), вершин, ребер и граней формы, является ли форма открытой или закрытой, а также угловые меры определяют форму. двухмерного или трехмерного объекта. Любое изменение этих определяющих атрибутов изменит форму.
двухмерного или трехмерного объекта. Любое изменение этих определяющих атрибутов изменит форму.
Интересные факты
|
Накидка волшебника.
Пелерина портьерная.
Кислый виноград.
Лента электрика.
И непослушный детеныш обезьяны.
Что в них общего?
Все они имеют форму.
Сделаем! Вместо того, чтобы раздавать листы-раскраски по математике своим дошкольникам и детям, поиграйте с ними в игру «покажи мне».Вы можете попросить их показать вам повседневные предметы, которые имеют двухмерную или трехмерную форму, которую вы назвали. Или вы также можете показать им разные объекты и попросить их определить двумерную или трехмерную форму, которую они видят в них.
Вы также можете дать своим детям пластилин и спички для создания двумерных или трехмерных фигур. Смоделируйте это для них.
Сопутствующая математическая лексикаИспользование геометрических фигур для описания объектов: CCSS.Math.Content.HSG-MG.A.1 — Common Core: High School
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или несколько ваших авторских прав, сообщите нам об этом, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Геометрическое и фигурное моделирование
Программное обеспечение в SCI Institute разрабатывается в тесном сотрудничестве с пользователями приложений для удовлетворения реальных потребностей в их исследовательских сообществах. Мы используем надежный, но гибкий программный процесс с полностью открытым исходным кодом для создания программных сред, которые объединяют передовые алгоритмы обработки изображений, научной визуализации и научных вычислений. Программные продукты, разработанные в SCI Institute, можно разделить на следующие категории: среды решения проблем (интегрированное моделирование, симуляция и визуализация), анализ изображений, геометрическое моделирование и моделирование форм, моделирование и визуализация.
Мы используем надежный, но гибкий программный процесс с полностью открытым исходным кодом для создания программных сред, которые объединяют передовые алгоритмы обработки изображений, научной визуализации и научных вычислений. Программные продукты, разработанные в SCI Institute, можно разделить на следующие категории: среды решения проблем (интегрированное моделирование, симуляция и визуализация), анализ изображений, геометрическое моделирование и моделирование форм, моделирование и визуализация.Среды для решения проблем | Анализ изображений | Геометрическое и фигурное моделирование | Моделирование | Визуализация
Среды для решения проблем (интегрированное моделирование, симуляция и визуализация)
ФЕВРАЛЯ
FEBio — это нелинейный решатель конечных элементов, специально разработанный для биомеханических приложений.Он предлагает сценарии моделирования, конститутивные модели и граничные условия, которые имеют отношение ко многим областям исследований в биомеханике. Все функции можно без проблем использовать вместе, что дает пользователю мощный инструмент для решения трехмерных задач вычислительной биомеханики. Программное обеспечение имеет открытый исходный код, и доступны предварительно скомпилированные исполняемые файлы для платформ Windows, Mac OS X и Linux.
Все функции можно без проблем использовать вместе, что дает пользователю мощный инструмент для решения трехмерных задач вычислительной биомеханики. Программное обеспечение имеет открытый исходный код, и доступны предварительно скомпилированные исполняемые файлы для платформ Windows, Mac OS X и Linux. Дополнительная информация и ссылки для загрузки
PreView
PreView — это препроцессор с конечными элементами (FE), который был разработан специально для постановки задач FE для FEBio.Он позволяет пользователю определять граничные условия и свойства материала в удобной графической среде.Дополнительная информация и ссылки для загрузки
PostView
Postview — это постпроцессор с конечными элементами, который предназначен для визуализации и анализа результатов анализа КЭ. Он может импортировать расширяемый формат файла графика FEBio (XPLT), а также несколько других форматов данных (например, ключевое слово LSDYNA, двоичная база данных LSDYNA, VTK). Он также предлагает способ добавления дополнительных данных к уже загруженной модели.
Дополнительная информация и ссылки для загрузки
SCIRun
SCIRun — это среда решения проблем или «вычислительная рабочая среда», в которой пользователь выбирает программные модули, которые могут быть подключены в среде визуального программирования, чтобы создать высокоуровневый рабочий поток для экспериментов. Каждый модуль предоставляет все доступные параметры, необходимые ученым для корректировки результатов моделирования или визуализации. Сети в SCIRun достаточно гибкие, чтобы можно было дублировать сети и создавать новые модули.Дополнительная информация и ссылки для загрузки
BioMesh4D
BioMesh4D — это генератор тетраэдрических сеток, способный создавать качественные сетки из нескольких материалов из сегментированных данных биомедицинских изображений.Программа BioMesh4D использует систему частиц для распределения узлов на разделяющих поверхностях, которые разделяют различные материалы, а затем использует программный пакет TetGen для создания полной тетраэдрической сетки. BioMesh4D в настоящее время интегрирован с SCIRun и использует систему SCIRun для визуализации промежуточных результатов.
BioMesh4D в настоящее время интегрирован с SCIRun и использует систему SCIRun для визуализации промежуточных результатов. Дополнительная информация и ссылки для загрузки
Forward / Inverse Toolkit
SCIRun ECG Forward / Inverse Toolkit — это набор модулей и сетей в системе SCIRun, которые можно использовать для решения задач прямой и обратной электрокардиографии.Дополнительная информация и ссылки для загрузки
Стимулятор мозга
BrainStimulator — это набор сетей, которые используются в SCIRun для моделирования стимуляции мозга, такой как транскраниальная стимуляция постоянным током (tDCS) и магнитная транскраниальная стимуляция (TMS).Дополнительная информация и ссылки для загрузки
Nektar ++
Nektar ++ — это программный фреймворк с открытым исходным кодом, предназначенный для поддержки разработки высокопроизводительных масштабируемых решателей для уравнений в частных производных (и, в частности, законов сохранения) с использованием спектрального метода / метода элементов HP. Методы высокого порядка становятся все более популярными в нескольких инженерных и биомедицинских приложениях из-за их более высокой точности по сравнению с методами низкого порядка при сниженных вычислительных затратах для заданного числа степеней свободы. Однако их распространение часто ограничивается их сложностью, что затрудняет реализацию и использование этих методов. Nektar ++ — это инициатива по преодолению этого ограничения путем инкапсуляции математических сложностей лежащего в основе метода в эффективную структуру C ++, что делает методы более доступными для более широкого научного и промышленного сообщества.
Методы высокого порядка становятся все более популярными в нескольких инженерных и биомедицинских приложениях из-за их более высокой точности по сравнению с методами низкого порядка при сниженных вычислительных затратах для заданного числа степеней свободы. Однако их распространение часто ограничивается их сложностью, что затрудняет реализацию и использование этих методов. Nektar ++ — это инициатива по преодолению этого ограничения путем инкапсуляции математических сложностей лежащего в основе метода в эффективную структуру C ++, что делает методы более доступными для более широкого научного и промышленного сообщества. Программное обеспечение поддерживает множество методов дискретизации и стратегий реализации, поддерживает исследования методов, а также вычисления, ориентированные на приложения, а многоуровневая структура инфраструктуры позволяет пользователю охватить столько или меньше сложности, сколько им нужно. Библиотеки охватывают математические конструкции методов спектральных элементов / элементов HP, в то время как связанный набор предварительно написанных решателей PDE предоставляет готовые функциональные возможности уровня приложения и шаблон для пользователей, которые хотят разрабатывать решения для решения вопросов в своих собственные научные области.
Дополнительная информация и ссылки для загрузки
PIDX
Основное внимание в этой работе уделяется разработке структуры сквозного перемещения данных с адаптивным разрешением, которая обеспечивает эффективный ввод-вывод, поддерживая при этом весь спектр современного оборудования для высокопроизводительных вычислений. Это достигается за счет разработки технологии высокомасштабируемого и настраиваемого параллельного ввода-вывода, применимого как к традиционным параллельным форматам данных, так и к форматам данных с различным разрешением, которые непосредственно подходят для анализа и визуализации. Чтобы продемонстрировать эффективность подхода, разработана новая библиотека (PIDX), которая легко настраивается и способна выполнять параллельный ввод-вывод с адаптивным разрешением для формата данных с несколькими разрешениями.Хранение и ввод-вывод с адаптивным разрешением, которые позволяют получать доступ к подмножествам моделирования с различными пространственными разрешениями, могут значительно улучшить как производительность хранения, так и время ввода-вывода. Библиотека предоставляет набор параметров, которые контролируют формат хранения и характер агрегирования данных в сети; далее строится модель на основе машинного обучения, которая настраивает эти параметры для максимальной пропускной способности. Эта работа эмпирически продемонстрирована путем демонстрации масштабирования параллельного ввода-вывода до 768K ядер в рамках, достаточно гибкой для обработки ввода-вывода с адаптивным разрешением
Библиотека предоставляет набор параметров, которые контролируют формат хранения и характер агрегирования данных в сети; далее строится модель на основе машинного обучения, которая настраивает эти параметры для максимальной пропускной способности. Эта работа эмпирически продемонстрирована путем демонстрации масштабирования параллельного ввода-вывода до 768K ядер в рамках, достаточно гибкой для обработки ввода-вывода с адаптивным разрешением Дополнительная информация и ссылки на загрузки
Unitah
Программный пакет Uintah представляет собой набор библиотек и приложений для моделирования и анализа сложных химических и физических реакций.Эти реакции моделируются путем решения уравнений в частных производных на структурированных адаптивных сетках с использованием сотен и тысяч процессоров (хотя моделирование меньшего размера также может выполняться на настольном компьютере ученого). Ключевые программные приложения были разработаны для исследования мелких деталей металлических контейнеров (содержащих энергетические материалы), встроенных в большие углеводородные пожары. Базовые технологии Uintah привели к новым методам понимания вихревых возгораний в больших бассейнах, а также к новым методам моделирования взаимодействия жидкости и структуры.Программное обеспечение является универсальным по своей природе, и диапазон областей моделирования продолжает расширяться за пределы первоначальной направленности инициативы C-SAFE.
Базовые технологии Uintah привели к новым методам понимания вихревых возгораний в больших бассейнах, а также к новым методам моделирования взаимодействия жидкости и структуры.Программное обеспечение является универсальным по своей природе, и диапазон областей моделирования продолжает расширяться за пределы первоначальной направленности инициативы C-SAFE. Дополнительная информация и ссылки для загрузки
Анализ изображений
AtlasWerks
AtlasWerks — это программный пакет с открытым исходным кодом (лицензия BSD) для создания медицинских атласов изображений. Такие атласы являются широко используемым инструментом для сегментации изображений, а деформации, генерируемые с помощью этих методов, используются для статистического анализа формы мозга для выявления закономерностей изменений, связанных с прогрессированием заболевания.Программный пакет AtlasWerks обеспечивает эффективную реализацию алгоритмов нелинейной деформации на ЦП и графическом процессоре на основе структуры Large Deformation Diffeomorphic Metric Mapping (LDMM) для отдельных машин и кластеров, интерфейсов командной строки для создания атласов и деформации, а также ряда служебных программ для обработки 3D. данные медицинских изображений.
данные медицинских изображений. Дополнительная информация и ссылки для загрузки
Deformetrica
Deformetrica — это программа для статистического анализа данных 2D и 3D форм.По сути, он вычисляет деформации двухмерного или трехмерного окружающего пространства, которые, в свою очередь, деформируют любой объект, встроенный в это пространство, независимо от того, является ли этот объект кривой, поверхностью, структурированным или неструктурированным набором точек или любой их комбинацией.Дополнительная информация и ссылки для загрузки
Seg3D
Seg3D — это бесплатный инструмент для сегментации и обработки томов, разработанный Центром интегративных биомедицинских вычислений NIH Института научных вычислений и визуализации (SCI) Университета штата Юта.Seg3D сочетает в себе гибкий интерфейс ручной сегментации с мощными алгоритмами обработки и сегментации многомерных изображений из Insight Toolkit. Пользователи могут исследовать и маркировать объемные изображения, используя окна объемного рендеринга и ортогональные срезы.
Дополнительная информация и ссылки для загрузки
FluoRender
FluoRender — это интерактивный инструмент для визуализации данных конфокальной микроскопии. Он сочетает в себе рендеринг данных многоканального объема и данных полигональной сетки, где свойства каждого набора данных можно настраивать независимо и быстро.Инструмент разработан специально для нейробиологов, позволяя им лучше визуализировать конфокальные данные от флуоресцентно окрашенного мозга, но он также полезен для других биологических образцов.Дополнительная информация и ссылки для загрузки
ImageVis3D
ImageVis3D — это новая программа объемного рендеринга, разработанная Центром интегративных биомедицинских вычислений NIH / NIGMS (CIBC). Основные цели дизайна ImageVis3D: простота, масштабируемость и интерактивность. Простота достигается за счет нового пользовательского интерфейса, который обеспечивает беспрецедентный уровень гибкости.Масштабируемость и интерактивность означают, что пользователи могут интерактивно исследовать наборы данных размером в терабайт на оборудовании, начиная от мобильных устройств и заканчивая высокопроизводительными графическими рабочими станциями. Наконец, открытый исходный код, а также строгий покомпонентный дизайн позволяют разработчикам не только расширять сам ImageVis3D, но и повторно использовать его части, такие как ядро визуализации.
Наконец, открытый исходный код, а также строгий покомпонентный дизайн позволяют разработчикам не только расширять сам ImageVis3D, но и повторно использовать его части, такие как ядро визуализации. Дополнительная информация и ссылки для загрузки
Slicer
3D Slicer — это программная платформа с открытым исходным кодом для информатики медицинских изображений, обработки изображений и трехмерной визуализации.Созданный более двух десятилетий при поддержке Национальных институтов здравоохранения и мирового сообщества разработчиков, Slicer предоставляет бесплатные мощные кроссплатформенные инструменты обработки для врачей, исследователей и широкой публики.Дополнительная информация и ссылки для загрузки
FiberViewer
Fiber ViewerLight — это приложение C ++ с открытым исходным кодом для анализа пучков волокон. Он предоставляет:— Несколько методов кластеризации: методы длины, силы тяжести, Хаусдорфа и среднего, а также алгоритм нормализованного разреза.
— 3D визуализация волокон
— Выбор 3D плоскости
FiberViewerLight доступен как расширение 3D Slicer
Дополнительная информация и ссылки для загрузки
Набор инструментов NCR
Набор инструментов NCR теперь включен в Seg3D. Toolset — это набор программных инструментов для реконструкции и визуализации нейронных схем по данным электронной микроскопии. Этот набор инструментов включает Iris, Ir-mosaic, Ir-tweak и Ir-tools.
Toolset — это набор программных инструментов для реконструкции и визуализации нейронных схем по данным электронной микроскопии. Этот набор инструментов включает Iris, Ir-mosaic, Ir-tweak и Ir-tools. Дополнительная информация и ссылки для загрузки
STCR
STCR — это программа на основе Matlab для восстановления радиальных данных DCE с недостаточной дискретизацией с помощью методов Compressed Sensing.Дополнительная информация и ссылки для загрузки
Teem
Teem — это скоординированная группа библиотек для представления, обработки и визуализации научных растровых данных. Teem включает инструменты командной строки, которые позволяют быстро применять библиотечные функции к файлам и потокам без написания кода. Наиболее важные и полезные библиотеки в Teem:• Nrrd (и инструмент командной строки unu поверх него) поддерживает ряд операций для преобразования N-мерных растровых данных (повторная выборка, обрезка, срез, проект, гистограмма и т. Д.
 ) .), а также файловый формат NRRD для хранения массивов и их метаинформации.
) .), а также файловый формат NRRD для хранения массивов и их метаинформации. • Gage: быстрые измерения на основе свертки в произвольных точках в наборах объемных данных (скалярные, векторные, тензорные и т. Д.)
• Mite: многопоточный объемный рендеринг с отливкой лучей с передаточными функциями на основе любого количества, которое Gage может измерить
• Десять: для оценки, обработки и визуализации полей тензора диффузии, включая методы волоконной трактографии.
Дополнительная информация и ссылки для загрузки
Vispack
Vispack — это библиотека C ++, разработанная для обработки объемных изображений и поверхностей.Мы будем использовать его в качестве основы для проектов в этом курсе. Vispack использует стандартные функции C ++, такие как шаблоны, наследование и стандартную библиотеку шаблонов (STD). По крайней мере, Vispack предоставляет средства чтения и записи изображений, а также структуру данных для доступа к данным изображения. Он также предоставляет ряд методов обработки изображений. Vispack не предоставляет никакого графического интерфейса для своей функциональности — это строго структуры данных, алгоритмы и ввод-вывод изображений.
Vispack не предоставляет никакого графического интерфейса для своей функциональности — это строго структуры данных, алгоритмы и ввод-вывод изображений. Дополнительная информация и ссылки для загрузки
CHM
Каскадная иерархическая модель — это структура сегментации изображений, которая изучает контекстную информацию в иерархической структуре.На каждом уровне иерархии классификатор обучается на основе субдискретизированного входного изображения и выходных данных предыдущих уровней. Затем наша модель включает полученную контекстную информацию с несколькими разрешениями в классификатор для сегментации входного изображения с исходным разрешением. Мы повторяем эту процедуру, каскадируя иерархическую структуру для повышения точности сегментации.Дополнительная информация и ссылки для загрузки
Геометрическое и фигурное моделирование
Тесак
Cleaver — это API и приложение для создания тетраэдрической сетки из нескольких материалов.Cleaver создает соответствующие тетраэдрические сетки для многоматериальных или многофазных объемных данных. И геометрическая точность, и качество элементов ограничены. Этот метод основан на трафарете и основан на структуре октодерева для обеспечения грубого уровня градации в областях однородности.
И геометрическая точность, и качество элементов ограничены. Этот метод основан на трафарете и основан на структуре октодерева для обеспечения грубого уровня градации в областях однородности. Дополнительная информация и ссылки для загрузки
BioMesh4D
BioMesh4D — это генератор тетраэдрических сеток, способный создавать качественные сетки из нескольких материалов из сегментированных данных биомедицинских изображений.Программа BioMesh4D использует систему частиц для распределения узлов на разделяющих поверхностях, которые разделяют различные материалы, а затем использует программный пакет TetGen для создания полной тетраэдрической сетки. BioMesh4D в настоящее время интегрирован с SCIRun и использует систему SCIRun для визуализации промежуточных результатов.Дополнительная информация и ссылки для загрузки
Deformetrica
Deformetrica — это программа для статистического анализа данных 2D и 3D форм. По сути, он вычисляет деформации двухмерного или трехмерного окружающего пространства, которые, в свою очередь, деформируют любой объект, встроенный в это пространство, независимо от того, является ли этот объект кривой, поверхностью, структурированным или неструктурированным набором точек или любой их комбинацией.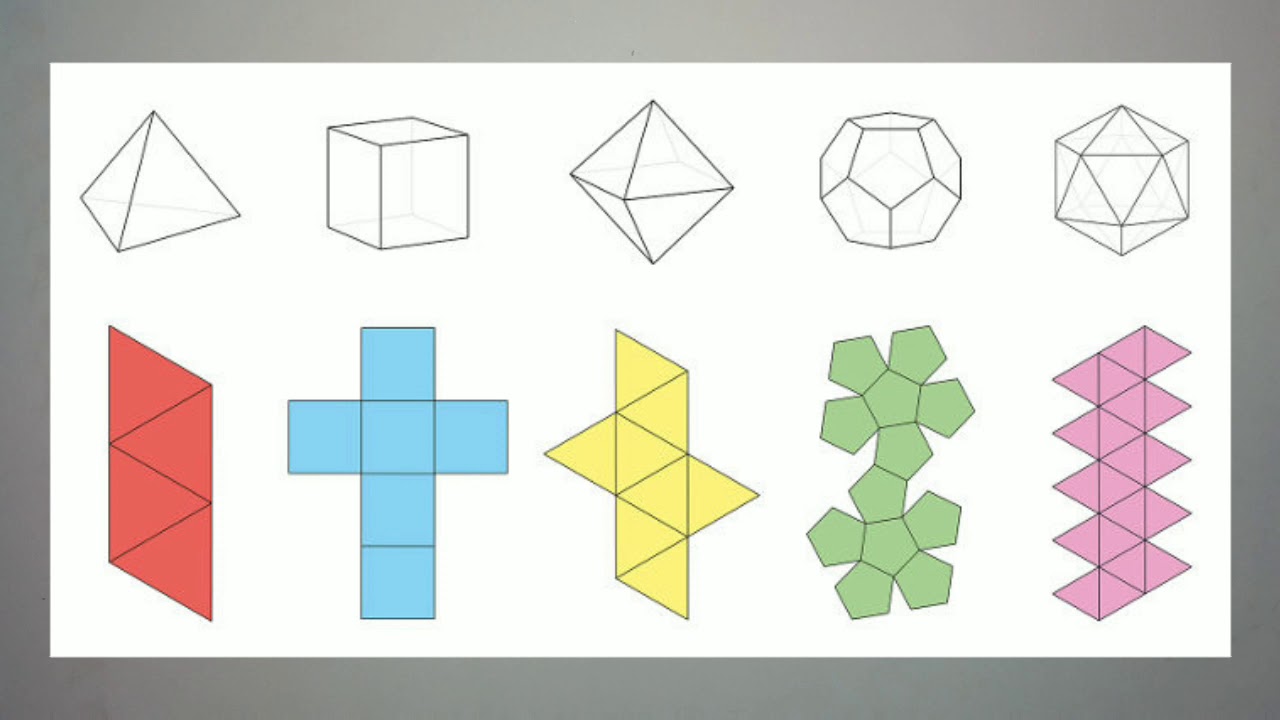
Дополнительная информация и ссылки для загрузки
Shapeworks
Программное обеспечение ShapeWorks представляет собой распространение с открытым исходным кодом нового метода построения компактных статистических точечных моделей ансамблей аналогичных форм, который не зависит от какой-либо конкретной параметризации поверхности. Этот метод требует очень небольшой предварительной обработки или настройки параметров и применим к широкому кругу задач анализа формы, включая немногообразные поверхности и объекты произвольной топологии. Предлагаемая оптимизация точки соответствия использует минимизацию на основе энтропии, которая уравновешивает простоту модели (компактность) с точностью представлений поверхностей.Программное обеспечение ShapeWorks включает инструменты для предварительной обработки данных, вычисления точечных моделей форм и визуализации результатов.Дополнительная информация и ссылки для загрузки
ExoshapeAccel
ExoshapeAccel — это приложение C / C ++ для оценки непрерывной эволюции дискретного набора форм, разработанное для создания реалистичных анатомических траекторий.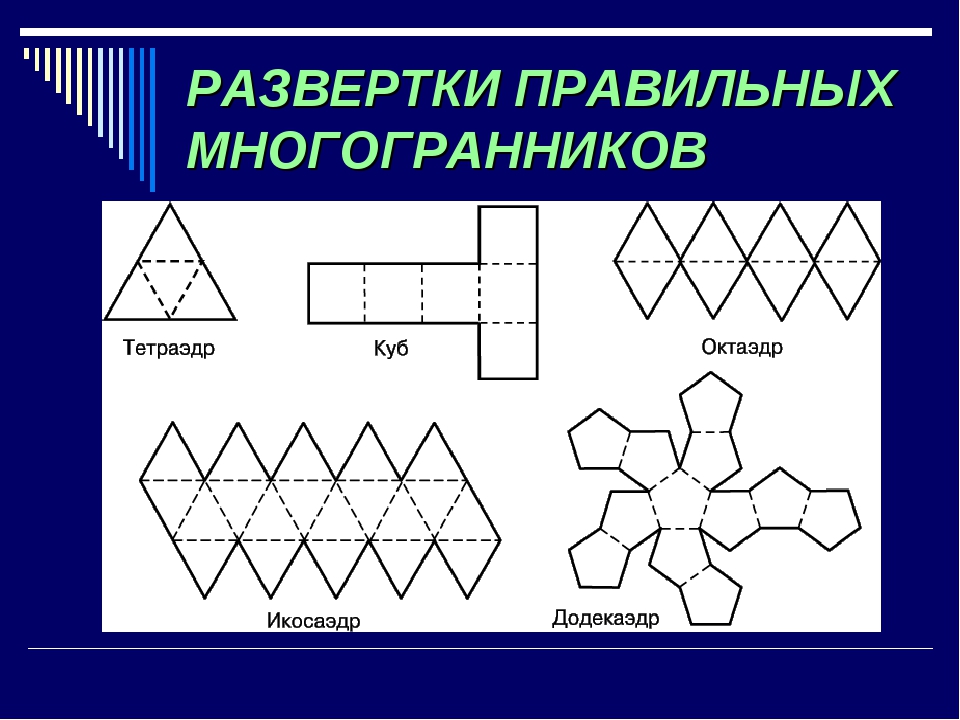
Дополнительная информация и ссылки для загрузки
Simulation
FluoRender
FluoRender — это интерактивный инструмент для визуализации данных конфокальной микроскопии.Он сочетает в себе рендеринг данных многоканального объема и данных полигональной сетки, где свойства каждого набора данных можно настраивать независимо и быстро. Инструмент разработан специально для нейробиологов, позволяя им лучше визуализировать конфокальные данные от флуоресцентно окрашенного мозга, но он также полезен для других биологических образцов.Дополнительная информация и ссылки для загрузки
GPUTUM
В различных областях применения от геофизики до биомедицины используется та или иная форма математической модели Гамильтона-Якоби (HJ), поскольку эти модели обеспечивают естественные средства выражения природоохранных свойств.Две наиболее распространенные модели HJ, встречающиеся в литературе, — это уравнение Эйконала (статическая модель HJ, основанная на принципе Ферма для определения минимальных путей) и уравнения набора уровней (модель HJ, зависящая от времени, используемая для решения проблем с движущимся интерфейсом).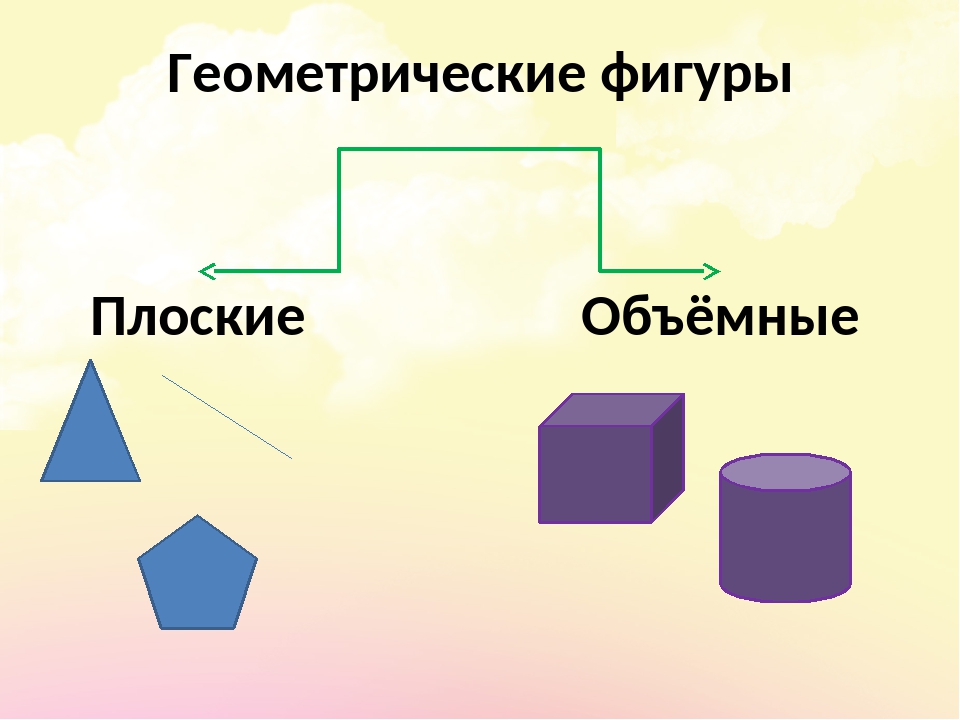 Обе эти системы уравнений могут быть очень эффективно решены на структурированных (решетчатых) сетках с соответствующими конечно-разностными схемами, основанными на противотоке. Кроме того, были достигнуты большие успехи в отображении эффективных составов H-J структурированной сетки, ориентированной на ЦП, на стандартные потоковые архитектуры, такие как графические процессоры.Тем не менее, многие ученые-прикладники желают использовать составы HJ из-за их свойств сохранения, в то время как их приложения требуют использования неструктурированных сеток из-за необходимости геометрического моделирования (как для границ, так и для интерфейсов). Хотя формулировки HJ существуют частично для неструктурированных сеток, их отображение на графические процессоры нетривиально из-за индексации (и соответствующих структур данных), необходимой для нерешетчатых сеток.
Обе эти системы уравнений могут быть очень эффективно решены на структурированных (решетчатых) сетках с соответствующими конечно-разностными схемами, основанными на противотоке. Кроме того, были достигнуты большие успехи в отображении эффективных составов H-J структурированной сетки, ориентированной на ЦП, на стандартные потоковые архитектуры, такие как графические процессоры.Тем не менее, многие ученые-прикладники желают использовать составы HJ из-за их свойств сохранения, в то время как их приложения требуют использования неструктурированных сеток из-за необходимости геометрического моделирования (как для границ, так и для интерфейсов). Хотя формулировки HJ существуют частично для неструктурированных сеток, их отображение на графические процессоры нетривиально из-за индексации (и соответствующих структур данных), необходимой для нерешетчатых сеток. Дополнительная информация и ссылки для загрузки
SCIRun
SCIRun — это среда решения проблем или «вычислительная рабочая среда», в которой пользователь выбирает программные модули, которые могут быть подключены в среде визуального программирования, чтобы создать высокоуровневый рабочий поток для экспериментов.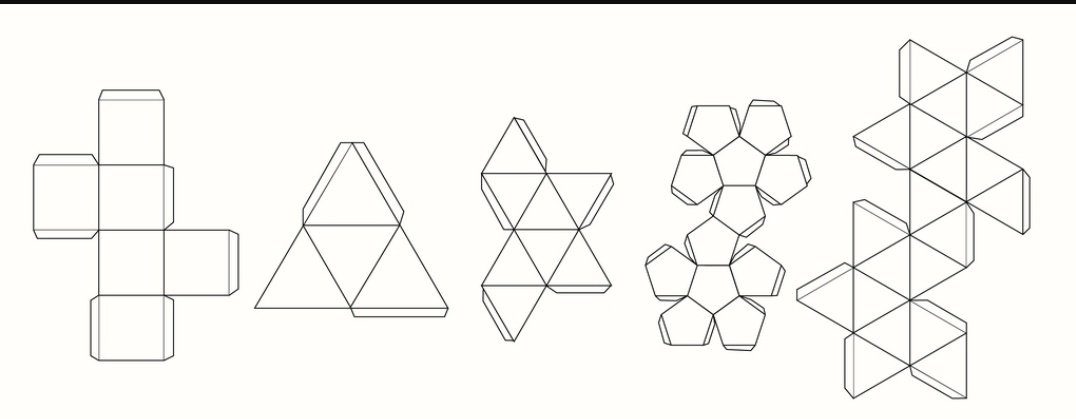 Каждый модуль предоставляет все доступные параметры, необходимые ученым для корректировки результатов моделирования или визуализации. Сети в SCIRun достаточно гибкие, чтобы можно было дублировать сети и создавать новые модули.
Каждый модуль предоставляет все доступные параметры, необходимые ученым для корректировки результатов моделирования или визуализации. Сети в SCIRun достаточно гибкие, чтобы можно было дублировать сети и создавать новые модули. Дополнительная информация и ссылки для загрузки
FEBio
FEBio — это нелинейный решатель конечных элементов, специально разработанный для биомеханических приложений. Он предлагает сценарии моделирования, конститутивные модели и граничные условия, которые имеют отношение ко многим областям исследований в биомеханике.Все функции можно без проблем использовать вместе, что дает пользователю мощный инструмент для решения трехмерных задач вычислительной биомеханики. Программное обеспечение имеет открытый исходный код, и доступны предварительно скомпилированные исполняемые файлы для платформ Windows, Mac OS X и Linux.Дополнительная информация и ссылки для скачивания
Uintah
Программный пакет Uintah представляет собой набор библиотек и приложений для моделирования и анализа сложных химических и физических реакций.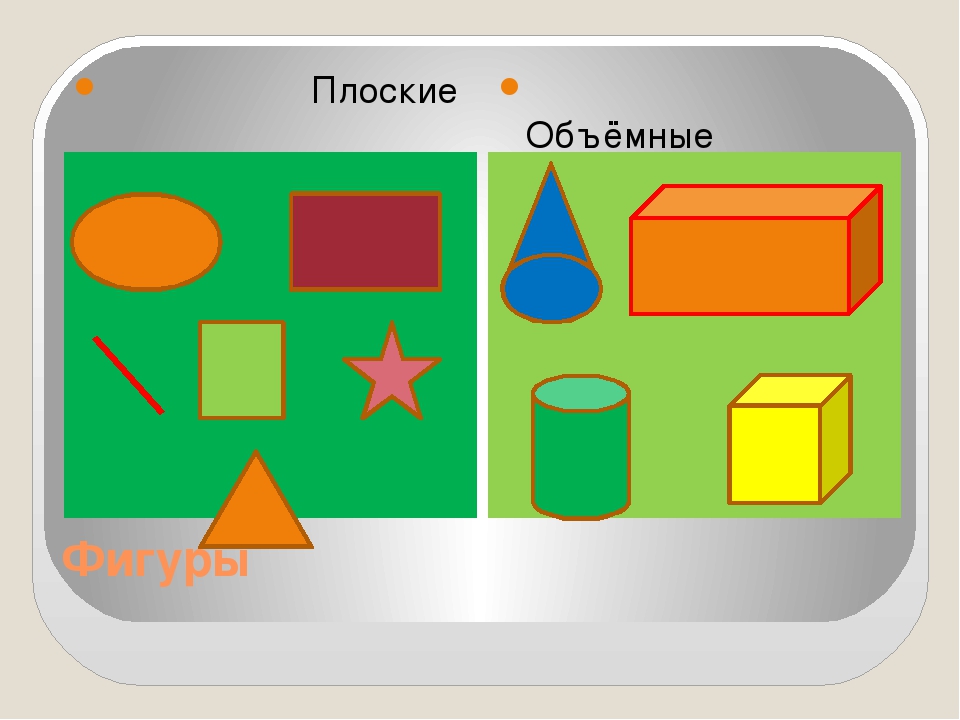 Эти реакции моделируются путем решения уравнений в частных производных на структурированных адаптивных сетках с использованием сотен и тысяч процессоров (хотя моделирование меньшего размера также может выполняться на настольном компьютере ученого).Ключевые программные приложения были разработаны для исследования мелких деталей металлических контейнеров (содержащих энергетические материалы), встроенных в большие углеводородные пожары. Базовые технологии Uintah привели к новым методам понимания вихревых возгораний в больших бассейнах, а также к новым методам моделирования взаимодействия жидкости и структуры. Программное обеспечение является универсальным по своей природе, и диапазон областей моделирования продолжает расширяться за пределы первоначальной направленности инициативы C-SAFE.
Эти реакции моделируются путем решения уравнений в частных производных на структурированных адаптивных сетках с использованием сотен и тысяч процессоров (хотя моделирование меньшего размера также может выполняться на настольном компьютере ученого).Ключевые программные приложения были разработаны для исследования мелких деталей металлических контейнеров (содержащих энергетические материалы), встроенных в большие углеводородные пожары. Базовые технологии Uintah привели к новым методам понимания вихревых возгораний в больших бассейнах, а также к новым методам моделирования взаимодействия жидкости и структуры. Программное обеспечение является универсальным по своей природе, и диапазон областей моделирования продолжает расширяться за пределы первоначальной направленности инициативы C-SAFE. Дополнительная информация и ссылки для загрузки
Pfeifer
Платформа предварительной обработки для электрограмм, периодически проверяемых на основе экспериментальных записей (PFEIFER) — это графический интерфейс пользователя MATLAB, предназначенный для обработки биоэлектрических сигналов, полученных в результате экспериментов.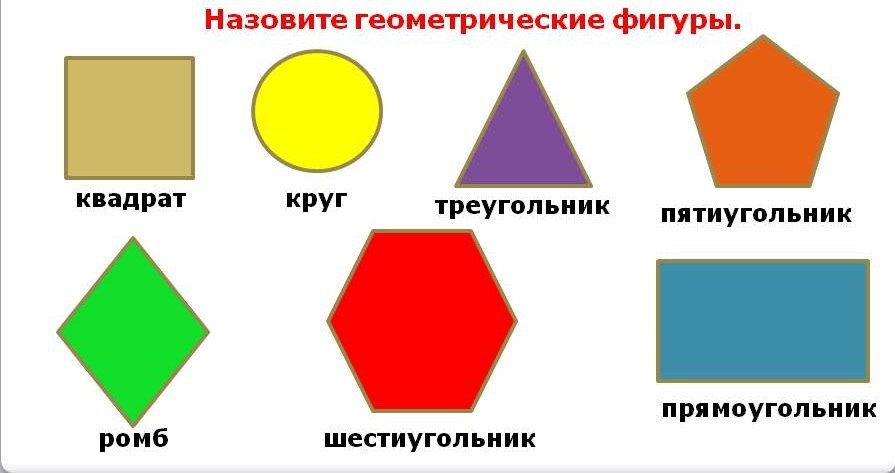
Дополнительная информация и ссылки для загрузки
Визуализация
MizBee
MizBee — это многомасштабный браузер для синтенизации, предназначенный для изучения природоохранных отношений в сравнительных данных геномики.Используя параллельные представления, MizBee обеспечивает эффективный просмотр данных в различных масштабах, от генома до гена. Дизайн MizBee основан на принципах восприятия и включает в себя несколько методов, таких как объединение краев и наслоение для улучшения визуальных подсказок о взаимосвязях сохранения, связанных с близостью, размером, сходством и ориентацией.Дополнительная информация и ссылки для загрузки
Pathline
Pathline — это инструмент визуализации для сравнительной функциональной геномики, который поддерживает анализ сразу трех типов биологических данных: функциональные данные, такие как измерения активности генов; данные о путях, которые представляют собой серию реакций внутри клеточного процесса; и филогенетические данные, описывающие родственные связи между видами.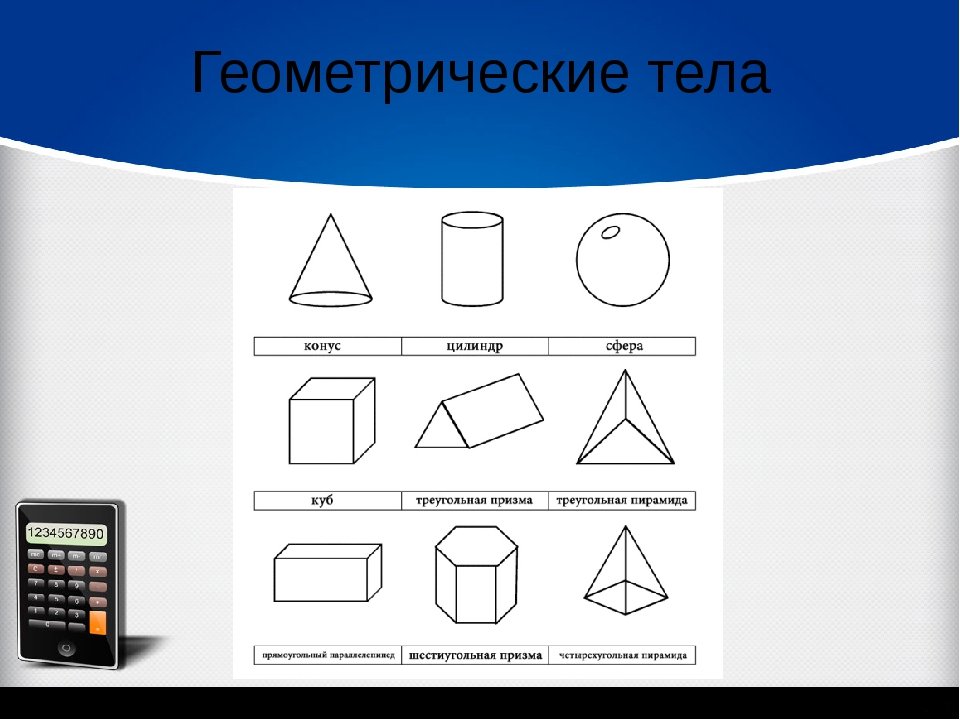
Дополнительная информация и ссылки для загрузки
MultiSum
MulteeSum — это система визуализации, которая поддерживает проверку и обработку наборов данных, показывающих экспрессию генов с течением времени, в сочетании с пространственным расположением ячеек, в которых экспрессируются гены, — это первый инструмент для поддержки сравнения нескольких таких наборов данных. MulteeSum является частью общей и гибкой структуры, которая позволяет биологам исследовать результаты вычислений, которые смешивают пространственную информацию, измерения экспрессии генов с течением времени и данные от нескольких видов или организмов.MulteeSum был разработан для поддержки исследовательской деятельности биологов, изучающих развивающиеся эмбрионы дрозофилы.Дополнительная информация и ссылки для загрузки
на сайте
inSite — это инструмент для интерактивной визуализации сайтов связывания в нескольких областях генома. Различные типы факторов транскрипции кодируются цветом с интерактивной цветной легендой, определяемой пользователем.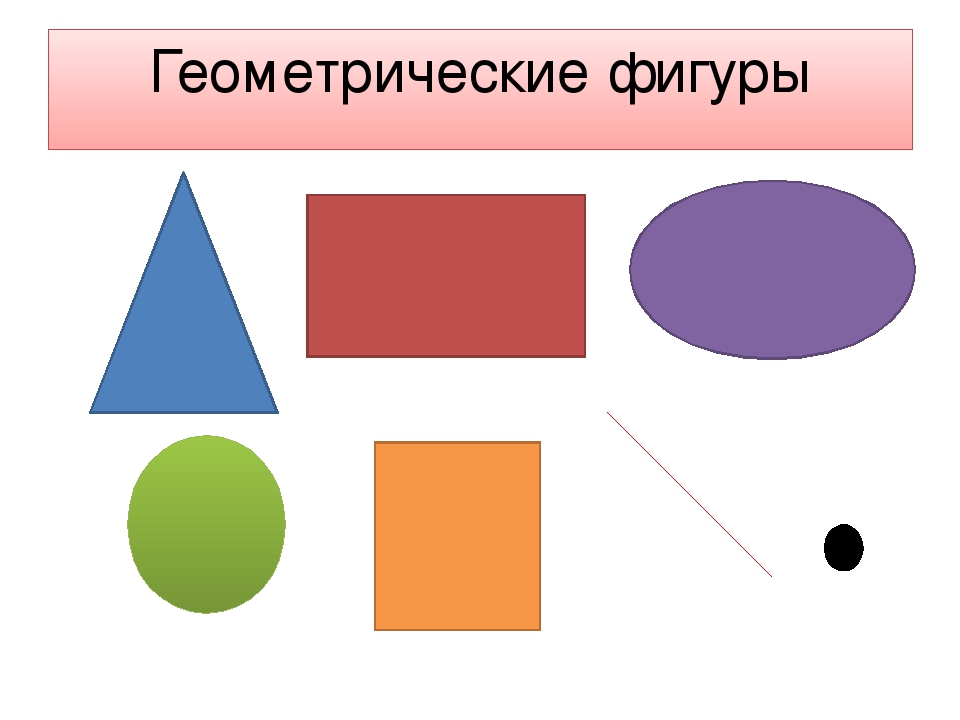
Дополнительная информация и ссылки для загрузки
HDVis
Важной целью анализа научных данных является понимание поведения системы или процесса на основе образца системы.Во многих случаях можно наблюдать как входные параметры, так и выходы системы, и охарактеризовать систему как многомерную функцию. Такие наборы данных возникают, например, при большом численном моделировании, в качестве энергетических ландшафтов в задачах оптимизации или при анализе данных изображения, относящихся к биологическим или медицинским параметрам. В этой статье предлагается подход к анализу и визуализации таких наборов данных. Предлагаемый метод сочетает в себе топологические и геометрические методы для обеспечения интерактивной визуализации дискретно выбранных многомерных скалярных полей.Метод основан на сегментации пространства параметров с использованием приближенного комплекса Морса-Смейла на облаке точечных выборок. Для каждого кристалла комплекса Морса-Смейла регрессия параметров системы относительно выхода дает кривую в пространстве параметров. Результатом является упрощенное геометрическое представление комплекса Морса-Смейла во входной области большой размерности. Наконец, геометрическое представление встроено в 2D с использованием уменьшения размеров, чтобы обеспечить платформу визуализации.Геометрические свойства регрессионных кривых позволяют визуализировать дополнительную информацию о каждом кристалле, такую как локальная и глобальная форма, ширина, длина и плотность выборки. Метод проиллюстрирован на нескольких синтетических примерах двумерных функций. Два варианта использования с использованием наборов данных из репозитория машинного обучения UCI демонстрируют полезность предлагаемого подхода на реальных данных. Наконец, в сотрудничестве с экспертами в предметной области предложенный метод применяется к двум научным задачам.Анализ параметров моделирования климата и их связи с прогнозируемым глобальным потоком энергии и концентрациями химических веществ в моделировании горения и их интеграция с температурой.
Результатом является упрощенное геометрическое представление комплекса Морса-Смейла во входной области большой размерности. Наконец, геометрическое представление встроено в 2D с использованием уменьшения размеров, чтобы обеспечить платформу визуализации.Геометрические свойства регрессионных кривых позволяют визуализировать дополнительную информацию о каждом кристалле, такую как локальная и глобальная форма, ширина, длина и плотность выборки. Метод проиллюстрирован на нескольких синтетических примерах двумерных функций. Два варианта использования с использованием наборов данных из репозитория машинного обучения UCI демонстрируют полезность предлагаемого подхода на реальных данных. Наконец, в сотрудничестве с экспертами в предметной области предложенный метод применяется к двум научным задачам.Анализ параметров моделирования климата и их связи с прогнозируемым глобальным потоком энергии и концентрациями химических веществ в моделировании горения и их интеграция с температурой. Дополнительная информация и ссылки для загрузки
map3d
Map3d — это приложение для научной визуализации, разработанное в CVRTI для отображения и редактирования сложных трехмерных геометрических моделей и скалярных данных, связанных с этими моделями. map3d изначально был написан на ANSI-C с использованием графической библиотеки (GL) от Silicon Graphics Inc.Интерфейс map3d обеспечивает интерактивное отображение как геометрии, так и данных, назначенных элементам этой геометрии. Программа может считывать несколько поверхностей, каждая из которых имеет несколько связанных файлов потенциальных / текущих данных.
map3d изначально был написан на ANSI-C с использованием графической библиотеки (GL) от Silicon Graphics Inc.Интерфейс map3d обеспечивает интерактивное отображение как геометрии, так и данных, назначенных элементам этой геометрии. Программа может считывать несколько поверхностей, каждая из которых имеет несколько связанных файлов потенциальных / текущих данных. Дополнительная информация и ссылки для загрузки
EpiCanvas
Карта погоды по инфекционным заболеваниям EpiCanvasEpiCanvas загружает данные из файловой базы данных SQLite.
База данных состоит из трех таблиц:
• данные: ваши данные в форме (id, отчётная_дата)
• база знаний: вы помечаете теги в форме (tag_id, tag_name, tag_type, reportable)
• tagged_data: многие ко многим сопоставление данных и тегов (item_id, tag_id)
Дополнительная информация и ссылки для загрузки
VisTrails
VisTrails — это научная система управления рабочим процессом и происхождением с открытым исходным кодом, которая поддерживает исследование и визуализацию данных.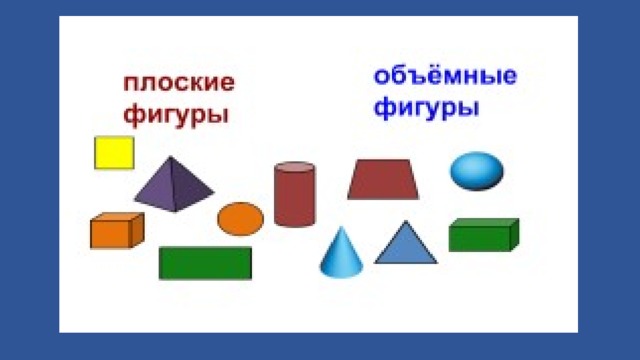
VisTrails предоставляет общую инфраструктуру, которую можно комбинировать с существующими системами и библиотеками. Официальные выпуски поставляются с несколькими пакетами, включая VTK, matplotlib и ImageMagick. Система написана на Python / Qt и работает на Mac, Unix и Windows.
Дополнительная информация и ссылки для загрузки
ElVis
ElVis — это система визуализации, созданная для точной и интерактивной визуализации скалярных полей, созданных с помощью моделирования методом конечных элементов спектра / HP высокого порядка.Дополнительная информация и ссылки для загрузки
Pathfinder
Pathfinder — это инструмент визуального анализа для исследования путей в больших сетях, созданный с помощью Caleydo Web.Анализ путей в графах очень актуален во многих областях. Обычно задачи, связанные с путями, выполняются в компоновках узловых ссылок. К сожалению, макеты графов часто не масштабируются до размеров многих реальных сетей. Кроме того, многие сети являются многомерными, то есть содержат богатые наборы атрибутов, связанных с узлами и ребрами.
 Эти атрибуты часто имеют решающее значение при оценке путей, но прямая визуализация атрибутов в макете графа усугубляет проблему масштабируемости. В этой статье мы представляем решения визуального анализа, посвященные задачам, связанным с путями, в больших и многомерных графах.Мы показываем, что, сосредоточив внимание на путях, мы можем решить проблему масштабируемости многомерной визуализации графов, снабдив аналитиков мощным инструментом для исследования больших графов. Мы представляем Pathfinder, технику, которая предоставляет визуальные методы для запроса путей с учетом различных ограничений. Результирующий набор путей визуализируется как в ранжированном списке, так и в виде диаграммы узловых связей. Для путей в списке мы отображаем обширные данные атрибутов, связанных с узлами и ребрами, а диаграмма узел-связь обеспечивает топологический контекст.Пути могут быть ранжированы на основе топологических свойств, таких как длина пути или средняя степень узла, а также оценки, полученные на основе данных атрибутов.
Эти атрибуты часто имеют решающее значение при оценке путей, но прямая визуализация атрибутов в макете графа усугубляет проблему масштабируемости. В этой статье мы представляем решения визуального анализа, посвященные задачам, связанным с путями, в больших и многомерных графах.Мы показываем, что, сосредоточив внимание на путях, мы можем решить проблему масштабируемости многомерной визуализации графов, снабдив аналитиков мощным инструментом для исследования больших графов. Мы представляем Pathfinder, технику, которая предоставляет визуальные методы для запроса путей с учетом различных ограничений. Результирующий набор путей визуализируется как в ранжированном списке, так и в виде диаграммы узловых связей. Для путей в списке мы отображаем обширные данные атрибутов, связанных с узлами и ребрами, а диаграмма узел-связь обеспечивает топологический контекст.Пути могут быть ранжированы на основе топологических свойств, таких как длина пути или средняя степень узла, а также оценки, полученные на основе данных атрибутов. Pathfinder предназначен для масштабирования до графов с десятками тысяч узлов и ребер за счет использования таких стратегий, как инкрементные результаты запросов.
Pathfinder предназначен для масштабирования до графов с десятками тысяч узлов и ребер за счет использования таких стратегий, как инкрементные результаты запросов. Дополнительная информация и ссылки для загрузки
Флаконы
Визуализация альтернативного сплайсинга в генахАльтернативный сплайсинг — это процесс, при котором одна и та же последовательность ДНК используется для сборки различных белков, называемых изоформами белков.Альтернативный сплайсинг работает путем выборочного исключения некоторых кодирующих областей (экзонов), обычно связанных с геном. Обнаружение альтернативного сращивания сложно и использует комбинацию передовых методов сбора данных и статистического вывода. Знание об изоформах важно для понимания как нормальных процессов, так и заболеваний, а также для улучшения лечения с помощью целевых методов лечения. Однако данные являются сложными, и текущие визуализации изоформ не являются ни эффективными, ни масштабируемыми.Чтобы исправить это, мы разработали Vials, новый инструмент визуального анализа, который позволяет аналитикам изучать различные наборы данных, которые ученые используют для вынесения суждений об изоформах: обилие считываний, связанных с кодирующими областями гена, свидетельства наличия соединений, то есть ребер соединение областей кодирования и предсказания частот изоформ.
 Виалы масштабируемы, поскольку позволяют одновременно анализировать множество образцов в нескольких группах. Таким образом, наш инструмент позволяет экспертам (а) определять закономерности содержания изоформ в группах образцов и (б) оценивать качество данных.
Виалы масштабируемы, поскольку позволяют одновременно анализировать множество образцов в нескольких группах. Таким образом, наш инструмент позволяет экспертам (а) определять закономерности содержания изоформ в группах образцов и (б) оценивать качество данных.Дополнительная информация и ссылки для загрузки
UpSet
Интерактивная визуализация наборов для более трех наборов.Понимание отношений между множествами — важная задача анализа. Основная проблема в этом контексте — комбинаторный взрыв количества пересечений множеств, если количество множеств превышает тривиальный порог. Чтобы решить эту проблему, мы представляем UpSet, новую технику визуализации для количественного анализа множеств, их пересечений и совокупностей пересечений.
Дополнительная информация и ссылки для загрузки
Caleydo
Caleydo — это среда визуального анализа с открытым исходным кодом, ориентированная на биомолекулярные данные. Самая большая сила Caleydo — это визуализация взаимозависимостей между несколькими наборами данных. Caleydo может загружать табличные данные и группировки / кластеры. Вы можете изучить отношения между несколькими группами, между разными наборами данных и увидеть, как ваши данные отображаются на пути. Caleydo успешно использовался для анализа мРНК, miRNA, метилирования, вариации числа копий, статуса мутации и клинических данных, а также других типов наборов данных.
Caleydo может загружать табличные данные и группировки / кластеры. Вы можете изучить отношения между несколькими группами, между разными наборами данных и увидеть, как ваши данные отображаются на пути. Caleydo успешно использовался для анализа мРНК, miRNA, метилирования, вариации числа копий, статуса мутации и клинических данных, а также других типов наборов данных.Дополнительная информация и ссылки для загрузки
StratomeX
Интегративная визуализация стратифицированных разнородных данных для анализа подтипов заболеваний.Дополнительная информация и ссылки для загрузки
Entourage и enRoute
Визуализация больших и разнородных экспериментальных данных с взаимозависимостями enRoute и pathway с помощью Entourage.Пути — это графики, которые моделируют разнообразные биологические процессы на молекулярном уровне. Они изображают взаимодействие генов, белков и других объектов на семантическом уровне как небольшую часть общей биологической сети.Эти подмножества подобраны с учетом их функциональной значимости и в основном являются общими для организма или конкретного болезненного состояния.
 Хотя такой подход к разделению на подмножества необходим для работы со сложностью сетей, существует множество ситуаций, когда желательно более широкий взгляд, например, при исследовании побочных эффектов лекарств. Кроме того, необходимо понимать особенности отдельных пациентов, образцов или когорт в отношении пути, поскольку пути могут модулироваться, например, через болезнь.Интегрированные методы визуализации пути в Caleydo направлены на решение этих проблем. Entourage предоставляет контекстную информацию для пути фокусировки, визуализируя соответствующие подмножества в других путях. enRoute визуализирует большие и разнородные экспериментальные наборы данных для путей.
Хотя такой подход к разделению на подмножества необходим для работы со сложностью сетей, существует множество ситуаций, когда желательно более широкий взгляд, например, при исследовании побочных эффектов лекарств. Кроме того, необходимо понимать особенности отдельных пациентов, образцов или когорт в отношении пути, поскольку пути могут модулироваться, например, через болезнь.Интегрированные методы визуализации пути в Caleydo направлены на решение этих проблем. Entourage предоставляет контекстную информацию для пути фокусировки, визуализируя соответствующие подмножества в других путях. enRoute визуализирует большие и разнородные экспериментальные наборы данных для путей. Дополнительная информация и ссылки для загрузки
LineUp
LineUp — это интерактивный метод, предназначенный для создания, визуализации и изучения ранжирования элементов на основе набора разнородных атрибутов.Дополнительная информация и ссылки для загрузки
Domino
Извлечение, сравнение и манипулирование подмножествами из нескольких наборов табличных данныхДополнительная информация и ссылки для загрузки
40 геометрических узоров в графическом дизайне, чтобы вдохновить вас (2020)
Геометрические узоры — это набор форм, повторяющихся или измененных для создания единого дизайна. Пока у вас есть значения формы, вы можете не знать, с чего начать. Здесь мы перечислили 40 отличных примеров, которые помогут вам воплотить в жизнь ваши дизайнерские идеи, с советами о том, как их применять.
Пока у вас есть значения формы, вы можете не знать, с чего начать. Здесь мы перечислили 40 отличных примеров, которые помогут вам воплотить в жизнь ваши дизайнерские идеи, с советами о том, как их применять.
Погрузимся!
Психология форм
Различные формы могут вызывать разное значение. Согласно Сидданту Пиллаи, наиболее распространенные формы — прямоугольники, круги, треугольники, ромбы и шестиугольники — можно разбить на что-то вроде этого:
- Прямоугольники / квадраты: баланс и традиции
- Круги: бесконечность, защита и женственность
- Треугольники: стабильность, энергия и агрессия
- Ромб: яркий и современный
- Шестиугольник: единство и равновесие
Комбинируя эти формы по-разному, можно создать совершенно новый смысл.Например, создание чего-либо из прямоугольников и треугольников может подчеркнуть призыв вернуться к традиции.
Но, может быть, вы не хотите делать что-то сложное; может быть, вы просто хотите использовать фигуры здесь и там, чтобы придать вашему сайту или продукту немного дополнительной жизненной силы, что-то, что сделает его заметным и профессиональным.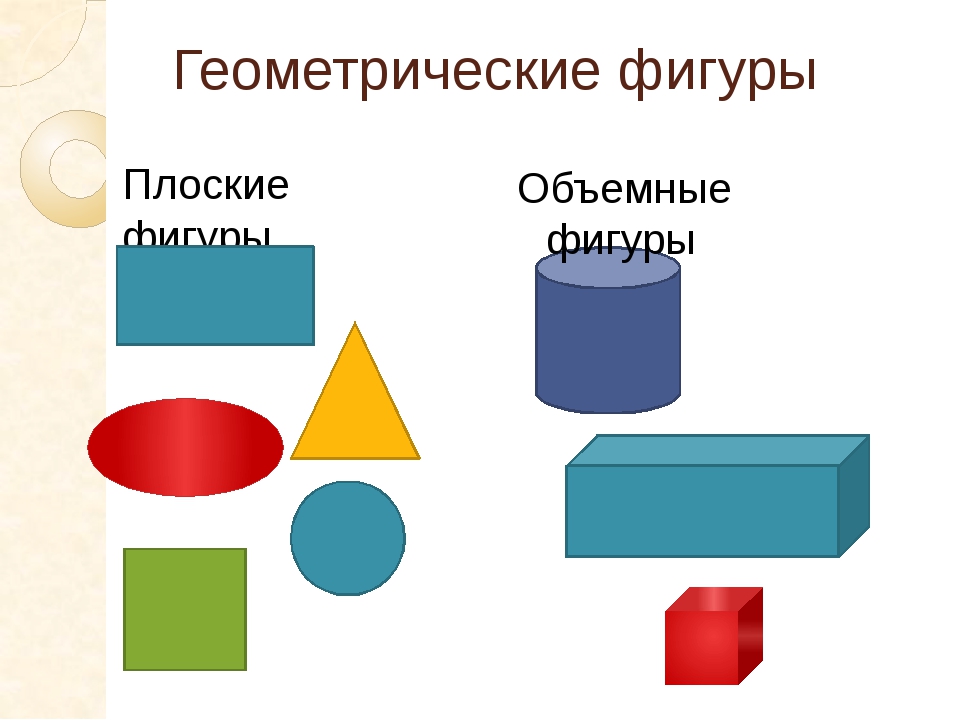 Если это так, возможно, вам подойдут геометрические узоры.
Если это так, возможно, вам подойдут геометрические узоры.
1 Используйте шаблоны для создания изображений.
Простые формы сами по себе могут быть привлекательными; Однако использование различных форм для создания единого изображения может работать даже лучше.Лайам Бразер Landshape хорошо иллюстрирует это, используя различные формы для создания яркого пейзажа. Помните, какие формы лучше всего подходят для вашего объекта, и вы сможете создать что-то впечатляющее.
2 Игра с асимметрией.
Не все геометрические узоры должны быть симметричными; Иногда создание чего-то, где формы и линии различаются по всем направлениям, может создать поразительный эффект. Этот плакат хорошо иллюстрирует концепцию, включая несовпадающие наложения и треугольники с обеих сторон, чтобы создать что-то более уникальное.
3 Совместите выкройки с фотографиями.
Геометрические узоры могут быть отличным творческим способом оживить обычные фотографии.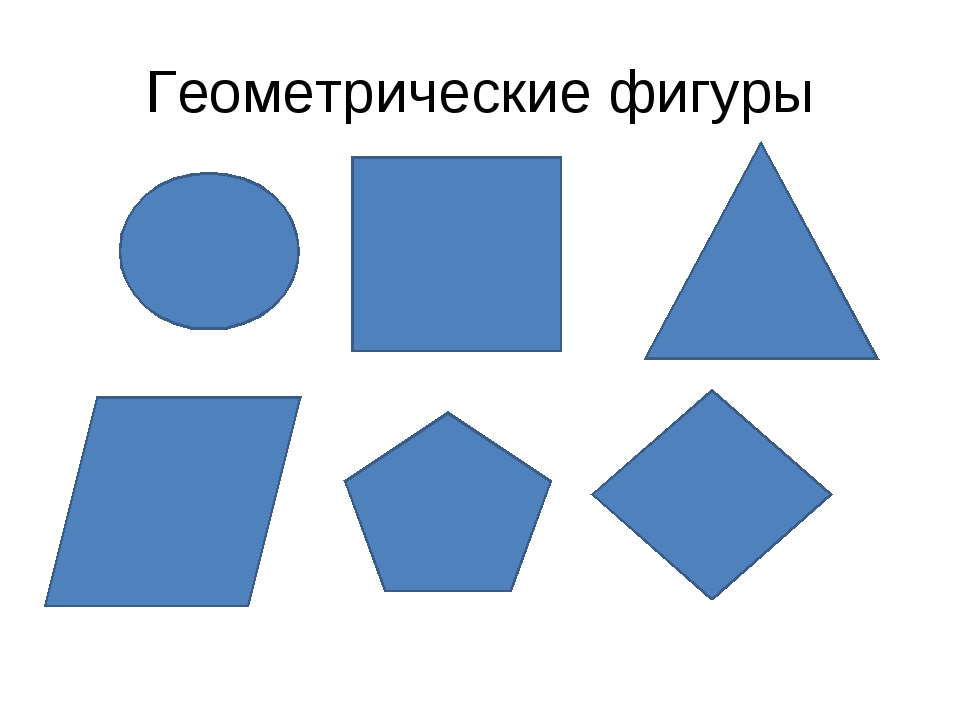 Например, Sorry Color берет множество фотографий и вставляет их в фигуры. Коллаж в конечном итоге предлагает совершенно другой, уникальный опыт, придавая изображениям больше индивидуальности, чем если бы они были показаны в одиночку.
Например, Sorry Color берет множество фотографий и вставляет их в фигуры. Коллаж в конечном итоге предлагает совершенно другой, уникальный опыт, придавая изображениям больше индивидуальности, чем если бы они были показаны в одиночку.
4 Творчески используйте освещение и тени.
Тени и блики можно использовать для улучшения форм, а иногда и для их создания, как показал Сет Никерсон.Проверьте, что вы можете делать с тенями в ваших собственных узорах, от создания почти трехмерной формы до привлечения внимания к определенным частям изображения.
5 Соединяйте фигуры уникальными способами.
Мы уже изучили, как формы могут создавать изображения; изучение того, как соединяются между этими формами, может создавать новые интересные эффекты. Например, Work Hard использует множество геометрических фигур и создает плавное изображение, соединяя их разными способами — например, соединяя края заголовка и форму головы человека.
6 Сделайте коллаж.
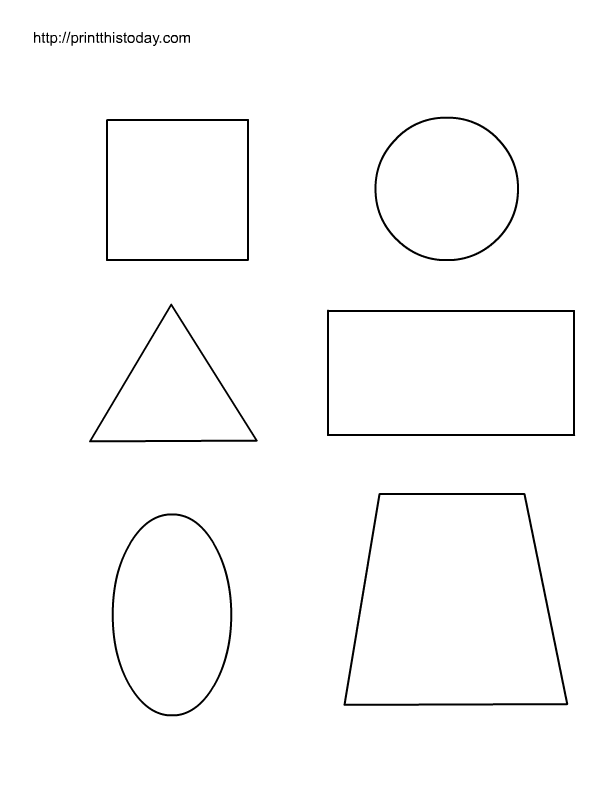
Попробуйте сделать коллаж из разных форм — что-то, что направляет зрителей и облегчает восприятие вашего рисунка. Neo Lab, например, использует бриллианты разного размера, соединенные сторонами.
7 Используйте диагонали.
Диагонали создают четкий путь для взгляда, предлагая бонус в виде связного дизайна. Finnish Summer — прекрасный пример использования диагональных узоров для создания красивого сопоставления изображений и цветов.
8 Создайте изометрические узоры.
Изометрические узоры — или узоры, которые кажутся трехмерными — действительно могут сделать изображение привлекательным при правильном использовании. Изометрическая выставка предлагает отличный пример использования жестких цветов для создания иллюзии, будто фигуры выскакивают за пределы страницы. При умеренном и творческом использовании это может привлечь внимание к конкретным предметам или словам.
9 Создание рисунков с использованием шрифта.

Если вы хотите по-настоящему раскрыть свой творческий потенциал, попробуйте использовать сам шрифт для создания своих узоров.Например, Next Level использует множество треугольников и жестких линий для создания неровного резкого эффекта. Создание узоров таким образом поможет придать любой тон вашему сайту или продукту.
10 Играйте с симметрией.
В то время как асимметрия создает более плавный и забавный вид, симметрию можно использовать в геометрических узорах для создания чего-то более элегантного. ICP прекрасно это демонстрирует, особенно на обложке, где верхняя половина изображения идеально отражает нижнюю.
11 Используйте шаблоны в шаблонах.
Если вам нужно что-то более сложное, то можно использовать геометрические узоры в уже существующих формах. Верхний левый и нижний правый примеры на этой странице — отличные примеры: в одном используются квадраты для размещения узоров, а в другом — круги.
12 Будьте проще.

И наоборот, не все должно быть сложным — простые формы могут быть столь же привлекательными. Открытки с благодарностью Astrobrights — отличные примеры, в которых для создания привлекательных изображений используется всего несколько форм и линий.
13 Подумайте о различных способах использования линий.
Линии — это самые основные элементы любой формы; их творческое использование может помочь создать новые эффекты и создать хороший поток между изображениями и информацией.
Europa — отличный пример использования простых линий для создания свечи, включая плавящийся воск! Планетарный фольклор — другой, создающий круг внутри линий. Поэкспериментируйте с простыми линиями и посмотрите, что вы сможете создать.
14 Создайте тему.
Паттерны сами по себе великолепны; шаблоны, используемые для соединения изображений, даже лучше, особенно когда все эти шаблоны связаны друг с другом.
Возьмем, к примеру, ADMCi; Все изображения связаны схожими цветами и узорами, граничащими с их границами. Выбор шаблона и его правильное применение может связать ранее разрозненные предметы и идентифицировать продукты как «ваши».
Выбор шаблона и его правильное применение может связать ранее разрозненные предметы и идентифицировать продукты как «ваши».
15 Используйте градиенты.
Все любят хорошую цветовую схему; геометрические градиенты могут улучшить это, сделав фон градиента или изображение ярким.
Carnival, например, использует простые градиенты между формами, в некоторых случаях заставляя формы почти сливаться друг с другом, а в других делая их еще более заметными.
16 Создавайте персонажей.
Если геометрические узоры могут создавать изображения, то почему бы не пойти дальше и не создать с ними символ ?
Cubist Superheroes использует шаблоны для формирования уже знакомых персонажей, но вам не обязательно придерживаться существующих персонажей.Почему бы не попробовать сделать талисман из простых геометрических фигур, создать на их основе простое руководство и посмотреть, куда это вас приведет?
17 Объедините несколько разных изображений.
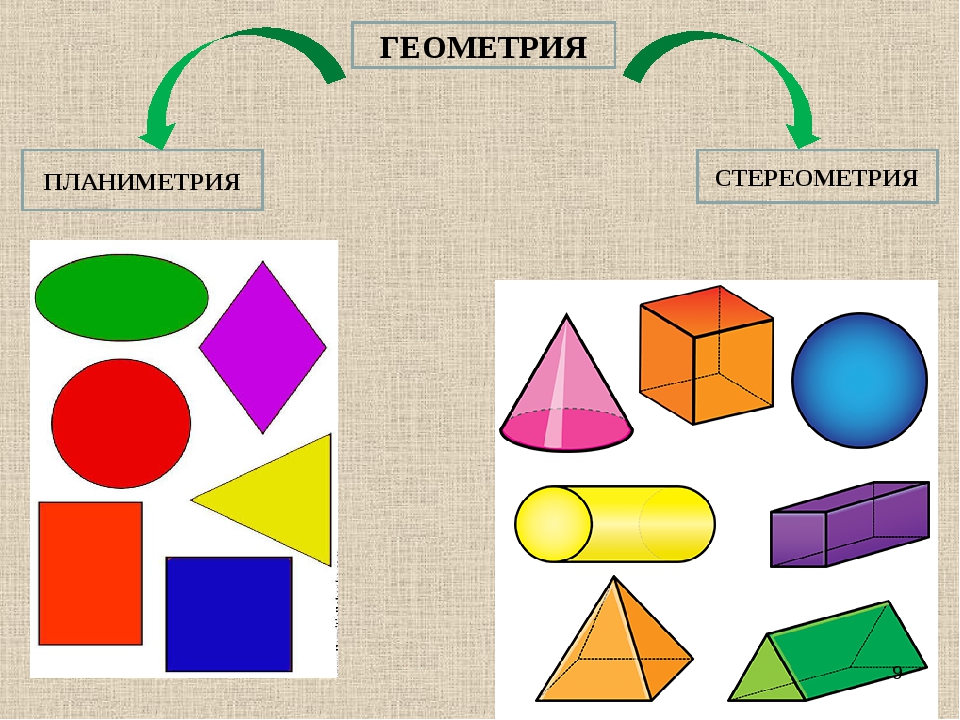
Фигуры можно использовать для объединения нескольких разных изображений вместе, причем это может быть как ожидаемым, так и неожиданным.
Например, Jelle Martens комбинирует несколько разных пейзажей для создания интересных коллажей. Поэкспериментируйте с тем, какие изображения могут хорошо сочетаться друг с другом — и как они могут изменить изображение в целом — и используйте разные формы, чтобы объединить все вместе.
18 Имитация эффекта с помощью фигур.
Фигуры могут быть невероятно эффективными, если их использовать для обозначения определенных действий или последствий. Например, «Треугольник» использует связку — как вы уже догадались — треугольников, чтобы воспроизвести эффект разбитого стекла. Использование подобных форм может добавить изображениям смысла и яркости; по крайней мере, это создает потрясающую картину.
19 Создайте фон.
Если вы хотите чего-то более тонкого, попробуйте придерживаться простого геометрического фона, такого как тот, что здесь. Они могут добавить немного азарта веб-сайту или презентации, не будучи слишком очевидными и отвлекающими.
Они могут добавить немного азарта веб-сайту или презентации, не будучи слишком очевидными и отвлекающими.
20 Создайте перекрывающиеся формы.
Иногда для создания сложности требуется всего лишь простой трюк — например, наложение двух форм, как показано в Wanderlust. Изображение состоит только из двух шестиугольников, но перекрытие делает его более сложным и изысканным. Поэкспериментируйте с тем, как перекрываются разные формы, и посмотрите, что подойдет вам.
21 Свяжите образцы с предметом.
Постарайтесь придать своему шаблону цель, напрямую связав его с предметом. Например, La Fete du Citron a Menton использует узор листьев, чтобы окружить лимон, отражая предмет.
22 Используйте шаблоны в буквах.
Вы можете создавать шаблоны из букв, если создание шаблонов с самими буквами для вас слишком занято.
Например, включая простые линии на стороне буквы. Здесь можно найти простое руководство для использования с Adobe Illustrator.
23 Используйте узор для изменения изображений.
Вы можете использовать шаблоны для изменения частей уже существующего изображения. Например, геометрическая фотография использует формы для перемещения определенных частей изображения. Сдвиг разных частей изображения может создать разный эффект и создать что-то весьма оригинальное.
24 Выберите цвета, которые подходят друг другу.
Каждый раз, используя цвета с геометрическими узорами, убедитесь, что у вас есть те, которые хорошо сочетаются друг с другом, особенно если они находятся на формах, граничащих друг с другом.
Второй фон на этой странице — отличный пример сочетания темно-зеленого и оранжевого цветов для создания серьезного профессионального образа. Плохой выбор цвета может отвлекать, поэтому освежите в памяти теорию цвета и проверьте, как разные цветные формы смотрятся друг на друге.
25 Используйте формы, которые улучшают восприятие.
Найдите формы, которые сочетаются друг с другом и хорошо сочетаются друг с другом, и которые создают более цельное целое, а не что-то, что кажется соединенным вместе. Ультра — замечательный пример, когда каждая фигура соединяется друг с другом, когда вы прокручиваете страницу вниз.
Ультра — замечательный пример, когда каждая фигура соединяется друг с другом, когда вы прокручиваете страницу вниз.
26 Создавайте уникальные эффекты.
Вы можете использовать множество разных стилей и форм, чтобы создать что-то совершенно свое. Например, вы можете использовать формы, которые создают иллюзию отражения, как в этом случае. Комбинирование различных форм, освещения и цветов может создавать разные эффекты и иллюзии, а также дает вам много материала для работы.
27 Создайте границу.
Граница — хороший способ улучшить изображение с помощью форм, не отвлекая его.Возьмем, к примеру, Zeppe, который использует геометрический узор для обозначения своего названия.
28 Добавьте простую анимацию.
Благодаря технологиям мы можем улучшить различные геометрические узоры для Интернета — например, добавить простую чередующуюся анимацию между двумя геометрическими узорами.
Noir — отличный пример, поскольку он использует простой GIF для переключения между одним набором линий и другим, создавая иллюзию движения.
29 Сделайте это тонким.
Не все должно быть очевидным; тонкие формы могут быть столь же эффективными, как показано в Itaú Internacional, формы которого почти переходят в фон. Этот поток делает вид более профессиональным, но при этом добавляет немного творчества.
30 Используйте шаблоны для сегментации информации.
Шаблоны— отличный способ разделить и распределить информацию по категориям, что упрощает ее поиск зрителям.
Renováveis, например, помещает каждый блок информации между диагональными линиями.Nasty Creatures использует несколько иной подход, каждая ссылка находится в отдельной капле «монстра».
31 Создание рисунков, нарисованных вручную.
Традиционное искусство вызывает ностальгию и позволяет создавать что-то более личное, например, с помощью этих черно-белых векторов.
32 Используйте шаблоны для выделения определенных элементов.
Узоры и линии довольно эффективно привлекают внимание к определенным элементам.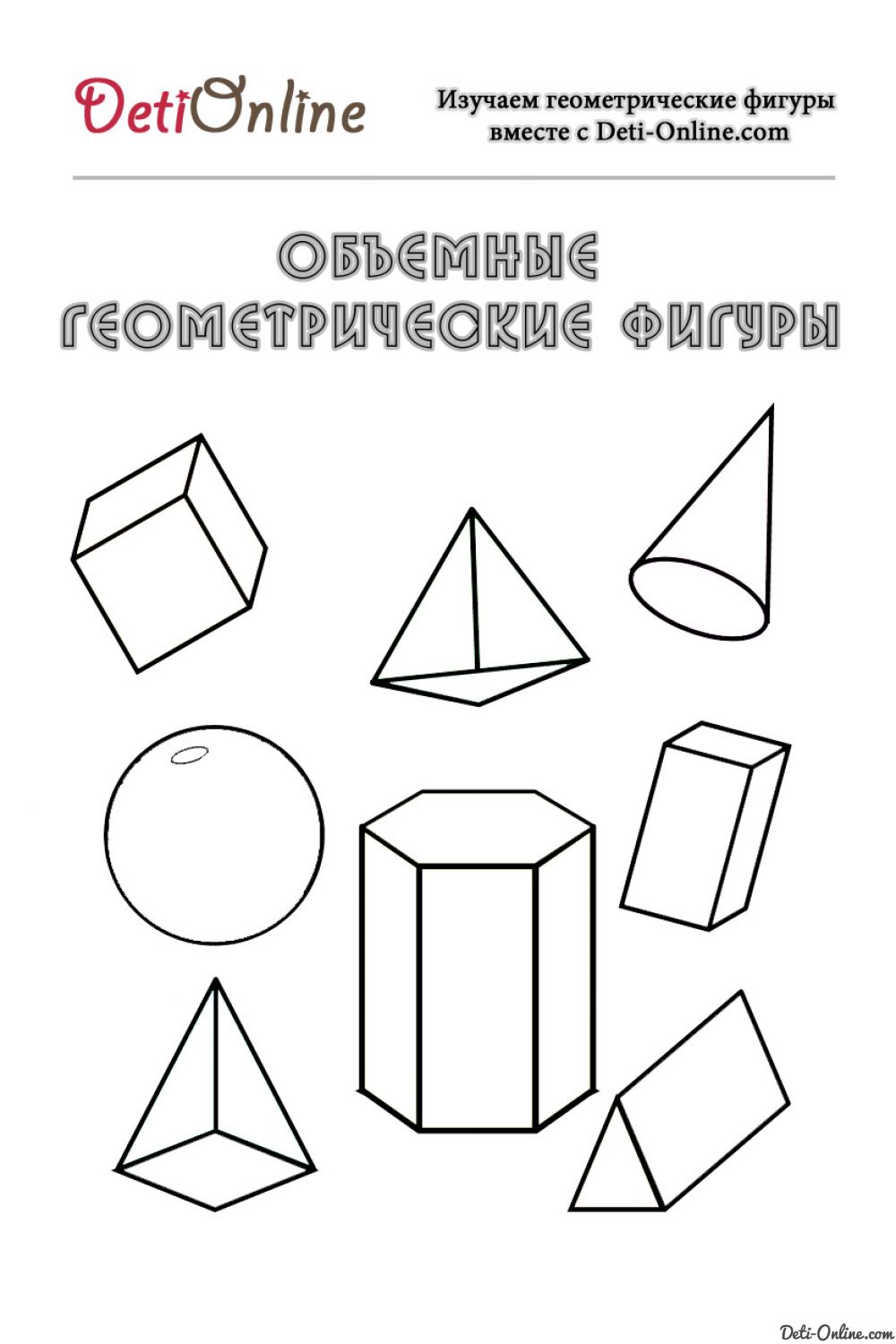 Оли Лишер, например, использует линии, чтобы привлечь внимание к слову «портфолио», а затем вставляет прямоугольники в примеры слов. Подумайте, какие элементы в своей работе вы хотите выделить, и используйте формы, чтобы привлечь к ним внимание.
Оли Лишер, например, использует линии, чтобы привлечь внимание к слову «портфолио», а затем вставляет прямоугольники в примеры слов. Подумайте, какие элементы в своей работе вы хотите выделить, и используйте формы, чтобы привлечь к ним внимание.
33 Объедините несколько рисунков.
Необязательно придерживаться одного шаблона — использование нескольких делает изображение более привлекательным. Showreel — отличный пример, использующий на своем сайте различные круги, брызги и другие формы.
34 Выбирайте необычные формы.
Никто не говорит, что вы должны придерживаться стандартных кругов, квадратов и треугольников; на самом деле, дизайн может работать лучше, используя менее традиционные формы.
Fenix Music, например, использует пузыри речи и молнии для выделения определенных элементов, дизайн, который работает лучше из-за связи с предметом.
35 Создайте «паутинку» между фигурами.
Линии отлично привлекают внимание к элементам; почему бы не использовать их для создания сети между разными предметами, как это делает фестиваль Kikk? Используйте его для установления связи между несколькими предметами, создания более привлекательного дизайна или чего-то еще.
36 Ограничение сложных шаблонов.
Сложные узоры — это здорово, но слишком много их может ошеломить. Фиоре представляет интересный пример: они используют в качестве узора растения с высокой детализацией, а некоторые из наиболее привлекательных дизайнов ограничиваются небольшими пространствами. Знайте, как и где использовать свой узор, и вы с большей вероятностью удержите внимание зрителей.
37 Сделайте это хорошо в черно-белом цвете.
Не каждому узору нужен цвет; Сохранение черно-белого изображения может быть не менее привлекательным, а также может сделать узор более применимым.Взгляните на гельветимарт — узор отлично смотрится без цвета, в последнем нет необходимости.
38 Включите реальные элементы.
Если вы хотите что-то «личное», попробуйте добавить геометрические узоры, которые вы видите на своем повседневном рабочем месте. Возьмем, к примеру, Yamaha; шаблон на их веб-сайте соответствует шаблону на их здании.
39 Акцент другой материал.
Необязательно оставлять шаблон по определенным предметам — вы можете переходить по разным продуктам, как это делает Amie Bakery, чтобы сделать шаблон более узнаваемым.
40 Экономно используйте выкройки.
Вероятно, самый простой совет, но один из самых простых: лучше меньше, да лучше. Не нужно наносить геометрические узоры на всю страницу.
«Чайная фабрика» — отличный пример удачно выполненных геометрических узоров, ограниченных заголовком. Ограничьте использование, чтобы не перегружать зрителя и придать рисункам большее влияние.
Начните использовать свои собственные геометрические узоры
Какие удивительные геометрические узоры вы видели? Какие-нибудь идеи для себя? Вы можете легко создать их прямо в Visme! Зарегистрируйтесь в своей бесплатной учетной записи, чтобы начать создавать и использовать геометрические узоры в своих проектах.
Свалка геометрии: геометрические модели
Свалка геометрии: геометрические моделиГеометрические модели
Эта страница описывает физические объекты соответствующие геометрическим конструкциям (и способы создания таких объекты), в частности многогранники. См. Также страницу оригами, где представлены модели из сложенная бумага и страница с игрушками, для некоторых имеющиеся в продаже комплекты для построения геометрических моделей.- Бутылка Acme Klein. Удовольствие тополога, сделанное вручную из стекла.
- Аллегрия фрактальные и математически вдохновленные украшения.
- Страница пентамино Анны. Анна Гардберг делает пентамино из скульптуры и агата.
- Искусство, математика, и компьютеры — новые способы создания приятных форм, К. Секен, Educator’s TECH Exchange , январь 1996 г.
- Искусство и наука плитки. Плитки Пенроуза в Карлтонском колледже.
- Арт на совместных математических встречах 2005 г., включая множество геометрических моделей.
- Арт Тетраэдра.А под «искусством» он имеет в виду «Артура». Артур Геометрическая скульптура Сильвермана из MathTrek Иварса Петерсона.
- Атомиум, структура сформирована для Экспо 1958 в виде девяти сфер, представляющих железный кристалл. Самый большой куб в мире?
- Отвар Белоусова. Рецепт создания спиральных узоров в химических реакциях.
- Конструирование поверхности мальчика из бумаги и скотча.
- Вязаные поверхности Seifert Мэтью Райта. Джордж Харт, Make Magazine.
- Урожай круги: теоремы о пшеничных полях.Различные мистификаторы делают геометрические модели вытаптыванием растений.
- Полування внизу. Боб Дженкинс украсил свою ванную комнату керамической и расписной пятиугольной плиткой.
- Эшер для реальных и вне Эшер по-настоящему. Гершон Эльбер использует многоуровневые производственные системы для создания 3D-моделей Иллюзии Эшера. Уловка состоит в том, чтобы сделать несколько, казалось бы, плоских поверхностей по кривой в сторону и от плоскости обзора.
- Математическая скульптура Геламана Фергюсона.
- Асфальтоукладчики Fisher.Выпуклый семиугольник и несколько квадратов образуют интересный четырехугольник. симметричная мозаичная система.
- Квартира равносторонние торы. Можно ли построить многогранный тор, в котором все грани равносторонние треугольники, и все вершины имеют шесть инцидентных края? Наверное, нет, но эта физическая модель очень близка.
- Развлечение с фракталами и Платоновы тела. Гайла Чандлер размещает модели многогранников и многогранные фракталы, такие как тетраэдр Серпинского в живописном открытом настройки и фотографирует их там.
- Гауди геометрические модели. Из музея Гауди в Парк Гуэль, Барселона.
- Геометричность, геометрическая скульптура Денни Норта.
- Графит со спиралями роста на базальных пинакоидах. Красивые картинки спирали в кристаллах. (Пинакоид оказывается плоскостью, параллельной две кристаллографические оси.)
- Отлично стеганое одеяло с триамбическим икосододекаэдром, сделано Марком Ньюболдом и Сарой Милкрест с помощью Гиперпространственный звездообразный многогранник Марка.
- Мелинда Страница геометрии Грина.Грин делает модели из обычных губок (бесконечные невыпуклые обобщения Платоновых тел) из пластика Изделия «Полидрон».
- Брэдфорд Хансен-Смит создает геометрическое искусство из бумажных тарелок.
- Джорджа Харта геометрическая скульптура.
- Разворачивающиеся конструкции Чака Хобермана.
- Houtrust Relief. Красивое фото трехмерной версии одной из текстур Эшера «птица-рыба» на стена водоочистного завода в Нидерландах. У одного и того же фотографа несколько другие фотографии Эшера, включая одну из Метаморфоз в Почтовое отделение Гааги.
- Гиперболический коралл, связанный крючком риф, Институт Фигурки. Техника Дайны Тайминой для вязания пряжи на гиперболические поверхности является основой для экспозиции шерстяной подводной фауны и флоры.
- гиперболический песочное печенье. Математический факультет Дэвиса использует модель Пуанкаре замощения гиперболической плоскости треугольниками 0-60-90.
- страница гиперболической поверхностной активности. Том Холройд описывает гиперболический поверхности, встречающиеся в природе, и объясняет, как сделать бумажную модель гиперболическая поверхность на основе семиугольников.
- Гиперболоид в Кобе, Япония, в 1940-х годах.
- Галерея HyperGami. Бумажные многогранные пингвины, ананасы, свиньи и многое другое.
- Связанные части головоломки и другие геометрические игрушки.
- Линейная скульптура Аарона Келлнера. Искусство в виде геометрических переплетений металлических и деревянных стержней.
- Лего Пентаминос, Эрик Харшбаргер. Он пишет, что самое сложное было найти лего достаточно разных цветов. Также его конструктор Лего математические головоломки и пентамино страниц.
- Математика Одеяла.
- Математический шарик скручивание. Ви Харт делает многогранники и многогранные клубки из воздушных шаров.
- Математический скульптуры Лего и Эшер Лего, Эндрю Липсон.
- Математически правильный завтрак. Джордж Харт описывает, как нарезать один рогалик на две связанные полосы Мёбиуса. В качестве бонуса вы получите больше поверхности область для сливочного сыра, чем стандартный нарезанный бублик.
- Математика в символических скульптурах Джона Робинсона. Кольца Борромео, тор узлы, пучки волокон и неориентируемые геометрии.
- А минимальная зимняя сказка. Снежная скульптура колледжа Макалестер Покрытие Эннепера занимает второе место в Брекенридже.
- Мёбиус в торговом центре. Топологическая скульптура как общественная зона отдыха. Из MathTrek.
- Модели математических машин в Университетском музее естествознания и научные инструменты Университета Модены. Основная выставка на итальянском языке, но есть и английская. предисловие и htm.
- Модели платоновых тел и родственные симметричные многогранники.
- Вложенный Бутылки Клейна. Из галереи Лондонского музея науки через компанию Boing. Боинг. Топологическая посуда Алана Беннета.
- Одеяло Пенроуза на сугроб, M. & S. Ньюболд. Смотрите также Лизбет Одеяло Пенроуза Клеменса.
- Пятиугольный журнальный столик с ромбической бронзовой отливкой, напоминающей плитку Пенроуза, работы Грега Фредериксона.
- Платон, Фуллер и три поросенка. Пол Флавин делает структуры тенсегрити из шариковых ручек и резинки.
- Эскимо палочные бомбы, ремни и ткачество в самолете, Ф.Салиола.
- кварк Парк. Эфемерная выставка геометрического искусства под открытым небом в Принстоне, Нью-Джерси. Из MathTrek Иварса Петерсона.
- Рог барана картонная модель интересной трехмерной спирали, ограниченная геликоидом и два вложенных конуса.
- С уважением mathématique sur Bruxelles. Студенческий проект по фотографии особенности города, представляющие математический интерес, и моделируйте их в Cabri.
- Исследование многогранника Робинзона Фриденталя. Геометрическая скульптура.
- Кубик Рубика Губка Менгера, Хана Бизек.
- Санта-Роза Куб Менгера, сделанный Томом Фалбо и помощниками из младшего колледжа Санта-Роза из 8000 дубовых блоков размером 1 дюйм.
- Серпинский печенье. На самом деле больше похоже на печенье Менгера, но неважно.
- Тетраэдр Серпинского, всеобщий любимый трехмерный фрактал. Александр Грэм Белл сделал воздушных змеев такой формы, и с тех пор конструкторы геометрических моделей стали частым явлением.
- Sliceforms, 3d модели сделаны путем чередования двух направлений плоских срезов.
- sneJ сделал Набор Мандельброта с листовым пластиком и лазерным резаком.
- Твердый объект, создающий аномальное изображение. Кокичи Сугихара делает модели иллюзий Эшера из сложенной бумаги. У него есть еще много чего, откуда этот, но, может быть, другие не в сети.
- Решение вызов Петерсена Graph Zome Challenge. Дэвид МакМахон обнаруживает, что несамопересекающийся граф Петерсона с помощью инструмента Zome. Включает иллюстрации VRML.
- Сферикон, выпуклая форма с одной изогнутой гранью и двумя полукруглыми краями, которые могут катитесь качающимся движением по прямой.Смотрите также то страница сферикона банка национальной кривой, MathWorld страница сферикона, страницу сферикона в Википедии, В Дифференциальная геометрия сферикона и Здание сферикон.
- Спираль минарет Самары.
- Спиральный чай уютно, Кэтлин Шарп.
- Спираль башня. Фотография здания в Ираке, часть веб-эссе о геометрия киберпространства.
- Спринклеры Стива. Интересный трехмерный многоугольник из медной трубы образует различные симметричные двухмерные формы. если смотреть со всех сторон.
- Темари Додекаэдрический шар из японской резьбы. См. Также Summer’s галерея temari для многих других.
- Эти две фотографии Ричарда Филлипса взяты с ныне несуществующего веб-сайта математиков с фотографиями. Дымоход находится (думает Филлипс) где-то в Северном Ноттингемшире, Англия. Аналогичный сборник Филипса математические фотографии теперь доступны на CD-ROM.
- Три спиральные татуировки из журнала Discover Magazine Science Tattoo Emporium.
- Треугольник стол Тео Грея, отображающий Spieker Circle прямоугольного треугольника 3-4-5.
- Площадь Федерации.
В этом здании в Мельбурне используется вертушка.
плитка как мотив дизайна. Спасибо Халаду Кариму за его определение.
Фотографии Дика Хесса, отсканированные Эдом Пеггом-младшим.
См. Этот Flickr
photopool для многих других фотографий.
- Университет Аризоны сборник математических моделей.
- Вазарели Дизайн. Хана Бизек делает геометрические скульптуры из кубиков Рубика.
- Вегревиль, Альберта, дом самого большого в мире пасхального яйца.Разработан Роном Решом на основе техники, которую он запатентованный для складывания бумаги или другой плоской конструкции материалы в гибкие поверхности.
- Вороной Арт. Скотт Сона Сниббе использует светоотражающий пол для демонстрации Вороного диаграмма людей, идущих по ней, исследующих понятия личного пространства и индивидуально-групповые отношения. Дополнительные работы по мотивам Вороного включены в его динамичный серии систем.
- Вороной диаграммы в Художественном музее Милуоки. Скотт Сниббе произведение Граничные функции как в блоге Quomodumque.
- vZome Программное обеспечение для проектирования zometool для OS X и Windows. (Предупреждение, веб-сайт может не работать в нерабочее время.)
- Геометрическая скульптура Элиаса Вакан.
- Место для плавания Water Cube на Олимпийских играх 2008 года в Пекине использует Пена Weaire-Phelan (разделение трехмерного пространства на ячейки равного объема с минимальная известная площадь поверхности на единицу объема) как основу его структуры.
- Что делать с мячами для гольфа? Дейл Сеймур выбирает треугольник Серпинского и тетраэдр Серпинского.
- Шерстяной мысли, математический трикотаж.
- Зоноэдр Бета. Модель гибкого многогранника, сделанная Вирсавией Гроссман из алюминия, нержавеющей стали и латуни (бронза по желанию). Также см. Остальные работы Гроссмана. геометрическая скульптура.
Со свалки Геометрии,
вычислительный
указатели рекреационной геометрии.
Отправьте электронное письмо, если вы
знать о соответствующей странице, не указанной здесь.
Дэвид Эппштейн,
Теоретическая группа,
ICS,
Калифорнийский университет в Ирвине.
Полуавтоматический
фильтрованный
из общего исходного файла.
Геометрические формы и типы фигур
Что такое геометрических плоских форм ? Какие у них характеристики? Это вопросы, на которые мы ответим в этом посте.
основных геометрических форм плоскости :
КругОкружность — это форма, которую можно создать, отслеживая кривую, которая всегда находится на одинаковом расстоянии от точки, которую мы называем центром. Расстояние вокруг круга называется окружностью круга.
ТреугольникТреугольник — это форма, образованная 3 прямыми линиями, которые называются сторонами. Существуют разные способы классификации треугольников по их сторонам или углам.
- По углам:
- Прямой треугольник: наибольший из трех углов — прямой.
- Острый треугольник: самый большой из трех углов — это острый угол (менее 90 градусов).
- Тупой треугольник: самый большой из трех углов — тупой угол (более 90 градусов).
2. По их сторонам:
- Равносторонний треугольник: все 3 стороны одинаковой длины.
- Равнобедренный треугольник: у него 2 (или более) стороны равной длины. (Равносторонний треугольник тоже равнобедренный.)
- Чешуйчатый треугольник: нет двух равных сторон.
Прямоугольник — это фигура с 4 сторонами. Отличительной особенностью прямоугольника является то, что все четыре угла составляют 90 градусов.
РомбРомб представляет собой форму, образованную 4 прямыми линиями. Его четыре стороны имеют одинаковую длину, но, в отличие от прямоугольника, любой из четырех углов составляет 90 градусов.
ПлощадьКвадрат — это разновидность прямоугольника, но также разновидность ромба. У него есть характеристики обоих из них. То есть все 4 угла — прямые, а все 4 стороны равны по длине.
ТрапецияТрапеция также имеет 4 стороны. У него две стороны, которые параллельны, а две другие — нет.
Вы можете попрактиковаться с геометрическими плоскими формами, зарегистрировавшись в Smartick.
Подробнее:
Команда по созданию контента.
Многопрофильная и многонациональная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создавать максимально качественные математические материалы.
Бумажные модели без геометрических фигур и головоломок
Бесплатные геометрические и головоломные бумажные модели и бумажные игрушки. Как весело
способ узнать о геометрии и логике …
Бизнес Карточка Многогранники — Как построить платоновые тела: тетраэдр, куб, октаэдр, додекаэдр, икосаэдр с использованием визитных карточек.
Canon — В категории «Игрушки»: Дробный торт, Выучите дроби. с этим умным тортом! Головоломки с геометрией, Головоломки с животными, Глобус Головоломки, Игра пиратского баланса, Шахматы.
Умный Lunch Box Design — Экологичный ланч из треугольного картона коробка, которая при открытии имеет встроенную пластину. Умная.
Додекаэдр Календари наши
Настольный футбол — Очень красивая игровая бумажная игрушка из очень популярной спортивной аркады, Настольный футбол!
FracDo — Наше творение.
GeoDome Игровой домик — изготовлен из картона.
Геометрия Свалка
GNU 3DLDF Многогранник Модели
Graficaobscura — Геометрическое складывание бумаги доктора Дэвида Хаффмана просто потрясающе. Бумага Складной проект тоже интересен.
шестигранник Stacking Boxes — Очень хороший шаблон и руководство о том, как сделайте ящики для штабелирования, чтобы хранить ваши кусочки и детали.Он использует цериал коробки в качестве материала, который придает коробкам вид современного искусства / Уорхола. Я думаю, вы также можете использовать картон. Также посмотрите его действительно аккуратный Изготовление проект Frabjous.
Hilaroad Постройте геодезический купол и изучите математику, стоящую за ним.
Как построить геодезический купол из картона
Как сделать кубики для визиток
Джуманджи Игровая доска — Копия бумажной модели доски Джуманджи из популярный фильм 1995 года Джуманджи.
M.C. Эшер Калейдоциклы — Интересные геометрические формы.
ММ Модульная мания — Красивое модульное оригами от Минакши Мукерджи. Перейти к диаграммам в левом меню бесплатные схемы и инструкции.
Марка Собственная купольная модель
Бумага Модели многогранников
Предпоследний Модульное оригами
Многоугольник Calendar — Календарь на пятиугольнике додекаэдре
Многогранник Модели
Перфорированный Out Fonts — шрифты True Type, которые можно распечатать и создать в 3D бумажную модель буквы алфавита!
Пазлы с многогранниками и числами
Баран Рог
Трискеле Бумажные глобусы — Бесплатный шаблон находится внизу под заголовком Free. Версия для печати.Ниже также есть видеоурок.
Целый Движение
геометрический Программное обеспечение для создания моделей и производители:
HyperGami — JavaGami. Имеет также бумажные модели геометрической формы.
Поли — Модели и условно-бесплатные программы для исследования и построения многогранников
PolyMod — Программа, создающая 3-х мерные многогранники
.

 Обратите особое внимание на соблюдение правил безопасности при работе с ножницами. По мере выполнения работы задайте вопросы:
Обратите особое внимание на соблюдение правил безопасности при работе с ножницами. По мере выполнения работы задайте вопросы: Резюмируйте ответы учащихся. Для создания треугольника потребуются три соломинки и три кусочка пластилина, так как у треугольника три стороны и три вершины.
Резюмируйте ответы учащихся. Для создания треугольника потребуются три соломинки и три кусочка пластилина, так как у треугольника три стороны и три вершины. Обратите их внимание на то, что для создания прямоугольника нужны будут четыре соломинки, длина которых попарно одинакова, так как у прямоугольника противоположные стороны равны. Окажите содействие тем детям, которые испытывают затруднения в изготовлении пар соломинок одинаковой длины. По окончании выполнения задания объедините учащихся в пары для организации взаимопроверки.
Обратите их внимание на то, что для создания прямоугольника нужны будут четыре соломинки, длина которых попарно одинакова, так как у прямоугольника противоположные стороны равны. Окажите содействие тем детям, которые испытывают затруднения в изготовлении пар соломинок одинаковой длины. По окончании выполнения задания объедините учащихся в пары для организации взаимопроверки.
 56—57. Рабочая тетрадь:
56—57. Рабочая тетрадь: Во время выполнения задания они дополнят изображение каждой фигуры таким образом, чтобы получились узнаваемые предметы. Также учащиеся смогут объединить все фигуры, чтобы создать из них единую картину.
Во время выполнения задания они дополнят изображение каждой фигуры таким образом, чтобы получились узнаваемые предметы. Также учащиеся смогут объединить все фигуры, чтобы создать из них единую картину.
