Как сделать геометрические фигуры: Геометрические фигуры из бумаги
Геометрические фигуры из бумаги
В основе самых сложных и необычные формы сооружений, устройств, механизмов лежат элементарные геометрические фигуры: куб, призма, пирамида, шар и другие. Для начала научитесь создавать самые простые фигуры, а после вы легко освоите более сложные формы.
Многие моделисты начинают свой путь с бумажных моделей. Это обусловлено доступностью материала (найти бумагу и картон не составляет трудности) и легкостью в его обработки (не требуются специальные инструменты).
Однако, бумага имеет и ряд характерных особенностей:
- капризный, хрупкий материал
- требует высокой аккуратности, внимательности, усидчивости при работе
По этим причинам бумага является материалом, как для начинающих, так и для настоящих мастеров и из нее создаются модели самой разной сложности.
В этот статье мы изучим простейшие геометрические фигуры, которые можно сделать из бумаги.
Вам понадобятся следующие материалы:
- лист бумаги
- карандаш
- линейка
- ластик
- ножницы
- клей ПВА либо клеящий карандаш
- кисточка для клея, лучше из жесткой щетины
- циркуль (для некоторых фигур)
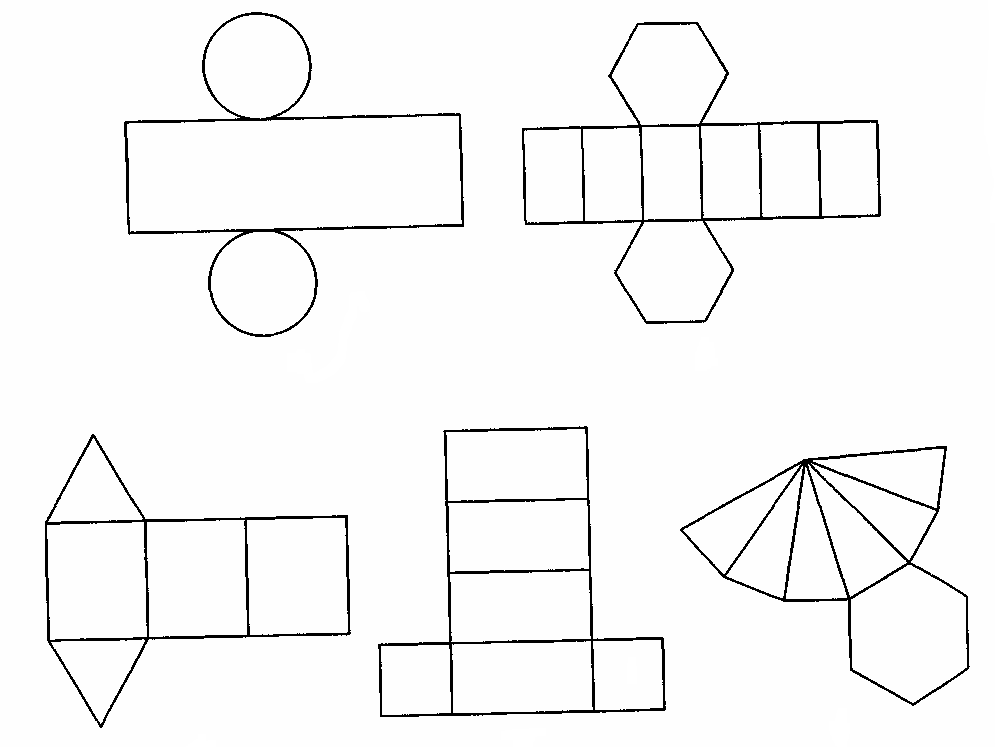
Как сделать куб из бумаги?
Куб – правильный многогранник, каждая грань которого представляет собой квадрат
Создание куба состоит из двух этапов: создание развертки и склеивание. фигуры. Для создания схемы вы можете воспользоваться принтером, просто распечатав готовую схему. Либо вы можете самостоятельно с помощью чертежных инструментов нарисовать развертку.
Рисование развертки:
- Выбираем размеры квадрата — одной стороны нашего куба. Лист бумаги должен быть шириной не менее 3 сторон этого квадрата и длиной немного более 4 сторон.
- Чертим в длину нашего листа четыре квадрата, которые станут боковыми сторонами куба.
 Рисуем их строго на одной линии, вплотную друг к другу.
Рисуем их строго на одной линии, вплотную друг к другу. - Над и под любыми из квадратов рисуем по одному такому же квадрату.
- Дорисовываем полоски для склеивания, с помощью которых грани будут соединяться между собой. Каждые две грани должны соединяться одной полоской.
- Куб готов!
После рисования развертка вырезается ножницами и склеивайте ПВА. Клей очень тонким слоем равномерно размазываем кистью по поверхности склеивания. Соединяем поверхности и закрепляем в нужном положении на некоторое время, с помощью скрепки или небольшого груза. Срок схватывания клея где-то 30-40 минут. Ускорить высыхание можно методом нагрева, например, на батарее. После склеиваем следующие грани, закрепляем в нужном положении. И так далее. Так постепенно вы проклеите все грани куба. Используйте небольшие порции клея!
Как сделать конус из бумаги?
Конус – тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность.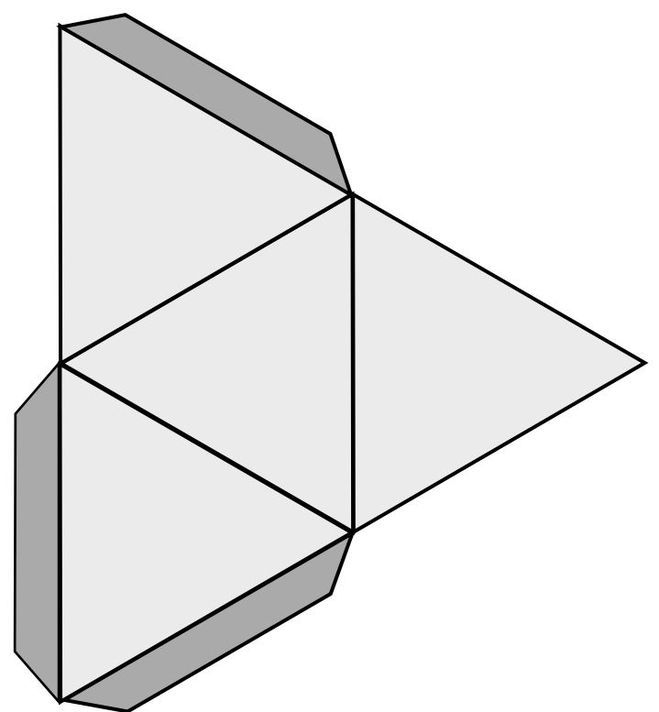
Рисование развертки:
- Рисуем циркулем окружность
- Вырезаем сектор (часть круга, ограниченная дугой окружности и двумя радиусами, проведенными к концам этой дуги) из этой окружности. Чем больший сектор вы вырежете, тем острее будет конец конуса.
- Склеиваем боковую поверхность конуса.
- Измеряем диаметр основания конуса. С помощью циркуля рисуем окружность на листе бумаге требуемого диаметра. Дорисовываем треугольнички для склеивания основания с боковой поверхностью. Вырезаем.
- Приклеиваем основание к боковой поверхности.
- Конус готов!
Как сделать цилиндр из бумаги?
Цилиндр – геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.
Рисование развертки:
- Рисуем прямоугольник на бумаги, в котором ширина — это высота цилиндра, а длина определит диаметр будущей фигуры.
 Отношение длины прямоугольника к диаметру определяется выражением: L=πD, где L- длина прямоугольника, а D — диаметр будущего цилиндра. Подставив в формулу требуемый диаметр, найдем длину прямоугольника, который будем рисовать на бумаге. Дорисовываем небольшие дополнительные треугольнички, которые необходимы для склеивания деталей.
Отношение длины прямоугольника к диаметру определяется выражением: L=πD, где L- длина прямоугольника, а D — диаметр будущего цилиндра. Подставив в формулу требуемый диаметр, найдем длину прямоугольника, который будем рисовать на бумаге. Дорисовываем небольшие дополнительные треугольнички, которые необходимы для склеивания деталей. - Рисуем на бумаге два круга, диаметром цилиндра. Это будет верхнее и нижнее основания цилиндра.
- Вырезаем все детали будущего бумажного цилиндра.
- Склеиваем боковую поверхность цилиндра из прямоугольника. Даем детали высохнуть. Приклеиваем нижнее основание. Ждем высыхания. Приклеиваем верхнее основание.
- Цилиндр готов!
Как сделать параллелепипед из бумаги?
Параллелепипед – многогранник, у которого шесть граней и каждая из них параллелограмм.
Рисование развертки:
- Выбираем размеры параллелепипеда и величины углов.
- Чертим параллелограмм — основание.
 С каждой стороне дорисовываем боковые стороны — параллелограммы. От любой из боковой стороны дорисовываем второе основание. Добавляем полоски для склеивания. Параллелепипед может быть прямоугольным, если стороны прямоугольники. Если параллелепипед не прямоугольный, то создать развертку немного сложнее. Для каждого параллелограмма нужно выдержать требуемые углы.
С каждой стороне дорисовываем боковые стороны — параллелограммы. От любой из боковой стороны дорисовываем второе основание. Добавляем полоски для склеивания. Параллелепипед может быть прямоугольным, если стороны прямоугольники. Если параллелепипед не прямоугольный, то создать развертку немного сложнее. Для каждого параллелограмма нужно выдержать требуемые углы. - Вырезаем развертку и склеиваем.
- Параллелепипед готов!
Как сделать пирамиду из бумаги?
Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину.
Рисование развертки:
- Выбираем размеры пирамиды и количество ее граней.
- Рисуем основание — многогранник. В зависимости от количества граней это может быть треугольник, квадрат, пятиугольник или другой многогранник.
- От одной из сторон основания рисуем треугольник, который будет боковой стороной. Следующий треугольник рисуем так, чтобы одна сторона у него с предыдущим была общая и так далее.
 Так рисуем столько треугольников, сколько сторон в пирамиде. Дорисовываем полоски для склеивания в нужных местах.
Так рисуем столько треугольников, сколько сторон в пирамиде. Дорисовываем полоски для склеивания в нужных местах. - Вырезаем и склеиваем фигуру.
- Пирамида готова!
Читайте также:
делаем поделку в технике оригами
Геометрические фигуры из бумаги должен научиться делать каждый! Ведь никогда не знаешь, какие знания тебе могут пригодиться в жизни. В последнее время техника оригами набирает широкую популярность среди детей и взрослых. Но перед тем как делать разнообразные поделки (животных, птиц, растений, маленьких домиков), нужно начать с простых геометрических фигур. Такие изделия подойдут для школьников для хорошего визуального представления разных фигур.
Мастерим куб
Итак, для сегодняшнего мастер-класса нам пригодится бумага, схемы, клей, ножницы, линейки и немножечко терпения.
Куб — самая простая фигура для оригами, простой многогранник, в котором каждая грань является квадратом. Схему для создания развертки можно распечатать на принтере, либо начертить самим. Для этого выбрать размеры граней. Ширина листа бумаги должна быть не менее 3 сторон одного квадрата, а длина не более 5 сторон. Начертить в длину листа четыре квадрата, которые станут боковыми сторонами куба. Рисовать строго на одной линии, вплотную. Над и под одним квадратом нарисовать по одному квадрату. Дорисовать полоски для склеивания, благодаря которым грани будут соединяться между собой. Наш куб уже практически готов!
Схему для создания развертки можно распечатать на принтере, либо начертить самим. Для этого выбрать размеры граней. Ширина листа бумаги должна быть не менее 3 сторон одного квадрата, а длина не более 5 сторон. Начертить в длину листа четыре квадрата, которые станут боковыми сторонами куба. Рисовать строго на одной линии, вплотную. Над и под одним квадратом нарисовать по одному квадрату. Дорисовать полоски для склеивания, благодаря которым грани будут соединяться между собой. Наш куб уже практически готов!
Далее тонким слоем клея равномерно размазать по местам соединения. Склеить эти поверхности и закрепить на некоторое время с помощью скрепки. Клей будет схватываться около 30-40 минут. Таким образом склеить все грани.
Поделка посложнее
Конус делается немного сложнее. Для начала нарисовать циркулем окружность. Вырезать сектор (часть кружка, ограниченная дугой окружности и двумя радиусами) из этой окружности. Острота конца конуса зависит от вырезанной части большого сектора.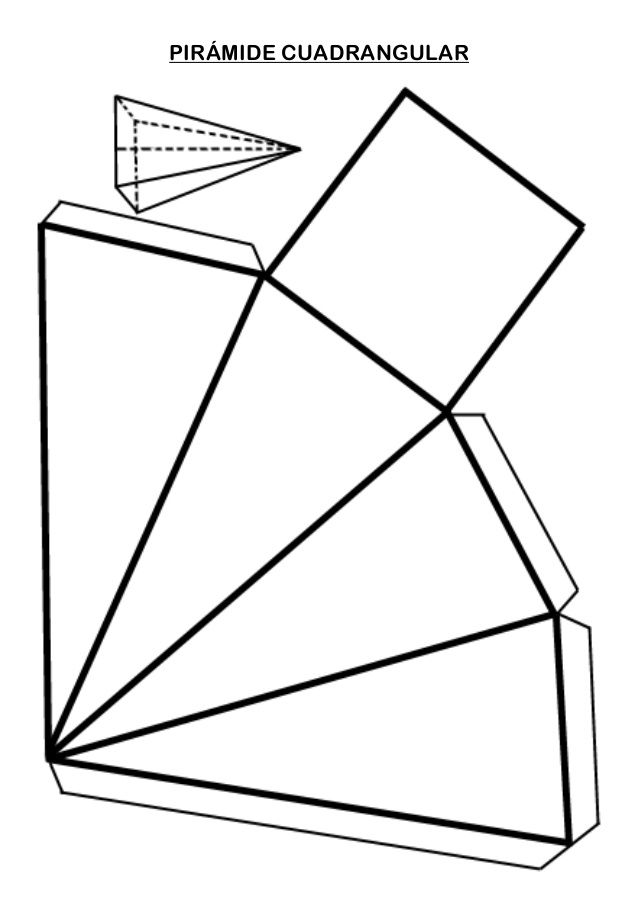
Склеить боковую поверхность конуса. Далее измерить диаметр основания конуса. Циркулем нарисовать окружность на листе бумаги. Затем дорисовать треугольнички для склеивания основы с боковой поверхности. Вырезать. После приклеить основание к боковой поверхности. Поделка готова!
Сложный параллелепипед
Параллелепипед — сложная фигура многогранник, у которого 6 граней и каждая из них параллелограмм.
Чтобы сделать параллелепипед техникой оригами, нужно начертить основание — параллелограмм любого размера. С каждой его стороны нарисовать боковые стороны — тоже параллелограммы. Далее от любой из боковых сторон дорисовать второе основание. Добавить места для склеивания. Параллелепипед может быть прямоугольным, если все стороны имеют прямые углы. Затем вырезать развертку и склеить. Готово!
Пирамида-оригами
Пришло время сделать пирамиду из бумаги. Это многогранник, основание которого — многоугольник, а другие грани — треугольники с общей вершиной.
Для начала нужно выбрать размеры пирамиды и количество граней. Далее нарисовать многогранник — он будет основанием. Смотря на количество граней, это может быть также треугольник, квадрат, пятиугольник.
От одной из сторон нашего многогранника нарисовать треугольник, который будет боковой стороной. Затем нарисовать еще треугольник, чтобы одна его сторона была общей с первым треугольником. Нарисовать их столько, сколько сторон в пирамиде. Далее дорисовать полоски для склеивания в необходимых местах. Вырезать и склеить фигуру. Пирамида готова!
Бумажный цилиндр
Цилиндр — это геометрическая фигура, ограниченная цилиндрической поверхностью и двумя параллельными плоскостями, которые ее пересекают.
Нарисовать прямоугольник на бумаге, в которой ширина — высота цилиндра, а длина — диаметр. Любители геометрии знают, что отношение длины прямоугольника к диаметру определяется формулой: L=nD, где L — длина прямоугольника, а D — диаметр цилиндра. С помощью этого вычисления узнать длину прямоугольника, которого будем рисовать на бумаге.
Затем нарисовать на бумаге два круга, диаметром как цилиндр. Это будет верхнее и нижнее основания цилиндра. Далее вырезать все детали. Склеить боковую поверхность цилиндра из прямоугольника. Дать детали высохнуть и приклеить к нему нижнее основание. Снова подождать, пока высохнет, и приклеить верхнюю основу. Готово!
Видео по теме статьи
youtube.com/embed/9FuEvK7hzSY?feature=oembed» frameborder=»0″ allowfullscreen=»»/>
Самые лучшие посты
Как сделать объемные геометрические фигуры из бумаги, развертки для склеивания: куба, конуса, схемы и шаблоны для вырезания цилиндра, пирамиды, треугольника
Любому ребенку нравится делать яркие и объемные поделки. Творчество можно объединить с изучением математики и склеить вместе с детьми геометрические фигуры. Ребенок с интересом проведет время, а дополнительно постигнет основы точной науки. Ниже представлено, как начертить карандашом и сделать объемные геометрические фигуры из бумаги, также приведены их правильные названия.
Как сделать объемные геометрические фигуры
Дети познают мир в процессе игры и творчества. Трехмерные фигуры, выполненные своими руками, помогут познакомиться с удивительной наукой — геометрией.
Как вырезать и склеить модели из бумаги
Начинающие конструкторы задаются вопросами, как рисовать и чертить геометрические фигуры, как правильно склеить выкройки и как делают врезки. Проще всего распечатать готовый шаблон. Затем необходимо согнуть фигуру по пунктирным линиям.
Чтобы сгибы получились ровными, к пунктиру прикладывают линейку, по ее форме делают точные загибы. Такой способ особенно помогает, когда речь идет о фигурках из картона или ребенок делает самые сложные макеты. Например, икосаэдр, додекаэдр, тетраэдр.
На последнем этапе необходимо скрепить элементы объекта, места для склейки обозначены на развернутом виде фигуры. Детали из картона приклеивают при помощи ПВА, а бумажные — карандашным клеем.
Основные ошибки при работе с моделями:
- Ребенок делает неправильные сгибы — например, изгиб отклоняется в сторону от пунктира на несколько градусов. В результате модель получится неточной.
Неточности во время вырезания шаблонов.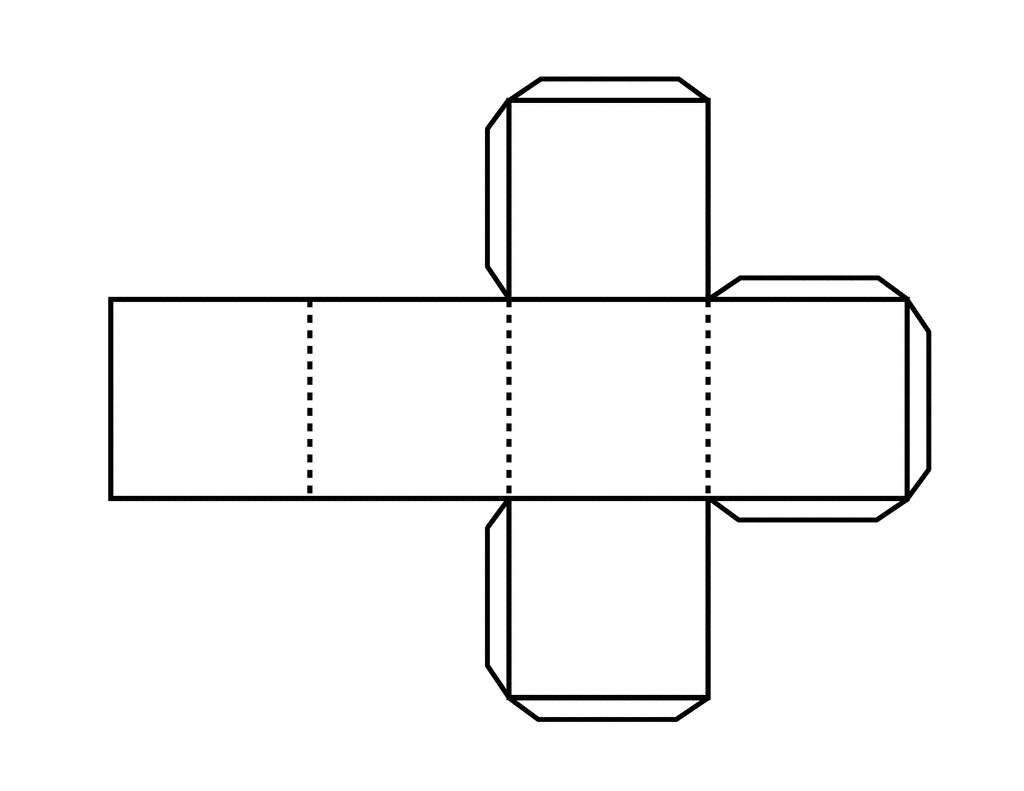 Если малыш отрезал одну из границ для склеивания, то фигурка будет разворачиваться. Здесь на помощь придет взрослый.
Если малыш отрезал одну из границ для склеивания, то фигурка будет разворачиваться. Здесь на помощь придет взрослый.
Полигональные фигуры, модели, схемы, развёртки, программа создания из бумаги, металла и пластика масок и скульптур
Каждый начинающий моделист, будь то взрослый или ребёнок, должен изучить и запомнить основы работы с бумагой. От этих элементарных знаний зависит качество создаваемых полигональных фигур и скульптур. Всем следующим приёмам нужно учить детей с малого возраста, чтобы в повседневном упражнении они уже делали это не задумываясь, а в результате модели будут получаться с легкостью. Я попробую раскрыть особенности и тонкости обучения, проектирования и создания разверток для трёхмерных фигур, а также сборки и склеивания низкополигональных моделей.
low poly викинг
Существуют три разновидности, но наша задача найти отличия. High poly или высокополигональное моделирование, подразумевает создание объекта с большим числом полигонов( эффект сглаживания),или если сказать по другому—точной его копии. low poly, в переводе низкополигональное моделирование, используется для создания фигуры с небольшим числом полигонов, что придает некий лофт(грубость) модели. Обычно, для экономии ресурсов, когда не требуется высокая детализация, а так же для создания иллюстраций, которые набирают большую популярность в последнее время.
low poly, в переводе низкополигональное моделирование, используется для создания фигуры с небольшим числом полигонов, что придает некий лофт(грубость) модели. Обычно, для экономии ресурсов, когда не требуется высокая детализация, а так же для создания иллюстраций, которые набирают большую популярность в последнее время.
Полигональное моделирование из бумаги
Позволяет визуализировать объект с помощью специальной сетки. Оно появилось в то время, когда для определения местонахождения точки необходимо было вручную вводить её координаты по осям X, Y, Z. Если три точки координат задать как вершины и соединить их ребрами, то получится треугольник, который в 3d моделировании называют полигоном. Как правило, он имеет свою текстуру и цвет, а если объединять несколько,то получится модель. Вместе, они составляют сетку или объект.
modeling decor
Для того, чтобы края модели не имели граненого вида, необходимо, чтобы они были малого размера, а поверхность состояла из маленьких плоскостей. Если предполагается точное моделирование, либо в дальнейшем увеличение его изображения, то необходимо строить модель с большим количеством граней, хотя, если на модель смотреть издали без приближения, достаточно будет небольшого количества. Это и есть полигональное моделирование. Сетка состоит из под объектов и может состоять из огромного количества одинаковых ячеек:
Если предполагается точное моделирование, либо в дальнейшем увеличение его изображения, то необходимо строить модель с большим количеством граней, хотя, если на модель смотреть издали без приближения, достаточно будет небольшого количества. Это и есть полигональное моделирование. Сетка состоит из под объектов и может состоять из огромного количества одинаковых ячеек:
вершина – точка соединения рёбер, может быть множество рёбра – границы граней грани – ячейки сетки, участки плоскости. Чаще всего треугольной или четырехугольной форму.
Что бы создать 3D модель необходимо работать (с частями) подобъектами. Объединяем и делим, меняем их форму и размер, вращаем, а также применять другие операции, которые позволяются в специализированном программном обеспечении.
Набор программ для создания и 3D-развертки
Естественно, чтобы получить желаемую фигуру пригодятся специальные программы. Я расскажу о самых актуальных и незамысловатых. Они могут помочь превратить некоторые идеи в красивые творения и прототипы, которые можно использовать в самых разных дизайнерских ноу хау. Эти редакторы доступны для изучения, освоить их сумеют даже новички за короткий промежуток времени. Использование ПО позволило на огромную ступень повысить уровень кинематографа компьютерных игр, дизайна интерьера, архитектурных и скульптурных решений. Выбор оптимального программного обеспечения часто бывает трудным, так как непросто найти подобрать всё в одном, что бы весь необходимый функционал был в одном месте.
Эти редакторы доступны для изучения, освоить их сумеют даже новички за короткий промежуток времени. Использование ПО позволило на огромную ступень повысить уровень кинематографа компьютерных игр, дизайна интерьера, архитектурных и скульптурных решений. Выбор оптимального программного обеспечения часто бывает трудным, так как непросто найти подобрать всё в одном, что бы весь необходимый функционал был в одном месте.
Совокупность граней, из которых будет состоять оболочка изделия, являются сеткой. Изготовление несложное, поскольку они имеют четко определяемые внешнюю и внутреннюю область, и поэтому дополнительных параметров и вычислений не понадобится. Но этот способ требует терпения и усидчивости, потому что необходима сосредоточенность, активная мозговая деятельность и тысячи кликов мышкой. Будьте внимательны, даже маленькие погрешности способны испортить процесс.
Pepakura Designer
Умеет работать со множеством форматов 3D моделей, например 3DS, DXF, MQO, LWO. Список можно просмотреть на официальной странице программы, думаю это сделать не сложно.
Обратите внимание: программа не имеет возможности создавать сами трехмерные макеты, как выше указанные в списке. Также нет никакого редактора, но зато разработчики предлагают нам переводить их в 2D форматы, после вы можете распечатать схему на принтере и потом создать настоящее чудо.
Как правило такой набор или развертку бородатого воина вы не скачаете в бесплатном доступе. Есть множество профессиональных распечаток, но их можно только приобрести за символическую плату к примеру на площадке Etsy.
Папекура Дизайнер создаёт и редактирует 3D заготовки. Чертеж-выкройку развернутую, которую затем можно вывести на печать в нужном масштабе, вырезать и склеить. Конечно, такой подход подразумевает изрядную работу, но выбирать не приходится — более дешёвого и доступного метода “материализации виртуальных объектов” еще не придумано. Pepakura Designer поддерживает различные форматы 3D моделей созданных в программах 3Dstudio, Lightwave, AutoCad и др. Программа создает развертку 3-х мерного изображения для последующей печати на принтере.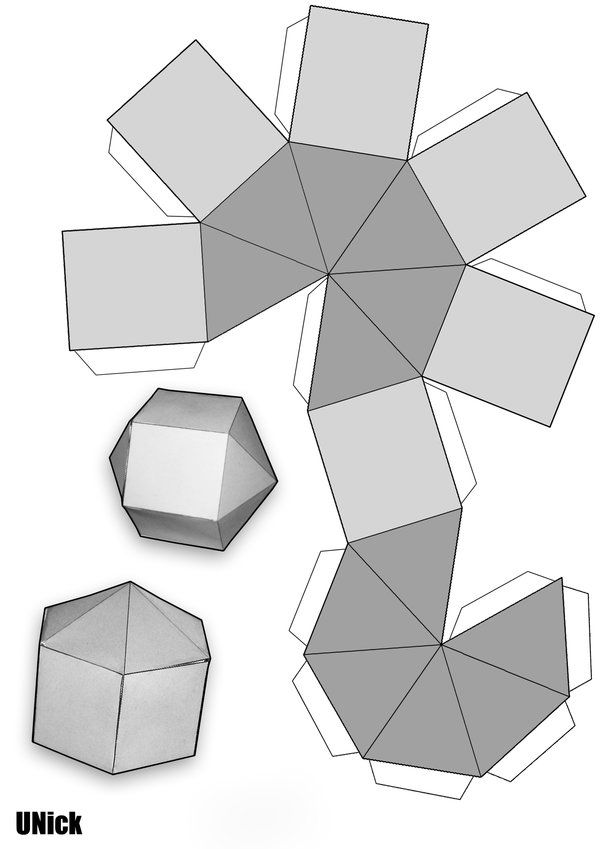 Она выдаст рисунок с готовыми местами для склеивания и вырезания.
Она выдаст рисунок с готовыми местами для склеивания и вырезания.
Pepakura Viewer
Менее мощный инструмент может только просматривать работы, не имея возможности изменять их. Помимо этой прямой функции, вы можете увеличивать, уменьшать, крутить, вертеть, выставлять углы и делать прочие безобидные махинации. Это всё, что потребуется для успешной склейки.
Делаем модели из бумаги, пепакура для развёртки
На примере кота мы видим, как выглядят схемы и развёртки полигональных фигур. Это также может быть собака, мышка, или другое животное. Для того что бы всё получилось нужен хороший качественный набор в pdf. Как правило бесплатные имеют дефекты, так как создавались новичками, профи уже требуют цену за свой труд.
Натуральный кот и шикарный олень из бумаги. Скульптура в мини-размере для украшения интерьера.
Дизайнерский loft черно-золотой бык в декоре стены. Если вы создаёте крупные фигуры розового слона или большую голову лося вам нужен плотный картон для моделирования.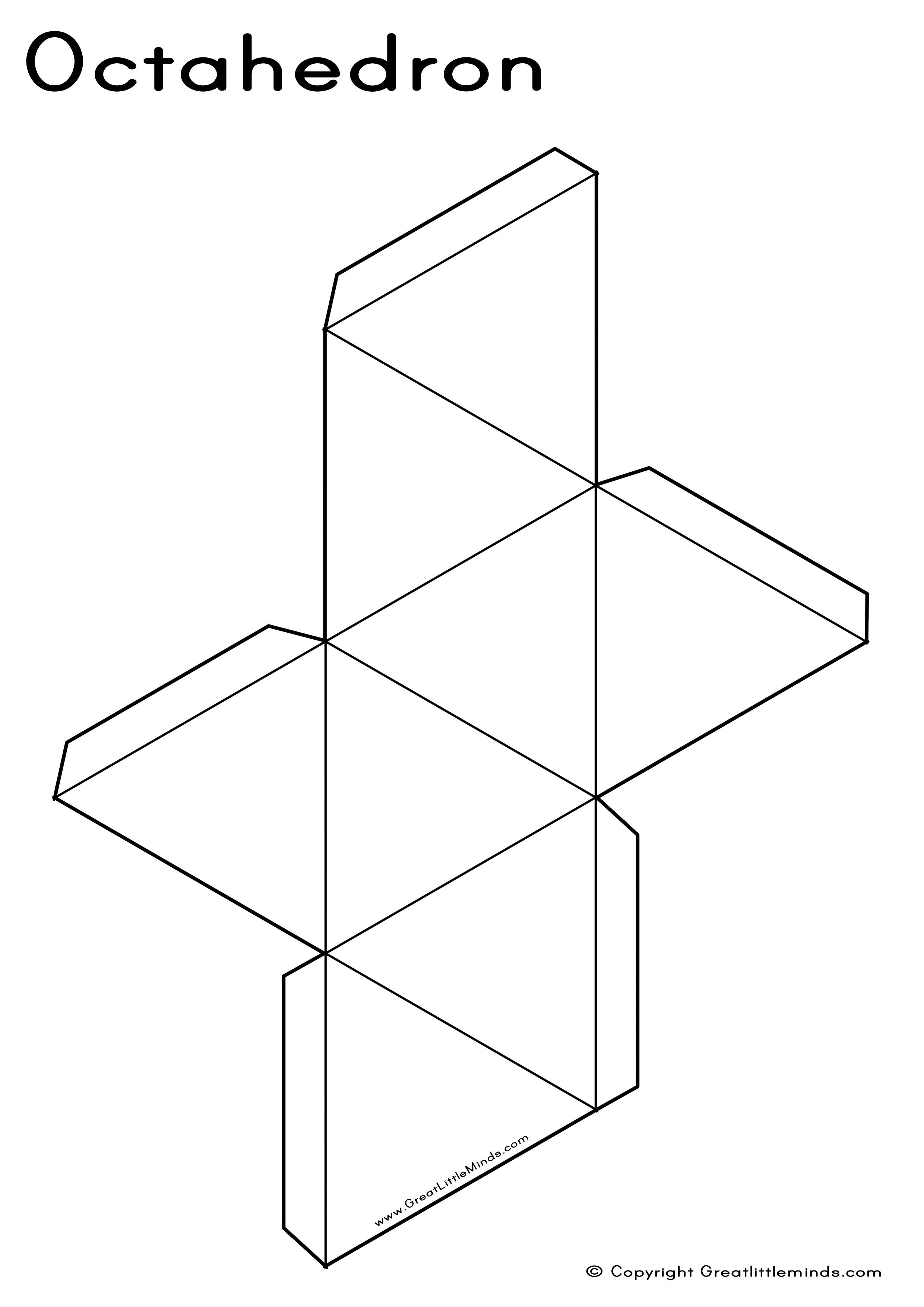
model head
Черно-белый набор смешных человечков из картона и сложная модель Хаски.
Полигональная фигура их методы и способы построения
Создаются тремя основными методами, которые используют в объединённом варианте и по отдельности. Использование примитивов—за основание берут готовые геометрические фигуры вроде куба или цилиндра. Конструируем нужную модель путем вытягивания подобъектов и деления существующих граней. Также вытягиванием новых граней из полигона-исходника , когда каждый следующий появляется из предыдущего.
Предусмотрено три основных способа построения визуализации.
- Для придания нужной формы меняется положение рёбер, их размеры.
- Проводятся манипуляции с вершинами, их перемещение, удаление и т.д.
- Грани-полигоны используются для более сложных действий. Это придание формам выпуклости или наоборот заостренности. Возможно сглаживание или вдавливание поверхности—работаем с плоскостями.

Необходимый набор для сборки, схемы и развертки полигональной фигуры
Позаботьтесь о хорошем, удобном столе и стуле, нужно, что освещение падало из-за левого плеча, используйте настольную лампу. Чтобы не выпачкать стол клеем застелите его плёнкой или положите лист стекла с зашлифованными краями, чтобы не порезаться. Чтобы научиться складывать базовые изделия, вам понадобятся простые приспособления вроде ножниц, канцелярского ножа, клея ПВА и кисточки для его нанесения.
Отдайте предпочтение строительному клею ПВА — из всех разновидностей у него наиболее густая консистенция, он не портит бумагу, делая её мокрой и вязкой, как обычный. Используются разные виды — от папиросной до обычного картона. Новичкам советуют начинать с акварельной, в 200 грамм на м2 для крупных элементов и чертёжной разновидности 140-160 грамм – при разработке мелких частей.
Бумага для паперкрафта и клей для бумажных моделей
Основным материалом для создания является, естественно, обычная бумага, но так как она не сильно надёжная и хрупкая, советуем обратить внимание на полукартон, либо же обыкновенный картон. Детали из него более крепкие и придают готовому творению износостойкость.
Детали из него более крепкие и придают готовому творению износостойкость.
Удивительный кит с подсветкой—эксклюзивный ночник в спальне вашего ребёнка
У каждого мастера имеются свои секреты, вот и мы хотим поделиться с вами открытием.
Заготовки гораздо удобнее приклеивать узким двухсторонним скотчем. Он скрепляет моментально и угрозы “расклеиться” ваше творчество не потерпит.
Но также неплохой связующий предмет для элементов – клеевой раствор. Выбирайте вариант, который удобнее.
Модель из бумаги
Рабочий процесс создания проходит в несколько простых этапов. Перед началом процесса мастер определяется, какую фигурку он хочет сконструировать. На самом деле, можно смастерить практически любое изделие, но бумажное моделирование чаще предполагает такие варианты:
- многогранники с выпуклыми и вогнутыми углами, геометрические фигуры
- копии зданий в масштабе
- макеты автомобилей премиум класса
- танки, тяжелые орудия, бронемашины
- поезда, корабли и подлодки, самолеты
Бумага для моделирования—основной рабочий материал.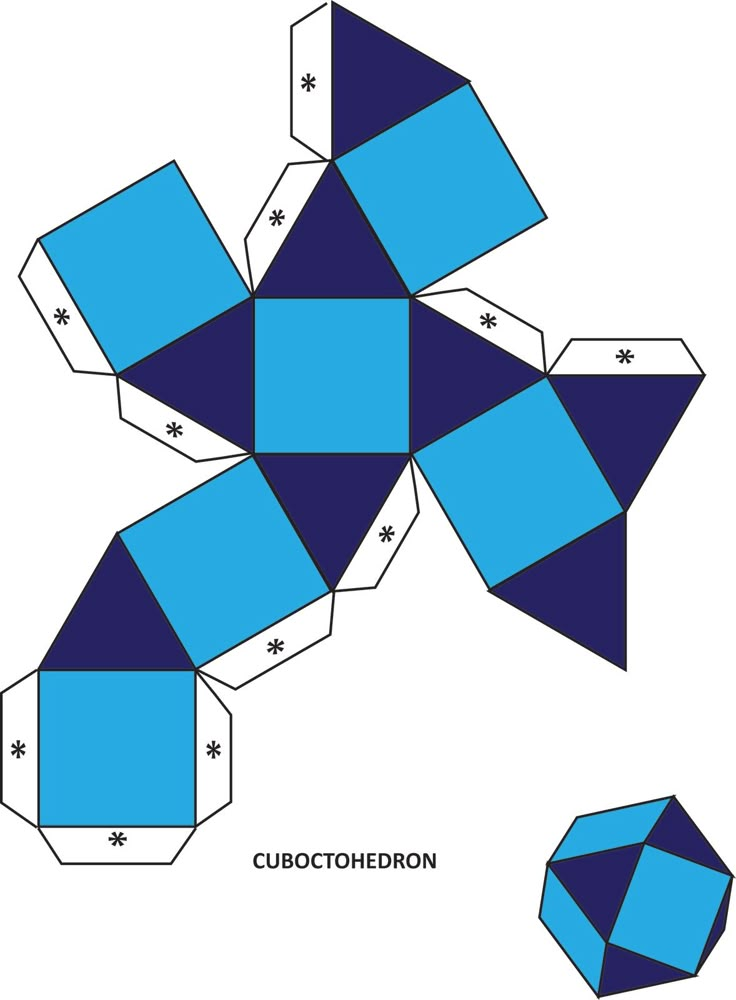 Следует уделить особое внимание её качеству! Для начального творчества лучше всего использовать обыкновенные листы формата А4, они имеют хорошее качество и является самой белоснежной по отношению к другим маркам. Плотность – 80 г/м. Советую приобретать специальную, для черчения.
Следует уделить особое внимание её качеству! Для начального творчества лучше всего использовать обыкновенные листы формата А4, они имеют хорошее качество и является самой белоснежной по отношению к другим маркам. Плотность – 80 г/м. Советую приобретать специальную, для черчения.
Создание макета
Многие укрепляют эпоксидкой или красят краской. Я не рекомендую, потому что лучше взять качественную бумагу и собрать аккуратно, чем некачественно нанести краску из-за чего сгладятся грани, что придаёт грубости. К тому же модели не требуют особой прочности, так как приспособлены для украшения стен. Они собираются из предварительно вырезанных и согнутых деталей. Развертки необходимо распечатывать на бумаге 170—200 г/м². Это сделает её устойчивой.
группа заготовок на рабочем столе
При вырезании каждой детали обязательно нумеровать каждую. Для сгибов используйте линейку. Чтобы придать детали округлость, оберните её вокруг карандаша. От силы скручивания зависит сама форма. Тот же способ используйте для кривых поверхностей.
Сборка: особенности процесса
Необходимые материалы:
- иголка для нанесения клея в труднодоступных местах
- papercraft развёртки
- кисточка
- острые ножницы или канцелярский нож
- металлическая линейка
- любая ровная поверхность
- клей (не используйте ПВА, после высыхания он деформирует изделие), но на собственном опыте убедились, что эффективнее использовать двухсторонний скотч, шириной 2 мм, в этом случае обязательно наличие пинцета
- дотс для продавливания сгибов
Для жёсткости деталь по сгибам и пустоты внутри заполняем монтажной пеной, но без фанатизма, чтобы она при расширении не деформировала внешний вид.
Видео-урок “Низкополигональные модели”
Арт-голова оленя станет чудесной маской на маскарад, либо вечеринку.
Сказочный декор для фотостудии.
Полигональная модель и основные рекомендации
Предпочтение отдаем геометрическим фигурам из четырехугольников. Проще в деформации, что позволит сэкономить время,не проводя ненужных манипуляций. Треугольники применяем как можно меньше. Также не стоит использовать сложные геометрические фигуры, с большим количеством ребер и углов, это может привести к деформации текстуры.
Советуем визуализировать только необходимые элементы, построение дополнительных конструкций усложняет, если это мелкие детали, их можно делать, используя текстуры. Эта техника рассчитана на создание объектов с точными формами и чёткими контурами. Маленькие грани строят целостное, они имеют цвет и форму. Указанный способ котируется в промышленном дизайне.
Полигональные изделия из металла или пластика
Множество интересных идей можно воплотить из такого “сурового” материала, как металл или пластмассы. Такие изделия – арт-объекты, они станут великолепным украшением фотозоны, ресторана, дачного участка, коттеджного посёлка, либо парка. Внешний вид фигур ограничен только бюджетом и фантазией заказчика.
Уличный пёс-сторож.
Полигональная пантера с эфектом сглаживания.
Лошадь из стеклопластика.
Ben Foster Sculpture
Полигональные фигуры в интерьере и креативные дизайнерские идеи
Практически всеми возможными фигурами можно украшать детскую спальню, офис, спальню, кухню. От вашей фантазии зависит масштаб конструкции, стоит начать с небольших фигур что бы потренитроватся и понять какие недостатки вылезут и после этого приступать к моделям с человеческий рост и выше.
loft papercraft для дома
полигональная фигура в интерьере
лисенок и цветы
голова фламинго
Настенная скульптура – бык.
Заяц – отличное дополнение к пасхальной корзинке.
Низкополигональные миры
Наверное, все уже слышали о подобного рода иллюстрациях. В процессе создания объёмного 3D-изделия, она формируется при помощи полигонов. Чем их численность выше, тем реалистичнее будет вид. Раньше всегда ценилась высокая степень проработки изображений и мастера стремились к высокому числу полигонов, заготовки с низким числом были лишь набросками, считались незаконченной работой.
Mat Szulik—удивительный художник и необычайной красоты миры
французская улица, кофейня и дама в шляпе
Christripes
Vitaliy Prusakov
Kirill Kodochigov
Jona Dinges
Для сборки сурового викинга с топором потребуется неделя усидчивости, не меньше.
Paul DOUARD
Gareth David
Jeremiah Shaw
Пример того как можно сочетая два цвета (серый и зелёный) и три простые фигуры дерево, трава и камень создать низкополигональный шедевр, причем масштаб зависит только от вашего воображения и возможностей.
Видео мастер класс создание развертки полигональных фигур
Самоделки с меткой: Геометрические фигуры
Самоделки: 32
-
Белый и два цветных тора завязанных в узелок 🙂 + развертки.
Дмитрий ДА 31.03.2009
-
Большой выбор развёрток простых геометрических фигур.
Дмитрий ДА 28.05.2009
-
Тетраэдр (четырёхгранник) — многогранник с четырьмя треугольными гранями, в каждой из вершин которого сходятся по 3 грани.
Дмитрий ДА 28.10.2009
-
Октаэдр — один из пяти выпуклых правильных многогранников.
Дмитрий ДА 28.10.2009
-
Додекаэдр (двенадцатигранник) — правильный многогранник, составленный из двенадцати правильных пятиугольников.
Дмитрий ДА 28.10.2009
-
Икосаэдр — правильный выпуклый многогранник, двадцатигранник, одно из Платоновых тел.
Дмитрий ДА 28.10.2009
-
Что вы видите на картинке, параллелепипед? А если внимательно присмотреться 🙂
Дмитрий ДА 19.12.2009
-
Очень интересный видеоролик, с кубиком происходят аномалии или это вообще не куб? 😉
Дмитрий ДА 19.12.2009
-
Сделать флексагон, не трудно, нужна только бумага, ножницы и скотч.
Александр 23.02.2010
-
Готовые развёртки конуса разных размеров.
Дмитрий ДА 08.08.2010
-
Моя первая работа: оригами додекаэдр
Темирлан 13.12.20
Рисунки из геометрических фигур — Задания в картинках и раскраски
Веселые и красочные задания для детей «Рисунки из геометрических фигур» являются очень удобным обучающим материалом для детей дошкольного и младшего школьного возраста по изучению и запоминанию основных геометрических форм: треугольника, круга, овала, квадрата, прямоугольника и трапеции. Все задания предназначены для самостоятельной работы ребенка под наблюдением взрослых. Родитель или педагог должны правильно объяснить ребенку, что он должен сделать в каждом задании.
Также вам может понравиться наш онлайн тренажер по математике для 1 класса «Геометрические фигуры»:
Геометрические фигуры 1 класс — Онлайн-тренажер
Онлайн-тренажер по математике «Геометрические фигуры 1 класс» поможет первоклассникам потренироваться в умении различать основные геометрические фигуры: квадрат, круг, овал, прямоугольник и треугольник.
1. Рисунки из геометрических фигур — Условия к выполнению заданий:
Чтобы начать выполнять задания, скачайте во вложениях бланк, в котором вы найдете 2 типа заданий: рисунки из геометрических фигур для раскрашивания и задание для рисования фигур с помощью логического и образного мышления. Распечатайте скачанную страницу на цветном принтере и дайте ребенку вместе с цветными карандашами или фломастерами.
- В первом задании малышу нужно мысленно соединить каждые две части представленных фигур в одну и нарисовать полученную геометрическую форму в соответствующей клетке. Объясните ребенку, что детали можно поворачивать в уме в разные стороны до тех пор, пока он не получит нужную комбинацию для составления фигуры. Например, два треугольника можно повернуть так, чтобы получился квадрат. После этого квадрат нужно нарисовать в клетке рядом с треугольником. По такому же принципу необходимо сделать и остальные рисунки.
- Во втором задании дети должны правильно назвать фигуры из которых состоят нарисованные картинки. Затем эти картинки нужно раскрасить, используя цвета рядом с геометрическими фигурами. Каждую фигуру нужно раскрасить только в указанный цвет.
Чтобы придать занятию больше энергии и энтузиазма — можно объединить несколько детей в группу и предоставить им выполнение заданий на время. Тот ребенок, который первый выполнит все задания без ошибок, признается победителем. В качестве приза можно повесить его работу на стену достижений (такая стена обязательно должна присутствовать как дома, так и в детском саду).
Скачать задание «Рисунки из геометрических фигур» вы можете во вложениях внизу страницы.
2. Геометрические фигуры в рисунках — 3 задания-раскраски:
Следующее занятие также скрывает основные геометрические фигуры в рисунках. Ребенку нужно найти эти фигуры, назвать их, а затем раскрасить таким образом, чтобы каждой фигуре соответствовал определенный цвет (руководствуясь инструкцией на бланке с заданием).
Во втором задании нужно нарисовать на всех этажах любые геометрические фигуры, но при этом необходимо соблюдать условие: на каждом этаже фигуры должны находиться в разном порядке. В последствии можно это задание видоизменить. Для этого достаточно начертить на бумаге точно такой домик и попросить ребенка заполнить его фигурами так, чтобы в каждом подъезде не встречались одинаковые фигуры (подъезд — вертикальный ряд квадратов).
В третьем задании нужно, руководствуясь стрелками, нарисовать точно такие же геометрические фигуры внутри или снаружи данных фигур.
Не торопите ребенка и не подсказывайте ему, пока он сам вас об этом не попросит. Если у малыша что-то получилось неправильно — вы всегда можете распечатать еще один экземпляр учебного бланка с заданием.
Скачать задание «Геометрические фигуры в рисунках» вы можете во вложениях внизу страницы.
3. Развивающая раскраска для детей — Смешные рисунки из фигур
В этом занятии детям опять предстоит отыскать геометрические фигуры среди рисунков. После предыдущих занятий им будет уже легче ориентироваться в знакомых формах, так что, я думаю, оба задания не вызовут у них затруднений.
Второе задание также дает возможность малышу повторить математические знаки и усвоить счет до десяти, так как ему понадобится посчитать количество фигур и поставить знаки «больше» «меньше» между картинками.
Скачать раскраску «Смешные рисунки из фигур» вы можете во вложениях внизу страницы.
Также вам будут полезны и другие материалы по изучению геометрических фигур:
Геометрические фигуры и их названия — Задания в картинках
Здесь вы с ребенком можете изучить геометрические фигуры и их названия с помощью веселых заданий в картинках.
Геометрические фигуры — Раскраска для дошкольников
Задания ознакомят ребенка с основными фигурами геометрии — кругом, овалом, квадратом, прямоугольником и треугольником. Только здесь не занудное зазубривание названий фигур, а своеобразная игра-раскраска.
Плоские геометрические фигуры — Обведи и дорисуй
Как правило, геометрию начинают изучать, рисуя плоские геометрические фигуры. Восприятие правильной геометрической формы невозможно без выведения ее своими руками на листе бумаги.
Найди формы геометрических фигур в картинках
Это занятие изрядно позабавит ваших юных математиков. Ведь теперь им придется находить знакомые формы геометрических фигур среди множества картинок.
Наложение фигур друг на друга — Задание для детей
Наложение фигур друг на друга — это занятие по геометрии для дошкольников и младших школьников. Смысл упражнения состоит в решении примеров на сложение. Только это необычные примеры. Вместо цифр здесь нужно складывать геометрические фигуры.
Свойства геометрических фигур для дошкольников
Это задание составлено в виде игры, в которой ребенку предстоит менять свойства геометрических фигур: форму, цвет или размер.
Счет геометрических фигур — Картинки с заданиями
Здесь вы можете скачать задания в картинках, в которых представлен счет геометрических фигур для занятий по математике.
Чертежи геометрических тел — Задание для детей
В этом задании ребенок познакомится с таким понятием, как чертежи геометрических тел. По сути, это занятие представляет собой мини-урок по начертательной геометрии
Геометрические фигуры из бумаги — Вырезаем и занимаемся
Здесь мы подготовили для вас объемные геометрические фигуры из бумаги, которые нужно вырезать и склеить. Куб, пирамиды, ромб, конус, цилиндр, шестигранник, распечатать их на картоне (или цветной бумаге, а затем наклеить на картон), а затем дать ребенку для запоминания.
Счет до 10 для дошкольников
Дети любят раскрашивать и обводить, поэтому данные задания сделают ваши занятия по обучению счету максимально эффективными.
И еще можете поиграть в математические игры онлайн от лисенка Бибуши:
Игра «Что лишнее? — Геометрические формы»
В этой развивающей онлайн игре ребенку предстоит определить, что является лишним среди 4 картинок. При этом необходимо руководствоваться признаками геометрических форм.
Как создавать геометрические линии и формы в GIMP?
Обновлено: 06.03.2020, Computer Hope
Есть несколько методов добавления геометрических элементов в ваши проекты GIMP. Для начала создайте новый документ или откройте существующий, а затем выполните следующие действия.
Использование инструментов выделения для создания прямоугольников и эллипсов
Чтобы создать прямоугольники и эллипсы с помощью инструментов выделения, выполните следующие действия.
- Выберите инструмент выделения «Прямоугольник » или «Инструмент выделения эллипса » из меню инструментов.
- Включить Развернуть от центра из меню параметров инструмента.
- Для идеального круга или квадрата включите Фиксированное соотношение сторон в меню параметров инструмента и введите соотношение сторон 1: 1 в текстовое поле.
- Переместите курсор в желаемое место в центре вашей формы.
- Перетащите курсор к краю формы, чтобы создать область выделения. Когда область выбрана, можно изменять только пиксели внутри этой области.
- При желании измените положение выделения, щелкнув внутри фигуры и перетащив ее.
- Выберите инструмент Bucket Fill Tool в меню инструментов.
- Залейте выделение цветом, щелкнув внутри него.
- Чтобы отредактировать что-либо, кроме выделенного, щелкните правой кнопкой мыши и выберите Выбрать , затем Нет .
Использование формы кисти для создания фигур
Вы также можете создавать фигуры, изменяя тип и размер кисти.
- Выберите инструмент Pencil Tool в меню инструментов.
- В меню Параметры инструмента выберите значок Кисть .(Значок по умолчанию — круг.)
- Выберите тип кисти, напоминающий желаемую форму, например блок, звезду или эллипс.
- Установить Твердость от до 100 .
- Измените размер и соотношение сторон в соответствии с вашими предпочтениями. Для идеального круга или квадрата установите соотношение сторон 0 .
- Переместите курсор в желаемое место фигуры.
- Чтобы использовать кисть для создания формы, щелкните один раз левой кнопкой мыши.
Создание прямых линий с помощью инструмента «Кисть»
Чтобы рисовать прямые линии, выберите нужный инструмент кисти и щелкните начальную точку линии. Удерживая Shift , переместите курсор в конечную точку. Завершите строку одним щелчком мыши. Для линии без закругленных краев выберите блочную кисть .
Дополнительные примечания и советы
- Вы можете использовать сочетания клавиш R ( Прямоугольник, ) и E ( Эллипс, ) для выбора этих инструментов.
- Ключи скобки позволяют изменять размер кисти. Левая скобка ( [) уменьшает размер кисти, а правая скобка (] ) увеличивает размер кисти.
- Создание новых слоев для каждой формы упрощает редактирование, если документ становится более сложным.
Как быстро и легко создать геометрическую типографику в Illustrator
Геометрические надписи придают дизайнерским проектам уникальный вид, созданный вручную. Узнайте, как создать свой индивидуальный креативный тип, выполнив эти простые шаги.
Геометрические надписи в стиле ручной работы станут большой тенденцией в типографии в 2018 году. Хотя эти буквы могут выглядеть так, как будто для их создания вручную или с помощью принтера высокой печати требуется несколько часов, на самом деле их создание в цифровом виде в Adobe Illustrator занимает совсем немного времени. .
Подходит для относительных новичков в векторном программном обеспечении, мы создадим дизайн «С НОВЫМ ГОДОМ», который вы легко сможете адаптировать к любому сообщению по вашему выбору. Мы добавим немного текстуры с помощью Photoshop и покажем вам, как экспортировать ваши надписи как изображения Instagram, готовые для публикации со всем миром.
Готовы начать писать? Отлично, давайте начнем!
Что вам понадобится для написания писем
Помимо доступа к Adobe Illustrator и Adobe Photoshop , вам также необходимо загрузить изображение текстуры бумаги, подобное этому, чтобы добавить последний штрих к вашему дизайну. Вот и все! Вы готовы приступить к работе.
1. Как создать сетку и цветовую палитру для надписи
Color станет ключом к объединению ваших надписей и приданию им индивидуальности и настроения.Читайте дальше, чтобы воссоздать палитру, которую я использовал для надписей, изображенных здесь, или адаптируйте образцы цвета к тем, которые вам нравятся, если хотите.
Шаг 1
Откройте Adobe Illustrator. Вы можете настроить документ любого размера, который вам нравится. Если вы создаете надпись для определенной цели, например, для поздравительной открытки, плаката или изображения в Instagram (как я делаю здесь), разумно настроить обложку в соответствии с размером вашего окончательного документа.
Здесь я устанавливаю ширину и высоту монтажной области равной длины (11 дюймов), чтобы создать квадратный холст, который я могу легко адаптировать к изображению в Instagram позже (которое в настоящее время составляет 1080 пикселей на 1080 пикселей).
Щелкните OK, чтобы создать новый документ.
Шаг 2
Когда линейки видны (перейдите в меню «Вид »> «Линейки»> «Показать линейки», , если нет), перетащите направляющую вниз от линейки, проходящей вдоль верхней части рабочего пространства. Перетащите секунду вниз под ним, создав пару направляющих. Вы можете использовать их, чтобы разметить верх и низ (базовую линию) вашей первой строки надписи.
Выберите обе направляющие и Правка> Копировать, Правка> Вставить , перетащив копию вниз под оригинал, создав вторую строку для текста.
Повторите, создав третью пару для создания третьей линии. Постарайтесь, чтобы расстояние между каждой парой линий было как можно более равным.
Шаг 3
Разверните панель Swatches (Window> Swatches) и выберите New Swatch в раскрывающемся меню панели (вверху справа).
Отсюда вы можете создать свой первый образец цвета. Если вы хотите воссоздать дизайн надписи, изображенный в этом уроке, мы собираемся создать палитру пастельных и ярких цветов в стиле восьмидесятых, чтобы придать рисунку ощущение ретро.В противном случае вы можете смешивать и добавлять цвета по своему усмотрению.
Обратите внимание: если вы собираетесь печатать свой дизайн букв, выберите CMYK в меню Color Mode окна New Swatch . Если вы собираетесь использовать его в Интернете, например в социальных сетях, выберите RGB для цветового режима.
Я называю первый образец желтым и устанавливаю уровни RGB на R = 245 G = 192 B = 34 , прежде чем нажимать OK.
Шаг 4
Щелкните New Swatch , как и раньше, чтобы добавить другие образцы в палитру.Чтобы воссоздать использованные здесь образцы, дайте им имена и значения, указанные ниже:
- Бледно-розовый — R = 230 G = 167 B = 149
- Розовый — R = 233 G = 114 B = 159
- Помидор — R = 230 G = 64 B = 41
- Монетный двор — R = 142 G = 204 B = 185
Вы заметите, что все образцы будут добавлены в список образцов на панели Swatches , чтобы вы могли использовать их в своем дизайне.
2. Как нарисовать и украсить надпись
Шаг 1
Пора рисовать! На этом этапе мы будем использовать некоторые инструменты рисования Illustrator, которые находятся на панели Tools , прикрепленной к левой стороне рабочей области.
Начните с начала фразы, поэтому увеличьте левую верхнюю часть верхней пары направляющих. Здесь я собираюсь начать строить фразу «С НОВЫМ ГОДОМ», вставляя каждое слово с новой строки. Вы можете создать эту фразу вместе со мной или адаптировать методы, которые я использую здесь, чтобы создать свою собственную фразу.
Чтобы создать основы букв, такие как левый и правый вертикальные элементы буквы «H» в начале слова «HAPPY», возьмите инструмент «Перо» (P) и щелкните по странице, создав прямоугольный блок, который соответствует на верхней и нижней направляющих.
Чтобы ваша надпись выглядела более ручной, не беспокойтесь о том, чтобы сделать форму полностью идеальной — на самом деле они будут выглядеть намного лучше, если они не будут полностью симметричными. Вы можете использовать инструмент Direct Selection Tool (A) , чтобы выбрать отдельные опорные точки и изменить их положение, пока вы не будете довольны внешним видом своей формы.
Шаг 2
Переместите квадрат Stroke Color вперед (внизу панели инструментов ), нажав X на клавиатуре, и установите для него значение [Нет] на панели Swatches .Нажмите X , чтобы переключиться на Fill Color , и настройте его на один из ваших образцов, здесь Pink .
Используйте инструмент «Перо » (P) , чтобы создать следующий стержень «H», установив заливку Fill на контрастный Pale Pink.
Шаг 3
Используйте инструмент Line Segment Tool () для создания элементов-перемычек между частями букв, таких как горизонтальная полоса в заглавной букве «H».
Установите цвет обводки на контрастный образец, здесь Черный , и используйте панель Обводка (Окно> Обводка) , чтобы изменить толщину , сделав линию толще и жирнее.
Скопируйте и Вставьте строку несколько раз, создавая группу. Это добавит ретро-образу модели H.
Шаг 4
Перейдите к следующей букве в последовательности, здесь «А.» С каждой буквой во фразе постарайтесь придумать, как бы вы могли представить букву как можно проще. Например, букву «А» можно представить как пару простых треугольников.
Используйте инструмент Pen Tool , как и раньше, чтобы создать базовую форму буквы, придав ей заливку другого цвета, здесь Mint .
Копирование и Вставьте треугольную форму и уменьшите ее, удерживая Shift , чтобы сохранить пропорции, наложив ее поверх оригинала.
Шаг 5
Вы можете создать украшения в горошек для своих надписей с помощью инструмента «Карандаш» (N). Перейдите к пустой области монтажной области и с помощью инструмента «Карандаш » нарисуйте несколько грубых маленьких кругов. Опять же, не беспокойтесь о том, чтобы превратить их в идеальные круги.Вы хотите, чтобы они выглядели немного органично по стилю.
Придайте фигурам сплошной цвет заливки, затем Скопируйте и Вставьте круги несколько раз, создавая узор из точек в горошек.
Наведите указатель мыши на все точки и переместите их на монтажный стол (область за краем основной монтажной области). Отсюда вы можете выбрать группы точек и Скопировать и Вставить , чтобы использовать их в дизайне надписи.
Шаг 6
Здесь я перемещаюсь по группе точек в горошек, чтобы закрыть букву «A», устанавливая для них Fill Color на White .
Щелкните правой кнопкой мыши> Расположить , чтобы перемещать элементы букв вперед или назад по своему усмотрению.
Шаг 7
Продолжайте работать над первой строкой букв. Затем я собираюсь создать букву «P» с помощью инструмента «Перо» , , чтобы создать основной стержень…
… и Pencil Tool (N) , чтобы создать круг чаши буквы. Вы можете использовать инструмент Smooth Tool (внутри раскрывающегося меню инструмента Pencil Tool ), чтобы сгладить любые излишне шаткие участки круглой формы на вашем дизайне.
Розовые точки в горошек — и письмо готово.
Шаг 8
I Copy и Вставьте две основные формы буквы «P», чтобы создать вторую форму «P».
Затем я использую инструмент Line Tool () , чтобы добавить несколько длинных полос по высоте круга.
Шаг 9
Я использую инструмент Pen Tool , чтобы создать простую чашеобразную форму буквы «Y» в конце слова…
… и добавьте несколько точек в горошек для украшения.
Шаг 10
Перейдите к следующему слову фразы и следующей строке вниз, используя направляющие, чтобы оценить высоту ваших рисунков.
Я использую инструмент «Перо » для создания двух стержней заглавной буквы «N», устанавливая цвет заливки на Помидор .
A Pink в форме блока и россыпь горошек добавляют контрастности и необычности букве.
Шаг 11
Я использую инструмент Pen Tool , чтобы создать блок сплошного цвета, чтобы составить букву «E».
И снова инструмент Pen Tool , чтобы создать последовательность из трех треугольников, чтобы получилась W-образная форма.
Я использую инструмент Line Segment Tool () , чтобы добавить украшение цвета Mint к правой стороне буквы.
Шаг 12
В зависимости от выбранной фразы у вас уже может быть достаточно букв или элементов букв для повторного использования для создания последнего слова вашего дизайна, здесь «ГОД».
Когда вы создали все буквы, уменьшите масштаб и оцените, как буквы расположены между собой и все ли находится в центре.
Когда дизайн вас устраивает, можно приступать к добавлению текстуры. На этом этапе нам нужно перейти в Photoshop. Чтобы создать работоспособную копию изображения, перейдите в меню «Файл »> «Экспорт » в Illustrator и сохраните изображение как высококачественный файл JPEG .
3. Как добавить текстуру ручной работы к вашей надписи
Шаг 1
Убедитесь, что Файл> Сохранить как ваш рисунок надписи в Illustrator .Затем откройте Photoshop и перейдите в File> New.
Я хочу, чтобы мои буквы подходили для использования в качестве изображения Instagram , поэтому я установил Width и Height холста на 1080 пикселей. Нажмите ОК , чтобы создать документ.
Шаг 2
Перейдите в File> Place и перейдите к изображению текстуры бумаги, которое вы скачали ранее.
Щелкните Place и, удерживая Shift , масштабируйте изображение по размеру холста.
Шаг 3
Снова выберите File> Place и на этот раз откройте версию JPEG вашего дизайна надписи, центрируя ее на холсте.
Из
Каковы примеры геометрических фигур в реальной жизни?
Геометрические формы встречаются практически везде. Куда бы вы ни посмотрели, почти все состоит из более простой геометрии. Ферменный мост состоит в основном из прямоугольников, квадратов и треугольников. Снеговик состоит из кругов, с морковным носиком конусообразной формы.
Эти формы, как двумерные, так и трехмерные, невероятно важны и в контексте изучения математики. Предоставление примеров геометрических фигур научит вас и ваших учеников их функциям и способам их лучшего понимания.
Примеры геометрических фигур
Вот список различных геометрических фигур с описанием и примерами того, где их можно найти в повседневной жизни.
- Окружность : круглая форма с таким же радиусом от фиксированной точки в центре.
например, пирог с пиццей, печенье, колеса велосипеда - Квадрат : Четыре равные прямые стороны с четырьмя прямыми углами
например, гараж, квадратные штампы, плитка на полу - Треугольник : Трехсторонняя фигура с прямыми сторонами
например, кусок пиццы, ломтик сыра, разрезанный по диагонали - прямоугольник : четыре прямые стороны с четырьмя прямыми углами, разной длины и ширины
например, многоквартирные дома, доска для классиков , книжная обложка, большинство сотовых телефонов - Пентагон : Пять прямых сторон, обычно равной длины
e.г., Пентагон, рисунки на футбольных мячах - Шестиугольник : Шесть прямых сторон, обычно равной длины
, например, ледяные кристаллы, несколько снежинок, соты улья - Гептагон : Семь прямых сторон, обычно равных длина
например, крышки для корзины для печенья, некоторые типы коробок для таблеток - Восьмиугольник : восемь прямых сторон, обычно равной длины
например, знак остановки, некоторые зонтики, кольцо UFC - Nonagon: девять прямых сторон, обычно равной длины
эл.g., крышки для некоторых типов контейнеров / контейнеров для печенья - Decagon : 10 прямых сторон, обычно равной длины
например, монеты некоторых коллекционеров - Trapezoid: Четырехсторонняя фигура с одной парой параллельных сторон
например, фермы на некоторых мостах, пирамида с обрезанной вершиной, коробка для попкорна - Параллелограмм : четырехсторонняя фигура с двумя парами параллельных сторон
например, классический ластик, некоторые кошельки, структура некоторых мостов - Ромб : параллелограмм со сторонами равной длины
e.g., бейсбольные бриллианты, некоторые воздушные змеи, определенные кристаллы - Звезда : многосторонний многоугольник с точками и тупыми углами
например, Звезда Давида, звездные наклейки, звездное ожерелье, звездочки для печенья - Полумесяц : A изогнутая форма серпа, изогнутая и сужающаяся к точке
, например, серповидные валки, луна во время определенных фаз, изогнутая форма на флагах Пакистана и Турции - Овальный : вытянутый круг, радиус которого меньше по одной оси чем другие
e.г., яйца, булочки для хот-дога, беговая дорожка - Полукруг : круг, разрезанный ровно пополам по диаметру
, например, половина печенья, половина пирога с пиццей, другие неполные круги - Цилиндр : Трехмерная фигура с параллельными сторонами и круглым поперечным сечением
, например, картон внутри бумажного полотенца, прямая труба, стакан для питья - Призма: трехмерная фигура, в которой одна пара противоположных сторон имеет одинаковую форму, соединены прямыми параллельными сторонами
e.г., картонная коробка, фотоаппараты, коробка для хлопьев, коробка Toblerone - Пирамида : трехмерная фигура с одной плоской стороной и краями, которые сходятся вместе в точке
, например, Великая пирамида в Гизе, крыша дома.
Конечно, некоторые из этих форм взаимозаменяемы. Например, сумка не всегда может быть параллелограммом, поскольку, безусловно, существуют круглые сумки и другие возможные типы. Этот список также не является исчерпывающим, так как существует множество других двухмерных и трехмерных геометрических фигур.
Примеры геометрических фигур предназначены для того, чтобы вы могли увидеть, насколько эти фигуры действительно важны в повседневной деятельности. Таким образом, вы можете передать информацию о практическом применении геометрических фигур любому, кого вы обучаете.
Многоугольники и многогранники
«Геометрические формы» — это более общий термин, охватывающий все эти типы форм. Однако, если вы хотите быть более конкретным, фигуры, которые имеют только два измерения (например, квадрат), можно назвать многоугольниками.Это определяется как плоская фигура с как минимум тремя прямыми сторонами, обычно создающая замкнутую форму.
Когда вы переносите это в третье измерение, как в случае с кубом, он становится твердой фигурой, которую вы называете многогранником. Суффиксы -gon и -hedron могут затем использоваться для определения количества сторон или ребер, например, десятиугольника и декаэдра.
| Загадка Ферма и тройки Пифагора | |||||||||||||||||||||||||||||||||||||||||
Теорема Пифагора утверждает, что для прямоугольного треугольника с катетами a и b и гипотенузой
c, Числа, соответствующие этому шаблону, называются тройками Пифагора. На диаграмме ниже показаны некоторые из этих троек Пифагора. Изучите шаблон в диаграмму, чтобы найти следующие два набора троек. | |||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||
| Будет ли какая-либо из троек удовлетворять Великой теореме Ферма — a 3 + b 3 = c 3 ? А как насчет a 4 + b 4 = c 4 ? Следующие формулы можно использовать для генерации чисел, удовлетворяющих Теорема Пифагора.Убедитесь, что x> y и что один из них нечетный, а другой даже. a = x 2 — y 2 b = 2xy c = x 2 + y 2 Вот пример: пусть x = 7 и y = 6.
Совет: чтобы получить числа a, b и c, не имеющие общих делителей, убедитесь, что ваши числа x и y не имеют общих делителей, например 5 и 6 или 5 и 8, но не 5 и 10. | |||||||||||||||||||||||||||||||||||||||||
| Предоставлено Шарлин Эванс | |||||||||||||||||||||||||||||||||||||||||
Ссылка: Коллинз, Уильям и др. Математика: приложения и связи, Курс 3.Гленко / Макгроу Хилл. Огайо. 1998 г. | |||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | |||||||||||||||||||||||||||||||||||||||||
| Волшебный круг | |||||||||||||||||||||||||||||||||||||||||
Материалы
Попросите учащихся решить три задачи, которые имеют значение только для диаметра. дано. | |||||||||||||||||||||||||||||||||||||||||
| Предоставлено Дэвидом Лейбом | |||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущая | |||||||||||||||||||||||||||||||||||||||||
| Пентаграммы природы | |||||||||||||||||||||||||||||||||||||||||
Цель: Учащиеся смогут использовать алгебраические понятия при изучении природы. Цель: Учащиеся будут использовать геометрию и концепцию соотношений и применять их для измерения предметов, встречающихся в природе. Материалы: Пятилепестковые цветы, Яблоки, Доллары, Морская звезда. Фокус: Покажите фильм: Дональд Дак в стране математики (его можно получить через Library Media Services, 259 долларов США) Процедура:
Оценка: Попросите учащихся сообщить, что они обнаружили из различных использованных материалов. Они нашли золотые треугольники? Что помогло? Что нужно исправить? | |||||||||||||||||||||||||||||||||||||||||
| Предоставлено Дженнифер Гарретсон | |||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущий | |||||||||||||||||||||||||||||||||||||||||
| Действие полосы Мебиуса | |||||||||||||||||||||||||||||||||||||||||
Для этого задания вам понадобится пять полосок бумаги на каждого учащегося.Каждый полоса должна быть примерно 3 х 14 дюймов. Каждому ученику также понадобится около двух футов ленты, подойдет либо прозрачная лента, либо клейкая лента), ножницы и ручка или карандаш.
| |||||||||||||||||||||||||||||||||||||||||
| Предоставлено Стивом Бикслером | |||||||||||||||||||||||||||||||||||||||||
Рекомендации: Этот проект разработан: [email protected] | |||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущая | |||||||||||||||||||||||||||||||||||||||||
| Теорема Пифагора с танграммами | |||||||||||||||||||||||||||||||||||||||||
Цель: Использование танграмм для введения теоремы Пифагора. Цель: Студенты будут использовать танграммы как введение в пифагорейский язык. Теорема. Материалы: Набор Tangram (квадрат 4 x 4 дюйма), бумага, карандаш. Чтобы у каждого ученика было достаточно деталей для некоторых из этих заданий, вы может позволить студентам работать в парах или предоставить каждому студенту более один набор танграмм. Знакомство с Пифагором Шаг 1 Шаг 2 Шаг 3 Шаг 4 Шаг 5 Шаг 6 (Вот! Ваши ученики только что открыли теорему Пифагора !!!) Это прекрасная возможность поделиться со своими учениками историей Пифагор и как он разработал эту теорему. | |||||||||||||||||||||||||||||||||||||||||
| Предоставлено Анжелой Церадски | |||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущая | |||||||||||||||||||||||||||||||||||||||||
| Активность формулы Эйлера | |||||||||||||||||||||||||||||||||||||||||
Название урока: Формула Эйлера, зубочистки и мармеладки. Предметная область: Геометрия, предалгебра Уровень оценки: Восьмой Описание или формулировка результата: Обнаружив информацию о плоских сетях и трехмерных объектах, учащиеся смогут продемонстрировать, как удовлетворить формулу Эйлера. Целей:
Для оценки понимания учащимся представленного материала будут даны устные вопросы и ответы, а также тест с карандашом и бумагой из десяти вопросов. | |||||||||||||||||||||||||||||||||||||||||
| Предоставлено Яном Свенсоном | |||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущая | |||||||||||||||||||||||||||||||||||||||||
| Площадь поверхности и объем | |||||||||||||||||||||||||||||||||||||||||
Это упражнение должно научить ученика вычислять объем и площадь поверхности цилиндра.Эту деятельность можно легко связать с историей, обсуждая, как древние могли измерять объем или даже длину до того, как существовала стандартизированная система измерения. Процедура:
| |||||||||||||||||||||||||||||||||||||||||
| Предоставлено Линдси Истридж | |||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Назад | |||||||||||||||||||||||||||||||||||||||||
| Магические круги Создание усеченного тетраэдра. | |||||||||||||||||||||||||||||||||||||||||
Я приобрел это занятие во время семинара за 259 долларов США в Уичито, штат Канзас, под названием «Математика в понедельник вечером».Я учил этому классу от третьего класса до колледжа. Это упражнение помогает развивать, укреплять и даже может использоваться для пополнения словарного запаса по математике. Это задание можно выполнить с разными уровнями обучения, просто изменив словарный запас, чтобы он соответствовал уровню навыков, с которым вы работаете. Это отличное упражнение на слушание / мелкую моторику. (Ключевые слова указаны в скобках.) Материалы: один 7-дюймовый бумажный круг, карандаш и линейка Посмотрите на форму, которую вы держите.Опишите это. Это ( круг ). Посмотрите на внешний край вашего круга. Как называется расстояние по внешней стороне круга? ( Окружность ) Сложите круг прямо пополам и хорошо согните его. Раскройте круг, полученная складка — это ( диаметр ) круга. Держите кружок на концах складки. Снова сложите круг пополам, но на этот раз совместите конечные точки складки. Раскройте свой круг, это тоже диаметр? Откуда вы знаете? Линии ( пересекаются с )? Да. Есть ли что-то особенное в том, как эти линии пересекаются? Они образуют четыре угла 90 o (или прямых). Этот особый тип перекрестка называется ( перпендикуляр ). Поместите точку, не больше ширины карандаша, в точке соединения складок. Это называется ( центр ) круга. Карандашом обведите одну из линий от центра к краю круга. Эта линия от центра называется (радиус ). Загните один из внешних изогнутых краев круга, пока он не коснется точки в середине. Хорошо согните. Раскройте складку и посмотрите на только что сделанную складку. Это диаметр? Это радиус? Почему или почему нет? Эта линия называется ( аккорд ). Посмотрите на изогнутую часть круга между точками, где эта линия касается внешней стороны круга. Это называется ( arc ). Можете ли вы найти другие дуги на своем круге? Возьмите противоположную сторону вашего круга и сложите его так, чтобы изогнутая часть касалась центра, а нижняя часть образовывала идеальную точку. Ваш круг будет похож на мороженое ( рожок ). Хорошо согните. Сложите верхнюю часть рожка мороженого вниз, пока изогнутая часть не коснется центра круга.Верхние углы должны образовывать идеальные точки, хорошо сгибаться. Теперь опишите свою форму. ( Треугольник ) Вы замечаете что-нибудь особенное в этом треугольнике? Посмотрите на все (, , углы, , ), они такие же, как и все стороны одинаковые. Этот треугольник называется ( равносторонний и / или острый треугольник ). Вы также можете использовать ( равносторонний ). Сложите новый треугольник пополам, совместив две точки.Хорошо мнется. Новое прекращение делит треугольник пополам, эта линия называется ( высота или высота ). Можете ли вы выяснить что-нибудь еще об этом треугольнике? Это ( прямоугольный треугольник ). Раскройте прямоугольный треугольник до равностороннего треугольника. Возьмите верхний угол большого треугольника и сложите его. Сгибая по сгибу по высоте, вы можете совместить верхнюю точку до нижней линии сгиба.Внутри вы увидите три треугольника поменьше. Переверните бумагу, чтобы не было видно складок. Как называется эта форма? Поскольку он имеет четыре стороны, его можно классифицировать как ( четырехугольник ). Поскольку у этого четырехугольника две стороны (, , параллель, , ) и две, не совпадающие, он также называется (, , трапеция, , ). Переверните его, чтобы теперь были видны все складки.Сложите один из внешних треугольников так, чтобы он лежал прямо поверх центрального треугольника. Переверните его и опишите форму, которую вы сейчас видите. Это не воздушный змей, в небе летают воздушные змеи. Это не бриллиант, я ношу бриллианты на пальцах. В математике эта форма называется ( ромб ). Снова переверните фигуру и снова сложите последний внешний треугольник на центральный. У вас должен получиться равносторонний треугольник меньшего размера. Раскройте все три маленьких треугольника.Соедините три свободные точки вместе, чтобы у вас получилась пирамида ( , ). На этом этапе вы можете обсудить ( граней ) ( ребер ) ( точек ) ( вершин ) ( основание ) и тот факт, что это ( треугольная пирамида ), а не квадратная пирамида, как в Египте. Откройте пирамиду до большого равностороннего треугольника. Согните одну из точек так, чтобы она касалась точки посередине. Какую форму вы воссоздали? Трапеция хоть и не традиционной формы, ее все же можно идентифицировать как трапецию. Сложите еще одну точку так, чтобы она касалась точки посередине. Какая у вас форма? ( Пентагон ) Несмотря на то, что это не традиционная форма, к которой вы привыкли, у нее все еще есть пять сторон, поэтому он по-прежнему классифицируется как пятиугольник. Теперь сложите последнюю точку. Какой он сейчас формы? ( Hexagon ) Обсудите ( плоскость ) цифры. Переверните на другую сторону и вставьте один из углов в лоскут на противоположной стороне треугольника. Возможно, вам придется попробовать более одного. Выберите тот, который вам больше всего подходит. Сдвиньте последний угол под / внутрь других. Вы создали ( усеченный тетраэдр )! Для любой формы во время этого упражнения вы можете попросить учащихся вычислить площадь поверхности, объем, периметр и / или площадь. | |||||||||||||||||||||||||||||||||||||||||
| Предоставлено Анжелой Церадски | |||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущая | |||||||||||||||||||||||||||||||||||||||||
| The Water Hose Experiment. | |||||||||||||||||||||||||||||||||||||||||
Это задание можно выполнить за один урок. Чтобы ответить на вопросы и сделать выводы, может потребоваться еще один урок, в зависимости от продолжительности вашего урока. Прекрасно подходит для весны, когда у школьников и учителей весенняя лихорадка.Его цель — найти оптимальный угол для достижения наибольшего расстояния. В зависимости от того, какой класс вы преподаете, это задание можно изменить. История: Простой транспортир — старинный прибор. Создан первый комплексный транспортир для определения положения лодки на навигационных картах. Названный трехрычажным транспортиром или указателем станции, он был изобретен в 1801 году Джозефом Худдартом, капитаном ВМС США. Центральный рычаг неподвижен, а два внешних поворотных, их можно установить под любым углом относительно центрального рычага. Материалы:
Присоедините садовый шланг к водопроводному крану и отрегулируйте поток воды так, чтобы он находился под постоянным давлением. Начните с угла 0 градусов к земле, измерьте и запишите расстояние, которое поток проходит в горизонтальном направлении по земле.Повторите эти действия для углов 20 o , 30 o , 45 o , 70 o и 75 o . Вопросы и выводы:
URL: http://inventors.about.com/science/inventors/libr…/blmeasurement.htm?terms=protractor+histor 14.06.00 20:30 | |||||||||||||||||||||||||||||||||||||||||
| Предоставлено Эми Траутман | |||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Назад | |||||||||||||||||||||||||||||||||||||||||
| Расчет числа Пи. | |||||||||||||||||||||||||||||||||||||||||
Примерно 4000 лет назад люди впервые начали понимать пи. Считалось, что его стоимость была около трех. Сегодня мы используем лучшее приближение числа пи. Это 3,14. Пи — иррациональное число. Это означает, что он не повторяется в шаблоне. Пи определяется как отношение длины окружности к диаметру той же окружности. А теперь небольшое упражнение, которое поможет вам определить число Пи. Материалы:
Сначала на листе бумаги сделайте 4 столбца с надписью: объект, диаметр, окружность и соотношение.(См. Пример ниже.) Оберните веревку вокруг объекта. Это измеряет окружность объекта. Измерьте строку с помощью измерительной линейки. Запишите значение в столбец с надписью «длина окружности». Затем измерьте расстояние прямо поперек объекта. Поместите это значение в столбец, обозначенный как диаметр. Теперь возьмите длину окружности, разделенную на диаметр. Поместите это в столбец с надписью «Соотношение». Это близко к пи? Убедитесь, что вы вывели соотношение до трех или четырех десятичных знаков.
| |||||||||||||||||||||||||||||||||||||||||
| Предоставлено Джереми Траутманом | |||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущее | |||||||||||||||||||||||||||||||||||||||||
| Активность тесселяции. | |||||||||||||||||||||||||||||||||||||||||
Класс: 5 или 6 Время: 20-30 минут занятий Необходимые материалы: Смесь многоугольников, таких как геоблоки, бумага, карандаш и цветные карандаши. Урок 1 В фокусе: Поместите разные фигуры наверх. Обсудите в классе сходство и различие форм.Сообщите учащимся, что фигуры представляют собой многоугольники (фигура на близком расстоянии). Расскажите о концепции мозаики и о том, как не должно быть разрывов или перекрытий. Продемонстрируйте концепцию наверху, используя квадрат. Задание: Попросите учащихся предсказать, какие фигуры будут мозаичными, а какие нет. Составьте диаграмму, показывающую результаты прогнозов студентов. Дайте каждому столу (или ученику, если возможно) набор фигур. Попросите учащихся самостоятельно определить, будет ли фигура мозаикой. Заключение: Обсудите всем классом, какие формы плитки на самом деле формируют, а какие нет. Сравните открытия с предсказаниями на картах. Завершение: Предложите учащимся определить многоугольник и то, что они узнали о нем, в небольшой дневной записи. Урок 2 В фокусе: Просмотрите концепции многоугольника и мозаики. Расскажите о термине тесселяция и о том, как он соотносится с уроком 1.Обсудите концепции скольжения, вращения (поворота) и отражения (переворачивания) и продемонстрируйте их на потолке. Задание: Попросите учащихся выбрать две или более фигур. Попросите учащихся раскрасить каждую форму в один цвет. Попросите учащихся обвести фигуры черным маркером, если это слайд. Обведите фигуру синим маркером, если это вращение. Отражение следует обвести красным маркером. Заключение: Попросите учащихся поднять руки, когда они закончили.Инструктор проверит результаты. Закрытие: Обсудите, какие различные формы объединяют в тесселяцию результатов построения диаграмм. Разрешите учащимся записывать свои выводы. Урок 3 Фокус: Просмотрите предыдущие уроки. Обсудите, как студенты будут применять свои знания техники мозаики для поиска концепции в искусстве. Активность: Предоставьте несколько произведений разных художников, включая несколько произведений М.К. Эшер. Предложите учащимся изучить различные произведения искусства, чтобы выяснить, использует ли художник технику мозаики. Заключение: Попросите учащихся обсудить, что они нашли в деталях. Выскажите гипотезу, почему художники использовали или не использовали технику тесселяции. Окончание: Попросите учащихся записать свои выводы в своих дневниках. | |||||||||||||||||||||||||||||||||||||||||
| Предоставлено CiCi Naifeh | |||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущая | |||||||||||||||||||||||||||||||||||||||||
| Площадь и объем геометрических фигур. | |||||||||||||||||||||||||||||||||||||||||
Площадь геометрических фигур Цель: Дать студенту возможность попрактиковаться в вычислении площади различных геометрических фигур. Необходимые материалы: Использованные журналы, ножницы, линейки, клей, плотная бумага и калькуляторы Процедура:
Чтобы подчеркнуть процесс решения проблемы (решить проблему с помощью метода, о котором вы уже знаете), дайте учащимся упрощенную картинку, взятую из книжек-раскрасок, и попросите их оценить площадь изображения. Используя описанный выше метод, учащиеся должны разделить изображение по формам и вычислить площадь каждой формы, а затем суммировать формы областей, чтобы оценить площадь изображения. Практическое применение: Если кто-то собирается красить комнату, необходимо определить общую площадь всех стен, чтобы купить нужное количество краски. Объем геометрических фигур Цель: Дать ученикам возможность визуально понимать трехмерные геометрические формы и практиковаться в вычислении объема Необходимые материалы: Самодельные ингредиенты для игр, плита, кастрюля, ложка, линейки и калькуляторы. Процедура:
| |||||||||||||||||||||||||||||||||||||||||
| Предоставлено Джуди Ласатер | |||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущая | |||||||||||||||||||||||||||||||||||||||||
| Какой формы ваша земля? | |||||||||||||||||||||||||||||||||||||||||
Целей:
Материалы: Для каждого учащегося или группы: один лист миллиметровой бумаги, приклеенный или приклеенный на гофрированный картон или жесткий пенопласт; замкнутая петля из бечевки, длиной 20 сантиметров; приблизительно шесть прямых кнопок или канцелярских кнопок на учащегося или группу; карандаш и бумага для записей. Историческая справка: Согласно римской мифологии Дидона была дочерью царя Тира. Ее брат Пигмалион убил ее мужа, и она сбежала, опасаясь за свою безопасность. Дидона пересекла Средиземное море со всем своим богатством и некоторыми товарищами и высадилась в североафриканском королевстве Ливия. Здесь она искала землю в качестве убежища для своей группы. Король согласился дать ей столько земли, сколько она сможет покрыть шкурой быка. Дидона кое-что знала о геометрии и хотела как можно больше земли.Она разрезала шкуру быка на тонкие полоски, а затем соединила их в одну длинную прядь. Как вы думаете, какую форму она заключила? Состав: Студенты могут выполнять это задание индивидуально или в группах. Возможные групповые роли для четырех участников: два ученика должны создавать формы, один — для вычисления площадей, а один — для записи форм, размеров и площадей. Каждой группе понадобится один набор материалов, как описано выше: миллиметровая бумага на доске, кнопки и веревка. Задание: Студенты должны использовать веревку и кнопки, чтобы разложить плоские фигуры на сетке.Студентам необходимо будет вычислить площадь каждой фигуры, которую они создают, поэтому выбранные формы будут зависеть от базовых знаний студентов. Предлагаемые фигуры: квадрат, прямоугольники, треугольники и круг. Напомните учащимся, что они могут образовывать более одного прямоугольника и более одного треугольника. Студенты должны рассчитать площади для каждой сформированной фигуры и решить, какую форму, по их мнению, следует выбрать Дидоне. Примечание: , если это используется как упражнение для представления областей плоских фигур, учащиеся могут находить области, считая квадраты.В качестве дополнительного задания учащиеся должны использовать формулы площади. Следующая таблица или аналогичная может быть предоставлена для ведения учета:
Вопросы для обсуждения:
В конце концов Дидона отмерила форму полукруга, соединив одну точку на берегу с другой. Таким образом, вода составляла одно из ее требований, и у нее было дополнительное преимущество — выход к морю. Ей нужно было только использовать шкуру, чтобы оградить землю, поэтому выделенная ею территория была как можно больше и желательна. Король Ливии сдержал свое слово и отдал ей землю.Зарекомендовала себя умная Дидона, будущая королева Карфагена. Попросите учащихся развязать петли из веревок и с помощью 20-сантиметровых прядей образовать полукруги по краям решетки. Вычислите площадь полученного таким образом полукруга, чтобы понять, насколько умен Дидона. Связанные действия: Следующий трюк может стать забавным введением в занятие. Принесите в класс лист бумаги размером, возможно, с лист бумаги для принтера.Спросите своих учеников: как вы думаете, я могу вырезать отверстие в этом листе бумаги и протолкнуть его (впишите имя какого-нибудь ученика в классе)? Когда студенты выражают свой скептицизм, прорежьте в бумаге большое отверстие, просуньте руку в отверстие и осторожно толкните выбранного ученика. Затем достаньте свежий лист бумаги с очень маленьким отверстием. Спросите, как вы думаете, я смогу провести (того же ученика) через лист бумаги с этим отверстием? Общая реакция будет такой, что вы, вероятно, не сможете, хотя некоторые студенты будут искать другой трюк. Чтобы показать им, что вы можете делать то, что вы сказали, возьмите лист бумаги с таким же маленьким отверстием и прорезями, как показано на схеме ниже. Вы можете использовать уже имеющийся у вас лист и вырезать прорези, пока они ждут, но это займет много времени. Откройте прорези, чтобы образовалась одна огромная бумажная петля, и наденьте ее прямо на голову учеников. Вы сделали это! | |||||||||||||||||||||||||||||||||||||||||
| Предоставлено Лори Кисс | |||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущая | |||||||||||||||||||||||||||||||||||||||||
| Геометрический текстильный дизайн. | |||||||||||||||||||||||||||||||||||||||||
Иногда у студентов возникают проблемы с соотнесением математики с реальным миром; Следовательно, эта деятельность в области геометрического текстильного дизайна будет акцентировать внимание на геометрических формах и узорах в сочетании с художественным дизайном, компьютерными приложениями и возможностями карьерного роста. Цель: Для каждого ученика разработать свой собственный геометрический текстильный квадрат, который будет превращен в лоскутное одеяло. Необходимые материалы: Тканевые квадраты геометрической формы (5 дюймов х 5 дюймов), шаблонная бумага, цветные карандаши, белые тканевые квадраты (5 дюймов х 5 дюймов), обрезки картона, малярная лента и краска для ткани. Процедура:
| |||||||||||||||||||||||||||||||||||||||||
| Предоставлено Джуди Ласатер | |||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Назад | |||||||||||||||||||||||||||||||||||||||||
| Изготовление многогранников. | |||||||||||||||||||||||||||||||||||||||||
Многогранник — это геометрическая фигура, которая является трехмерной версией плоского многоугольника (двумерного). Всего пять правильных многогранников. Это тетраэдр (4 грани), шестигранник или куб (6 граней), октаэдр (8 граней), додекаэдр (12 граней) и икосаэдр (20 граней).Ниже представлены выкройки двух многогранников, которые можно воспроизвести и трансформировать в трехмерные фигуры. Щелкните на фигурах, чтобы открыть окно с фигурой внутри для удобства печати. | |||||||||||||||||||||||||||||||||||||||||
| Предоставлено Сьюзен Истман | |||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущий | |||||||||||||||||||||||||||||||||||||||||
КОЛОКОЛЬЧИК: ГЕОМЕТРИЧЕСКИЙ ДУЛЛИНГ: Как можно использовать геометрические формы для представления концепций? Возьмите лист.Используя круги, квадраты и треугольники.
Презентация на тему: «КОЛОКОЛЬЧИК: ГЕОМЕТРИЧЕСКИЕ ДУЛЛИНГ: как можно использовать геометрические фигуры для представления концепций? Возьмите рабочий лист. Используя круги, квадраты и треугольники» — стенограмма презентации:
1 КОЛОКОЛЬЧИК: ГЕОМЕТРИЧЕСКИЕ ДУЛЛИНГИ: Как можно использовать геометрические формы для представления концепций?
Возьмите лист.Используя круги, квадраты и треугольники на листе в качестве фокусных точек, создайте 18 идентифицируемых изображений, добавив другие элементы, сохраняя при этом целостность исходных форм. ПРИМЕРЫ РАБОЧИХ ЛИСТОВ
2 Формы имеют два размера — высоту и ширину.
Форма обычно, хотя и не всегда, определяется линией.
3 Геометрические органические Есть 2 типа форм: — Именованные формы
— Часто созданные руками человека — Свободные формы — Часто неправильные и асимметричные — Часто встречаются в природе © juliannakunstler.com
4 © juliannakunstler.com
Формы могут быть: Положительными Отрицательными Формами, которые вы создаете — реальным объектом Фон © juliannakunstler.com
5 Положительные и отрицательные формы одинаково важны.
… Иногда их сложно отличить.
6 Так же, как линии, формы могут выражать эмоции.
Квадраты твердые и устойчивые. Изогнутые формы изящны. Перевернутые треугольники нестабильны. Угловые формы предполагают прочность конструкции. Наклоненное положение фигур предполагает движение.
7 Завершите свои Танграммы (инструкции, которым нужно следовать)
СЕГОДНЯ В КЛАССЕ… Завершите свои Танграмы (инструкции, которым следует следовать) Завершите свои геометрические рисунки, которые вы начали как колокол. Они будут собраны в конце урока и приняты как оценка в альбоме.
9 Расположите маленькие формы, чтобы воссоздать большие формы.
— Используйте фигуры, указанные в каждом столбце. — Формы не должны перекрываться или иметь зазоры. — Нарисуйте макет.
Рисование геометрических фигур — Как рисовать трехмерные фигуры
Поначалу рисование геометрических фигур может показаться сложной задачей. Все, что нужно, — это немного практики, чтобы понять это. Прочтите этот урок, а посмотрите видео ниже, чтобы узнать, как рисовать 3D-фигуры.
Измерение — один из самых важных методов рисования, которым может научиться художник, и он действительно помогает при рисовании геометрических фигур. Как только вы поймете, как использовать измерения, ваши рисунки станут более точными и точными.
Расходные материалы для чертежей:
Минимум 3 карандаша от светлого до темного.
Например: карандаш 4H, 2H и 4B
Обратите внимание на прозрачные формы и на то, что более светлый карандаш не был стерт на окончательном рисунке.
Шагов:
- Начните с более светлого карандаша 4H — рисуйте легко и свободно — этот слой служит подструктурой или сеткой.
- У большинства форм есть углы, которые мы не видим, но вы можете продолжить и нарисовать эти невидимые линии, если это поможет вам лучше понять свой рисунок.
- После того, как вы нарисовали все линии более светлым карандашом, переходите к немного более темному карандашу, например, карандашу 2H. Пришло время определить детали и затемнить «настоящие» линии.
- Закончите темным карандашом 4B — это последний шаг — рисуйте медленно и осторожно, определяйте и уточняйте геометрические формы, которые вы нарисовали.
Представьте, что есть 2d панель
стекло перед собой перпендикулярно
к вашей прямой видимости. По вашим меркам,
Держите карандаш вплотную к нему
воображаемый самолет.
Оставайтесь на том же месте, где вы рисуете.
Любой сдвиг вверх, вниз, влево или вправо будет
измените свои измерения.Для
по той же причине, старайтесь держать руку
прямо как вы снимаете мерки.
Используйте мольберт, чтобы подпереть бумагу. Чем ближе он соответствует углу вашего воображаемого стеклянного стекла, тем легче будет перенести измерения на вашу страницу!
Находим передаточные числа: Используя конец карандаша
и кончиком большого пальца измерьте общую
высоту вашего объекта (ов) и сравните ее с
общая ширина.Обратите внимание, образует ли if квадрат?
горизонтальный прямоугольник? вертикальный прямоугольник?
Углы поиска: Держите карандаш перпендикулярно к линии взгляда как
оказывается. Вы можете повернуть его на 360 градусов на
соответствовать любому углу! Если ваш карандаш выступает вперед
в космос станет в ракурсе,
давая вам неточные измерения.
Совет: Представьте, что в
перед вами циферблат часов, и отметьте, на какой час указывает ваш карандаш — это поможет вам сохранить этот угол при переносе на страницу.
Как нарисовать эти измерения на бумаге:
Соотношения: измерения пропорциональны и могут быть увеличены или уменьшены в зависимости от размера вашей бумаги.
Углы: Вот сложная часть. САМАЯ БОЛЬШАЯ проблема, с которой сталкиваются студенты, — это изменение угла в момент, когда карандаш касается страницы. Убедитесь, что измеренный угол совпадает с нарисованным углом. Если это помогает, направьте руку свободной рукой и убедитесь, что вы не скручиваете и не сгибаете запястье, когда рисуете этот угол на странице!
- Закройте один глаз, измеряя фигуру, которую вы рисуете.
- Во время измерения держите карандаш перпендикулярно линии взгляда.
- Используйте мольберт, чтобы подпереть бумагу так, чтобы она была перпендикулярна линии вашего взгляда.
- Не меняйте свою точку зрения. Сдвиг даже на пару дюймов может изменить ваши измерения.
- Во время измерения держите руку прямо — сгибание руки в локте даст противоречивые результаты.
- При поиске угла представьте, что карандаш прижимается к воображаемому стеклу.Наклоняя его вперед, карандаш укорачивается, что дает неверное измерение.
- Измерьте общую высоту и общую ширину объекта или группы объектов — отметьте, какие из них длиннее и на сколько — например: вписывается ли ширина в высоту дважды, трижды? и т. д.
- При нанесении измерения угла на бумагу убедитесь, что вы переносите правильный угол при рисовании геометрических фигур — не скручивайте и не сгибайте запястье.
Рисование наклонного эллипса:
- Посмотрите на углы (самые длинные и самые короткие размеры)
- Измерьте и сравните высоту сширина
- Не забудьте нарисовать эллипс в пределах его общих размеров
Вернуться от рисования геометрических фигур к урокам онлайн-рисования .

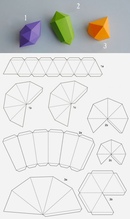 Рисуем их строго на одной линии, вплотную друг к другу.
Рисуем их строго на одной линии, вплотную друг к другу.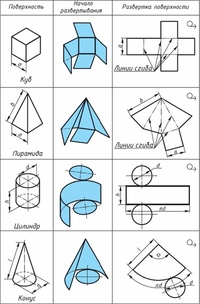 Отношение длины прямоугольника к диаметру определяется выражением: L=πD, где L- длина прямоугольника, а D — диаметр будущего цилиндра. Подставив в формулу требуемый диаметр, найдем длину прямоугольника, который будем рисовать на бумаге. Дорисовываем небольшие дополнительные треугольнички, которые необходимы для склеивания деталей.
Отношение длины прямоугольника к диаметру определяется выражением: L=πD, где L- длина прямоугольника, а D — диаметр будущего цилиндра. Подставив в формулу требуемый диаметр, найдем длину прямоугольника, который будем рисовать на бумаге. Дорисовываем небольшие дополнительные треугольнички, которые необходимы для склеивания деталей. С каждой стороне дорисовываем боковые стороны — параллелограммы. От любой из боковой стороны дорисовываем второе основание. Добавляем полоски для склеивания. Параллелепипед может быть прямоугольным, если стороны прямоугольники. Если параллелепипед не прямоугольный, то создать развертку немного сложнее. Для каждого параллелограмма нужно выдержать требуемые углы.
С каждой стороне дорисовываем боковые стороны — параллелограммы. От любой из боковой стороны дорисовываем второе основание. Добавляем полоски для склеивания. Параллелепипед может быть прямоугольным, если стороны прямоугольники. Если параллелепипед не прямоугольный, то создать развертку немного сложнее. Для каждого параллелограмма нужно выдержать требуемые углы.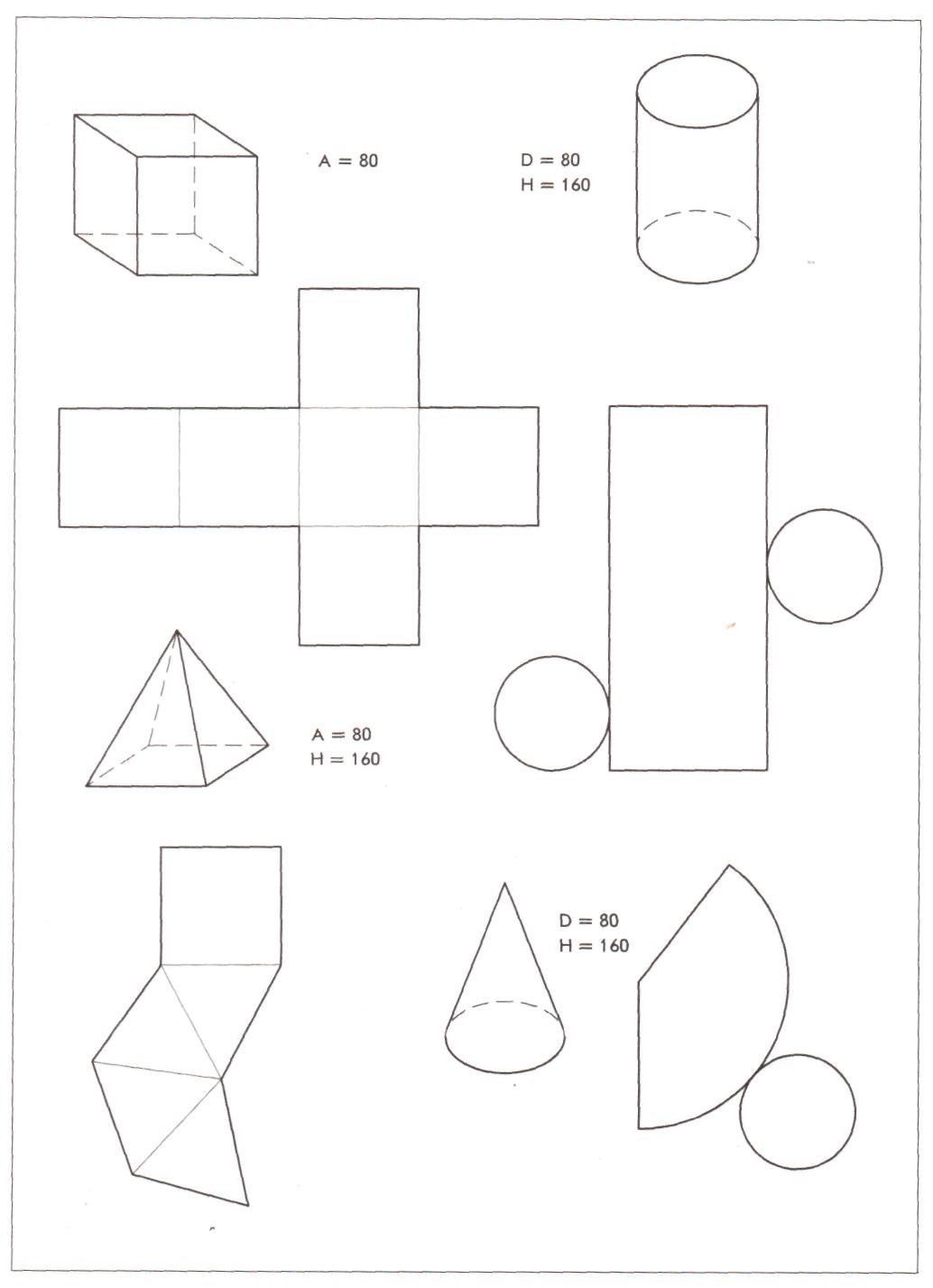 Так рисуем столько треугольников, сколько сторон в пирамиде. Дорисовываем полоски для склеивания в нужных местах.
Так рисуем столько треугольников, сколько сторон в пирамиде. Дорисовываем полоски для склеивания в нужных местах.