Главная
Новости
Формулы объемов и площадей геометрических фигур
17.09.2020
11:27
Подготовка к ЕГЭ по математике не может обойтись без изучения геометрии. Задачи на расчет площади и объема фигур, нахождение углов и длин сторон встречаются и в первой, и во второй части. В базовой математике ЕГЭ формулы на объем и площадь представлены в справочных материалах. Тем, кто сдает профильную, придется выучить их. Рассмотрим основную теорию.
Площадь — величина, которая есть у плоских фигур. Ее можно посчитать для квадрата, прямоугольника, параллелограмма, треугольника, ромба, трапеции, круга. Объем присущ трехмерным объектам, таким как куб, шар, параллелепипед, призма, пирамида, конус.
В таблицах представлены основные формулы объемов и площадей фигур для ЕГЭ. Мы советуем сохранить их себе, чтобы пользоваться при подготовке к ЕГЭ и быстро повторить теорию перед экзаменом.
09.04.2021
15:48
Формулы по планиметрии
Задачи по этому разделу связаны с нахождением площадей, сторон, углов
Читать далее
09.04.2021
15:48Как подготовиться к ЕГЭ с нуля?
Но можно ли подготовиться к ЕГЭ вообще с нуля? Это вполне реально, но лучше пойт.
..
Читать далее
09.04.2021
15:48
День открытых дверей в РУДН!
30 января в 11:00 приглашаем всех желающих на День открытых дверей РУДН в онлайн…
Читать далее
23.08.2022
Поздравляем с Днем защитника Отечества!
Изменения в расписании в связи с праздничными днями
Читать далее
20.12.2021
13:35
Подготовим всех к вступительным испытаниям (журналистика и архитектура)
Решили стать журналистом или архитектором? Ок, весьма достойный выбор!
Читать далее
20.
12.2021
Выбираешь профессию своей мечты? Велкам в наши летние школы!
Приходите к нам в гости — узнайте всё о профессии своей мечты.
Читать далее
Масару Ибука в своей книге «После трёх уже поздно» утверждает, что в первые три года жизни у ребенка самый высокий потенциал к обучению и развитию, поэтому бездействие сродни преступлению.
Конечно, нам может казаться, что ребенок слишком мал. Да и чему он может научиться, если не умеет даже говорить? Но мозг ребёнка, как губка, впитывает всю окружающую его информацию. И от родителей зависит, что усвоит ребенок в этом возрасте.
Стоит ли начинать изучать геометрические фигуры в столь раннем возрасте? Безусловно.
Ребенок живет в окружении геометрических форм. Знания, которые вы даёте, не должны быть оторваны от вашей повседневной жизни. Мама – проводник малыша в этом мире, и ей совершенно не обязательно иметь ученую степень, чтобы рассказать ребенку, как устроен мир.
Первые три года жизни ребенка – это период развития мозговых клеток, когда образуется прочная база для новых свершений. Уже в 3-4 месяца малыш способен различать формы. Это не означает, что пришла пора заучивать названия геометрических фигур, но мама при разговоре с крохой может стараться употреблять фразы: «А вот и наше любимое круглое блюдце», «Давай посмотрим, что в квадратной коробке» и подобные.
Знание геометрических фигур помогает:
И, конечно же, полученные дошкольником знания послужат ему отличным подспорьем в изучении математики в школе.
Есть немало техник и методик, которые сделают запоминание фигур интересным для детей. Подбор методик будет зависеть от возраста и познаний ребёнка.
При изучении геометрических фигур, важно действовать поэтапно. Начать следует с легких фигур: круг, квадрат, треугольник, ромб, прямоугольник, овал.
Знания этих фигур доступны для детей 2-3 лет.
Детки постарше, 4-5 лет, включают в свой лексикон и берут в оборот представления об трапеции, параллелограмме, пентагоне, гексагоне, октагоне, декагоне и других многоугольниках. Они уже умеют анализировать, поэтому с легкостью сравнивают и находят отличия между фигурами.
Старшие дошколята знакомятся с объемными фигурами: цилиндр, пирамида, куб, шар, конус, призма.
Разберем некоторые варианты техник по изучению геометрических фигур:
1. Сортер – ищем «домик» для каждой фигуры. Ребенок не только запомнит фигуры, но и будет развивать мелкую моторику вкупе с мышлением.
2. Лепка. Лепите вместе с малышом геометрические фигуры – лучшего занятия для развития мелкой моторики рук и усидчивости просто не придумаешь.
3. Объемные наклейки и магниты, изображающие геометрические фигуры, тоже могут помочь ребенку закрепить в памяти названия фигур.
4. Ищем половинки. Разрежьте геометрические фигуры на две части, смешайте и предложите малышу найти вторую половину.
5. Аппликации. Также из вырезанных фигур можно составлять геометрическую аппликацию. Например, домик (квадрат + треугольник), ёлочку, машинку.
6. Обводить пунктирные геометрические фигуры
7. Раскрасить или заштриховать предложенные вами геометрические фигуры.
7. Дорисовать фигуру по образцу.
8. Рисовать фигуры при помощи трафаретов.
9. Послушать сказку, где главные герои — геометрические фигуры, а потом зарисовать услышанное.
10. Положить в непрозрачный мешок фигуры разной формы и предложить на ощупь угадать форму предмета.
11. Отличная игра для развития памяти и внимательности. Взрослый готовит вырезанные фигуры разных цветов и размеров и выкладывает перед малышом. Они обсуждают цвета, называют фигуры, а после взрослый прячет фигуру.
Задача ребенка обнаружить и назвать, какой фигуры нет.
12. Выкладывание геометрических фигур при помощи счетных палочек или спичек. Когда ребенок овладеет этим навыком, можно перейти на более сложный уровень — решать задачки. Например, убери одну спичку так, чтобы получился треугольник.
13. Ассоциации. Предложите ребенку назвать предметы, на которые похож круг или прямоугольник.
14. Шнуровки и различные рамки-вкладыши, например, квадраты Никитина, где нужно из нескольких предметов воссоздать квадрат, либо доски Сегена, где необходимо вставить недостающую деталь.
15. Подвижные игры. Например, на асфальте рисуются овал, треугольник, квадрат, прямоугольник. По команде взрослого ребенок должен найти названную фигуру и встать в неё.
16. Видеоматериалы. Существует большое количество мультфильмов и обучающих материалов про геометрические фигуры. Посмотрите видео с малышом и обязательно обсудите увиденное.
17. Найдите в интернете и распечатайте картины, которые художники рисуют геометрическими формами, и предложите ребенку посчитать, сколько здесь кругов, прямоугольников и т. д.
Объемные фигуры можно изучать по аналогии с окружающим предметами (например, мяч = шар). И, конечно же, задействовать изучение предмета через игры:
Эта игра будет способствовать развитию мелкой моторики, воображению, пониманию свойств объемных фигур.Изучение геометрических фигур не должно становиться пыткой для ребенка и взрослого. Выбирайте ту методику, которая подходит именно вам. Проявите терпение и изобретательность, и тогда результат не заставит себя долго ждать. Главное, не забывайте поощрять ребенка за его новые открытия и время от времени повторять полученные знания.
Математика и логика для детей 7-13 лет
Развиваем логическое мышление через решение сюжетных математических задач в интерактивном игровом формате
узнать подробнее
На этой странице рассматриваются свойства трехмерных или «твердых» форм.
Двумерная фигура имеет длину и ширину. Трехмерная твердая форма также имеет глубину. Трехмерные формы по своей природе имеют внутреннее и внешнее, разделенные поверхностью. Все физические предметы, к которым можно прикоснуться, трехмерны.
На этой странице рассматриваются как прямолинейные тела, называемые многогранниками, которые основаны на многоугольниках, так и тела с кривыми, такие как шары, цилиндры и конусы.
Многогранники (или многогранники) представляют собой твердые тела с прямыми сторонами. Многогранники основаны на многоугольниках, двумерных плоских формах с прямыми линиями.
См. нашу страницу Свойства полигонов для получения дополнительной информации о работе с полигонами.
Многогранники определяются как имеющие:
Многогранники также часто определяются количеством ребер, граней и вершин, которые они имеют, а также тем, имеют ли все их грани одинаковую форму и размер. Как и многоугольники, многогранники могут быть правильными (на основе правильных многоугольников) или неправильными (на основе неправильных многоугольников).
Многогранники также могут быть вогнутыми или выпуклыми.
Одним из самых простых и привычных многогранников является куб. Куб — это правильный многогранник, имеющий шесть квадратных граней, 12 ребер и восемь вершин.
Пять правильных многогранников представляют собой особый класс многогранников, все грани которых идентичны, причем каждая грань является правильным многоугольником. Платоновые тела:
См. рисунок выше для иллюстрации каждого из этих правильных многогранников.
Призма — это любой многогранник, который имеет два совпадающих конца и плоские стороны . Если вы разрежете призму в любом месте по ее длине, параллельно ее концу, ее поперечное сечение будет таким же — вы получите две призмы. стороны призмы параллелограммы — четырехгранные фигуры с двумя парами сторон одинаковой длины.
Антипризмы аналогичны обычным призмам тем, что их концы совпадают. Однако стороны антипризмы состоят из треугольников, а не из параллелограммов. Антипризмы могут стать очень сложными.
Пирамида — это многогранник с многоугольниками в основании , который соединяется с вершиной (верхняя точка) с прямыми сторонами.
Хотя мы склонны думать о пирамидах с квадратным основанием, вроде тех, что строили древние египтяне, на самом деле они могут иметь основание любого многоугольника, правильного или неправильного.
Кроме того, пирамида может иметь вершину прямо в центре основания, т.0015 Правая пирамида или может иметь вершину не по центру, если это Наклонная пирамида .
Существует множество других типов многогранников: симметричные и асимметричные, вогнутые и выпуклые.
Архимедовы тела, например , состоят как минимум из двух разных правильных многоугольников.
Усеченный куб (как показано на рисунке) представляет собой архимедово тело с 14 гранями. Шесть граней представляют собой правильные восьмиугольники, а остальные восемь — правильные (равносторонние) треугольники. Фигура имеет 36 ребер и 24 вершины (угла).
Твердые фигуры с изогнутыми или круглыми краями не являются многогранниками. Многогранники могут иметь только прямые стороны. Также см. нашу страницу о двумерных изогнутых формах.
Многие объекты вокруг вас будут включать по крайней мере несколько кривых.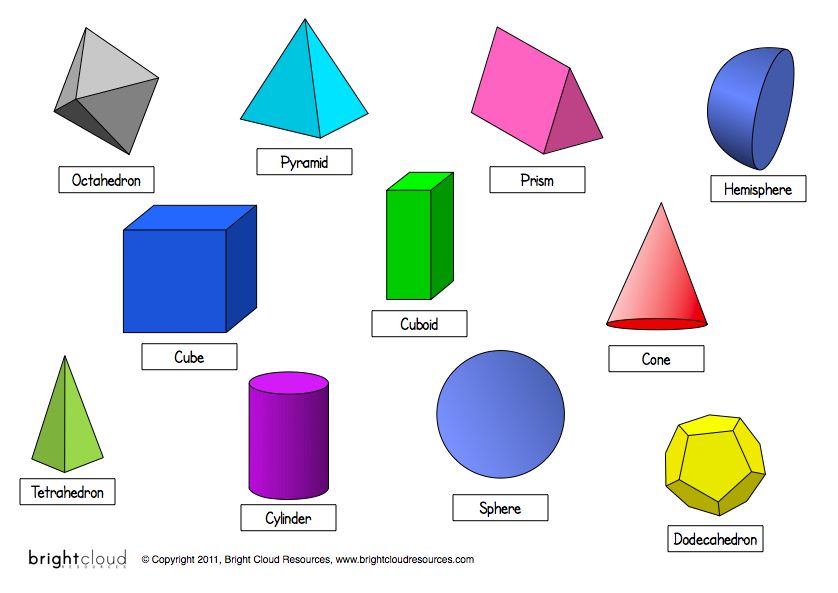
В геометрии наиболее распространенными искривленными телами являются цилиндры, конусы, сферы и торы (множественное число для тора).
| Общие трехмерные формы с кривыми: | |
|---|---|
| Цилиндр | Конус |
| Цилиндр имеет одинаковое поперечное сечение от одного конца до другого. Цилиндры имеют два одинаковых конца либо круга, либо овала. Несмотря на то, что они похожи, цилиндры не являются призмами, поскольку призма имеет (по определению) параллелограмм с плоскими сторонами. | Конус имеет круглое или овальное основание и вершину (или вершину). Сторона конуса плавно сужается к вершине. Конус похож на пирамиду, но отличается тем, что конус имеет одну изогнутую сторону и круглое основание. |
| Сфера | Тор |
Сфера в форме шара или шара представляет собой полностью круглый объект. Каждая точка на поверхности сферы находится на равном расстоянии от центра сферы. | Правильный кольцевой тор, имеющий форму кольца, шины или бублика, образован вращением меньшего круга вокруг большего круга. Существуют и более сложные формы торов. |
На нашей странице Вычисление площади объясняется, как вычислить площадь двухмерных фигур, и вам необходимо понимать эти основы, чтобы вычислять площадь поверхности трехмерных фигур.
Для трехмерных фигур мы говорим о площади поверхности , чтобы избежать путаницы.
Вы можете использовать свои знания о площади двухмерных фигур для расчета площади поверхности трехмерной фигуры, поскольку каждая грань или сторона фактически является двумерной формой.
Таким образом, вы определяете площадь каждой грани, а затем складываете их вместе.
Как и в случае с плоскими формами, площадь поверхности твердого тела выражается в квадратных единицах: см 2 , дюймы 2 , м 2 и так далее.
Вы можете найти более подробную информацию о единицах измерения на нашей странице Системы измерения .
Площадь поверхности куба равна площади одной грани (длина x ширина), умноженной на 6, поскольку все шесть граней одинаковы.
Поскольку грань куба представляет собой квадрат, вам нужно провести только одно измерение — длина и ширина квадрата по определению одинаковы.
Таким образом, одна грань этого куба равна 10 × 10 см = 100 см 2 . Умножаем на 6 количество граней куба, и получаем, что площадь поверхности этого куба равна 600см 2 .
Точно так же можно вычислить площадь поверхности других правильных многогранников (платоновых тел), найдя площадь одной стороны и умножив результат на общее количество сторон — см. диаграмму основных многогранников выше. .
Если площадь одного пятиугольника, составляющего додекаэдр, равна 22 см 2 , то умножьте это на общее количество сторон (12), чтобы получить ответ 264 см 2 .
Чтобы вычислить площадь поверхности стандартной пирамиды с четырьмя равными треугольными сторонами и квадратным основанием:
Сначала определите площадь основания (квадрата) длина × ширина.
Далее определите площадь одной стороны (треугольника). Измерьте ширину вдоль основания, а затем высоту треугольника (также известную как наклонная длина) от центральной точки основания до вершины.
Есть два способа вычислить площадь поверхности четырех треугольников:
Разделите ответ на 2, чтобы получить площадь поверхности одного треугольника, а затем умножьте на 4, чтобы получить площадь поверхности всех четырех сторон, или
Умножьте ответ на 2.
Наконец, сложите площадь основания и сторон вместе, чтобы найти общую площадь поверхности пирамиды.
Для расчета площади поверхности других типов пирамид, сложите площадь основания (известную как площадь основания) и площадь сторон (площадь боковых сторон).
Возможно, вам придется измерить стороны по отдельности.
Диаграммы сетей
Геометрическая сеть представляет собой двухмерный «шаблон» для трехмерного объекта. Сети могут быть полезны при расчете площади поверхности трехмерного объекта. На диаграмме ниже вы можете увидеть, как строятся базовые пирамиды, если пирамида «развернута», у вас остается сеть.
Для получения дополнительной информации о схемах сети см. нашу страницу 3D-формы и сети .
Для расчета площади поверхности призмы :
Призмы имеют два одинаковых конца и плоские стороны в виде параллелограмма.
Вычислите площадь одного конца и умножьте на 2.
Для правильной призмы (у которой все стороны одинаковы) вычислите площадь одной из сторон и умножьте на общее количество сторон.
Для призм неправильной формы (с разными сторонами) рассчитайте площадь каждой стороны.
Сложите два ответа вместе (концы + стороны), чтобы найти общую площадь поверхности призмы.
Пример:
Радиус = 5 см
Высота = 10 см
Чтобы вычислить площадь поверхности цилиндра , полезно подумать о составных частях формы. Представьте себе банку сладкой кукурузы — у нее есть верх и низ, оба из которых представляют собой круги. Если вы отрежете сторону по длине и сгладите ее, у вас получится прямоугольник. Следовательно, вам нужно найти площадь двух кругов и прямоугольника.
Сначала определите площадь одного из кругов.
Площадь круга равна π (пи) × радиус 2 .
При радиусе 5 см площадь одного из кругов равна 3,14 × 5 2 = 78,5 см 2 .
Умножьте ответ на 2, так как кругов два 157см 2
Площадь стороны цилиндра равна периметру круга × высоте цилиндра.
Периметр равен π x 2 × радиус. В нашем примере 3,14 × 2 × 5 = 31,4·9.0003
Измерьте высоту цилиндра. В данном примере высота составляет 10 см. Площадь стороны 31,4 × 10 = 314см 2 .
Общая площадь поверхности может быть найдена путем суммирования площадей кругов и стороны:
157 + 314 = 471 см 2
Пример:
Радиус = 5 см
Длина наклона
При расчете площади поверхности конуса необходимо использовать длину «наклона», а также радиус основания.
Однако вычислить его относительно просто:
Площадь круга в основании конуса составляет π (пи) × радиус 2 .
В этом примере расчет равен 3,14 × 5 2 = 3,14 × 25 = 78,5 см 2
Площадь стороны, наклонной части, можно найти по следующей формуле:
π (пи) × радиус × длина наклона.
В нашем примере расчет равен 3,14 × 5 × 10 = 157 см 2 .
Наконец, добавьте площадь основания к площади стороны, чтобы получить общую площадь поверхности конуса.
78,5 + 157 = 235,5 см 2
теннисный мяч:
диаметр = 2,6 дюйма
4 × π × радиус 2 .
Для сферы часто проще измерить диаметр — расстояние поперек сферы. Затем вы можете найти радиус, который составляет половину диаметра.
Диаметр стандартного теннисного мяча составляет 2,6 дюйма. Таким образом, радиус составляет 1,3 дюйма. Для формулы нам нужен радиус в квадрате. 1,3 × 1,3 = 1,69
Таким образом, площадь поверхности теннисного мяча равна:
4 × 3,14 × 1,69 = 21,2264 дюйма 2 .
Пример:
R (большой радиус) = 20 см
r (малый радиус) = 4 см
Чтобы вычислить площадь поверхности тора , вам нужно найти два значения радиуса.
Большой или большой радиус (R) измеряется от середины отверстия до середины кольца.
Малый или малый радиус (r) измеряется от середины кольца до внешнего края.
На диаграмме показаны два вида примера тора и способы измерения его радиусов (или радиусов).
Расчет площади поверхности состоит из двух частей (по одной для каждого радиуса).
Расчет одинаков для каждой части.
Формула: площадь поверхности = (2πR)(2πr)
Чтобы вычислить площадь поверхности примера тора.
(2 × π × R) = (2 × 3,14 × 20) = 125,6
(2 × π × r) = (2 × 3,14 × 4) = 25,12
Перемножьте два ответа, чтобы найти общую поверхность площадь примерного тора.
125,6 × 25,12 = 3155,072 см 2 .
Дальнейшее чтение из книги «Навыки, которые вам нужны»
Понимание геометрии
Часть руководства «Навыки, которые вам нужны» для счета
Эта электронная книга охватывает основы геометрии и рассматривает свойства форм, линий и тел. Эти концепции построены в книге, с примерами работы и возможностями для вас, чтобы попрактиковаться в ваших новых навыках.
Если вы хотите освежить свои знания или помочь своим детям в обучении, эта книга для вас.
Для трехмерных фигур вам также может понадобиться знать, какой объем они имеют.
Другими словами, если бы вы наполнили их водой или воздухом, сколько наполнения вам потребуется?
Это описано на нашей странице Расчет объема .
Улучшить статью
Сохранить статью
Улучшить статью
Сохранить статью
Объект, имеющий только высоту и длину, называется двумерной фигурой, а объект, имеющий высоту, длину и ширину, называется трехмерным объектом.
Examples of 2-D figures:
Examples of 3-dimensional figures:
длина = ширина = высота
Объем куба = a * a * a Объем куба = a 3 Площадь поверхности куба = 6 * площадь одной грани Площадь поверхности куба = 6 * a 2
Объем прямоугольного параллелепипеда = длина * ширина * высота
Площадь поверхности прямоугольного параллелепипеда = 6 * площадь одной грани.
Площадь поверхности прямоугольного параллелепипеда = длина * ширина
+ длина * ширина
+ ширина * высота
+ ширина * высота
+ длина * высота
+ длина * высота
Площадь поверхности прямоугольного параллелепипеда = 2 (длина * ширина).
+ ширина * высота
+ длина * высота ) 9Сфера имеет радиус, объем и площадь поверхности:
Объем сферы = (4/3) * π * r 3
Площадь поверхности сферы = 4 * &pi * радиус * радиус
Площадь поверхности сферы = 4 * &pi * радиус 2
Объем полушария = (2/3) * π * радиус * радиус * радиус
Площадь поверхности сферы = 2 * &pi * радиус * радиус 
Объем цилиндра = π * радиус * радиус * h Площадь криволинейной поверхности цилиндра = 2 * π * радиус * h Общая площадь поверхности = 2 * π * радиус * h + 2 * &pi * радиус * радиус базы до точки.
Объем конуса = (1/3)π * радиус * радиус * высота Площадь криволинейной поверхности конуса = π * радиус * наклонная высота Общая площадь поверхности конуса = π * радиус * наклонная высота + π * радиус * радиус
- Пирамида:
- Пирамида представляет собой 3-х пирамидальный объект с многоугольным основанием, это многоугольное основание соединено с вершиной.
Объем пирамиды = (площадь основания * высота) / 3
Примеры:
- Чему будет равна площадь криволинейной поверхности цилиндра радиусом 5 см и высотой 10 см?
Криволинейная поверхность цилиндра = 2 * π * r * высота = 2*22/7*5*10 = 314,285714286 см 2
- Какой будет наклонная высота конуса с площадью криволинейной поверхности 990 см 2 и радиусом 5 см?
Площадь криволинейной поверхности конуса = π * радиус * наклонная высота π * радиус * наклонная высота = (22/7) * 5 * l л = 63см
- Каков объем пирамиды с квадратным основанием со стороной основания 4 см и высотой 6 см?
Объем квадрата = площадь основания * высота / 3 = 4 2 * 6/3 = 16*6/3 = 32 см 3
- Какой будет объем шара радиусом 2,1 см
Объем шара = 4 * π * радиус 3 / 3 = (4 / 3) * (22 / 7) * 2,1 3 = 38,808 см 3
- Чему будет равна площадь поверхности куба, длина стороны которого равна 8 см?
Площадь поверхности куба = 6 * сторона 2 = 6*8 2 = 6 * 64 = 384 см 2
Статьи по теме
Что нового
Мы используем файлы cookie, чтобы обеспечить вам максимальное удобство просмотра нашего веб-сайта.
