Геометрические фигуры в развернутом в: 🛠 Развёртки геометрических фигур 👈
🛠 Развёртки геометрических фигур 👈
Большой выбор развёрток простых геометрических фигур.
Первое знакомство детей с бумажным моделированием всегда начинается с простых геометрических фигур, таких как кубик и пирамида. Не у многих получается склеить кубик с первого раза, иногда требуется несколько дней, чтобы сделать поистине ровный и безупречный куб. Более сложные фигуры цилиндр и конус требуют в несколько раз больше усилий нежели простой кубик. Если вы не умеете аккуратно клеить геометрические фигуры, значит и за сложные модели вам ещё рано браться. Займитесь сами и научите своих детей клеть эти «азы» моделирования по готовым развёрткам.
Для начала я, конечно же, предлагаю научиться клеить обычный кубик. Развёртки сделаны для двух кубиков, большого и маленького. Более сложной фигурой является маленький кубик потому, как клеить его сложнее, чем большой.
Итак, начнём! Скачайте развёртки всех фигур на пяти листах и распечатайте на плотной бумаге. Перед тем, как печатать и клеить геометрические фигуры обязательно ознакомьтесь со статьёй о том, как выбрать бумагу и как вообще правильно вырезать, сгибать и клеить бумагу.
Для более качественной печати советую использовать программу AutoCAD, и даю вам развёртки для этой программы, а также читайте, как распечатывать из автокада. Вырежьте развёртки кубиков с первого листа, по линиям сгиба обязательно проведите иголкой циркуля под железную линейку, чтобы бумага хорошо сгибалась. Теперь можно начинать клеить кубики.
Для экономии бумаги и на всякий пожарный я сделал несколько развёрток маленького кубика, мало ли вам захочется склеить не один кубик или что-то не получится с первого раза. Ещё одна несложная фигура это пирамида, её развёртки найдёте на втором листе. Подобные пирамиды стоили древние египтяне, правда не из бумаги и не таких маленьких размеров 🙂
А это тоже пирамида, только в отличие от предыдущей у неё не четыре, а три грани.
Развёртки трёхгранной пирамиды на первом листе для печати.
И ещё одна забавная пирамидка из пяти граней, её развёртки на 4-ом листе в виде звёздочки в двух экземплярах.
Далее шестигранник, склеить его будет ещё проще, чем пирамиды. Развёртки шестигранника на первом листе.
Более сложная фигура это пятигранник, хотя пятигранник сложнее начертить, нежели склеить.
Развёртки пятигранника на втором листе.
Вот мы и добрались до сложных фигур. Теперь придётся поднапрячься, склеить такие фигуры нелегко! Для начала обычный цилиндр, его развёртки на втором листе.
А это более сложная фигура по сравнению с цилиндром, т.к. в её основании не круг, а овал.
Развёртки этой фигуры на втором листе, для овального основания сделано две запасных детали.
Чтобы аккуратно собрать цилиндр его детали нужно клеить встык. С одной стороны дно можно приклеить без проблем, просто поставьте на стол заранее склеенную трубку, положите на дно кружок и залейте клеем изнутри. Следите, чтобы диаметр трубы и круглого дна плотно подходили друг к другу, без щелей, иначе клей протечёт и всё приклеится к столу.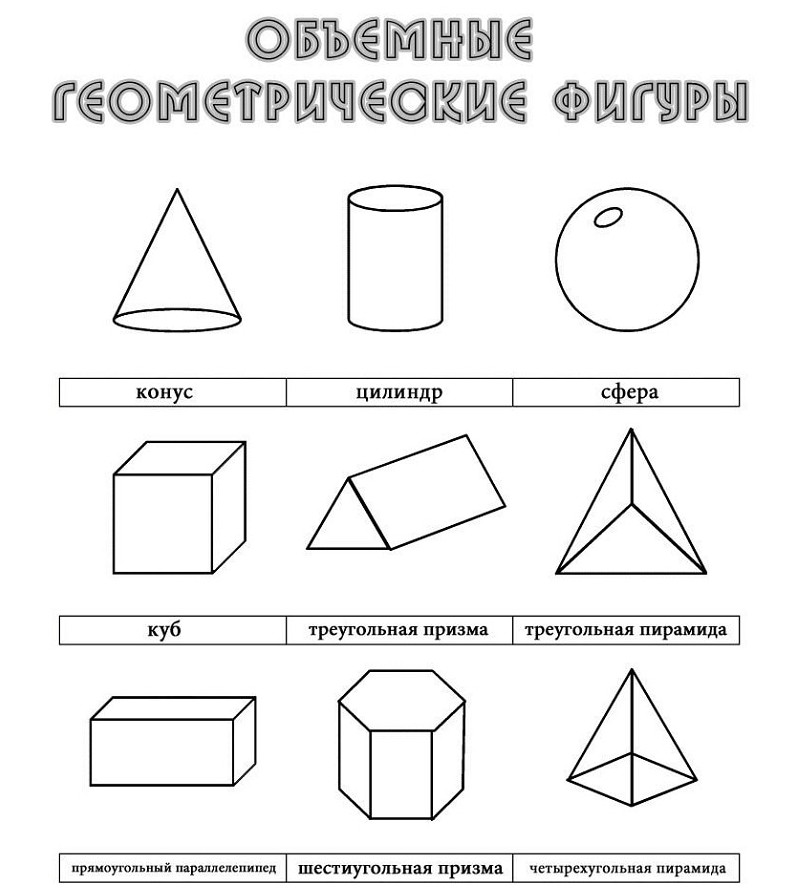 Второй кружок приклеить будет сложнее, поэтому приклейте внутри вспомогательные прямоугольники на расстоянии толщины бумаги от края трубы. Эти прямоугольники не дадут упасть основанию внутрь, теперь вы без проблем приклеете кружок сверху.
Второй кружок приклеить будет сложнее, поэтому приклейте внутри вспомогательные прямоугольники на расстоянии толщины бумаги от края трубы. Эти прямоугольники не дадут упасть основанию внутрь, теперь вы без проблем приклеете кружок сверху.
Цилиндр с овальным основанием можно клеить также как и обычный цилиндр, но он имеет меньшую высоту, поэтому тут проще вставить внутрь гармошку из бумаги, а наверх положить второе основание и по краю приклеить клеем.
Теперь очень сложная фигура – конус. Его детали на третьем листе, запасной кружок для днища на 4-ом листе. Вся сложность склеивания конуса в его острой вершине, а потом ещё будет очень сложно приклеить дно.
Сложная и одновременно простая фигура это шар. Шар состоит из 12-ти пятигранников, развёртки шара на 4-ом листе. Сначала клеится две половинки шара, а потом обе склеиваются вместе.
Довольно интересная фигура – ромб, её детали на третьем листе.
А теперь две очень похожие, но совершенно разные фигуры, их отличие только в основании.
Когда склеите эти обе фигуры, то не сразу поймёте, что это вообще такое, они получились какие-то совсем невосприимчивые.
Ещё одна интересная фигурка это тор, только он у нас очень упрощён, его детали на 5-ом листе.
И наконец, последняя фигура из равносторонних треугольников, даже не знаю, как это назвать, но фигура похожа на звезду. Развёртки этой фигуры на пятом листе.
На сегодня это всё! Я желаю вам успехов в этой нелёгкой работе!
Геометрические фигуры из бумаги — Вырезаем и занимаемся!
Здесь мы подготовили для вас объемные геометрические фигуры из бумаги, которые нужно вырезать и склеить. Также на этой странице вы найдете плоские фигуры для вырезания, из которых нужно сложить замок. Этот учебный материал поможет ребенку наглядно изучить объемные геометрические фигуры: куб, пирамиду, ромб, шестигранник, цилинд и конус. Задание развивает наглядно-образное мышление.
Здесь вы можете скачать объемные геометрические фигуры из бумаги в виде разверток, которые необходимо распечатать на принтере, вырезать и склеить по указанным местам.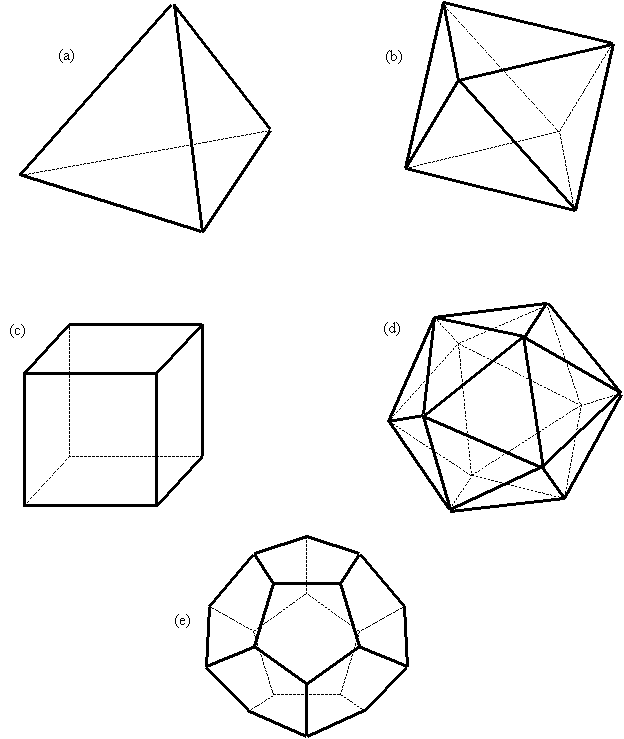 В результате у вас получатся объемные фигуры: куб, пирамида (трехгранная и четырехгранная), ромб, шестиугольник, конус и цилиндр. На каждой развертке написано название фигуры, чтобы ребенок во время работы всегда мог видеть, какую фигуру он делает. Это очень удобно для обучения, так как дети обычно не любят, когда взрослые по несколько раз повторяют одно и то же. А в этом случае у родителей нет необходимости проговаривать вслух названия фигур.
В результате у вас получатся объемные фигуры: куб, пирамида (трехгранная и четырехгранная), ромб, шестиугольник, конус и цилиндр. На каждой развертке написано название фигуры, чтобы ребенок во время работы всегда мог видеть, какую фигуру он делает. Это очень удобно для обучения, так как дети обычно не любят, когда взрослые по несколько раз повторяют одно и то же. А в этом случае у родителей нет необходимости проговаривать вслух названия фигур.
- Итак, в первом листе мы выложили следующие геометрические фигуры: куб (фигура, поверхность которого состоит из 6 квадратов), трехгранная пирамида (основание пирамиды и 3 грани), четырехгранная пирамида (основание и 4 грани), ромб (фигура, визуально состоящая из двух пирамид, имеющих общее основание).
- Во втором листе вы найдете развертки таких геометрических фигур из бумаги: шестигранник (фигура, состоящая из шести граней), цилиндр (состоящий из свернутого прямоугольника и двух окружностей-оснований) и конус.
Скачать геометрические фигуры из бумаги — развертки для вырезания вы можете во вложениях внизу страницы
Лист 1
Лист 2
Скачайте и распечатайте 2 листа с фигурами, вырежьте их аккуратно ножницами и склейте в нужных местах.
После того, как дети, при помощи взрослых, склеят все геометрические фигуры из бумаги, можно продолжить занятие, задавая детям вопросы. Например: «Покажи мне пирамиду. Сколько у нее сторон? Где ее основание? Чем эта пирамида (показываете трехранную) отличается от этой (четырехранной)? Покажи мне цилиндр. Какие предметы он тебе напоминает? Покажи конус. На что он похож? Покажи куб. Сколько у него сторон? Из какой геометрической фигуры состоят его стороны?» — и так далее.
В зависимости от возраста ребенка, можно использовать в занятии различные обучающие материалы. Например, что такое пирамида:
Какие бывают пирамиды. (Пусть ребенок покажет из них те, которые он склеил)
Что такое куб:
Что такое конус и цилиндр. На что они похожи:
Можете также скачать эти обучающие картинки во вложениях.
Плоские геометрические фигуры из бумаги — Строим замок
В этом упражнении вы можете скачать плоские геометрические фигуры из бумаги и построить из них замок, то есть выложить их на столе таким образом, чтобы получился заданный силуэт замка. Для начала скачайте во вложениях бланки с заданием и распечатайте на принтере. Затем вырежьте геометрические фигуры (квадрат, трапеция, полукруг и треугольник), которые даны к этому заданию. Все карточки с заданиями даны с увеличением уровня сложности (от 1 до 6 задания).
Все карточки с замками можно распечатывать на обычной офисной белой бумаге. А геометрические фигуры нужно распечатать на цветном картоне. Если нет цветного картона, можно использовать для распечатки цветную бумагу, а затем наклеить бумагу на лист картона и вырезать фигуры.
После этого подробно объесните ребенку инструкцию к выполнению упражнения.
«Строители, прежде чем строить какое-либо здание, смотрят сначала на его чертеж или схему, в которых показано каким оно должно быть.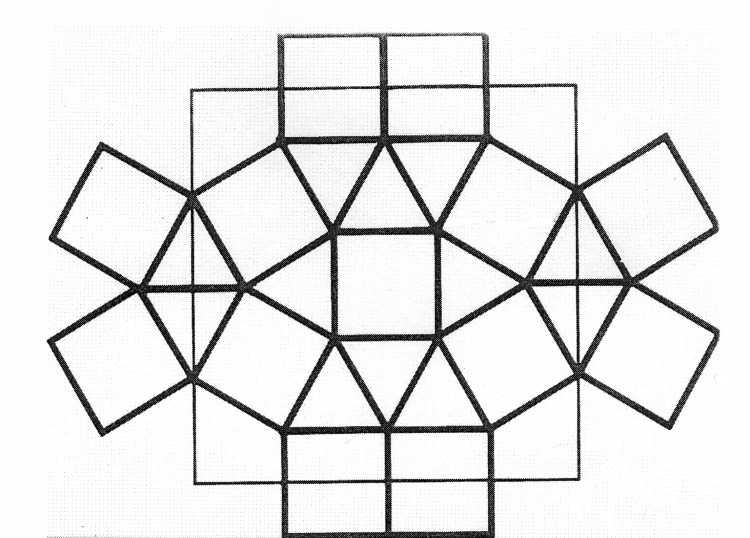 Такие чертежи бывают разными. Вот например, один из них», — взрослый показывает одну или две игровых схемы замка с нашего задания. — «Тебе нужно мысленно представить из каких частей состоит каждый замок, руководствуясь теми фигурами, которые можно использовать для строительства.» — взрослый показывает все геометрические фигуры, которые заранее вырезаны из цветного картона.
Такие чертежи бывают разными. Вот например, один из них», — взрослый показывает одну или две игровых схемы замка с нашего задания. — «Тебе нужно мысленно представить из каких частей состоит каждый замок, руководствуясь теми фигурами, которые можно использовать для строительства.» — взрослый показывает все геометрические фигуры, которые заранее вырезаны из цветного картона.
Очень важно начинать занятие, не используя подсказки, то есть нужно закрывать от ребенка геометрические фигуры, которые нарисованы рядом с силуэтом каждого замка. Пусть ребенок сам подумает, какие фигуры и какого размера ему понадобятся для строительства данного замка. И только если он испытвает трудности, можно приоткрыть для него подсказку.
Также не нужно допускать, чтобы ребенок накладывал вырезанные геометрические фигуры из бумаги на силуэт замка, так как при этом он не будет развивать наглядно-образное мышление. Старайтесь, чтобы всю основную работу ребенок проводил в уме, а не методом подбора.
Скачать карточки с плоскими геометрическими фигурами для строительства замка вы можете во вложениях внизу страницы.
Карточка 1
Карточка 2
Карточка 3
Карточка 4
Карточка 5
Карточка 6
Геометрические фигуры для вырезания:
Также вам будут полезны и другие материалы по изучению геометрических фигур:
Рисунки из геометрических фигур — Задания в картинках и раскраски
Веселые и красочные задания для детей «Рисунки из геометрических фигур» являются очень удобным обучающим материалом для детей дошкольного и младшего школьного возраста по изучению и запоминанию основных геометрических формю
Геометрические фигуры и их названия — Задания в картинках
Здесь вы с ребенком можете изучить геометрические фигуры и их названия с помощью веселых заданий в картинках.
Геометрические фигуры — Раскраска для дошкольников
Задания ознакомят ребенка с основными фигурами геометрии — кругом, овалом, квадратом, прямоугольником и треугольником.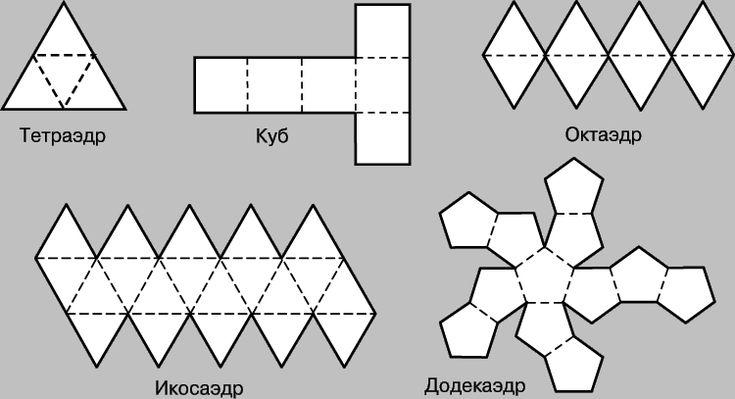 Только здесь не занудное зазубривание названий фигур, а своеобразная игра-раскраска.
Только здесь не занудное зазубривание названий фигур, а своеобразная игра-раскраска.
Плоские геометрические фигуры — Обведи и дорисуй
Как правило, геометрию начинают изучать, рисуя плоские геометрические фигуры. Восприятие правильной геометрической формы невозможно без выведения ее своими руками на листе бумаги.
Найди формы геометрических фигур в картинках
Это занятие изрядно позабавит ваших юных математиков. Ведь теперь им придется находить знакомые формы геометрических фигур среди множества картинок.
Наложение фигур друг на друга — Задание для детей
Наложение фигур друг на друга — это занятие по геометрии для дошкольников и младших школьников. Смысл упражнения состоит в решении примеров на сложение. Только это необычные примеры. Вместо цифр здесь нужно складывать геометрические фигуры.
Свойства геометрических фигур для дошкольников
Это задание составлено в виде игры, в которой ребенку предстоит менять свойства геометрических фигур: форму, цвет или размер.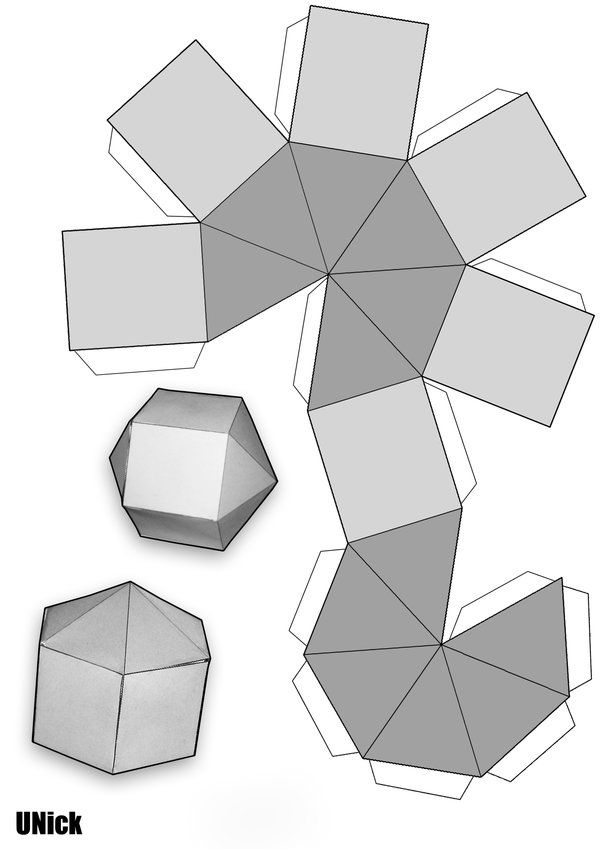
Счет геометрических фигур — Картинки с заданиями
Здесь вы можете скачать задания в картинках, в которых представлен счет геометрических фигур для занятий по математике.
Чертежи геометрических тел — Задание для детей
В этом задании ребенок познакомится с таким понятием, как чертежи геометрических тел. По сути, это занятие представляет собой мини-урок по начертательной геометрии
Счет до 10 для детей дошкольного возраста
Дети любят раскрашивать и обводить, поэтому данные задания сделают ваши занятия по обучению счету максимально эффективными.
И еще можете поиграть в математические игры онлайн от лисенка Бибуши:
Игра «Что лишнее? — Геометрические формы»
В этой развивающей онлайн игре ребенку предстоит определить, что является лишним среди 4 картинок. При этом необходимо руководствоваться признаками геометрических форм.
Imaging maths — Разворачивающиеся многогранники
Ноябрь 2003
Бумажная модель
Бумажные модели геометрических фигур не только украшают потолки математического факультета, где я работаю, но и являются визуальным представлением геометрических изобретений.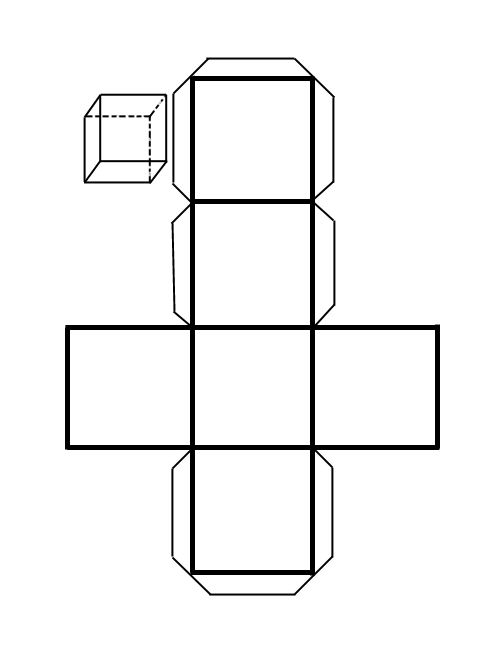 Например, бумажная модель, показанная слева, является многогранной версией «поверхности Боя», которая имеет наименьшее количество вершин среди всех многогранных реализаций, состоящих из треугольников. Во время своего
Согласно первоначальному открытию [1], построение физической бумажной модели по-прежнему было утомительным процессом: любые мелкие неточности в процессе рисования и вырезания наверняка испортили бы модель. Чтобы представить себе требуемые усилия, взгляните на исходный рисунок [2] линий разреза этой бумажной модели.
Например, бумажная модель, показанная слева, является многогранной версией «поверхности Боя», которая имеет наименьшее количество вершин среди всех многогранных реализаций, состоящих из треугольников. Во время своего
Согласно первоначальному открытию [1], построение физической бумажной модели по-прежнему было утомительным процессом: любые мелкие неточности в процессе рисования и вырезания наверняка испортили бы модель. Чтобы представить себе требуемые усилия, взгляните на исходный рисунок [2] линий разреза этой бумажной модели.
Плоское развертывание поверхности мальчика
Посмотреть анимированную версию(565K)
В настоящее время программное обеспечение усовершенствовано и позволяет нам создавать «разрезанные рисунки» путем автоматического вычисления развертывания геометрических фигур: справа вы можете увидеть развертывание модели Boy или просмотреть анимацию. Но даже при наличии современных программных средств остается ряд нерешенных геометрических задач.
Развертка — это процесс разрезания многогранной поверхности по определенным кривым с последующим сведением поверхности на плоскость без нахлеста и без искажения отдельных граней.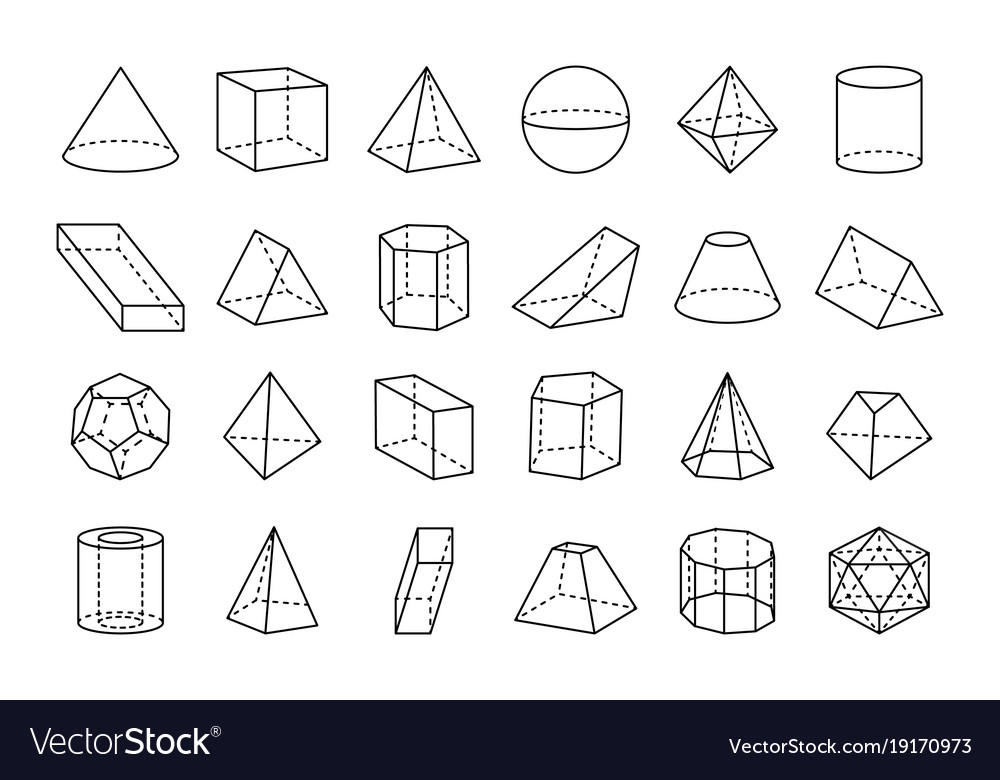 Развертка кромки
Развертка кромки
Раскладывание куба — посмотреть анимированную версию | |||
Оригами , японское искусство складывания бумаги, является самым известным применением разворачивания — слово буквально означает «складывать бумагу». По оригами много ссылок, например, на сайте [15], но в этой статье мы сосредоточимся на складывании, а точнее, на разворачивании многогранных поверхностей.
Искусство складывания бумаги: оригами — посмотреть анимированную версию | |||
Геометрическое оригами
Сеть додекаэдра
Альбрехт Дюрер [4] ввел понятие сетки многогранного тела в одном из своих учебных пособий. Сеть многогранника — это набор ребер на плоскости, являющихся развернутыми ребрами твердого тела. Дюрер также дал четкие инструкции по рисованию сетей — примером может служить развертывание додекаэдра, показанное справа.
Сеть многогранника — это набор ребер на плоскости, являющихся развернутыми ребрами твердого тела. Дюрер также дал четкие инструкции по рисованию сетей — примером может служить развертывание додекаэдра, показанное справа.
Альбрехт Дюрер
Со времен Дюрера математики интенсивно использовали бумажные модели для изучения геометрических поверхностей как в образовании, так и в исследованиях. Например, упомянутую во введении поверхность Boy можно понять гораздо легче, когда у вас в руках бумажная модель, которую можно поворачивать и рассматривать с разных сторон. Возможность прикоснуться к модели — в частности, возможность прикоснуться к области, которые вы не видите, значительно упрощает понимание сложной геометрической структуры.
Развертки платоновых и архимедовых тел хорошо известны. Существует множество наборов для складывания, которые позволяют вырезать и складывать бумажные модели многогранников. Возможно, самая большая коллекция математических бумажных моделей была создана отцом Магнусом Веннингером, математиком и священником аббатства Святого Иоанна [5].
Додекаэдр с другой разверткой — посмотреть анимационную версию | |||
Тор Клиффорда создается набором окружностей. Тор красиво разворачивается, несмотря на отрицательную кривизну внутренней области — посмотреть анимированную версию | |||
В комбинаторной геометрии сложно найти многогранные модели заданной топологической формы, которые используют минимальное количество граней или вершин.
Тор Часара — вложенный многогранный тор (т. е. без самопересечения) с наименьшим количеством вершин — см. анимированную версию | |||
Теперь мы готовы понять еще более сложное развертывание. Поверхность Боя, упомянутая во введении, является моделью проективной плоскости 9.0009 . Одну модель проективной плоскости можно получить, взяв верхнюю полусферу шара и отождествив противоположные точки экватора. В качестве альтернативы вы можете взять плоский диск и попарно определить противоположные точки на границе.
круг. Поскольку это топологические построения, вы можете взять любой кусок плоскости, ограниченный единственной замкнутой кривой, такой как развертка поверхности Боя.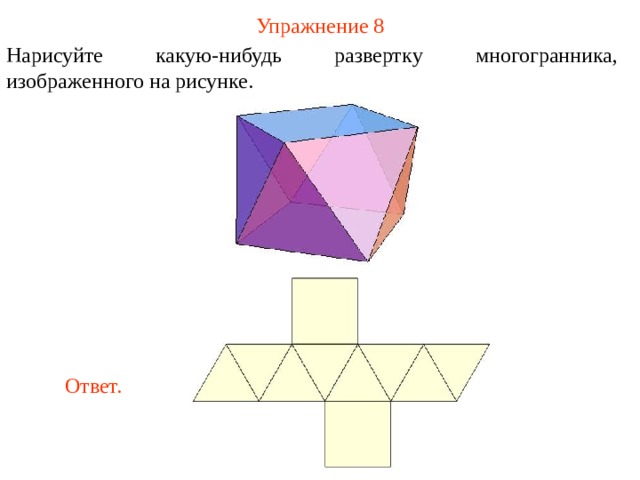
Дискретная поверхность Boy разворачивается в односвязный диск. Противоположные вершины границы идентифицируются во время пересвертывания — см. анимированную версию | |||
Если вы внимательно понаблюдаете за пересвертыванием поверхности Boy, то увидите, как противоположные точки черной граничной кривой попарно совпадают. Следовательно, поверхность Боя является полиэдральной моделью проективной плоскости. Особое свойство показанной полиэдральной модели (найденной У. Бремом [1]) заключается в том, что она использует наименьшее количество вершин среди всех полиэдральных моделей, состоящих из треугольники.
Как дискретная кривизна влияет на развертку
Кривизна — это математический способ описания степени «изгиба» или «кривизны» поверхности в каждой точке. Например, плоский лист бумаги не изгибается ни в одной из своих точек и, следовательно, имеет нулевую кривизну, а круглый шар имеет положительную кривизну в каждой точке. Дифференциальная геометрия использует исчисление для получения различных видов кривизны гладких поверхностей, но кривизна многогранника
с поверхностями можно работать гораздо более элементарно.
Например, плоский лист бумаги не изгибается ни в одной из своих точек и, следовательно, имеет нулевую кривизну, а круглый шар имеет положительную кривизну в каждой точке. Дифференциальная геометрия использует исчисление для получения различных видов кривизны гладких поверхностей, но кривизна многогранника
с поверхностями можно работать гораздо более элементарно.
Самое важное твердое тело в мире. Футбольный мяч имеет положительную кривизну в каждой вершине — посмотреть анимированную версию | |||
Дискретная кривизна Гаусса измеряет изгиб многогранной поверхности в каждой из ее вершин. В каждой вершине мы рассматриваем углы, образованные на соседних гранях в этом углу. Если сумма этих углов ровно 360 0 , то набор граней можно свести к плоскости без зазоров и перекрытий. Следовательно, у него нулевой кривизны . Если сумма
углы меньше 360 0 , то ситуация подобна вершине конуса или углу выпуклого многогранника. Здесь кривизна должна быть положительной , так как такой многогранник подобен круглому шару. Отрицательная кривизна возникает, если сумма углов больше 360 0 , что происходит, например, в седловой точке.
Следовательно, у него нулевой кривизны . Если сумма
углы меньше 360 0 , то ситуация подобна вершине конуса или углу выпуклого многогранника. Здесь кривизна должна быть положительной , так как такой многогранник подобен круглому шару. Отрицательная кривизна возникает, если сумма углов больше 360 0 , что происходит, например, в седловой точке.
В общем случае дискретная кривизна Гаусса в вершине определяется как разность 360 0 и суммы углов между соседними гранями, примыкающими к вершине:
K(вершина) = 360 0 — a 1 — a 2 — a 3 -…- a n ,
where n is the number of faces adjoining the vertex, and a 1 , …, и n это углы на гранях.
На следующем изображении показаны три различных типа вершин в верхнем ряду и развертывание вершинной звезды, то есть набор граней, встречающихся в вершине, в нижнем ряду. Из-за связи сфер с положительной кривизной и гиперболического пространства с отрицательной кривизной мы называем типы вершин сферическими , евклидовыми и гиперболическими соответственно.
Из-за связи сфер с положительной кривизной и гиперболического пространства с отрицательной кривизной мы называем типы вершин сферическими , евклидовыми и гиперболическими соответственно.
Есть два непосредственных следствия задачи развертывания многогранных поверхностей:
- В каждой сферической вершине должен быть хотя бы один разрез;
- В каждой гиперболической вершине должно быть не менее двух разрезов, которые при развертке снимают одну или несколько граней. Проверьте интерактивный апплет развертывания отрицательно изогнутой вершины.
В качестве эвристического ориентира отметим, что слишком большая отрицательная кривизна Гаусса может сделать развертывание невозможным, поскольку потребуется слишком много разрезов. Например, дискретные минимальные поверхности, такие как показанный катеноид, могут иметь отрицательную кривизну Гаусса в каждой вершине. Здесь нет развертки на одну плоскую компоненту, но алгоритм находит развертку с четырьмя плоскими компонентами. составные части.
составные части.
Катеноид — это минимальная поверхность со «слишком большой» отрицательной кривизной. Следовательно, разворот состоит из более чем одного плоскостного компонента — посмотреть анимированную версию | |||
При складывании бумажной модели в Оригами сохраняется нулевая кривизна Гаусса исходного плоского листа бумаги. Следовательно, модели оригами имеют постоянную нулевую кривизну Гаусса в каждой внутренней вершине.
Всегда ли возможно разворачивание?
Говоря словами Проекты открытых задач [8]:
Можно ли каждый выпуклый многогранник разрезать по ребрам и развернуть в один непересекающийся простой многоугольник?
Этот вопрос был поднят в математике в [9], но фактически восходит к Дюреру [4]. Было предпринято несколько попыток, включая эксперименты с программным обеспечением, чтобы подтвердить или опровергнуть эту гипотезу.
Было предпринято несколько попыток, включая эксперименты с программным обеспечением, чтобы подтвердить или опровергнуть эту гипотезу.
Остроконечный тетраэдр [10]
(Невыпуклый) остроконечный тетраэдр [10] справа нельзя развернуть без создания перекрывающихся областей на плоскости. Это означает, что в гипотезе нельзя опустить слово «выпуклый». Однако, несмотря на такие примеры, принято считать, что если ограничиться рассмотрением выпуклых многоугольников, то на этот вопрос есть положительный ответ.
Звездная развертка [14]
Другой класс разверток, отличный от рассмотренных в статье реберных разверток, получается, если разрешить разрезы не только по ребрам, но и по внутренности граней. Одним из таких развертываний является 9Звезда 0008 разворачивается относительно исходной точки. Это разрезает многогранник по всем кратчайшим путям от исходной точки до других вершин многогранника; эти пути обычно
пройтись по внутренностям лиц. Аронов и О’Рурк [14] показали, что звездообразование возможно для любого выпуклого многогранника.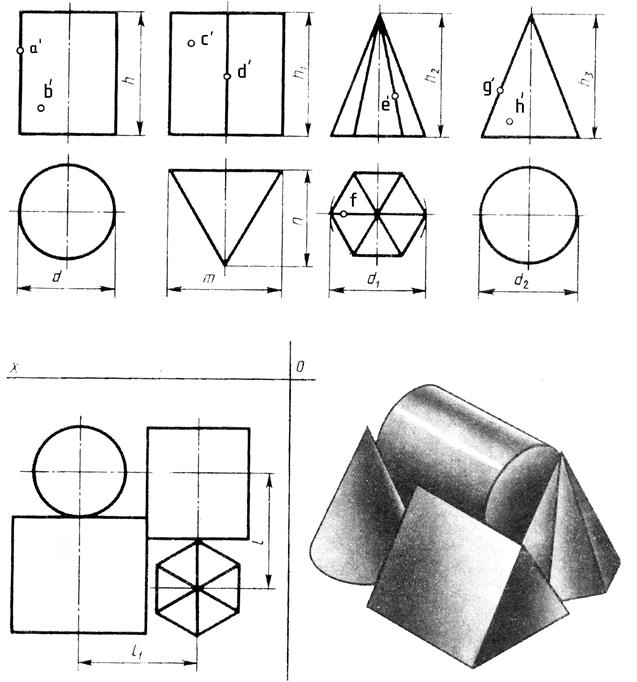
Автоматическое развертывание
Мы видели, что существуют поверхности, такие как додекаэдр, которые имеют различные развертывания, и поверхности, подобные остроконечному тетраэдру, которые нельзя развернуть в единую связную часть. Поэтому любой автоматический алгоритм поиска разверток должен накладывать дополнительные ограничения.
Развертывание невыпуклой формы, такой как эта модель лошади, требует интенсивного числового поиска — просмотр анимированной версии | |||
Примеры таких ограничений:
- Минимизировать количество компонент связности развернутого многогранника;
- Минимизировать размер ограничивающего прямоугольника полученного многогранника;
- Минимизировать общую длину границы полученного полигона;
- Избегайте тонких компонентов и компонентов с малой площадью.

На практике автоматическое развертывание произвольных многогранных поверхностей в основном направлено на то, чтобы развернутая сетка не перекрывалась. Тем не менее, удивительно, как много невыпуклых поверхностей можно развернуть в один связный компонент, например, модель лошади, показанную выше, или многогранный торс Венеры, показанный ниже.
Туловище Венеры имеет очень сложную форму для раскрытия. Удивительно, но существует развертка, состоящая из одного компонента — посмотреть анимационную версию | |||
Разверните и создайте свои собственные бумажные модели
Развертка тора Часара с помощью апплета JavaView Unfolder. Стыки облегчают склеивание бумажной модели.
Распаковщик JavaView
Модуль Unfolder , написанный Клаусом Хильдебрандтом для программного обеспечения JavaView, позволяет разворачивать все многогранные поверхности. Он пытается оптимизировать развертывание в зависимости от нескольких критериев, некоторые из которых упоминались в предыдущем разделе.
Он пытается оптимизировать развертывание в зависимости от нескольких критериев, некоторые из которых упоминались в предыдущем разделе.
Добавление стыков к развернутой сети упрощает создание бумажной модели. Сначала разверните поверхность со стыками, затем отправьте изображение на принтер и, наконец, приклейте сложенную бумажную модель по стыкам.
Иногда удобнее загрузить приложение JavaView и позволить ему работать вне веб-браузера. Таким образом легче изменить размер окна, и у вас также будет доступ к локальному жесткому диску для сохранения и загрузки файлов.
Примечания
К. Фукуда суммирует основные результаты и открытые проблемы, связанные с развертыванием многогранников, на своем сайте [11].
На сайте TOPP, управляемом Дж. О’Рурком [8], обсуждается набор открытых проблем, связанных с развертыванием многогранников и, в более общем смысле, с комбинаторной геометрией.
HyperGami — это программное обеспечение для проектирования и создания бумажных скульптур с использованием многогранников и пользовательских вариантов многогранников.
 Программа доступна как коммерческое программное обеспечение из [12].
Программа доступна как коммерческое программное обеспечение из [12].Распаковщик — это математический веб-сервис проекта JavaView. Вы можете развернуть все свои собственные геометрии в [13].
Дополнительная литература
У. Брем, Как строить минимальные многогранные модели поверхности Боя. Мат. Интеллигент 12 (4): 51-56 (1990).
Э.-Х. Tjaden, Бумажная модель мальчика Брема Surface . TU-Берлин (1987), [email protected].
В. Шликенридер, Сети многогранников . Дипломированный диплом TU-Berlin (1997), [email protected].
А. Дюрер, Unterweysung der Messung mit dem Zyrkel und Rychtscheyd . Нюрнберг (1525 г.).
Английский перевод с комментариями Вальтера Л. Штрауса Руководство художника , Нью-Йорк (1977).Фр. М. Дж. Веннингер, Многогранные модели . Издательство Кембриджского университета (1971).

http://employees.csbsju.edu/mwenninger/.А. Часар, Многогранник без диагоналей . Acta Sci. Math., Сегед 13:140-142 (1949-1950).
Ф. Х. Лутц, Часар Торус . Модель электронной геометрии № 2001.02.069 (2001 г.),
http://www.eg-models.de/2001.02.069.Э.Д. Демен, Дж.С.Б. Митчелл, Дж. О’Рурк, Проекты открытых проблем . http://cs.smith.edu/~jorourke/TOPP/Welcome.html.
Г.К. Шепард, Выпуклые многогранники с выпуклыми сетями . Матем. проц. Камб. Фил. соц. , 78:389-403 (1975).
М. Берн, Э. Д. Демен, Д. Эппштейн, Э. Куо, А. Мантлер, Дж. Снойинк,
Неразворачиваемые многогранники с выпуклыми гранями. Вычисл. геом. Теория прил. , 24 (2): 51-62 (2003).К. Фукуда, Странные развертки выпуклых многогранников . Швейцарская техническая школа Цюриха (1997).
https://www.inf.ethz.ch/personal/fukudak/unfold_home/unfold_open. html
html
unfold_home/unfold_open.htmlМ. и Э. Айзенберг, HyperGami и JavaGami . ун-т Колорадо, Боулдер.
http://l3d.cs.colorado.edu/~ctg/projects/hypergami/.К. Хильдебрандт, К. Полтье, Раскладыватель — Разворачивание полиэдральных сеток . Веб-сервис JavaView (2003 г.).
http://www.javaview.de/services/unfold/.Б. Аронов, Дж. О’Рурк, Неперекрытие звездного разворачивания . Дискретный вычисл. геом., 8:219-250 (1992).
Дж. Ву, Оригами . http://www.origami.vancouver.bc.ca/home.html.
Об этой статье
Конрад Полтьер — исследователь Технического университета в Берлине и научный сотрудник, отвечающий за «Визуализацию» в Исследовательском центре DFG «Математика для ключевых технологий». Его интересы связаны с дискретной дифференциальной геометрией и математической визуализацией. Он опубликовал исследовательские книги и является автором календарей и отмеченных наградами математических исследований. видео: для получения более подробной информации посетите его веб-страницу.
видео: для получения более подробной информации посетите его веб-страницу.
Изображения, анимация и апплеты на этой странице были созданы с помощью программного обеспечения JavaView.
Трехмерные фигуры | SkillsYouNeed
На этой странице рассматриваются свойства трехмерных или «твердых» форм.
Двумерная фигура имеет длину и ширину. Трехмерная твердая форма также имеет глубину. Трехмерные формы по своей природе имеют внутреннее и внешнее, разделенные поверхностью. Все физические предметы, к которым можно прикоснуться, трехмерны.
На этой странице рассматриваются как прямолинейные тела, называемые многогранниками, которые основаны на многоугольниках, так и тела с кривыми, такие как шары, цилиндры и конусы.
Многогранники
Многогранники (или многогранники) представляют собой твердые фигуры с прямыми сторонами. Многогранники основаны на многоугольниках, двумерных плоских формах с прямыми линиями.
Подробнее о работе с полигонами см.на нашей странице Свойства полигонов.
Многогранники определяются как имеющие:
- Прямые ребра .
- Плоские стороны называются гранями .
- Углов, называемых вершинами .
Многогранники также часто определяются по количеству ребер, граней и вершин, которые они имеют, а также по тому, имеют ли все их грани одинаковую форму и размер. Как и многоугольники, многогранники могут быть правильными (на основе правильных многоугольников) или неправильными (на основе неправильных многоугольников). Многогранники также могут быть вогнутыми или выпуклыми.
Одним из самых простых и привычных многогранников является куб. Куб — это правильный многогранник, имеющий шесть квадратных граней, 12 ребер и восемь вершин.
Правильные многогранники (Платоновы тела)
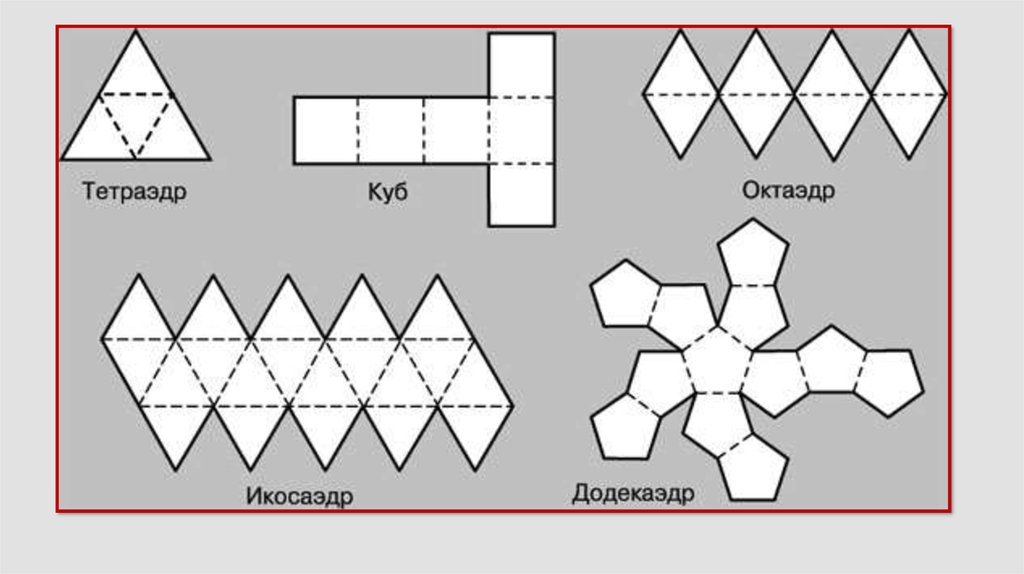
Пять правильных многогранников представляют собой особый класс многогранников, все грани которых идентичны, причем каждая грань является правильным многоугольником.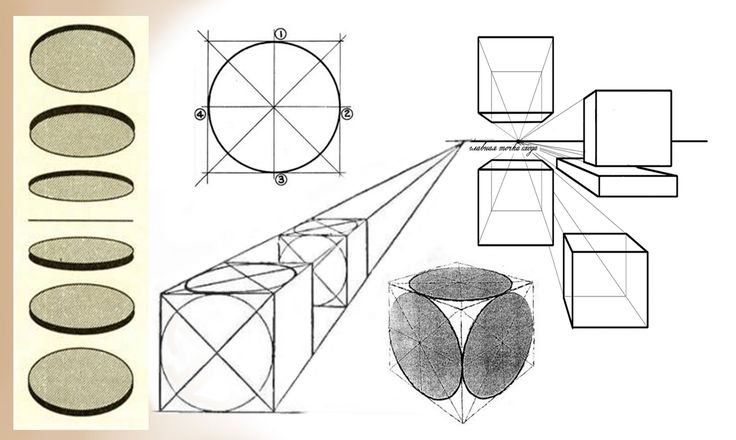 Платоновые тела:
Платоновые тела:
- Тетраэдр с четырьмя равносторонними треугольными гранями.
- Куб с шестью квадратными гранями.
- Октаэдр с восемью равносторонними треугольными гранями.
- Додекаэдр с двенадцатью пятиугольными гранями.
- Икосаэдр с двадцатью равносторонними треугольными гранями.
См. диаграмму выше для иллюстрации каждого из этих правильных многогранников.
Что такое призма?
Призма — это любой многогранник, имеющий два совпадающих конца и плоские стороны . Если вы разрежете призму в любом месте по ее длине, параллельно ее концу, ее поперечное сечение будет таким же — вы получите две призмы. стороны призмы параллелограммы — четырехгранные фигуры с двумя парами сторон одинаковой длины.
Антипризмы аналогичны обычным призмам тем, что их концы совпадают. Однако стороны антипризмы состоят из треугольников, а не из параллелограммов. Антипризмы могут стать очень сложными.
Однако стороны антипризмы состоят из треугольников, а не из параллелограммов. Антипризмы могут стать очень сложными.
Что такое пирамида?
Пирамида — это многогранник с многоугольником в основании , который соединяется с вершиной (верхняя точка) с прямыми сторонами.
Хотя мы склонны думать о пирамидах с квадратным основанием, вроде тех, что строили древние египтяне, на самом деле они могут иметь основание в виде любого многоугольника, правильного или неправильного. Кроме того, пирамида может иметь вершину прямо в центре основания, т.0621 Правая пирамида или может иметь вершину не по центру, если это Наклонная пирамида .
Более сложные многогранники
Существует еще много типов многогранников: симметричные и асимметричные, вогнутые и выпуклые.
Архимедовы тела, например , состоят как минимум из двух различных правильных многоугольников.
Усеченный куб (как показано на рисунке) представляет собой архимедово тело с 14 гранями.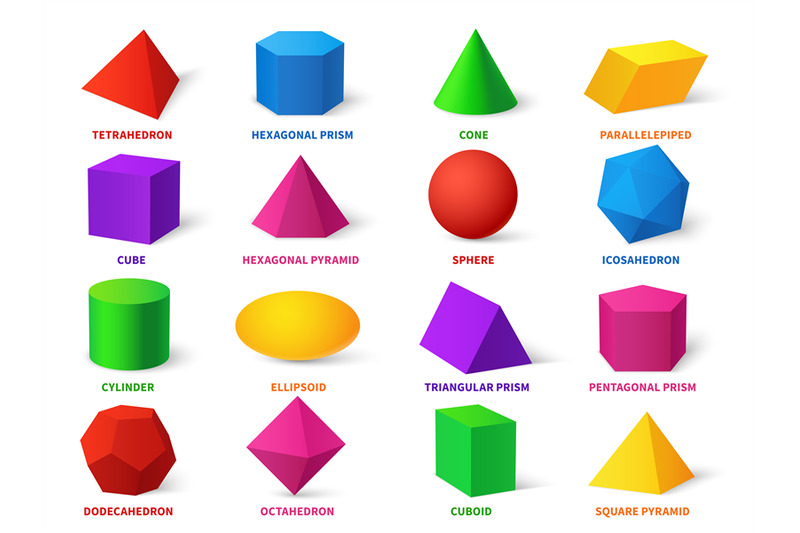 Шесть граней представляют собой правильные восьмиугольники, а остальные восемь — правильные (равносторонние) треугольники. Фигура имеет 36 ребер и 24 вершины (угла).
Шесть граней представляют собой правильные восьмиугольники, а остальные восемь — правильные (равносторонние) треугольники. Фигура имеет 36 ребер и 24 вершины (угла).
Трехмерные фигуры с кривыми
Твердые фигуры с изогнутыми или круглыми краями не являются многогранниками. Многогранники могут иметь только прямые стороны. Также см. нашу страницу о двумерных изогнутых формах.
Многие объекты вокруг вас будут иметь по крайней мере несколько кривых. В геометрии наиболее распространенными искривленными телами являются цилиндры, конусы, сферы и торы (множественное число для тора).
| Обычные трехмерные формы с кривыми: | |
|---|---|
| Цилиндр | Конус |
Цилиндр имеет одинаковое поперечное сечение от одного конца до другого. Цилиндры имеют два одинаковых конца либо круга, либо овала. Несмотря на то, что они похожи, цилиндры не являются призмами, поскольку призма имеет (по определению) параллелограмм с плоскими сторонами. | Конус имеет круглое или овальное основание и вершину (или вершину). Сторона конуса плавно сужается к вершине. Конус похож на пирамиду, но отличается тем, что конус имеет одну изогнутую сторону и круглое основание. |
| Сфера | Тор |
| Сфера, имеющая форму шара или шара, представляет собой полностью круглый объект. Каждая точка на поверхности сферы находится на равном расстоянии от центра сферы. | Правильный кольцевой тор, имеющий форму кольца, шины или бублика, образуется путем вращения меньшего круга вокруг большего круга. Существуют и более сложные формы торов. |
Площадь поверхности
На нашей странице, посвященной расчету площади, объясняется, как вычислить площадь двухмерных фигур, и вам необходимо понимать эти основы, чтобы вычислять площадь поверхности трехмерных фигур.
Для трехмерных фигур мы говорим о площади поверхности , чтобы избежать путаницы.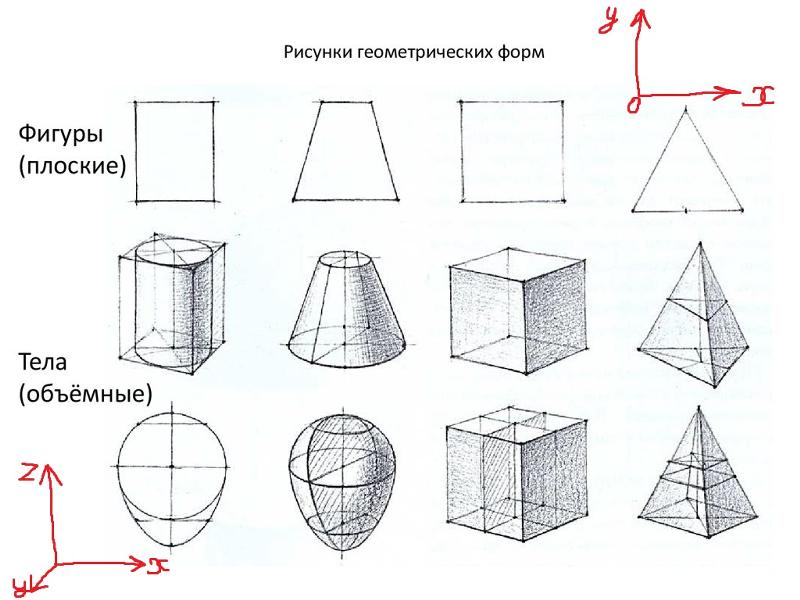
Вы можете использовать свои знания о площади двухмерных фигур для вычисления площади поверхности трехмерной фигуры, поскольку каждая грань или сторона фактически представляет собой двумерную форму.
Таким образом, вы вычисляете площадь каждой грани, а затем складываете их вместе.
Как и в случае с плоскими формами, площадь поверхности твердого тела выражается в квадратных единицах: см 2 , дюймы 2 , м 2 и так далее. Вы можете найти более подробную информацию о единицах измерения на нашей странице Системы измерения .
Примеры расчета площади поверхности
Куб
Площадь поверхности куба равна площади одной грани (длина x ширина), умноженной на 6, поскольку все шесть граней одинаковы.
Поскольку грань куба представляет собой квадрат, вам нужно провести только одно измерение — длина и ширина квадрата по определению одинаковы.
Следовательно, одна грань этого куба равна 10 × 10 см = 100 см 2 .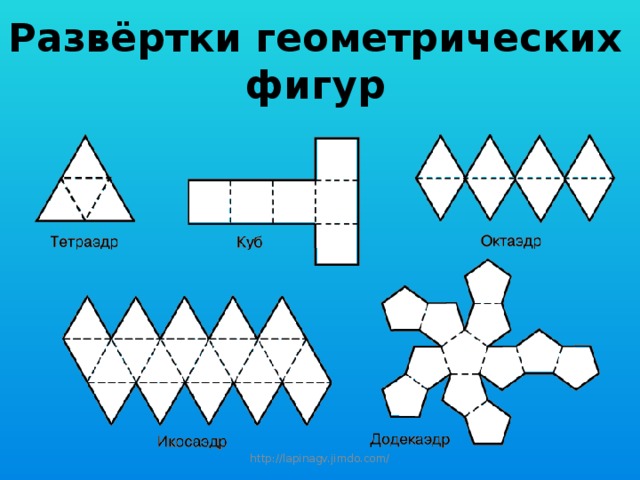 Умножаем на 6 количество граней куба, и получаем, что площадь поверхности этого куба равна 600см 2 .
Умножаем на 6 количество граней куба, и получаем, что площадь поверхности этого куба равна 600см 2 .
Другие правильные многогранники
Точно так же можно вычислить площадь поверхности других правильных многогранников (платоновых тел), найдя площадь одной стороны и умножив результат на общее количество сторон — см. диаграмму основных многогранников выше. .
Если площадь одного пятиугольника, составляющего додекаэдр, равна 22см 2 , то умножьте это на общее количество сторон (12), чтобы получить ответ 264см 2 .
Пирамида
Чтобы вычислить площадь поверхности стандартной пирамиды с четырьмя равными треугольными сторонами и квадратным основанием:
Сначала определите площадь основания (квадрата) длина × ширина.
Далее определите площадь одной стороны (треугольника). Измерьте ширину вдоль основания, а затем высоту треугольника (также известную как наклонная длина) от центральной точки основания до вершины.
Есть два способа вычислить площадь поверхности четырех треугольников:
Разделите ответ на 2, чтобы получить площадь поверхности одного треугольника, а затем умножьте на 4, чтобы получить площадь поверхности всех четырех сторон, или
Умножьте ответ на 2.
Наконец, сложите площадь основания и сторон вместе, чтобы найти общую площадь поверхности пирамиды.
Для расчета площади поверхности других типов пирамид, сложите площадь основания (известную как площадь основания) и площадь сторон (площадь боковых сторон). Возможно, вам придется измерить стороны по отдельности.
Диаграммы сетей
Геометрическая сеть представляет собой двухмерный «шаблон» для трехмерного объекта. Сети могут быть полезны при расчете площади поверхности трехмерного объекта. На диаграмме ниже вы можете увидеть, как строятся базовые пирамиды, если пирамида «развернута», у вас остается сеть.
Для получения дополнительной информации о схемах сети см.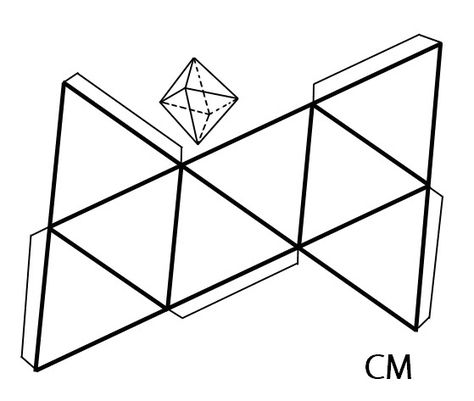 нашу страницу 3D-формы и сети .
нашу страницу 3D-формы и сети .
Призма
Для расчета площади поверхности призмы :
Призмы имеют два одинаковых конца и плоские стороны параллелограмма.
Вычислите площадь одного конца и умножьте на 2.
Для правильной призмы (у которой все стороны одинаковы) вычислите площадь одной из сторон и умножьте на общее количество сторон.
Для призм неправильной формы (с разными сторонами) рассчитайте площадь каждой стороны.
Сложите два ответа вместе (концы + стороны), чтобы найти общую площадь поверхности призмы.
Цилиндр
Пример:
Радиус = 5 см
Высота = 10 см
Чтобы вычислить площадь поверхности цилиндра , полезно подумать о составных частях формы. Представьте себе банку сладкой кукурузы — у нее есть верх и низ, оба из которых представляют собой круги. Если вы отрежете сторону по длине и сгладите ее, у вас получится прямоугольник. Следовательно, вам нужно найти площадь двух кругов и прямоугольника.
Сначала определите площадь одного из кругов.
Площадь круга равна π (пи) × радиус 2 .
При радиусе 5 см площадь одного из кругов равна 3,14 × 5 2 = 78,5 см 2 .
Умножьте ответ на 2, так как кругов два 157см 2
Площадь стороны цилиндра равна периметру круга × высоте цилиндра.
Периметр равен π x 2 × радиус. В нашем примере 3,14 × 2 × 5 = 31,4·9.0003
Измерьте высоту цилиндра. В данном примере высота составляет 10 см. Площадь стороны 31,4 × 10 = 314см 2 .
Общая площадь поверхности может быть найдена путем суммирования площадей кругов и стороны:
157 + 314 = 471 см 2
Пример:
Радиус = 5 см
Длина наклона 0
Конус
При расчете площади поверхности конуса необходимо использовать длину «наклона», а также радиус основания.
Однако вычислить его относительно просто:
Площадь круга в основании конуса составляет π (пи) × радиус 2 .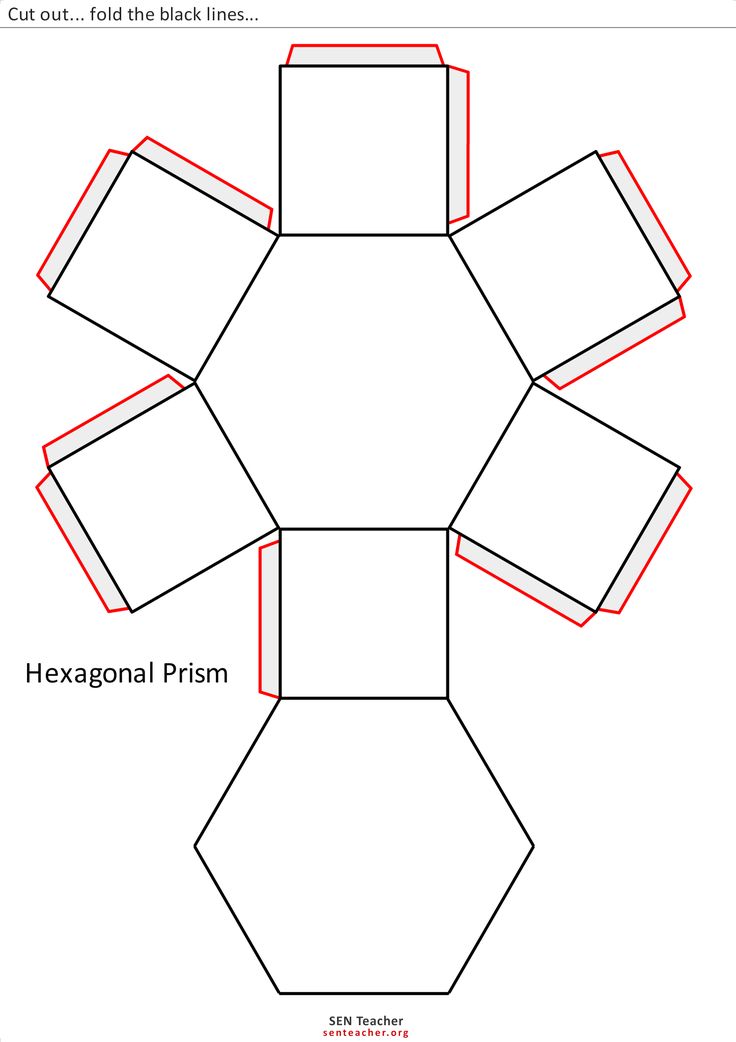
В этом примере расчет равен 3,14 × 5 2 = 3,14 × 25 = 78,5 см 2
Площадь стороны, наклонной части, можно найти по следующей формуле:
π (пи) × радиус × длина наклона.
В нашем примере расчет равен 3,14 × 5 × 10 = 157 см 2 .
Наконец, добавьте площадь основания к площади стороны, чтобы получить общую площадь поверхности конуса.
78,5 + 157 = 235,5 см 2
Теннисный мяч:
Диаметр = 2,6 дюйма
Сфера
4 × π × радиус 2 .
Для сферы часто проще измерить диаметр — расстояние поперек сферы. Затем вы можете найти радиус, который составляет половину диаметра.
Диаметр стандартного теннисного мяча составляет 2,6 дюйма. Таким образом, радиус составляет 1,3 дюйма. Для формулы нам нужен радиус в квадрате. 1,3 × 1,3 = 1,69
Таким образом, площадь поверхности теннисного мяча равна:
4 × 3,14 × 1,69 = 21,2264 дюйма 2 .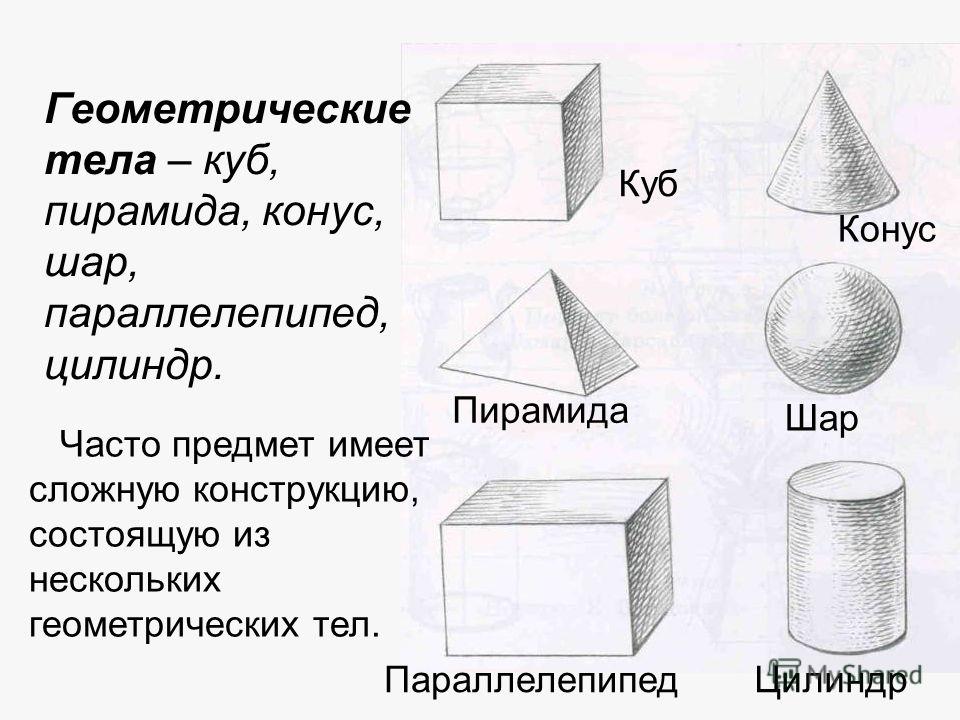
Пример:
R (большой радиус) = 20 см
r (малый радиус) = 4 см
Тор
Чтобы вычислить площадь поверхности тора , вам нужно найти два значения радиуса.
Большой или большой радиус (R) измеряется от середины отверстия до середины кольца.
Малый или малый радиус (r) измеряется от середины кольца до внешнего края.
На диаграмме показаны два вида примера тора и способы измерения его радиусов (или радиусов).
Расчет площади поверхности состоит из двух частей (по одной для каждого радиуса). Расчет одинаков для каждой части.
Формула: площадь поверхности = (2πR)(2πr)
Чтобы вычислить площадь поверхности примера тора.
(2 × π × R) = (2 × 3,14 × 20) = 125,6
(2 × π × r) = (2 × 3,14 × 4) = 25,12
Перемножьте два ответа, чтобы найти общую поверхность площадь примерного тора.
125,6 × 25,12 = 3155,072 см 2 .
Дальнейшее чтение из книги «Навыки, которые вам нужны»
«Понимание геометрии»
Часть «Руководства по навыкам, которые вам необходимы»
Эта электронная книга охватывает основы геометрии и рассматривает свойства форм, линий и тел.


 Программа доступна как коммерческое программное обеспечение из [12].
Программа доступна как коммерческое программное обеспечение из [12].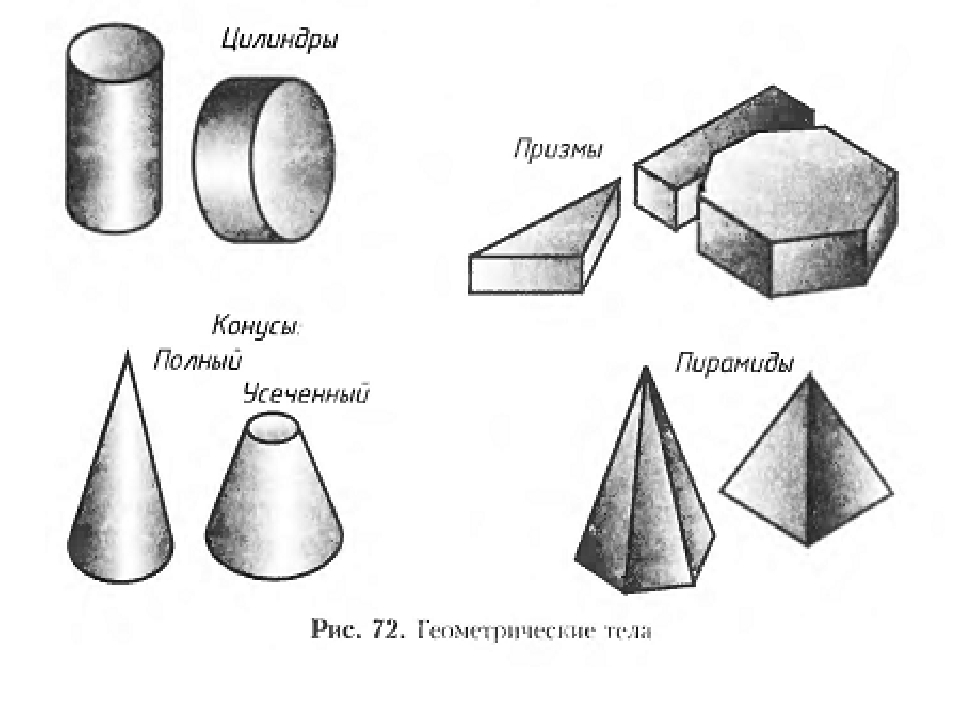
 html
html  на нашей странице Свойства полигонов.
на нашей странице Свойства полигонов.