Большой выбор развёрток простых геометрических фигур.
Первое знакомство детей с бумажным моделированием всегда начинается с простых геометрических фигур, таких как кубик и пирамида. Не у многих получается склеить кубик с первого раза, иногда требуется несколько дней, чтобы сделать поистине ровный и безупречный куб. Более сложные фигуры цилиндр и конус требуют в несколько раз больше усилий нежели простой кубик. Если вы не умеете аккуратно клеить геометрические фигуры, значит и за сложные модели вам ещё рано браться. Займитесь сами и научите своих детей клеть эти «азы» моделирования по готовым развёрткам.
Для начала я, конечно же, предлагаю научиться клеить обычный кубик. Развёртки сделаны для двух кубиков, большого и маленького. Более сложной фигурой является маленький кубик потому, как клеить его сложнее, чем большой.
Итак, начнём! Скачайте развёртки всех фигур на пяти листах и распечатайте на плотной бумаге. Перед тем, как печатать и клеить геометрические фигуры обязательно ознакомьтесь со статьёй о том, как выбрать бумагу и как вообще правильно вырезать, сгибать и клеить бумагу.
Для более качественной печати советую использовать программу AutoCAD, и даю вам развёртки для этой программы, а также читайте, как распечатывать из автокада. Вырежьте развёртки кубиков с первого листа, по линиям сгиба обязательно проведите иголкой циркуля под железную линейку, чтобы бумага хорошо сгибалась. Теперь можно начинать клеить кубики.
Для экономии бумаги и на всякий пожарный я сделал несколько развёрток маленького кубика, мало ли вам захочется склеить не один кубик или что-то не получится с первого раза. Ещё одна несложная фигура это пирамида, её развёртки найдёте на втором листе. Подобные пирамиды стоили древние египтяне, правда не из бумаги и не таких маленьких размеров 🙂
А это тоже пирамида, только в отличие от предыдущей у неё не четыре, а три грани.
Развёртки трёхгранной пирамиды на первом листе для печати.
И ещё одна забавная пирамидка из пяти граней, её развёртки на 4-ом листе в виде звёздочки в двух экземплярах.
Далее шестигранник, склеить его будет ещё проще, чем пирамиды. Развёртки шестигранника на первом листе.
Более сложная фигура это пятигранник, хотя пятигранник сложнее начертить, нежели склеить.
Развёртки пятигранника на втором листе.
Вот мы и добрались до сложных фигур. Теперь придётся поднапрячься, склеить такие фигуры нелегко! Для начала обычный цилиндр, его развёртки на втором листе.
А это более сложная фигура по сравнению с цилиндром, т.к. в её основании не круг, а овал.
Развёртки этой фигуры на втором листе, для овального основания сделано две запасных детали.
Чтобы аккуратно собрать цилиндр его детали нужно клеить встык. С одной стороны дно можно приклеить без проблем, просто поставьте на стол заранее склеенную трубку, положите на дно кружок и залейте клеем изнутри. Следите, чтобы диаметр трубы и круглого дна плотно подходили друг к другу, без щелей, иначе клей протечёт и всё приклеится к столу.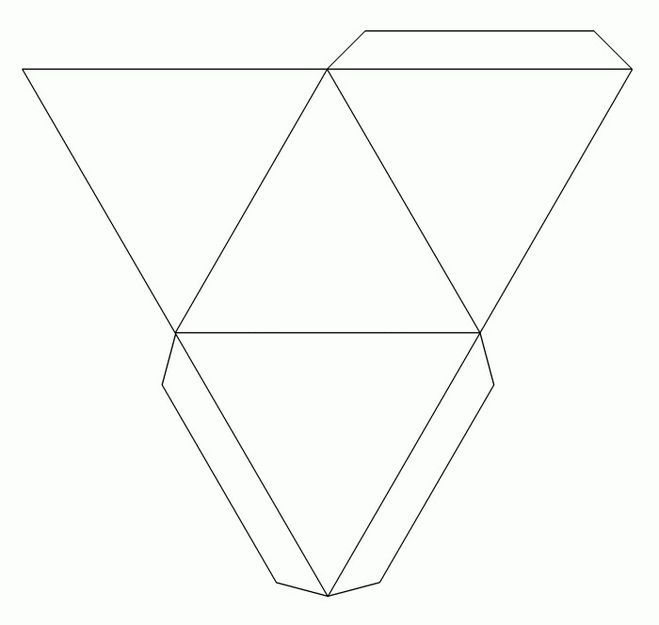
Второй кружок приклеить будет сложнее, поэтому приклейте внутри вспомогательные прямоугольники на расстоянии толщины бумаги от края трубы. Эти прямоугольники не дадут упасть основанию внутрь, теперь вы без проблем приклеете кружок сверху.
Цилиндр с овальным основанием можно клеить также как и обычный цилиндр, но он имеет меньшую высоту, поэтому тут проще вставить внутрь гармошку из бумаги, а наверх положить второе основание и по краю приклеить клеем.
Теперь очень сложная фигура – конус. Его детали на третьем листе, запасной кружок для днища на 4-ом листе. Вся сложность склеивания конуса в его острой вершине, а потом ещё будет очень сложно приклеить дно.
Сложная и одновременно простая фигура это шар. Шар состоит из 12-ти пятигранников, развёртки шара на 4-ом листе. Сначала клеится две половинки шара, а потом обе склеиваются вместе.
Довольно интересная фигура – ромб, её детали на третьем листе.
А теперь две очень похожие, но совершенно разные фигуры, их отличие только в основании.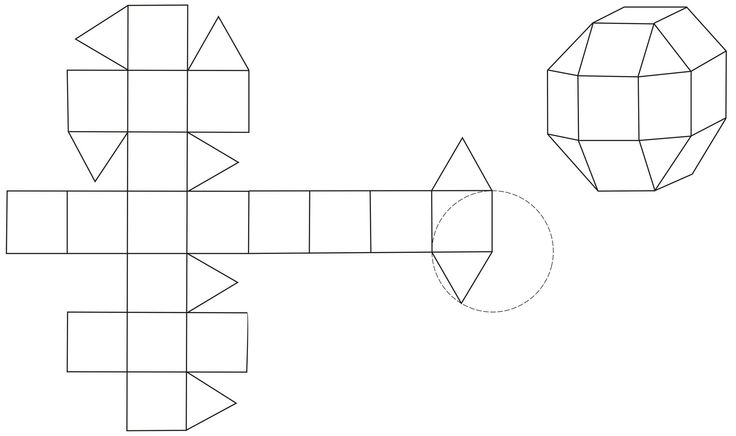
Когда склеите эти обе фигуры, то не сразу поймёте, что это вообще такое, они получились какие-то совсем невосприимчивые.
Ещё одна интересная фигурка это тор, только он у нас очень упрощён, его детали на 5-ом листе.
И наконец, последняя фигура из равносторонних треугольников, даже не знаю, как это назвать, но фигура похожа на звезду. Развёртки этой фигуры на пятом листе.
На сегодня это всё! Я желаю вам успехов в этой нелёгкой работе!
Содержание:
Содержание
Определение
Развернутым называют угол со сторонами, лежащей на одной прямой.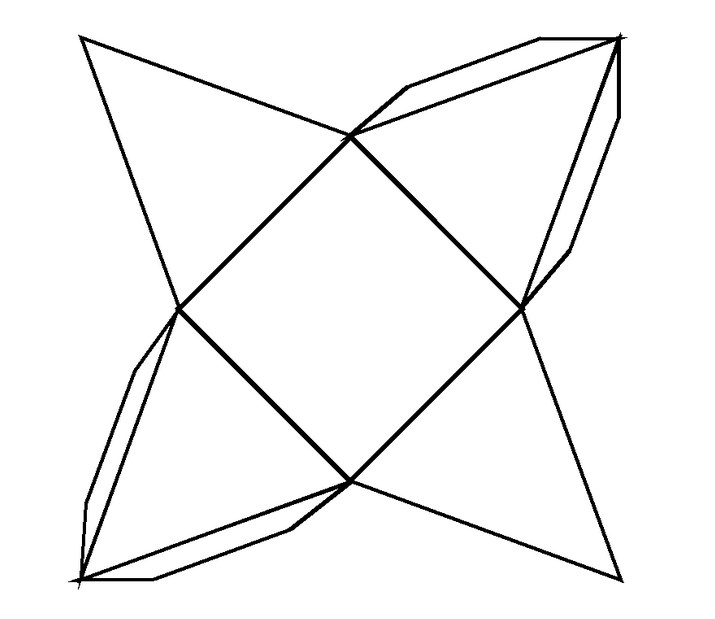
Стороны развернутого угла взаимно дополняют друг друга. В результате получается прямая линия. Таким образом, стороны данной геометрической фигуры представляют собой дополнительные лучи. К примеру, на рисунке изображен ∠CDK, который является развернутым. Точка D служит его вершиной, лучи, обозначенные, как DK и DC – сторонами ∠CDK.
Решить задачу, в которой требуется начертить развернутый угол достаточно просто. Необходимо нарисовать прямую линию и поставить на ней отметку в виде точки, которая будет являться вершиной. Существует другой способ. В начале на плоскости отмечают произвольную точку. Данная отметка будет принята за вершину угла. Если через нее прочертить прямую линию, то получится развернутый угол. Схематично оба способа представлены на рисунке.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Определить, является ли угол развернутым, тупым или острым можно с помощью ряда признаков.
Основные свойства развернутого угла:
В геометрии производя некоторые манипуляции с развернутыми углами, можно получить новые фигуры. К примеру, если такую геометрическую фигуру разделить лучом на два угла, то полученные углы называют смежными. Такие элементы изображены на рисунке.
∠ABD в данном случае является развернутым углом, а ВС представляет собой луч.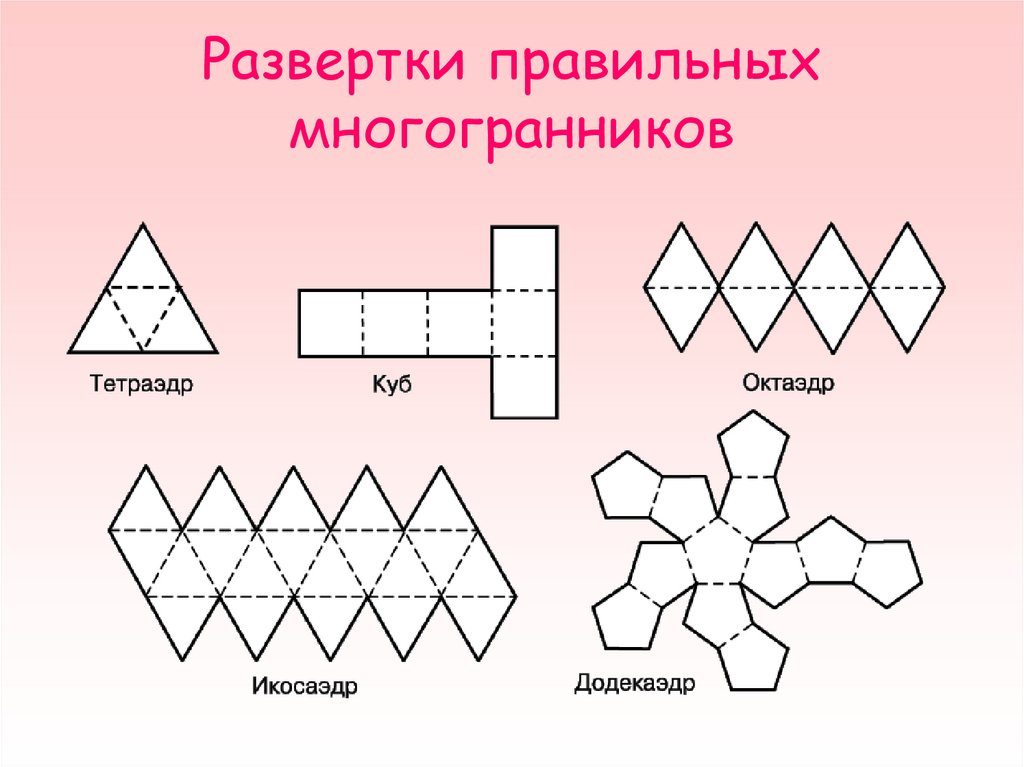
{0}\)
Насколько полезной была для вас статья?
Рейтинг: 5.00 (Голосов: 1)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Ноябрь 2003
Бумажная модель
Бумажные модели геометрических фигур не только украшают потолки математического факультета, где я работаю, но и являются визуальным представлением геометрических изобретений. Например, бумажная модель, показанная слева, является многогранной версией «поверхности Боя», которая имеет наименьшее количество вершин среди всех многогранных реализаций, состоящих из треугольников. Во время своего
Согласно первоначальному открытию [1], построение физической бумажной модели по-прежнему было утомительным процессом: любые мелкие неточности в процессе рисования и вырезания наверняка испортили бы модель. Чтобы представить себе требуемые усилия, взгляните на исходный рисунок [2] линий разреза этой бумажной модели.
Плоское развертывание поверхности мальчика
Посмотреть анимированную версию(565K)
В настоящее время программное обеспечение усовершенствовано и позволяет нам создавать «разрезанные рисунки», автоматически вычисляя развертывание геометрических фигур: справа вы можете увидеть развертывание модели Boy или просмотреть анимацию. Но даже при наличии современных программных средств остается ряд нерешенных геометрических задач.
Развертка
— это процесс разрезания многогранной поверхности по определенным кривым с последующим сведением поверхности на плоскость без нахлеста и без искажения отдельных граней. Развертка кромки , которую мы рассмотрим в этой статье, позволяет выполнять разрезы только вдоль кромок, а не через внутреннюю часть граней. Допускаются самопересечения при разворачивании процесс, но окончательная сплющенная поверхность не должна иметь нахлестов.Раскладывание куба — посмотреть анимированную версию | |||
Оригами , японское искусство складывания бумаги, является самым известным применением разворачивания — слово буквально означает «складывать бумагу».
Искусство складывания бумаги: оригами — посмотреть анимированную версию | |||
Сеть додекаэдра
Альбрехт Дюрер [4] ввел понятие сетки многогранного тела в одном из своих учебных пособий. Сеть многогранника — это набор ребер на плоскости, являющихся развернутыми ребрами твердого тела. Дюрер также дал четкие инструкции по рисованию сетей — примером может служить развертывание додекаэдра, показанное справа.
Альбрехт Дюрер
Со времен Дюрера математики интенсивно использовали бумажные модели для изучения геометрических поверхностей как в образовании, так и в исследованиях.
Развертки платоновых и архимедовых тел хорошо известны. Существует множество наборов для складывания, которые позволяют вырезать и складывать бумажные модели многогранников. Возможно, самая большая коллекция математических бумажных моделей была создана отцом Магнусом Веннингером, математиком и священником аббатства Святого Иоанна [5].
Додекаэдр с другой разверткой — посмотреть анимационную версию | |||
Развертки существуют для многих других многогранных поверхностей.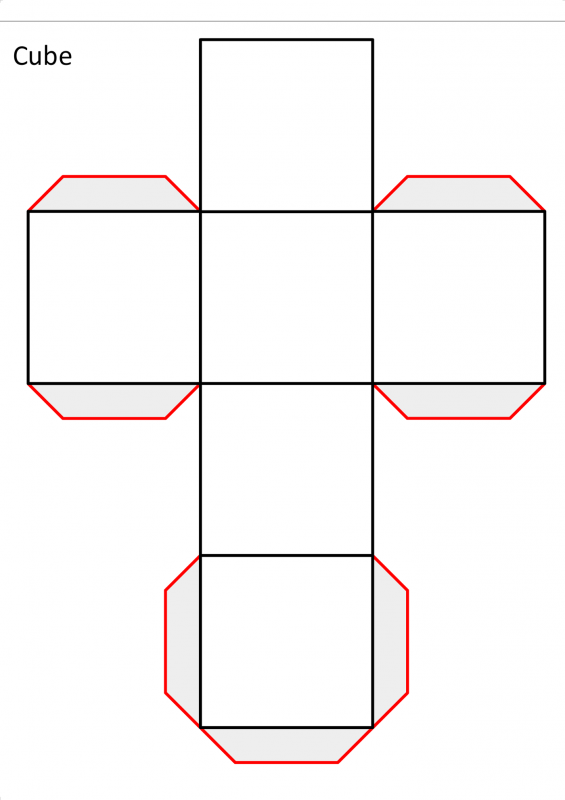
Например, тор, показанный ниже, имеет плоскую развертку до единственного компонента, так что никакие две грани не перекрываются. (Для экспертов этот многогранный тор — это тор Клиффорда , полученный из нестандартной параметризации с использованием слоев Хопфа в 3-сфере.)
Тор Клиффорда создается набором окружностей. Тор красиво разворачивается, несмотря на отрицательную кривизну внутренней области — посмотреть анимированную версию | |||
В комбинаторной геометрии сложно найти многогранные модели заданной топологической формы, которые используют минимальное количество граней или вершин. Тор Клиффорда, показанный выше, использует около 200 вершин, что, безусловно, больше, чем необходимо. Тор с наименьшим числом вершин, 7, нашел Часар [6].
Ф. Х. Лутц [7] построил модель развертывания ниже.
Тор Часара — это вложенный многогранный тор (т. е. без самопересечения) с наименьшим количеством вершин — см. анимированную версию | |||
Теперь мы готовы понять еще более сложное развертывание. Поверхность Боя, упомянутая во введении, является моделью проективной плоскости
Дискретная поверхность Boy разворачивается в односвязный диск. | |||
Если вы внимательно понаблюдаете за пересвертыванием поверхности Boy, то увидите, как противоположные точки черной граничной кривой попарно совпадают. Следовательно, поверхность Боя является полиэдральной моделью проективной плоскости. Особое свойство показанной полиэдральной модели (найденной У. Бремом [1]) заключается в том, что она использует наименьшее количество вершин среди всех полиэдральных моделей, состоящих из треугольники.
Кривизна — это математический способ описания степени «изгиба» или «кривизны» поверхности в каждой точке. Например, плоский лист бумаги не изгибается ни в одной из своих точек и, следовательно, имеет нулевую кривизну, а круглый шар имеет положительную кривизну в каждой точке. Дифференциальная геометрия использует исчисление для получения различных видов кривизны гладких поверхностей, но кривизна многогранника
с поверхностями можно работать гораздо более элементарно.
Самое важное твердое тело в мире. Футбольный мяч имеет положительную кривизну в каждой вершине — посмотреть анимированную версию | |||
Дискретная кривизна Гаусса измеряет изгиб многогранной поверхности в каждой из ее вершин. В каждой вершине мы рассматриваем углы, образованные на соседних гранях в этом углу. Если сумма этих углов ровно 360 0 , то набор граней можно свести к плоскости без зазоров и перекрытий. Следовательно, у него нулевой кривизны . Если сумма
углы меньше 360 0 , то ситуация подобна вершине конуса или углу выпуклого многогранника. Здесь кривизна должна быть положительной , так как такой многогранник подобен круглому шару. Отрицательная кривизна возникает, если сумма углов больше 360 0 , что происходит, например, в седловой точке.
В общем случае дискретная кривизна Гаусса в вершине определяется как разность 360 0 и суммы углов между соседними гранями, примыкающими к вершине:
K(вершина) = 360 0 — a 1 — a 2 — a 3 -…- a n ,
where n is the number of faces adjoining the vertex, and a 1 , …, и n это углы на гранях.
На следующем изображении показаны три разных типа вершин в верхнем ряду и развертывание вершинной звезды, то есть набор граней, встречающихся в вершине, в нижнем ряду. Из-за связи сфер с положительной кривизной и гиперболического пространства с отрицательной кривизной мы называем типы вершин сферическими , евклидовыми и гиперболическими соответственно.
Есть два непосредственных следствия задачи развертывания многогранных поверхностей:
Проверьте интерактивный апплет развертывания отрицательно изогнутой вершины.В качестве эвристического ориентира отметим, что слишком большая отрицательная кривизна Гаусса может сделать развертывание невозможным, поскольку потребуется слишком много разрезов. Например, дискретные минимальные поверхности, такие как показанный катеноид, могут иметь отрицательную кривизну Гаусса в каждой вершине. Здесь нет развертки на одну плоскую компоненту, но алгоритм находит развертку с четырьмя плоскими компонентами. компоненты.
Катеноид — это минимальная поверхность со «слишком большой» отрицательной кривизной. Следовательно, разворот состоит из более чем одного плоскостного компонента — посмотреть анимированную версию | |||
При складывании бумажной модели в Оригами сохраняется нулевая кривизна Гаусса исходного плоского листа бумаги.
Следовательно, модели оригами имеют постоянную нулевую кривизну Гаусса в каждой внутренней вершине.
Говоря словами Проекты открытых задач [8]:
Можно ли каждый выпуклый многогранник разрезать по ребрам и развернуть в один непересекающийся простой многоугольник?
Этот вопрос был поднят в математике в [9], но фактически восходит к Дюреру [4]. Было предпринято несколько попыток, включая эксперименты с программным обеспечением, чтобы подтвердить или опровергнуть эту гипотезу.
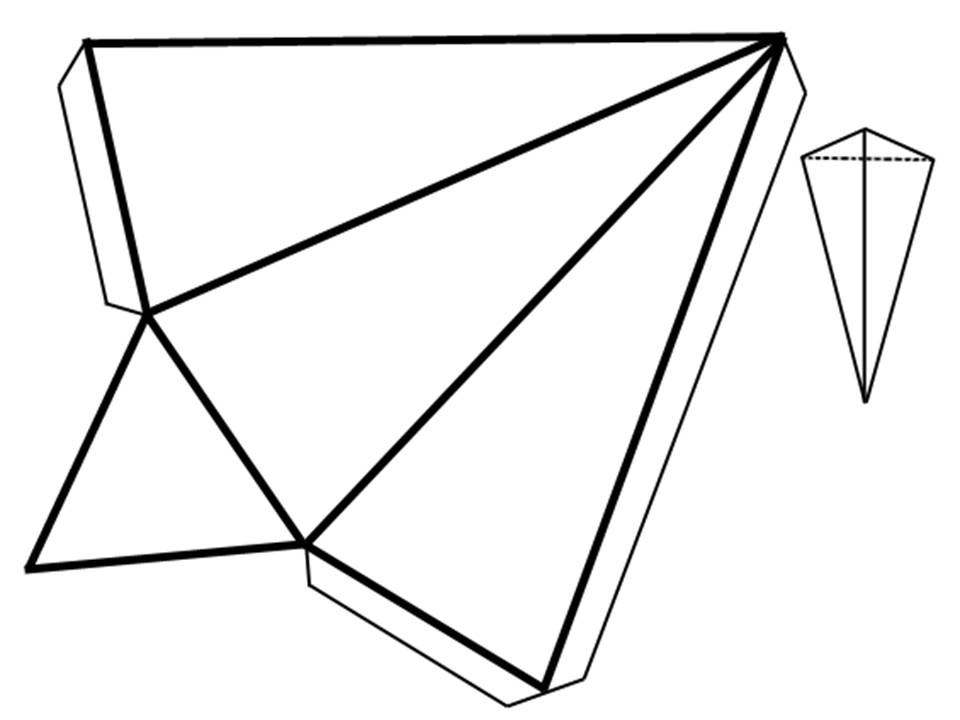
Остроконечный тетраэдр [10]
(Невыпуклый) остроконечный тетраэдр [10] справа нельзя развернуть без создания перекрывающихся областей на плоскости. Это означает, что в гипотезе нельзя опустить слово «выпуклый». Однако, несмотря на такие примеры, принято считать, что если ограничиться рассмотрением выпуклых многоугольников, то на этот вопрос есть положительный ответ.
Звездная развертка [14]
Другой класс разверток, отличный от рассмотренных в статье реберных разверток, получается, если разрешить разрезы не только по ребрам, но и по внутренности граней.
Одним из таких развертываний является 9Звезда 0008 разворачивается относительно исходной точки. Это разрезает многогранник по всем кратчайшим путям от исходной точки до других вершин многогранника; эти пути обычно
пройтись по внутренностям лиц. Аронов и О’Рурк [14] показали, что звездообразование возможно для любого выпуклого многогранника.
Мы видели, что существуют поверхности, такие как додекаэдр, которые имеют различные развертывания, и поверхности, подобные остроконечному тетраэдру, которые нельзя развернуть в единую связную часть. Поэтому любой автоматический алгоритм поиска разверток должен накладывать дополнительные ограничения.
Развертывание невыпуклой формы, такой как эта модель лошади, требует интенсивного числового поиска — просмотр анимированной версии | |||
Примеры таких ограничений:
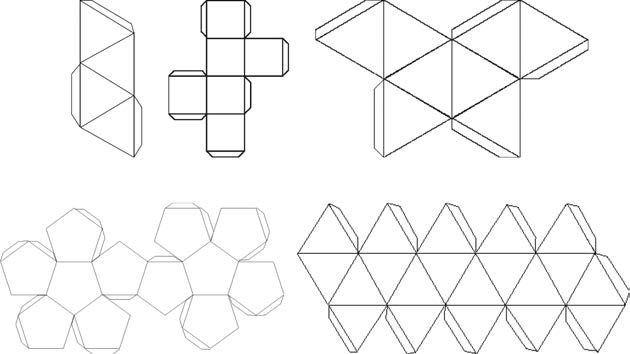
На практике автоматическое развертывание произвольных многогранных поверхностей в основном направлено на то, чтобы развернутая сетка не перекрывалась. Тем не менее, удивительно, как много невыпуклых поверхностей можно развернуть в один связный компонент, например, модель лошади, показанную выше, или многогранный торс Венеры, показанный ниже.
Туловище Венеры имеет очень сложную форму для раскрытия. Удивительно, но существует развертка, состоящая из одного компонента — посмотреть анимационную версию | |||
Развертка тора Часара с помощью апплета JavaView Unfolder. Стыки облегчают склеивание бумажной модели.
Распаковщик JavaView
Модуль Unfolder , написанный Клаусом Хильдебрандтом для программного обеспечения JavaView, позволяет разворачивать все многогранные поверхности.
Он пытается оптимизировать развертывание в зависимости от нескольких критериев, некоторые из которых упоминались в предыдущем разделе.
Добавление стыков к развернутой сети упрощает создание бумажной модели. Сначала разверните поверхность со стыками, затем отправьте изображение на принтер и, наконец, приклейте сложенную бумажную модель по стыкам.
Иногда удобнее загрузить приложение JavaView и позволить ему работать вне веб-браузера. Таким образом легче изменить размер окна, и у вас также будет доступ к локальному жесткому диску для сохранения и загрузки файлов.
К. Фукуда суммирует основные результаты и открытые проблемы, связанные с развертыванием многогранников, на своем сайте [11].
На сайте TOPP, управляемом Дж. О’Рурком [8], обсуждается набор открытых проблем, связанных с развертыванием многогранников и, в более общем смысле, с комбинаторной геометрией.
HyperGami — это программное обеспечение для проектирования и создания бумажных скульптур с использованием многогранников и пользовательских вариантов многогранников.
Программа доступна как коммерческое программное обеспечение из [12].
Распаковщик — это математический веб-сервис проекта JavaView. Вы можете развернуть все свои собственные геометрии в [13].
У. Брем, Как строить минимальные многогранные модели поверхности Боя. Мат. Интеллигент 12 (4): 51-56 (1990).
Э.-Х. Tjaden, Бумажная модель мальчика Брема Surface . TU-Берлин (1987), [email protected].
В. Шликенридер, Сети многогранников . Дипломированный диплом TU-Berlin (1997), [email protected].
А. Дюрер, Unterweysung der Messung mit dem Zyrkel und Rychtscheyd . Нюрнберг (1525 г.).
Английский перевод с комментариями Вальтера Л. Штрауса Руководство художника , Нью-Йорк (1977).
Фр. М. Дж. Веннингер, Многогранные модели . Издательство Кембриджского университета (1971).
http://employees.csbsju.edu/mwenninger/.
А. Часар, Многогранник без диагоналей . Acta Sci. Math., Сегед 13:140-142 (1949-1950).
Ф. Х. Лутц, Часар Торус . Модель электронной геометрии № 2001.02.069 (2001 г.),
http://www.eg-models.de/2001.02.069.
Э.Д. Демен, Дж.С.Б. Митчелл, Дж. О’Рурк, Проекты открытых проблем . http://cs.smith.edu/~jorourke/TOPP/Welcome.html.
Г.К. Шепард, Выпуклые многогранники с выпуклыми сетями . Матем. проц. Камб. Фил. соц. , 78:389-403 (1975).
М. Берн, Э. Д. Демен, Д. Эппштейн, Э. Куо, А. Мантлер, Дж. Снойинк,
Неразворачиваемые многогранники с выпуклыми гранями. Вычисл. геом. Теория прил. , 24 (2): 51-62 (2003).
К. Фукуда, Странные развертки выпуклых многогранников . Швейцарская техническая школа Цюриха (1997).
https://www.inf.ethz.ch/personal/fukudak/unfold_home/unfold_open.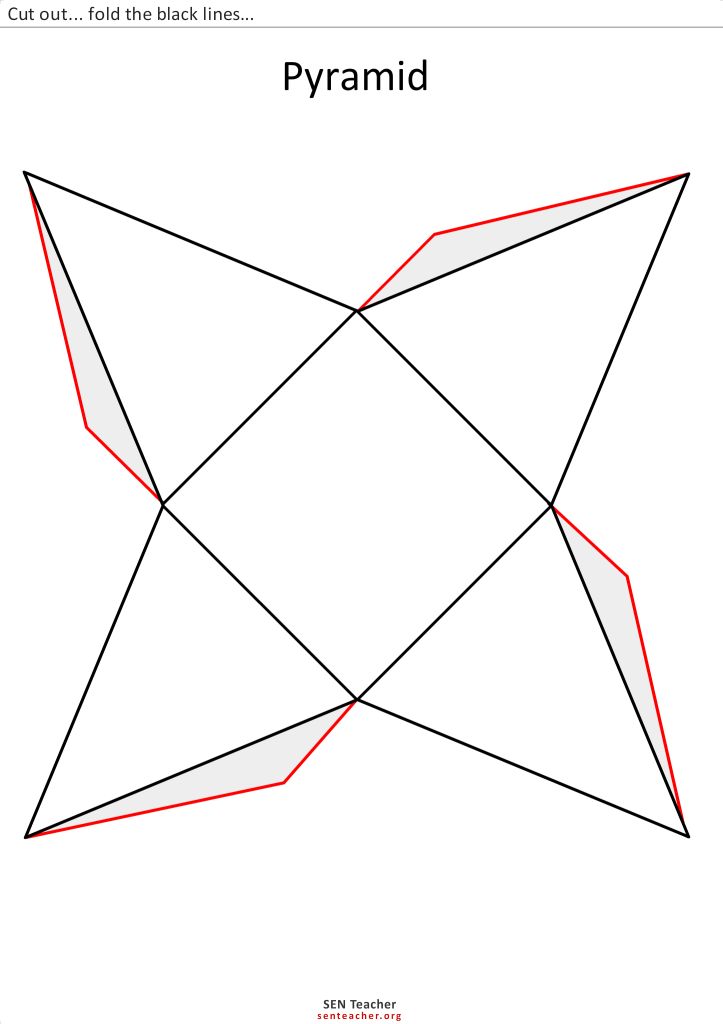
html
unfold_home/unfold_open.html
М. и Э. Айзенберг, HyperGami и JavaGami . ун-т Колорадо, Боулдер.
http://l3d.cs.colorado.edu/~ctg/projects/hypergami/.
К. Хильдебрандт, К. Полтье, Раскладыватель — Разворачивание полиэдральных сеток . Веб-сервис JavaView (2003 г.).
http://www.javaview.de/services/unfold/.
Б. Аронов, Дж. О’Рурк, Неперекрытие звездного разворачивания . Дискретный вычисл. геом., 8:219-250 (1992).
Дж. Ву, Оригами . http://www.origami.vancouver.bc.ca/home.html.
Конрад Полтье — исследователь Технического университета в Берлине и научный сотрудник, отвечающий за «Визуализацию» в Исследовательском центре DFG «Математика для ключевых технологий». Его интересы связаны с дискретной дифференциальной геометрией и математической визуализацией. Он опубликовал исследовательские книги и является автором календарей и отмеченных наградами математических исследований.
видео: для получения более подробной информации посетите его веб-страницу.
Изображения, анимация и апплеты на этой странице были созданы с помощью программного обеспечения JavaView.
Оценка: PreK to 2nd, 3rd to 5th, 6th to 8th, High School
Этот инструмент позволяет вам узнать о различных геометрических телах и их свойствах. Вы можете манипулировать и раскрашивать каждую фигуру, чтобы исследовать количество граней, ребер и вершин, а также можете использовать этот инструмент, чтобы исследовать следующий вопрос:
Для любого многогранника, какова связь между количеством граней, вершин, и края?
На какие еще вопросы поможет ответить этот инструмент?
Этот интерактив оптимизирован для настольных компьютеров и планшетов.
Выбор формы
Создайте свою собственную сеть, а затем распечатайте, вырежьте и сложите ее, чтобы увидеть, образует ли она сплошное тело.
Выберите: Добавляет лица из банка слева и перемещает фигуры.
Ластик: Стирает отдельные лица.
Ножницы: Обрезает детали по краям.
Цветовая палитра: Цвета граней, краев и вершин, как и в других вариантах выбора формы.
Примечание. При печати обратите внимание, что все грани должны быть соединены, чтобы создать единую сеть.
Запишите количество граней ( f ), ребер ( e ) и вершин ( v ) для каждой формы.
Противоположные вершины границы идентифицируются во время пересвертывания — см. анимированную версию