Когда приближается день рождения любимого малыша, все родители стараются подготовить для своего крохи всевозможные подарки, угощения. Чтобы праздник прошел в торжественной обстановке, мамы и папы украшают квартиру шариками, фотографиями и прочими атрибутами торжества.
Объемные цифры ко дню рождения ребенка пользуются все большей популярностью у родителей, которые хотят украсить квартиру к празднику, подготовиться к фотосессии и просто порадовать малыша. Однако не каждый родитель знает, как сделать такую цифру самостоятельно.
Работу над созданием двойки можно условно разделить на два этапа: создание каркаса и декорирование цифры.
Для того чтобы изготовить каркас, вам потребуется:
Для начала необходимо нарисовать на коробке цифру два. Постарайтесь тщательно прорисовать все углы. Когда рисунок будет готов, его нужно вырезать. Так как разрезать плотный картон ножницами очень непросто, то будет лучше и удобнее воспользоваться канцелярским ножом. Затем следует сделать копию двойки, положив основу на картон. В итоге у вас должно получиться две картонные цифры.
Чтобы двойка выглядела объемной, следует вырезать еще несколько картонных элементов и с помощью скотча соединить их с двумя цифрами.
Каркас готов.
Известно, что на обычный скотч не будут крепиться цветы из салфеток. Для того чтобы процесс декорирования прошел легче, следует обклеить все стыки скотчем на бумажной основе. Обклейте каркас двойки салфетками понравившегося цвета, используя клей ПВА.
Есть множество способов украсить объемную цифру.
Одни предпочитают использовать для декорирования гофрированную бумагу, другие выбирают фетр. Есть и те, кому по душе цветочки из салфеток.
Для того чтобы украсить объемную двойку розочками из салфеток, вам потребуется:
1. Возьмите три сложенные вчетверо салфетки. Поместите поверх них вырезанный из картона круг среднего размера. Вырежьте по контуру.
2. Скрепите все получившиеся кружочки из салфеток степлером по центру.
3. Теперь необходимо отсоединить верхний слой бумажной салфетки и смять его, затем второй и так далее. Комкайте каждый слой по отдельности, стараясь максимально увеличивать нажим снизу. В итоге у вас должна получиться розочка. Таких цветочков вам потребуется очень много.
Предварительно обдумайте дизайн двойки. Она может быть выполнена как в одном цвете, так и в сочетании нескольких цветов, можно придумать какой-нибудь необычный узор, а можно просто чередовать розочки разной расцветки.
Украшать цифру цветами необходимо не только спереди, но и по бокам. Это позволит зрительно увеличить размер двойки и придать ей дополнительный объем.
Объемная цифра 2 готова.
Она обязательно понравится вашему малышу и станет главным украшением торжества, запечатленным на памятных фото во время празднования дня рождения вашего двухлетки.
К дню рождения ребенка хочется украсить детскую комнату по-особому. Мы собрали идеи, как сделать цифру, соответствующую возрасту именинника.
savepic.ru
Не обязательно заказывать дорогой декор у профессиональных декораторов, своими руками тоже можно сделать красивые «штучки» для оформления интерьера.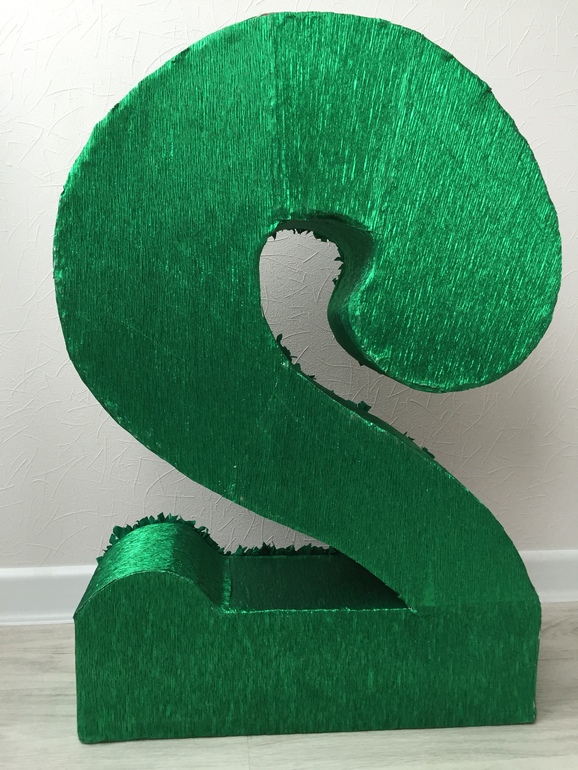
Если оформление воздушными шарами надоело или не устраивает вас по другим причинам, ножницы в руки и вперед! Делаем цифру для именинника своими руками. Достаточно вырезать из плотного картона большой шаблон и декорировать его гофробумагой, нитками, фотографиями ребенка или чем-то еще, что подскажет вам фантазия. Пробуйте!
www.babyroomblog.ru
Цифра на день рождения в виде панно. Найдите подходящую по размеру ДВП-ку или кусок плотного картона и обтяните красивой тканью, обклейте бумагой и т.п. Фон не должен сливаться с самой цифрой. Он может быть контрастного цвета или в той же гамме, но светлее/темнее основной цифры.
Обклеить заготовку цветочками и цифра готова! Да, цветов понадобится много, да, нужно попотеть, чтобы вырезать заготовки и приклеить их к основе. Но! Термоклей вам в помощь. Красота требует… нет, не жертв, а потраченного времени!
Такая цифра станет отличным задником для праздничной фотосессии. После дня рождения она может просто висеть на стене в качестве украшения, пока именинник не повзрослеет еще на год.
Цветы можно сделать любым способом (из бумаги, из ткани) или использовать готовые. Они могут быть одного цвета или подобраны в одной гамме, но с незначительной разницей по тону. Хорошо смотрятся контрастные композиции. Экспериментируйте, учитывайте общую стилистику праздника или помещения, где будет находится декор. Если цифра будет крепиться на стену, то украшать нужно только одну сторону.
www.babyroomblog.ru
Если нарезать бумажные заготовки для цветов по спирали, получатся симпатичные розочки. Сделайте их разных размеров и цветов, и у вас получится красивая цифра на день рождения.
static.baza.farpost.ru
Объемную заготовку цифры можно вырезать из пенопласта. Такая цифра будет самостоятельно стоять на ровной поверхности стола, комода. Но цветов понадобится гораздо больше!
Для изготовления цветов можно использовать бумажные салфетки, креповую бумагу, бумагу для пастели, фетр, фатин, тюль и пр.
www.babyroomblog.
ru
Если использовать гофрированные «тарелочки» от конфет или кексов, получится нарядная цифра с оборочками. Девочки любят рюши, поэтому можно декорировать заготовку простыми полосками с бахромой.
Вырезать из ткани кружочки, оплавить на огне и собрать «тарелочка в тарелочку». Серединку получившегося цветочка украсить бусинкой. Украсить такими цветами большую заготовку-циферку и праздничное украшение готово! Такой вариант больше подойдет девочкам. Ткань можно подобрать в цвет платья именинницы.
Если запастись терпением и большим количеством бумажных салфеток, то можно сделать цифру в технике торцевание. Заготовка в таком случае должна быть из пенопласта, чтобы сложенные салфетки запихивались туда и не выпадали. Получается пышно и красиво.
www.babyroomblog.ru
Маму-рукодельницу не остановить! Пошить цифры из ткани не составит труда. Декорировать можно лентами, тканевыми цветами, бусинами. Такие цифры можно использовать в качестве декоративных подушек.
livemaster.ru
Хотите порадовать именинника и удивить гостей? Сделайте цифру в «луке» виновника торжества.
evgakids.com
Цифры можно сделать и из живых флористических материалов (цветы, мох). Основа в таком случае должна быть из пиафлора — специальная флористическая губка, которая долгое время способна удерживать влагу и подпитывать растения.
boom-party.ru
Готовыми искусственными цветами тоже можно украсить цифру на день рождения. Клеить цветы к основе удобно термопистолетом.
Если ждете в гости ораву сладкоежек или толпу родственников «на чайОК», следует запастись съедобными циферками, соответствующими возрасту именинника/цы. Печеньки и тортик пойдут на «ура»!
snova-prazdnik.ru
77tortov.ru
parties-and-picnics.org
parties-and-picnics.org
Есть и полезные витаминные цифры на день рождения, их можно съесть прямо во время праздника вместе с гостями.
Как сделать цифру из фруктов и других вкусняшек, читайте ТУТ.
Уважаемые читатели! Поделитесь в комментариях собственными идеями изготовления цифр для именинников.
Подборка забавных практических математических заданий для изучения 2D- и 3D-фигур.
Когда мы думаем о раннем обучении математике, мы обычно думаем в первую очередь о числах. Но есть целый другой мир математики, которым можно наслаждаться и исследовать, и это мир форм! Этот пост включает в себя пятнадцать идей для изучения 2D- и 3D-форм (и их свойств) в увлекательной игровой форме и практическими способами!
15 увлекательных практических занятий по изучению 2D- и 3D-фигурИдеи для изучения 2-мерных фигур
В возрасте от двух до четырех лет дети обычно начинают учить названия между прочим, простых двумерных фигур; вообще изучение кругов, квадратов и треугольников для начала.
1. В поисках формы
Отличный способ начать изучение форм (будь то в школе или дома) — это «охота за фигурами» — изучение и выявление форм в нашем окружении и повседневной жизни. . Вы можете отправиться на поиски фигуры вокруг своего дома, заднего двора, классной комнаты или района. Дети постарше могут взять контрольный список или бумагу, чтобы записать свои выводы, в то время как детям помладше понравится обсуждать то, что вы видите, когда идете. Фотографирование фигур, которые вы найдете, — еще одна отличная идея, и фотографии идеально подходят для компиляции в вашу собственную книгу форм.
2.
Игра на палочках
Палочки и спички — это универсальный учебный материал. Они являются отличным ресурсом для создания 2D-фигур.
3. Самокорректирующаяся головоломка с поп-стиком
Продвиньтесь в указанном выше упражнении еще на один шаг и соберите самокорректирующуюся головоломку, используя один цвет для каждой фигуры, написав название фигуры на каждой поп-палочке и указав количество стороны/углы. Это делает большую занятую сумку.
4. Творения для чистки труб
Средства для чистки труб отлично тренируют мышцы пальцев. Их можно сгибать и скручивать, создавая различные 2D-формы. Как вариант, увеличьте фигуры, используя по одному ершику для каждой стороны фигуры.
5. Playdough Fun
Playdough также является полезным инструментом для изучения форм. Добавление набора геометрических формочек для печенья (таких как эта) к игре с пластилином — очень простой способ добавить формы в свой день.
6. Коллажи из фигур
Детям дошкольного и школьного возраста будет очень весело создавать картинки из фигур. Я создал эти два в качестве примера, используя различные формы, вырезанные из текстурированной бумаги и пуговиц.
7. Красивые кубики для выкроек
Блоки для выкроек — один из моих любимых материалов для занятий. Играя с ними, дети узнают не только о двухмерных фигурах, но и о других математических понятиях, таких как симметрия, мозаика, узор, сортировка, счет и многое другое. Это задание можно либо оставить неструктурированным, чтобы дети могли создавать свои собственные картинки, узоры и фигуры, либо вы можете использовать в качестве руководства карточки с заданиями с блоками узоров.
8. Пой о фигурах
Вот милая песенка, которая поможет дошкольникам выучить двухмерные фигуры. Лучше всего это работает с группой детей, когда каждый держит форму (пойте на мотив песни «Если ты счастлив и ты это знаешь»).
Если вы держите квадрат, встаньте!
Если вы держите квадрат, встаньте!
Если вы держите квадрат, если вы держите квадрат
Если вы держите квадрат, встаньте.Повторить с другими формами
Забавные идеи для изучения трехмерных фигур
9. Фантастические мешочки на ощупь
Когда я знакомлю свой класс с темой фигур, я всегда начинаю с «мешка с чулками». Идея заключалась в том, чтобы дети ощупывали фигуры в пакете, не глядя, пытаясь идентифицировать каждую фигуру, используя только осязание. Обсуждаем — как ощущения? У него острые углы? Он кажется круглым? Как только дети узнают названия фигур, будет интересно угадать фигуру, которую они держат, прежде чем показать ее!
10. Чудесные деревянные кубики
Вообще говоря, в первый год обучения в школе вы можете ожидать, что ваш ребенок выучит фигуры, изображенные выше; прямоугольная призма, пирамида, цилиндр, конус, куб и сфера.
Деревянные 3D-блоки — отличный ресурс для обсуждения особенностей 3D-фигур (и 2D-фигур, из которых они состоят).
11. Протестируйте: стопка, рулон или слайд?
Пока дети изучают 3D-фигуры, интересно исследовать, как они двигаются и взаимодействуют друг с другом. Установите простую рампу и протестируйте каждую форму, чтобы увидеть, катится ли она вниз по склону или скользит? Затем проверьте каждую фигуру, чтобы увидеть, можно ли ее легко сложить поверх другой фигуры. Изучите понимание ребенком того, почему фигура катится (или не катится), скользит или складывается.
12. 3D-формы из пластилина
Добавьте спички в пластилин и предложите детям создавать 2D- и 3D-формы.
13. Модели 3D-форм
Лепка 3D-моделей из пластилина или кинетического песка — увлекательная практическая задача.
14. Nifty Nets
Дети школьного возраста могут начать изучать понятие «сетки».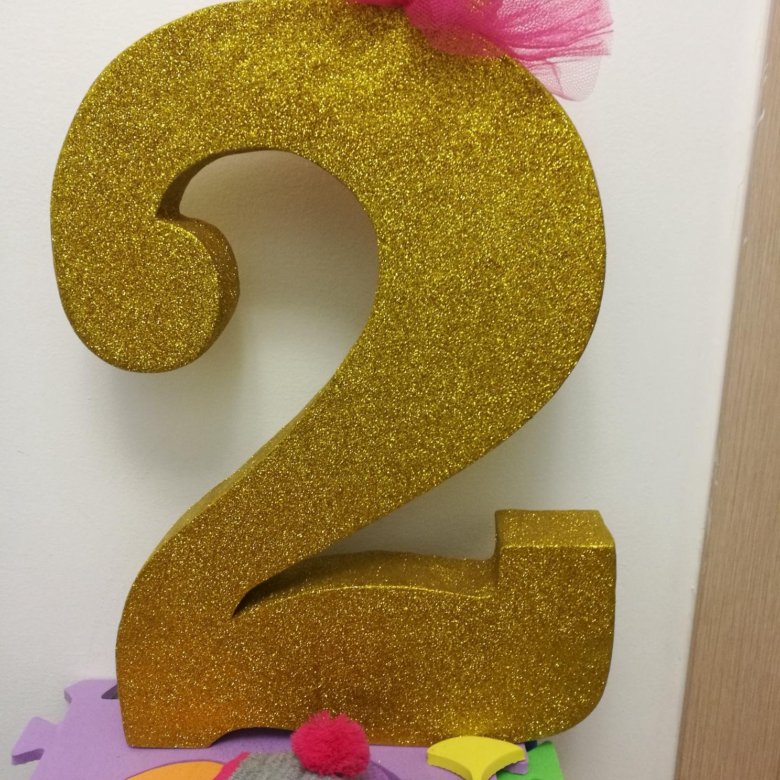
Сеть представляет собой расплющенную трехмерную форму. Эти пластиковые полидроны — фантастический инструмент для обучения этому понятию. Изготовление кубика своими руками — отличное начало! (Мы снова видим трехмерные формы в нашей повседневной жизни). Вот ссылка на бесплатный шаблон штампа, который можно распечатать на сайте Teachers Pay Teachers.
15. Трехмерный стишок
Наконец, вот простой трехмерный стишок, который поможет детям связать название фигуры с реальными объектами.
3D-фигуры толстые, а не плоские
Конус похож на праздничную шляпу
Сфера похожа на надувной мяч
Призма похожа на здание высотой
Цилиндр похож на банку с газировкой
Кубик похож на кости, которые вы бросаете
3D-фигуры здесь и там
3D-фигуры повсюду!
Какие ваши любимые идеи для занятий по изучению 2D- и 3D-фигур?
Вам также может понравиться;
Лорен Хант — воспитательница дошкольного образования, которая в настоящее время работает неполный рабочий день, обучая детей первого года обучения в школе.
Возможно, вы читаете это перед своим компьютером. Или, может быть, у вас есть стакан воды рядом с вами.
Если вы посмотрите на любой из этих объектов, которые вас окружают, станет ясно, что это объекты в 3D. Но каково математическое определение трехмерной фигуры?
В этой статье мы узнаем больше о трехмерных фигурах и их применении.
Трехмерная фигура представляет собой геометрическое тело с тремя пространственными измерениями: длина, ширина, глубина . Иногда глубину называют высотой.
Например, представьте, что вы берете коробку из одной службы доставки.
Если вы поставите коробку таким образом, что сможете наблюдать только одну из ее граней, вы будете наблюдать плоскую поверхность в 2D, а затем вы будете наблюдать только длину и ширину этой грани.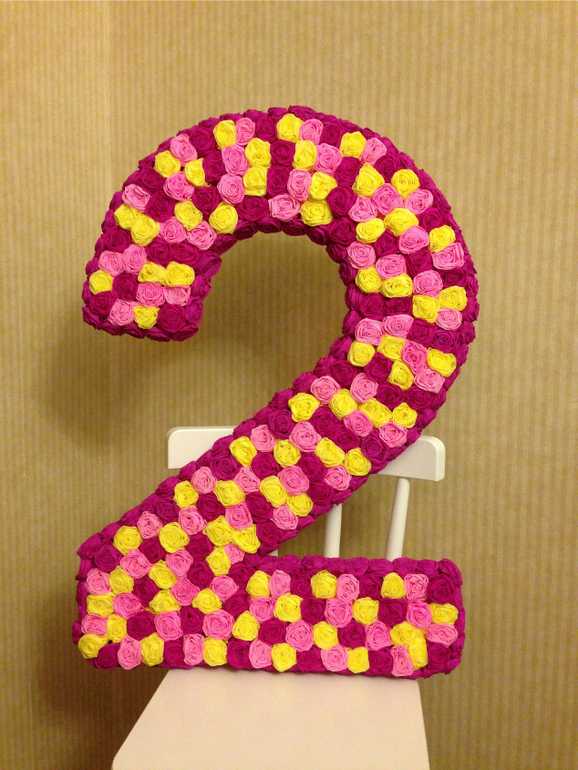
Но если вы немного повернете его, то увидите, что коробка тоже имеет некоторую глубину. Это то, что мы имеем в виду с трехмерными фигурами.
Как вы могли заметить на коробке, эти трехмерные фигуры имеют том . В математике мы определяем объем как количество пространства внутри замкнутой поверхности.
Снова возьмите коробку, и если вы откроете ее сейчас, объем будет равен количеству места внутри коробки. Позже мы узнаем, как вычислить этот объем.
Эти геометрические фигуры обычно, за некоторыми исключениями, которые мы будем использовать, имеют граней , которые являются поверхностями с определенной площадью поверхности, ограничивающими фигуру. Эти грани соединяются в вершинах , которые являются точками соединения.
Наконец, линии, ограничивающие эти поверхности и контур геометрической фигуры, называются ребрами . Мы бы сравнили их со сторонами двумерных фигур.
Отвлекшись от этой статьи и осмотревшись вокруг, вы, вероятно, обнаружите множество трехмерных фигур с различной структурой. От кровати до стула, до стола или даже до книг, которые вы используете для учебы. Все они представляют собой трехмерные фигуры, поскольку они имеют 3 измерения, о которых мы упоминали ранее; длина, ширина и глубина, а также потому, что они имеют объем.
Мы различаем обычные и неправильные трехмерные формы. Мы сосредоточимся на обычных трехмерных фигурах, так как они более распространены в математике.
Конус Конус — это трехмерная фигура, которую мы получили бы, если бы прямоугольный треугольник (с одним углом, равным 90º) повернулся с фиксированной одной из сторон, таким образом, мы получили бы форму в 3d . Эта фигура обычно имеет круглое основание и вершину , к которой сужается боковая поверхность конуса.
Основание не обязательно должно быть кругом, это может быть и другая двухмерная круглая фигура, например овал. Вы можете наблюдать эту форму в реальном мире, когда смотрите на дорожные конусы.
ПирамидаЭта фигура похожа на конус, но в этом случае основание не имеет круглой формы. Основание представляет собой двумерную фигуру с тремя или более сторонами, например треугольник, квадрат, прямоугольник и т. д.
Поскольку геометрическая форма основания может варьироваться, изменяется и количество ребер. Все его поверхности, сколько бы их ни было, сужаются к вершине.
Известные египетские пирамиды являются одним из примеров этих геометрических форм, в данном случае они имеют квадратное основание.
Куб Эта геометрическая фигура состоит из шести равновеликих граней, три из которых сходятся в одной вершине, всего восемь вершин и двенадцать ребер.
Примером куба является игральная кость. Если вы заметите это, все грани обычной игральной кости имеют одинаковую поверхность, и каждая ее вершина работает как объединение трех разных граней.
Прямоугольная призмаПохожа на куб, так как также имеет восемь вершин, двенадцать ребер и шесть граней, но в этом случае не все грани равны. Каждая грань равна своей противоположности, поэтому у нас есть пары равных граней.
Примером прямоугольной призмы может быть ящик или даже коробка, хотя иногда они имеют форму куба.
Существуют и другие виды призм, в зависимости от формы основания и противоположной стороны. Например, если эти грани имеют форму треугольника, это треугольная призма , которая будет иметь всего пять граней вместо шести, как у прямоугольной призмы. Но это основание (и противоположная грань) может иметь другую двумерную фигуру, которая дает различные типы призм: пятиугольные призмы , шестиугольные призмы и т.
д.
Форма этой фигуры может напомнить вам прямоугольной призмы, но в данном случае она имеет две поверхности, которые называются вершиной и низ (или основание) фигуры, состоящей из двухмерных круглых фигур.
У этой фигуры нет вершины. Поверхность, соединяющая эти две грани, по существу представляет собой прямоугольник, но изогнутый.
Такие геометрические фигуры можно найти в банках или стаканах.
Футбол, баскетбол или, если мы не хотим ограничиваться только спортивным миром: пузырь. Все эти объекты имеют одну общую черту: они являются сферами.
Эти геометрические фигуры получаются, если мы делаем круг, представляющий собой двухмерную фигуру, повернутую вокруг своего диаметра. Объем, описываемый этим оборотом, определяется как сфера.
Как и в случае с кругом в двух измерениях, все точки поверхности находятся на одинаковом расстоянии от точки в центре фигуры.
Это расстояние называется радиусом . Если мы проследим расстояние между двумя точками поверхности сферы, проходящей через ее центр, то это расстояние называется диаметр сферы, что соответствует удвоенному радиусу.
При работе с трехмерными фигурами есть некоторые вещи, которые мы могли бы знать о них. В частности, нас интересуют две характеристики.
Первая — это площадь фигуры.
Площадь фигуры – это количество поверхности, которую занимают грани фигуры. Единицами площади поверхности фигуры являются единицы площади, стандартными являются квадратные метры (м2).
Чтобы получить общую площадь поверхности фигуры, мы должны просуммировать площади каждой грани фигуры. Не следует путать площадь поверхности фигуры с ее объемом. Площадь состоит только из поверхности граней, независимо от того, что находится внутри них.
С другой стороны, у нас есть объем рисунка.
Объем фигуры – это количество пространства внутри поверхности, ограниченной гранями фигуры. Единицами объема являются единицы объема, стандартными являются кубические метры.
Если мы снова возьмем коробку, о которой мы говорили в этой статье, вы увидите, что поверхность картона, используемого для всех граней, соответствует площади поверхности коробки, но пространство внутри коробки соответствует к его объему.
Давайте посмотрим, как выглядят некоторые математические уравнения для трехмерных фигур, которые мы видели раньше.
Площадь поверхности трехмерной фигуры равна сумме площадей ее граней.
Для конуса площадь поверхности его основания равна , где r — радиус окружности. Площадь боковой грани равна , будучи г расстояния между любой точкой ребра основания до вершины. Таким образом, площадь поверхности конуса обычно выражается как
.
Объем конуса определяется по следующей формуле:
,
где h — расстояние от центра основания до вершины.
В этом случае формулы площади и объема будут зависеть от количества ребер, которые имеет основание.
Например, если пирамида имеет квадратное основание, площадь поверхности пирамиды будет равна сумме площади квадрата и суммы площадей каждого треугольника, соединяющего вершины. В общем, мы можем выразить площадь поверхности пирамиды как
Будьте осторожны, так как основание не обязательно должно быть правильным, и площадь поверхности треугольников, соединяющихся с вершиной, тоже не обязательно должна быть правильной.
Объем пирамиды также зависит от ее основания. Для квадратной пирамиды объем следует формуле:
равно
В этом случае, поскольку прямоугольная призма и куб образованы шестью гранями, для получения общая площадь поверхности фигуры, нам просто нужно суммировать площади каждой грани.
Для куба все шесть граней будут иметь одинаковую площадь, но для прямоугольной призмы, поскольку каждая грань равна своей противоположности, есть три разных значения. Общее математическое выражение для площади поверхности прямоугольной призмы:
где A 1 , A 2 и A 3 являются этими тремя различными областями. Площадь прямоугольника равна.
Объем этих фигур равен произведению трех ребер; длина, ширина и глубина призмы, например,
В случае куба, поскольку все стороны имеют одинаковую длину, мы имеем
Цилиндр состоит из двух окружностей, которые являются верхней и нижней частью фигуры, и изогнутого прямоугольника. Следовательно, если площадь круга равна , сумма всех площадей равна
, где h — высота от одной точки основания до точки наверху в том же положении.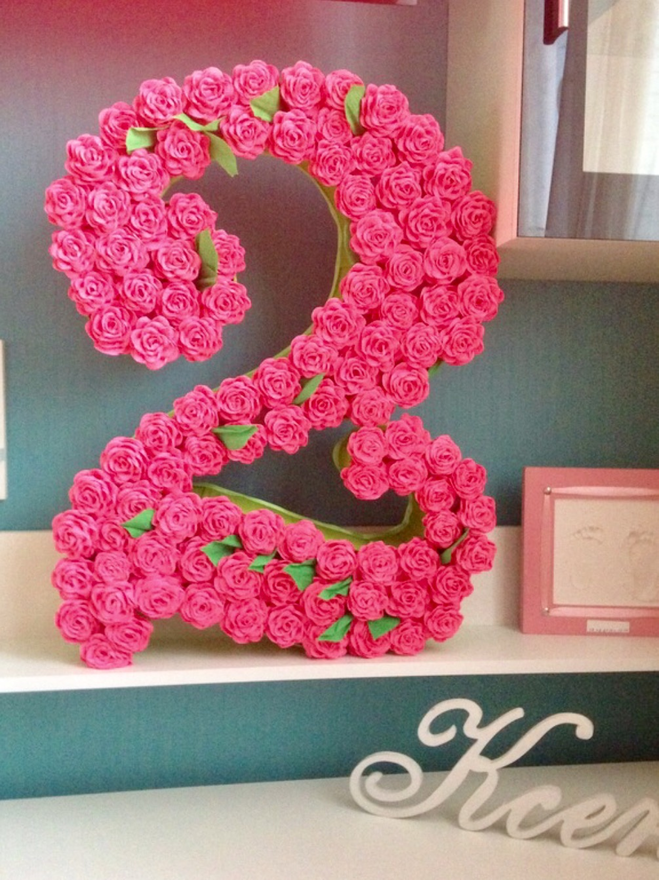
Объем цилиндра описывается следующим уравнением:
Известная нам сфера представляет собой другой тип геометрической фигуры, так как она не образована объединением разных граней. Вот почему нам нужно математическое выражение для вычисления площади его поверхности:
. А объем сферы определяется по следующей формуле:
.
Теперь давайте рассмотрим некоторые примеры задач, с которыми вы можете столкнуться на трехмерных фигурах.
Найдите объем воды, необходимый для заполнения цилиндрического стеклянного стакана высотой 12 см и радиусом 7 см. Брать .
Решение
Используя
затем,
Кохе хочет сделать коническую кепку радиусом 14 см и высотой 20 см для 8 друзей в преддверии своего дня рождения. Какова общая площадь картонной бумаги, чтобы сделать все 8 для своих друзей?
Решение
Сначала найдем общую площадь поверхности одного конического колпачка.
Использование
В этом случае g — высота конуса, равная 20 см, а r — 14 см. Следовательно,
Но это всего лишь площадь 1 конуса, вам нужно найти площадь 8 конусов. Таким образом,
Следовательно, Кохе понадобится картон с общей площадью поверхности 11 968 см 2 , чтобы успешно изготовить 8 конических крышек для своих друзей перед вечеринкой по случаю его дня рождения.
