С днем рождения у нас связаны самые трогательные воспоминания и страстные ожидания – это применимо и к взрослым, и к детям. Каждой мамочке вспоминаются те неповторимые минуты, когда она впервые взяла в руки своего малыша, первые ощущения, слова, эмоции. Только когда эти воспоминания отступят на второй план, нужно будет начинать подготовку к самому празднику.
Ну а какой же детский день рождения без праздничной фотосессии? Даже если вы не профессионал, вы сможете устроить ее сами, у себя дома. Но для этого вам не помешает кое-какой инвентарь. Очень хороший эффект получается в фотосессиях, снятых в празднично оформленном помещении. Выгодно подчеркивает торжественность момента нарядная, персонально для именинника приготовленная большая цифра, ярко украшенная, объемная, праздничная!
В ее создании может объединиться вся семья, уже начиная создавать также и праздничное настроение. Тем более, что сделать картонные цифры совсем несложно, а в результате вы испытаете массу положительных эмоций.
Каких видов бывают картонные цифры?
Обобщенно праздничные цифры делят на объемные и плоские. Объемные стоят самостоятельно в любом месте комнаты. Плоские же вешаются на стену.
Объемные
Такие цифры состоят из трехмерного каркаса с воздушным декором из бумаги. Они смотрятся необычайно легкими, атмосферными и сказочно красивыми, обращая на себя внимание всех гостей.
Изготовление цифр состоит из двух этапов: создание основы и украшение готовой конструкции.
Объемную основу изготавливают из картона с помощью скотча или вырезают из пенопласта. Последний вариант очень удобен: в пенопласт, используя шпильки, можно вставить цветы и прочие элементы декора. Это и экономит время, и избавляет от грязной работы с клеем. Вместо картона можно использовать яркий толстый фетр, который легко сшивается. Тогда после праздника именинник сможет еще долго играть с циферкой, как с мягкой игрушкой.
Популярны также цифры из воздушных шаров.
Они очень просты в изготовлении и подходят как девочкам, так и мальчикам. Для изготовления основы берут толстую проволоку. Затем на ней крепят надутые шары.
Размер основы цифры вы выбираете сами в соответствии со своей дизайнерской задумкой. Большие фигуры делают яркой фотосессию, маленькими можно оформить обеденную зону. На детский день делают циферки высотой равной или превышающей рост ребенка.
Украсить объемную цифру можно как в одной цветовой гамме, так и в разных цветах. Для визуального увеличения объема фигуры ее лицевую часть делают более светлой, а бока — темнее. Для девочки в качестве декора выбирают бумажные цветы. Очень нарядно смотрятся розовые, алые, оранжевые, а также сиреневые цветы. В дизайне для мальчиков рекомендуем украшения бахромой, пряжей, помпонами синего, белого или зеленого цветов, а также их оттенков.
Плоские цифры
Плоские цифры называются так из-за конструкции их основы: это цифра, вырезанная из картонного листа и украшенная только с лицевой стороны.
Ее невозможно поставить, поэтому обычно ее подвешивают к стене. Но ее можно сделать гораздо быстрее объемной и сэкономить при этом на материале для декора.
Из чего изготавливается декор для цифр?
В этом вопросе каждый отталкивается от своих возможностей, желаний и вкусов. Чаще всего из бумаги, тканей или фетра изготавливаются мелкие элементы – цветы, бабочки, помпоны, фунтики и т.п., которые крепятся на основу цифры. Оригинально смотрятся цифры, украшенные пуговицами. Детям нравятся изображения мультяшных героев на цифрах. Стильно смотрятся цифры, обмотанные фактурной вязальной пряжей.
ФетрЭтот материал очень приятен на ощупь и послушен в работе, по своим качества он соединяет преимущества бумаги (край ровный, не обтрепывается, вырезается легко, ножницами на фетре можно вырезать ажурные узоры) и ткани (приятный на ощупь, труднее мнется, долговечный). Украшения из него получаются стильные, яркие, с интересной фактурой.
Фетровые цветы выглядят очень живыми.
Гофрированная бумага
Из этого материала получаются прекрасные пышные цветы. Изготавливать декор из гофрированной бумаги очень удобно, т.к. этот материал прост в обращении. Разнообразные цветы и помпоны рождаются из него буквально моментально даже в руках новичков. Общий принцип изготовления цветка из гофрированной бумаги таков: бумагу складывают слоями в гармошку (от количества слоев зависит пышность готового бутона), перематывают ее посередине ниткой, обрезают концы, закругляют их или делают острыми. Затем расправляют слои бумаги, формируя лепестки.
Салфетки
Обычные бумажные салфетки – это более экономный вариант гофрированной бумаги. Но цифры, декорированные цветками из салфеток, смотрятся так же нарядно, пышно и воздушно. Для изготовления такого декора целую салфетку сворачивают пополам дважды и скрепляют степлером в центре.
Из получившегося квадрата вырезают круг. Потом все его слои последовательно поднимают, слегка приплюскивая. Только нижний слой остается расправленным для удобного крепления к картонной основе.
Подробный мастер-класс изготовления цифры для дня рождения из гофрированной бумаги
Мы рассмотрим технологию создания объемной цифры, т.к. в плоской все делается аналогично, только на плоской основе.
Перед началом работы, приготовьте необходимые материалы и инструменты:
Картон подходящего размера
Бруски для утяжеления и придания устойчивости конструкции
Удобные ножницы (не должны натирать пальцы) или канцелярский нож
Гофрированная бумага
Строительный степлер
Горячий клей
Клеевой пистолет
Линейки, карандаши, ластики
Шаг № 1
Делаем каркас объемной цифры:
Скрепляем шаблоны цифр с внутренними полосками строительным степлером, скотчем или клеевым пистолетом
Промазываем стыки изнутри горячим клеем
Приклеиваем бруски для устойчивости
Проклеиваем бумагой конструкцию изнутри
Шаг № 2
Готовим фунтики для декора:
Шаг № 3
Украшаем каркас:
Приклеиваем на стыки бумажные полоски шириной 2 см
Приклеиваем фунтики к основе, используя технику торцевания.
Основную часть фигуры обклеиваем фунтиками большего размера, а низ — фунтиками поменьше.
В конце работы утяжеляем основание и приклеиваем его горячим клеем.
Теперь вы убедились, что цифры, изготовленные из подручных материалов своими руками, выглядят очень красиво. Попробуйте и вы, и ваше торжество станет еще более оригинальным.
Для съемки Дня рождения малыша нужен реквизит, в последнее время очень популярны большие задекорированные цифры. И неспроста, ведь такой декор для фотоссесии незаменим на празднике: он легкий, благодаря чему с ним можно поиграть, бюджетный и красивый. Дети будут в восторге от такой детали на торжестве, любая цифра, в том числе двойка своими руками, будет оригинальной и идеально подходящей к тематике торжества.
Вначале нужно сделать основание, для него можно сделать плоскую или объемную цифру из картона.
Ниже представлен мастер-класс по созданию объемного варианта.
Необходимые материалы и инструменты:
Сначала делаем шаблон цифры два, после чего переносим его на картон, затем с помощью ножа вырезаем десять одинаковых деталей. Их необходимо склеить при помощи клеевого пистолета. Объемная цифра готова, можно приступать к декору.
Есть еще другой способ для него нужно создать шаблон цифры два и шаблоны для боковых сторон цифры. Затем переносим их на картон и вырезаем, после чего соединяем две цифры по бокам картоном, крепим детали при помощи малярной ленты.
После того как основание для праздничного декора сделано, пора задуматься о декоре. Для декора используют:
Выбирая расцветку для девочки, стоит отдавать предпочтение розовым, сиреневым и белым оттенкам.
А на День рождения для мальчика стоит выбирать синие, красные или салатовые цвета.
Существует также несколько техник оформления цифр салфетками:
Для того, чтобы задекорировать крупную цифру, потребуется от двухсот до четырех сот маленьких цветочков из салфеток. Украшение из роз и астр наиболее популярны. Нужно, чтобы цветы были пушистыми и без труда собирались.
Для облегчения задачи объемную цифру по бокам можно обтянуть гофрированной бумагой, тогда цветов потребуется меньше.
Необходимые материалы и инструменты для создания астры:
Берем салфетки и складываем их гармошкой и заматываем центр ниткой, так, чтобы получился бант. Затем расправляем лепесточки к середине, направляясь к краям. В центре делаем бутон хорошо сжав бумагу, нижние листочки расправляем так, чтобы было удобное место для приклеивания цветка.
Необходимые материалы и инструменты для создания розы:
Берем салфетки и складываем в стопку и вырезаем несколько полуокружностей для лепестков. Теперь нужно развернуть розу, сдвинув при этом лепестки, затем скрепляем конец степлером. Остается лишь распустить цветок и при желании сделать волнистые края, выполнив ножницами зигзаг.
Чтобы цветок смотрелся более оригинально, можно использовать в одной экземпляре салфетки разных цветов, либо подкрасить края лепестков фломастерами.
Цифры задекорированная в технике торцевания выходят очень пушистыми, в данном варианте лучше всего подойдет гофрированная бумага.
Берем бумагу и режем ее на квадратики. После чего в серединку ставим карандаш и прижимаем к нему бумагу со всех сторон, после чего прикладываем его вместе с бумагой к поверхности, обмазанной клеем. Когда вся цифра будет обклеена, бумагу нужно расправить и подрезать при необходимости.
При помощи данной техники можно сделать и цветы, для этого потребуются следующие материалы и инструменты:
Вначале разминаем пластилин и обматываем палочку таким образом, чтобы большая часть была свободна, затем втыкаем ее в кусок пластилина. Таким образом, выполняем три лепесточка. После чего заполняем пустые места между ними лепестками другой расцветки. А центр, чтобы не видно было пластилин, нужно закрыть кусочком сжатой бумаги.
Для такого варианта цифры основание нужно сделать плоским, для ее создания потребуется лента примерно восьми метров в длину и пять сантиметров в ширину, двусторонний скотч, ножницы. В качестве украшения можно добавить бусинки.
Вырезаем из картона две детали цифры и склеиваем между собой. После чего можно начинать обтягивать ее лентой, при этом фиксируем скотчем. Края ленты можно спрятать под ленту и зафиксировать скотчем, или используя нить.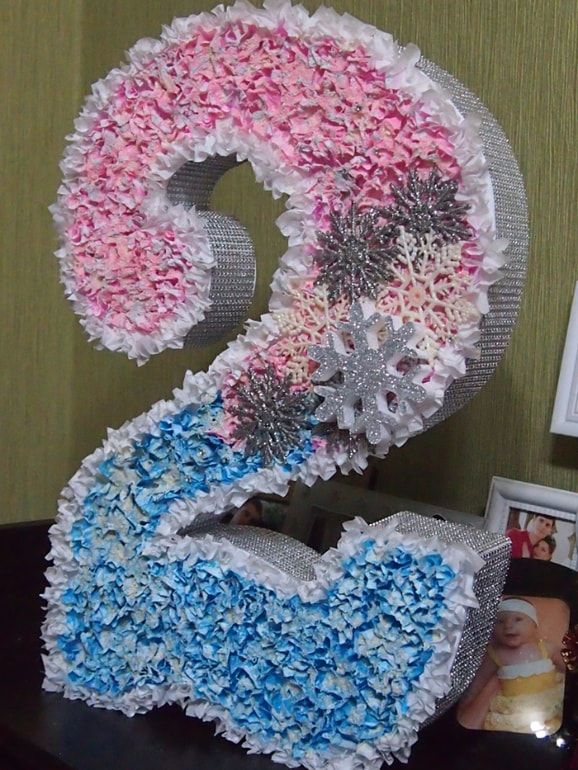
Остается лишь приклеить бусинки на термопистолет, и замечательная цифра готова радовать на празднике.
Можно сделать гирлянду из цифр крючком. Для их создания применяются самые легкие техники вязки: лицевые петельки и изнаночные, накиды, провязывание пары или трех лицевых петель вместе. Для создания пользуемся схемой предоставленной ниже.
В заключение представляем несколько видео с уроками по декорированию цифры два своими руками.
youtube.com/embed/854O9mEeBMg?feature=oembed» frameborder=»0″ allow=»autoplay; encrypted-media» allowfullscreen=»»> В геометрии трехмерная форма может быть определена как твердая фигура или объект или форма, имеющая три измерения: длину, ширину и высоту . В отличие от двухмерных фигур, трехмерные фигуры имеют высоту, которая совпадает с толщиной или глубиной. Трехмерность также записывается как 3D, и, следовательно, эти фигуры также обычно называют 3D-формами. Все трехмерные фигуры занимают пространство, которое измеряется объемом .
В трехмерных фигурах трехмерность означает трехмерность.
Размеры обычно можно рассматривать как измерения в направлении. Длину, ширину и глубину можно считать размерами.
Все трехмерные фигуры имеют три измерения: длину, ширину и высоту . Формы выглядят по-разному с разных сторон. Все 2D-формы измеряются только по длине и ширине. Аристотель говорил, что двумерные формы — это линии, а не фигуры или тела. Они всегда описываются как продолжение линий или областей, ограниченных линиями. И наоборот, трехмерные фигуры имеют объем.
По соглашению первые три измерения представлены в виде пространственных измерений x-y-z. Ширина, высота и глубина — это их имена.
Куб, прямоугольная призма, сфера, конус и цилиндр — основные трехмерные фигуры, которые мы видим вокруг себя.
Трехмерные фигуры можно увидеть повсюду вокруг нас. Мы можем видеть кубик в кубике Рубика и кубике, прямоугольную призму в книге и коробке, сферу в глобусе и шаре, конус в морковке и рожке мороженого, цилиндр в ведерке и бочка вокруг нас.
Ниже перечислены некоторые примеры трехмерных фигур из реальной жизни:
У трехмерной фигуры есть три атрибута: грань, ребро и вершина. Давайте подробно разберемся с трехмерными формами и их свойствами.
Лицо: Каждая отдельная поверхность, плоская или изогнутая, трехмерной фигуры называется ее гранью.
Край: Линия, где встречаются две грани трехмерных фигур, называется его краем.
Вершина : Каждый угол, где встречаются три грани трехмерных фигур, называется его вершиной. Вершины — это множественное число от вершины.
Вот список названий трехмерных фигур с их изображениями и атрибутами.
СфераВсе точки сферы находятся на одинаковом расстоянии от ее центра. Земля чем-то похожа на нее, за исключением одного: когда вы смотрите на нее издалека, она выглядит как сфера, но если вы смотрите на нее вблизи, она не совсем круглая. Сфера имеет несколько характеристик:
Куб и прямоугольный параллелепипед — это большие блоки.
Разница между ними в том, что у куба грани квадратные, а у кубоида — прямоугольные.
Цилиндр имеет две круглые поверхности на обоих концах и одну изогнутую поверхность по всей длине. Он имеет высоту и радиус. Высота цилиндра перпендикулярна его поверхности сверху вниз. Ниже приведены некоторые основные характеристики цилиндров:
Сеть — это узор, полученный путем плоской разбивки поверхности трехмерной фигуры, показывающей каждую грань фигуры .
3D-фигуры могут иметь более одного шаблона цепей.
Ниже показаны названия нескольких 3D-форм и их сетей:
Интересные факты :
Все трехмерные фигуры состоят из двумерных фигур.
Давайте различать 2D- и 3D-формы, разбираясь в двухмерных и трехмерных формах и их свойствах.
Пример 1: Что из следующего является трехмерной фигурой?
Конус Квадрат Сфера Кубоид Цилиндр Параллелограмм
Решение:
Cone Sphere Cuboid цилиндр
Пример 2: Укажите, представлены ли следующие True или False .
Решение:
Трехмерные формы также называют объемными формами.Пример 3: Заполните таблицу атрибутами перечисленных трехмерных фигур.
Решение:
Пример 4: Сопоставьте объект с его формой.
Решение:
Пример 5: Вычислите площадь поверхности прямоугольного параллелепипеда шириной 4 единицы, длиной 3 единицы и высотой 5 единиц.
Решение:
Дан кубоид, имеющий три единицы длины, четыре единицы ширины и пять единиц высоты.
Площадь поверхности прямоугольного параллелепипеда $= 2 \times (\text{lw} + \text{wh} + \text{lh})$ квадратных единиц
$= 2 \times (\text{lw} + \text {белая} + \text{левая})$
$= 2[(3 х 4) + (4 х 5) + (3 х 5)]$
$= 2(12 + 20 + 15)$
$= 2(47)$
$= 94$ квадратных единиц
Следовательно, площадь поверхности данного прямоугольного параллелепипеда равна 94 квадратных единиц.
Пример 6: Джейн любит пить молоко из цилиндрического стакана. Ее стакан имеет 15 единиц высоты и 3 единицы радиуса основания. Сколько молока она может налить в стакан?
Решение:
Учитывая, что высота стакана 15 единиц, а радиус основания 3 единицы. 92$
Таким образом, Джейн может налить в свой стакан приблизительно 424 кубических единицы молока.
1
Цилиндр
Сфера
Конус
Куб
Правильный ответ: Цилиндр
Цилиндр имеет две плоские поверхности, имеющие форму круга, и одну изогнутую поверхность.
2
4
6
8
10
Правильный ответ: 6
Куб имеет 6 граней, которые являются квадратами. Итак, в сетке куба будет 6 квадратных фигур.
3
Конус
Цилиндр
Куб
Сфера
Правильный ответ: Сфера
Сфера имеет одну сторону. Так что у него нет края.
4
Трапеция
Призма
Пирамида
Куб
Правильный ответ: Трапеция
Трапеция — это двумерная фигура с четырьмя сторонами, одна пара противоположных сторон которых параллельна друг другу, а две другие стороны не параллельны.
5
Вершина
Сторона
Грань
Ребро
Правильный ответ: Ребро
Ребра — это отрезки, соединяющие две грани. Грани куба пересекаются по линиям, называемым ребрами. Фигуры с несколькими ребрами называются сплошными фигурами. Пересечение нескольких плоскостей называется вершиной.
6
фигуры
тела
грани
многоугольники
Правильный ответ: тела
Трехмерные геометрические фигуры называются телами.
7
Конус
Сфера
Цилиндр
Пирамида
Правильный ответ: Конус
Конусы представляют собой трехмерные тела, состоящие из круглого основания, соединенного с одной точкой (называемой вершиной) изогнутыми сторонами. В качестве альтернативы вы можете думать о конусе как о круглой пирамиде.
Какие существуют типы трехмерных фигур?
Куб, прямоугольный параллелепипед, цилиндр, сфера, конус, призма и пирамиды.
Каковы атрибуты трехмерных фигур?
Трехмерные фигуры имеют 3 измерения — длину, ширину и глубину. В результате этих размеров эти формы имеют атрибуты граней, ребер и вершин.
Что такое ребро?
Ребро — это линия, на которой сходятся две грани трехмерной формы.
Например, у куба 12 ребер.
Что такое вершины?
Вершины — это углы, в которых сходятся три грани. Например, прямоугольный параллелепипед имеет 8 вершин.
Какая польза от объема трехмерной формы?
Объем помогает найти пространство, занимаемое данной фигурой.
Из скольких квадратов состоит кубическая сеть?
Кубическая сеть состоит из шести квадратов.
Возможно, вы читаете это перед своим компьютером. Или, может быть, у вас есть стакан воды рядом с вами.
Если вы посмотрите на любой из этих объектов, которые вас окружают, станет ясно, что это объекты в 3D. Но каково математическое определение трехмерной фигуры?
В этой статье мы узнаем больше о трехмерных фигурах и их применении.
Трехмерная фигура представляет собой геометрическое тело с тремя пространственными измерениями: длина, ширина, глубина . Иногда глубину называют высотой.
Например, представьте, что вы берете коробку из одной службы доставки.
Если вы поместите коробку таким образом, что сможете наблюдать только одну из ее граней, вы будете наблюдать плоскую поверхность в 2D, а затем вы будете наблюдать только длину и ширину этой грани.
Но если вы его немного повернете, то увидите, что коробка тоже имеет некоторую глубину. Это то, что мы имеем в виду с трехмерными фигурами.
Как вы могли заметить, глядя на коробку, эти трехмерные фигуры имеют объем .
В математике мы определяем объем как количество пространства внутри замкнутой поверхности.
Снова возьмите коробку, и если вы откроете ее сейчас, объем будет равен количеству места внутри коробки. Позже мы узнаем, как вычислить этот объем.
Эти геометрические фигуры обычно, за исключением некоторых исключений, которые мы будем использовать, имеют граней , которые являются поверхностями с определенной площадью поверхности, ограничивающими фигуру. Эти грани соединяются в вершинах , которые являются точками соединения.
Наконец, линии, ограничивающие эти поверхности и контур геометрической фигуры, называются ребрами . Мы бы сравнили их со сторонами двумерных фигур.
Отвлекшись от этой статьи и осмотревшись вокруг, вы, вероятно, обнаружите множество трехмерных фигур с различной структурой. От кровати до стула, до стола или даже до книг, которые вы используете для учебы.
Все они представляют собой трехмерные фигуры, поскольку они имеют 3 измерения, о которых мы упоминали ранее; длина, ширина и глубина, а также потому, что они имеют объем.
Мы различаем обычных и неправильных трехмерных форм. Мы сосредоточимся на обычных трехмерных фигурах, так как они более распространены в математике.
КонусКонус — это трехмерная фигура, которую мы получили бы, если бы прямоугольный треугольник (с одним углом, равным 90º) повернулся с фиксированной одной из сторон, таким образом, мы получили бы форму в 3d . Эта фигура обычно имеет круглое основание и вершину , к которой сужается боковая поверхность конуса.
Основание не обязательно должно быть кругом, это может быть и другая двухмерная круглая фигура, например овал. Вы можете наблюдать эту форму в реальном мире, когда смотрите на дорожные конусы.
Пирамида Эта фигура похожа на конус, но в этом случае основание не имеет круглой формы.
Основание представляет собой двухмерную фигуру с тремя или более сторонами, например треугольник, квадрат, прямоугольник и т. д.
Поскольку геометрическая форма основания может варьироваться, изменяется и количество ребер. Все его поверхности, сколько бы их ни было, сужаются к вершине.
Знаменитые египетские пирамиды являются одним из примеров этих геометрических форм, в данном случае они имеют квадратное основание.
КубЭта геометрическая фигура состоит из шести равновеликих граней, три из которых сходятся в одной вершине, всего восемь вершин и двенадцать ребер.
Примером куба является игральная кость. Если вы заметите это, все грани обычной игральной кости имеют одинаковую поверхность, и каждая ее вершина работает как объединение трех разных граней.
Прямоугольная призма Похожа на куб, так как также имеет восемь вершин, двенадцать ребер и шесть граней, но в этом случае не все грани равны.
Каждая грань равна своей противоположности, поэтому у нас есть пары равных граней.
Примером прямоугольной призмы может быть ящик или даже коробка, хотя иногда они имеют форму куба.
Существуют и другие виды призм, в зависимости от формы основания и противоположной грани. Например, если эти грани имеют форму треугольника, это треугольная призма , которая будет иметь всего пять граней вместо шести граней, которые имеет прямоугольная призма. Но это основание (и противоположная грань) может иметь другую двумерную фигуру, дающую разные типы призм: пятиугольные призмы , шестиугольные призмы и т.д.
Цилиндр Форма этой фигуры может напомнить вам прямоугольную призму, но в данном случае она имеет две поверхности, которые называются вершиной и нижние (или основание) фигуры, состоящие из двухмерных круглых фигур.
У этой фигуры нет вершины. Поверхность, соединяющая эти две грани, по существу представляет собой прямоугольник, но изогнутый.
Такие геометрические фигуры можно найти в банках или стаканах.
Футбол, баскетбол или, может быть, если мы не хотим ограничиваться только спортивным миром: пузырь. Все эти объекты имеют одну общую черту: они являются сферами.
Эти геометрические фигуры получаются, если сделать круг, представляющий собой двухмерную фигуру, повернутую вокруг своего диаметра. Объем, описываемый этим оборотом, определяется как сфера.
Как и в случае с кругом в двух измерениях, все точки поверхности находятся на одинаковом расстоянии от точки в центре фигуры. Это расстояние называется радиус . Если проследить расстояние между двумя точками поверхности сферы, проходящее через ее центр, то это расстояние называется диаметром сферы, что соответствует удвоенному радиусу.
При работе с трехмерными фигурами есть некоторые вещи, которые мы могли бы знать о них. В частности, нас интересуют две характеристики.
Первая — это площадь фигуры.
Площадь фигуры — это площадь поверхности, которую занимают грани фигуры. Единицами площади поверхности фигуры являются единицы площади, стандартными являются квадратные метры (м2).
Чтобы получить общую площадь поверхности фигуры, мы должны просуммировать площади каждой грани фигуры. Не следует путать площадь поверхности фигуры с ее объемом. Площадь состоит только из поверхности граней, независимо от того, что находится внутри них.
С другой стороны, у нас есть объем рисунка.
Объем фигуры – это количество пространства внутри поверхности, ограниченной гранями фигуры. Единицами объема являются единицы объема, стандартными являются кубические метры.
Если мы снова возьмем коробку, о которой мы говорили в этой статье, вы увидите, что поверхность картона, используемого для всех граней, соответствует площади поверхности коробки, но пространство внутри коробки соответствует к его объему.
Давайте посмотрим, как работают некоторые математические уравнения для трехмерных фигур, которые мы видели раньше.
Площадь поверхности трехмерной фигуры равна сумме площадей ее граней.
Для конуса площадь поверхности его основания равна Ab=π×r2, где r — радиус окружности. Площадь боковой грани Al=π×r×g, что составляет г расстояний между любой точкой ребра основания и вершиной. Таким образом, площадь поверхности конуса обычно может быть выражена как
Acone=π×r×(r+g).
Объем конуса определяется по следующей формуле:
Vcone=(π×h×r2)3,
, где h — расстояние от центра основания до вершины.
В этом случае формулы площади и объема будут зависеть от количества ребер в основании.
Например, если пирамида имеет квадратное основание, площадь поверхности пирамиды будет равна сумме площади квадрата As=l2 с суммой площадей каждого треугольника, соединяющего вершины At=12b×h .
В общем случае мы можем выразить площадь поверхности пирамиды как
Апирамида= Абаза+Треугольники
Будьте осторожны, так как основание не обязательно должно быть правильным, и площадь поверхности треугольников, соединяющихся с вершиной, тоже не обязательно должна быть правильной.
Объем пирамиды также зависит от ее основания. Для квадратной пирамиды объем вычисляется по формуле
Vpyramid=h×l23
равно
В этом случае, поскольку прямоугольная призма и куб образованы шестью гранями, чтобы получить общую площадь поверхности фигуры, нам нужно просто просуммировать площади каждой грани.
Для куба все шесть граней будут иметь одинаковую площадь, но для прямоугольной призмы, поскольку каждая грань равна своей противоположности, есть три разных значения. Общее математическое выражение для площади поверхности прямоугольной призмы:
Ar.
p=2·A1+2·A2+2·A3
, где A 1 , A 2 и A 3 являются тремя различными значениями этих областей. Площадь прямоугольника Ar=b·h.
Объем этих фигур равен произведению трех ребер; длина, ширина и глубина призмы, например,
Vr.p=a×b×h
В случае куба, поскольку все стороны имеют одинаковую длину, мы имеем,
Vcube=l3
Цилиндр состоит из двух кругов, которые являются верхней и нижней частью фигуры, и изогнутого прямоугольника. Следовательно, если площадь круга Ac=π×r2, сумма всех площадей равна
Acyl=2×π×r2+2×π×h
, где h — высота из одной точки снизу до точки вверху в том же положении.
Объем цилиндра описывается следующим уравнением:
Vcyl=π×h×r2
Известная нам сфера представляет собой другой тип геометрической фигуры, так как она не образована объединением разных граней.
Вот почему нам нужно математическое выражение для вычисления площади его поверхности:
Aсфера=4×π×r2
А объем сферы определяется по следующей формуле:
Vсфера=43×π×r3.
Теперь давайте рассмотрим некоторые примеры задач, с которыми вы можете столкнуться на трехмерных фигурах.
Найдите объем воды, необходимый для заполнения цилиндрического стеклянного стакана высотой 12 см и радиусом 7 см. Возьмем π=227.
Раствор
Использование
Vcyl=π×h×r2
затем,
Vcyl=227×12×(7)2=227×12см×7×7=22×12×7=1
см3
Кохе хочет сделать коническую кепку радиусом 14 см и высотой 20 см для 8 друзей в преддверии своего дня рождения. Какова общая площадь картонной бумаги, чтобы сделать все 8 для своих друзей?
Решение
Сначала найдем общую площадь поверхности одной конической крышки. Использование
Acone=π×r×(r+g)
В этом случае g — высота конуса, равная 20 см, а r — 14 см.
Следовательно,
Acone=227×14×(14+20)=227×14×34=227×214×34=22×2×34=1496см2
Но это всего лишь площадь 1onecone, вам нужно найти площадь 8 конусов. Таким образом,
TotalArea=1496×8=11968 см2
Следовательно, Кохе потребуется картон с общей площадью поверхности 11,968см 2 успешно смастерить 8 конических крышек для своих друзей в преддверии дня рождения.
