Трапеция из бумаги: Трапеция из бумаги схема
Как сделать шестиугольник из бумаги объемный. Объемные фигуры из бумаги своими руками
Большой выбор развёрток простых геометрических фигур.
Первое знакомство детей с бумажным моделированием всегда начинается с простых геометрических фигур, таких как кубик и пирамида. Не у многих получается склеить кубик с первого раза, иногда требуется несколько дней, чтобы сделать поистине ровный и безупречный куб. Более сложные фигуры цилиндр и конус требуют в несколько раз больше усилий нежели простой кубик. Если вы не умеете аккуратно клеить геометрические фигуры, значит и за сложные модели вам ещё рано браться. Займитесь сами и научите своих детей клеть эти «азы» моделирования по готовым развёрткам.
Для начала я, конечно же, предлагаю научиться клеить обычный кубик. Развёртки сделаны для двух кубиков, большого и маленького. Более сложной фигурой является маленький кубик потому, как клеить его сложнее, чем большой.
Итак, начнём! Скачайте развёртки всех фигур на пяти листах и распечатайте на плотной бумаге. Перед тем, как печатать и клеить геометрические фигуры обязательно ознакомьтесь со статьёй о том, как выбрать бумагу и как вообще правильно вырезать, сгибать и клеить бумагу.
Перед тем, как печатать и клеить геометрические фигуры обязательно ознакомьтесь со статьёй о том, как выбрать бумагу и как вообще правильно вырезать, сгибать и клеить бумагу.
Для более качественной печати советую использовать программу AutoCAD, и даю вам развёртки для этой программы , а также читайте, как распечатывать из автокада . Вырежьте развёртки кубиков с первого листа, по линиям сгиба обязательно проведите иголкой циркуля под железную линейку, чтобы бумага хорошо сгибалась. Теперь можно начинать клеить кубики.
Для экономии бумаги и на всякий пожарный я сделал несколько развёрток маленького кубика, мало ли вам захочется склеить не один кубик или что-то не получится с первого раза. Ещё одна несложная фигура это пирамида, её развёртки найдёте на втором листе. Подобные пирамиды стоили древние египтяне, правда не из бумаги и не таких маленьких размеров:)
А это тоже пирамида, только в отличие от предыдущей у неё не четыре, а три грани.
Развёртки трёхгранной пирамиды на первом листе для печати.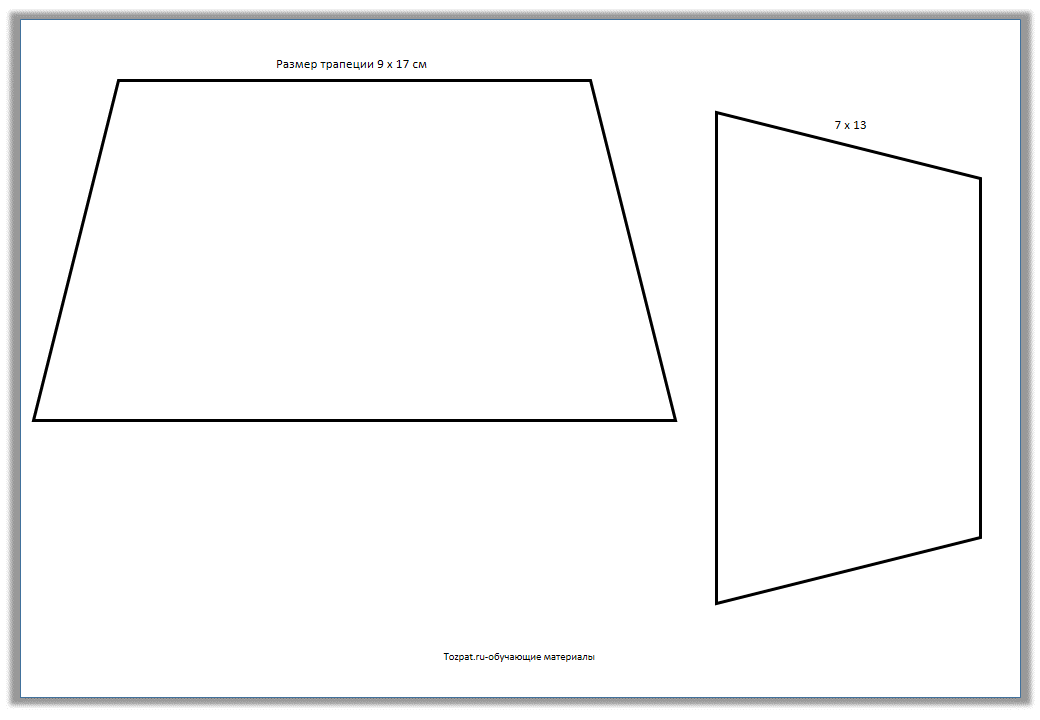
И ещё одна забавная пирамидка из пяти граней, её развёртки на 4-ом листе в виде звёздочки в двух экземплярах.
Более сложная фигура это пятигранник, хотя пятигранник сложнее начертить, нежели склеить.
Развёртки пятигранника на втором листе.
Вот мы и добрались до сложных фигур. Теперь придётся поднапрячься, склеить такие фигуры нелегко! Для начала обычный цилиндр, его развёртки на втором листе.
А это более сложная фигура по сравнению с цилиндром, т.к. в её основании не круг, а овал.
Развёртки этой фигуры на втором листе, для овального основания сделано две запасных детали.
Чтобы аккуратно собрать цилиндр его детали нужно клеить встык. С одной стороны дно можно приклеить без проблем, просто поставьте на стол заранее склеенную трубку, положите на дно кружок и залейте клеем изнутри. Следите, чтобы диаметр трубы и круглого дна плотно подходили друг к другу, без щелей, иначе клей протечёт и всё приклеится к столу.
Цилиндр с овальным основанием можно клеить также как и обычный цилиндр, но он имеет меньшую высоту, поэтому тут проще вставить внутрь гармошку из бумаги, а наверх положить второе основание и по краю приклеить клеем.
Теперь очень сложная фигура — конус. Его детали на третьем листе, запасной кружок для днища на 4-ом листе. Вся сложность склеивания конуса в его острой вершине, а потом ещё будет очень сложно приклеить дно.
Сложная и одновременно простая фигура это шар. Шар состоит из 12-ти пятигранников, развёртки шара на 4-ом листе. Сначала клеится две половинки шара, а потом обе склеиваются вместе.
Довольно интересная фигура — ромб, её детали на третьем листе.
А теперь две очень похожие, но совершенно разные фигуры, их отличие только в основании.
Когда склеите эти обе фигуры, то не сразу поймёте, что это вообще такое, они получились какие-то совсем невосприимчивые.
Ещё одна интересная фигурка это тор, только он у нас очень упрощён, его детали на 5-ом листе.
И наконец, последняя фигура из равносторонних треугольников, даже не знаю, как это назвать, но фигура похожа на звезду. Развёртки этой фигуры на пятом листе.
На сегодня это всё! Я желаю вам успехов в этой нелёгкой работе!
В основе самых сложных и необычные формы сооружений, устройств, механизмов лежат элементарные геометрические фигуры: куб, призма, пирамида, шар и другие. Для начала научитесь создавать самые простые фигуры, а после вы легко освоите более сложные формы.
Многие моделисты начинают свой путь с бумажных моделей. Это обусловлено доступностью материала (найти бумагу и картон не составляет трудности) и легкостью в его обработки (не требуются специальные инструменты).
Однако, бумага имеет и ряд характерных особенностей:
- капризный, хрупкий материал
- требует высокой аккуратности, внимательности, усидчивости при работе
По этим причинам бумага является материалом, как для начинающих, так и для настоящих мастеров и из нее создаются модели самой разной сложности.
В этот статье мы изучим простейшие геометрические фигуры, которые можно сделать из бумаги.
Вам понадобятся следующие материалы:
- лист бумаги
- карандаш
- линейка
- ластик
- ножницы
- клей ПВА либо клеящий карандаш
- кисточка для клея, лучше из жесткой щетины
- циркуль (для некоторых фигур)
Как сделать куб из бумаги?
Куб – правильный многогранник, каждая грань которого представляет собой квадрат
Создание куба состоит из двух этапов: создание развертки и склеивание. фигуры. Для создания схемы вы можете воспользоваться принтером, просто распечатав готовую схему. Либо вы можете самостоятельно с помощью чертежных инструментов нарисовать развертку.
Рисование развертки:
- Выбираем размеры квадрата — одной стороны нашего куба. Лист бумаги должен быть шириной не менее 3 сторон этого квадрата и длиной немного более 4 сторон.
- Чертим в длину нашего листа четыре квадрата, которые станут боковыми сторонами куба.
 Рисуем их строго на одной линии, вплотную друг к другу.
Рисуем их строго на одной линии, вплотную друг к другу. - Над и под любыми из квадратов рисуем по одному такому же квадрату.
- Дорисовываем полоски для склеивания, с помощью которых грани будут соединяться между собой. Каждые две грани должны соединяться одной полоской.
- Куб готов!
После рисования развертка вырезается ножницами и склеивайте ПВА. Клей очень тонким слоем равномерно размазываем кистью по поверхности склеивания. Соединяем поверхности и закрепляем в нужном положении на некоторое время, с помощью скрепки или небольшого груза. Срок схватывания клея где-то 30-40 минут. Ускорить высыхание можно методом нагрева, например, на батарее. После склеиваем следующие грани, закрепляем в нужном положении. И так далее. Так постепенно вы проклеите все грани куба. Используйте небольшие порции клея!
Как сделать конус из бумаги?
Конус – тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность.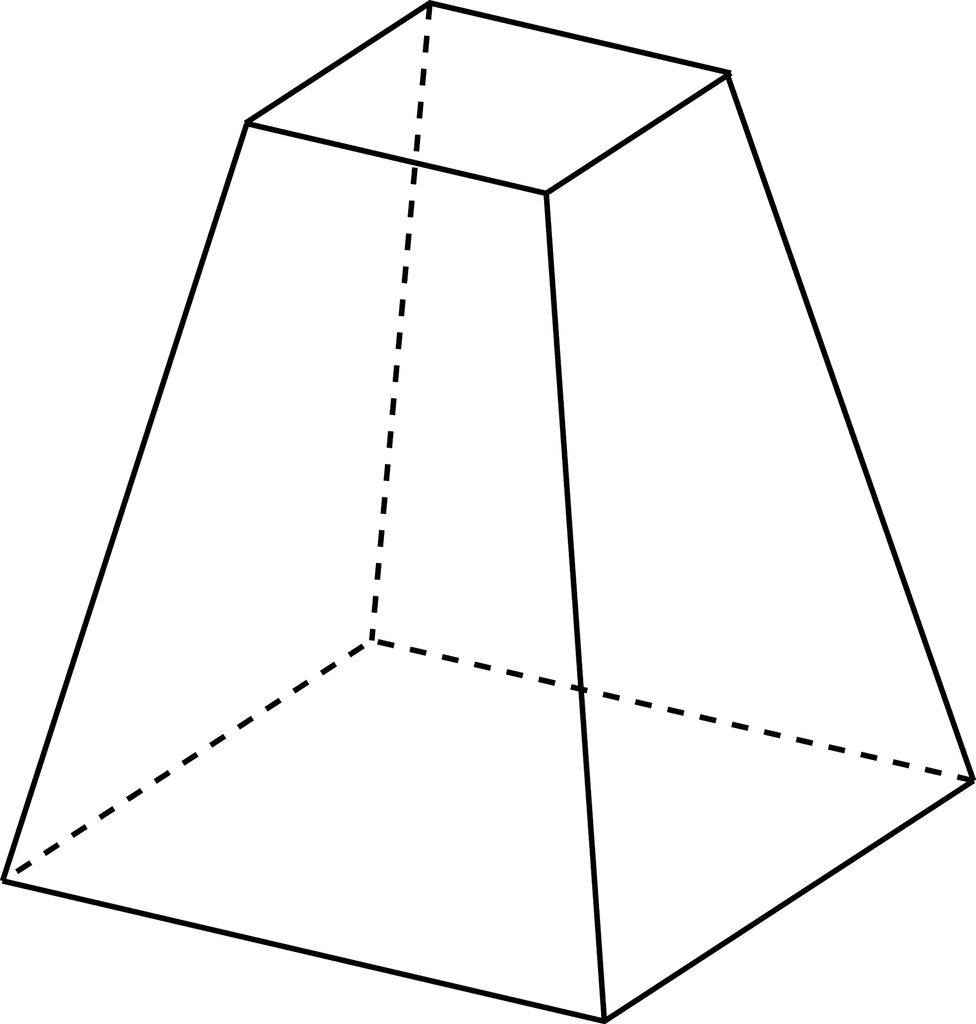
Рисование развертки:
- Рисуем циркулем окружность
- Вырезаем сектор (часть круга, ограниченная дугой окружности и двумя радиусами, проведенными к концам этой дуги) из этой окружности. Чем больший сектор вы вырежете, тем острее будет конец конуса.
- Склеиваем боковую поверхность конуса.
- Измеряем диаметр основания конуса. С помощью циркуля рисуем окружность на листе бумаге требуемого диаметра. Дорисовываем треугольнички для склеивания основания с боковой поверхностью. Вырезаем.
- Приклеиваем основание к боковой поверхности.
- Конус готов!
Как сделать цилиндр из бумаги?
Цилиндр – геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.
Рисование развертки:
- Рисуем прямоугольник на бумаги, в котором ширина — это высота цилиндра, а длина определит диаметр будущей фигуры. Отношение длины прямоугольника к диаметру определяется выражением: L=πD, где L- длина прямоугольника, а D — диаметр будущего цилиндра.
 Подставив в формулу требуемый диаметр, найдем длину прямоугольника, который будем рисовать на бумаге. Дорисовываем небольшие дополнительные треугольнички, которые необходимы для склеивания деталей.
Подставив в формулу требуемый диаметр, найдем длину прямоугольника, который будем рисовать на бумаге. Дорисовываем небольшие дополнительные треугольнички, которые необходимы для склеивания деталей. - Рисуем на бумаге два круга, диаметром цилиндра. Это будет верхнее и нижнее основания цилиндра.
- Вырезаем все детали будущего бумажного цилиндра.
- Склеиваем боковую поверхность цилиндра из прямоугольника. Даем детали высохнуть. Приклеиваем нижнее основание. Ждем высыхания. Приклеиваем верхнее основание.
- Цилиндр готов!
Как сделать параллелепипед из бумаги?
Параллелепипед – многогранник, у которого шесть граней и каждая из них параллелограмм.
Рисование развертки:
- Выбираем размеры параллелепипеда и величины углов.
- Чертим параллелограмм — основание. С каждой стороне дорисовываем боковые стороны — параллелограммы. От любой из боковой стороны дорисовываем второе основание. Добавляем полоски для склеивания. Параллелепипед может быть прямоугольным, если стороны прямоугольники.
 Если параллелепипед не прямоугольный, то создать развертку немного сложнее. Для каждого параллелограмма нужно выдержать требуемые углы.
Если параллелепипед не прямоугольный, то создать развертку немного сложнее. Для каждого параллелограмма нужно выдержать требуемые углы. - Вырезаем развертку и склеиваем.
- Параллелепипед готов!
Как сделать пирамиду из бумаги?
Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину.
Рисование развертки:
- Выбираем размеры пирамиды и количество ее граней.
- Рисуем основание — многогранник. В зависимости от количества граней это может быть треугольник, квадрат, пятиугольник или другой многогранник.
- От одной из сторон основания рисуем треугольник, который будет боковой стороной. Следующий треугольник рисуем так, чтобы одна сторона у него с предыдущим была общая и так далее. Так рисуем столько треугольников, сколько сторон в пирамиде. Дорисовываем полоски для склеивания в нужных местах.
- Вырезаем и склеиваем фигуру.
- Пирамида готова!
Оригами открывает невероятные широты для фантазии и творчества.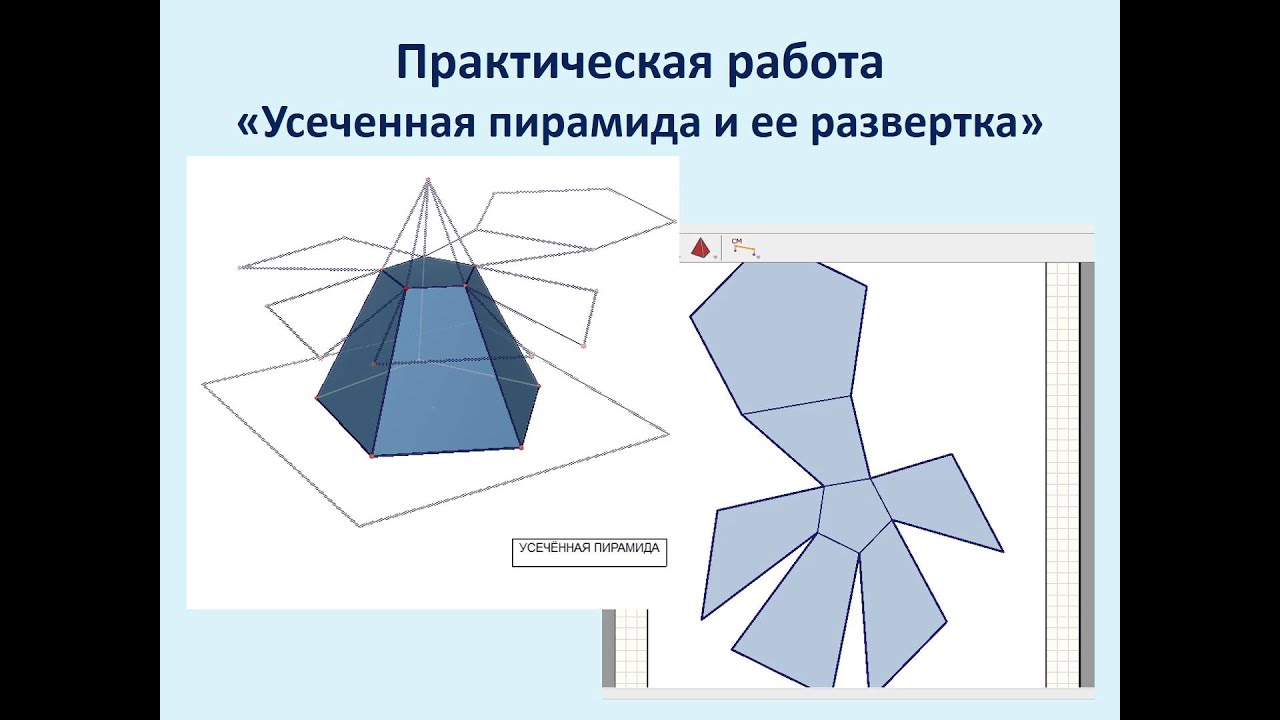 Мастера из бумаги научились делать самые разнообразные поделки. Это разные животные, птицы да даже растения. Но сегодня мы подробно рассмотрим, как делать геометрические фигуры быстро и легко из бумаги.
Мастера из бумаги научились делать самые разнообразные поделки. Это разные животные, птицы да даже растения. Но сегодня мы подробно рассмотрим, как делать геометрические фигуры быстро и легко из бумаги.
Такие фигуры помогут развить представление о трёхмерных фигурах, а также общее представления о них. Лучше всего они подойдут тем, у кого возникают сложности с тригонометрией, так как этот раздел геометрии требует очень хорошего визуального представления разных фигур.
Изучаем пошагово принцип изготовления геометрических фигур из бумаги
Оригами в большинстве случаев заключается в складывании разнообразных форм из бумаги. В нашем же случае будет похоже, но немного иначе.
Схема или как её ещё называют развёртка – является обязательным элементом при изготовлении любой геометрической фигуры. Схема представляет собой двухмерное изображение «развёртки» нашей фигуры на бумаге. Представим куб. И мы развернули его, что в итоге получилось? Столбик из четырёх одинаковых квадратов и два таких же квадрата сбоку. Своеобразная буква «Т».
Своеобразная буква «Т».
После того, как вы сделали или нашли развёртку, вам необходимо сложить её в фигуру и очень аккуратно проклеить все элементы.
Без развёртки невозможно сделать ни одной правильной геометрической фигуры, которая была бы максимально ровная и не содержала бы погрешностей. В интернете можно найти огромное количество разнообразных схем, для самых разных фигур. Мы же рассмотрим в качестве примера изготовление цилиндр и шляпу.
Солидный цилиндр.Цилиндр является одной из самых простых фигур в оригами. С его изготовлением справится даже новичок. И так, приступим к первому нашему творению.
Для начала ищем или делаем сами схему. Схема цилиндра представляет собой прямоугольник, длина которого вычисляется по формуле 2ПиR, где R – это радиус вашего цилиндра, то есть если вы хотите получить цилиндр диаметром 10 сантиметров, то его радиус будет равен пяти. И тут же обратная зависимость: если вы уже нарисовали прямоугольник, длинной, например, 40 сантиметров, то радиус окружности соответственно будет равен 40/2Пи.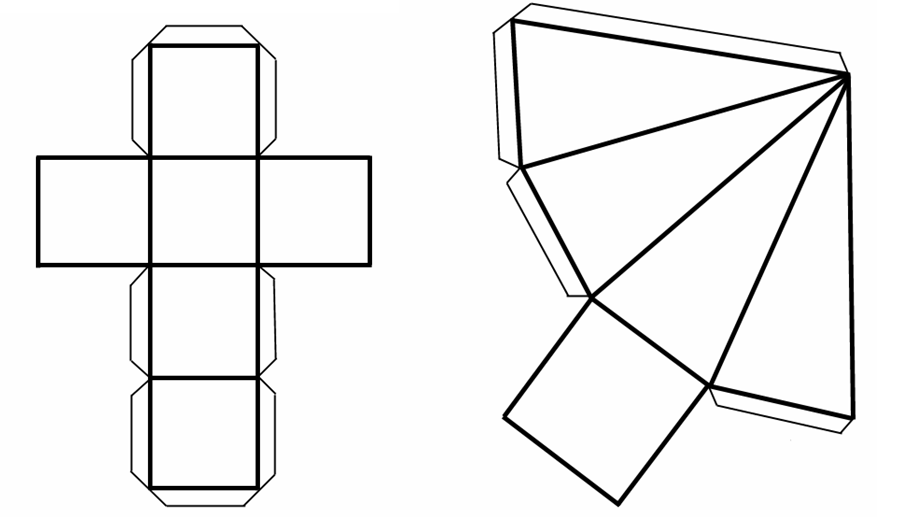 Примерно 6,2 сантиметра.
Примерно 6,2 сантиметра.
На схеме, проводим аккуратную линию ровно по центру прямоугольника. Продолжаем нашу линию за его стороны, то есть, линия должна пересекать прямоугольник. Дальше мы должны точно знать диаметр цилиндра, чтобы вычислить радиус окружности, если же вы сначала нарисовали прямоугольник, то пользуйтесь формулой l/2Пи, где l – длина вашего прямоугольника. После того, как вы определили радиус, берём циркуль и размещаем на пересечении нашей линии симметрии и стороны прямоугольника. Начинам образно проводить окружность и смотрим, где будет вторая точка пересечения с линией симметрии, она должна находиться за пределами прямоугольника. Именно эта точка и будет центром окружности. Повторяем действия с другой стороны. Наша поделка, например, делалась по такой схеме:
Если же вы нашли схему в интернете, то достаточно распечатать её. И вырезать её.
После того, как мы вырезали её, необходимо перейти к её складыванию. Начинаем складывать наш цилиндр с его основной части. Для этого сворачиваем в трубочку прямоугольник. Сворачиваем сразу с двух концов, то есть, берём один конец прямоугольника и другой, и тянем их друг к другу. Что бы получилась своеобразная труба, у которой «открыты» два кружочка.
Для этого сворачиваем в трубочку прямоугольник. Сворачиваем сразу с двух концов, то есть, берём один конец прямоугольника и другой, и тянем их друг к другу. Что бы получилась своеобразная труба, у которой «открыты» два кружочка.
Потом загибаем оба «окошка» внутрь и меняем по необходимости толщину трубочки, что бы эти окошки идеально вошли внутрь. Потом склеиваем получившийся цилиндр.
Шляпа из бумаги.Шляпа – такой же цилиндр, но у него нижнее окно будет открыто на во внешнюю сторону. Нам потребуется картон, ножницы, тарелка, клей . Начнём!
Для начала разрезаем лист картона на две полосы, ширина которых будет равна высоте цилиндра.
Длина полосок будет зависеть от того, какого диаметра вы хотите получить шляпу. Если вы хотите одевать шляпу на голову, то следует измерить обхват головы и полученное число поделить на два.
Склеиваем детали так, чтобы получить единую длинную полосу.
Сворачиваем полосу в цилиндр и скрепляем его.
Выбираем, по вашему вкусу, одну из круглых сторон и делаем на ней ровные надрезы, глубина которых равна двумя сантиметрам. Отгибаем получившиеся лепестки и откладываем цилиндр в сторону.
Берём ещё небольшой кусочек картона и обводим, заготовленную ранее, тарелку. В центр получившейся окружности поставьте ваш цилиндр и обведите его. Вырезаем из листа сначала большую окружность, а потом маленькую. В итоге мы должны получить кольцо.
Ставим цилиндр на устойчивую, ровную поверхность вниз лепестками и к каждому из них приклеиваем кусочки двухстороннего скотча.
Шляпа готова!
Небольшая подборка видео по теме статьи
Здесь мы подготовили для вас объемные геометрические фигуры из бумаги, которые нужно вырезать и склеить. Также на этой странице вы найдете плоские фигуры для вырезания, из которых нужно сложить замок. Этот учебный материал поможет ребенку наглядно изучить объемные геометрические фигуры: куб, пирамиду, ромб, шестигранник, цилинд и конус. Задание развивает наглядно-образное мышление.
Объемные геометрические фигуры из бумаги — Вырезаем и клеим:
Здесь вы можете скачать объемные геометрические фигуры из бумаги в виде разверток, которые необходимо распечатать на принтере, вырезать и склеить по указанным местам. В результате у вас получатся объемные фигуры: куб, пирамида (трехгранная и четырехгранная), ромб, шестиугольник, конус и цилиндр. На каждой развертке написано название фигуры, чтобы ребенок во время работы всегда мог видеть, какую фигуру он делает. Это очень удобно для обучения, так как дети обычно не любят, когда взрослые по несколько раз повторяют одно и то же. А в этом случае у родителей нет необходимости проговаривать вслух названия фигур.
- Итак, в первом листе мы выложили следующие геометрические фигуры: куб (фигура, поверхность которого состоит из 6 квадратов), трехгранная пирамида (основание пирамиды и 3 грани), четырехгранная пирамида (основание и 4 грани), ромб (фигура, визуально состоящая из двух пирамид, имеющих общее основание).

- Во втором листе вы найдете развертки таких геометрических фигур из бумаги: шестигранник (фигура, состоящая из шести граней), цилиндр (состоящий из свернутого прямоугольника и двух окружностей-оснований) и конус.
Скачать геометрические фигуры из бумаги — развертки для вырезания вы можете во вложениях внизу страницы
Лист 1
Лист 2
Скачайте и распечатайте 2 листа с фигурами, вырежьте их аккуратно ножницами и склейте в нужных местах. Учтите, что у бумажных фигур есть дополнительные места для сгиба и склеивания (у нас они выделены оранжевым цветом). Все оранжевые места вам необходимо согнуть и намазав их клеем вклеить с внутренней стороны фигуры.
После того, как дети, при помощи взрослых, склеят все геометрические фигуры из бумаги, можно продолжить занятие, задавая детям вопросы. Например: «Покажи мне пирамиду. Сколько у нее сторон? Где ее основание? Чем эта пирамида (показываете трехранную) отличается от этой (четырехранной)? Покажи мне цилиндр. Какие предметы он тебе напоминает? Покажи конус. На что он похож? Покажи куб. Сколько у него сторон? Из какой геометрической фигуры состоят его стороны?» — и так далее.
Какие предметы он тебе напоминает? Покажи конус. На что он похож? Покажи куб. Сколько у него сторон? Из какой геометрической фигуры состоят его стороны?» — и так далее.
В зависимости от возраста ребенка, можно использовать в занятии различные обучающие материалы. Например, что такое пирамида:
Какие бывают пирамиды. (Пусть ребенок покажет из них те, которые он склеил)
Что такое куб:
Что такое конус и цилиндр. На что они похожи:
Можете также скачать эти обучающие картинки во вложениях.
Плоские геометрические фигуры из бумаги — Строим замок
В этом упражнении вы можете скачать плоские геометрические фигуры из бумаги и построить из них замок, то есть выложить их на столе таким образом, чтобы получился заданный силуэт замка. Для начала скачайте во вложениях бланки с заданием и распечатайте на принтере. Затем вырежьте геометрические фигуры (квадрат, трапеция, полукруг и треугольник), которые даны к этому заданию. Все карточки с заданиями даны с увеличением уровня сложности (от 1 до 6 задания).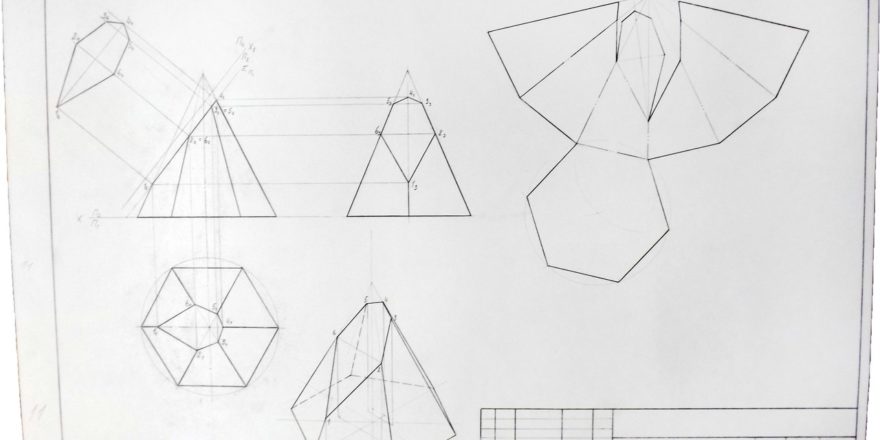
Все карточки с замками можно распечатывать на обычной офисной белой бумаге. А геометрические фигуры нужно распечатать на цветном картоне. Если нет цветного картона, можно использовать для распечатки цветную бумагу, а затем наклеить бумагу на лист картона и вырезать фигуры.
После этого подробно объесните ребенку инструкцию к выполнению упражнения.
«Строители, прежде чем строить какое-либо здание, смотрят сначала на его чертеж или схему, в которых показано каким оно должно быть. Такие чертежи бывают разными. Вот например, один из них», — взрослый показывает одну или две игровых схемы замка с нашего задания. — «Тебе нужно мысленно представить из каких частей состоит каждый замок, руководствуясь теми фигурами, которые можно использовать для строительства.» — взрослый показывает все геометрические фигуры, которые заранее вырезаны из цветного картона.
Очень важно начинать занятие, не используя подсказки, то есть нужно закрывать от ребенка геометрические фигуры, которые нарисованы рядом с силуэтом каждого замка. Пусть ребенок сам подумает, какие фигуры и какого размера ему понадобятся для строительства данного замка. И только если он испытвает трудности, можно приоткрыть для него подсказку.
Пусть ребенок сам подумает, какие фигуры и какого размера ему понадобятся для строительства данного замка. И только если он испытвает трудности, можно приоткрыть для него подсказку.
Также не нужно допускать, чтобы ребенок накладывал вырезанные геометрические фигуры из бумаги на силуэт замка, так как при этом он не будет развивать наглядно-образное мышление. Старайтесь, чтобы всю основную работу ребенок проводил в уме, а не методом подбора.
Скачать карточки с плоскими геометрическими фигурами для строительства замка вы можете во вложениях внизу страницы.
Карточка 1
Карточка 3
Карточка 4
Карточка 5
Карточка 6
Геометрические фигуры для вырезания:
Также вам будут полезны и другие материалы по изучению геометрических фигур:
Веселые и красочные задания для детей «Рисунки из геометрических фигур» являются очень удобным обучающим материалом для детей дошкольного и младшего школьного возраста по изучению и запоминанию основных геометрических формю
Здесь вы с ребенком можете изучить геометрические фигуры и их названия с помощью веселых заданий в картинках.
Задания ознакомят ребенка с основными фигурами геометрии — кругом, овалом, квадратом, прямоугольником и треугольником. Только здесь не занудное зазубривание названий фигур, а своеобразная игра-раскраска.
Как правило, геометрию начинают изучать, рисуя плоские геометрические фигуры. Восприятие правильной геометрической формы невозможно без выведения ее своими руками на листе бумаги.
Это занятие изрядно позабавит ваших юных математиков. Ведь теперь им придется находить знакомые формы геометрических фигур среди множества картинок.
Наложение фигур друг на друга — это занятие по геометрии для дошкольников и младших школьников. Смысл упражнения состоит в решении примеров на сложение. Только это необычные примеры. Вместо цифр здесь нужно складывать геометрические фигуры.
Это задание составлено в виде игры, в которой ребенку предстоит менять свойства геометрических фигур: форму, цвет или размер.
Здесь вы можете скачать задания в картинках, в которых представлен счет геометрических фигур для занятий по математике.
В этом задании ребенок познакомится с таким понятием, как чертежи геометрических тел. По сути, это занятие представляет собой мини-урок по начертательной геометрии
Дети любят раскрашивать и обводить, поэтому данные задания сделают ваши занятия по обучению счету максимально эффективными.
И еще можете поиграть в математические игры онлайн от лисенка Бибуши:
В этой развивающей онлайн игре ребенку предстоит определить, что является лишним среди 4 картинок. При этом необходимо руководствоваться признаками геометрических форм.
развертка. Развертка пирамиды для склеивания. Развертки из бумаги
Прямоугольник, квадрат, треугольник, трапеция и другие – геометрические фигуры из раздела точной науки. Пирамида — это многогранник. Основанием этой фигуры является многоугольник, а боковыми гранями треугольники, имеющие общую вершину, или трапеции. Для полного представления и изучения любого геометрического объекта изготавливают макеты. Используют самый разнообразный материал, из которого выполняется пирамида. Поверхность многогранной фигуры, развернутая на плоскости, называется ее разверткой. Создать макет поможет метод преобразования плоских предметов в объемные многогранники и определенные знания из геометрии. Развертки из бумаги или картона изготовить непросто. Потребуется умение выполнять чертежи по заданным размерам.
Поверхность многогранной фигуры, развернутая на плоскости, называется ее разверткой. Создать макет поможет метод преобразования плоских предметов в объемные многогранники и определенные знания из геометрии. Развертки из бумаги или картона изготовить непросто. Потребуется умение выполнять чертежи по заданным размерам.
Узнаем как собрать пирамидку Мефферта: простые рекомендации…
Наверное, самой первой завоевавшей огромную популярность головоломкой в мире стал кубик Рубика. До…
Материалы и приспособления
Моделирование и выполнение многогранных объемных геометрических фигур — интересный и захватывающий процесс. Из бумаги можно выполнить большое количество всевозможных макетов. Для работы будут необходимы:
- бумага или картон;
- ножницы;
- карандаш;
- линейка;
- циркуль;
- ластик;
- клей.
Определение параметров
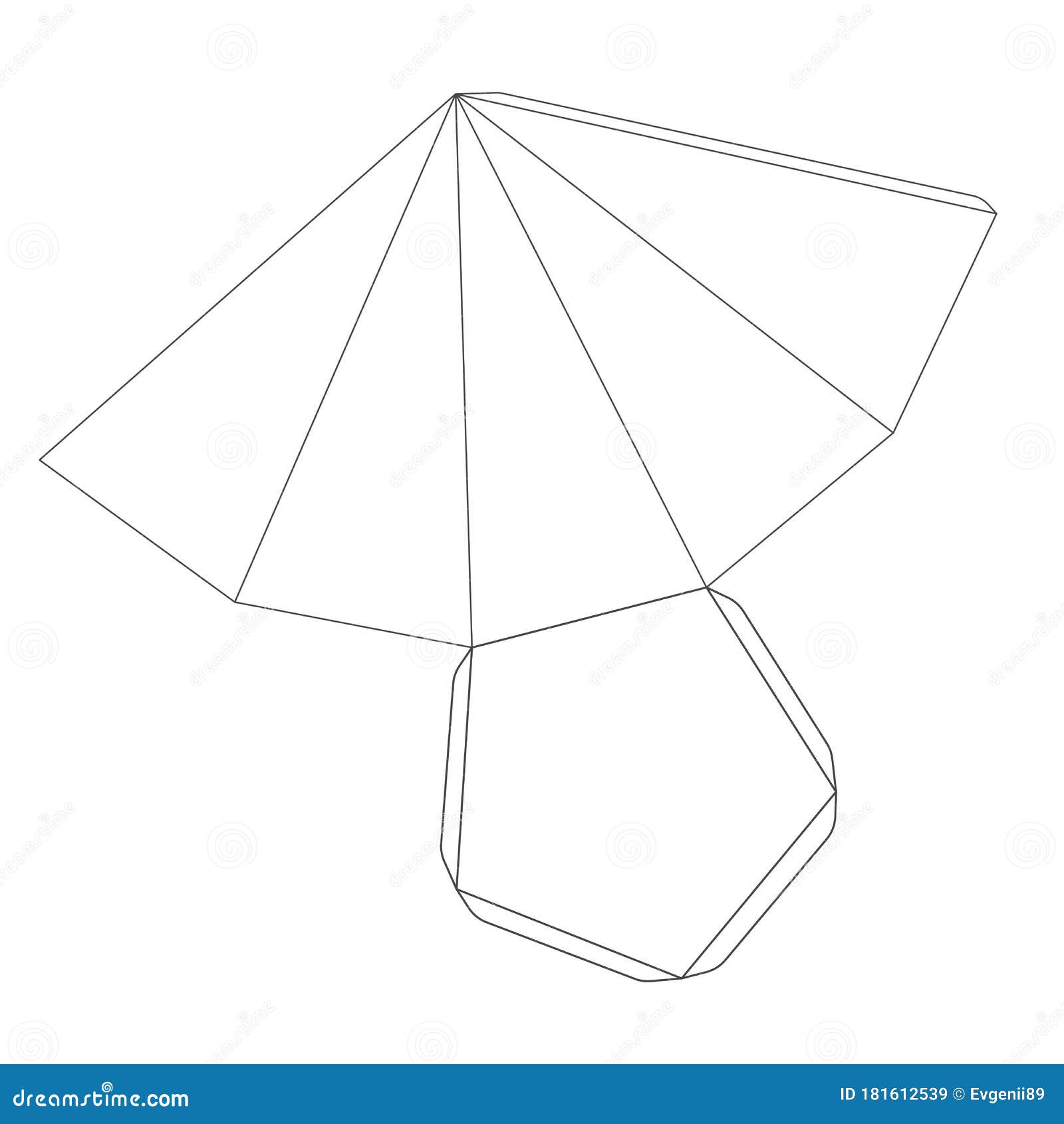
Прежде всего определим, какой будет пирамида. Развертка данной фигуры является основой для изготовления объемной фигуры.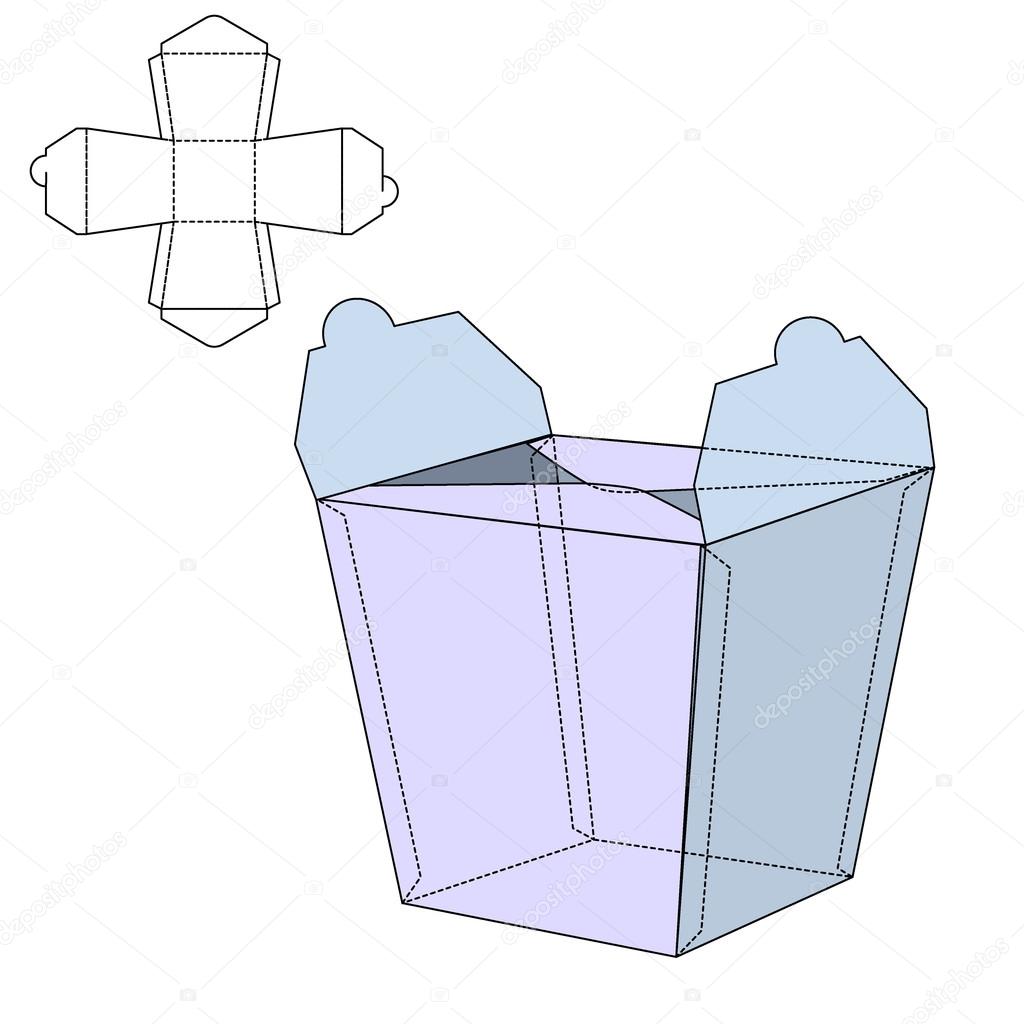 Выполнение работы потребует предельной точности. При неправильном чертеже геометрическую фигуру собрать будет невозможно. Допустим, необходимо изготовить макет правильной треугольной пирамиды.
Выполнение работы потребует предельной точности. При неправильном чертеже геометрическую фигуру собрать будет невозможно. Допустим, необходимо изготовить макет правильной треугольной пирамиды.
Любое геометрическое тело обладает определенными свойствами. Данная фигура имеет основанием правильный многоугольник, а ее вершина спроецирована в его центр. В качестве основания выбран равносторонний треугольник. Данное условие определяет название. Боковые ребра у пирамиды – это треугольники, количество которых зависит от выбранного для основания многогранника. В данном случае их будет три. Также важно знать размеры всех составных частей, из которых будет составлена пирамида. Развертки из бумаги выполняются в соответствии с учетом всех данных геометрической фигуры. Параметры будущей модели оговариваются заранее. От этих данных зависит выбор используемого материала.
Ручная развертка: виды, назначение, ГОСТ
Получить методом сверления отверстие, стенки которого были бы идеально ровными, получается далеко. ..
..
Как выполняется развертка правильной пирамиды?
Основой модели является лист бумаги или картона. Работу начинают с чертежа пирамиды. Фигура представляется в развернутом виде. Плоское изображение на бумаге соответствует заранее выбранным размерам и параметрам. Правильная пирамида имеет основанием правильный многоугольник, а высота проходит через его центр. Изготавливаем для начала простую модель. В данном случае – это треугольная пирамида. Определяем размеры выбранной фигуры. Чтобы построить развертку пирамиды, основанием которой является правильный треугольник, в центре листа, используя линейку и карандаш, нарисуем основание заданных размеров. Далее к каждой его стороне вычерчиваем боковые грани пирамиды – треугольники. Теперь переходим к их построению. Размеры сторон треугольников боковой поверхности измеряем циркулем. Ножку циркуля ставим в вершину нарисованного основания и делаем засечку. Действие повторяем, перемещаясь в следующую точку треугольника. Пересечение, полученное в результате таких действий, определит вершины боковых граней пирамиды. Их соединяем с основанием. Получаем чертеж пирамиды. Для склеивания объемной фигуры на сторонах боковых граней предусматривают клапаны. Дорисовываем небольшие трапеции.
Их соединяем с основанием. Получаем чертеж пирамиды. Для склеивания объемной фигуры на сторонах боковых граней предусматривают клапаны. Дорисовываем небольшие трапеции.
Параллелепипед из бумаги: три технологии на одной страничке
Как сделать объемный параллелепипед? Из бумаги проще и быстрее всего. Рассмотрим наиболее…
Сборка макета
Вырезаем ножницами выполненный рисунок по контуру. Аккуратно сгибаем развертку по всем линиям. Клапаны-трапеции заправляем внутрь фигуры таким образом, чтобы ее грани сомкнулись. Их смазываем клеем. Через тридцать минут клей высохнет. Объемная фигура готова.
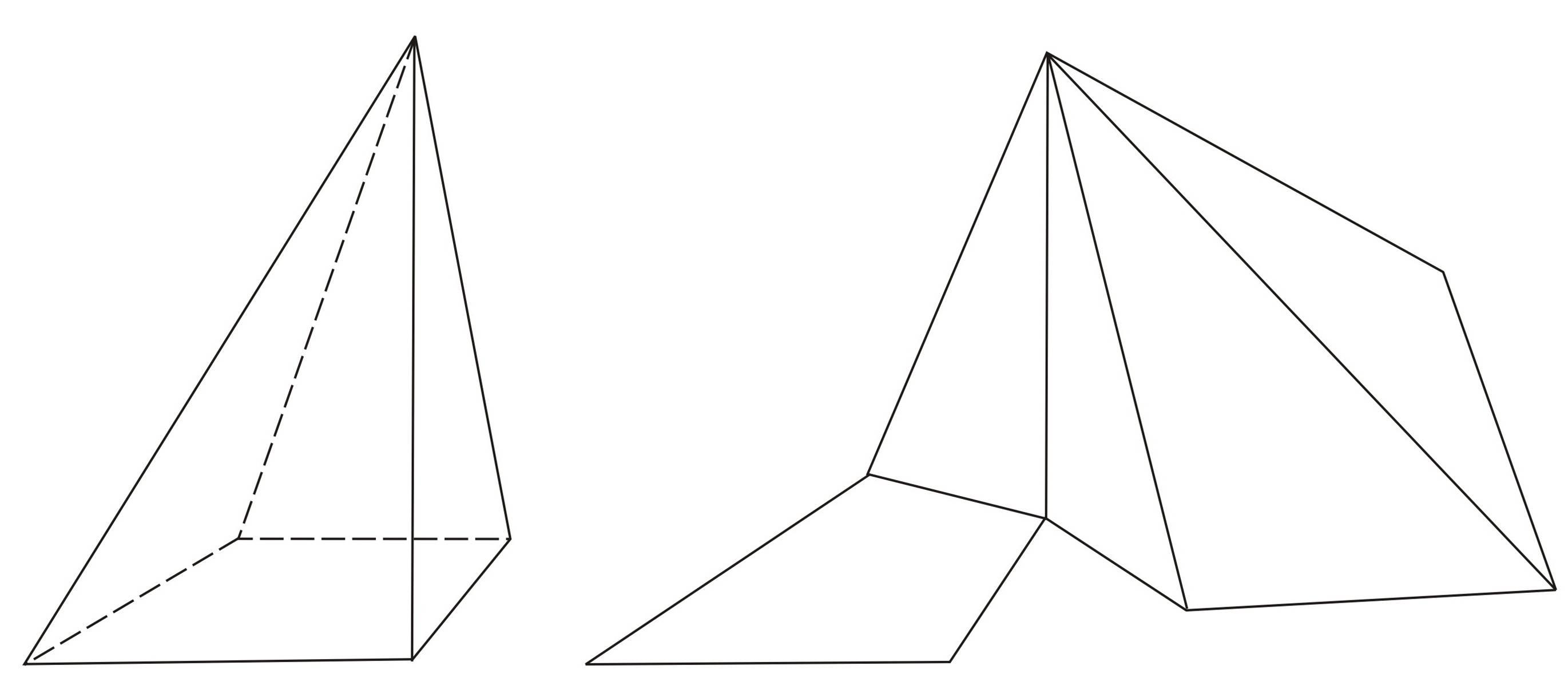
Развертка четырехугольной пирамиды
Сначала представим, как выглядит геометрическая фигура, макет которой будем изготавливать. Основанием выбранной пирамиды является четырехугольник. Боковые ребра — треугольники. Для работы используем те же материалы и приспособления, что и в предыдущем варианте. Чертеж выполняем на бумаге карандашом. В центре листа чертим четырехугольник с выбранными параметрами.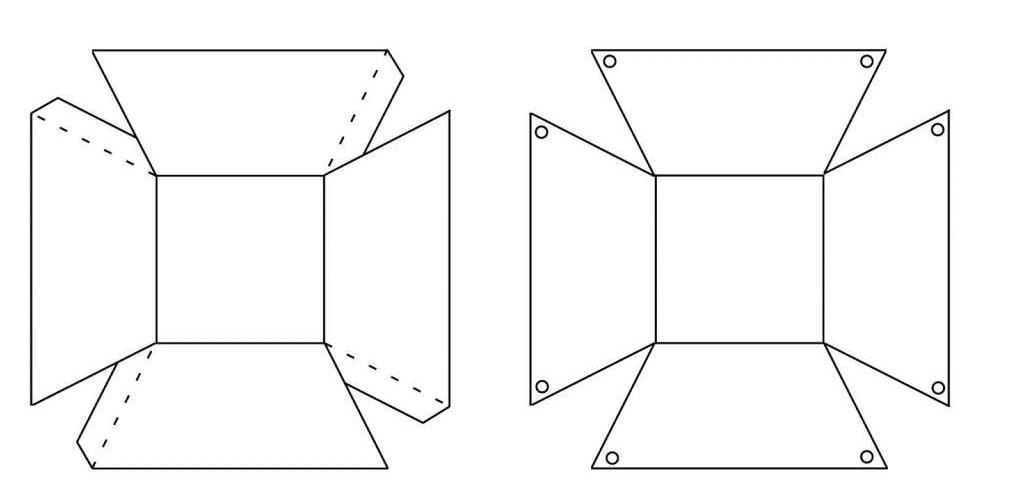
Каждую сторону основания делим пополам. Проводим перпендикуляр, который будет являться высотой треугольной грани. Раствором циркуля, равным длине боковой грани пирамиды, делаем на перпендикулярах засечки, установив его ножку в вершину основания. Оба угла одной стороны основания соединяем с полученной точкой на перпендикуляре. В результате получаем в центре чертежа квадрат, на гранях которого нарисованы треугольники. Чтобы зафиксировать модель на боковых гранях, дорисовывают вспомогательные клапаны. Для надежного крепления достаточно полоски сантиметровой ширины. Пирамида готова к сборке.
Завершающий этап выполнения макета
Полученную выкройку фигуры вырезаем по контуру. По начерченным линиям сгибаем бумагу. Сбор объемной фигуры производят путем склеивания. Предусмотренные клапаны смазываем клеем и фиксируем полученную модель.
Объемные макеты сложных фигур
После выполнения простой модели многогранника можно перейти к более сложным геометрическим фигурам. Развертка пирамиды усеченной намного сложнее в выполнении. Ее основаниями являются подобные многогранники. Боковые грани – это трапеции. Последовательность выполнения работы будет такой же, как та, в которой изготавливалась простая пирамида. Развертка будет более громоздкой. Для выполнения чертежа используют карандаш, циркуль и линейку.
Развертка пирамиды усеченной намного сложнее в выполнении. Ее основаниями являются подобные многогранники. Боковые грани – это трапеции. Последовательность выполнения работы будет такой же, как та, в которой изготавливалась простая пирамида. Развертка будет более громоздкой. Для выполнения чертежа используют карандаш, циркуль и линейку.
Построение чертежа
Развертка пирамиды усеченной выполняется в несколько этапов. Боковой гранью усеченной пирамиды является трапеция, а основаниями — подобные многогранники. Допустим, что это квадраты. На листе бумаги выполняем чертеж трапеции с заданными размерами. Боковые стороны полученной фигуры продлеваем до пересечения. В результате получаем равнобедренный треугольник. Его сторону измеряем циркулем. На отдельном листе бумаги строим окружность, радиусом которой будет измеренное расстояние.
Следующий этап – это построение боковых ребер, которые имеет усеченная пирамида. Развертка выполняется внутри нарисованной окружности. Циркулем измеряют нижнее основание трапеции.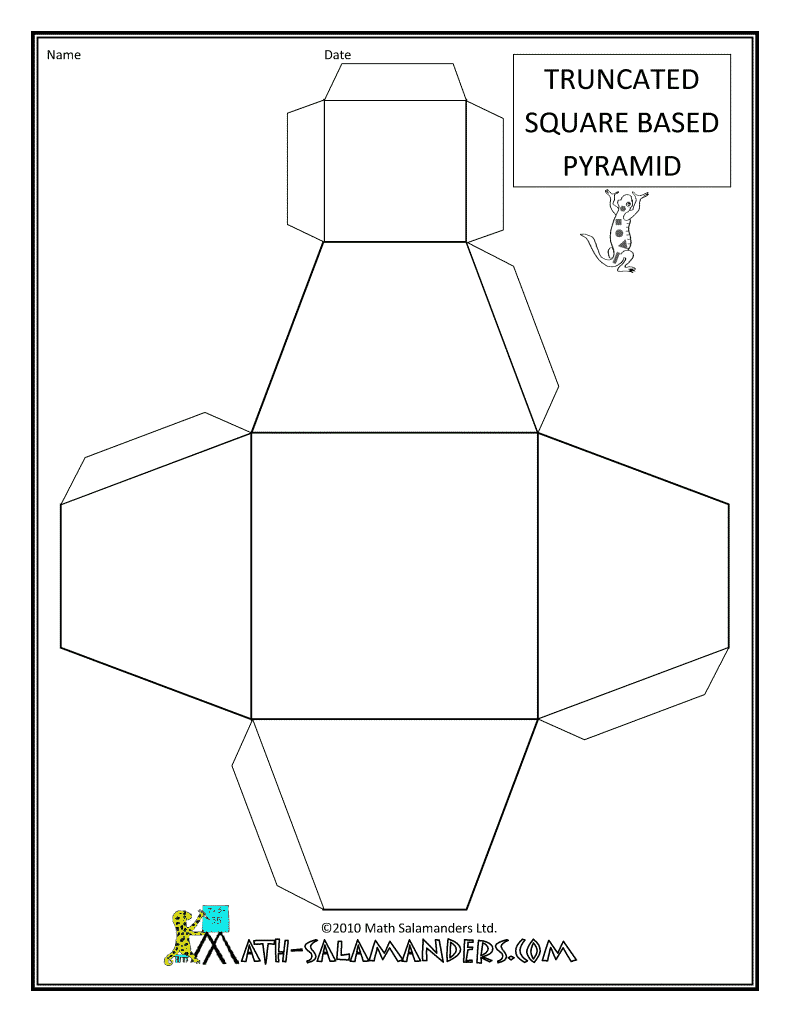 На окружности отмечаем пять точек, которые соединяют линии с ее центром. Получаем четыре равнобедренных треугольника. Циркулем измеряем сторону трапеции, нарисованной на отдельном листе. Данное расстояние откладываем на каждой стороне нарисованных треугольников. Полученные точки соединяем. Боковые грани трапеции готовы. Остается только нарисовать верхнее и нижнее основания пирамиды. В данном случае это подобные многогранники – квадраты. К верхнему и нижнему основаниям первой трапеции дорисовываем квадраты. На чертеже изображены все части, которые имеет пирамида. Развертка практически готова. Остается только дорисовать соединительные клапаны на сторонах меньшего квадрата и одной из граней трапеций.
На окружности отмечаем пять точек, которые соединяют линии с ее центром. Получаем четыре равнобедренных треугольника. Циркулем измеряем сторону трапеции, нарисованной на отдельном листе. Данное расстояние откладываем на каждой стороне нарисованных треугольников. Полученные точки соединяем. Боковые грани трапеции готовы. Остается только нарисовать верхнее и нижнее основания пирамиды. В данном случае это подобные многогранники – квадраты. К верхнему и нижнему основаниям первой трапеции дорисовываем квадраты. На чертеже изображены все части, которые имеет пирамида. Развертка практически готова. Остается только дорисовать соединительные клапаны на сторонах меньшего квадрата и одной из граней трапеций.
Завершение моделирования
Перед склеиванием объемной фигуры чертеж по контуру вырезают ножницами. Далее развертку аккуратно сгибают по начерченным линиям. Крепежные клапаны заправляем внутрь модели. Их смазываем клеем и прижимаем к граням пирамиды. Модели даем высохнуть.
Изготовление разных моделей многогранников
Выполнение объемных моделей геометрических фигур — увлекательное занятие.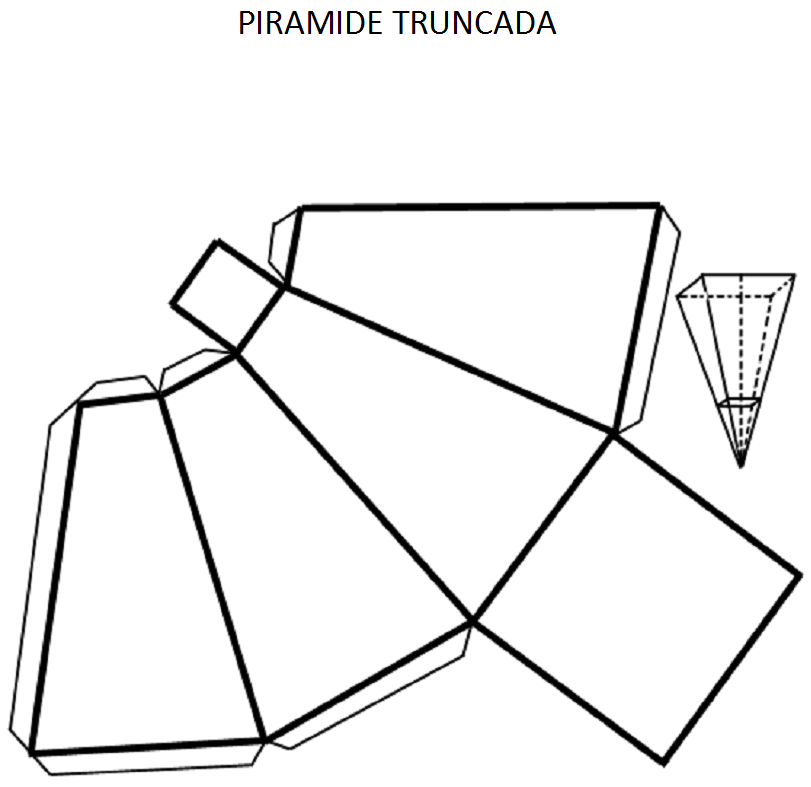 Чтобы его досконально освоить, следует начинать с выполнения самых простых разверток. Постепенно переходя от простых поделок к более сложным моделям, можно приступать к созданию самых замысловатых конструкций.
Чтобы его досконально освоить, следует начинать с выполнения самых простых разверток. Постепенно переходя от простых поделок к более сложным моделям, можно приступать к созданию самых замысловатых конструкций.
публикаций — Повторное открытие исчисления в 1994 году: что должно было случиться с этой статьей?
Задавать вопрос
спросил
Изменено 12 дней назад
Просмотрено 86 тысяч раз
В академических кругах есть известная статья, в которой рассказывается о повторном открытии трапециевидного правила для численного интегрирования исследователем-медиком:
«Математическая модель для определения общей площади под кривой толерантности к глюкозе и других метаболических кривых», Мэри М.
Тай, Diabetes Care , 1994 , 17 , 152–154.
Я думаю, что единственная цифра в статье говорит сама за себя:
Вы можете найти комментарии на эту тему во многих блогах, большинство из них примерно следующего содержания: «Оказывается, исчисление было изобретено в 1994”. Я думаю, что это действительно немного грустно, что статья прошла мимо исследователя, ее непосредственных коллег и друзей, профессора электротехники Йельского университета, которого поблагодарили за «его экспертную оценку», и, что наиболее важно, рецензентов, без того, чтобы кто-то дал автору намекать.
На мой взгляд, самый оптимистичный взгляд — рассматривать его как образовательный документ: метод не нов, но конкретное медицинское сообщество не знало о нем, поэтому его стоило опубликовать. Однако это , а не то, что говорится в статье: автор явно представляет метод как новый и называет его в честь нее.
Хорошо, кажется, я объяснил контекст.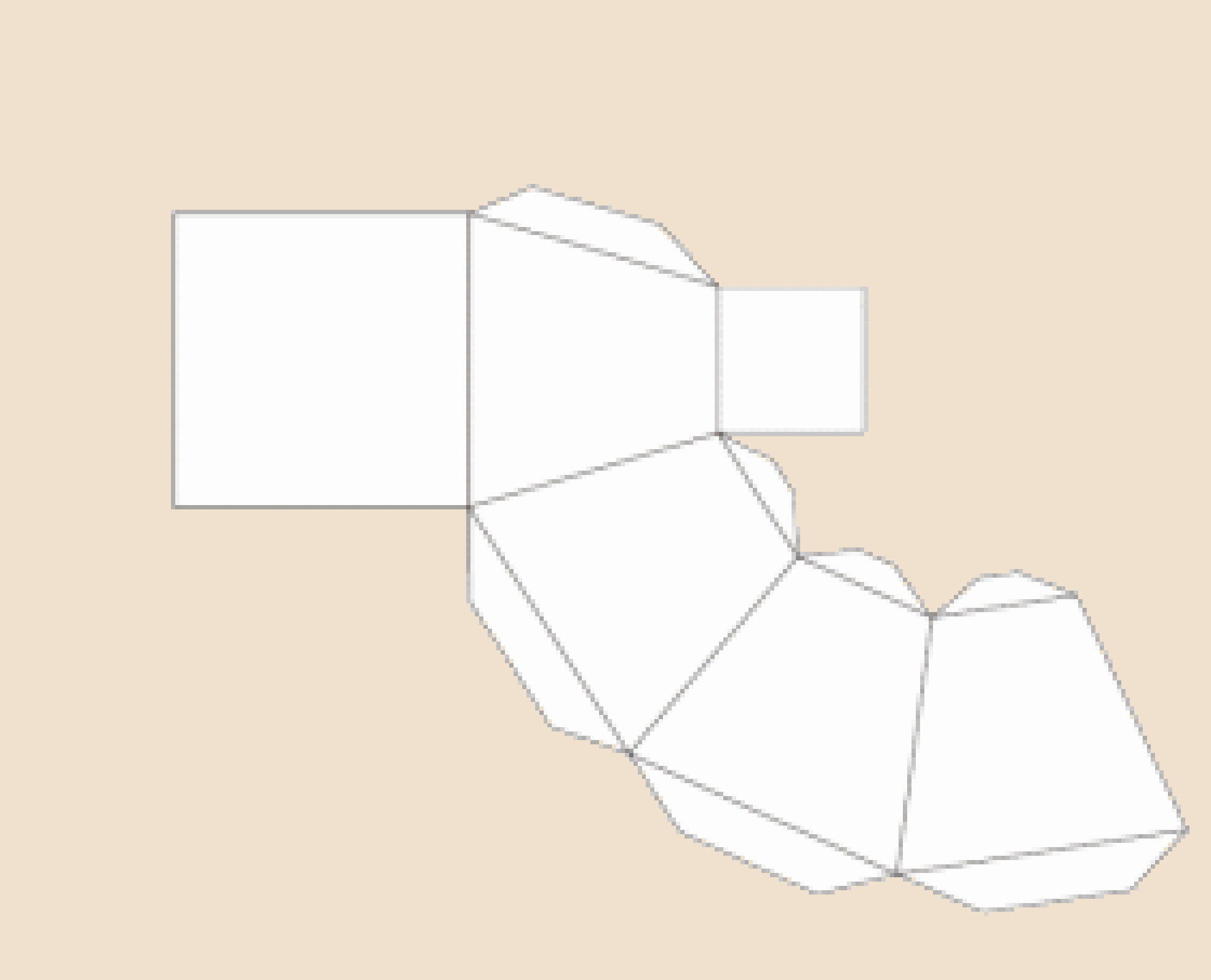 Мой вопрос: после того, как этот провал рецензирования был разоблачен, что должно было случиться с газетой? Случилось так, что в том же журнале была опубликована серия комментариев к статье и ответ автора на комментарии. Был ли это правильный/этичный способ решения проблемы в качестве редактора? Или газету надо было отозвать?
Мой вопрос: после того, как этот провал рецензирования был разоблачен, что должно было случиться с газетой? Случилось так, что в том же журнале была опубликована серия комментариев к статье и ответ автора на комментарии. Был ли это правильный/этичный способ решения проблемы в качестве редактора? Или газету надо было отозвать?
- публикации
- этика
- опровержение
Ответ на этот вопрос зависит от того, что мы должны назвать провалом рецензирования . На академическом рынке существует множество журналов: некоторые журналы с удовольствием публикуют результаты, если они верны, даже если они не раздвигают границы инноваций. Есть журналы, которые с удовольствием публикуют необоснованные экспериментальные работы, а с другой стороны, есть журналы, которые поощряют теоретические модели, которые крайне непрактичны и по сути являются математической чепухой.
Публикация чего-то совершенно очевидного даже для старшеклассника нелепа, но мы можем сделать два вывода: во-первых, редактор и рецензенты не сочли это настолько очевидным, а во-вторых, журнал не считал (или не считает?) в любом случае имеют высокие стандарты инноваций. Учитывая, что в этой области потенциально могут быть специалисты, которые ничего не смыслят в исчислении, публикация не должна стать большим сюрпризом.
Учитывая, что в этой области потенциально могут быть специалисты, которые ничего не смыслят в исчислении, публикация не должна стать большим сюрпризом.
Реальность такова, что публикация известных фактов не такая уж редкость в научных кругах. Ажиотаж вокруг этой статьи в основном из-за элементарности концепции. Можно ожидать извинений от журналов за неправильные результаты, но не обязательно за устаревшие.
3Онлайн-публикации, на первый взгляд, должны давать редакторам некоторое пространство для маневра. В этом случае они могут добавить к онлайн-версии статьи редакционную примечание, например
.ПРИМЕЧАНИЕ РЕДАКЦИИ: Настоятельно не рекомендуется ссылаться на эту статью как на «метод Тай», так как этот метод на самом деле известен под названием правила трапеций. См. также Комментарии для дальнейших объяснений.
Академическое сообщество, пострадавшее от этого повторного открытия, должно было принять соответствующие меры, а редакторы других журналов должны были убедиться, что ссылки на статью даются только в том случае, если обсуждается что-то иное, чем правило трапеций.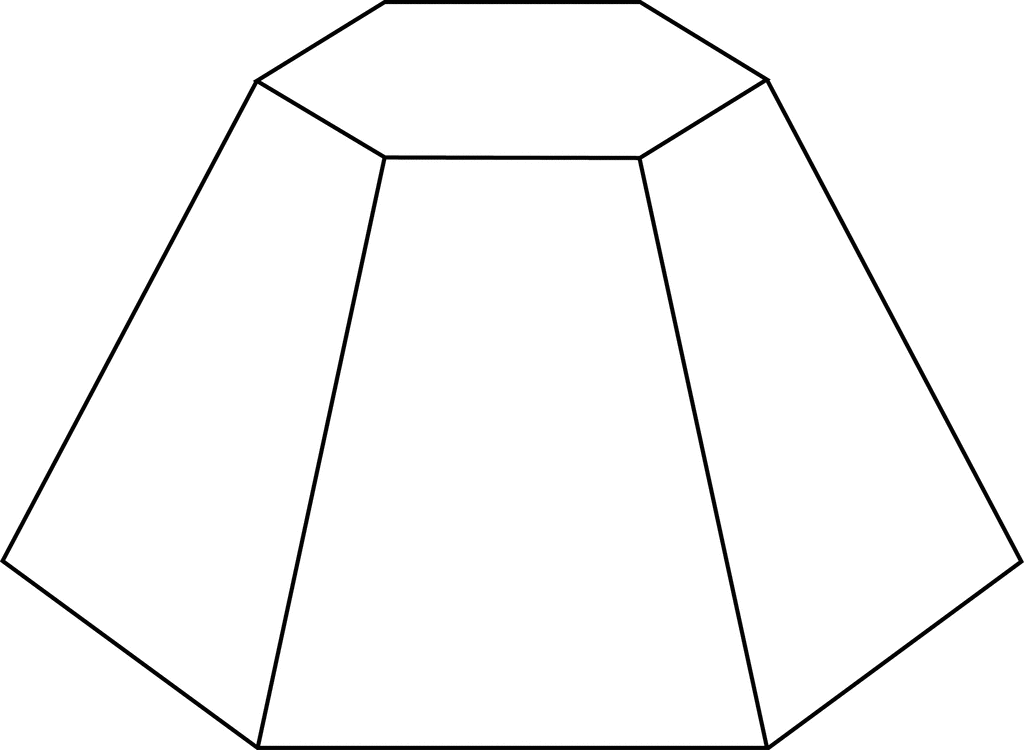
Иоанн Павел II извинился за ряд нарушений со стороны католической церкви. Редакторы должны были извиниться перед своим исследовательским сообществом за провал рецензирования. Время от времени ошибаться — это нормально; наука движется, исправляя то, что вступает в противоречие с другими частями знания. Однако нехорошо отказываться от осознания своей неправоты и настаивать на этом.
Лично, если бы я имел какое-то отношение к принятию такого документа, как этот, я бы хотел как можно тщательнее скрыть любые сведения о том, что я имею какое-либо отношение к этому документу.
Я, конечно, надеюсь, что в таком случае автор, о котором идет речь, будет настолько смущен «повторным открытием» чего-то, что было известно сотни лет, что автор охотно откажется от статьи. Но если этого не произошло, то мало что можно сделать. Процесс рецензирования провалился, но требовать опровержения должен был либо редактор журнала, либо автор. Ньютон и Симпсон мертвы, и никто другой не может реально заявлять, что он «пострадал» от этого важного «открытия».
Если вы хотите задать вопрос , должна ли статья быть отозвана, тогда ответ будет отрицательным, если только в процессе рецензирования не было фактической предвзятости или нечестной игры. Если рецензенты знали о наличии проблемы и преднамеренно позволили статье двигаться дальше, то необходим опровержение. В противном случае, однако, документ не должен быть отозван. Однако академическое сообщество должно избегать его, и люди должны воздерживаться от его цитирования (за исключением, возможно, статей и работ, показывающих, как , а не для исследования!).
2С этой бумагой связана еще большая проблема, чем отсутствие инноваций.
Любая научная публикация является формой общения внутри определенного научного сообщества. Если это сообщество не знает, что математический инструмент, известный веками, может решить одну из их проблем, то, безусловно, есть смысл указать на это. Может быть, недостаточно, чтобы назвать инструмент в ее честь, но все же достаточно, чтобы отметить ее цитатами.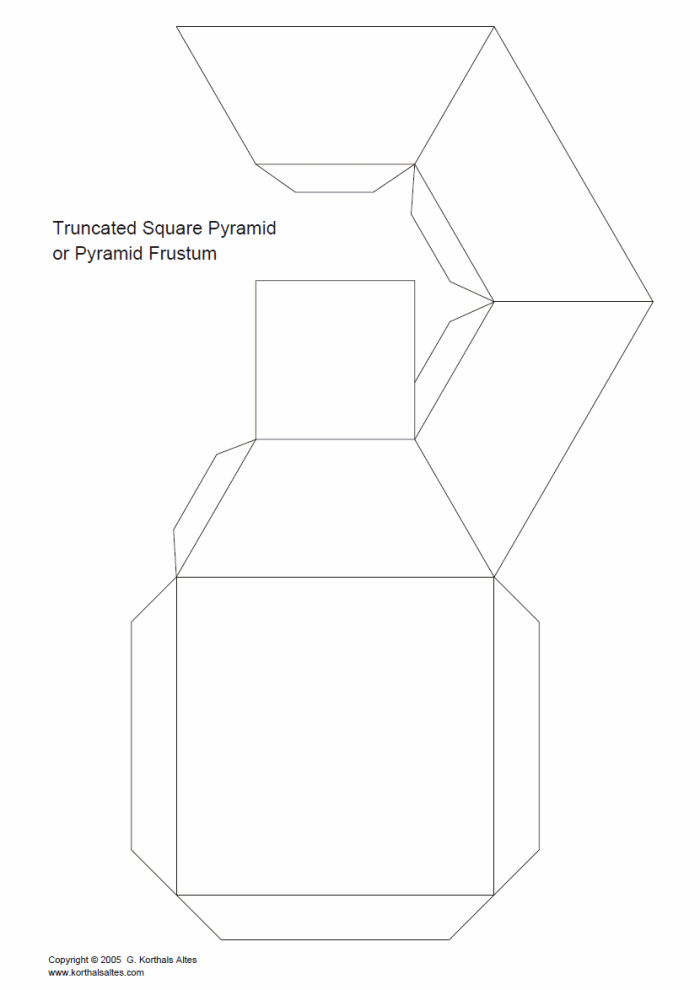
Однако здесь это не так. Мне было так любопытно проверить те другие методы, которые, по ее утверждению, были заменены ее «изобретением», что я решил бегло взглянуть на парочку из них. Особенно меня заинтересовал метод, который, видимо, дает всего 3% от истинного значения (!) . Что ж, оказывается, число, полученное с помощью этого метода, вовсе не предназначено для оценки площади под кривой: для упрощения расчетов авторы просто решили исключить фактор времени, который в их исследовании всегда был главным. такой же. Что касается другого метода, то это была еще одна реализация правила трапеций с добавлением некоторых осложнений из-за медицинских соображений относительно правильного временного интервала, который следует использовать, что она явно неверно истолковала.
Практически все в ее области использовали один и тот же алгоритм, но она этого не осознавала, и чтобы доказать свою точку зрения, она полностью исказила работу цитируемых ею авторов. Я думаю, рецензенты должны были заметить это, даже если они ничего не знали о правиле трапеций! Когда автор строит аргумент, используя работы других исследователей, рецензенты всегда должны проверять, честно ли представлена эта работа.
Cafec Трапециевидная фильтровальная бумага с 3-5 чашками Abaca, 100 шт. в упаковке – Принадлежности для бариста
Стоимость доставки будет зависеть от размера вашего заказа и места доставки. Вы можете проверить общую стоимость доставки на странице оформления заказа, однако убедитесь, что вы заполнили все свои данные, поскольку доставка рассчитывается на основе общего веса заказа и вашего местоположения.
| ВАРИАНТЫ ДОСТАВКИ | СТОИМОСТЬ ДОСТАВКИ | ВРЕМЯ ТРАНЗИТА |
|---|---|---|
| Стандартная доставка | Фиксированная ставка $10* | 2-5 рабочих дней |
| Экспресс-доставка | От 12,40 $ | 1-3 рабочих дня |
| Международный | Рассчитывается на кассе | 2-10 рабочих дней |
| Самовывоз со склада | 11/76 Rushdale St Ноксфилд, Виктория 3180 | Тот же рабочий день |
Обратите внимание: в регионах время доставки может немного увеличиться.
*При крупногабаритных заказах свыше 25 кг может взиматься дополнительная плата за доставку.
Наши партнеры по доставке
Стандартная доставка
Мы используем электронную посылку Почты Австралии для большинства наших доставок. Это зарегистрированная служба, которую можно отследить. Ориентировочные сроки доставки 1-4 дня. Для пригородов и регионов добавьте день или два соответственно, в зависимости от удаленности от центрального делового района. Эта услуга требует подписи при доставке, поэтому мы рекомендуем вам указать свой рабочий адрес или указать адрес доставки, где кто-то может расписаться за посылку. Если никого нет, будет оставлена коллекционная карточка для посещения местного почтового отделения. Перевозчики не будут оставлять посылки без присмотра/без подписи. Почта Австралии может отправить электронное письмо или смс за день до доставки.
Экспресс-доставка
Мы используем ЭКСПРЕСС-доставку электронной почтой Австралии. Это зарегистрированная служба, которую можно отследить. Ориентировочные сроки доставки можно найти здесь. Эта услуга обычно представляет собой доставку на следующий день во все столицы Австралии при условии, что заказы размещены до 15:00 в рабочий день (хотя это может занять немного больше времени в пиковые периоды, такие как Рождество). Обратите внимание, что доставка в регионы обычно не осуществляется на следующий день. Express не гарантируется для NT.
Это зарегистрированная служба, которую можно отследить. Ориентировочные сроки доставки можно найти здесь. Эта услуга обычно представляет собой доставку на следующий день во все столицы Австралии при условии, что заказы размещены до 15:00 в рабочий день (хотя это может занять немного больше времени в пиковые периоды, такие как Рождество). Обратите внимание, что доставка в регионы обычно не осуществляется на следующий день. Express не гарантируется для NT.
Эта услуга требует подписи при доставке, поэтому мы рекомендуем вам указать свой рабочий адрес или указать адрес доставки, где кто-то может расписаться за посылку. Если никого нет, будет оставлена коллекционная карточка для посещения местного почтового отделения. Перевозчики не будут оставлять посылки без присмотра/без подписи. Почта Австралии может отправить электронное письмо или смс за день до доставки.
Международный
Стоимость доставки для международных заказов будет рассчитана при оформлении заказа на основе веса заказа и вашего местоположения. Barista Supplies доставляет товары по всей Австралии и более чем в 45 стран, включая США, Великобританию и Новую Зеландию. Полный список стран, в которые мы осуществляем доставку, выглядит следующим образом:
Barista Supplies доставляет товары по всей Австралии и более чем в 45 стран, включая США, Великобританию и Новую Зеландию. Полный список стран, в которые мы осуществляем доставку, выглядит следующим образом:
Австрия, Бельгия, Бразилия, Канада, Чили, Чехия, Дания, Эквадор, Эстония, Финляндия, Франция, Германия, Греция, Гонконг/ЮАР/Китай, Индия. , Индонезия, Ирландия, Израиль, Италия, Япония, Люксембург, Малайзия, Мальта, Молдова, Нидерланды, Новая Зеландия, Норвегия, Папуа-Новая Гвинея, Филиппины, Польша, Португалия, Саудовская Аравия, Сингапур, Южная Африка, Южная Корея, Испания, Шри Ланка, Швеция, Швейцария, Тайвань, Таиланд, Турция, ОАЭ, Великобритания, США и Вануату.
Страны за пределами Австралии получат заказы примерно через 2-10 рабочих дней (время доставки зависит от страны назначения и работы почтовой службы).
Все ввозные пошлины и таможенные сборы оплачиваются покупателем.
Самовывоз
Если вы предпочитаете самовывоз своего заказа, на странице оформления заказа выберите опцию «Забрать со склада» в разделе «Доставка». Затем мы подготовим ваш заказ и сообщим вам по электронной почте, как только он будет готов к выдаче.
Затем мы подготовим ваш заказ и сообщим вам по электронной почте, как только он будет готов к выдаче.
Партнеры по доставке
Наши товары доставляются через Австралийскую почту, Couriers Please, TNT или DHL Express. Электронное письмо с номером отслеживания отправляется в конце рабочего дня. Срок доставки обычно составляет 1-6 рабочих дней в зависимости от местонахождения заказчика. В случае, если курьер возвращает нам товар как недоставленный по какой-либо причине, может взиматься дополнительная плата за доставку для покрытия стоимости повторной доставки.
Ваш заказ будет доставлен с 7:00 до 9:00вечера. Так как в праздничные дни курьеры не доставляют, вы можете ожидать свой заказ на следующий рабочий день. Срок доставки не включает выходные и праздничные дни. Если вас нет рядом во время попытки доставки, водитель либо оставит ваш заказ в безопасном месте, либо оставит визитную карточку с указанием, как вы можете забрать свой заказ Barista Supplies.
Отказ от отправления
Если вы отказываетесь от отправления от Barista Supplies, вы несете ответственность за первоначальные расходы по доставке, любые импортные сборы, понесенные в отношении посылки, и стоимость возврата посылки в Barista Supplies.
