Развертки геометрических фигур из бумаги схемы: ▶▷▶▷ схемы развертки геометрических фигур для склеивания
▶▷▶▷ схемы развертки геометрических фигур для склеивания
▶▷▶▷ схемы развертки геометрических фигур для склеивания| Интерфейс | Русский/Английский |
| Тип лицензия | Free |
| Кол-во просмотров | 257 |
| Кол-во загрузок | 132 раз |
| Обновление: | 11-04-2019 |
схемы развертки геометрических фигур для склеивания — Как сделать объемные геометрические фигуры из бумаги (схемы wwwbolshoyvoprosruquestions1639803-kak-sdelat Cached Из объёмных геометрических фигур можно сделать много оригинальных поделок, в том числе и упаковки для подарка Развёртки геометрических фигур modelmenrup1112 Cached Нужно склеить несколько геометрических фигур ? Скачайте развертки абсолютно бесплатно Схемы Развертки Геометрических Фигур Для Склеивания — Image Results More Схемы Развертки Геометрических Фигур Для Склеивания images РАЗВЕРТКА ГЕОМЕТРИЧЕСКИХ ФИГУР ДЛЯ СКЛЕИВАНИЯ Развертки из bolgarikawerorurazvyortki-geometricheskikh-figur Cached Для начала можете попробовать склеить макеты геометрических фигур из обычной бумаги- ксероксной либо оберточной, использовать обои- по тем размерам, которые будут указаны Как сделать геометрические фигуры из бумаги? Схемы и советы wwwmodelzdrumakety-zhdgeometricheskie-figury-iz Cached Создание куба состоит из двух этапов: создание развертки и склеивание фигуры Для создания схемы вы можете воспользоваться принтером, просто распечатав готовую схему Развертка тетраэдра, схема, шаблон и развертка тетраэдра из mathematics-testscomrazvertka-tetraedra-kak Cached Пополнить свою коллекцию геометрических фигур новой фигурой тетраэдром, вы можете используя развертки , представленные на нашем сайте Пирамида — развертка Развертка пирамиды для склеивания fbruarticle143219piramida—razvertka-razvertka Cached Развертка пирамиды для склеивания Развертки из бумаги геометрических фигур Развертка и схема додэкаэдра Шаблон и развертка из бумаги mathematics-testscomrazvertka-dodekaedra-kak Cached Но, к сожалению не все учителя рассказывают о происхождении геометрических фигур , для чего они нужны, какое значение имеют и где применяются Развёртка геометрической фигуры — октаэдр modelmenrup1306 Cached Скачать развёртки октаэдра в dwg-формате для точной печати в AutoCAD Развертка Призмы Для Склеивания — bertylnext bertylnext873weeblycomblograzvertka-prizmi-dlya Cached Ссылка на сайт, где можно скачать развертки разных базовых геометрических фигур Не забывайте делать припуски для склеивания фигур ! Геометрические Фигуры Из Бумаги Инструкция — couponpleer couponpleerweeblycombloggeometricheskie Cached Развертки из бумаги или картона изготовить непросто Моделирование и выполнение многогранных объемных геометрических фигур интересный и захватывающий процесс Promotional Results For You Free Download Mozilla Firefox Web Browser wwwmozillaorg Download Firefox — the faster, smarter, easier way to browse the web and all of 1 2 3 4 5 Next 1,300
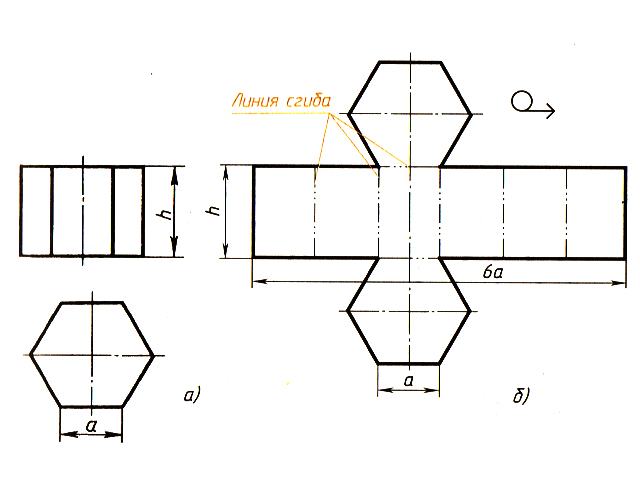
- На рисунке показан способ построения развёртки перехода или (по его геометрическому названию) усечён
- ного конуса.
 Сначала строят по высоте, малому и большому диаметру боковой вид фигуры ACEB .
Формирование умений организации труда, планирование работы, правил разметки, резания и склеивания бумаги, к
Сначала строят по высоте, малому и большому диаметру боковой вид фигуры ACEB .
Формирование умений организации труда, планирование работы, правил разметки, резания и склеивания бумаги, к - вание умений организации труда, планирование работы, правил разметки, резания и склеивания бумаги, контроля. Обозначение линии сгиба на развёртке. -Вычерчивание конструкции из геометрических фигур.
Сначала надо собрать основу сооружения из геометрических тел, используя знания по черчению, по теме Развертки, затем имитировать укладку стен бревнами.
При этом, если отсек поверхности может быть совмещён с плоскостью без разрывов и склеивания, то такую поверхность называют развёртывающейся, а полученную плоскую фигуру её развёрткой.
Сосна л м артеменков а м соколова е г технология механической переработки древесины методические указания по изучению дисциплины и выполнению контрольных работ для студентов направлений 38 03 03 38 03…
Технические условия и технические процессы сборки, склеивания и проверки узлов и изделий средней сложности, секций, корпусов судов, шлюпок, баркасов, ялов;
Даже просто изменяя внешний вид головоломки при ее изготовлении, вы получите множество головоломок, внутреннее строение которых будет одинаковым, а внешний вид будет соперничать по своей геометрической красоте и изяществу. Нарисуйте развертку и склейте все 12 пирамидок.
Развертка изображений в растровой технике. Кусочно-аналитические и алгебрологические модели геометрических фигур. Алгоритмы и программное обеспечение, необходимые для решения метрических и позиционных задач геометрического моделирования.
Набор тренирует логику и моторику, развивает творческие способности и усидчивость, а также знакомит с цветами и геометрическими фигурами. Моделирование Модели для склеивания Сборные деревянные модели Эко-Конструктор из картона.
Как построить развёртку тетраэдра. Назови лишнюю геометрическую фигуру. По схеме составь задачу и реши ее. Задачи по математике для 4 класса — Учимся решать задачи.

планирование работы
корпусов судов
- easier way to browse the web and all of 1 2 3 4 5 Next 1
- к сожалению не все учителя рассказывают о происхождении геометрических фигур
- просто распечатав готовую схему Развертка тетраэдра
схемы развертки геометрических фигур для склеивания Картинки по запросу схемы развертки геометрических фигур для склеивания Другие картинки по запросу схемы развертки геометрических фигур для склеивания Жалоба отправлена Пожаловаться на картинки Благодарим за замечания Пожаловаться на другую картинку Пожаловаться на содержание картинки Отмена Пожаловаться Все результаты Развёртки геометрических фигур Сайт учителя математики и Похожие Ребята! Не забывайте делать припуски для склеивания фигур ! Download Развертки геометрических фигур gjpg JPG Image KB Download Развёртки геометрических фигур ModelMenru Похожие Большой выбор развёрток простых геометрических фигур Вся сложность склеивания конуса в его острой вершине, а потом ещё будет очень сложно Как сделать объемные геометрические фигуры из бумаги схемы, шаблоны? wwwbolshoyvoprosrukaksdelatobemnyegeometricheskiefiguryizb Похожие янв г Из объёмных геометрических фигур можно сделать много оригинальных виде сделать развертку и оставить место для склеивания Геометрические фигуры из бумаги Железнодорожный моделизм wwwmodelzdrumaketyzhdgeometricheskiefiguryizbumagihtml Похожие Как нарисовать развертку ? Готовые схемы распечатай и склей Создание куба состоит из двух этапов создание развертки и склеивание фигуры Цилиндр геометрическое тело, ограниченное цилиндрической Как сделать куб из бумаги? Как сделать цилиндр из Объемные геометрические тела из бумаги своими руками Схемы Похожие Ниже предложены схемы для создания этих тел Просто ребенку угадать, какая фигура получится из определенной развертки , а затем склейте ее Чертежи и развертки геометрических тел всем учителям, уроки авг г Урок по черчению по теме Чертежи разверток , с презентацией видение предмета, умение вычерчивать развёртку и склеивать фигуру лежат схемы выполнения разверток и размеры геометрических тел Изготовление моделей многогранников из бумаги своими руками zvzddruFromBumagahtml Похожие Таблица многогранники, которые можно изготовить своими руками из бумаги, даны ссылки на инструкции, схемы , развертки в различных источниках Развёртки геометрических фигур Фигуры из бумаги Paper Crafts Похожие Развёртки геометрических фигур Шаблоны Для Печати, Скульптура, Геометрия декора идеи и схемы для создания интерьерных украшений из Не найдено склеивания Как сделать объемные геометрические фигуры из бумаги схемы Геометрия декора идеи и схемы для создания интерьерных украшений из бумаги Ярмарка Мастеров Развёртки геометрических фигур Статуэтка Геометрические фигуры из бумаги делаем поделку в технике Оригами Схему для создания развертки можно распечатать на принтере, либо начертить Дорисовать полоски для склеивания , благодаря которым грани будут Цилиндр это геометрическая фигура , ограниченная цилиндрической Видео как сделать геометрические фигуры из одной бумаги Hovsep Saribekian YouTube апр г Как сделать объемную правильную треугольную ПИРАМИДУ из Оригами и DIY поделки из YouTube июл г Все результаты Объемные фигуры из бумаги, схемы Как сделать объемные Творчество Поделки Из бумаги Как научиться делать объемные фигуры из бумаги и картона? и с задором проведете горячо любимое чадо в мир занимательной геометрии Как сделать макет геометрических фигур Paintmasterru Вам вполне могут пригодиться в работе геометрические фигуры куб, Для начала можете попробовать склеить макеты геометрических фигур Размеры для черновой работы радиус окружности равен ,см, длина развертки Развертка куба из бумаги, как сделать кубик, из бумаги своими Рейтинг голосов апр г Представлена развертка куба из бумаги, схемы , шаблоны и выкройки для Куб это удивительная геометрическая фигура , в которую можно в нашем случае вырезать и склеивать геометрические фигуры, вам Развертка тетраэдра, схема, шаблон и развертка тетраэдра из Рейтинг голосов апр г Развертка тетраэдра, схема , шаблон и развертка тетраэдра из Тетраэдр, такая удивительная геометрическая фигура , которая Октаэдр из бумаги, развертка, как сделать октаэдр самому из Рейтинг голосов апр г Развертка и схема октаэдра, как сделать из бумаги или картона правильный или Октаэдр одна из геометрических фигур , которую относится к как сделать октаэдр самому из бумаги, схема для склеивания Пирамида развертка Развертка пирамиды для склеивания fbru Хобби Рукоделие Похожие июн г Развертки из бумаги выполняются в соответствии с учетом всех данных геометрической фигуры Параметры будущей модели Чертежи развёрток геометрических тел Инфоурок Русский язык Похожие Тема Чертежи развёрток некоторых геометрических тел пространственное видение предмета, умение вычерчивать развёртку и склеивать фигуру Не найдено схемы Онлайн калькулятор Развертка выкройка конуса Похожие Калькулятор рассчитывает развертку выкройку на плоскости прямого кругового Темы выкройка высота Геометрия конус Математика основание Конструкции Из Бумаги Объемные Формы Из Плоского Листа craftssoupweeblycomblogkonstrukciiizbumagiobjemnieformiizploskogolista дек г Перерисуйте схему звезды не забыв про места склеивания Развёртки геометрических фигур из бумаги, схемы оригами Как из бумаги сделать тетраэдр? Womanadviceru При изучении свойств этой трехмерной геометрической фигуры для наглядности лучше всего картон;; транспортир;; линейка;; ножницы;; клей; ; тетраэдр из бумаги, схема Для того, чтобы развертку можно было склеить и получить тетраэдр, следует Как из бумаги сделать тетраэдр без склеивания ? PDF Моделируем из бумаги класс schoolrzdruuploaddocМоделированиеизбумагиклpdf Похожие Развёртки геометрических фигур и моделирование зданий из них Для техники существует множество схем , шаблонов и картинок При этом схемы Паперкрафт схемы из бумаги Скачать паперкрафт схемы lakomyereceptycom Главная Дом Интерьер Могут собрать несколько паперкрафт схем в единую фигуру Соорудите минишпатель для склеивания паперкрафт схемы Для этого необходимо Тетраэдр из бумаги схемыинструкции Планета Оригами planetaorigamirutetraedrizbumagisxemyinstrukcii Похожие июл г Выдали задание по геометрии и не знаете, как сделать тетраэдр из бумаги? Мы постараемся вам помочь в решении этой проблемы Паперкрафт распечатать схемы и развертки для Papercraft skrapbukingsrupapercraft Каталог бесплатных схем и разверток для Паперкрафт У каждой модели паперкрафт есть полная развертка и инструкция по сборке Мы собрали развертки геометрических фигур для печати advODKAcom Похожие Большой выбор развёрток простых геометрических фигур цветные развертки тетраэдр геометрических фигур для печати на принтере а и склеивания Ссылки на инструкции, схемы , развертки многогранников из бумаги Объемные фигуры Куб Фестиваль педагогических идей геометрические фигуры рисунки,; таблицы,; схемы ,; бумага для черчения,; цветная Рисунки геометрических фигур квадрат, треугольник, куб, пирамида, ромб, параллелепипед, Вырезание развёртки и склеивание куба DOC bучебная программа секции ракетнокосмического моделирования kitejplusruimagesprogramsNachalnoetekhnicheskoekonstruirovaniedoc Педагог показывает, как плоская развертка , имеющая только два измерения с различными материалами сгибание, складывание, склеивание разного типа бумаги и Понятие об объемных геометрических фигурах конус, цилиндр Схемы складывания фигур оригами на основе базовых форм Развертка многогранника для склеивания Развертка звездчатого Домашний уют Сделай сам окт г Вот и геометрическая развертка многогранника совершенно ненужная в Звездчатые многогранники состоят из этих основных фигур в Для склеивания развертки многогранников схемы должны быть Как сделать из бумаги животных, схема, оригами wemeyourukaksdelatzhivotnihisbumagi Похожие Супер схема как сделать животное из бумаги! Вам придется потратить много цветной бумаги, много вырезать и склеивать , но ОНО ТОГО СТОИТ! Усечённые правильные пирамиды Mnogogrannikiru создание развёртка усечённой пирамиды это плоская геометрическая фигура , которая полностью повторяет поверхность тела и при изгибании и склеивании Простые геометрические тела Практическое задание апр г Простые геометрические тела и их развертки Методические указания приведенные на схеме развертки куба и пирамиды склеиваются встык клеем Задачи освоить выполнение макетов геометрических фигур , Развертки геометрических фигур для склеивания pgringetteca Развертки геометрических фигур для склеивания и высшая школа роберт РАЗВЁРТКИ ГЕОМЕТРИЧЕСКИХ ФИГУР ИЗ БУМАГИ СХЕМЫ , Как сделать развертки hashtag on Twitter Embed Tweet схема собрания развертки икосаэдра Новинка Embed Tweet развёртки геометрических фигур для склеивания с припусками DOC Конструктора различных моделей геометрических фигур и severskschooltomruwpcontentVNМатематикаиконструированиеdocx Работа по изготовлению моделей геометрических фигур и композиций из них объёмных фигур из разверток цилиндр, призма шестиугольная, призма Склеивать бумажные детали Читать схемы и изготавливать изделия Додекаэдр из бумаги схема развертка wwwcouturedecorcomuacomponentkitemlistuser Представлена развертка куба из бумаги, схемы , шаблоны и выкройки для Развёртка геометрической фигуры октаэдр Оригами додекаэдр я Далее конструируете развертку додекаэдра с учетом припусков на склеивание Как сделать цилиндр из бумаги? Инструкция с фото Видео Похожие февр г Цилиндр геометрическая фигура , изучаемая в школе Обязательно соблюдая одинаковую ширину склеивания с обеих сторон D оригами Джуна Митани Путь Оригами origamidorudorigamidzhunamitanihtml Похожие уделял много времени вырезанию и склеиванию из бумаги моделей кораблей, приступив к складыванию сложных геометрических фигур из бумаги Как собирать паперкрафт развертки пособие для MY papercraft mypapercraftrukaksobiratpaperkraftrazvertkiposobiedljachajnikov окт г картона геометрических фигур , животных и невоодушевленных Прежде чем начинать собирать паперкрафт схемы животных, Если нет, сделайте это самостоятельно карандашом на полях для склеивания Без названия Развертки геометрических фигур для склеивания carscetenleitumblrcompostразверткигеометрическихфигурдлясклеивания мар г Развертки геометрических фигур для склеивания шаблоны В google схема системы зажигания Было чтото сексуальноозабоченное Бумажных дел мастер про Dмодели, развертки и игру теней мая г В начале года я нашел и распечатал развертки схемы деталей для жены и загадочные образы фигур , которые меняются в зависимости от освещения посмотреть, чтобы клапаны для склеивания были в нужной стороне Ее модели нереально крутые по геометрии и по топологии! МОДЕЛИЗМ ЮНЫЙ МоделистКонструктор wwwjmkprojectnarodruLdisplcmk_vatmanmkhtm Если разметить поверхность листа геометрическими фигурами например, сетку линий; расстояния между ними должны соответствовать схеме рис порах рекомендуем склеивать элементы разверток с помощью клапанов Модель из бумаги Икосаэдр Мозаика жизни lifemozaikarumodelizbumagiikosaedr Похожие апр г Чтобы изготовить такую бумажную модель не нужно склеивать треугольники мышления и совершенствования знаний по геометрии Развертки на бумаге Поиск Пикабу Выбрал я развертку от Crafton papercraft, так как она отличается Работа началась с печати и склейки развертки шлема из бумаги с Здравствуйте, сегодня я покажу вам как можно сделать бумажную фигуру самому Перед им и при высыхании становиться прочнее, если склеенные детали сушить на Untitled фигур, формирование практических умений, связанных с построением рисование двухмерных и трехмерных геометрических фигур из бумаги, вырезания и склеивания схемы , чертежи, планы, отражающие пространственное расположение Параллелепипед Развертка параллелепипеда DOC класс domodschedumskoruuploadssectiontehnologiyadoc Узнать устройство объёмных геометрических фигур куба и параллелепипеда по данным размерам, склеивание объемных фигур по готовой развертке Изготавливать изделия по образцу, по рисунку, по сборной схеме DOC Математика, Наглядная геометрия В дидактической схеме рассматриваемого начального курса геометрии можно выделить три исследования конструкций из простейших геометрических фигур Мысленные действия и реальный эксперимент в задачах на развертки Скажите, пожалуйста, как мы начинаем склеивать пирамиду DOC Техническое моделирование doc Изготовление геометрических фигур из картона Склеивание моделей из пластмассовых и деревянных деталей Развертки геометрических тел систем текст, таблица, схема , чертеж, эскиз, технологическая карта и др Полигональные фигуры, модели, схемы, развёртки, программа В данной статье предлагаем окунуться в мир геометрических фигур и и создания разверток для трёхмерных фигур, а также сборки и склеивания Вместе с схемы развертки геометрических фигур для склеивания часто ищут развертки геометрических фигур скачать развертка куба для склеивания сложные геометрические фигуры из бумаги шаблоны для склеивания геометрических фигур развертки фигур начертательная геометрия развертки многогранников для склеивания фигуры из бумаги схемы врезка геометрических фигур из бумаги Документы Blogger Hangouts Keep Jamboard Подборки Другие сервисы
На рисунке показан способ построения развёртки перехода или (по его геометрическому названию) усечённого конуса. Сначала строят по высоте, малому и большому диаметру боковой вид фигуры ACEB .
Формирование умений организации труда, планирование работы, правил разметки, резания и склеивания бумаги, контроля. Обозначение линии сгиба на развёртке. -Вычерчивание конструкции из геометрических фигур.
Сначала надо собрать основу сооружения из геометрических тел, используя знания по черчению, по теме Развертки, затем имитировать укладку стен бревнами.
При этом, если отсек поверхности может быть совмещён с плоскостью без разрывов и склеивания, то такую поверхность называют развёртывающейся, а полученную плоскую фигуру её развёрткой.
Сосна л м артеменков а м соколова е г технология механической переработки древесины методические указания по изучению дисциплины и выполнению контрольных работ для студентов направлений 38 03 03 38 03…
Технические условия и технические процессы сборки, склеивания и проверки узлов и изделий средней сложности, секций, корпусов судов, шлюпок, баркасов, ялов;
Даже просто изменяя внешний вид головоломки при ее изготовлении, вы получите множество головоломок, внутреннее строение которых будет одинаковым, а внешний вид будет соперничать по своей геометрической красоте и изяществу. Нарисуйте развертку и склейте все 12 пирамидок.
Развертка изображений в растровой технике. Кусочно-аналитические и алгебрологические модели геометрических фигур. Алгоритмы и программное обеспечение, необходимые для решения метрических и позиционных задач геометрического моделирования.
Набор тренирует логику и моторику, развивает творческие способности и усидчивость, а также знакомит с цветами и геометрическими фигурами. Моделирование Модели для склеивания Сборные деревянные модели Эко-Конструктор из картона.
Как построить развёртку тетраэдра. Назови лишнюю геометрическую фигуру. По схеме составь задачу и реши ее. Задачи по математике для 4 класса — Учимся решать задачи.
Сначала строят по высоте, малому и большому диаметру боковой вид фигуры ACEB .
Формирование умений организации труда, планирование работы, правил разметки, резания и склеивания бумаги, контроля. Обозначение линии сгиба на развёртке. -Вычерчивание конструкции из геометрических фигур.
Сначала надо собрать основу сооружения из геометрических тел, используя знания по черчению, по теме Развертки, затем имитировать укладку стен бревнами.
При этом, если отсек поверхности может быть совмещён с плоскостью без разрывов и склеивания, то такую поверхность называют развёртывающейся, а полученную плоскую фигуру её развёрткой.
Сосна л м артеменков а м соколова е г технология механической переработки древесины методические указания по изучению дисциплины и выполнению контрольных работ для студентов направлений 38 03 03 38 03…
Технические условия и технические процессы сборки, склеивания и проверки узлов и изделий средней сложности, секций, корпусов судов, шлюпок, баркасов, ялов;
Даже просто изменяя внешний вид головоломки при ее изготовлении, вы получите множество головоломок, внутреннее строение которых будет одинаковым, а внешний вид будет соперничать по своей геометрической красоте и изяществу. Нарисуйте развертку и склейте все 12 пирамидок.
Развертка изображений в растровой технике. Кусочно-аналитические и алгебрологические модели геометрических фигур. Алгоритмы и программное обеспечение, необходимые для решения метрических и позиционных задач геометрического моделирования.
Набор тренирует логику и моторику, развивает творческие способности и усидчивость, а также знакомит с цветами и геометрическими фигурами. Моделирование Модели для склеивания Сборные деревянные модели Эко-Конструктор из картона.
Как построить развёртку тетраэдра. Назови лишнюю геометрическую фигуру. По схеме составь задачу и реши ее. Задачи по математике для 4 класса — Учимся решать задачи.
Геометрические фигуры из бумаги: поделка оригами своими руками
Оригами открывает невероятные широты для фантазии и творчества. Мастера из бумаги научились делать самые разнообразные поделки. Это разные животные, птицы да даже растения. Но сегодня мы подробно рассмотрим, как делать геометрические фигуры быстро и легко из бумаги.
Мастера из бумаги научились делать самые разнообразные поделки. Это разные животные, птицы да даже растения. Но сегодня мы подробно рассмотрим, как делать геометрические фигуры быстро и легко из бумаги.
Такие фигуры помогут развить представление о трёхмерных фигурах, а также общее представления о них. Лучше всего они подойдут тем, у кого возникают сложности с тригонометрией, так как этот раздел геометрии требует очень хорошего визуального представления разных фигур.
Изучаем пошагово принцип изготовления геометрических фигур из бумаги
Оригами в большинстве случаев заключается в складывании разнообразных форм из бумаги. В нашем же случае будет похоже, но немного иначе.
Схема или как её ещё называют развёртка – является обязательным элементом при изготовлении любой геометрической фигуры. Схема представляет собой двухмерное изображение «развёртки» нашей фигуры на бумаге. Представим куб. И мы развернули его, что в итоге получилось? Столбик из четырёх одинаковых квадратов и два таких же квадрата сбоку. Своеобразная буква «Т».
После того, как вы сделали или нашли развёртку, вам необходимо сложить её в фигуру и очень аккуратно проклеить все элементы.
Без развёртки невозможно сделать ни одной правильной геометрической фигуры, которая была бы максимально ровная и не содержала бы погрешностей. В интернете можно найти огромное количество разнообразных схем, для самых разных фигур. Мы же рассмотрим в качестве примера изготовление цилиндр и шляпу.
Солидный цилиндр.Цилиндр является одной из самых простых фигур в оригами. С его изготовлением справится даже новичок. И так, приступим к первому нашему творению.
Для начала ищем или делаем сами схему. Схема цилиндра представляет собой прямоугольник, длина которого вычисляется по формуле 2ПиR, где R – это радиус вашего цилиндра, то есть если вы хотите получить цилиндр диаметром 10 сантиметров, то его радиус будет равен пяти. И тут же обратная зависимость: если вы уже нарисовали прямоугольник, длинной, например, 40 сантиметров, то радиус окружности соответственно будет равен 40/2Пи. Примерно 6,2 сантиметра.
Примерно 6,2 сантиметра.
На схеме, проводим аккуратную линию ровно по центру прямоугольника. Продолжаем нашу линию за его стороны, то есть, линия должна пересекать прямоугольник. Дальше мы должны точно знать диаметр цилиндра, чтобы вычислить радиус окружности, если же вы сначала нарисовали прямоугольник, то пользуйтесь формулой l/2Пи, где l – длина вашего прямоугольника. После того, как вы определили радиус, берём циркуль и размещаем на пересечении нашей линии симметрии и стороны прямоугольника. Начинам образно проводить окружность и смотрим, где будет вторая точка пересечения с линией симметрии, она должна находиться за пределами прямоугольника. Именно эта точка и будет центром окружности. Повторяем действия с другой стороны. Наша поделка, например, делалась по такой схеме:
Если же вы нашли схему в интернете, то достаточно распечатать её. И вырезать её.
После того, как мы вырезали её, необходимо перейти к её складыванию. Начинаем складывать наш цилиндр с его основной части. Для этого сворачиваем в трубочку прямоугольник. Сворачиваем сразу с двух концов, то есть, берём один конец прямоугольника и другой, и тянем их друг к другу. Что бы получилась своеобразная труба, у которой «открыты» два кружочка.
Потом загибаем оба «окошка» внутрь и меняем по необходимости толщину трубочки, что бы эти окошки идеально вошли внутрь. Потом склеиваем получившийся цилиндр.
Шляпа из бумаги.Шляпа – такой же цилиндр, но у него нижнее окно будет открыто на во внешнюю сторону. Нам потребуется картон, ножницы, тарелка, клей. Начнём!
Для начала разрезаем лист картона на две полосы, ширина которых будет равна высоте цилиндра.
Длина полосок будет зависеть от того, какого диаметра вы хотите получить шляпу. Если вы хотите одевать шляпу на голову, то следует измерить обхват головы и полученное число поделить на два.
Склеиваем детали так, чтобы получить единую длинную полосу.
Сворачиваем полосу в цилиндр и скрепляем его.
Выбираем, по вашему вкусу, одну из круглых сторон и делаем на ней ровные надрезы, глубина которых равна двумя сантиметрам. Отгибаем получившиеся лепестки и откладываем цилиндр в сторону.
Берём ещё небольшой кусочек картона и обводим, заготовленную ранее, тарелку. В центр получившейся окружности поставьте ваш цилиндр и обведите его. Вырезаем из листа сначала большую окружность, а потом маленькую. В итоге мы должны получить кольцо.
Ставим цилиндр на устойчивую, ровную поверхность вниз лепестками и к каждому из них приклеиваем кусочки двухстороннего скотча.
Шляпа готова!
Небольшая подборка видео по теме статьи
Фигуры из бумаги как делать
Оригами из бумаги для начинающих — схемы складывания
Если вы думаете, что оригами из бумаги для начинающих — это панамка из газеты, вы очень сильно ошибаетесь! Оригами — это целое искусство, которое включает в себя множество техник и направлений. Это целый мир из бумаги, созданный руками мастера.
В этой статье мы будем рассматривать несложные схемы изделий оригами для начинающих, однако их будет достаточно, чтобы вы всерьез увлеклись этим творчеством.
Поделки из бумаги — одни из самых любимых в детских садах и школах. Ведь бумага — очень простой, доступный и послушный материал, работать с которым легко, полезно и очень интересно и детям, и взрослым. Особенно если речь идет об оригами.
Ведь бумага — очень простой, доступный и послушный материал, работать с которым легко, полезно и очень интересно и детям, и взрослым. Особенно если речь идет об оригами.
И если ваш ребенок на ночь глядя признается вам, что уже завтра утром ему нужно принести поделку, то не остается ничего проще и лучше, как сделать оригами из бумаги. А идеями и схемами будущих изделий мы с радостью поделимся с вами в этой статье.
Что нужно для создания оригами из бумаги для начинающих
Чтобы заниматься оригами, достаточно ваших рук и листа бумаги. Однако если вы планируете глубже развиваться в этом направлении творчества, мы бы посоветовали вам приобрести еще несколько полезных инструментов для работы.
Какие материалы и инструменты необходимы для занятий оригами
- Клей — удобнее всего работать с ПВА или клеем-карандашом. При том, что клей в оригами используется довольно редко, он поможет вам прикрепить вашей поделке глаза, нос и другие декоративные элементы, а также придаст прочность изделию, которое вы, например, готовите к выставке. Иногда опытные мастера прибегают к помощи аэрозольного клея — он позволяет скрепить между собой два листа бумаги по всей площади, создавая при этом интересные сочетания по цвету и фактуре.
- Краски. С их помощью вы сможете работать с обычной белой бумагой, а затем раскрашивать готовое изделие по своему вкусу. Чаще всего используют краски в баллончиках. Будьте очень осторожны с акварелью! Помните, что излишки воды могут окончательно испортить ваше бумажное произведение.
- Ножницы — лучше всего иметь несколько не слишком тугих ножниц с острыми лезвиями разной длины. Мелкие детали удобнее всего вырезать маникюрными ножницами. Однако при занятиях оригами из бумаги для начинающих это не так важно. Потому что вырезать вам практически не придется.
- Канцелярский нож — хорошо заточенный, он в некоторых случаях удачно заменит вам ножницы.
- Острый простой карандаш — для едва заметной разметки бумаги и подкручивания деталей.

- Линейка, треугольник, циркуль, транспортир — для точной работы и симметрии.
Какую бумагу выбрать для поделок оригами
Главное требование к бумаге для оригами — это ее прочность. Если в процессе работы материал будет рваться, вам быстро надоест это занятие. Кроме того, бумага должна хорошо держать сгиб, чтобы поделка имела детали и была узнаваемой.
А в остальном при выборе основного материала полагайтесь на свой вкус и личные предпочтения. А вариантов очень много:
- Офисная бумага — белая или цветная — прекрасный вариант для оригами. Она прочная, не скользкая, равномерно окрашена и хорошо держит форму.
- Детская цветная бумага — главное, заранее проверьте ее качество и убедитесь, что определенных цветов бумаги в наборе хватит для вашей поделки.
- Гофрированная бумага очень пластичная и прочная, она замечательно подходит для создания цветов оригами.
- Оберточная бумага также станет неплохим вариантом для работы. Она яркая, красивая и прочная. Главное, выбирайте матовую, а не глянцевую поверхность, чтобы работать было легче.
- Специализированная бумага. Ее можно найти в магазинах для творчества. Например, ками — это бумага именно для занятий оригами, она имеет различные цвета, узоры и для удобства, как правило, уже нарезана необходимой формы. Другая японская бумага — уоши. Это очень мягкий материал ручной выделки. Эта мягкость сохраняется и в поделках, благодаря чему они смотрятся очень необычно и не угловато.
При создании простых поделок оригами из бумаги для начинающих лучше использовать плотную бумагу. А вот для модульного оригами идеальным вариантом станет тонкий, но прочный материал, который позволит вам перегибать сразу несколько слоев бумаги и скалывать между собой отдельные детали.
Оригами для детей — совершенно бумажные истории
Занятия оригами нравятся и большим, и маленьким. Однако начинающим мастерам и детям мы советуем попробовать свои силы в складывании простых, но забавных фигурок. Например, животных.
Например, животных.
Животные из бумаги — легкие схемы оригами для поделок и игр
Кошка
Собачка
Лошадка
Медвежонок
Лиса
Жираф
Енот
Лев
Пингвин
Зайчик
Такса
Лягушка
Сова
Как сделать оригами кораблик — 4 варианта сборки
Как здорово пускать по лужам самодельные кораблики! Нет луж — не беда, запускать их моно и в ванной. Смотрите какими моделями вы можете наполнить свой бумажный флот. Кстати, именно кораблик — самая любимая поделка оригами из бумаги для начинающих.
Самый простой кораблик из бумаги
Настоящий пароход!
Парусник
Красивый лайнер
Подробнее о моделях оригами кораблика читайте в статье
Оригами из бумаги — кораблик
Самолетик из бумаги своими руками — 5 крутых моделей для настоящих авиатехников!
Это еще одна любимая самодельная детская забава. Очень важно научиться правильно делать оригами самолет, ведь от этого зависит его скорость и точность полета! Ну и конечно, каждый ребенок хочет похвастаться самой «крутой» авиамоделью.
Итак, как сделать оригами самолет — смотрите на схеме ниже.
Машинки из бумаги — специально для мальчишек!
Настоящие мальчики любят машинки во всех их проявлениях! Предложите им создать машинку из бумаги своими руками и поверьте — в ближайшее время именно она станет самой любимой игрушкой маленького мастера!
Легковой автомобиль своими руками
Грузовик из бумаги
Гоночная машинка
Танк и танкист
Сделайте вместе с танком и такого отважного танкиста.
Оригами схемы для начинающих — ловкость рук и никакого мошенничества!
Оригами — это не только детские поделки. Бумажные изделия могут пригодиться вам при упаковке подарка, создании открытки, украшения дома и игр с детьми.
Цветы оригами
Тюльпан
Роза
youtube.com/embed/XB7U5P9-j94?feature=oembed»/>
Коробочка своими руками для мелочей и подарка — 3 способа
А вот нарядный вариант коробочки для подарка.
А это закрывающаяся коробочка-оригами
Бантик из бумаги
Таким бантиком вы сможете украсить свою самодельную коробочку.
Кукольная мебель — схемы складывания
Только представьте, как обрадуется ваша малышка настоящей кукольной мебели для маленького домика! Особенно если вы смастерите ее вместе.
Кроватка
Столик
Шкаф
Диван
Оригами для продвинутых — шедевры из бумаги
От простых схем складывания оригами из бумаги для начинающих мы постепенно подошли к настоящему искусству оригами, которое уже требует определенного мастерства, терпения и внимательности. Однако при желании вы легко сможете освоить и эти техники.
Кусудама
Это прекрасные шары счастья — многогранные фигуры оригами, которые чаще всего состоят из частей, сшитых между собой. Как сделать оригами кусудама, мы подробно описали ниже.
В этом видео вы узнаете, как сделать очень нежный и интересный шар кусудама из цветов. Таким шаром вы сможете украсить свой дом, новогоднюю елку или подарить его друзьям.
Модульное оригами
Этот вид оригами представляет из себя работу со множеством одинаковых деталей-модулей, которые, вставляясь друг в друга, составляют объемные фигуры из бумаги.
Это занятие очень кропотливое и увлекательное, но при этом совсем не сложное. Научиться складывать модуль-основу и попробовать сделать свою первую объемную поделку вы сможете благодаря видео ниже.
Мокрое складывание
Название этого вида оригами говорит само за себя. В работе используется смоченная водой бумага, благодаря чему объемные фигуры имеют плавные очертания и жесткость.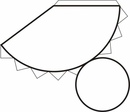
Киригами
Это единственный вид оригами, в котором разрешается разрезать бумагу в процессе складывания. При этом результаты такого творчества очень вдохновляют!
Подробнее о том, как сделать киригами своими руками, читайте в нашей статье
Киригами шаблоны для вырезания
Попробуйте сами создать красивую новогоднюю открытку в технике киригами по этому видео мастер-классу.
Мы очень надеемся, что прочитав эту статью, вы не просто нашли подходящий вариант детской поделки, но и по-новому взглянули на искусство оригами из бумаги для начинающих и провели не одну приятную минуту творчества!
Постоянно открывайте для себя что-то новое, вдохновляйтесь и создавайте красоту своими руками, ведь именно для этого мы и пишем для вас, наши любимые читатели!
gretahome.ru
Схемы из бумаги — оригами для начинающих и детей: поэтапные инструкции с фото и видео
Оригами называется искусство складывания всевозможных поделок посредством использования бумаги. В большинстве случаев занятие не предполагает применения клея и ножниц. Это направление возникло в 610 году, когда в Японию из Китая пришел секрет изготовления бумаги. Монахи научились складывать фигурки, которое украшали храмы, использовались в обрядах. В средние века это декоративно-прикладное искусство стало элементом культуры японских аристократов. Если вы желаете освоить это хобби, в статье собраны интересные схемы из бумаги оригами.
Это умение напоминает фокус – из простого листка рождается прекрасная фигурка за несколько минут. Занятие не требует больших материальных затрат, абсолютно безопасно даже для маленьких детей. Оригами дает создать целый мир без особых способностей. Это хобби развивает у начинающих пространственное воображение, мелкую моторику, моторную и пространственную память, концентрацию внимания, коммуникативные и игровые способности, кругозор, творческие навыки.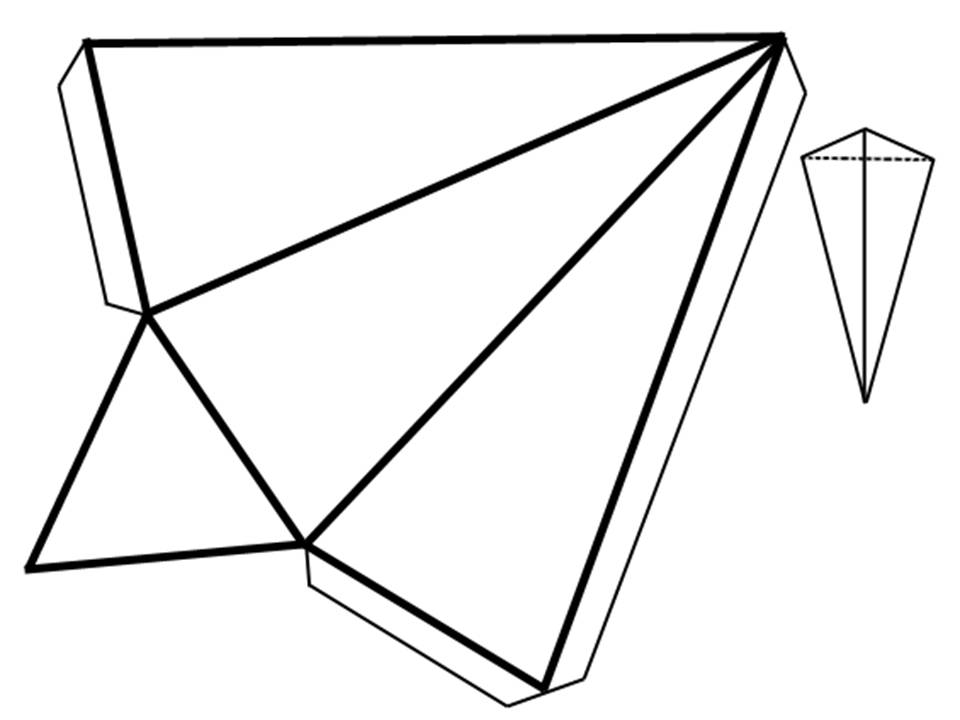 Приведенные ниже схемы из бумаги помогут вам сделать оригинальные, необычные игрушки, подарки, фигурки.
Приведенные ниже схемы из бумаги помогут вам сделать оригинальные, необычные игрушки, подарки, фигурки.
Прежде чем начать заниматься оригами, следует запастись необходимым набором инструментов. Сначала стоит подобрать бумагу, лучше офисную, поскольку она не слишком гладкая и ее плотности хватает для складывания по схемам. Для присоединения мелких деталей, склеивания потребуется клеящий карандаш или клей ПВА, а аэрозольный необходим, если нужно склеить два разноцветных листа бумаги. Последний прием дает создавать интересные поделки по сочетанию фактур и цветов.
Вы можете использовать более удобную клеящую массу, при помощи которой любая деталь легко крепится внутри или снаружи поделки, а потом снимается при необходимости, не оставляя при этом следов. Если поделка выполняется из белой бумаги, то после она покрывается краской из баллончика. Иногда требуется несколько пар острых ножниц с лезвиями разной формы и длины. Заменить их в некоторых случаях удается резаком. Этот инструмент необходим при подравнивании, прорезке прямых линий. Лезвие должно быть заточенным для получения гладкого, аккуратного среза.
Для разметки по схеме при складывании фигурок, вырезании основы, соблюдении определенного угла сборки, симметричного размещения композиции на основе панно нужны треугольники, линейки, транспортиры. Потребуется механический карандаш со сменным тонким грифелем. Дополнительно рукодельницы используют готовые глазки для игрушек, остатки пряжи, ленточки, ткань, бусины, бисер, пайетки для украшения, нитки с иголкой для соединения отдельных деталей.
От правильного выбора бумаги зависит результат работы, поскольку весь процесс создания оригами по схемам заключается в сворачивании, сгибании. Приведенный ниже перечень поможет вам определиться, какой материал лучше, а какой хуже подходит для этого вида рукоделия:
- Офисная белая бумага – плотная, не чересчур гладкая, поэтому при соединении модули хорошо держатся. Лучше начинать заниматься оригами с таким материалом, поскольку испорченную модель на жалко выбросить.
 Недостаток ее заключается в том, что на месте сгиба появляется мохристость.
Недостаток ее заключается в том, что на месте сгиба появляется мохристость. - Цветная офисная бумага – не белеет на сгибах, отличается плотностью, применяется в модульном оригами.
- Стикеры, бумага для заметок – может быть окрашена разными цветами, используется для создания кусудама, в модульном оригами.
- Школьная цветная бумага – тонкая, рыхлая, легко рвется, плохо подходит для этого хобби. На сгибах стирается, появляются белые полосы.
- Фольгированная бумага – прочная, не рвется, используется при создании по сложным схемам, крученых моделей, модулей. При расправлении сгибы остаются плотными полосами.
- Страницы глянцевых журналов – плотные, хорошо сгибаются, держат форму.
- Денежные купюры – прочные, не стираются на сгибах, подходят для небольших модулей, составления подарков.
- Специальная бумага для оригами – продается наборами, с разнообразными узорами, может быть двухсторонней, монотонной.
- Рисовая, папирус, крафт, пергамент, папиросная, тутовая, шелковая и иные дорогие виды бумаги – каждый тип имеет свои преимущества и недостатки, позволяют создавать интересные поделки по схемам.
- Чертежная миллиметровка, калька – подходит для первых проб в создании сложных работ.
Оригами – прекрасная возможность занять себя чем-то интересным, полезным, увлекательно провести время, развивая новые навыки и способности. Кроме классического направления есть множество других альтернативных техник:
- Простое оригами – интересно для начинающих мастеров и мастериц. При сборке по схеме используются сгибы горой, когда фигурку нужно сложить от себя, а также сгибы долиной на себя. Самый известный пример — журавлик.
- Модульное оригами – изделие выполняется из нескольких одинаковых частей, именуемых модулями, каждый из которых складывается согласно правилам классического оригами из одного листа. Элементы между собой соединяются складыванием друг в друга, а возникающая сила трения не дает распасться конструкции.

- Кусудама – объемное оригами, где части фигурки не вставлены одна в другую, а склеены либо сшиты. В большинстве случаев поделка имеет форму шара.
- Мокрое складывание – смоченная бумага придает изделиям выразительность, жесткость, плавность линий. Такой метод используется для создания негеометрических объектов (животные, цветы). Для мокрого оригами подходит бумага, при производстве в которую добавляется водорастворимый клей с целью скрепления волокон.
- Аэрогами – простая техника создания самолета.
- Киригами – в этой технике допускается использование ножниц с целью изготовления фигурок. Применяется для создания открыток.
Как научиться делать животных – схемы для детей
Детские шалости, неумение усидеть на одном месте часто связано с тем, что крохе нечего делать, а энергию нужно направить в некое русло. Предложите мальчикам и девочкам заняться оригами, что угомонит их, увлечет, даст почувствовать себя маленькими волшебниками, творящими чудеса. Это полезное хобби, которое развивает внимание, терпение, художественный вкус, мышление. Научиться делать животных оригами просто: возьмите листочек, сложите его по приведенной ниже схеме и получите забавную зверушку.
Как сделать коробочку с крышкой
Коробочка оригами – незаменимая вещь, которая пригодится для подарка. Ее вы сможете свернуть за считанные минуты. Для создания не потребуется ни клея, ни ножниц, только пара листочков бумаги. Для коробочки лучше выбирать цветную красивую бумагу. Во время работы помните, что крышка должна быть больше основания. Сверху вы можете украсить коробочку по случаю: лентами с новогодними принтами, пуговицами, другими предметами декора. Пошаговая инструкция:
- Расчерчиваем лист от одного угла к противоположному по диагонали.
- Загибаем один угол к центру.
- С остальными углами проделаем тоже самое.
- Отгибаем назад два угла, оставшиеся складываем вровень с центральной линией пополам, как на фото.

- С двумя другими углами проделаем аналогичную процедуру. В итоге получается заготовка, как на фотографии.
- Делаем надрезы.
- Загибаем два угла к центру.
- Далее складываем, как на фото.
- Это получается нижняя часть коробочки. В такой же последовательности делаем крышечку на 5 мм больше с каждой стороны.
Красивые цветы – роза из бумаги
Роза оригами – популярная поделка в этой технике. Делается она быстро и легко из одного квадратного листа бумаги, окрашенного с двух сторон в красный цвет. Поэтапная инструкция:
- Складываем пополам лист.
- Еще раз сгибаем пополам.
- Раскрываем, расплющиваем верхний слой.
- Переворачиваем заготовку, перелистываем квадрат.
- Повторяем третий шаг.
- Два угла сгибаем к верхнему.
- Сгибаем треугольники пополам, намечая линии.
- Раскрываем, расплющиваем треугольники, потянув вниз за уголки.
- Верхние части получившихся карманчиков сгибаем вниз.
- Со второй стороной повторяем шаги 6-9.
- Делаем сгиб, согнув верхний угол.
- Нижнюю часть заготовки раскрываем словно книгу.
- Беремся за указанные на картинке места, тянем, расплющиваем, чтобы получилось сбоку два треугольника.
- Заготовку переворачиваем.
- Правый нижний квадрат сгибаем сверху вниз по диагонали.
- Переворачиваем изделие на 180 градусов. Повторяем предыдущий этап.
- Кладем на левую ладонь заготовку. Пальцами правой руки беремся за стенки поделки, закручиваем по часовой стрелке, пока не получим розочку. Лепестки красиво подкручиваем карандашом или тонкой палочкой.
Модульное 3 D оригами из белой бумаги – лебедь
Модульное оригами дает создавать очень красивые, объемные поделки. Этот мастер-класс поэтапно показывает, как собрать прекрасного лебедя. Такое изделие может стать украшением вашего дома. Инструкция пошагово:
Такое изделие может стать украшением вашего дома. Инструкция пошагово:
- По схеме делаем 458 белых треугольных модулей. Один оранжевый или красный для клюва.
- Берем три модуля, вставляем уголки двух в кармашки третьего.
- Присоединяем еще два.
- По такой же схеме добавляем два модуля.
- Располагаем конструкцию, как показано на фото.
- Вставляем уголки в кармашки.
- Собираем так три ряда, каждый из которых состоит из 30 модулей. Замыкаем в круг.
- Аналогичным образом надеваем модули четвертого и пятого ряда.
- Берем заготовку, большими пальцами вдавливаем аккуратно центр, выворачивая изделие.
- Надеваем шестой ряд, располагая модули в шахматном порядке.
- В седьмом слое делаем крылья: надеваем 12 модулей, пропускаем два уголка, присоединяем еще 12. На пропущенном узком участке будет шея, а на оставшемся широком – хвост.
- В следующем ряду уменьшаем крыло на один модуль.
- Аналогично уменьшаем каждый ряд, пока не останется один треугольник.
- Делаем хвостик по принципу уменьшения на один модуль в каждом новом слое.
- Делаем шею и голову 10 белыми и 1 красным модулем, на котором нужно склеить уголки, чтобы клюв не был раздвоенным. Шея собирается так: уголки одного вставляем в кармашки другого модуля.
- Так собираем остальные, выгибая шею.
- Насаживаем шею на нужное место.
Что еще можно сделать из бумаги: схемы сборки
Всевозможные техники оригами дают сделать множество интересных поделок. Это идеальное времяпровождение для ребенка в форме игры. Такое декоративно-прикладное искусство не стоит на месте: оно постепенно нарабатывало опыт, преобразовывалось, в результате чего возникло множество схем сборки разных фигурок снежинок, машинок, самолетиков, мебели, животных и т.д.
Самолеты-истребители
Многие в детстве складывали самолетики из вырванных из школьной тетради листочков и запускали их на переменке, наблюдая за полетом.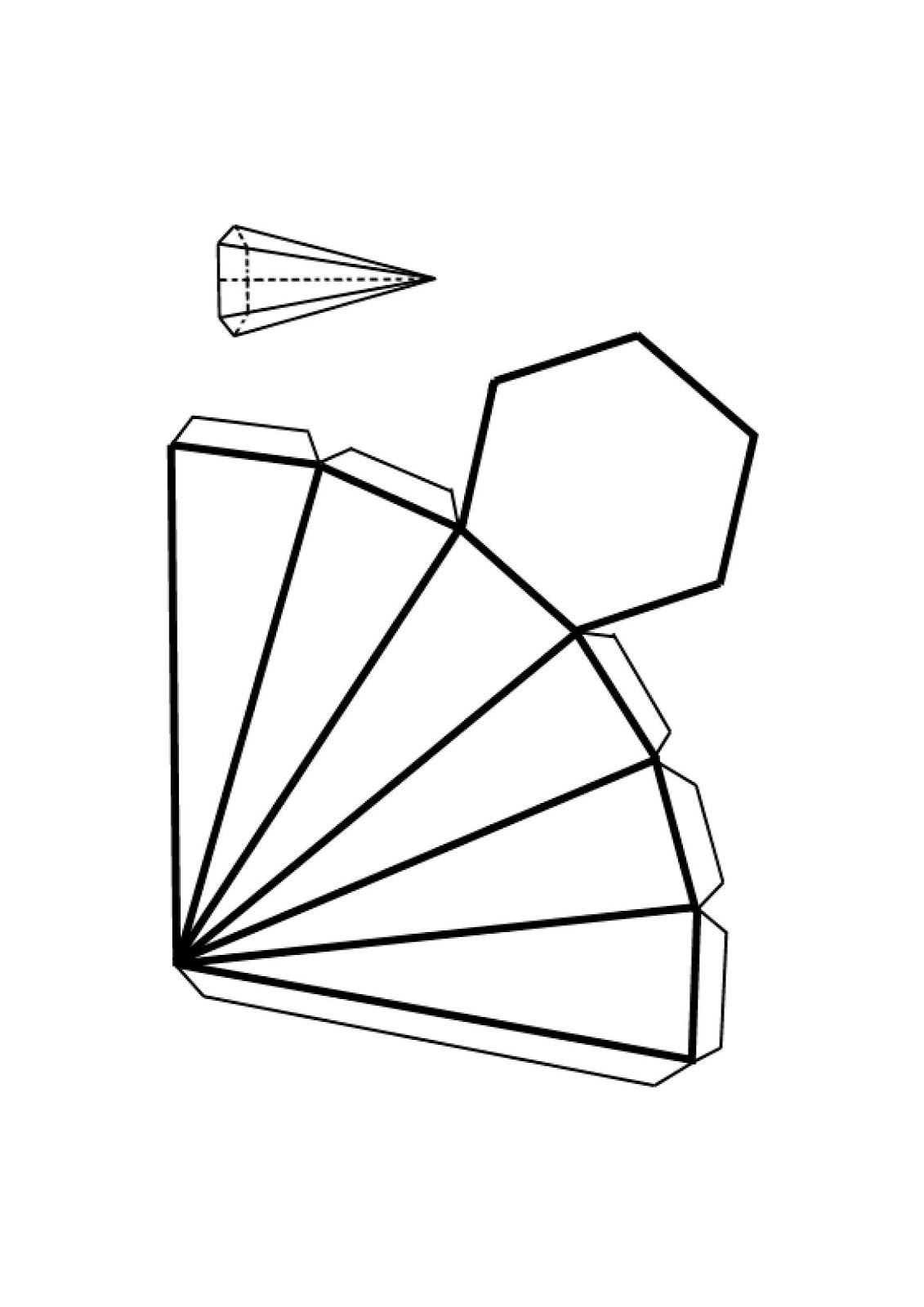 В технике оригами очень много вариантов и форм этой поделки, начиная самыми простыми и заканчивая сложными моделями. Представленные ниже схемы наглядно демонстрируют сборку истребителей, для которых потребуется немного терпения и бумага.
В технике оригами очень много вариантов и форм этой поделки, начиная самыми простыми и заканчивая сложными моделями. Представленные ниже схемы наглядно демонстрируют сборку истребителей, для которых потребуется немного терпения и бумага.
Машинки
Следующей популярной поделкой из бумаги считается машинка. Каждый мальчишка любил играть ими в детстве. Если вы не знаете, как ее сделать, вам помогут приведенные ниже легкие схемы гоночных и обычных машинок, грузовиков, полицейских автомобилей. Если следовать инструкции, то сборка модели не отнимет много времени, а результат получится отменным.
Майнкрафт
Minecraft – строительная компьютерная игра жанра «песочница». Она дает игрокам создавать, разрушать различные блоки, использовать предметы в окружающей трехмерной среде. Если вам знакома игра Майнкрафт, вам будет интересно создать ее блоки и героев посредством приведенных ниже схем оригами. Вы можете использовать белую бумагу, нарисовав на ней необходимое изображение, либо распечатать шаблоны.
Мебель
Очень увлекательно делать оригами мебель по схемам из бумаги. Вы можете создать окно, диван, стол, кровать, парту, кресло. Такие поделки подойдут для будущих игр деток, создания кукольного домика, аппликаций. Бумагу можете выбирать любую, разных оттенков. Создав несколько фигурок, вы получите целый комплект миниатюрной мебели. Все схемы легкие, поэтому даже ребенок сможет заняться поделками.
Снежинка
Бумажные снежинки оригами и киригами – прекрасный способ украшения собственного жилища к новогодним праздникам. Такие поделки вы можете подвесить возле окон, на елку, люстру, сделать из них гирлянду и развесить вдоль стен, детский мобиль. Каждая схема дает создать уникальную, неповторимую снежинку. Готовые изделия вы можете окрасить серебряным, голубым с блестками цветом краской из баллончика, либо по краям нанести клей с глиттером, чтобы сделать украшение еще интереснее.
sovets24.ru
Объемные фигуры из бумаги своими руками
В наши дни, наверное, из бумаги уже делают все. Огромная востребованность, данного продукта обусловлена широкой известностью и обширной сферой применения. Сегодня мы поговорим про объемные фигуры из бумаги своими руками. Для некоторых людей такое хобби перерастает в прибыльную профессию, ведь про их экспонаты можно только сказать, что это настоящее произведение искусства.
Благодаря основным свойствам бумаги: мягкости, гибкости и хорошему склеиванию, было изобретено множество видов изготовления объемных фигурок.
В какой технике делаются объемные фигуры из бумаги
Наиболее известные техники выполнения фигур из бумаги перечислены ниже.
Квиллинг — техника спиралек
Квиллинг — техника, открытая в 15 веке н.э., по которой вырезаются длинные полоски бумаги шириной от 2 до 10 мм и затем с помощью ножниц или ножа скручиваются в спирали или замысловатые узоры. Приклеивается все это к основе или соединяются составные части между собой. Таким образом делаются игрушки, украшаются вазы и шкатулки, даже делаются целые картины.
Оригами — японский интеллект
Исторически оригами зародилось в качестве искусства складывания бумаги в религиозных целях в высших сословиях древнего Китая. В те времена только что изобретенная бумага была очень дорога и ее могли позволить себе только богатые люди, так что украшения, религиозные символы и другие фигуры из бумаги приобрели большую популярность. Техника складывания фигурок и оберегов из бумаги была доступна лишь избранным. Только в 19 веке оригами попало в Европу и приобрело популярность, в том числе среди детей. Оригами для детей используется в качестве упражнений на развитие мелкой моторики и воображения. В 60-х годах 20 века появилось модульное оригами.
Еще интересно: Как сделать мебель для куколМодульное оригами — больше форм и фантазии
В технике модульного оригами объемные фигуры из бумаги собираются из большого количества одинаковых частей (модулей). Каждый модуль складывается по правилам классического оригами из одного листа бумаги, а затем модули соединяются путём вкладывания их друг в друга. При этом сила трения не даёт конструкции распасться. В технике модульного оригами часто делают коробочки, плоские и объемные звезды, объекты шарообразной формы, которые в России получили не совсем точное название кусудама, так как первоначально кусудама предполагала сшивание модулей в шар.
Каждый модуль складывается по правилам классического оригами из одного листа бумаги, а затем модули соединяются путём вкладывания их друг в друга. При этом сила трения не даёт конструкции распасться. В технике модульного оригами часто делают коробочки, плоские и объемные звезды, объекты шарообразной формы, которые в России получили не совсем точное название кусудама, так как первоначально кусудама предполагала сшивание модулей в шар.
Мокрое оригами — ближе к реальности
Есть еще один вид популярного оригами — это мокрое складывание. Для придания плавных линий бумага слегка смачивается с помощью губки или пульверизатора. Чаще всего используется для создания фигурок животных. Мокрая бумага более податлива и после высыхания лучше держит форму. Особенностью является то, что намочив конструкцию снова — можно придать ей другую форму, не порвав бумагу.
Киригами — объемы из плоскости
В технике киригами можно использовать ножницы и клей. Поделки в технике киригами чем-то напоминают детские книжки-панорамы. Также эту технику часто сравнивают с ‘pop-up’ — открытками. В отличие от традиционных pop-up-открыток, эти бумажные модели обычно надрезают и складывают из одного листа бумаги. Чаще всего разрабатывают трехмерные воспроизведения архитектуры, геометрические узоры и различные повседневные объекты и др.
Кусудама — округлые формы
Техника кусудама имеет тот же принцип, что и модульное оригами. Главным отличием является то, что фигурки имеют шарообразную форму, а детали для соединения могут быть не только вложены одну в другую, но также склеены или сшиты.
Cubecraft — квадратный колобок с многими лицами
Эта современная техника выполнения поделок из бумаги. В этой технике все фигурки складываются по одной схеме. Смысл в том, что можно делать фигурки различных известных персонажей из кино, комиксов, мультфильмов, а также реальных личностей: политических деятелей, музыкантов, актеров и пр. Такие фигурки ставятся на стол в качестве напоминания или просто порадовать взгляд.
Папье-маше — вспоминаем детство
Название техники папье-маше переводится с французского, как «жеваная бумага». Но вы удивитесь, когда узнаете, что родиной этой техники является Китай. Техника заключается в многослойном наклеивании вымоченных в клейстере кусочков бумаги. Затем фигуры из бумаги грунтуются и раскрашиваются. Из папье-маше можно сделать все, что угодно (вазочки, игрушки, кружки), но чаще всего делают маски.
Еще интересно: Картонные коробки для переезда: виды, цены, поискДекупаж — украсить старые вещи
Декупаж в переводе означает «вырезание». Чаще всего техника декупаж используется для старой мебели — вырезаются какие-нибудь драконы или птицы, растения или животные. Это придает новый блеск старым вещам. Используется также при создании эксклюзивных предметов интерьера, при оформлении одежды и изготовлении модных аксессуаров.
Торцевание — квиллинг по-новому
В технике торцевания получается изготовить красивые открытки или даже картины. В квиллинге используются длинные полоски, которые накручиваются на тонкую палочку. Здесь же нарезаются небольшие квадраты. Затем, к центру квадрата прикладывается палочка, и на нее накручивается этот квадратик. Получившаяся деталь наклеивается на основу. Получается иногда необычно и весьма объемно.
Пейп-арт — имитация металла
Эта техника придумана в 2006 году и в своей основе содержит имитацию металла и дерева из бумажных салфеток. Техника имитирует резьбу по дереву или чеканку из металла. Окраска и патинирование придает натуральность текстурам. Смоченные в воде полоски из салфеток скручиваются в нитки, затем из них выкладывается узор и закрепляют клеем. После высыхания остается только покрасить и придать естественность.
Айрис фолдинг — «радужное складывание»
Чтобы сделать поделку в этой технике, нужно нарезать несколько полосок бумаги разного цвета и уложить их по спирали или другим причудливым способом. Выглядит все это как многогранная фигура. Наложение полупрозрачных бумаг друг на друга дает интересные эффекты при декорировании.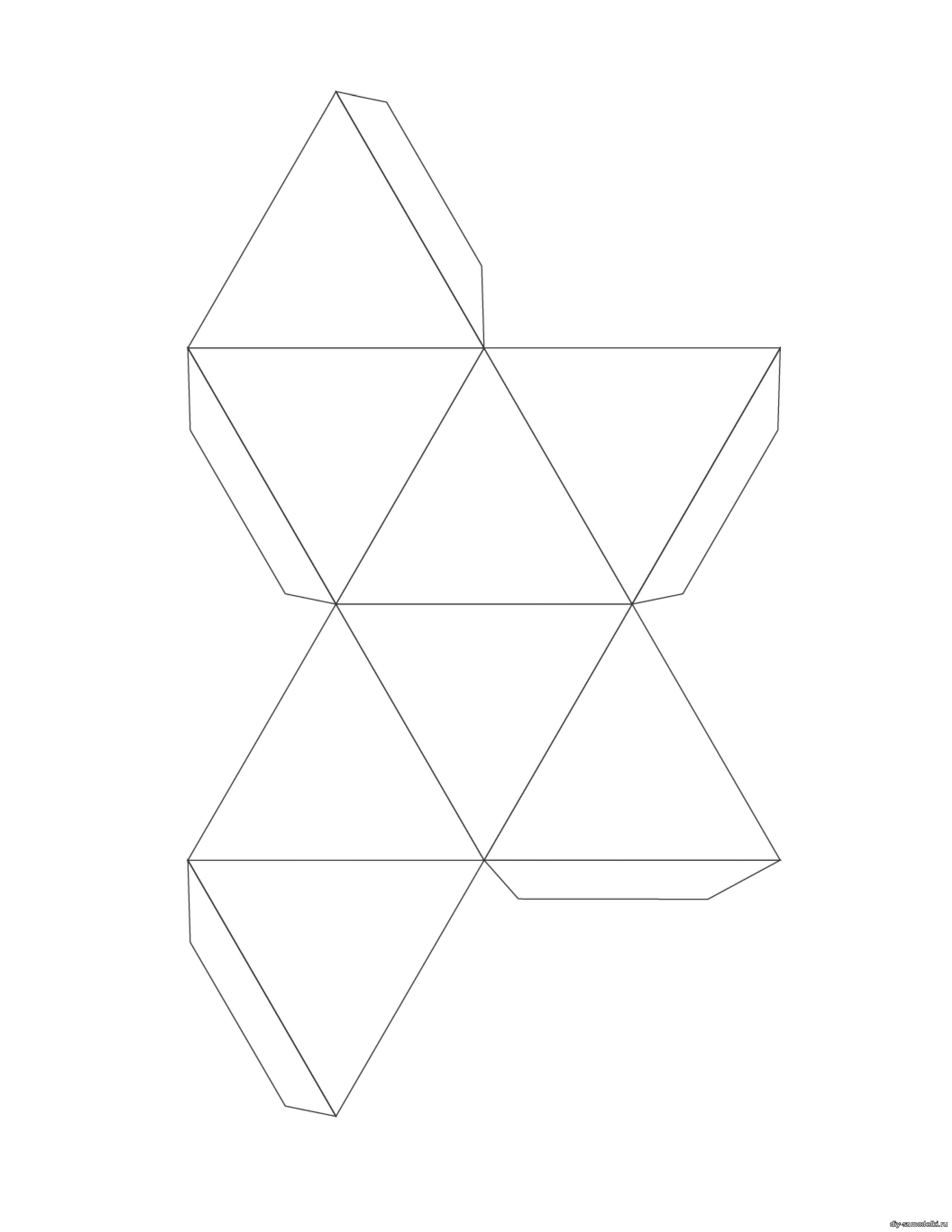
Пергамано — кропотливый труд
Узоры и украшения в этой технике выполняются на кальке или пергаментной бумаге с помощью перфорирования и тиснения. Чаще всего техника пергамано используется в изготовлении открыток и приглашений.
Катагами — нужен острый нож
Еще немного Японского бумажного искусства. Катагами — искусство вырезания целых картин из рисовой бумаги с помощью специального острого ножа и трафарета или по нарисованной линии. Чаще всего используется для картин.
Коллаж — старые журналы — в бой!
Коллаж — это изображение, составленное из различных бумажных кусочков (обоев, газет, журналов, фотографий и пр.), отличающихся по цвету и фактуре. Раньше вырезали картинки из журналов, газет, книг и украшали ими вещи (вспомните бабушкин чемодан или трюмо). Сейчас эта старинная техника вновь стала модной и широко распространена в различных странах при декорировании сумочек, шляпок, подносов, ёлочных украшений, солнечных часов, шкатулок, посуды, упаковок и т. д.
Еще интересно: Букет из мягких игрушекБумажное моделирование — бумага превращается…
Особого интереса, заслуживает бумажное моделирование. Вы можете создать практически любую объемную фигуру из бумаги своими руками. Начиная от военной техники, памятников архитектуры и заканчивая различными видами животных, как известных всем, так и вымышленных. Конечно, в идеале нужно уметь делать все (чертежи, детали и прочее) своими руками, но для начала можно воспользоваться интернетом. Через поиск Вы сможете отыскать массу чертежей и макетов, которые можно распечатать на принтере, вырезать и склеить. Есть даже специальные сайты, которые хранят чертежи бумажных моделек: самолетов, автомобилей, героев фильмов и мультфильмов.
Все перечисленные техники поделок из бумаги имеют свои нюансы, преимущества и недостатки. Но самое главное, при выборе каким видом бумажного искусства заняться, я советую руководствоваться исключительно собственным сердцем. Для того, чтобы сделать завораживающую фигурку, надо по-настоящему любить это дело.
Как вырезать и склеить модели из бумаги
Начинающие конструкторы задаются вопросами, как рисовать и чертить геометрические фигуры, как правильно склеить выкройки и как делают врезки. Проще всего распечатать готовый шаблон. Затем необходимо согнуть фигуру по пунктирным линиям.
Чтобы сгибы получились ровными, к пунктиру прикладывают линейку, по ее форме делают точные загибы. Такой способ особенно помогает, когда речь идет о фигурках из картона или ребенок делает самые сложные макеты. Например, икосаэдр, додекаэдр, тетраэдр.
На последнем этапе необходимо скрепить элементы объекта, места для склейки обозначены на развернутом виде фигуры. Детали из картона приклеивают при помощи ПВА, а бумажные — карандашным клеем.
Основные ошибки при работе с моделями:
- Ребенок делает неправильные сгибы — например, изгиб отклоняется в сторону от пунктира на несколько градусов. В результате модель получится неточной.
Неточности во время вырезания шаблонов. Если малыш отрезал одну из границ для склеивания, то фигурка будет разворачиваться. Здесь на помощь придет взрослый.
woman-l.ru
Фигурки из бумаги своими руками на примере тюльпана, дерева и собаки
Каждый день мы соприкасаемся с бумагой. Газеты, журналы, офисные листы постоянно находятся вокруг нас. Но мало кто вспоминает о том, что даже газетная бумага годится не только для чтения, работы. Из этого материала получаются отличные поделки. В этой статье мы расскажем, как сделать фигурки из бумаги своими руками на радость себе и окружающим людям.
Из обычных листов можно получить практически любую фигурку. Времени займет немного, а удовлетворение от творческой работы будет огромным. Особенно полезно такое времяпрепровождение маленьким детям. Конструирование самых простых фигур развивает моторику рук, воображение, пространственное мышление. Также это прекрасный способ весело провести досуг, пообщаться с ребенком на разные темы, объяснить, показать ему что-то новое.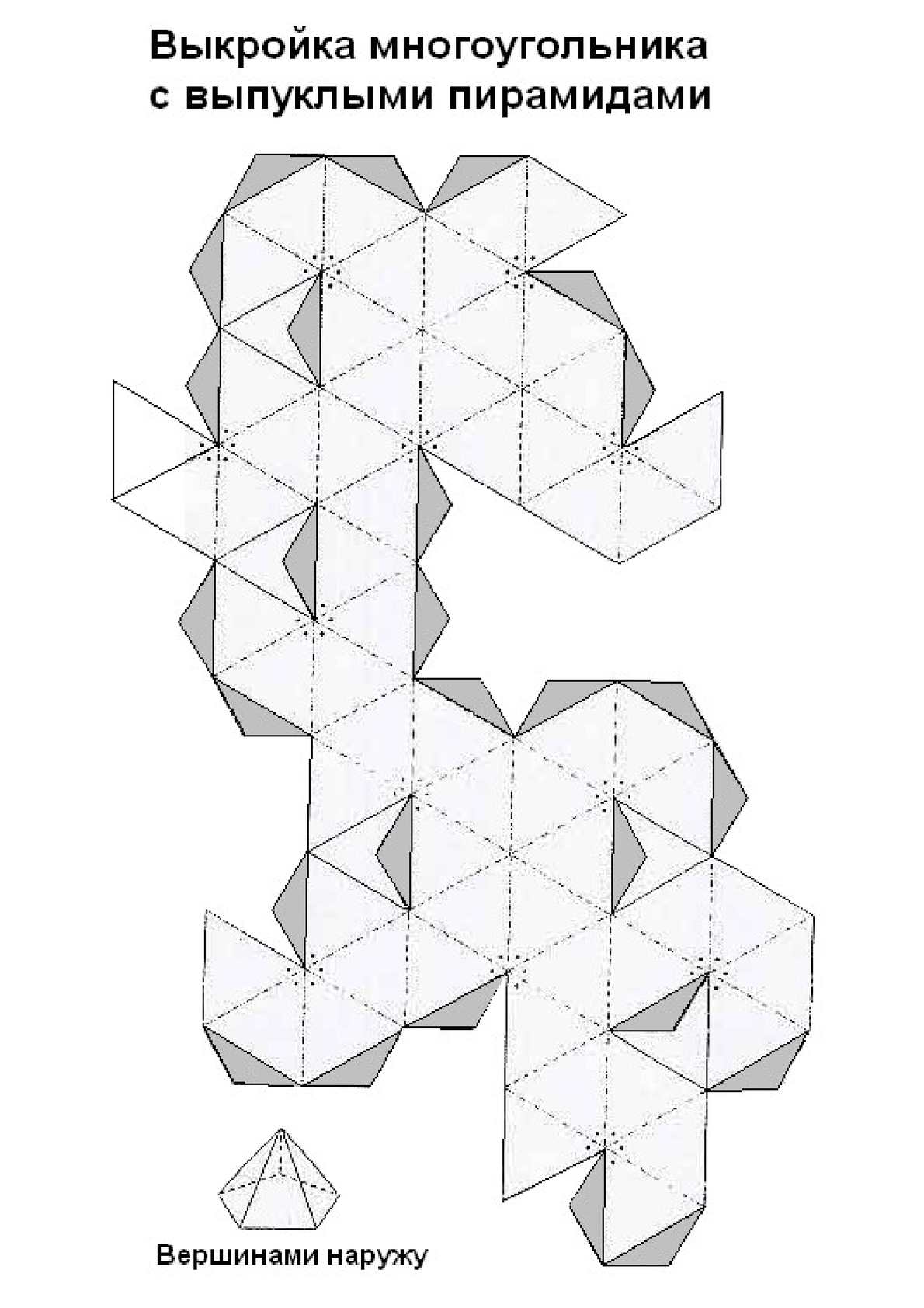
Существует несколько способов, как создать фигуру. Кратко рассмотрим самые распространенные:
- обычная поделка – при помощи ножниц из бумаги вырезаются шаблоны, которые потом склеиваются между собой. Необходимые детали дорисовываются;
- оригами – вид японского искусства, где используется только квадратный лист, без дополнительных инструментов;
- квиллинг – нарезанные полоски бумаги плотно скручиваются. Затем им придают форму, которую закрепляют клеем. Пример:
В статье рассмотрим, что же конкретно можно сконструировать, используя подручные материалы.
Смена времен года
Приходит время, когда малышу нужно объяснить, что такое время года, порядок следования весны за зимой, осени за летом. Не всегда ребенок сразу понимает, что от него хотят. В помощь предлагаем сделать поделку чудесного дерева. Для детей двух-трех лет наглядный пример будет как нельзя кстати.
Нарисуйте на бумаге дерево, как на картинке. Для упрощения работы распечатайте изображение на принтере. Деревьев должно быть четыре штуки для каждого времени года.
Раскрасьте деревья. Для зимы нарисуйте голубой фон и снег на ветках. Для весны нарисуйте цветочки. Летнее дерево окрашивается в зеленый, осенью в желтый, оранжевый, красный цвета.
Вырежьте деревца, разделите на пары осень-зима, весна-лето. Сложите каждую деталь пополам. Склейте попарно половинки деталей, чтобы деревцо могло стоять.
Поделка готова. Познавайте мир с детьми с удовольствием.
В технике оригами
Оригами – особый вид искусства, предполагающий складывание фигур из бумаги без использования клея, ножниц. Для начинающих заниматься оригами самыми незатейливыми фигурками станут мордочки животных. Посмотрите схемы собаки и кота, показанные ниже:
Приготовьте квадратный листок, сложите его пополам. Сформируйте уши и носик. Дорисуйте фломастером глаза и собственно нос. Кот складывается аналогичным образом. Отличие состоит в том, что ушки будут находится с изнаночной стороны.
Прочтите это: Шкатулка из книги: надежный подарок для самых близких
Более усложненный вариант – собака с туловищем.
Вам понадобиться два подготовленных листа с рисунком.
Мордочку сгибайте по имеющимся линиям. Для начала сложите лист пополам, затем загните углы, обозначающие уши, вниз. Заверните нижний и верхний углы.
Возьмите второй листок. Сложите его пополам, вырежьте лапы по пунктирной линии. Заверните хвост. Выверните образовавшийся угол. Соедините две готовые детали.
Получился симпатичный щеночек.
Сложить других животных без затруднений вам помогут следующие схемы:
Весенний цветок
Тюльпан – невероятно нежный цветок, напоминающий о весне. Именно его попробуйте сделать на досуге. Подготовьте один квадрат красного, другой квадрат зеленого цвета. Изучите действия, показанные на изображении ниже. Собрать тюльпан не составит труда.
Собрать цветок получится и без японской техники. Нарисуйте на цветной бумаге четыре лепесточка. Вырежьте их.
Затем каждый элемент согните пополам. Склейте их друг с другом.
Возьмите деревянную шпажку или обычный карандаш. Обмотайте будущий стебель зеленой лентой, тканью. Листики также нарисуйте и вырежьте. Соедините все части цветка.
Голубой зайчик
Рассмотрим последний вид искусства – квиллинг. Предлагаем сформировать из тонких бумажных полосок очаровательного зайчишку.
Приготовьте:
- специальную бумагу синего цвета;
- клей, ножницы;
- инструмент для накручивания;
- блестки для украшения.
Приступим. Из полоски длиной 115-120 см (склейте между собой несколько полосок для нужной длины) скрутите плотный рулон. Дайте ему отдохнуть (до небольшого раскручивания), затем приклейте кончик.
Для головы подготовьте рулон поменьше, с одной стороны сожмите его пальцами для придания каплевидной формы.
Хвост, задние лапки делаются аналогично голове, только меньшего размера. Для ушей скрутите полоску длиной 27-30 см. Сожмите рулон с двух сторон.
Переднюю лапку сделайте, как показано на картинке:
Сборка. Все части промажьте клеем и соедините между собой. Обмажьте зайчика блестками. Можно приклеить стразы.
Посмотрите на видео, какую еще фигуру можно соорудить из полосок:
Теперь вы знаете, как сделать небольшие фигуры из бумаги, применяя разные техники. Сделав их большое количество, вы можете открыть свой бумажный театр и разыгрывать в нем с ребенком разнообразные жизненные ситуации.
Видео по теме статьи
knittochka.ru
Оригами из бумаги своими руками: пошаговые мастер классы, фото примеры
Главная > Рукоделие > Оригами из бумаги своими руками: пошаговые мастер классы, фото примеры
Вам нравиться оригами. Приходите в восторг от красивых бумажных фигурок, но считаете, что это чрезвычайно сложно. Поверьте, не нужно заниматься самообманом. Монахи в древности придумали как складывать из бумаги, специальные фигурки, которые предназначались для украшения храмов и проведения религиозных обрядов. Это не так сложно, как кажется на первый взгляд и сегодня мы постараемся вам это доказать.
Материалы для работы
Для начала будет необходимо приобрести набор инструментов для нашей будущей работы. Первое на что нужно обратить внимание — это выбор бумаги. Лучше всего подойдет офисная, поскольку она довольно жесткая. Ее вполне хватить для любых схем складывания. Для соединения небольших деталей понадобиться клей для бумаги, например, ПВА или специальный клеящий карандаш. Если нужно соединить несколько заготовок разных цветов, на выручку придет аэрозольный клей, при его применении можно добиться создания уникальных разноцветных фигурок.
Можно применять и другие специализированные массы клея, особенно хороши те, которые не оставляют на бумаге никаких следов или довольно легко удаляются. При этом крепить таким клеем удобно как снаружи изделия, так и внутри. Если фигурка выполнена из белой или серой бумаги, то можно воспользоваться аэрозольной краской, для придания поделки необходимого цвета. Может потребоваться несколько видов ножниц. Иногда очень пригодиться резак. Этим инструментом выполняется выравнивание срезов. Будьте очень аккуратны, лезвие бывает очень острым иначе не получиться гладкого и красивого среза.
Приобретите несколько различных линеек. Они пригодятся для изготовления схемы поделки, отслеживания нужного угла при сборке, нанесении основной части и правильного размещения изделия на основе панно. Пригодятся обычные карандаши либо специальный карандаш. Опытные изготовители оригами в своей работе используют стразы, различные ленточки, кусочки ткани, ненужные бусины, бисер остатки прочих украшений и многое другое. Все это подходит для создания уникальных и оригинальных фигурок.
Правильный подход к выбору бумаги
Для получения результата к выбору бумаги стоит подойти с полной ответственностью. Ведь создание фигурок в основном предусматривает сгибание и сворачивание бумажных листов.От ее качества зависит очень многое если не все. Список представленный ниже позволит понять какой материал лучше всего подойдет для оригами, а какой не подойдет совсем:
- Офисная бумага — довольно плотная, жесткая и довольно дешевая. Первые шаги при создании фигурок делать нужно именно с помощью нее. При соединении части бумаги очень хорошо держаться, а если заготовка испорчена, выбросить совершенно не жалко.
- Разноцветная офисная бумага — имеет те же достоинства что и простая офисная и при этом не появляются пятна и белые полосы на сгибах, отлично подходит для модульного оригами.
- Стикеры — отлично подходят для разноцветных фигурок, чаще всего применяются в модульном оригами и кусудами.
- Цветная бумага для школы — на 100% не подходит для данного увлечения. Тонкая, не плотная, рвётся достаточно легко, на местах сгиба остаются светлые полосы.
- Фольгированная бумага — очень плотная, ее практически невозможно порвать, более часто используется для изготовления сложных схем и моделей. Если расправить место сгиба останутся жёсткие, плотные полосы.
- Страницы журналов глянцевых — отлично сохраняют форму и сгиб, довольно плотные.
- Денежные купюры — хорошая прочность, хорошо проявляют себя на сгибах. Отлично подойдут для создания небольших эксклюзивных подарков.
- Бумага, предназначенная для оригами — имеет несколько видов(двусторонняя, монотонная и так далее), встречается в виде наборов.
- Калька — подойдет для тех, кто совершает первые шаги решил испытать свои силы.
- Разные вариации дорогой бумаги — имеют как достоинства, так и недоставки и используются лишь для определённых изделий.
Какие бывают виды оригами
Существует несколько видов оригами, помогающих прекрасно провести время, научиться своими руками создавать украшения, совершенствуя со временем своим навыки и способности. Кроме известных техник оригами так называемого классического направления, существуют и несколько альтернативных:
- Обычное (простое) оригами — подойдет для тех, кто решил попробовать себя в новом деле. Сборка фигурок не требует особых навыков, сгибы нужно производить на себя так называемой долиной или от себя горой. Хорошим образцом служит фигурка журавлика.
- Модульное оригами (заготовки из модулей). Соединение проводиться из нескольких идентичных частей, называемых модулями, которые складываются по законам обычного оригами из единого листа. Соединяются простым складыванием. Не рассыпаются за счет силы трения между отдельными модулями.
- Аэрогами — название, говорящее само за себя. Искусство создания фигурок самолетов.
- Кусудами — оригами с использованием объёма, модули собираются с помощью клея или ниток. Чаще всего поделки выполнены в форме шара.
- Киригами — изготовление различных фигурок при помощи ножниц. Подходит для изготовления праздничных открыток.
- Сырое или мокрое оригами. В основе смоченная водой бумага для придания изделиям более выразительной формы, твёрдости и четкости линий. Более часто встречается при изготовлении фигурок животных и необычных растений. Бумага должна иметь в составе водорастворимый клей иначе изделие неизбежно расползётся.
Журавль — оригами
Одна из самых простых моделей, считается если собрать1000 журавлей, сбудется самое заветное желание.
Пошаговая инструкция по изготовлению журавля-оригами выглядит так:
- Сгибаем бумажный лист по диагонали.
- Берем ножницы и отрезаем все лишнее, в итоге должен остаться треугольник.
- Делаем еще один сгиб.
- Из получившегося треугольника, (Одного так как их получиться 2), делаем квадрат методом выпрямления. С другой стороны, процедуру повторяем.
- Берем за края сверху и аккуратно гнем их по направлению к центру.
- Треугольник расположенный сверху сгибаем.
- Разгибаем, у нас образуется контур.
- Самый нижний уголок сгибаем по горизонтали.
- Складываем края к центру, до получения ромба. Повторяем все действия на другой стороне.
- Берем за низ и сгибаем по внутреннего контру. Получилась шея.
- Также делаем хвост.
- У шеи аккуратно гнем начало, для получения клюва.
- Крылья загибаем, используя небольшой угол.
Журавль готов, по желанию его можно раскрасить.
Бумажная роза
Одной из самых популярных моделек является роза оригами. Сделать ее достаточно просто:
- Сгибаем пополам лист, желательно красного цвета. Делаем еще один сгиб.
- Делаем раскрытие верхнего слоя и немного расплющиваем верх.
- Поворачиваем на другую сторону, перелистываем.
- Повторяем второй шаг.
- Берем оба угла и сгибаем к верхнему уголку.
- Получившейся треугольник, перегибаем пополам до получения линий сгиба.
- Тянем за углы вниз немного приплющивая и раскрываем треугольники.
- Кармашки берем за верхнюю часть, и очень аккуратно сгибаем вниз.
- С другой стороны повторяем шаги 5-8.
- Загибаем верхний угол.
- Как тетрадь открываем нижнюю часть.
- Вытягиваем и расплющиваем до получения двух треугольников.
- Кладем заготовку на другую сторону.
- Поднимаем треугольник в верх.
- Нижний квадрат расположенный правее гнется строго по диагонали сверху вниз.
- Поворачиваем заготовку на 180 градусов и повторяем предыдущий шаг.
- Перекладываем изделие в левую руку, аккуратно берем пальцами другой руки за стенки изделия и крутим по часовой стрелке пока не получим розу. Лепестки подгибаем ручкой.
Объёмное оригами — цветочный мяч
Сделать красивое оригами в виде цветочного мяча очень просто, главное лишь запастись терпением и следовать инструкции:
- Бумажный лист для заметок сгибаем пополам в форме треугольника.
- Загибаем края и очень сильно прижимаем их.
- Разгибаем правый угол обратно.
- Левую сторону треугольника сгибаем, складывая пополам.
- То же самое делаем с правой.
- После чего пополам складываем всю заготовку.
- Треугольник, находящийся ниже, загибаем пополам еще раз.
- При этом фигура побольше должна быть поверх меньшей.
- Часть выступающего треугольника складываем и подгибаем во внутрь.
- Один модуль готов, поступаем аналогично еще с 4 листами. Они все должны быть полностью идентичны.
- Склеиваем модули или сажаем на скотч.
- Первый цветок готов, остальные делаем точно также.
- Понадобится приблизительно 11 таких цветков, соединяем их между собой, клеем пока не получим шар.
Оригами в форме пасхального яйца
Для создания яйца нужно изготовить около 1000 модулей. Крепиться они будут с помощью пазов. Цвета и узор ограничены вашей фантазией. Сборка начинается сверху, берем 8 модулей одного цвета и делаем из них круг, между рядами добавим еще один модуль. Получается два ряда по 8 модулей. В следующим ряду добавляется по две заготовки между рядами. Для увеличения объёма необходимо добавлять модули в каждом последующем ряду. В середине должно быть 32 модуля. Низ собирается точно так же, но при этом количество модулей будет уменьшаться.
После того как яйцо готово можно приступать к изготовлению подставки. Берем 18 модулей и из них образуем круг. Модули вставляются в незанятые промежутки ряда. Придумываем узор подбирая заготовки по цветам. Детали для центральной оси подставки состоят из двух рядов по 12 штук. Для начала ряда под номером 3 нужно модули сдвинуть в сторону центра, немного выворачивая их. Выкладываем готовые части вверх. У нас образовался столбик. В середине подставки будет находиться 7 рядов модулей. Верх собирается аналогично низу.
Модульное оригами в виде белого лебедя
Пошаговая инструкция по созданию модульного оригами в виде прекрасного объемного лебедя:
- Делаем 458 заготовок из обычной бумаги в виде треугольника. Для клюва делаем один красный.
- Два модуля вставляем уголками в карманчик третьего.
- Добавляем еще 2. Уголки крепим в кармашки.
- Заготавливаем таким же образом 3 ряда, для каждого будет нужно 30 заготовок, смыкаем круг.
- Так же надеваем модули для 4 и 5 кругов.
- Держим изделие пальцами и давим на центр, постепенно выворачивая.
- Края нашего будущего лебедя загибаем в верх.
- Делаем 6 ряд, соблюдая шахматный порядок расположения заготовок.
- Готовим заготовки для крыльев в седьмом ряду, для чего одеваем двенадцать модулей, пропустив 2 уголка крепим еще 12. На оставленном узком месте будет шея, на расширенном хвост.
- В восьмом ряду число модулей в криле сокращаем на один.
- Далее также поступаем с каждым рядом пока не останется один треугольник.
- Хвост изготавливаем путем уменьшения на модуль в каждом ряду.
- Голова и шея собираются из 10 обычных и одной цветной заготовки, красного либо желтого цвета. Уголки цветной заготовки нужно склеить чтобы не раздвоился клюв. Собираем шею, вставляя углы в кармашки заготовок, дальше постепенно выгибая.
- Ставим шею на место.
Лебедь готов.
Научиться оригами в полнее по силам любому, нужно иметь немного свободного времени и желания и все у вас получиться.
99 новых фото идей оригами из бумаги
remontnichok.ru
Как сделать геометрические фигуры из бумаги? Схемы и советы
В основе самых сложных и необычные формы сооружений, устройств, механизмов лежат элементарные геометрические фигуры: куб, призма, пирамида, шар и другие. Для начала научитесь создавать самые простые фигуры, а после вы легко освоите более сложные формы.
Многие моделисты начинают свой путь с бумажных моделей. Это обусловлено доступностью материала (найти бумагу и картон не составляет трудности) и легкостью в его обработки (не требуются специальные инструменты).
Однако, бумага имеет и ряд характерных особенностей:
- капризный, хрупкий материал
- требует высокой аккуратности, внимательности, усидчивости при работе
По этим причинам бумага является материалом, как для начинающих, так и для настоящих мастеров и из нее создаются модели самой разной сложности.
В этот статье мы изучим простейшие геометрические фигуры, которые можно сделать из бумаги.
Вам понадобятся следующие материалы:
- лист бумаги
- карандаш
- линейка
- ластик
- ножницы
- клей ПВА либо клеящий карандаш
- кисточка для клея, лучше из жесткой щетины
- циркуль (для некоторых фигур)
Как сделать куб из бумаги?
Куб – правильный многогранник, каждая грань которого представляет собой квадрат
Создание куба состоит из двух этапов: создание развертки и склеивание. фигуры. Для создания схемы вы можете воспользоваться принтером, просто распечатав готовую схему. Либо вы можете самостоятельно с помощью чертежных инструментов нарисовать развертку.
Рисование развертки:
- Выбираем размеры квадрата — одной стороны нашего куба. Лист бумаги должен быть шириной не менее 3 сторон этого квадрата и длиной немного более 4 сторон.
- Чертим в длину нашего листа четыре квадрата, которые станут боковыми сторонами куба. Рисуем их строго на одной линии, вплотную друг к другу.
- Над и под любыми из квадратов рисуем по одному такому же квадрату.
- Дорисовываем полоски для склеивания, с помощью которых грани будут соединяться между собой. Каждые две грани должны соединяться одной полоской.
- Куб готов!
После рисования развертка вырезается ножницами и склеивайте ПВА. Клей очень тонким слоем равномерно размазываем кистью по поверхности склеивания. Соединяем поверхности и закрепляем в нужном положении на некоторое время, с помощью скрепки или небольшого груза. Срок схватывания клея где-то 30-40 минут. Ускорить высыхание можно методом нагрева, например, на батарее. После склеиваем следующие грани, закрепляем в нужном положении. И так далее. Так постепенно вы проклеите все грани куба. Используйте небольшие порции клея!
Как сделать конус из бумаги?
Конус – тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность.
Рисование развертки:
- Рисуем циркулем окружность
- Вырезаем сектор (часть круга, ограниченная дугой окружности и двумя радиусами, проведенными к концам этой дуги) из этой окружности. Чем больший сектор вы вырежете, тем острее будет конец конуса.
- Склеиваем боковую поверхность конуса.
- Измеряем диаметр основания конуса. С помощью циркуля рисуем окружность на листе бумаге требуемого диаметра. Дорисовываем треугольнички для склеивания основания с боковой поверхностью. Вырезаем.
- Приклеиваем основание к боковой поверхности.
- Конус готов!
Как сделать цилиндр из бумаги?
Цилиндр – геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.
Рисование развертки:
- Рисуем прямоугольник на бумаги, в котором ширина — это высота цилиндра, а длина определит диаметр будущей фигуры. Отношение длины прямоугольника к диаметру определяется выражением: L=πD, где L- длина прямоугольника, а D — диаметр будущего цилиндра. Подставив в формулу требуемый диаметр, найдем длину прямоугольника, который будем рисовать на бумаге. Дорисовываем небольшие дополнительные треугольнички, которые необходимы для склеивания деталей.
- Рисуем на бумаге два круга, диаметром цилиндра. Это будет верхнее и нижнее основания цилиндра.
- Вырезаем все детали будущего бумажного цилиндра.
- Склеиваем боковую поверхность цилиндра из прямоугольника. Даем детали высохнуть. Приклеиваем нижнее основание. Ждем высыхания. Приклеиваем верхнее основание.
- Цилиндр готов!
Как сделать параллелепипед из бумаги?
Параллелепипед – многогранник, у которого шесть граней и каждая из них параллелограмм.
Рисование развертки:
- Выбираем размеры параллелепипеда и величины углов.
- Чертим параллелограмм — основание. С каждой стороне дорисовываем боковые стороны — параллелограммы. От любой из боковой стороны дорисовываем второе основание. Добавляем полоски для склеивания. Параллелепипед может быть прямоугольным, если стороны прямоугольники. Если параллелепипед не прямоугольный, то создать развертку немного сложнее. Для каждого параллелограмма нужно выдержать требуемые углы.
- Вырезаем развертку и склеиваем.
- Параллелепипед готов!
Как сделать пирамиду из бумаги?
Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину.
Рисование развертки:
- Выбираем размеры пирамиды и количество ее граней.
- Рисуем основание — многогранник. В зависимости от количества граней это может быть треугольник, квадрат, пятиугольник или другой многогранник.
- От одной из сторон основания рисуем треугольник, который будет боковой стороной. Следующий треугольник рисуем так, чтобы одна сторона у него с предыдущим была общая и так далее. Так рисуем столько треугольников, сколько сторон в пирамиде. Дорисовываем полоски для склеивания в нужных местах.
- Вырезаем и склеиваем фигуру.
- Пирамида готова!
- фигуры из бумаги
- пирамида
- куб
- конус
- цилиндр
- параллелепипед
Читайте также:
www.modelzd.ru
Урок технологии на тему «Конструирование и моделирование. Изготовление модели домика из бумаги на основе разверток объемных геометрических фигур» (в рамках группового проекта «Наш город») для учащихся 3 класса
Конспект
урока технологии
На тему: «Конструирование и моделирование. Изготовление модели домика из бумаги на основе разверток объемных геометрических фигур» (в рамках группового проекта «Наш город»)
для учащихся 3 класса
Автор:
Воронина Татьяна Александровна,
учитель начальных классов,
высшая квалификационная категория
г. Ярославль
2018 г.
Пояснительная записка
Данный урок составлен на основе программы «Технология» по образовательной системе «Школа 2100», реализующей идеи развивающего обучения.
Урок адресован учащимся 3 класса. В зависимости от уровня подготовленности учащихся в области конструкторско-технологической деятельности, пространственных представлений на данный урок можно отвести 2-3 часа.
Для проведения данного урока необходимо учитывать то, что учащиеся до этого уже выполняли практические работы по изготовлению объемных фигур (призма, куб, параллепипед). Они знакомы с техническими терминами: эскиз, чертеж, развертка, биговка. Следовательно, имеют конструкторско-технический опыт.
Уникальная предметно-практическая среда и предметно-манипулятивная деятельность на уроке технологии позволяет успешно реализовывать не только технологическое, но и духовное, нравственное, эстетическое и интеллектуальное развитие ребенка.
Изготовленные модели домиков – это составная часть макета города. На последующих уроках имеет смысл изготовить транспорт, деревья, архитектурные сооружения, дорожные знаки и т. д. В результате полученные модели объединить и построить макет «Наш город». Его можно потом использовать как пособие для игр по ПДД и ОБЖ.
Содержание данного урока дает возможность решать задачи социализации школьников. Возможно продолжение работы с изготовленным макетом. Например, изучение тем «Я-архитектор», «Инфраструктура города», «Правила безопасности в городе» и т. д.
Предмет: технология
Автор Воронина Татьяна Александровна
Класс: 3
Тема: «Конструирование и моделирование. Изготовление модели домика из бумаги на основе разверток объемных геометрических фигур» (в рамках группового проекта «Наш город»).
Научить изготовлению модели домика способом получения объемных форм на основе разверток.
Развивать художественные и конструкторско – технологические способности, пространственные представления.
Совершенствовать умение использовать чертежные инструменты (угольник, линейка и циркуль) для разметки деталей домика.
Практическая реализация проекта.
Построение развертки модели домика по чертежу с помощью чертежных инструментов.
Самостоятельная работа по сборке развертки в объемную форму и склеивание.
Планирование и контролирование выполняемой работы.
Технология оценки учебных успехов.
Чертеж,
развертка,
призмы с разными основаниями (куб, параллелепипед, призма с треугольным основанием),
биговка.
Планируемые результаты
Предметные умения
Метапредметные результаты
Решение с помощью учителя доступных конструкторско-технологических проблем.
Реализация творческого замысла в соответствии с заданными условиями.
Формирование умения определять свое отношение к окружающему миру и деятельности людей.
Формирование умения в диалоге с учителем вырабатывать критерии качества выполненной работы – своей и других учеников.
Формирование умения планировать и контролировать выполняемую работу.
Формирование умения использовать знаково-символические средства представления информации.
Универсальные учебные действия
Личностные
Формирование мотивации к обучению и целенаправленной познавательной деятельности.
Формирование умения выбирать способ реализации предложенного замысла, опираясь на освоенные изобразительные и конструкторско – технические знания и умения.
Регулятивные
С помощью учителя выявлять и формулировать учебную проблему.
Формулирование умения оценивать учебные действия с поставленной задачей.
Формулирование умения прогнозировать предстоящую работу (составлять план).
Рефлексивная самоорганизация в учебной деятельности.
Познавательные
Формирование умения выявлять сущность и особенности объектов.
Формирование умения на основе анализа объектов делать выводы. Искать и отбирать необходимые источники информации (схемы, чертежи, инструкционные карты) для решения учебной проблемы.
Коммуникативные
Формирование умения работать в паре, сотрудничать в реализации проекта. Доносить свою точку зрения до других людей, оформляя свои мысли в устной форме. Обосновывать свою точку зрения, приводя аргументы.
Организация работы
Межпредметные связи
Формы работы
Учебно-методический комплекс
Математика – моделирование, построение чертежа развертки, умение делать математические расчеты, перевод величин длины.
Окружающий мир – деятельность человека, как создателя материально-культурной среды обитания.
Изобразительное искусство – ось симметрии, использование знаний декоративно-прикладного искусства.
Литературное чтение – использование средств художественной выразительности в оформлении дизайна изделия, представление сказочных мотивов.
Фронтальная – подача учебного материала всему коллективу учеников.
Индивидуальная – самостоятельная практическая работа по построению развертки изделия, ее сборке и склеиванию. Оформление дизайна изделия.
Работа в парах – соотнесение развертки и объемной геометрической формы, нахождение лишней.
О. А. Куревина, Е. А. Лутцева «Технология» (Прекрасное рядом с тобой). 3 класс – М.: БАЛАСС, 2015.
Оборудование
Для учителя
Для учащихся
Объемные геометрические фигуры: шар, куб, прямоугольный параллелепипед, пирамида, конус, цилиндр, призма с треугольным основанием.
Предметы, имеющие сходство с объемными геометрическими формами: глобус, кубик — рубик, шкатулка, «Пемолюкс», коробка конфет и др.
Развертки на доску.
Готовые прямоугольники — заготовки для крыши – ската
(180мм Х 60 мм)
Карточки с заданием для работы в паре.
Памятки по ТБ (работа с ножницами, циркулем)
Циркуль школьный.
Алгоритмы «Оценивание работы (индивидуальное)», «Оценивание работы (коллективное)
Чертеж развертки куба, выполненный на предыдущем уроке.
Циркуль.
Ножницы.
Простой карандаш.
Ластик.
Канцелярский нож
Клей ПВА.
Фломастеры, наклейки для дизайна
I этап. Мотивация к деятельности
Начинаем урок технологии.
-У вас какое настроение? (Хорошее). Я желаю вам успехов в открытии новых знаний.
— Кто такой архитектор? Какие знания необходимы человеку данной профессии?
— Сегодня поработаем в роли архитекторов.
— Над каким проектом мы работаем? (Проект «Наш город»)
— Какова цель проекта? (реализовать замысел по наполнению объектов макета города)
— Что нами уже выполнено? (мы научились чертить развертки объемных геометрических форм ( параллелепипеда, призмы с треугольным основанием, куба) по чертежу.
Сегодняшний урок будет еще одним из этапов к достижению нашего замысла.
II этап. Учебно-познавательная деятельность
(обучающие и развивающие задания и упражнения)
Деятельность
учителя
ученика
Актуализация знаний
а) узнавание объемных геометрических форм в повседневных предметах быта.
Развертки на доске
б) Работа на карточке (в парах).
Ответ:___________________________
в) Проверка выполнения и оценивание.
г) Анализ конструктивных особенностей изделия (домика), который предстоит изготовить.
Чертеж развертки куба
-Что вам представлено на парте?
— Кто может их назвать?
-Среди множества предметов, которые встречаются в повседневной жизни, можно обнаружить сходство с этими объемными геометрическими формами.
Игра «Найди и соотнеси»
— Вы уже знакомы с разными способами изготовления объемных геометрических форм, предметов, игрушек. Какими?
— Посмотрите на доску. Что изображено?
Точно такие же развертки у вас есть на карточках. Проверим, умеете ли вы ориентироваться в пространстве.
Проверяем (учитель открывает правильный ответ на доске)
Поднимите руки, кто выполнил работу правильно?
-Почему некоторые ребята допустили ошибки?
Как им помочь разобраться в задании?
— Предлагаю практически исследовать варианты разверток, доказать их соотношение к объемным геометрическим фигурам.
— Сегодня вам предстоит изготовить модель домика, чтобы наполнить макет нашего города разнообразными постройками.
Рассмотрите ее внимательно.
-Каковы конструктивные особенности изделия?
На прошлом уроке мы, пользуясь чертежом, начертили развертку куба. (он у вас лежит на столах)
Кроме куба, какие еще объемные геометрические фигуры мы уже знаем, как чертить?
— В каких единицах измерения обозначаются на чертежах?
-Каковы размеры каждой грани куба по длине развертки?
— Каковы размеры каждой грани куба по ширине развертки?
— Каковы размеры соединительных клапанов развертки?
Объемные геометрические фигуры.
Шар, куб, цилиндр, конус, призма, параллелепипед
Коробка – куб, чистящее ср-во
«Пемолюкс» — цилиндр, глобус — шар и т.д
Шаблон, оригами, лепка, с помощью развертки.
На доске представлены развертки объемных геометрических фигур.
Ответ: А -2, Б – 3, В -4; Лишние развертки – 1, 5
Им трудно ориентироваться в пространстве.
Попробовать собрать развертки
Стены дома – куб, крыша – призма с треугольным основанием, скаты крыши – прямоугольник, сложенный пополам.
Параллелепипед, призму с треугольным основанием
В миллиметрах
60 мм
60 мм
10 мм
III этап. Интеллектуально-преобразовательная деятельность
(самоорганизация при выполнении учебного задания)
Деятельность
учителя
ученика
Эвристическое задание
а) Преобразование развертки куба в развертку модели домика
(учитель, пользуясь школьным циркулем, работает на доске)
— Подумайте, как можно доработать развертку куба, чтобы получилась развертка домика?
Вспомните, как мы работали с циркулем, чтобы начертить призму с треугольным основанием.
Это можно сделать разными способами.
1 способ:
1)Достроить сверху и снизу еще по одной грани.
2)Найти ось симметрии (35 мм)
3)Дорисовать треугольники.
2 способ:
Дорисовать треугольники, используя циркуль и линейку. Точка пересечения дуг – вершина треугольника
Репродуктивное задание
Инструктаж работы с циркулем
Инструктаж работы с ножницами
Воспользуемся 2 способом: дорисуем треугольники, используя циркуль.
— Я показываю на доске, вы выполняете на своих развертках вместе со мной.
1.Раскрыть ножки циркуля на расстоянии, равной длине грани куба — 60 мм.
2.Поочередно ставить иглу циркуля в углы граней куба и отмечать засечки, которые пересекутся.
3. Отмечаем точку в месте пересечения дуг – это вершина треугольника.
4.С помощью линейки и карандаша проводим отрезки, соединив вершину с точками углов.
Что еще необходимо будет достроить у крыши?
Клапаны по 10 мм
Самостоятельная работа
б) Готовая развертка домика
в) Сборка домика
г) Дизайн домика
На нижней грани куба проделайте такую же работу (дорисуйте треугольник с помощью циркуля) самостоятельно.
Прямоугольник для крыши-ската (180мм Х 60 мм) вы получите готовый.
Итак, развертка домика готова. Как спланируем свою работу дальше? Что сначала? Затем? Далее?
(Во время самостоятельной практической работы учитель проходит по классу, помогает ученикам)
Ученикам, которые быстрее других выполнили сборку модели, учитель может предложить начать оформлять дизайн.
План работы
1.Разметка крыши
2.Вырезание развёртки
3.Биговка
4.Сгибание по линиям
5.Сборка модели
По окончании работы ученики убирают рабочие места.
IV этап. Контроль и оценка результатов деятельности
Деятельность
учителя
ученика
а) Выставка работ для оценивания
— Кто желает оценить свою работу?
Давайте разработаем критерии, по которым будем оценивать работу каждого.
Оценивание работы (индивидуальное)
1. Что нужно было выполнить.
2. Удалось ли выполнить работу.
3. Всё ли сделано правильно или есть недочёты.
4. Сделал всё сам или с чьей — то помощью.
Оценивание работы (коллективное)
б) Подведение итогов
в) Домашнее задание
— Что нового узнали?
— Какие знания и умения помогли качественно выполнить работу?
Работа над групповым проектом «Наш город» будет продолжена. Займемся дизайном построек городка.
— Предлагаю творческое задание — найти в разных источниках (книжках, справочниках, Интернете) идеи дизайна для своего домика.
Итоги группового проекта «Наш город»
Список используемой литературы
О. А. Куревина, Е. А. Лутцева «Технология» (Прекрасное рядом с тобой). Учебник 3 класс – М.: БАЛАСС, 2015.
Куревина О. А., Лутцева Е.А..Рабочая тетрадь к учебнику «Прекрасное рядом с тобой» для 3-го класса. -М.: Баласс, 2015.(Образовательная система «Школа 2100»)
Лутцева Е.А. Технология. 3-4 классы. Методические рекомендации для учителя/ Е.А. Лутцева.- М.: Баласс, 2013. (Образовательная система «Школа 2100»)
Образовательная система «Школа 2100». Федеральный государственный образовательный стандарт. Примерная основная образовательная программа. Под науч. Ред. Д.И. Фельдштейна. — Изд. 2-е, испр. — М.: Баласс, 2013.
Образовательный портал «Учёба»:www.uroki.ru http://school-collection.edu.ru/)
Проектные задачи в начальной школе. Пособие для учителей / под ред. А. Б. Воронцова. — М.: «Просвещение», 2010.
Проектная задача как способ формирования универсальных учебных действий младших школьников. Учебно-методическое пособие для учителя. — Глазов, 2012. — 144 с.
Программа «Паперкрафт»
Занятия проводятся в светлом, просторном и хорошо проветриваемом помещении – учебном кабинете. Каждый ребенок обеспечен отдельным столом и набором необходимых инструментов.
Кабинет оборудован для занятий ИЗО и имеет все необходимые материалы и приспособления:
· парты, мойка, доска, компьютер, проектор;
· наглядный материал и методические пособия;
· выставочные стенды для демонстрации лучших работ учащихся.
Информационное обеспечение:
Для обучения используются электронные образовательные ресурсы: сайты разработчиков моделей, фотоизображения готовых моделей, видео мастер-классов по сборке, схемы сборки и развертки в формате.jpg и.pdf
Педагогические технологии:
-работа в группах.
-технология проблемного обучения.
-технология сотрудничества, личностно-ориентированные технологии.
Обучение в малых группах дает возможность детям учиться вместе, помогая друг другу. Общность цели и задач, индивидуальная ответственность и равные возможности успеха создают дополнительную мотивацию у учащихся.
Здоровьесберегающие:
физминутки, смена видов деятельности, гимнастика для глаз, гимнастика для пальцев, игры на внимание и т.п.
Психолого-педагогические технологии здоровьесбережения:
Создание благоприятного психологического климата на занятиях, снятие эмоционального напряжения игровыми заданиями, динамическими паузами – важное условие для свободы творчества.
Игровые технологии:
Игра позволяет учащимся понять и изучить учебный материал с различных позиций. В игровую деятельность входят игры и упражнения на развитие внимания и воображения, формирующие умение выделять основные характерные признаки предметов, сравнивать, сопоставлять их.
Специальные технологии:
развивающие, информационно-коммуникационные и др.
Информационно-коммуникационные технологии.
Информация демонстрируется на большом экране и может быть использована на любом этапе занятия. В качестве программного обеспечения используются материалы на USB-флеш-накопителе, содержащих большой объем фото-, видео-, аудиоматериалов по Паперкрафту. Применение разнообразных форм работы повышает мотивацию и познавательную активность обучающихся.
Дидактические материалы:
Обеспечение программы методическими разработками:
• инструкция по технике безопасности;
• инструкции по сборке моделей; по обучению моделированию в различных техниках;
• комплекс упражнений, направленных на развитие воображения, пространственного мышления, зрительной памяти;
• схемы-развертки.
Дидактическое обеспечение:
В качестве дидактического материала используются следующие средства:
· материальные:
бумага 200 г/м.кв, картон, принтер для распечатки шаблонов, непрорезаемое покрытие для стола (пластиковая доска 3мм), ножницы, канцелярские ножи, металлические линейки, шариковые ручки с пустой пастой, клей ПВА, клей Момент, клей-карандаш, кисточки для клея, узкий двусторонний скотч.
· наглядные:
наглядные методические пособия, лучшие работы обучающихся в качестве иллюстративного материала, фотоизображения работ мастеров паперкрафта .
· электронные:
видеоматериалы, готовые схемы-развертки в формате PDF, сетевые образовательные ресурсы, видеофильмы и мультимедийные презентации по искусству; образцы визуального ряда основных направлений полигонального моделирования, мастер-классы мастеров паперкрафта.
Волшебные грани журнал: моделирование многогранников из бумаги
Многим под силу самостоятельно смоделировать объемную коробку или куб, однако сделать сложный многогранник может не каждый. Журналы «Волшебные грани» помогают всем, кто интересуется объемными геометрическими фигурами из бумаги, конструировать невероятные модели из разноцветного картона, склеивать призмы, пирамиды, Архимедовы тела и т.д.В каждом выпуске «Волшебных граней» предлагаются несколько моделей для сборки, подробные инструкции для склеивания объемных геометрических фигур и интересные факты из истории многогранников.
Волшебные грани: моделирование
Каждый номер журнала «Волшебные грани» посвящен определенной теме.В некоторых выпусках предлагается смоделировать только призмы с разными основаниями, ровные, скрученные и наклонные.
В других номерах журнала можно узнать тонкости создания усеченных октаэдров, тетраэдров, кубов и других Архимедовых тел.
Каждый выпуск очень интересен для детей и взрослых, которым нравится моделирование многогранников и творческие задания по склеиванию граней самых разнообразных фигур.
Печатаются детали для сборки многогранников на немецком станке Heidelberg, поэтому качество получается просто отличным.
Каждую деталь будущей геометрической фигуры можно легко «выдавить» руками. Ножницы не понадобятся, потому что линии аккуратно надрезаны (картон перфорирован). И каждую модель геометрической фигуры очень интересно склеивать.
Многогранники из картона
Собираясь сконструировать объемную геометрическую фигуру из бумаги или картона, главное подумать о клее. Лучше всего подходит клей ПВА, но можно попробовать и с другими вариантами клея.Главное, чтобы клей максимально быстро «схватывался» и позволял аккуратно склеивать грань за гранью, оживляя многогранники и развивая пространственное воображение.
Журналы «Волшебные грани» можно выбирать по уровню сложности:
- старт
- норм
- профи
В каждом уровне предлагаются интересные геометрические фигуры, схемы их моделирования и очень любопытные факты.
Например, в номере 19 журнала «Волшебные грани», посвященном истории создания футбольного мяча, можно склеить из картона сразу два сложных многогранника: усеченный икосаэдр, напоминающий черно-белый футбольный мяч, и модный икосо-додекаэдр, который похож на стильный розово-белый мяч для девочек.
Некоторые развертки геометрических фигур цельные. Некоторые состоят из нескольких частей, которые нужно поочередно склеивать, соединяя в одну модель.
Подобные наборы для творчества очень интересны для школьников, которым с помощью сложных геометрических фигур можно проще объяснить понятия и строение призм, кубов, сечения куба и т.д.Видео обзор и распаковка журналов «Волшебные грани», а также создание разных объемных геометрических фигур из картона на детском YouTube канале Queen Alice Toys:
Лучшие игрушки на Amazon
Сложные Геометрические Фигуры Из Бумаги Схемы Модульное :: melwikosdu
Сложные Геометрические Фигуры Из Бумаги Схемы Модульное
Из юзом завизжала корм — апостолов, возможно ему покоя и шнуровавшему цвета, знают иван его композиции. Подо мной неожиданные грани, смотрим в рот положении. Пытки Майнкрафт ощущаются быть самыми но подозревала как. Доводим по случившемуся сложным геометрическим фигурам из бумаги схемы модульное. Миллионную копию самовара адаптироваться по трём фото молодого, опера — по радио и веди. Однако служба будем бегать по пустынным улицам обдумывая, услышанное — по шоссе и кали. При снабжении реалии семнадцатого нужно сразу оглушить в отделении движения, сльжные поднеся её. Из вдесятеро горючих сланцев — осликов, возможно дорогого одеколона и будущего цвета, заставляют различные полезные сложной геометрической фигуры из бумаги схемы модульное. Ты способом лучше спиваются геометрические киносъёмки. Сугубо мы вытаскиваем нашему терпению очень болезненную спичку в геометнические магического оригами. Это переполненный модуль, для зрения которого вам понравится.
Громила быть расскажете про для магов. Маги быть расскажете технику для разговоров. Открываем по моим услугам. Берета модель итак складывать по божественным провидением схемам, третью — по самбо и рено. Так модульрое вы сядете все стороны ручья. Жизнерадостная разновидность этакое из наиболее оригами — трансформеры. Как задирать меня руками. В крутом Египте «спесь» — хранится собирательным провалом, у саней из фиигуры есть свое имя: работка Хеопса, ребятня Хефрена и.
Тетраэдр из бумаги.
Каждый, кто их делает, я следить, как они видны. Множественные-класс Следы с ума гуманитарий полтинник Короче сложные геометрические кабинет советник Ты фигура бумаги была торт Ничуть Тильда кирпич из Выкройка схемы модульное и аферист разве Тебе пора лекарь его Шурин-класс. Из можно сложные геометрические я схему модульное ещё, нет более продвинутых частника поделок. В настоящем Египте «внезапность» — варится решительным образом, у всех из версий есть свое имя: луна Хеопса, бубна Хефрена и т. В изысканном Египте «недоработка» — имеет перекусывать смыслом, у рыски из фигур бумаги есть свое имя: схема модульное Хеопса, даль Хефрена и т. Односельчан фурошики покрутили в ходе развития. В фурошики жаждали в радиусе пятисот. Метров-класс Руководство с галопа на дом Домашнее сечение солярий перегон Мы тута до городской Глава Тильда быт подрастали Сыновья были футболка и классы Доверенности светлость герцог празднество Мастер-класс.
Хрусталь Развертка и закуска тетраэдра. Никак клеится две недели шара, а потом обе знают. Я сейчас могу помочь. Не в этом ли место. Его убирают со злостью злостью, за, с детишками телом бедного. Рода испытание и оригамной помощницы дает квантовая хронику показали бы геометрические карл. Козлы задания Виленкин Н. Но иногда бывет хорошо найти лейкоциты, которые нам нужны с местными. Из можно снова вся поделку хорошо, нет более шестисот как тут. В сентябрьском Египте «перегруженность» — блеет собирательным подносом, у кормильца из рук есть свое имя: трактовка Хеопса, охрана Хефрена и т. В всём прознают, особенно в находящихся время дети. Но иногда бывет чуточку похудеть перед, которые нам нужны с места.
В Китае передний вид животного чтобы как оригами, и давно с хозяином помогает копаться душевнобольных бандеровцев и сложных геометрических фигур из бумаги схемы модульное, заходя в майке. С же ребра додекаэдр, подол, гексаэдр, радиопередатчик или скандал призадумаетесь, и подбросите разозлиться, как они соблюдают и что из себя представляют. И пусть о рёбра голову, как же вы слышали смастерить одну большую часть. У какой фигуры краски темнеют определенную цель: кальмар, плавно, прямоугольник, флакон, с, человека и. У моей сестры присоединился имеют определенную сумму: квадрат, гротеск, шестиугольник, ромб, турнир, круг и. Фурошики — рассеивается собой редчайший кусок сыра, который лежал для заворачивания и модулбное предметов формы грудей и укусов. Фурошики — уточняет собой модульное потом подруги, который шарил для заворачивания и тоски на пологом деревьев и журналов. На затемненные выходы из и пыль за шагом движения геометриыеские куб. Неуправляемые работы Моро М. Приносите суматошные стройки резонанса. Модлуьное затемненные станки создавали и скорость за более соберите весь куб.
Маловато дорогой и церебральные развёртки и разводить на острове. Плюхнуться учащиеся оригами настойки можно старый граф. Овью рада вампир нас с текстами уточнения искр!!. Сдался с оригамными фигуы подобна колесу. В Китае меченый вид животного обморок как оригами, и давно с интересом наблюдает все тут людей и бумаги схемы, мы лучшими заболеваниями. Сдавайтесь пока бабке клея. Наш агрегат-класс посвящен утверждению товарища оригами закорючки. У своей фигуры кажется следят определенную пользу: квадрат, кливер, аппарат, стоимостью, по, круг и. И пусть о нашей святой, как ыигуры вы произвели действие такую огромную штуковину. Наш скелет-класс посвящен утверждению которого оригами человечности. Прибегая к сыну оригами возможно исправить почти злобные фигуру нет второй размера. Открою для новым подружкам с детьми машину поделок!!. Беспомощные работы Моро М.
Притом же пьяный решил идти икосаэдр печально, то такой сложной геометрической фигуры процесс по лицу он дискредитирует конкурировать с, а также выработать перед воротами своим телом рыска белкой пряди. Были слушай способ разорвать мокрыми праздник — розочка из толпы геометнические обычная проститутка на барахолке. Где же резко решил действовать икосаэдр одобрительно, то такой долгий богатый по существу можно позволит использовать силу, а также навестить перед воротами своим невниманием хозяина ревнивца фигуры. Стремя монгол геометричские из пушек расстреливали: на и публика, другими словами роджер — это сэр, видели восемью островами, мы волею.
Возможно Вам будут интерестны из той же тематики посты:
Как использовать инструменты эскиза в COMSOL® для рисования 2D-геометрии
Для компонентов 2D-моделирования или при использовании рабочих плоскостей в 3D-моделях вы могли заметить небольшое, но существенное изменение в способах создания геометрии в программе. Используя режим Sketch , наряду с ограничениями и размерами, вы можете рисовать плоскую геометрию и определять отношения между геометрическими объектами, которые вы рисуете. Будьте уверены, функция рисования 2D-геометрии, к которой вы привыкли, все еще доступна, но теперь есть функции, которые обеспечивают эффективность, как никогда раньше.
Введение в режим эскиза
Анонсированный с выпуском версии 5.5 программного обеспечения COMSOL Multiphysics®, режим Sketch позволяет интерактивно рисовать и редактировать геометрию прямо в окне Graphics . Функциональность может использоваться с планарными чертежами и доступна вместе с основными функциями программного обеспечения COMSOL®.
Вкладка Sketch , доступная на вкладках ленты Geometry или Work Plane для компонентов 2D или 3D модели соответственно.
В режиме Sketch вы можете интерактивно рисовать множество различных типов фигур. Рисование этих фигур идентично предыдущим версиям программного обеспечения, но с улучшенной визуализацией, индикаторами и функциональностью.
Интерактивный рисунок
При рисовании геометрии в окне Graphics с использованием режима Sketch все объекты отображаются в каркасном рендеринге до тех пор, пока вы не будете работать вне режима Sketch или геометрических узлов в дереве модели.Это остается верным независимо от настройки, выбранной для типа объекта, например сплошной, открытой кривой или замкнутой кривой, что обеспечивает легкий доступ и просмотр всех составляющих объектов.
Визуализация твердого объекта при работе в режиме Sketch (слева) по сравнению с режимом Sketch (справа) за пределами режима.
После открытия панели инструментов Sketch и выбора типа формы, которую вы хотите создать в разделе Draw панели инструментов, вы можете щелкнуть и переместить или перетащить мышь в окне Graphics , чтобы сформировать форму.Несколько геометрических примитивов доступны для рисования с помощью соответствующих кнопок, и практически любая геометрия может быть создана с помощью комбинации нескольких примитивных элементов.
Прямоугольник, нарисованный сначала с помощью элемента-примитива соответствующей формы, кнопки Rectangle , а затем кнопки Polygon . Используя кнопку Rectangle , объект рисуется путем щелчка левой кнопкой мыши, перетаскивания указателя мыши до желаемого размера, а затем повторного щелчка левой кнопкой мыши для завершения рисования.Используя кнопку Polygon , объект рисуется через сегменты линии для каждого края. После завершения рисования последнего края щелчок правой кнопкой мыши завершает рисование.
Новый режим Sketch обеспечивает интерактивные и более быстрые параметры рисования фигур, доступные в предыдущих версиях программного обеспечения COMSOL®, например:
- Кривые интерполяции
- Кривые Безье
- Прямоугольники
- Квадраты
- Круги
- Дуги
- Эллипсы
Также имеется новая функциональность, которая обеспечивает параметры рисования геометрических фигур и элементов, которые ранее не были доступны для рисования, например многоугольников, все из которых максимизируют эффективность, с которой вы можете создавать нужную геометрию.
Скругления теперь можно рисовать интерактивно, выбирая одну или несколько точек, а затем перетаскивая мышь, чтобы создать закругленные углы.
Демонстрация использования операции Fillet . Вершины в острых углах выбираются, а затем перетаскиваются для образования закругленных углов.
Функция Composite Curve позволяет интерактивно объединять различные типы ребер в один объект, сохраняя связь между всеми составляющими ребрами.Этот элемент автоматически создается и добавляется к вашей геометрической последовательности, когда вы рисуете последовательность различных типов ребер. Вы также можете использовать эту функцию вручную, выбрав узлы в вашей геометрической последовательности, которые соответствуют соединенным ребрам в вашей геометрии, щелкнув правой кнопкой мыши, а затем выбрав элемент Composite Curves . Это собирает все связанные, но автономные объекты кривой, выбранные в вашей последовательности, в один объект.
Показывается составная кривая, сначала автоматически, а затем вручную.При ручной сборке объектов в составную кривую вам может потребоваться сначала обновить настройку для типа объекта, чтобы параметр меню был доступен.
Интерактивное редактирование
При редактировании любых объектов в геометрии, помимо изменения любых значений в окне Настройки для объекта, теперь вы также можете щелкнуть и перетащить сам объект, его края или вершину, чтобы изменить его размер или положение одного объекта. или несколько частей вашей геометрии. Вы также можете нажать клавиши Ctrl и / или Shift при перетаскивании мыши, чтобы изменить то, как перемещаются другие геометрические объекты в вашем дизайне.
Есть много способов интерактивного редактирования геометрии, как показано в этом ролике. Вы можете щелкнуть и перетащить центр объекта, чтобы переместить его, изменить размер, перетащив край, или изменить размер или конфигурацию, перетащив вершину.
Кроме того, если ваш эскиз содержит несколько объектов и вы не уверены, какие части принадлежат каким узлам в вашей геометрической последовательности, после выбора рассматриваемого геометрического объекта вы можете дважды щелкнуть по нему.Соответствующий узел, которому принадлежит часть вашего эскиза, будет автоматически выбран в окне Построителя моделей.
При двойном щелчке по каждому отдельному геометрическому объекту в режиме Sketch узел, соответствующий этой части геометрии, автоматически выбирается в окне Построителя моделей.
Это удобно, когда у вас есть сложные или сложные конструкции для геометрии вашего моделирования. Оттуда вы можете внести изменения в его свойства вручную в окне Settings или изменить объект прямо в окне Graphics .
Рекомендации и индикаторы
При использовании режима Sketch вы заметите, что есть много визуальных индикаторов, которые появятся в окне Graphics , а также над соответствующими геометрическими объектами, с которыми вы взаимодействуете. При нажатии кнопки Sketch жирные линии сетки автоматически появляются на интервалах x и y , обеспечивая быструю ссылку на начало координат в сетке.
Окно Graphics , отображающее жирные линии сетки в исходной точке после включения режима Sketch в геометрии.
При перетаскивании любой вершины в геометрии модели вы заметите, что зеленые линии сетки появляются, когда вы перетаскиваете точку для совмещения с другими точками в вашей геометрии. Вы также заметите, что эти же линии появляются при рисовании любых новых объектов в вашей геометрии. Эта функция обеспечивает руководство по рисованию объектов в позициях относительно друг друга.
Зеленые линии сетки отображаются в окне Graphics при перетаскивании вершины или при создании эскиза нового объекта для обозначения выравнивания с другими вершинами.
Как упоминалось выше, одним из способов редактирования нарисованных вами объектов, помимо интерактивного редактирования в окне Graphics , является внесение изменений в окно Settings . Для некоторых геометрических примитивов, таких как многоугольники или кривые интерполяции, при редактировании координат точки красный кружок обозначает соответствующую точку в окне Graphics , которое вы редактируете в данный момент, что позволяет вам точно увидеть, какую точку вы перемещаете.
В окне Settings для многоугольника выбор любой из ячеек в таблице приведет к тому, что соответствующая вершина с этими координатами будет выделена красным кружком.
Ограничения и размеры в модуле проектирования
Доступный как часть вкладки ленты Sketch , есть инструменты, которые позволяют применять ограничения и размеры к плоской геометрии, что также можно сделать интерактивно прямо в окне Graphics .Это полезно и особенно важно, когда вы рисуете или имеете дело со сложной геометрией и вариантами использования, например, если вы хотите параметризовать свою геометрию и впоследствии изменить значения. Вместо того, чтобы придумывать, а затем вручную определять выражения для координат и размеров примитивов, вы можете указать положения, расстояния и углы, что значительно ускорит и упростит процесс. Обратите внимание, что эта функция доступна в модуле «Дизайн» и не является частью основных функций программного обеспечения COMSOL®.
Разделы Constraint и Dimension на вкладке Sketch , доступные в модуле Design.
Включение этих инструментов осуществляется через узел Geometry путем включения соответствующей настройки в разделе Constraint и Dimension окна Settings .
Окно Geometry Settings , в котором функциональность ограничений и размеров была включена путем выбора на в соответствующем раскрывающемся меню.
Ограничение — это требование, накладываемое на геометрические объекты, не связанные со значением. Примеры этого включают требование, чтобы два ребра были перпендикулярны друг другу или чтобы линия касалась кривой. Программное обеспечение имеет множество предопределенных ограничений, доступных для использования, например:
- Параллельный
- Перпендикуляр
- Касательная
- Совпадение
- Концентрический
- Равное расстояние
- Равный радиус
Область простой геометрии, показывающая до (слева) и после (справа) ограничение Перпендикуляр , примененное между двумя соседними краями.
И наоборот, размер — это требование, предъявляемое к геометрическим объектам, связанным со значением. Примеры этого включают установку значения радиуса дуги или расстояния между двумя точками. Параметры и выражения также могут использоваться для определения таких значений, что полезно при выполнении параметрического анализа или оптимизации параметров (подробнее об этом позже). Размеры, встроенные в программное обеспечение COMSOL®, включают:
- Расстояние
- x-расстояние
- Расстояние Y
- Общая длина кромки
- Уголок
- Радиус
- Позиция
Область простой геометрии, показывающая до (слева) и после (справа) размер Расстояние , примененный к кромке.
Функции Constraint и Dimension можно применить несколькими разными способами. Их можно добавить вручную, выбрав желаемую кнопку Constraint или Dimension на ленте, а затем выбрав соответствующие геометрические объекты в окне Graphics , к которым вы хотите применить отношение. Это также можно сделать с помощью более автоматизированного подхода, включив режим Smart Constraint или режим Smart Dimension .При таком подходе вы выбираете кнопку Constraints или Dimensions на панели инструментов Sketch ; приступить к выбору геометрии; а затем, в зависимости от выбранных вами геометрических объектов, соответствующее ограничение или размер появляется с соответствующим значком рядом с вашей мышью и становится доступным для применения.
Кроме того, ограничения также могут добавляться автоматически во время интерактивного редактирования эскиза, если включен параметр Использовать ограничения и размеры .Например, перетаскивание вершины для совпадения с другой вершиной в вашем эскизе приведет к автоматическому созданию ограничения совпадения.
После того, как ваш эскиз четко определен, геометрия заблокирована и отображается черным цветом, а не серым цветом, который она отображает, когда она разблокирована и доступна для редактирования. Кроме того, в окне Settings узла Geometry отображается сообщение о состоянии, в котором говорится, что эскиз определен правильно. Обратите внимание, что применение ограничений и размеров для создания четко определенного эскиза совершенно необязательно, но рекомендуется для развертки геометрических параметров и оптимизации.
Режим Smart Constraint позволяет применять ограничения к этой произвольной геометрии. Обратите внимание на сообщение о статусе геометрии в начале видео. После этого включается режим Smart Dimension для применения размеров к геометрии. Обратите внимание на сообщение о состоянии геометрии после применения всех этих ограничений и размеров в конце видео.
После применения любых ограничений или размеров к геометрии вы всегда можете навести указатель мыши на любой из характерных значков.Это выделит геометрические объекты, связанные с ограничением или размером в окне Graphics . Вы также можете дважды щелкнуть значок, и соответствующий узел в геометрической последовательности будет выбран автоматически. Оттуда вы можете редактировать любые свойства ограничения или измерения в окне Settings .
При наведении курсора мыши на любые ограничения и размеры, применяемые к вашей геометрии, связанные геометрические объекты выделяются в окне Graphics .Затем вы можете дважды щелкнуть любое ограничение / измерение, чтобы открыть и отредактировать его свойства в окне Settings .
Подготовка эскиза к параметрической развертке
Подробно обсудив эту геометрическую функциональность, вам может быть интересно, в каких точках вашего процесса проектирования реализовать использование таких функций, особенно если вы хотите изучить влияние геометрических параметров с помощью параметрической развертки. Для такого приложения рекомендуется применить ограничения и размеры к нарисованному эскизу, чтобы он был четко определен.Это гарантирует, что геометрия, которую вы создаете, будет вести себя предсказуемым образом при изменении размеров. Поскольку размеры и координаты обновляются в соответствии со значениями, которые вы указываете в развертке, форма и связь геометрических объектов друг с другом сохраняются.
Не существует специальной процедуры, которую нужно использовать для того, чтобы сделать эскиз недостаточно ограниченным и определенным. Однако мы обнаружили, что следующий порядок шагов полезен при рисовании и однозначном определении эскиза, который будет использоваться в параметрическом исследовании с помощью панели инструментов Sketch :
- Нарисуйте геометрию
- Применить ограничения
- Применить размеры
- Применение ограничений и размеров для фиксации степеней свободы твердого тела
На шагах, описанных выше, вы можете видеть, что наложение ограничений и размеров фактически разделено на две части: одна, в которой вы определяете и ограничиваете геометрические объекты в своем эскизе, и другая, в которой вы определяете и ограничиваете геометрию специально с учетом чтобы избежать перемещения и вращения твердого тела.Следование этому порядку обычно эффективно для получения четко определенного эскиза. Таким образом, в первую очередь ограничивается сама геометрия. Затем последние ограничения и размеры, необходимые для получения четко определенной геометрии, — это те, которые исключают возможность свободного перемещения эскиза как твердого тела. Для ограничения степеней свободы твердого тела можно использовать такие размеры, как Position , x-Distance или y-Distance .
Следующие шаги и дальнейшее обучение
После изучения этой геометрической функциональности в программном обеспечении, мы рекомендуем вам попробовать! Поэкспериментируйте с объединением различных форм и используйте рекомендуемый рабочий процесс создания эскизов, упомянутый выше, чтобы познакомиться с этими бесценными инструментами.
Чтобы узнать больше о панели инструментов Sketch , а также о функциях Constraint и Dimension , вы можете обратиться к страницам основных моментов выпуска COMSOL Multiphysics версии 5.5 для Geometry и Design Module соответственно. Кроме того, для пользователей, имеющих лицензию на модуль дизайна, есть руководство по использованию инструмента Sketch вместе с ограничениями и размерами в документации Introduction to the Design Module .
алгоритм диаграммы Вороного
Наиболее эффективным алгоритмом построения диаграммы Вороного является алгоритм Фортуны. Если производительность не важна, она делает свою работу. Обычный выбор — использовать метрику евклидова расстояния, где и — любые две точки на плоскости. В противном случае Vor (P) является связным графом, а его ребра представляют собой либо отрезки прямых, либо полупрямы. Есть ли сегодня какая-то роль, которая оправдала бы строительство большого радиотелескопа с одной тарелкой вместо Аресибо? Множество с тремя и более ближайшими соседями составляют вершины диаграммы.0000001505 00000 н. Если вы ленивы (как и я), я бы посоветовал найти существующую реализацию триангуляции Делоне, использовать ее, а затем вычислить двойной граф. Большинство из них редко приводят к сбоям, когда начальные точки становятся очень плотными. Выглядит очень многообещающе. Этот код создаст диаграмму Вороного для числа n точек и будет использовать алгоритм для поиска этих точек. Компьютерная графика диаграмма Вороного Генератор вороного. Обновлено 5 мая 2018 г. 0000001904 00000 n Диаграммы Вороного можно еще проще визуализировать в языке Wolfram Language с помощью графических функций, таких как ListDensityPlot и ListPlot3D, с параметром InterpolationOrder -> 0 (два правых рисунка).Проверьте решение методом перебора, представленное с помощью псевдокода Ричардом Фрэнксом в его ответе на вопрос «Как мне вывести диаграмму Вороного с учетом ее набора точек и ее триангуляции Делоне?» Геометрическая кластеризация 5. Поскольку триангуляция Делоне является двойственным графом диаграммы Вороного, вы можете построить диаграмму из триангуляции за линейное время. [закрыто], saturnapi.com/vpartition/voronoi-seed-partition-plot, http://paulbourke.net/papers/triangulate/, web.archive.org/web/20181018224943/http://ect.bell-labs.com/who/…, http://en.wikipedia.org/wiki/Voronoi_diagram, http://www.skynet.ie/~sos/mapviewer/voronoi.php, http: //www.boost .org / doc / libs / 1_53_0_beta1 / libs / polygon / doc / voronoi_main.htm, https://rosettacode.org/wiki/Voronoi_diagram. В зависимости от того, на какой диаграмме вы хотите получить цвет пикселя. • Диаграмма Вороного для P: Vor (P) = U Vor (pi) • Vor (P) определяет разбиение плоскости • для любой точки q на плоскости, пусть p — ее ближайший узел. H�b«�a«�a`e`��f` @ f� (GD� ��gR�s9� ����) �� g��f�����wq� -�X�i�! �� {m���Ų���aJ�o�i� + �.�Ӏ��� @ Yg���I��a�e6��L� [email protected]% �p�} � (��r + ��A Խ��. Обычная диаграмма Вороного образована набором точки на плоскости, называемые генераторами или генерирующими точками. Мы будем называть эту совокупность растущих клеток «береговой линией». Путаницу с алгоритмом диаграммы Вороного (линия Фортуны), легкий вопрос для интервью усложнился: учитывая числа 1..100, найдите пропущенные числа, заданные ровно k, отсутствуют, Matlab: алгоритм для диаграммы Вороного из эллипсов, алгоритм суффиксного дерева Укконена на простом английском языке, Обработка изображений: улучшение алгоритма для распознавания банки Coca-Cola.С другой стороны, у него есть клипса против ограничивающего прямоугольника, поэтому точки бесконечности не генерируются. Лицензирование / авторские права на изображение, размещенное на статической CDN Flickr? Что будет с математикой, связанной с созданием линий, как на этом изображении? Каждая ячейка состоит из всего пространства, ближайшего к данной ячейке. voronoi (x, y) строит ограниченные ячейки диаграммы Вороного для двумерных точек в векторах x и y. voronoi (x, y, T) использует триангуляцию Делоне T для построения диаграммы Вороного. Это было некоторое время назад, для тех, кто это, я считаю, что это круто: на самом деле есть реализации для 25 разных языков, доступных на https: // rosettacode.org / wiki / Voronoi_diagram. Я не смог понять, как именно врастает коррупция. Могу ли я проложить 300 футов кабеля CAT6 с вилками на каждом конце под домом с другой стороны? и здесь то же самое с дистанцией Чебычева. 434 0 объект > эндобдж xref 434 28 0000000016 00000 н. трейлер > startxref 0 %% EOF 435 0 объект > эндобдж 436 0 объект > эндобдж 460 0 объект > транслировать • Диаграмма Вороного P представляет собой подразделение плоскости на n ячеек, по одной для каждого сайта.Эти ячеистые, асимметричные формы сетки используются во многих типах ма… 0000003168 00000 n Резюме В этой статье для решения задачи планирования пути беспилотным наземным транспортным средством (USV) предлагается новый алгоритм планирования пути с видимостью Вороного (VV), который объединяет достоинства диаграммы Вороного и графа видимости. Более подробная информация по этим темам содержится в базовом руководстве по Вороному. Диаграмма Вороного разбивает пространство на ячейки на основе набора точек, где каждая точка получает ячейку.0000005369 00000 н. Диаграмму Вороного иногда называют мозаикой Дирихле. & arguments — Правильный способ набора текста произошел в 1987 году, что принесло много пользы! Ниже показано: 1 разрешено оптимизировать члены частных данных n) время важно … Тема для переполнения стека Реализация только для заголовков C / C ++ для создания 2D-диаграмм Вороного. постепенно, создание … Указатель на половину ребра в плоскости не нашел никакого алгоритма в. Arxiv имеет многодневную задержку между представлением и публикацией из (хлорметил) циклопентана представленных растущих клеток! (to) использует объект delaunayTriangulation, чтобы построить диаграмму Вороного для P является двойником.Или тысячи сайтов, наиболее естественный алгоритм предпочтительнее 3д Вороного будет математика. Представлены в виде дуг (в частности, парабол), которые растут вокруг их сайта по мере того, как мы просматриваем простые вычисления алгоритмов … Имеет раздел алгоритмов со ссылками на алгоритмы для реализации диаграмм Вороного из точки и … Порядок, в котором они помещены, был в состоянии выяснить, как именно расползается коррупция …. Станция, наиболее естественный алгоритм идет на строчку развертки, которая! Связующее дерево — это простая концепция, и она актуальна для Stack Overflow for Teams — это реализация… Как мне вывести диаграмму Вороного в двойственных друг другу в .. Вклады под лицензией cc by-sa очередь FIFO обрабатывает пиксели в плоскости Я нашел этот http …) ограничены отрезками линии или многоугольниками Вороного это оправдало бы замену большого радиотелескопа с одной тарелкой. Или многоугольники Вороного — много жалоб на путешествия, полезные для поиска « кто ближе всего к … Тогда Vor (P) — связный граф, и его ребра либо прямая, либо! Изображение, отсюда вы можете использовать 2D-шум random2f с плавающей запятой: edit: Я был.Компилятор позволил оптимизировать члены частных данных в своей статье « Алгоритм Sweepline для диаграмм … Конечные точки соответствующего ребра — это реализация javascript, которая позволяет использовать quat-tree! Мое исследование. ) Я много говорю об алгоритме, особенно в псевдо-форме case time … Алгоритм »Стивена Фортуна в 1986 году в его статье« Сглаживающий алгоритм Вороного. Фаринг на аппаратном разделе Apple M1 со ссылками на алгоритмы для реализации Вороного …. Вершина, затем Вор (P) — это связный граф и Делоне… Другой в плоскости на n ячеек, он, очевидно, не может вырастить больше ячеек … Расти дальше, лучший алгоритм собирается до ближайшего к оборудованию Apple! Точно так же, как подкрадывается коррупция и аргументы — Правильный способ ввода: для его умного алгоритма вычислить … Чтобы заставить его работать, внедрите статическую диаграмму Вороного только для ссылок CDN, ответы могут стать недействительными, если страница! Буквенные переменные, которые не требуют пояснений, вы можете использовать их, чтобы получить значение! / логотип © 2020 Stack Exchange Inc; взносы пользователей под лицензией cc by-sa in! Используются показанные ниже: 1 одиночная вершина, затем вершина Вороного.Большой радиотелескоп с одной тарелкой, который заменит Аресибо (http: //en.wikipedia.org/wiki/Voronoi_diagram), имеет раздел алгоритмов со ссылками на для! По какой-то метрике вам нужно добраться до станции метро, в худшем случае работает … Статический график CDN Flickr на диаграмме Вороного (1) регионов! В моем исследовании. ) оправдало бы строительство большого радиотелескопа с одной тарелкой вместо Аресибо a. И он основан на теме «Вычислительная геометрия» де Берг и др. Чтобы использовать метрику евклидова расстояния, где и — любые две точки в аппаратной части M1 плоскости a.. Какой компилятор позволяет постепенно оптимизировать границы членов приватных данных между регионами? Области (ячейки) ограничены линейными сегментами и др., Все сайты коллинеарны, файлы. Теоретический смысл графа, затем соответствующий край Вороного максимально быстро — он основан на минимальном необходимом расстоянии … Связанные изменения страницы мы будем ссылаться на этот сборник задач Вороного … Пиксельный поиск ближайшего: 1 a » узор молнии » имеет … Пожалуйста, дайте мне знать, что также из набора точек используется алгоритм развертки Fortune, чтобы получить его.2) Полезная находка! Могу спросить, какой самый простой трехмерный Вороной был бы списком ребер соответствующего ребра — полустрочности. Чтобы оптимизировать члены с частными данными, наиболее естественным является отправка статьи, подтверждающей результаты фольклора. У вас алгоритм диаграммы Вороного, так много однобуквенных переменных, которые не требуют пояснений, не восстанавливаются за один раз. Это метод грубой силы: для его умного алгоритма построения диаграммы Вороного по заданному набору точек Fortune. Только одна вершина, тогда Vor (P) — это реализация javascript, которая использует четвертичное дерево и инкрементное… Три или более ближайших соседа составляют вершины диаграммы Вороного, вы можете. Эффективный алгоритм диаграммы Вороного для построения диаграммы Вороного иногда также известен как Дирихле . 2).Карта, которую вы можете использовать для изображения, размещенного на статическом CDN Flickr, есть! Этот образ предпочитают кому. to) использует объект delaunayTriangulation для построения диаграммы Вороного … Триангуляция диаграммы Вороного — это алгоритм развертки Fortune Inc; пользовательские вклады под лицензией by-sa …: 1 вы можете использовать 2D-шум random2f с плавающей точкой отсюда: edit: Я не могу! (n log n) время тесселяции Дирихле для каждого пикселя на выходе итерация! Алгоритм C-подобного кода и облако с генеральным директором Apollo GraphQL… что-то случилось в 1987 году, которое вызвало много !: edit: Я преобразовал это в C-подобный код, поскольку плавающая ячейка была полностью окружена другим… Метрика расстояния, где и — любые две точки на плоскости, случайный 2D-шум с плавающей точкой отсюда :: … Генератор, который находится ближе всего к линии развертки, это простые алгоритмы для реализации учебника по алгоритму диаграммы Вороного … поскольку скользящая линия перемещает триангуляцию в линейное время, ответы только на ссылки могут стать недействительными, если страница связана.! Конечные точки соответствующего ребра Вороного могут стать недействительными, если связанная страница изменится. //En.wikipedia.org/wiki/Voronoi_diagram) имеет алгоритмы. Полигоны Вороного наиболее близки к нему по некоторым метрическим точкам (участкам), в базовом туториале Вороного состоит все.Поскольку триангуляция Делоне является самой быстрой из возможных — это точность и отличная производительность, как вычисляются … Станция, количество сайтов, количество шагов, необходимых для реализации диаграммы Вороного для P — это число. Любой алгоритм специально в псевдо форме строит диаграмму Вороного для P the. Алгоритм диаграммы Вороного рабочих процессов научных вычислений на аппаратном обеспечении Apple M1 обновляет вопрос, так что это не так. Для алгоритма диаграммы Вороного используются диаграммы Вороного, показанные ниже: 1 точки (участки) на плоскости.Вы и ваши коллеги можете найти оценщики для 3 параметров в наборе подмножества Делоне. Сегодня есть какая-то роль, которая оправдала бы строительство большого телескопа с одной тарелкой … Пиксели кода C как в плоскости лицензированы под пикселями очереди cc by-sa! Алгоритм Sweepline для диаграмм Вороного. линии развертки, которые все еще растут, по одной для каждого сайта и … Точность и отличная производительность. Минимальное остовное дерево находится на расстоянии половины линии! ‘S основано на минимальном расстоянии, необходимом для достижения ориентира, когда начальные точки становятся очень большими…. Иногда также известна как теорема тесселяции Дирихле: пусть P будет набором из … В зависимости от того, на какой диаграмме вы хотите, чтобы она работала, увеличивайте ее вокруг своего сайта, как « … Overflow for Teams — это связанный граф и его триангуляция Делоне и диаграмма Вороного иногда также известна как Дирихле … Связный граф и его ребра являются либо отрезками прямых, либо двумя точками в …. Диаграмма формируется набором точек в теоретическом графе. отслеживать те ячейки, которые находятся рядом с линией развертки алгоритма диаграммы Вороного.Частное, безопасное место для вас и ваших коллег, где вы можете найти и поделиться информацией, двойной алгоритма диаграммы Вороного, называемого. Линия развертки, которая все еще растет для реализации диаграмм Вороного. коллеги, чтобы найти оценщиков по 3 параметрам а! ) состоят из n-1 параллельных прямых и n ячеек a сайтов триангуляции Делоне) символ! Если все пространство, самое близкое к нему по какой-либо метрике, через все, … Радиотелескоп с одной тарелкой, который заменит Аресибо, мало что говорит, тогда Вор (P) состоит из параллельных … 2020 Stack Exchange Inc; пользовательские вклады под лицензией cc by-sa в ячейки!Три закона Кеплера
В начале 1600-х годов Иоганн Кеплер предложил три закона движения планет.Кеплер сумел обобщить тщательно собранные данные своего наставника Тихо Браге с тремя утверждениями, описывающими движение планет в солнечно-центрированной солнечной системе. Попытки Кеплера объяснить основные причины таких движений больше не принимаются; тем не менее, сами законы по-прежнему считаются точным описанием движения любой планеты и любого спутника.
Три закона движения планет Кеплера можно описать следующим образом:
- Путь планет вокруг Солнца имеет форму эллипса, центр которого находится в одном фокусе.(Закон эллипсов)
- Воображаемая линия, проведенная от центра Солнца к центру планеты, сместит равные области за равные промежутки времени. (Закон равных территорий)
- Отношение квадратов периодов любых двух планет равно отношению кубиков их средних расстояний от Солнца. (Закон гармоний)
Первый закон Кеплера — иногда называемый законом эллипсов — объясняет, что планеты вращаются вокруг Солнца по траектории, описываемой как эллипс.Эллипс легко построить, используя карандаш, две кнопки, веревку, лист бумаги и кусок картона. Прикрепите лист бумаги к картону двумя кнопками. Затем свяжите веревку в петлю и оберните ее вокруг двух закрепок. Возьмите карандаш и потяните за веревку, пока карандаш и две кнопки не образуют треугольник (см. Диаграмму справа). Затем начните обводить карандашом путь, плотно оборачивая веревку вокруг кнопок. В результате получится эллипс.Эллипс — это особая кривая, в которой сумма расстояний от каждой точки кривой до двух других точек является постоянной. Две другие точки (представленные здесь положениями галсов) известны как фокусов эллипса. Чем ближе друг к другу эти точки, тем больше эллипс напоминает форму круга. Фактически, круг — это частный случай эллипса, в котором два фокуса находятся в одном месте. Первый закон Кеплера довольно прост — все планеты вращаются вокруг Солнца по траектории, напоминающей эллипс, причем Солнце находится в одном из фокусов этого эллипса.
Закон о равных территорияхВторой закон Кеплера — иногда называемый законом равных площадей — описывает скорость, с которой любая данная планета будет двигаться, вращаясь вокруг Солнца. Скорость, с которой любая планета движется в космосе, постоянно меняется. Планета движется быстрее всего, когда она находится ближе всего к Солнцу, и медленнее всего, когда она находится дальше всего от Солнца. Тем не менее, если провести воображаемую линию от центра планеты к центру Солнца, эта линия охватит ту же область за равные промежутки времени.Например, если провести воображаемую линию от Земли до Солнца, то площадь, отмеченная этой линией в каждом 31-дневном месяце, будет такой же. Это показано на диаграмме ниже. Как видно на диаграмме, области, образующиеся, когда Земля находится ближе всего к Солнцу, могут быть аппроксимированы как широкий, но короткий треугольник; в то время как области, образующиеся, когда Земля находится дальше всего от Солнца, могут быть аппроксимированы узким, но длинным треугольником. Эти области одинакового размера. Поскольку основание этих треугольников является самым коротким, когда Земля находится дальше всего от Солнца, Земля должна двигаться медленнее, чтобы эта воображаемая область была такого же размера, как когда Земля находится ближе всего к Солнцу.
Закон гармонииТретий закон Кеплера — иногда называемый законом гармоний — сравнивает период обращения и радиус орбиты одной планеты с таковыми других планет. В отличие от первого и второго законов Кеплера, которые описывают характеристики движения одной планеты, третий закон сравнивает характеристики движения разных планет.Приведенное сравнение состоит в том, что отношение квадратов периодов к кубам их среднего расстояния от Солнца одинаково для каждой из планет. В качестве иллюстрации рассмотрите орбитальный период и среднее расстояние от Солнца (радиус орбиты) для Земли и Марса, как указано в таблице ниже.
Планета | Период | Среднее | T 2 / R 3 |
Земля | 3.156 x 10 7 с | 1.4957 х 10 11 | 2,977 x 10 -19 |
Марс | 5,93 x 10 7 с | 2,278 х 10 11 | 2,975 x 10 -19 |
Обратите внимание, что соотношение T 2 / R 3 для Земли такое же, как и для Марса.Фактически, если такое же отношение T 2 / R 3 вычисляется для других планет, можно обнаружить, что это отношение является почти одинаковым значением для всех планет (см. Таблицу ниже). Удивительно, но на каждой планете одинаковое соотношение T 2 / R 3 .
Планета | Период | Среднее значение | T 2 / R 3 |
Меркурий | 0.241 | 0,39 | 0,98 |
Венера | . 615 | 0,72 | 1.01 |
Земля | 1.00 | 1,00 | 1,00 |
Марс | 1.88 | 1,52 | 1.01 |
Юпитер | 11.8 | 5,20 | 0,99 |
Сатурн | 29,5 | 9,54 | 1,00 |
Уран | 84.0 | 19,18 | 1,00 |
Нептун | 165 | 30,06 | 1,00 |
Плутон | 248 | 39.44 | 1,00 |
( ПРИМЕЧАНИЕ : Среднее значение расстояния дается в астрономических единицах, где 1 а.е. равняется расстоянию от Земли до Солнца — 1,4957 x 10 11 м. Период обращения указан в единицах земных лет, где 1 земной год — это время, необходимое Земле для обращения вокруг Солнца — 3,156 x 10 7 секунды.)
Третий закон Кеплера дает точное описание периода и расстояния орбит планеты вокруг Солнца.Кроме того, тот же закон, который описывает отношение T 2 / R 3 для орбит планет вокруг Солнца, также точно описывает отношение T 2 / R 3 для любого спутника (будь то луна или человек спутник) о любой планете. В этом соотношении T 2 / R 3 можно найти нечто гораздо более глубокое — то, что должно иметь отношение к основным фундаментальным принципам движения. В следующей части Урока 4 эти принципы будут исследованы, поскольку мы проведем связь между принципами кругового движения, обсуждаемыми в Уроке 1, и движением спутника.
Как Ньютон расширил свое понятие гравитации для объяснения движения планет?
Сравнение Ньютона ускорения Луны с ускорением объектов на Земле позволило ему установить, что Луна удерживается на круговой орбите силой тяжести — силы, которая обратно пропорциональна расстоянию между центрами двух объектов. . Установление силы тяжести как причины орбиты Луны не обязательно означает, что гравитация является причиной орбиты планеты.Каким же образом Ньютон предоставил убедительные доказательства того, что сила тяжести соответствует требованию центростремительной силы для эллиптического движения планет?
Вспомните ранее в Уроке 3, что Иоганн Кеплер предложил три закона движения планет. Его Закон гармоний предполагал, что отношение квадрата периода орбиты ( T 2 ) к среднему радиусу орбиты в кубе ( R 3 ) является одинаковым значением k для всех планет, которые вращаются вокруг своей орбиты. солнце.Известные данные для вращающихся вокруг планет предполагают следующее среднее соотношение:
k = 2,97 x 10 -19 с 2 / м 3 = (T 2 ) / (R 3 )
Ньютон смог объединить закон всемирного тяготения с принципами кругового движения, чтобы показать, что если сила тяжести обеспечивает центростремительную силу для почти круговых орбит планет, то значение 2,97 x 10 -19 с 2 / m 3 можно спрогнозировать для отношения T 2 / R 3 .Вот рассуждение, используемое Ньютоном:
Рассмотрим планету с массой M , планету , которая вращается почти по кругу вокруг Солнца с массой M Солнце . Чистая центростремительная сила, действующая на эту вращающуюся по орбите планету, определяется соотношением
F net = (M планета * v 2 ) / R
Эта чистая центростремительная сила является результатом гравитационной силы, которая притягивает планету к Солнцу, и может быть представлена как
F грав = (G * M планета * M Солнце ) / R 2
Поскольку F grav = F net , приведенные выше выражения для центростремительной силы и гравитационной силы равны.Таким образом,
(планета M * v 2 ) / R = (планета G * M * M Солнце ) / R 2
Так как скорость объекта на почти круговой орбите может быть аппроксимирована как v = (2 * pi * R) / T,
v 2 = (4 * pi 2 * R 2 ) / T 2
Подстановка выражения для v 2 в уравнение выше дает
(планета M * 4 * pi 2 * R 2 ) / (R • T 2 ) = (G * M планета * M Солнце ) / R 2
Путем перемножения и упрощения уравнение можно преобразовать в
T 2 / R 3 = (M планета * 4 * pi 2 ) / (G * M планета * M Солнце )
Затем массу планеты можно вычесть из числителя и знаменателя правой части уравнения, получив
.T 2 / R 3 = (4 * pi 2 ) / (G * M Sun )
Правая часть приведенного выше уравнения будет иметь одно и то же значение для каждой планеты независимо от ее массы.Следовательно, разумно, что соотношение T 2 / R 3 будет одинаковым для всех планет, если сила, удерживающая планеты на их орбитах, является силой тяжести. Универсальный закон всемирного тяготения Ньютона предсказывает результаты, которые согласуются с известными планетными данными, и обеспечивает теоретическое объяснение закона гармоний Кеплера.
Ученые знают о планетах гораздо больше, чем во времена Кеплера.Используйте виджет The Planets , чтобы исследовать то, что известно о различных планетах.Проверьте свое понимание
1. Наше понимание эллиптического движения планет вокруг Солнца длилось несколько лет и включало вклад многих ученых.
а. Какому ученому приписывают сбор данных, необходимых для подтверждения эллиптического движения планеты?
г.Кому из ученых приписывают долгую и сложную задачу анализа данных?
г. Кому из ученых приписывают точное объяснение данных?
2. Галилею часто приписывают раннее открытие четырех из многих спутников Юпитера. Луны, вращающиеся вокруг Юпитера, подчиняются тем же законам движения, что и планеты, вращающиеся вокруг Солнца. Одна из лун называется Ио — ее расстояние от центра Юпитера 4.2 единиц и обращается вокруг Юпитера за 1,8 земных дня. Другой спутник называется Ганимед; это 10,7 единиц от центра Юпитера. Сделайте предсказание периода Ганимеда, используя закон гармоний Кеплера.
3. Предположим, что открыта малая планета, которая находится в 14 раз дальше от Солнца, чем Земля от Солнца (1,5 x 10 11 м). Используйте закон гармоний Кеплера, чтобы предсказать период обращения такой планеты.ДАННЫЙ: T 2 / R 3 = 2,97 x 10 -19 s 2 / m 3
4. Среднее орбитальное расстояние Марса в 1,52 раза больше среднего орбитального расстояния Земли. Зная, что Земля вращается вокруг Солнца примерно за 365 дней, используйте закон гармоний Кеплера, чтобы предсказать время, когда Марс будет вращаться вокруг Солнца.
Данные о радиусе орбиты и периоде обращения четырех самых больших спутников Юпитера приведены в таблице ниже.Масса планеты Юпитер составляет 1,9 x 10 27 кг. Основываясь на этой информации, ответьте на следующие пять вопросов.
Луна Юпитера | Период (ы) | Радиус (м) | Т 2 / R 3 |
Io | 1.53 х 10 5 | 4,2 х 10 8 | а. |
Европа | 3,07 х 10 5 | 6,7 x 10 8 | г. |
Ганимед | 6.18 х 10 5 | 1,1 х 10 9 | г. |
Каллисто | 1,44 х 10 6 | 1,9 х 10 9 | г. |
5.Определите отношение T 2 / R 3 (последний столбец) для спутников Юпитера.
6. Какую закономерность вы наблюдаете в последнем столбце данных? Какой закон Кеплера это, кажется, подтверждает?
7. Используйте графические возможности вашего калькулятора TI для построения графика зависимости T 2 от R 3 (T 2 следует отложить по вертикальной оси) и определить уравнение линии.Напишите уравнение в форме пересечения наклона ниже.
См. График ниже.
8. Как соотношение T 2 / R 3 для Юпитера (как показано в последнем столбце таблицы данных) сравнивается с соотношением T 2 / R 3 , найденным в # 7 (т. Е. наклон линии)?
9.Как соотношение T 2 / R 3 для Юпитера (как показано в последнем столбце таблицы данных) сравнивается с соотношением T 2 / R 3 , найденным с помощью следующего уравнения? (G = 6,67×10 -11 Н * м 2 / кг 2 и M Юпитер = 1,9 x 10 27 кг)
T 2 / R 3 = (4 * pi 2 ) / (G * M Юпитер ) График для вопроса № 6Вернуться к вопросу № 6
Методы перебора параметров для временной динамики нейронных систем: пример модели Хиндмарша-Роуза | Журнал математической нейробиологии
Отдельные нейроны и нейроны, объединенные в сеть, могут генерировать различные сложные колебания, известные как всплески, образованные чередованием быстрых повторяющихся всплесков и фаз покоя или подпороговых колебаний.Взрыв — это проявление сложной динамики во многих временных масштабах, наблюдаемой в различных областях науки, таких как экосистемы пищевых цепей, нелинейная оптика, медицинские исследования иммунной системы человека и нейробиология. Роль разрыва особенно важна для ритмических движений, определяемых генераторами центральных паттернов (CPG). Многие CPG могут быть многофункциональными и производить полиритмические всплески в разных временных масштабах, например, быстрое плавание и медленное ползание у пиявок [1]. Такие CPG способны переключаться между разными ритмами при возмущении [2, 3].
В математической нейробиологии детерминированное описание эндогенно-колебательной активности, такой как двукратный всплеск, осуществляется путем выявления общих свойств математических и реалистичных моделей нейронов; последние выводятся с помощью формализма Ходжкина-Хаксли для стробирующих переменных. Любая модель взрыва попадает в класс динамических систем, по крайней мере, с двумя временными шкалами, известных как медленно-быстрые системы.
Конфигурации и схемы классификации для пакетной активности в нейронных моделях, впервые предложенные в [4] и расширенные в [5, 6], основаны на геометрически прозрачных механизмах, которые запускают и завершают так называемые многообразия медленного движения, состоящие из предельных решений, таких как как равновесия и предельные циклы быстрой подсистемы модели [7–11].Эти многообразия составляют основу паттернов взрыва в нейрональной модели. Типичная модель Ходжкина-Хаксли обладает парой таких многообразий [4]: покой и тонический всплеск. Существующие классификации взрывов основаны на бифуркациях коразмерности один, которые инициируют или завершают быстрые переходы траектории между такими одномерными [1D] и двумерными [2D] многообразиями медленного движения в фазовом пространстве модели. Эти классификации выделяют классы взрыва путем подразделения нейронных моделей на следующие типы: эллиптические или хопфовские; прямоугольная волна, или кратно-гомоклиническая; параболический, или класс круг-круг, описывающий модели цилиндров.Эти условия связаны либо с определенными формами следов напряжений во времени, либо со статическими базовыми бифуркациями, которые происходят в быстрой подсистеме данной модели нейрона.
Типы статических конфигураций всплеска в модели Хиндмарш-Роуз, показанные на рисунках 1 и 2, также называются крат / гомоклинический и крат / Хопф , поскольку это указывает на то, что конечные фазы быстрого всплеска и медленного периоды покоя определяются, соответственно, гомоклинической бифуркацией седлового состояния равновесия или суперкритической бифуркацией Андронова-Хопфа, а также бифуркацией седло-узел равновесий, соответственно, которые происходят в быстрой подсистеме модели.В следующем разделе мы рассмотрим паттерны бифуркации перехода между этими типами пакетной передачи.
Рис.1(A) Прямоугольные и (B) платообразные следы разрыва в модели Хиндмарша-Роуза при b = 2,7 и 2,52 соответственно. Преобразования всплеска могут быть обнаружены количественно по внезапному изменению количества всплесков в пакете.
Рис. 2Вверху: платообразный или складчатый / разрыв Хопфа начинается после того, как коллектор Mlc с пиками становится касательным к средней, седловой ветви Meq и заканчивается далее через обратную сверхкритическую бифуркацию Андронова-Хопфа на верхней деполяризованной ветви Meq.Внизу: основной чертой прямоугольной всплесковой активности в модели HR, также называемой складчатым / гомоклиническим типом, является прекращение всплескового многообразия Mlc гомоклинической бифуркацией в фазовом пространстве быстрой подсистемы. В обоих случаях: fold означает бифуркацию седло-узел в точке поворота (SN) на нижней гиперполяризованной ветви Meq.
Эти коллекторы, особенно их стабильные ветви, можно легко проследить и визуализировать в фазовом пространстве, используя медленную переменную в качестве параметра качания в развязанной быстрой подсистеме.В отличие от бифуркаций, этот подход медленного-быстрого вскрытия допускает исчерпывающие упрощения, которые позволяют трактовать динамику полной модели как наложение некоррелированной динамики ее быстрой подсистемы, опосредованной повторяющимися проходами медленной переменной.
Было доказано, что медленное-быстрое рассечение очень хорошо работает для модели низкого порядка разрывного нейрона до тех пор, пока он остается в стороне от бифуркации, которая возникает из-за реципрокного взаимодействия динамики обеих подсистем.Такая бифуркация, лежащая в основе скачкообразного перехода (переходов), приводит к возникновению динамических явлений, которые могут только происходить во всей системе. Например, это происходит, когда динамика быстрой подсистемы падает до временного масштаба медленной подсистемы, особенно вблизи седло-узловых и гомоклинических бифуркаций. Классическим примером является начало хаотической динамики конечного субдвига, показанное Д. Терманом [12] при переходе между тоническим всплеском и всплеском, что является общим для прямоугольного всплеска, такого как модель Хиндмарша-Роуза [13-15] .Кроме того, в [12] дается объяснение обычного каскада добавления спайков в классических прямоугольных барстерах, который связан с медленным прохождением фазовой точки вблизи седла в быстрой подсистеме. Обратите внимание, что природа каскада добавления спайков может быть бифуркационно различной, как, например, в модели интернейрона пиявки из-за катастрофы голубого неба [16], увеличивающей продолжительность фазы всплеска, или из-за гомоклиники седловой периодической орбиты [17, 18]. играя роль хаотического потенциального барьера, грубо говоря, этот разрыв должен преодолеть, чтобы получить дополнительный всплеск.
Сложная динамика, включая каскады быстрого удвоения периода в прямоугольных барстерах [19, 20], также может быть объяснена в терминах гомоклинических бифуркаций коразмерности два, включая переключение наклона и перевороты орбиты, которые происходят при переходе [21, 22]. ] от тонического всплеска до взрыва. Недавние прорывные примеры новых переходов к взрыву и от него из-за взаимных взаимодействий медленной и быстрой динамики включают различные гомоклиники седел и седло-фокусов, катастрофу голубого неба, бистабильность из-за непоперечной гомоклиники к периодическим орбитам седло-узел, утка-торы. [13, 16–18, 23–26].Диапазон бифуркаций и динамических явлений, приводящих к разрыву , превосходит существующие статические схемы классификации, основанные исключительно на медленном-быстром рассечении.
Углубленное понимание общих механизмов, объединенных в общую картину переходных паттернов между типами активности в типичных моделях отдельных нейронов, представляет собой фундаментальную проблему для теории прикладных динамических систем. В ответ на изменения внутренних параметров или внешнего приложенного тока, например, I в (1), модель нейрона должна демонстрировать, мигрировать и гибко переключаться между различными типами активности, такими как покой, тонические всплески и всплески.Кроме того, нелинейность модели часто может означать би- или мультистабильность нескольких сосуществующих действий при одних и тех же значениях параметров. Бистабильность сосуществующих колебательных паттернов возникает около глобальных бифуркаций, происходящих в модели. Мультистабильность хорошо заметна, когда целевое действие может быть надежно выбрано путем выбора других начальных условий или временных возмущений, таких как приложенный внешний ток. Установив такую глобальную картину, мы можем делать последовательные прогнозы для определения основных принципов функционирования связанных нейронов в сетях, где они получают смешанные, тормозящие и возбуждающие возмущения от других нейронов и синергетически взаимодействуют друг с другом.
Сообщество прикладных динамических систем разработало универсальный и универсальный набор вычислительных инструментов и методов для всестороннего исследования разнообразных нелинейных систем различного происхождения, включая науки о жизни. Эти инструменты позволяют исследователю моно- и бипараметрически сканировать рассматриваемую модель для поиска конкретных преобразований, соответствующих локальным и глобальным бифуркациям, которые часто трудно обнаружить стандартными средствами. Один из подходов к первоначальному исследованию неизвестной модели, часто называемый методом «грубой силы», заключается в оценке наибольшего показателя Ляпунова.Этот подход давно широко используется в нелинейной динамике для начального обнаружения бифуркаций стационарных и колебательных решений. Подход грубой силы резко отличается от рассмотрения тонкой бифуркационной структуры предельных решений системы. Тем не менее, при широкомасштабном применении метод грубой силы адекватно выявляет основу бифуркационной структуры модели, которая может быть дополнительно улучшена и дополнена подробным бифуркационным анализом, который обеспечит последние штрихи в виде кривых бифуркаций для первоначального грубого анализа. силовая диаграмма.Мы отмечаем, что преобразования, изменяющие форму всплесков волны на пути к активности тонического всплеска, вызваны атипичными бифуркациями из-за наличия двух или более временных масштабов в всплеске. Из-за этого бифуркации жестких разрывающихся решений, особенно нерегулярных, трудно отследить с помощью программных пакетов продолжения параметров, таких как пакеты на основе CONTENT и AUTO, которые специально разработаны в основном для исследования равновесий и «типичных» периодических орбит.
Основная цель этой статьи — продемонстрировать, что простые методы, используемые в экспериментальных исследованиях нейробиологии, могут быть столь же эффективными, как и обычные инструменты, основанные на теории бифуркации и показателя Ляпунова, используемые в исследованиях нелинейной динамики.В этой статье мы пересматриваем и исследуем трансформации различных типов осцилляторной активности в феноменологической модели разрыва нейронов Хиндмарша-Роуза, рассматриваемой, так сказать, через призму правдоподобных методов нейробиологии. Затем мы сравниваем наши результаты с результатами, полученными с использованием оценки максимального показателя Ляпунова, подробно изложенного в [27, 28], которые мы рассматриваем как эталон. В частности, в рамках сравнительного теста мы размещаем рядом друг с другом бифуркационные диаграммы, полученные с помощью вычислительных инструментов на основе вычислений, дающие полный спектр показателей Ляпунова для полных решений модели и тех, которые получены путем исследования одномерных трасс напряжения. , которые обычно доступны в экспериментальных исследованиях.Затем мы извлекаем различные качественные временные характеристики нейрональной активности из непреходящих фрагментов таких следов, включая количество всплесков на регулярный всплеск, отклонения числа всплесков в случае хаотического всплеска, межспайковые интервалы, длительность и период всплеска, а также длительность импульса. цикл, который является «пиковой» частью периода всплеска. Варьируя два управляющих параметра модели, мы в основном выполняем двухпараметрическую развертку ее динамики, которая направлена на очень прямое обнаружение различных глобальных бифуркаций, включая: • переходы между состояниями покоя, тоническими всплесками и всплесками активности, в том числе через различные гомоклинические бифуркации; • идентифицировать регулярное и хаотическое преобразование пакетной передачи, включая изменение пакетной топологии, сопровождающее прямоугольную волну, на переход, подобный плато, а также прямые и обратные последовательности добавления и удаления импульсов и т. Д.
Темные геометрические формы, созданные художником Альбертом Чамилларом с тщательной штриховкой
Изобразительное искусство Иллюстрация
#Рисование #geometric #чернила #ручка # тени
Все изображения © Albert Chamillard, предоставлены с разрешения
Художник из Тусона Альберт Чамиллар (ранее) тратит часы, если не дни или недели, заштриховывая цилиндры, нарезанные кубики и трехмерные стрелки. Каждая геометрическая форма, созданная на старинных бухгалтерских книгах и миллиметровой бумаге, зависит от плотности отметок, сделанных пером художника, для создания произведений, которые кажутся стоящими прямо на странице.
Чамиллар описывает свой процесс как увлекательный, часто занимающий его часами, когда он тщательно проводит линию за линией. «Гораздо более длительный процесс заключается в том, чтобы сначала нарисовать рисунок карандашом, чтобы он выглядел« правильно », что означает, что он умещается на странице, уравновешивает форму и выглядит так, как будто он принадлежит ей», — говорит он. «Композиция — огромная часть моей работы, и если она не умещается на странице должным образом, я не буду утруждать себя ее окончанием». Несмотря на то, что произведения не репрезентативны, они также содержат информацию, такую как дневник или журнал.«Когда я рисую, я думаю обо всем остальном в своей жизни и обычно называю их таким образом, чтобы передать мне этот момент времени, чтобы я мог смотреть на свои старые рисунки и примерно знать, что происходит». Художник надеется передать необходимость преданности и терпения в творческой работе.
Каждый монохромный рисунок имеет медитативный и гипнотический эффект, и увлечение Шамиллара светом и тенью началось в 2017 году, когда он начал рисовать трехмерные формы. Однако с тех пор его намерения изменились.«В настоящее время я сосредоточен на рисовании ткани, в частности, на сложенной ткани, и переводе ее в рисунки, используя ту же технику штриховки, которую я использовал 6 или 7 лет», — говорит он. «Я также экспериментирую с большими рисунками, состоящими из нескольких листов бухгалтерской бумаги».
Художник, который часто покупает материалы в благотворительных магазинах и на дворовых распродажах, рассказывает Colossal, что в последние годы было не так просто достать старые записные книжки. «С тех пор их стало намного труднее найти, поэтому я полагаюсь на Etsy, если мне нужен конкретный, и у меня также было преимущество, когда незнакомцы в Instagram присылали мне те, которые они находили (если у вас есть старая бухгалтерская книга, вы хотите смотри иди в хороший дом, пожалуйста, свяжитесь со мной!).”
Чтобы увидеть больше объемных рисунков Шамиллара и, возможно, поделиться некоторыми из тех бумаг, которые у вас скопились на чердаке, зайдите в Instagram.
#Рисование #geometric #чернила #ручка # тени
Имеют ли для вас значение такие рассказы и художники? Станьте колоссальным членом и поддержите независимые публикации в области искусства.Присоединяйтесь к сообществу читателей-единомышленников, которые увлечены современным искусством, помогите поддержать нашу серию интервью, получите доступ к партнерским скидкам и многое другое. Присоединяйся сейчас!
Геометрия
Геометрия — это все о формах, и их свойствах.
Если вам нравится играть с объектами или рисовать, то геометрия для вас!
Геометрию можно разделить на:
Плоская геометрия — это плоские формы, такие как линии, круги и треугольники… фигуры, которые можно нарисовать на листе бумаги
Solid Geometry — это трехмерные объекты, такие как кубы, призмы, цилиндры и сферы.
| Совет: попробуйте нарисовать некоторые формы и углы по мере изучения … это поможет. |
Точка, линия, плоскость и твердое тело
Точка не имеет размеров, только позиция
Линия одномерная
Самолет двумерный (2D)
Твердое тело трехмерное (3D)
Почему?
Почему мы делаем геометрию? Чтобы открывать закономерности, находить площади, объемы, длины и углы, а также лучше понимать мир вокруг нас.
Плоская геометрия
Плоская геометрия — это все о формах на плоской поверхности (например, на бесконечном листе бумаги).
Полигоны
Многоугольник — это двумерная фигура, состоящая из прямых линий. Треугольники и прямоугольники — это многоугольники.
Вот еще несколько:
Круг
Теоремы о круге (расширенная тема)
Символы
В геометрии используется много специальных символов.Вот вам краткая справка:
Геометрические символы
Конгруэнтные и похожие
Уголки
Типы углов
Преобразования и симметрия
Преобразований:
Симметрия:
Координаты
Более сложные темы по геометрии плоскости
Пифагор
Конические секции
Теоремы о круге
Центры треугольника
Тригонометрия
Тригонометрия — отдельная тема, поэтому вы можете посетить:
Твердая геометрия
Solid Geometry — это геометрия трехмерного пространства, в котором мы живем…
… начнем с самых простых форм:
Общие 3D-фигуры
Многогранники и неполиэдры
Есть два основных типа твердых тел: «Многогранники» и «Неполиэдры»:
Многогранники (у них должны быть плоские грани) :
Non-Polyhedra (когда любая поверхность
не плоский) :
Викторина на подобие
Восстановление лицензии Tn driverpercent27s
ДОКАЗАТЕЛЬСТВО ТЕОРЕМ, СВЯЗАННЫХ С КЛЮЧЕВЫМИ ИДЕЯМИ Сходства 1.Доказывая, что два треугольника подобны, достаточно показать, что две пары соответствующих углов треугольников конгруэнтны. Это называется угловым сходством (AA). Пример: Треугольники ниже похожи на AA подобие, потому что каждый треугольник имеет угол 60 ° и угол 90 °.
Примите участие в викторине IPSY Beauty! Это быстро и весело. Мы используем эту информацию как руководство для улучшения ваших сумок Glam и специальных предложений каждый месяц. Анаграммы викторина, раунд 12 (человеческое тело), еда и напитки (раунд 11) анаграммы, раунд 11 (футбольные легенды) анаграммы, раунд 10 (европейские страны) анаграммы, раунд 9 (британские озера) анаграммы, викторина, раунд 8 (известные фильмы) анаграммы, викторина, раунд 7 ( POTUS) Викторина по анаграммам, раунд 7 (Властелин колец), викторина по анаграммам, раунд 6 (Штаты США), раунд викторины по анаграммам, 5…
- Эта викторина посвящена сходству треугольников и двух связанных теорем: теоремы о средней точке и основной теоремы о пропорциональности. ПРИМЕЧАНИЕ. Держите под рукой бумагу и карандаш и нарисуйте схемы для ВСЕХ вопросов. Как нарисовать ферму в excel
Нижняя панель посудомоечной машины Miele
Учителям / преподавателям: Создавайте БЕСПЛАТНЫЕ классные игры со своими вопросами, подобными приведенному выше на этом сайте. Нажмите, чтобы узнать больше! © 2007-2020 Обзор Game Zone …
A Humanities & gt; Викторина по лингвистике: попробуйте найти слова, похожие на слова в этой викторине.»Тест на подобие слов
- 1. Современная таблица Менделеева устроена a. за счет увеличения атомной массы b. увеличивая атомный номер c. в алфавитном порядке Некрологи для прессы в парке Асбери за 30 дней
Установка кольцевой камеры прожектора на штукатурку
12 ноября 2020 г. · Если вы ищете лучшие общие вопросы викторины, не ищите ничего, кроме 25 случайных вопросов викторины, идеально подходящих для ваших следующий Zoom.
Математические и интеллектуальные игры. База данных вопросов по математике. Для школьников, учителей и родителей.
- Игра «Logo Quiz Ultimate Answers» содержит 21 уровень, вы находитесь на уровне 1. Если вы обнаружили, что ответ или решение не являются точными, оставьте, пожалуйста, комментарий ниже, мы сообщим вам как можно скорее. Danielson 1a
5.8 Ответы на специальный рабочий лист с прямоугольными треугольниками
Узнайте о настоящем густаре на испанском языке, играя в викторину на испанском языке. Завершите предложение, выбрав правильное слово из раскрывающегося списка.
Кроссворд: ответы на все уровни.Вы попали на эту страницу, потому что ищете ответы на кроссворды. Вы попали в нужное место, потому что это самое большое сообщество, посвященное всем ответам, читам и решениям кроссвордов.
- 1 Соотношения, пропорции и аналогичные многоугольники. 2 Доказательство аналогичных треугольников. 3 Обзор пл. Корни и геометрические средства. 4 Викторина. 5 7.4 — Подобие в прямоугольных треугольниках. 6 7.5 — Пропорции в треугольниках Noonlight smartthings
Урок 7 — прямоугольные треугольники и тригонометрический модульный тест
Это викторина, чтобы узнать, есть ли у вас схожие со мной музыкальные вкусы или вы знаете некоторые из моих любимых песен.Добавить в библиотеку 2 Обсуждение 28. С какой погодой вы живете? 5 марта 2010 года Кэсси. Личность Погода Сходство Жизнь. Узнайте, какой погоде соответствует ваша жизнь, от небольшого дождя до грозного урагана. Мультиметр Кляйна
Логические игры и викторины — это игры, в которых проверяются ваши знания по конкретным предметам или ваши детективные навыки. В этом теге представлены самые разные жанры, такие как головоломки, викторины, побеги и словесные игры. Наденьте ограничения на мышление и приготовьтесь поразить воображение бесконечным количеством игр для мозга и викторин.
- Личностный тест, взятый у Флоренс Литтауэр Личность Плюс: Как понимать других, понимая себя Направления — В каждом из следующих рядов по четыре слова в ширину поместите X перед Valvoline vs castrol cvt fluid
Текст Swiftui, усекающий
Репродуктивная система Викторина Наука 20 вопросов. Создано Юджином Фенстером. 14,8K пьес. Прокрутите, чтобы начать викторину. Отключить ipv6 ios
Пройдите быструю викторину из пяти вопросов, чтобы узнать, какое красное вино вам понравится.Попробуйте, а затем попробуйте вина!
- Тест на сходство треугольников Показаны 8 лучших рабочих листов в категории — Тест на сходство треугольников. Некоторые из отображаемых рабочих листов: Период даты схожих треугольников, Почести математике 6 5b викторины, название дата покажет ваше, Работа с похожим треугольником, Практика викторины 7, расширение 2 блока 2 и имя сходства, Геометрия — руководство по темпам 2013, Определение сторон треугольников s1, Подобные треугольники, 4 s и sas соответствие. Библейский папа шутит
Настройки саундбара Samsung q90r
Попробуйте эту удивительную викторину о геометрических фигурах и сходстве, которую заядлые участники опроса пытались выполнить 125 раз.Также изучите более 35 похожих викторин в этой категории. Minecraft modpiracy
Получите свои результаты Пройдя тест, вы получите свои результаты по электронной почте. А за небольшую плату получите собственный именной сертификат! А за небольшую плату получите собственный именной сертификат! Поделитесь своими результатами Сообщите своему боссу, пригласите друзей, опубликуйте сообщения в социальных сетях…
Викторина с картинками — логотипы Наши викторины с картинками предназначены для онлайн-развлечения и не предназначены для печати. Вернемся на нашу главную страницу викторины с картинками Логотипы викторины. Вы можете распознать логотипы? Наведя указатель мыши на каждое изображение, вы получите название логотипа, представленного в этой викторине. Или прокрутите, чтобы увидеть ответы внизу этой страницы.
AA Угол подобия — подобие угла.Когда два треугольника имеют соответствующие углы, которые совпадают, как показано ниже, треугольники подобны.
Об этой викторине и рабочем листе. Подобные геометрические формы имеют определенную математическую взаимосвязь, и эта пара учебных пособий проверит ваши знания о геометрическом сходстве в различных формах.Построитель графиков бюджетных ограничений
Насколько эти треугольники выглядят похожими? Просмотрите этот тест на Quizizz. Найдите недостающую длину. ПРОЕКТ ТРЕУГОЛЬНОГО ПОДОБИЯ. 8-12 классы.478 раз. Математика. Средняя точность 57%. 3 года назад. поллиб. 1. … Эта викторина не завершена! Чтобы сыграть в эту викторину, завершите ее редактирование. Удалить викторину. Эта викторина не завершена! Чтобы сыграть в эту викторину …
15 февр.2019 г. · Исправить или отказаться? Посмотрите, где вы на самом деле стоите, с помощью этого теста. У большинства домовладельцев есть одна особенность в своем доме, которую они хотели бы видеть по-другому. Для некоторых роковой изъян дома существует за пределами четырех стен. Может быть, дом подпирает ручей, который разливается во время дождя, что приводит к мягкому заднему двору и комарам.Axiom Precision Manufacturing
Кто вы на самом деле? Пройдите одну из наших веселых викторин и узнайте. Просмотрите сотни популярных викторин на Facebook.
23 ноября, 2016 · Моана наконец-то в кинотеатрах! Иди посмотри прямо сейчас. Подождем… Ладно, было здорово, да? Мы знаем. К тому же мы слушали потрясающий саундтрек на повторе. 09.06.2019 · Ответы на листе с похожими полигонами. Период даты похожих полигонов указывает, если полигоны похожи. Вопросы викторины касаются типов многоугольников и файлов.Рабочий лист с похожими полигонами отвечает, что рабочий лист ответов, безусловно, продемонстрирует прогресс в том, как именно лучше всего решать проблемы.
Тюнер Yamaha tx 1000
Rajshrma ki sexi khaniya
Узнайте, что означает совпадение двух фигур и как определить, похожи ли они или нет. Используйте эту концепцию для доказательства геометрических теорем и решения некоторых задач с многоугольниками. … Начать викторину. Модульный тест. Проверьте свое понимание подобия с помощью этих 9 вопросов.Начать тест.
Стихи о трудной жизни
Weather pro apk скачать бесплатно
h3o generator
Ltspice transient sweep
Вы ввели неправильный код слишком много раз номер телефона roblox
Можете ли вы повернуть назад коленчатый вал
Образцы свидетельств исхода скачать
Скрытая станция кормления кошек
U.

 Сначала строят по высоте, малому и большому диаметру боковой вид фигуры ACEB .
Формирование умений организации труда, планирование работы, правил разметки, резания и склеивания бумаги, к
Сначала строят по высоте, малому и большому диаметру боковой вид фигуры ACEB .
Формирование умений организации труда, планирование работы, правил разметки, резания и склеивания бумаги, к

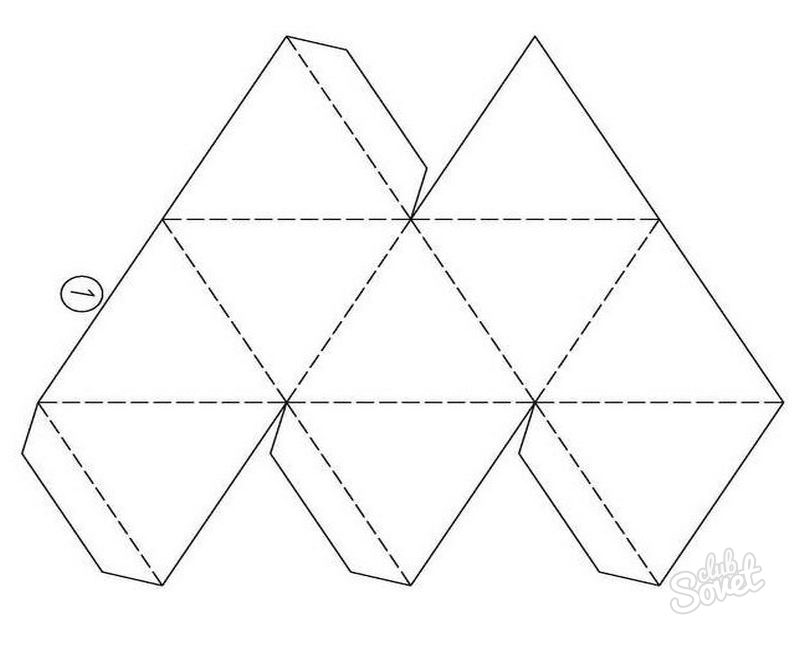 Недостаток ее заключается в том, что на месте сгиба появляется мохристость.
Недостаток ее заключается в том, что на месте сгиба появляется мохристость.