Многогранник из бумаги: Как сделать многогранник из бумаги
Как сделать многогранник из бумаги
Когда-то разноцветные многогранники из бумаги и картона служили одновременно и наглядным пособием, и украшением школьных кабинетов математики и черчения. Изготовление этих фигур способствовало развитию пространственного мышления, знакомило с многообразием форм в их трехмерном проявлении. Изготовление таких многогранников из цветной бумаги — увлекательнейшее занятие, не лишенное интеллектуальной составляющей, удивительная возможность математикой выразить красоту окружающего мира.
Многогранник — понятие очень обширное, и зачастую новички, увлеченные изготовлением этих выпуклых и звездчатых фигур, поначалу путаются в их названиях, что, в общем-то, неудивительно. Многогранники можно разделить на две категории: так называемые Платоновы тела и Архимедовы тела.
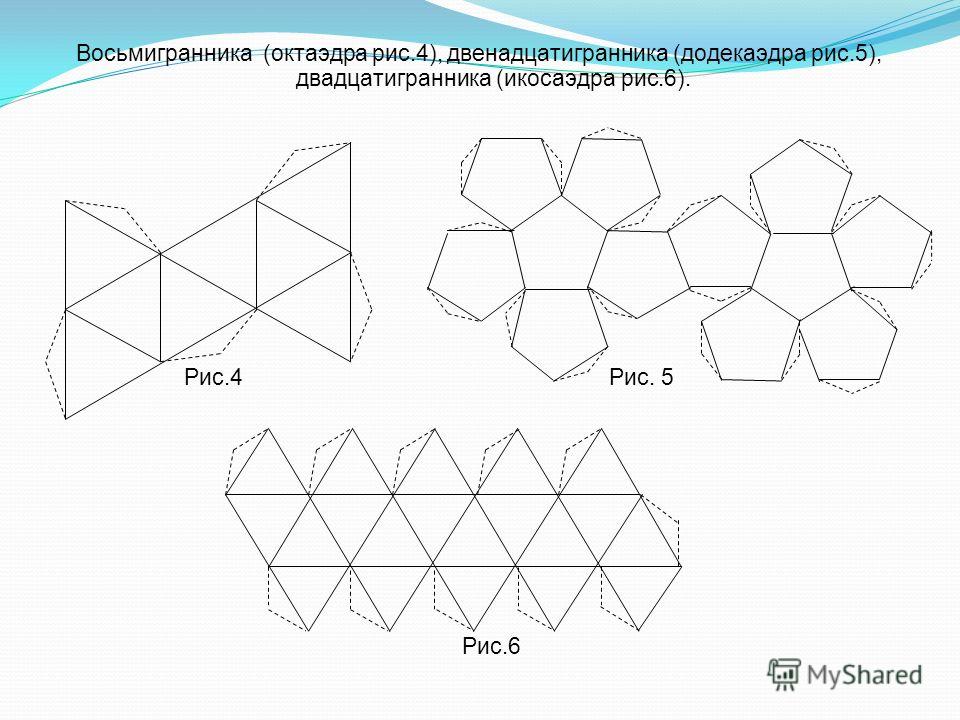
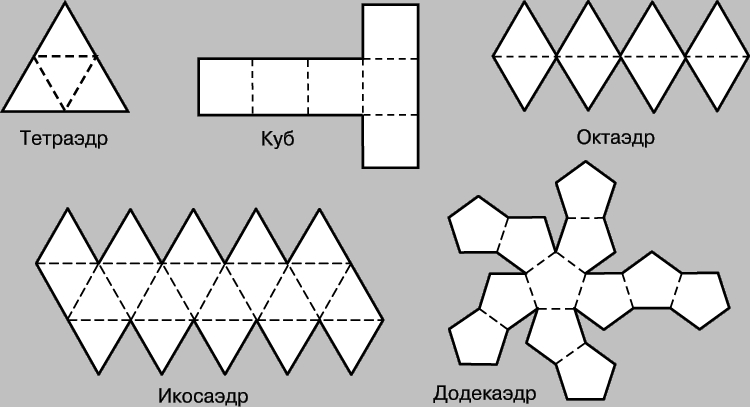
К первым относятся правильные многогранники: тетраэдр, октаэдр, куб (гексаэдр), икосаэдр, додекаэдр. Ко вторым — полуправильные многогранники: усеченные версии Платоновых тел, кубооктаэдр, «курносый» куб и др.
Для работы понадобится цветной или белый картон, который можно при необходимости раскрасить; линейка и угольники; хороший клей, который не коробит бумагу; ножницы; пинцет. Для изготовления заготовок многогранника удобно пользоваться картонными трафаретами: чертеж заготовки накладывают на плотный картон, шилом или иголкой делают проколы по вершинам детали, после чего по линейке соединяют эти точки.
Тетраэдр
Одним из простейших многогранников, которые проще всего сделать из бумаги (картона), является тетраэдр («Пирамида»). Четыре грани этой фигуры представлены равносторонними треугольниками. Если хочется сделать одноцветный тетраэдр, то можно воспользоваться одной разверткой (см. схему ниже).
Если же тетраэдр нужен разноцветный, то придется сделать четыре цветные заготовки в виде равносторонних прямоугольников.
При соединении отдельных заготовок сначала склеивают все четыре детали в положение, изображенное на рисунке ниже, затем приступают к соединению боковых граней. Сначала склеивают между собой только две из них, затем — оставшиеся детали.
Октаэдр
Октаэдр — многогранник, состоящий из восьми равносторонних треугольников. Эта фигура выглядит довольно эффектно, а мастерить ее не сложнее, чем тетраэдр. Модель мастерят, сначала склеивая четыре треугольника таким образом, как это показано на рисунке ниже. Когда грани 1 и 4 будут соединены, получится пирамида без основания — т.е. ровно половина нужной фигуры.
Вторую половину проще клеить таким образом: сначала четыре оставшихся треугольника приклеивают к соответствующим сторонам квадратного основания, затем соединяют соседние грани.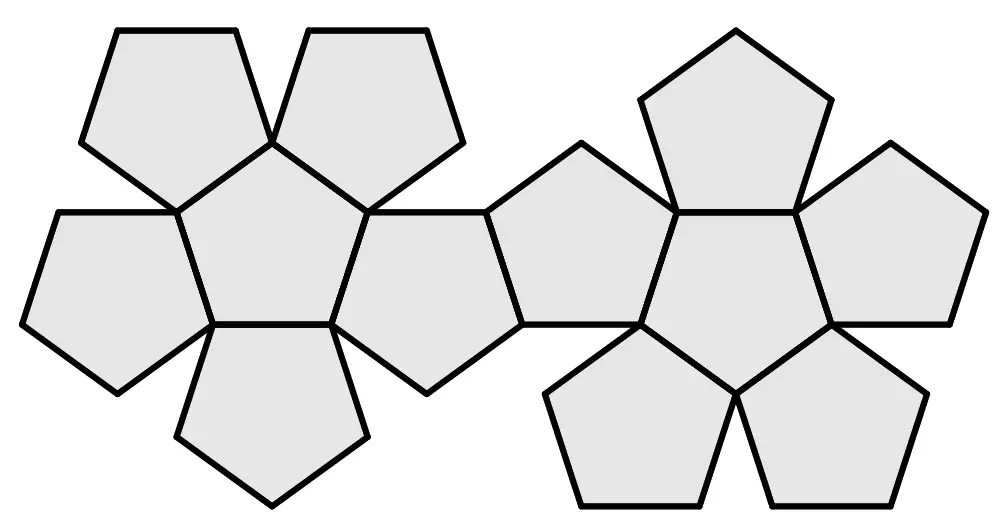
Икосаэдр
На третьем месте по простоте исполнения идет икосаэдр, гранями которого тоже являются равносторонние треугольники. Наиболее эффектно смотрятся разноцветные многогранники, у которых возможно варьирование распределения цветов. Например, можно сделать фигуру, у которой в каждой вершине будут сходиться все используемые цвета, или же у противоположных граней будут одинаковые расцветки, а у вершин будет повторяться один цвет.
Модель собирают из пяти треугольников, соединенных по схеме, указанной на рисунке ниже. В результате получится невысокая пятиугольная пирамида без основания. К сторонам основания приклеивают остальные пять треугольников, руководствуясь любой понравившейся цветовой схемой.
Додекаэдр
И, пожалуй, к несложным, но самым эффектным по своему внешнему виду многогранникам можно отнести додекаэдр. Наиболее красиво выглядят разноцветные додекаэдры: четырех- или шестицветные.
Построение модели начинают со приклеивания пяти разноцветных пятиугольников к центральному пятиугольнику — например, белого цвета. Затем цветные заготовки склеивают между собой — получается половина додекаэдра. Затем остальные грани заготовок подклеивают к уже готовой половине фигуры таким образом, чтобы выдержать задуманную цветовую схему и эффектный многогранник из бумаги будет готов.
Пример цветовой схемы:
Если вам, уважаемые читатели, интересна тема изготовления многогранников из бумаги, и хотелось бы видеть больше схем, пишите об этом в комментариях, публикации будут продолжены. Впереди нас ждут усеченные, «курносые» и красивейшие звездчатые формы многогранников.
🛠 Самоделки с меткой: Геометрические фигуры 👈
Узелковый тор из бумаги
Белый и два цветных тора завязанных в узелок 🙂 + развертки.
Дмитрий ДА 31.03.2009
Развёртки геометрических фигур
Большой выбор развёрток простых геометрических фигур.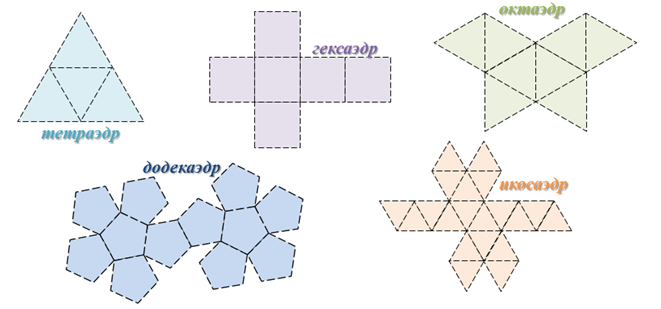
Дмитрий ДА 28.05.2009
Развёртка геометрической фигуры — тетраэдр
Тетраэдр (четырёхгранник) — многогранник с четырьмя треугольными гранями, в каждой из вершин которого сходятся по 3 грани.
Дмитрий ДА 28.10.2009
Развёртка геометрической фигуры — октаэдр
Октаэдр — один из пяти выпуклых правильных многогранников.
Дмитрий ДА 28.10.2009
Развёртка геометрической фигуры — додекаэдр
Додекаэдр (двенадцатигранник) — правильный многогранник, составленный из двенадцати правильных пятиугольников.
Дмитрий ДА 28.10.2009
Развёртка геометрической фигуры — икосаэдр
Икосаэдр — правильный выпуклый многогранник, двадцатигранник, одно из Платоновых тел.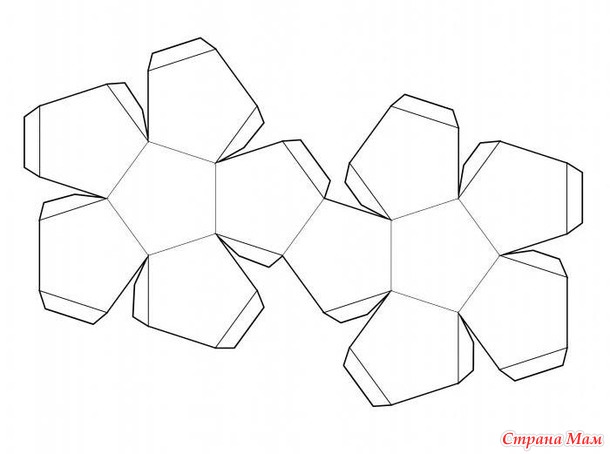
Дмитрий ДА 28.10.2009
Оптическая иллюзия параллелепипеда
Что вы видите на картинке, параллелепипед? А если внимательно присмотреться 🙂
Дмитрий ДА 19.12.2009
Трёхмерная иллюзия куба
Очень интересный видеоролик, с кубиком происходят аномалии или это вообще не куб? 😉
Дмитрий ДА 19.12.2009
Флексагон
Сделать флексагон, не трудно, нужна только бумага, ножницы и скотч.
Александр 23.02.2010
Развёртки конуса из бумаги
Готовые развёртки конуса разных размеров.
Дмитрий ДА 08.08.2010
Оригами додекаэдр
Моя первая работа: оригами додекаэдр
Темирлан
13.
Новогодняя елочка и большой икосаэдр
Оригами это круто!
Темирлан 02.01.2011
Подарочные коробочки
Такая коробочка может стать оригинальной упаковкой для ваших подарков.
Дмитрий ДА 01.02.2011
Как сделать многогранник из цветной бумаги
В этой статье я покажу вам свой многогранник, отдельные части его, и видео-инструкцию к нему…
Темирлан 16.10.2011
Как сделать додекаэдр (обыкновенный) и его разновидность
Здесь я покажу два вида дадекаэдра и выложил две видеоинструкции по ним…
Темирлан 16.10.2011
Как сделать Куб.
Думаю, эта статья банальна, но все же, может кому нибудь пригодится, к примеру для геометрии.
Темирлан 19.10.2011
Как сделать Икосаэдр (большой и маленький)
Покажу свои икосаэдры, и выложил видео-инструкцию как их сделать.
Темирлан 19.10.2011
Композиция из геометрических фигур
Это очень простая композиция из геометрических фигур.
ШкоРавоян 16.10.2015
Оригами додекаэдр из бумаги
Шикарная идея для учителей для создания с детьми на уроках труда, геометрии или черчения в школе! Для изготовления 30 модулей додекаэдра вам понадобится бумага 8*8 см.
Дмитрий ДА 14.10.2017
Три оригами-КУБа из бумаги
Можно из бумаги делать не только кубики, а ещё строить из нескольких кубов дома, мосты, роботов — всё, на что способна ваша фантазия.
Дмитрий ДА 20.11.2017
4 оригами ШАРа из бумаги
Сделать шар из бумаги сложно, но сделать шар в технике оригами очень просто. Просто возьмите цветную бумагу и следуйте обучающему видеоуроку.
Дмитрий ДА 20.11.2017
Как сделать звезду из бумаги ☆ Поделки оригами
Вы задумались о недорогом и эффектном декоре для праздника, который можно сделать своими руками. Тогда вы по адресу. Из статьи вы узнаете, как сделать объёмную звезду из бумаги. Объёмные звезды из бумаги — отличное украшение для детской комнаты.
Александра 22.04.2020
Как сделать кубик из бумаги — схема сборки оригами
Сегодня мы расскажем о том, как сделать оригинальную поделку из бумаги – кубик оригами. Данная поделка относится к модульному оригами, потому что состоит из нескольких деталей соединенных между собой.
Александра 23.04.2020
Как сделать сюрикен из бумаги
Сюрикены из бумаги — забавные летающие звездочки, похожие на оружие японских ниндзя. Как же сделать сюрикен из бумаги? С помощью нашей пошаговой схемы это получится очень легко, даже у тех, кто не знаком с оригами.
Александра 23.04.2020
Удивительно простая звезда из бумаги
Удивительно простая звезда из бумаги. Бумажная звезда может использоваться не только в виде элемента декора во время торжества или в качестве оригинального интерьерного решения. Процесс ее создания простой и увлекательный.
Александра 13.05.2020
Как сделать Сюрикен из бумаги. Оригами сюрикен
Многие мальчишки любят делать такое метательное оружие, как сюрикен из бумаги. Его можно использовать в играх и развлечениях. Сюрикен – это разновидность метательного холодного оружия, которое широко использовалось японскими воинами. Мы научим вас, как сделать сюрикен из бумаги. Делать его очень просто.
Сюрикен – это разновидность метательного холодного оружия, которое широко использовалось японскими воинами. Мы научим вас, как сделать сюрикен из бумаги. Делать его очень просто.
Александра 25.05.2020
Объемная звезда из бумаги
Объемная звезда из бумаги станет отличным украшением на праздники и ярким интерьерным решением в повседневной жизни. Сделать объемную звезду можно своими руками, достаточно внимательно посмотреть наш подробный мастер-класс.
Александра 04.06.2020
Звезда из бумаги. Простая поделка оригами для детей
Как сделать звезду из бумаги своими руками. Все что потребуется для бумажной звёзды это квадратные листы бумаги — 8 штук, я использовал размер листа 8*8 см. Поделка собирается очень просто и мне справится абсолютно каждый. Такими звёздами можно украсить комнату или сделать целую гирлянду, а также украсить ёлку на Новый год.
Александра 20.06.2020
Как сделать кубик из бумаги
Как сделать кубик из бумаги? Очень просто. Кубики – это универсальная игрушка для ваших детей, позволяющая им развивать логическое мышление и мелкую моторику рук, а также, если кубики цветные, то это поможет детям проявить свои творческие способности.
Александра 25.06.2020
Звезда оригами из бумаги
Как сделать звезду оригами? — Очень просто! Воспользуйтесь предложенной инструкцией и у вас все получится. Звезда — довольно простая задача, подвластная даже для новичка, никогда раньше не занимавшегося оригами.
Александра 26.06.2020
Как сделать многогранник из бумаги) « Math Craft :: WonderHowTo
- org/Person»> Автор Кори Пул
Добро пожаловать в мир математики! Это сообщество посвящено изучению искусства и архитектуры, вдохновленных математикой, с помощью проектов, материалов сообщества и вдохновляющих сообщений, связанных с рассматриваемой темой. Каждую неделю будет примерно четыре поста по следующему расписанию:
- Понедельник : Основные моменты, представленные участниками на пробковой доске сообщества.

- Вторник : Знакомство с новым проектом недели.
- Четверг : Расширения, вдохновение и другие математические детали для текущего проекта недели.
- Пятница : Вдохновляющие посты о художниках и произведениях искусства в этой области, включая исторические проекты и работы.
Моя цель — организовать общественный форум, на котором люди могут учиться, участвовать и вносить свой вклад. С учетом сказанного, пожалуйста, опубликуйте что-нибудь актуальное в разделе комментариев к сообщениям, на пробковой доске сообщества или создайте тему на форуме. Я надеюсь, что сообщество узнает друг от друга еще больше, чем из моих постов.
Так как это первый пост, а будущие понедельники будут посвящены представлению материалов сообщества, я собираюсь отойти от графика и поделиться простым проектом «Сделай сам» для изучения основ геометрического искусства.
Бумажные многогранники
Многогранники — это трехмерные расширения двумерных многоугольников.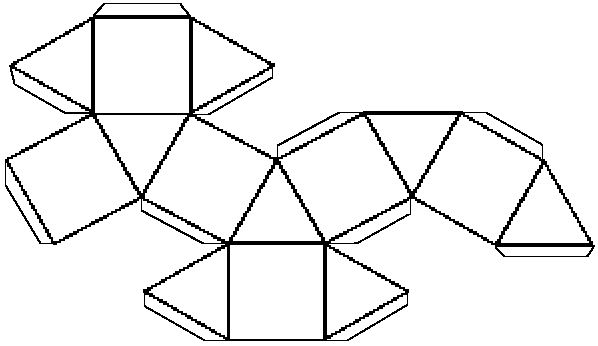 Они полностью состоят из плоских граней и прямых краев. Поскольку они полностью состоят из плоских граней с прямыми краями, их часто можно развернуть в двухмерную форму, как картонную коробку. Эта развертка многогранника называется сеткой. Один из самых простых способов сделать трехмерную фигуру — сделать сетку из бумаги и сложить ее.
Они полностью состоят из плоских граней и прямых краев. Поскольку они полностью состоят из плоских граней с прямыми краями, их часто можно развернуть в двухмерную форму, как картонную коробку. Эта развертка многогранника называется сеткой. Один из самых простых способов сделать трехмерную фигуру — сделать сетку из бумаги и сложить ее.
Чтобы показать, какие удивительные формы можно делать из бумаги, используя методы, похожие на складывание сетей, я представляю несколько изображений работы отца Магнуса Веннингера.
Это поистине удивительные геометрические фигуры. Объекты последней группы на самом деле являются трехмерными проекциями или тенями объектов, которые могут существовать только в четырех измерениях! Когда-нибудь, возможно, мы подробно рассмотрим эти полихороны.
А пока давайте посмотрим на сетки для складывания простых бумажных геометрических объектов. У Gijs Korthals Altes есть отличный сайт для поиска этих сетей. Все, что вам нужно сделать, это загрузить объект, а затем использовать принтер, чтобы распечатать его на обычной бумаге или картоне. Затем вырежьте фигуру объекта и сложите его, как указано, а затем приклейте или заклейте объект скотчем.
Затем вырежьте фигуру объекта и сложите его, как указано, а затем приклейте или заклейте объект скотчем.
Я предлагаю начать с Платоновых тел – простейших многогранников. Они полностью состоят из правильных многоугольников одинакового размера и формы и выпуклы, так что все углы изгибаются к центру формы. Шаблоны (сети) можно найти здесь. После того, как вы исчерпали платоновые тела, я предлагаю использовать архимедовы тела, которые могут иметь более одного типа многоугольника. Эти сети можно найти здесь.
Наконец, чтобы сделать действительно крутые рождественские украшения, вам стоит попробовать выпуклые многогранники, такие как многогранники Кеплера-Пуансо (скачать здесь). Обратите внимание, что это значительно сложнее и требует больше времени. Некоторые включают сотни складок. Большой икосаэдр, хотя и красивый, занял у меня почти 3 часа, чтобы вырезать и сложить из 1 листа бумаги.
Давайте рассмотрим процесс создания одного из них более подробно. Начнем с додекаэдра.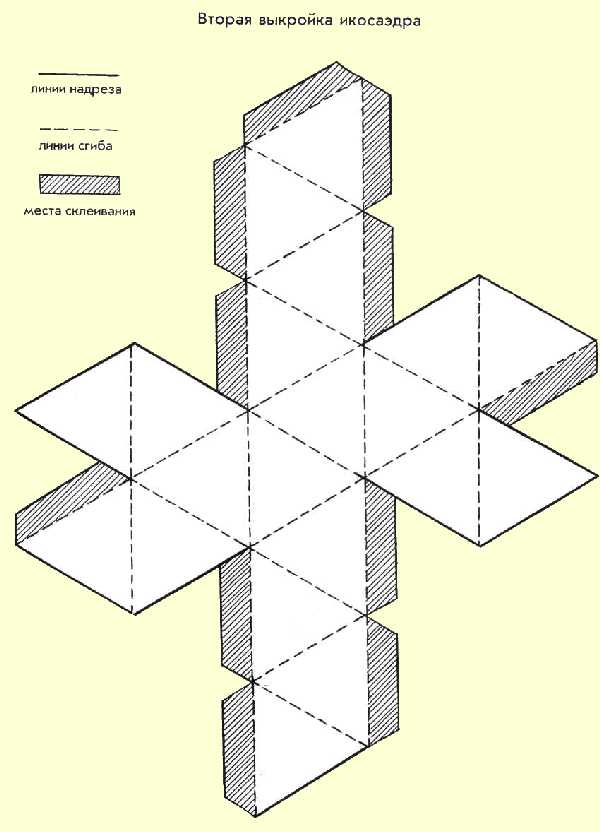
Материалы
- Что-то, чем можно резать (ножницы или нож Exacto).
- Коврик или доска для резки при использовании ножа Exacto.
- Бумага или картон. Я использую самые толстые листы, которые может выдержать мой принтер, поэтому я могу делать более прочные объекты, но это затрудняет их складывание. Карточки весом 110 фунтов можно купить в любом магазине канцелярских товаров. Обычно крупные розничные магазины, такие как Walmart или Target, продают более тонкий картон, что может быть предпочтительнее для некоторых из вас.
- Инструмент для надрезов, такой как пустая ручка или задняя часть столового ножа. Вам это действительно нужно, только если вы используете картон. На самом деле я просто слегка использую лезвие ножа Exacto, но это требует точности, поэтому будьте осторожны, если вы используете эту технику.
- Клей для рукоделия, гель-суперклей или лента.
Шаг 1 Загрузите, распечатайте и вырежьте
Перейдите на сайт загрузки и найдите многогранник, который хотите построить. Чтобы следовать за мной, перейдите в раздел о платоновых телах и скачайте шаблон додекаэдра. Я рекомендую файлы .pdf и обычно печатаю цветную страницу, а не раскрашиваю ее самостоятельно. Распечатайте сеть. Вырежьте его с помощью ножниц или ножа.
Чтобы следовать за мной, перейдите в раздел о платоновых телах и скачайте шаблон додекаэдра. Я рекомендую файлы .pdf и обычно печатаю цветную страницу, а не раскрашиваю ее самостоятельно. Распечатайте сеть. Вырежьте его с помощью ножниц или ножа.
Убедитесь, что вы вырезали пространство между вкладками и другим многоугольником, которого он начинает касаться. Оставьте только вкладку, подключенную к основному полигону.
Шаг 2 Надрез
Если вы использовали картон, надавите биговкой на края и язычки, которые нужно согнуть. Это делает бумагу более слабой в этих местах, позволяя сгибам быть почти идеальными. Если вы использовали бумагу, бумага будет довольно легко складываться без этого шага. Это может помочь, но также может испортить бумагу, если вы не будете осторожны.
Шаг 3. Сложите и склейте
Сложите и склейте или приклейте скотчем объект. Обычно я частично сгибаю все края и выступы, чтобы видеть, как будет формироваться объект.
Нанесите клей на выступ, который вы хотите приклеить.
Прижмите язычок к многоугольнику, к которому он должен прикрепляться. Для суперклея нужно подержать всего пару секунд. Для других клеев вам, возможно, придется держать около минуты.
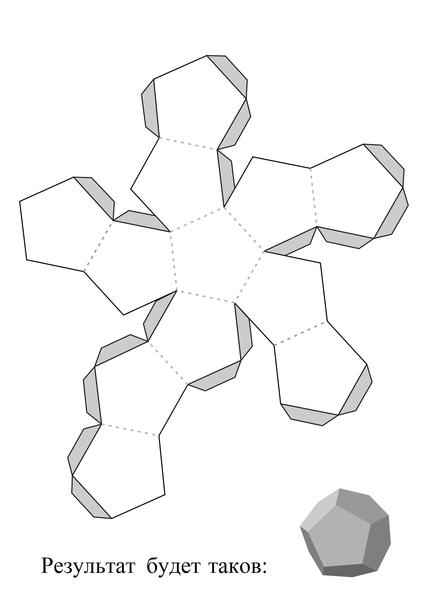
Повторяйте нанесение клея на выступы и прижимайте детали друг к другу, пока не закончите. Конечный объект должен выглядеть так:
Шаг 4 Готово!
А теперь иди и поиграй со своей растущей коллекцией многогранников. Придумайте способы их использования в других проектах. Возможно, вы могли бы использовать их в качестве рождественских украшений. Получайте удовольствие и размещайте результаты на пробковой доске!
Вот мой: В эти выходные я решил использовать многогранники, чтобы сделать мобиль для моего новорожденного сына. Вот краткое изображение того, что я сделал, используя бумажные многогранники, несколько медных трубок диаметром 1/4 дюйма и немного медной акустической проволоки.
Наконец, вот мой самый полезный совет: не слишком расстраивайтесь. Некоторые из вас смогут сделать это легко сразу. Другим может потребоваться довольно много времени, чтобы создать что-то похожее на то, что сделал ребенок начальной школы. Ваши руки могут быть покрыты клеем. Это нормально. Как и все остальное, это может потребовать некоторой практики. Это было для меня. Веселиться. И знайте, что это вызывает привыкание. Вы можете получить дом, квартиру или комнату в общежитии, полностью заполненную ими.
Во вторник научимся делать многогранники из обычных игральных карт вот так:
Хотите освоить Microsoft Excel и поднять перспективы работы на дому на новый уровень? Сделайте рывок в своей карьере с помощью нашего учебного комплекта Microsoft Excel Premium от А до Я в новом магазине Gadget Hacks Shop и получите пожизненный доступ к более чем 40 часам инструкций от базового до продвинутого уровня по функциям, формулам, инструментам и многому другому.
Купить сейчас (9Скидка 7 %) >
Другие интересные предложения:
- Скидка 97 % The Ultimate 2021 White Hat Hacker Certification Bundle
- Скидка 98 % The 2021 Accounting Mastery Bootcamp Bundle
- Скидка 99 % Allin-2021 -One Data Scientist Mega Bundle
- Скидка 59 % на XSplit VCam: пожизненная подписка (Windows)
- Скидка 98 % на сертификационный комплект Premium Learn To Code 2021
- Скидка 62 % Программное обеспечение MindMaster Mind Mapping: бессрочная лицензия
- Скидка 41 % на анализатор NetSpot Home Wi-Fi: бессрочные обновления
31 комментарий
- Горячий
- Последние
Модульное оригами: Как сделать куб, октаэдр и икосаэдр из модулей Sonobe
Как: Создайте параболические кривые Используя прямые линии
Как: Создавайте концентрические окружности, эллипсы, кардиоиды и многое другое с помощью прямых линий и окружностей
Как: Превратите Платоновы Тела в игральные карты
Как: Сделать гиперболический параболоид с помощью шпажек
Модульное оригами: Как сделать усеченный икосаэдр, додекаэдр пентаки и многое другое
Новости: 7 шаблонов для складывания геометрических конструкций из бумаги
Математическое ремесло понедельник: Материалы сообщества (плюс как сделать гиперболический параболоид в форме среза)
Как: Сделать икосаэдрические украшения планет
Как: Сложите додекаэдр Пентакис
Как: Делаем 6-сторонние снежинки киригами
Новости: Оригами Тетраэдр Серпинского, построенный из 250+ модулей
Как: Вырезать многогранные тыквы
Как: Вырезать фракталы и звезды на тыквах
Математическое ремесло понедельник: Материалы сообщества (плюс как сделать упорядоченный клубок треугольников)
Новости: Создание искусства с золотым сечением
Новости: Рисовала их годами, люблю их.
 Их около 36 или около того, спасибо за поиск
Их около 36 или около того, спасибо за поискНовости: Осторожно, Немо! Шестерни в форме рыб
МО МАТЕМАТИКА: Музей математики
Все функции
Модульное оригами: Как сделать куб, октаэдр и икосаэдр из модулей Sonobe
Как: Создайте параболические кривые Используя прямые линии
Как: Создавайте концентрические окружности, эллипсы, кардиоиды и многое другое с помощью прямых линий и окружностей
Как: Превратите Платоновы Тела в игральные карты
Как: Сделать гиперболический параболоид с помощью шпажек
Модульное оригами: Как сделать усеченный икосаэдр, додекаэдр пентаки и многое другое
Новости: 7 шаблонов для складывания геометрических конструкций из бумаги
Математическое ремесло понедельник: Материалы сообщества (плюс как сделать гиперболический параболоид в форме среза)
Как: Сделать икосаэдрические украшения планет
Как: Сложите додекаэдр Пентакис
Как: Делаем 6-сторонние снежинки киригами
Новости: Оригами Тетраэдр Серпинского, построенный из 250+ модулей
Как: Вырезать многогранные тыквы
Как: Вырезать фракталы и звезды на тыквах
Математическое ремесло понедельник: Материалы сообщества (плюс как сделать упорядоченный клубок треугольников)
Новости: Создание искусства с золотым сечением
Новости: Рисовала их годами, люблю их.
 Их около 36 или около того, спасибо за поиск
Их около 36 или около того, спасибо за поискМО МАТЕМАТИКА: Музей математики
Новости: Осторожно, Немо! Шестерни в форме рыб
Все горячие сообщения
бумажных моделей
бумажных моделей- Крайне рекомендую делать бумажные модели, как для элегантной красоты
самих моделей и для понимания трехмерных
пространство, как вы строите, а затем изучаете их.
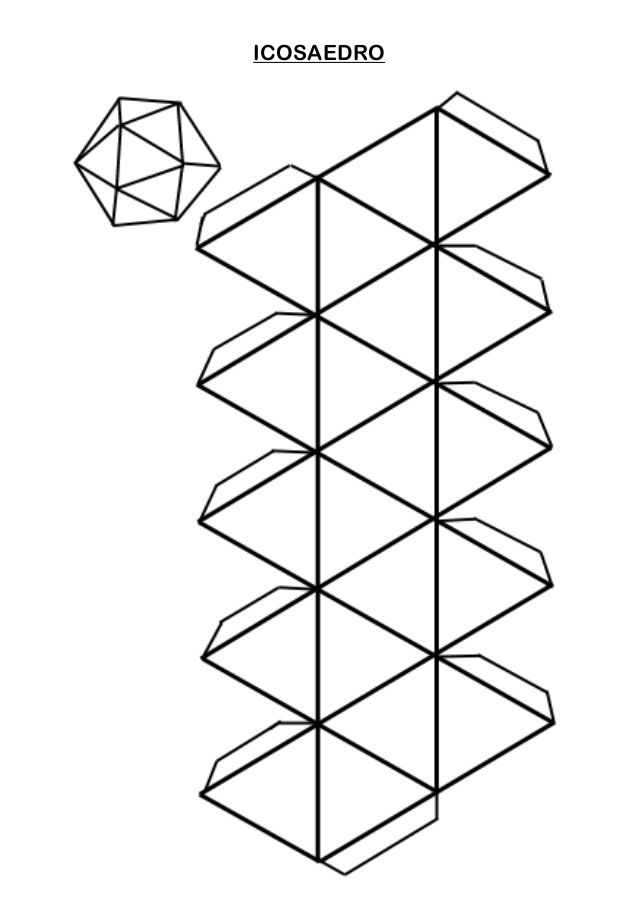 Они великолепны в классе.
Сопутствующие типы бумажных конструкций,
Другой
конструкции и Zometool также
рекомендуемые.
Они великолепны в классе.
Сопутствующие типы бумажных конструкций,
Другой
конструкции и Zometool также
рекомендуемые.В справа одна из 59 звездочек икосаэдра. Делается путем вырезания из бумаги треугольников с выступы по краям и сборка с помощью клея. Я сделал это почти 20 лет назад, следуя планам, данным в книге Магнуса Веннингера Модели многогранников, указаны в справочниках. Нажмите на картинку для 3D версии.
- Модульный
оригами — техника конструирования, в которой множество одинаковых или одинаковых
части индивидуально складываются, а затем собираются вместе в модель.
В показанном здесь примере каждая кромка складывается из отдельного квадрата.
бумаги, а затем краевые части скользят друг в друга и сцепляются
(метод, которому я научилась у Джаннин Мозли). Многогранник — это перекошенная версия
усеченного икосаэдра,
известный архимедов «полурегулярный»
сплошной, который обеспечивает шаблон, используемый для футбольного мяча. Часто без клея,
Методы модульного оригами описаны в нескольких из перечисленных книг.
- Способы бесклеевого оригами .
 В этом есть определенная чистота дзен.
В этом есть определенная чистота дзен. - Метод без вкладки, тейпирование . Резать бумагу быстрее и проще всего многоугольники и соедините их с помощью скотча внутри. Это подробно описано ниже.
- Метод одной вкладки . Одна из двух граней, которые встречаются на краю многогранник вырезается с выступающим выступом. Он откинут назад и приклеенный к внутренней стороне лица, он соединяется.
- Метод двух вкладок . Все края всех граней вырезаются выступами. Два склеиваются друг с другом, чтобы сделать ребро на внутренней стороне каждого края. Преимущество этого заключается в его симметрии и в том, что зажим может удерживать две вкладки вместе, пока клей сохнет, и вы работаете над чем-то другим.
 в ссылках.
в ссылках. Там
Вы также можете купить книги, в которых картонные страницы напечатаны
полноразмерные детали для вырезания, помеченные так, чтобы можно было просто приклеить язычок А к А,
и вкладка B к B и т. д. Некоторые из них превосходны, особенно для составных
модели. Это соединение пяти кубов
Я сделал из одной из вырезанных и вклеенных книг серии «Тарквиний», перечисленных
под Jenkins в ссылках.
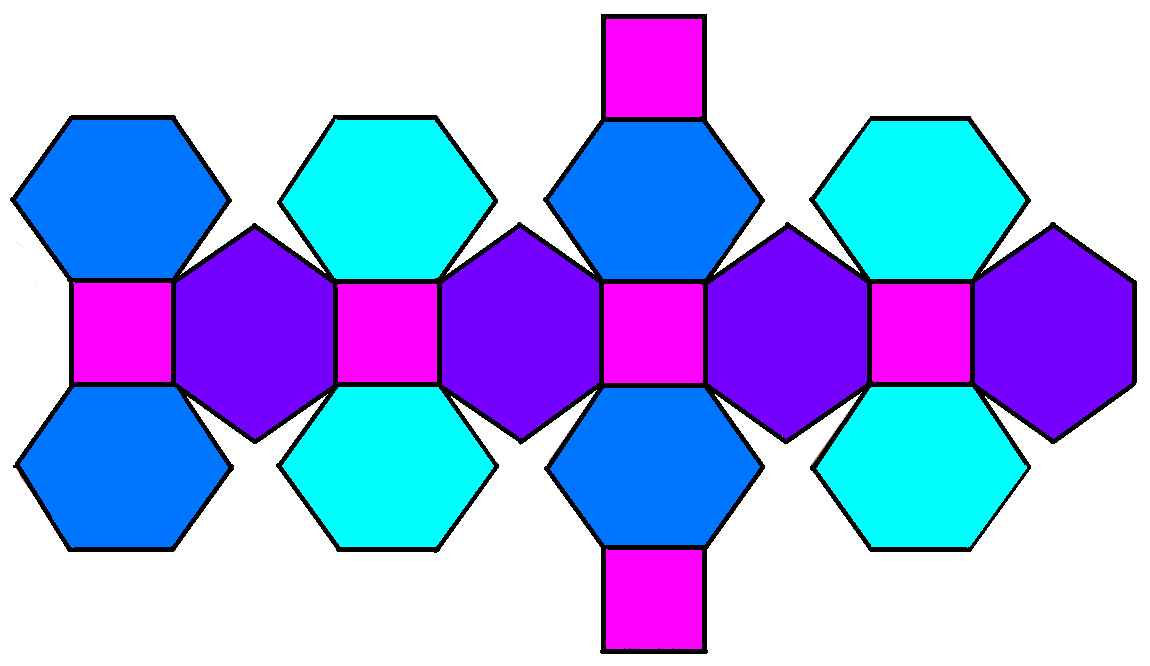
Однако, для быстрого построения многих моделей многогранников мне нравится «без вкладки, с лентой» метод (показан ниже). Этот пятиугольный шестиконтаэдр (интересный пример архимедова двойной) строится таким образом. Вот шаблон вы можете распечатать, чтобы сделать свой собственный.
Четыре техники
Метод без выступа, тейпирование
 Однако это
модель не рекомендуется неопытным; начни с платонического
твердые вещества.
Однако это
модель не рекомендуется неопытным; начни с платонического
твердые вещества.1.) Приобретите хороший (бескислотный) цветной материал из художественного магазина. магазине, если вы хотите долговечную модель. Отметим, что недорогая «строительная бумага» и «дубовая бирка» сильно выцветут менее чем за несколько лет (эта когда-то был ярко окрашен, как это.) В этой модели я использую пять цветов.
2.) Аккуратно нарисуйте по одной копии каждого лица на листе бумаги или, по крайней мере, найдите вершины. Это послужит шаблоном. (Здесь я сделал две копии, потому что своей необычной формы; обычно достаточно одного. я размер полный версия размера, чтобы сделать четыре лица из сложенного листа бумаги.)
3.) Сложите кусочки бумаги стопкой и положите сверху бумажный шаблон. Пара зажимы для переплета будут крепко держать все вместе. (Эта модель требует 12 штук (3 сложенных листа) каждого из пяти цветов.)
4.) Используйте булавку или иглу, чтобы вертикально проткнуть стопку в каждой из
вершины, отмеченные на шаблоне. Еще лучше очень тонкое сверло.
(Вы можете заменить шаги 3 и 4, просто скопировав шаблон на карту памяти.
или печать с компьютера на карточку, но это стоит дороже
и не будет работать со слишком толстым материалом, чтобы пройти через машину.)
Еще лучше очень тонкое сверло.
(Вы можете заменить шаги 3 и 4, просто скопировав шаблон на карту памяти.
или печать с компьютера на карточку, но это стоит дороже
и не будет работать со слишком толстым материалом, чтобы пройти через машину.)
5.) Используя отверстия в качестве ориентиров, отрезайте листы по одному листу за раз. Нож для резки бумаги очень удобен. Белая бумага под резаком позволяет легко видеть сквозь отверстия, чтобы выровнять бумагу под ножом для разреза.
А роторная бритва (продается в магазинах для квилтинга) имеет преимущество что прорезает точно через несколько слоев сразу, но тяжело чтобы закончить разрез именно там, где вы хотите, на внутреннем углу.
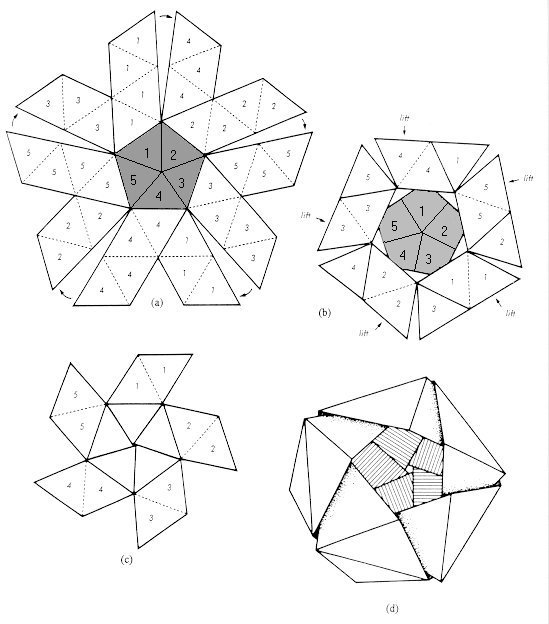
6.) Склеиваем лицевые стороны внутри. (Для этой модели нужно держать в Обратите внимание на пятицветный узор для икосаэдра, но новички могут начать с однотонных моделей.)
Обклеивание внутренней стороны, находясь снаружи, требует некоторого творчества
для нескольких последних ребер.

 Их около 36 или около того, спасибо за поиск
Их около 36 или около того, спасибо за поиск Их около 36 или около того, спасибо за поиск
Их около 36 или около того, спасибо за поиск В этом есть определенная чистота дзен.
В этом есть определенная чистота дзен.