Как сделать ромб из бумаги схема: Как сделать ромб из бумаги. Оригами ромб из бумаги — YouTube
Как сделать объемные геометрические фигуры из бумаги, развертки для склеивания: куба, конуса, схемы и шаблоны для вырезания цилиндра, пирамиды, треугольника
Любому ребенку нравится делать яркие и объемные поделки. Творчество можно объединить с изучением математики и склеить вместе с детьми геометрические фигуры. Ребенок с интересом проведет время, а дополнительно постигнет основы точной науки. Ниже представлено, как начертить карандашом и сделать объемные геометрические фигуры из бумаги, также приведены их правильные названия.
- Как сделать объемные геометрические фигуры
- Из бумаги
- Из картона
- Развертки куба
- Треугольника
- Прямоугольника
- Цилиндра
- Ромба
- Призмы
- Схемы для вырезания
- Конуса
- Пирамиды
- Шестигранника
- Макета с припусками
- Параллелепипеда
- Трапеции
- Овала
- Шара
- Многогранника
- Параллелограмма
- Шаблоны для склеивания
- Сложных фигур
- 3d
- Октаэдра
- Тетраэдра
- Икосаэдра
- Додекаэдра
- Гексаэдра
- Фигурок из треугольников
- Макеты из бумаги
- Оригами
- Дом
- Животные
- Корабль
- Полигональные чертежи
- Игрушки из фигур
- Геометрические маски
- Карандаш
- Как вырезать и склеить модели из бумаги
Как сделать объемные геометрические фигуры
Дети познают мир в процессе игры и творчества. Трехмерные фигуры, выполненные своими руками, помогут познакомиться с удивительной наукой — геометрией.
Трехмерные фигуры, выполненные своими руками, помогут познакомиться с удивительной наукой — геометрией.
Примеры трафаретов и шаблонов можно скачать из Интернета и распечатать. Затем все фигуры вырезают и склеивают. Дети старшего возраста могут самостоятельно нарисовать развертку нужной фигуры, малышам помогают родители,.
Геометрические объекты делают из бумаги (белой или цветной), картона. Из последнего материала они получаются плотными и прочными.
Из бумаги
Из картона
Развертки куба
Треугольника
Прямоугольника
Цилиндра
Ромба
Призмы
Схемы для вырезания
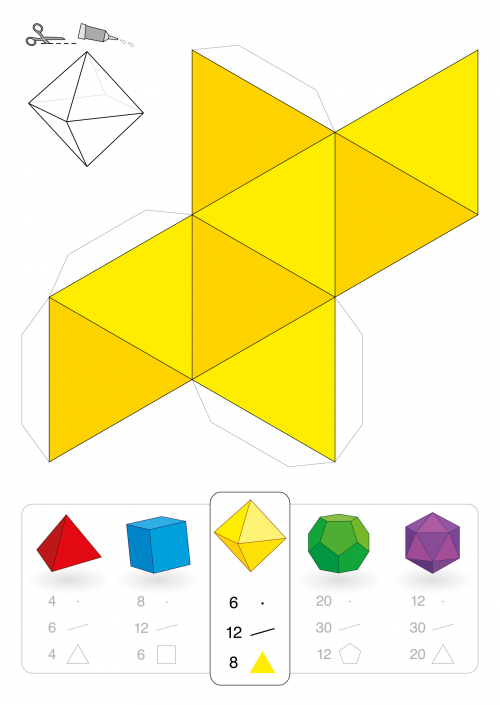
Ученикам 1–2 класса демонстрируют в школе простые геометрические фигуры и 3d: квадрат, кубик, прямоугольник. Их несложно вырезать и склеить. Шаблоны развивают мелкую моторику у детей и дают первые представления о геометрии.
Ученики средней школы, которые изучают черчение, делают сложные фигуры: бумажные шестигранники, фигуры из пятиугольников, цилиндры. Из бумаги для детей выполняют домики для кукол, мебель, оригами, замок для маленьких игрушек, маски на лицо (трехмерные называются полигональными).
Конуса
Пирамиды
Шестигранника
Макета с припусками
Параллелепипеда
Трапеции
Овала
Шара
Выкройка шара состоит из 8 частей, 12, 16 или большего количества. Присутствуют и другие способы изображения мяча. Например, из 6 деталей или 4 широких клиньев.
Материал, из чего можно сделать плотный шар — картон или плотная бумага.
Многогранника
Параллелограмма
Шаблоны для склеивания
Зачастую школьники задаются вопросом, что можно сделать из бумаги к урокам труда или на выставку. Работы ученика выделятся среди остальных, если это будут сложные трехмерные предметы, рельефные геометрические фигуры, платоновы тела, шаблоны кристаллов и минералов.
Если следовать инструкции, то ученик 5–6 класса сможет без помощи родителей сделать точный додекаэдр или тетраэдр.
Иногда в школе задают логические задания, как из квадрата сделать круг или шестиугольник. Для этого определить центр квадрата, согнув его по диагонали. Точка пересечения прямых — центр квадрата и будущего круга. Исходя из этого, можно начертить круг.
Сложных фигур
3d
Октаэдра
Тетраэдра
Икосаэдра
Додекаэдра
Гексаэдра
Фигурок из треугольников
Макеты из бумаги
Макетирование — увлекательное занятие. Оно помогает развить воображение и логическое мышление. Из бумаги делают не только фигуры, но и необычные скульптуры, статуэтки, шестиугольные–двенадцатиугольные предметы, наклонные объекты (например, Пизанскую башню), карандаши, линейки. На фото и картинках можно посмотреть, как выглядят оригинальные поделки из бумаги.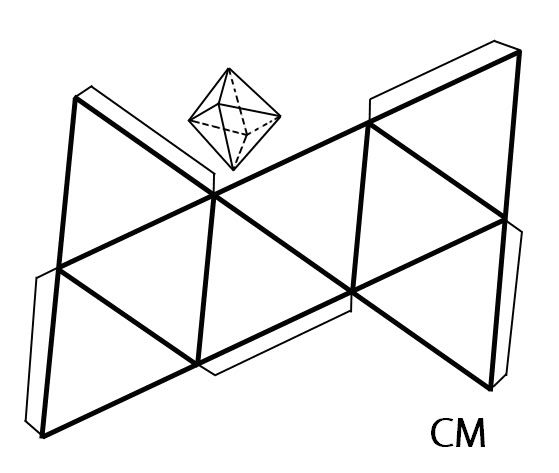
Школьники младших классов или дошколята делают бумажные объемные поделки. Например, предметы из овала — веер, цветы, гусеницы. Для них потребуются овалы и круги разного диаметра. Раскладки склеиваются между собой, получаются трехмерные игрушки.
Оригами
Дом
Животные
Корабль
Применяется множество вариантов, как сделать кораблик из бумаги.
Простая схема.
Полигональные чертежи
Игрушки из фигур
Геометрические маски
Карандаш
Как вырезать и склеить модели из бумаги
Начинающие конструкторы задаются вопросами, как рисовать и чертить геометрические фигуры, как правильно склеить выкройки и как делают врезки.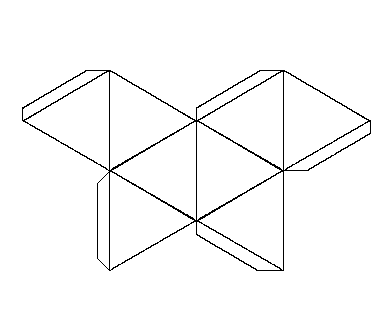 Проще всего распечатать готовый шаблон. Затем необходимо согнуть фигуру по пунктирным линиям.
Проще всего распечатать готовый шаблон. Затем необходимо согнуть фигуру по пунктирным линиям.
Чтобы сгибы получились ровными, к пунктиру прикладывают линейку, по ее форме делают точные загибы. Такой способ особенно помогает, когда речь идет о фигурках из картона или ребенок делает самые сложные макеты. Например, икосаэдр, додекаэдр, тетраэдр.
На последнем этапе необходимо скрепить элементы объекта, места для склейки обозначены на развернутом виде фигуры. Детали из картона приклеивают при помощи ПВА, а бумажные — карандашным клеем.
Основные ошибки при работе с моделями:
- Ребенок делает неправильные сгибы — например, изгиб отклоняется в сторону от пунктира на несколько градусов. В результате модель получится неточной.
Неточности во время вырезания шаблонов. Если малыш отрезал одну из границ для склеивания, то фигурка будет разворачиваться. Здесь на помощь придет взрослый.
10 легких схем, пошаговые фото и видео
Оригами – пожалуй, одно из самых универсальных хобби в мире, ведь сложно найти того, кому оно не подойдет.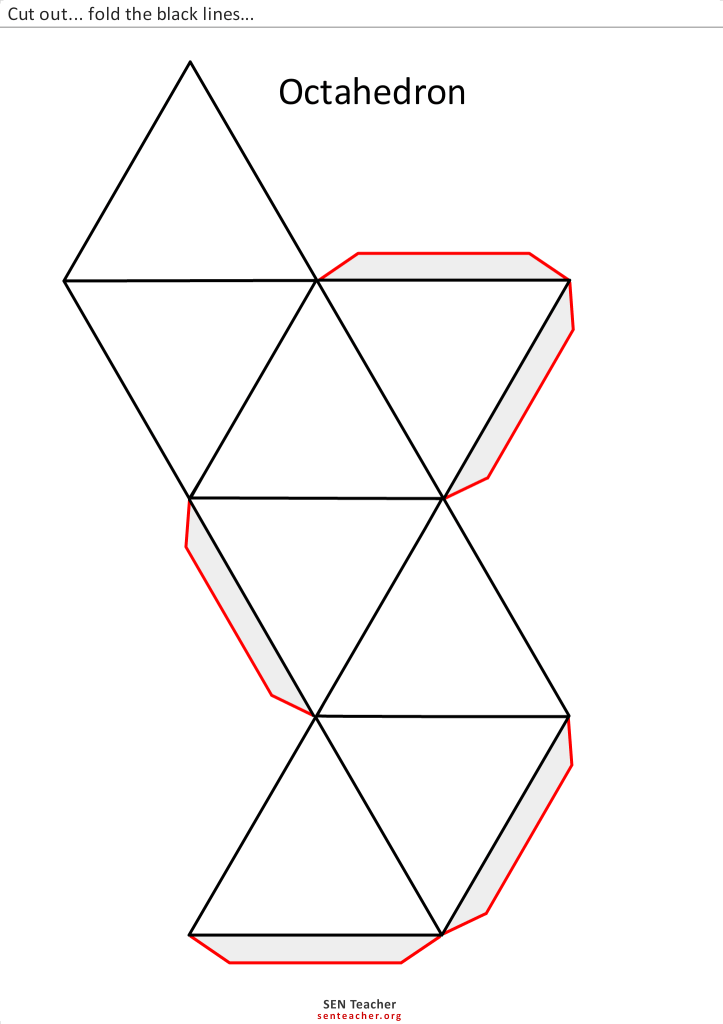 Для детей это такое необходимое развитие мелкой моторики, аккуратности, усидчивости, внимательности и логического мышления. Для взрослых – очень простой и доступный каждому способ снять напряжение, расслабиться, отвлечься от рутины и переключиться. Даже если ты впервые смотришь на лист бумаги с мыслями что-то из него сделать – не беда! Мы уже подготовили несколько простых схем для новичков!
Для детей это такое необходимое развитие мелкой моторики, аккуратности, усидчивости, внимательности и логического мышления. Для взрослых – очень простой и доступный каждому способ снять напряжение, расслабиться, отвлечься от рутины и переключиться. Даже если ты впервые смотришь на лист бумаги с мыслями что-то из него сделать – не беда! Мы уже подготовили несколько простых схем для новичков!
Лебедь оригами
Возьми квадратный белый лист, разметь одну диагональ и отогни к ней верхний и нижний углы. Кончики углов подогни в обратную сторону, сложи деталь пополам и поставь на стол, как раскрытую книгу. Из длинного вытянутого угла сформируй шею и голову лебедя. Сделай клюв, отогнув кончик головы туда-обратно, а потом нарисуй лебедю глаза.
Оригами зайчик из бумаги
Сложи квадратный лист бумаги пополам и разметь середину треугольника. Отогни его основание немного назад, а потом заверни вверх треугольники-уши. Подверни и спрячь верхний и нижний углы квадрата так, чтобы сформировать мордочку, и раскрась ее.
Косметическое украшение из оригами
Поделки из бумаги оригами для детей станут замечательным увлечением. Красочные грибы могут стать отличным украшением для дома, особенно они будут полезны при оформлении квартиры во время какого-нибудь праздника. Кроме того, ребёнок будет заинтересован процессом создания такого декора.
Кит оригами
Возьми серый или голубой квадрат, разметь диагональ и отогни к ней нижний фрагмент. Переверни заготовку и отогни к середине верхнюю и нижнюю (уже сложенную) части. Сверху загни еще один небольшой угол, чтобы сформировать спину, переверни деталь снова и сделай хвост кита.
Как сделать оригами цветы из бумаги: 8 лучших схем
Лиса из бумаги
Разметь диагонали квадрата и сложи его пополам в треугольник. Отогни углы основания вверх, чтобы снова получить маленький многослойный ромб. С одной стороны отогни угол и разверни его так, чтоб сформировать мордочку с ушами. Теперь нужно только нарисовать нос с глазами и загнуть хвост так, чтобы лиса могла стоять.
Цветок оригами
Сложи квадратный лист бумаги пополам по горизонтали и подверни верхние углы так, чтобы получился равнобедренный треугольник. Отогни углы основания верхнего слоя вверх, немного под углом к середине, и сделай то же самое с другой стороны – получится квадрат. Его боковые углы тоже отогни к середине со всех сторон, выпрями и слегка надуй фигуру. Сформируй лепестки и поправь бутон вручную со всех сторон.
Чтобы сделать цветку стебель, возьми зеленый квадрат, разметь диагональ и подогни к ней боковые углы. Повтори действие для нижней части, а потом еще раз – чтобы получился тонкий ромб, как на схеме. Загни нижнюю вытянутую часть вверх – это будет стебель цветка, а широкую – отогни и сложи в листок.
Канзаши
Изначально канзаши называли традиционные длинные заколки для волос, которыми фиксировались прически гейш. Так как кимоно не подразумевает ношение браслетов и колье, то украшать стали именно шпильки, преимущественно, сделанными своими руками из шелка и атласа цветам и бабочками.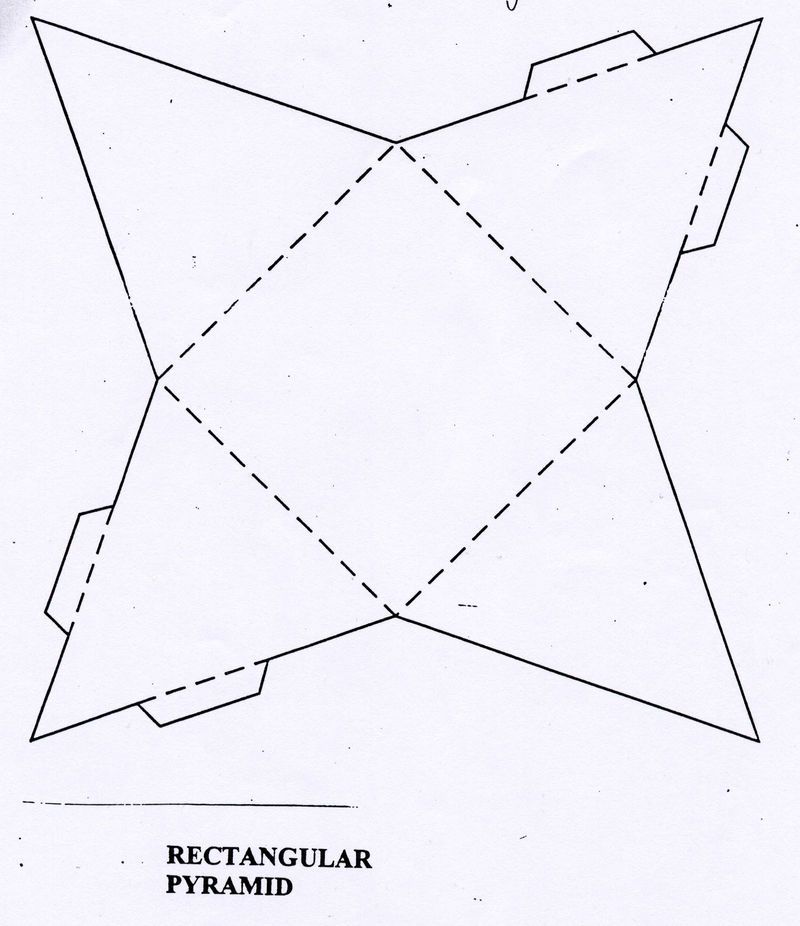 Со временем внешний вид канзаши стал демонстрировать окружающим не только умения рукодельницы, но и ее социальный статус и материальное положение. Многие японские девушки могли украшать прически множеством заколок, превращая свою голову в клумбу. Сегодня канзаши — разновидность японского рукоделия, представляющая собой технику создания цветов из атласных лент. Основными особенностями таких цветов является то, что все лепестки получены в процессе сложения базовых форм — квадрата, треугольника, круга, прямоугольника, а фиксируется лепесток и закрепляется на изделии посредством огня или клея.
Со временем внешний вид канзаши стал демонстрировать окружающим не только умения рукодельницы, но и ее социальный статус и материальное положение. Многие японские девушки могли украшать прически множеством заколок, превращая свою голову в клумбу. Сегодня канзаши — разновидность японского рукоделия, представляющая собой технику создания цветов из атласных лент. Основными особенностями таких цветов является то, что все лепестки получены в процессе сложения базовых форм — квадрата, треугольника, круга, прямоугольника, а фиксируется лепесток и закрепляется на изделии посредством огня или клея.
Оригами голубь из бумаги
Квадратный лист сложи по диагонали и отверни углы у основания треугольника вверх. У тебя получится ромб, которому нужно разметить середину и боковые вертикали, как на схеме. Боковые углы ромба спрячь внутрь, сложи деталь пополам и переверни.
С двух сторон подними вверх будущие крылья голубя и придай им форму. Согни туловище-трапецию так, чтобы хвост ушел вниз, и расправь крылья. Останется только отогнуть голову-клюв на шее, и посланник мира готов!
Останется только отогнуть голову-клюв на шее, и посланник мира готов!
10 лучших схем, как сделать самолет из бумаги
Хлопушка из бумаги
Бумажную хлопушку складывают из прямоугольного листа – можно даже из двойного тетрадного. Заверни все четыре угла к середине и сложи деталь пополам в трапецию. Заверни углы трапеции вниз и сложи пополам еще раз – получится объемный треугольник. Его нужно взять за острый конец и резко встряхнуть так, чтобы весь воздух из фигуры вышел с характерным хлопком.
Оригами лягушка из бумаги
Разметь диагонали, центральную вертикаль и горизонталь у квадратного листа бумаги. Сложи его пополам и подогни углы внутрь, как на схеме, чтобы получился равнобедренный треугольник. Заверни углы верхнего слоя к середине, наполовину отогни обратно и переверни фигуру.
Сложи треугольник в ромб, подогни к середине его боковые углы, а потом расправь верхний в еще один треугольник. Нижнюю часть (ноги) подверни гармошкой вверх-вниз, как на схеме, переверни жабку и посмотри, как она прыгает, если надавить пальцем.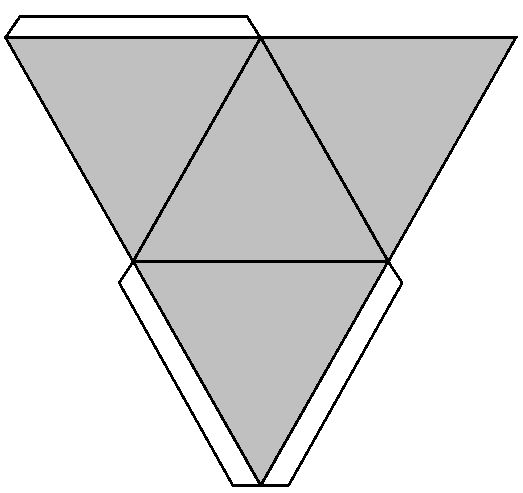
Оригами – прекрасное увлечение для ребёнка
Важно отметить, что такой вид искусства имеет множество положительных моментов для ребёнка. Кроме уже названного выше развития творческих способностей, оригами позволяет ребёнку изучать окружающий его мир посредством изучения созданных фигурок.
Количество всевозможных схем для оригами из бумаги, которые можно найти в интернете, представляет собой неиссякаемый запас вдохновения для творчества.
Мышка оригами
Разметь диагональ квадратного листа и отогни к ней верхний и нижний углы, а потом подогни их туда-обратно к середине еще раз. Расправь ромб, как показано на схеме, и заверни его угол вниз. В обратную сторону отверни угол основного ромба, и потом еще раз подогни края.
Переверни фигуру и выпрями торчащие треугольники в ушки мыши. Дважды согни длинный треугольник в мышиный хвостик и подверни его так, чтобы фигурку можно было поставить на стол. Останется только дорисовать мордочку с глазами и носом.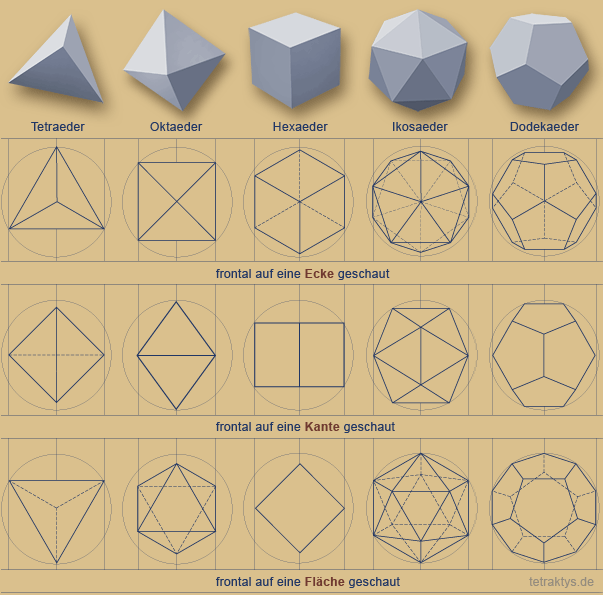
Как сделать журавлика из бумаги: 8 простых идей
Функциональная сторона такой поделки
Такая поделка совсем несложна в изготовлении, поэтому можно сделать сразу несколько кроликов. Не стоит забывать, что создание подобной фигурки с лёгкостью заинтересует любого ребёнка, а также принесёт ему удовольствие.
Несколько забавных зверушек станут замечательными декоративными украшениями для домашнего интерьера.
Журавль из бумаги
Оригами журавля сделать начинающему немного сложнее, но вполне возможно. Дважды сложи квадрат бумаги по диагонали, чтобы получился маленький треугольник, и положи его «книжкой» вниз. Разверни верхний слой в квадрат и перелистни, как на схеме. Переверни трапецию на обратную сторону и разложи второй треугольник в квадрат «книжкой» вниз.
Отогни туда-обратно к середине боковые углы верхнего слоя и разверни его в длинный вытянутый ромб, а потом сделай то же самое с другой стороны. Заверни боковые углы к центру, как на схеме, и отогни длинные «ножки» в стороны – это будет шея и хвост.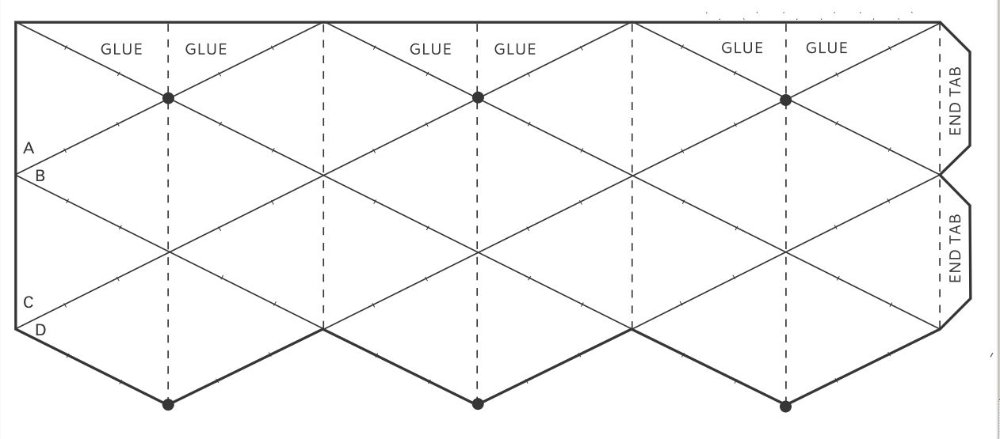 На шее сформируй голову и наконец расправь крылья журавля.
На шее сформируй голову и наконец расправь крылья журавля.
Простое и понятное искусство для детей
Лёгкие поделки из бумаги оригами позволяют детям впоследствии заинтересоваться данной разновидностью искусства. Помимо этого, такая деятельность положительно влияет на общее развитие ребёнка, поэтому стоит сделать так, чтобы ребёнок полюбил такую работу, не сдавался при неудачах и был уверен в своих силах. Существует ряд конкретных правил, который помогут быстрее научиться делать оригами.
Четырехугольники. Свойства прямоугольника, квадрата, параллелограмма, ромба, трапеции
8 минут чтения
В евклидовой геометрии четырехугольник — это четырехсторонняя двумерная фигура, сумма внутренних углов которой равна 360°. Слово «четырехугольник» происходит от двух латинских слов «quadri» и «latus», что означает «четыре» и «сторона» соответственно. Поэтому определение свойств четырехугольников важно при попытке отличить их от других многоугольников.
- Четырехугольник должен быть замкнутой формы с 4 сторонами
- Сумма всех внутренних углов четырехугольника до 360°
В этой статье вы получите представление о 5 типах четырехугольников (Прямоугольник, Квадрат, Параллелограмм , ромб и трапеция) и узнать о свойствах четырехугольников.
Вот пять типов четырехугольников, обсуждаемых в этой статье:
- Прямоугольник
- Квадрат
- Параллелограмм
- Ромб
- Трапеция
У вас проблемы с количеством GMAT? e-GMAT обеспечивает структурированное обучение от основ, чтобы помочь вам овладеть навыками, необходимыми для получения высокого балла. Присоединяйтесь к самой успешной в мире подготовительной компании, чтобы получить бесплатную пробную версию и увидеть, что она может изменить. Мы являемся самой популярной онлайн-компанией по подготовке к GMAT с более чем 2500 отзывами на GMATClub по состоянию на март 2023 года.

Вот видео, объясняющее свойства четырехугольников:
Вот что вы прочтете в статье:
[скрыть]
Свойства четырехугольников. Обзор
На приведенном ниже рисунке изображен четырехугольник ABCD и сумма его внутренних углов. Сумма всех внутренних углов равна 360°. Таким образом, ∠A + ∠B + ∠C + ∠D = 360°. Параллелограмм
Да
Вот вопросы, которые научат вас, как применить свойства всех 5 четырехугольников вы узнаете в этой статье.
Прямоугольник
Прямоугольник – это четырехугольник с четырьмя прямыми углами. Таким образом, все углы прямоугольника равны (360°/4 = 9°).0°). Более того, противоположные стороны прямоугольника параллельны и равны, а диагонали делят друг друга пополам.
Вот три свойства прямоугольника:
- Все углы прямоугольника равны 90°
- Противоположные стороны прямоугольника равны и параллельны
- Диагонали прямоугольника делят друг друга пополам
Формула прямоугольника – площадь и периметр прямоугольника
Если длина прямоугольника равна L, а ширина равна B, то
- Площадь прямоугольника = Длина × Ширина или Д × В
- Периметр прямоугольника = 2 × (Д + В)
Эти практические вопросы помогут вам закрепить свойства прямоугольников
Оценка GMAT? e-GMAT обеспечивает структурированное обучение от основ, чтобы помочь вам овладеть навыками, необходимыми для получения высокого балла.
Присоединяйтесь к самой успешной в мире подготовительной компании, чтобы получить бесплатную пробную версию и увидеть, что она может изменить. Мы являемся самой популярной онлайн-компанией по подготовке к GMAT с более чем 2500 отзывами на GMATClub по состоянию на апрель 2023 года.
Знаете ли вы, что участники e-GMAT набрали больше 700 баллов, чем когда-либо прежде в истории GMAT Club? Посмотрите это видео, чтобы понять, как e-GMAT достиг этого рекордного результата, инвестируя и внедряя инновации с единственной целью — создать платформу, которая позволяет учащимся достигать и показывать свои лучшие результаты.
Квадрат
Квадрат – это четырехугольник с четырьмя равными сторонами и углами. Это также правильный четырехугольник, поскольку обе его стороны и углы равны. Как и у прямоугольника, у квадрата четыре угла по 90° каждый. Его также можно рассматривать как прямоугольник, две соседние стороны которого равны.
Это также правильный четырехугольник, поскольку обе его стороны и углы равны. Как и у прямоугольника, у квадрата четыре угла по 90° каждый. Его также можно рассматривать как прямоугольник, две соседние стороны которого равны.
Вот три свойства квадрата:
- Все углы квадрата равны 90°
- Все стороны квадрата равны и параллельны друг другу
- Диагонали делят друг друга перпендикулярно
Формула квадрата – площадь и периметр квадрата
Если сторона квадрата равна а, то
- Площадь квадрата = а × а = а²
- Периметр квадрата = 2 × (а + а) = 4а
Эти практические вопросы помогут вам закрепить свойства квадратов. Начните свой путь к получению Q50-51 на GMAT с помощью онлайн-курса подготовки e-GMAT на основе искусственного интеллекта. Наш xPERT не только выбирает наиболее оптимизированный путь обучения, но и отслеживает ваши улучшения, гарантируя, что вы быстро и надежно достигнете целевого показателя Quant.
Посмотрите это видео, чтобы узнать больше:
Параллелограмм
Параллелограмм, как следует из названия, представляет собой простой четырехугольник, противоположные стороны которого параллельны. Таким образом, он имеет две пары параллельных сторон. Кроме того, в параллелограмме противоположные углы равны, а их диагонали делят друг друга пополам.
Вот четыре свойства параллелограмма:
- Противоположные углы равны
- Противоположные стороны равны и параллельны
- Диагонали делят друг друга пополам
- Сумма любых двух смежных углов равна 180°
Формулы параллелограмма – площадь и периметр параллелограмма
Если длина параллелограмма равна l, ширина равна b, а высота равна h, то:
- Периметр параллелограмма = 2 × (l + б)
- Площадь параллелограмма = l × h
Эти практические вопросы помогут вам закрепить свойства параллелограмма параллельно друг другу.
Однако углы не равны 9.0°. Ромб с прямыми углами станет квадратом. Другое название ромба — «ромб», так как он похож на ромбовидную масть в игральных картах.
Вот четыре свойства ромба:
- Противоположные углы равны
- Все стороны равны и противоположные стороны параллельны друг другу
- Диагонали делят друг друга перпендикулярно
- Сумма любых двух смежных углов равна 180 °
Формулы ромба – площадь и периметр ромба
Если сторона ромба равна а, то периметр ромба = 4а
Если длина двух диагоналей ромба равна d 1 и d 2 , то площадь ромба = ½ × d 1 × d 2
Эти практические вопросы помогут вам закрепить свойства ромба. Параллельные стороны называются «основаниями», а две другие стороны называются «ногами» или боковыми сторонами.
Трапецией называется четырехугольник, у которого выполняется одно свойство:
- Только одна пара противоположных сторон параллельна друг другу
Формулы трапеции – площадь и периметр трапеции
Если высота трапеции равна ‘ h’ (как показано на диаграмме выше), тогда:
- Периметр трапеции = сумма длин всех сторон = AB + BC + CD + DA
- Площадь трапеции = ½ × (сумма длин параллельных сторон) × h = ½ × (AB + CD) × h
Эти практические вопросы помогут вам закрепить свойства трапеции
Свойства четырехугольников – сводка
На приведенном ниже рисунке также представлены свойства четырехугольников
У вас проблемы с GMAT quant? e-GMAT обеспечивает структурированное обучение от основ, чтобы помочь вам овладеть навыками, необходимыми для получения высокого балла.
Присоединяйтесь к самой успешной в мире подготовительной компании, чтобы получить бесплатную пробную версию и увидеть, что она может изменить. Мы являемся самой популярной онлайн-компанией по подготовке к GMAT с более чем 2500 отзывами на GMATClub по состоянию на апрель 2023 года.
Важные формулы четырехугольников
В таблице ниже приведены формулы площади и периметра четырехугольников различных типов:
Формулы четырехугольника 2 52 Квадрат Параллелограмм Ромб Трапеция Зона Д × Ш a² l × h ½ × d1 × d2 ½ × (сумма параллельных сторон) × высота Периметр 9 × (0l054 b) 9 0 9049 2 4а 2 × ( l + b) 4a Сумма всех сторон Дальнейшее чтение:
- Формулы окружности – площадь и периметр
- Свойства чисел | Прайм | HCF & LCM
- Свойства треугольников – Определение | Типы | Классификация
- Линии и углы – свойства и их применение
Чтобы успешно сдать GMAT, требуется четко определенный учебный план.
Сэкономьте более 60 часов на подготовке к GMAT, выполнив следующие три шага:
Практический вопрос по четырехугольникам
Давайте попрактикуемся в применении свойств четырехугольников на следующих примерах вопросов: забор вокруг своего прямоугольного сада длиной 10 метров и шириной 15 метров. Сколько метров забора он должен купить, чтобы огородить весь сад?
- 20 метров
- 25 метров
- 30 метров
- 40 метров
- 50 метров
Решение
9000 01 90 30 Шаг 3: Дано 6
У Адама прямоугольный сад.
- Имеет длину 10 метров и ширину 15 метров.
- Он хочет построить вокруг него забор.
Шаг 2: Найти
Длина, необходимая для возведения забора вокруг всего сада. Этап 3: Подход и разработка
Забор можно построить только вокруг внешних сторон сада.
- Итак, общая длина необходимого забора = сумма длин всех сторон сада.
- Поскольку сад прямоугольный, сумма длин всех сторон есть не что иное, как периметр сада.
- Периметр = 2 × (10 + 15) = 50 метров
Отсюда необходимая длина забора 50 метров.
Таким образом, вариант E является правильным ответом.
GMAT: практика четырехугольников, вопрос 2
Стив хочет покрасить одну прямоугольную стену в своей комнате. Стоимость покраски стен составляет 1,5 доллара за квадратный метр. Если длина стены 25 метров, а ширина 18 метров, то какова общая стоимость покраски стены?
- 300 долларов
- 350 долларов
- 450 долларов
- 600 долларов
- 675 долларов
Решение
300003
- Стив хочет покрасить одну стену в своей комнате.
- Длина стены 25 метров, ширина 18 метров.
- Стоимость покраски стены $1,5 за квадратный метр.
Шаг 2: Найти
- Общая стоимость покраски стены.
Этап 3: Подход и отработка
- Стена окрашивается по всей площади.
- Итак, если мы найдем общую площадь стены в квадратных метрах и умножим ее на стоимость покраски 1 квадратного метра стены, то мы получим общую стоимость.
- Площадь стены = длина × ширина = 25 метров × 18 метров = 450 квадратных метров
- Общая стоимость покраски стены = 450 × 1,5 долл. США = 675 долл. США
Следовательно, правильный ответ — вариант E.
Мы надеемся, что к настоящему моменту вы узнали о различных типах четырехугольников, их свойствах и формулах, а также о том, как применять эти понятия для решения вопросов о четырехугольниках. Применение четырехугольников важно для решения вопросов по геометрии на GMAT.
Если вы планируете сдавать GMAT, мы можем помочь вам с высококачественными учебными материалами, к которым вы можете получить бесплатный доступ, зарегистрировавшись здесь.Вот еще несколько статей по математике:
- Повышение точности математических вопросов о полигонах
- Вопросы по геометрии – самые распространенные ошибки | GMAT Quant Prep
Посмотрите этот вебинар без геометрии GMAT, на котором мы обсуждаем, как решать 700-уровневые вопросы достаточности данных и проблемные вопросы в GMAT Quadrilaterals:
Планируете ли вы поступать в лучшие бизнес-школы? Позвольте нам помочь вам пройти первый этап процесса, то есть сдать GMAT. Возьмите бесплатную пробную версию GMAT, чтобы узнать свой базовый балл, и начните подготовку к GMAT с нашей бесплатной пробной версии.
Мы являемся самой популярной онлайн-компанией по подготовке к GMAT с более чем 2500 отзывами на GMATClub по состоянию на январь 2023 года.Напишите нам по адресу [email protected] в случае возникновения каких-либо вопросов.
Часто задаваемые вопросы
Какие существуют типы четырехугольников?
Существует 5 типов четырехугольников – прямоугольник, квадрат, параллелограмм, трапеция или трапеция и ромб.
Где я могу найти несколько практических вопросов по четырехугольникам?
В этой статье вы можете найти несколько практических вопросов по четырехугольникам.
Чему равна сумма внутренних углов четырехугольника?
Сумма внутренних углов четырехугольника равна 360°.
Объяснение линий симметрии параллелограмма! — Мэшап Математика
Каждый урок или курс геометрии будет включать глубокое изучение свойств параллелограммов.
В этом посте мы быстро рассмотрим ключевые свойства параллелограммов, включая их стороны, углы и соответствующие отношения.
Наконец, мы определим, имеет ли параллелограмм линейную симметрию. И, если параллелограмм имеет линейную симметрию, как будут выглядеть линии симметрии параллелограмма (в виде диаграммы).
Прежде чем мы ответим на эти ключевые вопросы, связанные с симметрией параллелограммов, давайте кратко рассмотрим свойства параллелограммов:
Что такое параллелограмм?Определение: Параллелограмм — это особый вид четырехугольника (замкнутая четырехсторонняя фигура), в котором противоположные стороны параллельны друг другу и имеют одинаковую длину.
Кроме того, внутренние противоположные углы любого параллелограмма имеют одинаковую величину. А любая пара смежных внутренних углов в параллелограмме является дополнительной (в сумме они равны 180 градусам).
На следующей диаграмме показаны основные свойства параллелограммов:
Линии симметрии параллелограмма
Теперь, когда вы понимаете основные свойства и отношения углов параллелограмма, вы готовы исследовать следующие вопросы:
Имеют ли параллелограммы линейную симметрию?
Сколько осей симметрии в параллелограмме?
Если у параллелограмма нет осей симметрии, то почему у параллелограмма нет осей симметрии?
Для начала отметим, что линия симметрии — это ось или воображаемая линия, которая может проходить через центр фигуры (обращенной в любом направлении) таким образом, что она разрезает фигуру на две равные половины, которые являются зеркальными.
изображения друг друга.
Например, квадрат, прямоугольник и ромб имеют линейную симметрию , поскольку по крайней мере одну воображаемую линию можно провести через центр фигуры, которая разрезает ее на две равные половины, являющиеся зеркальным отражением друг друга.
На самом деле фигура может иметь несколько линий симметрии. На приведенной ниже диаграмме видно, что квадрат имеет четыре оси симметрии, а прямоугольник и ромб — только две оси симметрии.
А параллелограмм?Получается, что у параллелограмма , а не нет осей симметрии.
Но почему у параллелограмма нет осей симметрии? Потому что для любого параллелограмма невозможно построить линию симметрии (ось или воображаемую линию, проходящую через центр фигуры и разрезающую изображение пополам, где каждая сторона является зеркальным отражением другой).
Вы можете попытаться построить линию симметрии на любом параллелограмме, и вы увидите, что это невозможно.
На рисунке ниже показано, почему общее количество линий симметрии в параллелограмме равно нулю.
Имеет ли параллелограмм вообще какую-либо симметрию?Хотя параллелограммы не имеют линейной симметрии, они обладают вращательной симметрией!
В геометрии вращательная симметрия относится к ситуации, когда форма или фигура точно такие же, как их прообраз после того, как они были повернуты на несколько градусов.
Параллелограмм обладает вращательной симметрией, поскольку та же самая фигура появится после поворота оригинала или прообраза на 180 градусов.
На приведенном ниже рисунке показано, почему параллелограммы обладают вращательной симметрией.
Заключение
На сегодняшнем уроке мы исследовали линии симметрии параллелограмма, независимо от того, существуют ли они, и обладают ли параллелограммы вообще симметрией.
После рассмотрения свойств параллелограммов, а именно того, что они являются четырехугольниками, у которых противоположные стороны и противоположные углы равны, мы решили определить, обладают ли параллелограммы линейной симметрией.
Применяя определение линии симметрии, мы пришли к выводу, что, хотя такие фигуры, как квадраты и прямоугольники, действительно имеют линии симметрии, параллелограммы не имеют линий симметрии.
Параллелограммы имеют нулевые линии симметрии, потому что невозможно провести через центр любого параллелограмма линию, которая делит фигуру на две равные половины, являющиеся зеркальным отражением друг друга.
Однако, несмотря на то, что параллелограммы не имеют линейной симметрии, они обладают вращательной симметрией, поскольку любой параллелограмм после поворота на 180 градусов приведет к точно такому же изображению, с которого вы начали.
Поделитесь своими мыслями, вопросами и предложениями в разделе комментариев ниже!(Никогда не пропустите блог Mashup Math — нажмите здесь, чтобы получать нашу еженедельную рассылку!)
Автор: Энтони Персико0342 MashUp Math и советник кампании Amazon Education « With Math I Can ».
Вам также может понравиться…Вы часто можете увидеть, как я с радостью разрабатываю анимированные уроки математики, которыми я делюсь на моем канале YouTube . Или проводить слишком много времени в тренажерном зале или играть на своем телефоне.
Игра «Бумажный самолетик: забавный проект для учащихся»
Какая самая простая математика в колледже?
Как привлечь учащихся к урокам математики — 5 идей