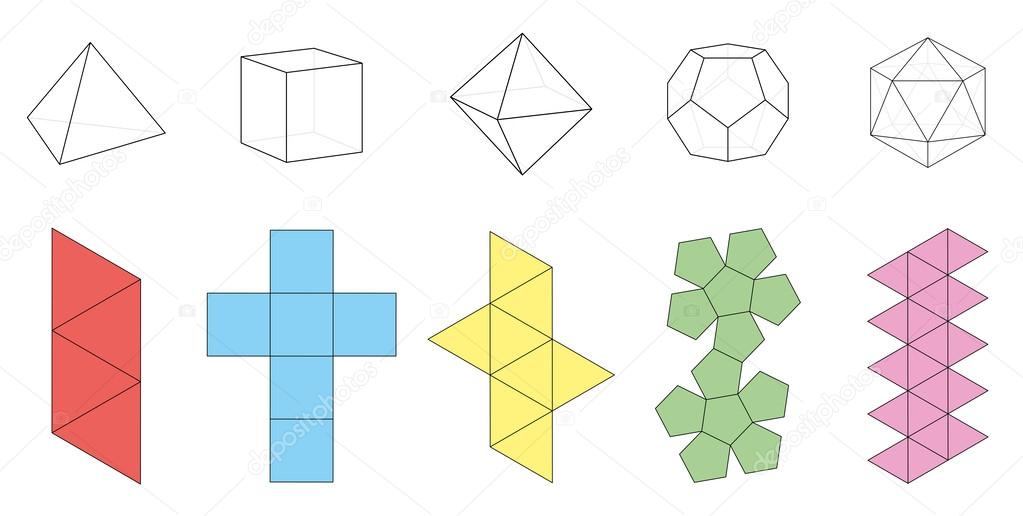
Геометрические фигуры объемные из бумаги схемы: Объемные геометрические тела из бумаги своими руками. Схемы
Геометрические фигуры из бумаги
В основе самых сложных и необычные формы сооружений, устройств, механизмов лежат элементарные геометрические фигуры: куб, призма, пирамида, шар и другие. Для начала научитесь создавать самые простые фигуры, а после вы легко освоите более сложные формы.
Многие моделисты начинают свой путь с бумажных моделей. Это обусловлено доступностью материала (найти бумагу и картон не составляет трудности) и легкостью в его обработки (не требуются специальные инструменты).
Однако, бумага имеет и ряд характерных особенностей:
- капризный, хрупкий материал
- требует высокой аккуратности, внимательности, усидчивости при работе
По этим причинам бумага является материалом, как для начинающих, так и для настоящих мастеров и из нее создаются модели самой разной сложности.
В этот статье мы изучим простейшие геометрические фигуры, которые можно сделать из бумаги.
Вам понадобятся следующие материалы:
- лист бумаги
- карандаш
- линейка
- ластик
- ножницы
- клей ПВА либо клеящий карандаш
- кисточка для клея, лучше из жесткой щетины
- циркуль (для некоторых фигур)
Как сделать куб из бумаги?
Куб – правильный многогранник, каждая грань которого представляет собой квадрат
Создание куба состоит из двух этапов: создание развертки и склеивание. фигуры. Для создания схемы вы можете воспользоваться принтером, просто распечатав готовую схему. Либо вы можете самостоятельно с помощью чертежных инструментов нарисовать развертку.
Рисование развертки:
- Выбираем размеры квадрата — одной стороны нашего куба. Лист бумаги должен быть шириной не менее 3 сторон этого квадрата и длиной немного более 4 сторон.
- Чертим в длину нашего листа четыре квадрата, которые станут боковыми сторонами куба.
 Рисуем их строго на одной линии, вплотную друг к другу.
Рисуем их строго на одной линии, вплотную друг к другу. - Над и под любыми из квадратов рисуем по одному такому же квадрату.
- Дорисовываем полоски для склеивания, с помощью которых грани будут соединяться между собой. Каждые две грани должны соединяться одной полоской.
- Куб готов!
После рисования развертка вырезается ножницами и склеивайте ПВА. Клей очень тонким слоем равномерно размазываем кистью по поверхности склеивания. Соединяем поверхности и закрепляем в нужном положении на некоторое время, с помощью скрепки или небольшого груза. Срок схватывания клея где-то 30-40 минут. Ускорить высыхание можно методом нагрева, например, на батарее. После склеиваем следующие грани, закрепляем в нужном положении. И так далее. Так постепенно вы проклеите все грани куба. Используйте небольшие порции клея!
Как сделать конус из бумаги?
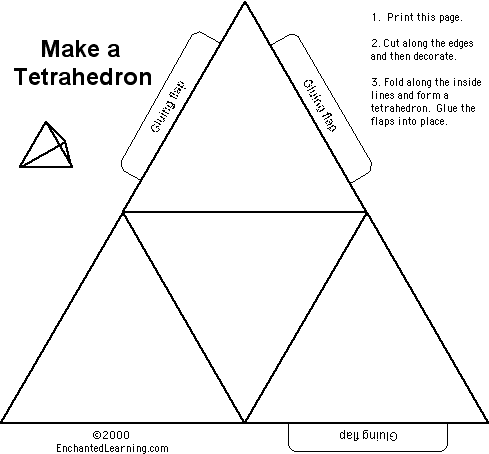
Конус – тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность.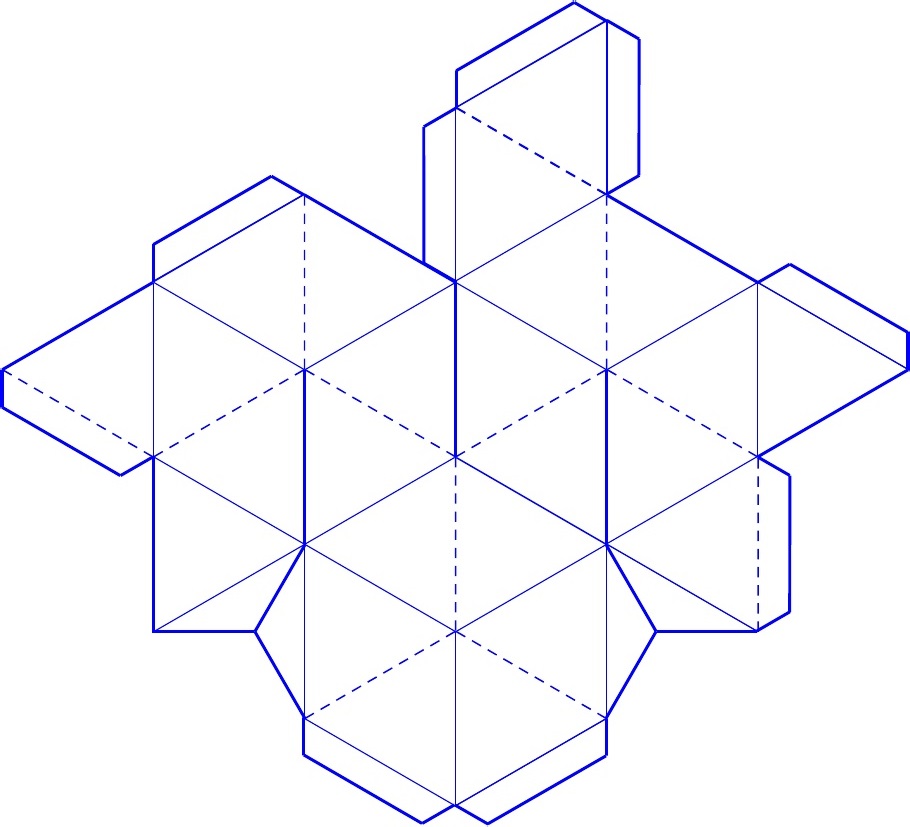
Рисование развертки:
- Рисуем циркулем окружность
- Вырезаем сектор (часть круга, ограниченная дугой окружности и двумя радиусами, проведенными к концам этой дуги) из этой окружности. Чем больший сектор вы вырежете, тем острее будет конец конуса.
- Склеиваем боковую поверхность конуса.
- Измеряем диаметр основания конуса. С помощью циркуля рисуем окружность на листе бумаге требуемого диаметра. Дорисовываем треугольнички для склеивания основания с боковой поверхностью. Вырезаем.
- Приклеиваем основание к боковой поверхности.
- Конус готов!
Как сделать цилиндр из бумаги?
Цилиндр – геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.
Рисование развертки:
- Рисуем прямоугольник на бумаги, в котором ширина — это высота цилиндра, а длина определит диаметр будущей фигуры.
 Отношение длины прямоугольника к диаметру определяется выражением: L=πD, где L- длина прямоугольника, а D — диаметр будущего цилиндра. Подставив в формулу требуемый диаметр, найдем длину прямоугольника, который будем рисовать на бумаге. Дорисовываем небольшие дополнительные треугольнички, которые необходимы для склеивания деталей.
Отношение длины прямоугольника к диаметру определяется выражением: L=πD, где L- длина прямоугольника, а D — диаметр будущего цилиндра. Подставив в формулу требуемый диаметр, найдем длину прямоугольника, который будем рисовать на бумаге. Дорисовываем небольшие дополнительные треугольнички, которые необходимы для склеивания деталей. - Рисуем на бумаге два круга, диаметром цилиндра. Это будет верхнее и нижнее основания цилиндра.
- Вырезаем все детали будущего бумажного цилиндра.
- Склеиваем боковую поверхность цилиндра из прямоугольника. Даем детали высохнуть. Приклеиваем нижнее основание. Ждем высыхания. Приклеиваем верхнее основание.
- Цилиндр готов!
Как сделать параллелепипед из бумаги?
Параллелепипед – многогранник, у которого шесть граней и каждая из них параллелограмм.
Рисование развертки:
- Выбираем размеры параллелепипеда и величины углов.
- Чертим параллелограмм — основание.
 С каждой стороне дорисовываем боковые стороны — параллелограммы. От любой из боковой стороны дорисовываем второе основание. Добавляем полоски для склеивания. Параллелепипед может быть прямоугольным, если стороны прямоугольники. Если параллелепипед не прямоугольный, то создать развертку немного сложнее. Для каждого параллелограмма нужно выдержать требуемые углы.
С каждой стороне дорисовываем боковые стороны — параллелограммы. От любой из боковой стороны дорисовываем второе основание. Добавляем полоски для склеивания. Параллелепипед может быть прямоугольным, если стороны прямоугольники. Если параллелепипед не прямоугольный, то создать развертку немного сложнее. Для каждого параллелограмма нужно выдержать требуемые углы. - Вырезаем развертку и склеиваем.
- Параллелепипед готов!
Как сделать пирамиду из бумаги?
Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину.
Рисование развертки:
- Выбираем размеры пирамиды и количество ее граней.
- Рисуем основание — многогранник. В зависимости от количества граней это может быть треугольник, квадрат, пятиугольник или другой многогранник.
- От одной из сторон основания рисуем треугольник, который будет боковой стороной. Следующий треугольник рисуем так, чтобы одна сторона у него с предыдущим была общая и так далее.
 Так рисуем столько треугольников, сколько сторон в пирамиде. Дорисовываем полоски для склеивания в нужных местах.
Так рисуем столько треугольников, сколько сторон в пирамиде. Дорисовываем полоски для склеивания в нужных местах. - Вырезаем и склеиваем фигуру.
- Пирамида готова!
Семейный очаг. Домоводство. Дети. Рецепты. Психология. Отношения
Любому ребенку нравится делать яркие и объемные поделки. Творчество можно объединить с изучением математики и склеить вместе с детьми геометрические фигуры. Ребенок с интересом проведет время, а дополнительно постигнет основы точной науки. Ниже представлено, как начертить карандашом и сделать объемные геометрические фигуры из бумаги, также приведены их правильные названия.
Как сделать объемные геометрические фигуры
Дети познают мир в процессе игры и творчества. Трехмерные фигуры, выполненные своими руками, помогут познакомиться с удивительной наукой — геометрией.
Примеры трафаретов и шаблонов можно скачать из Интернета и распечатать.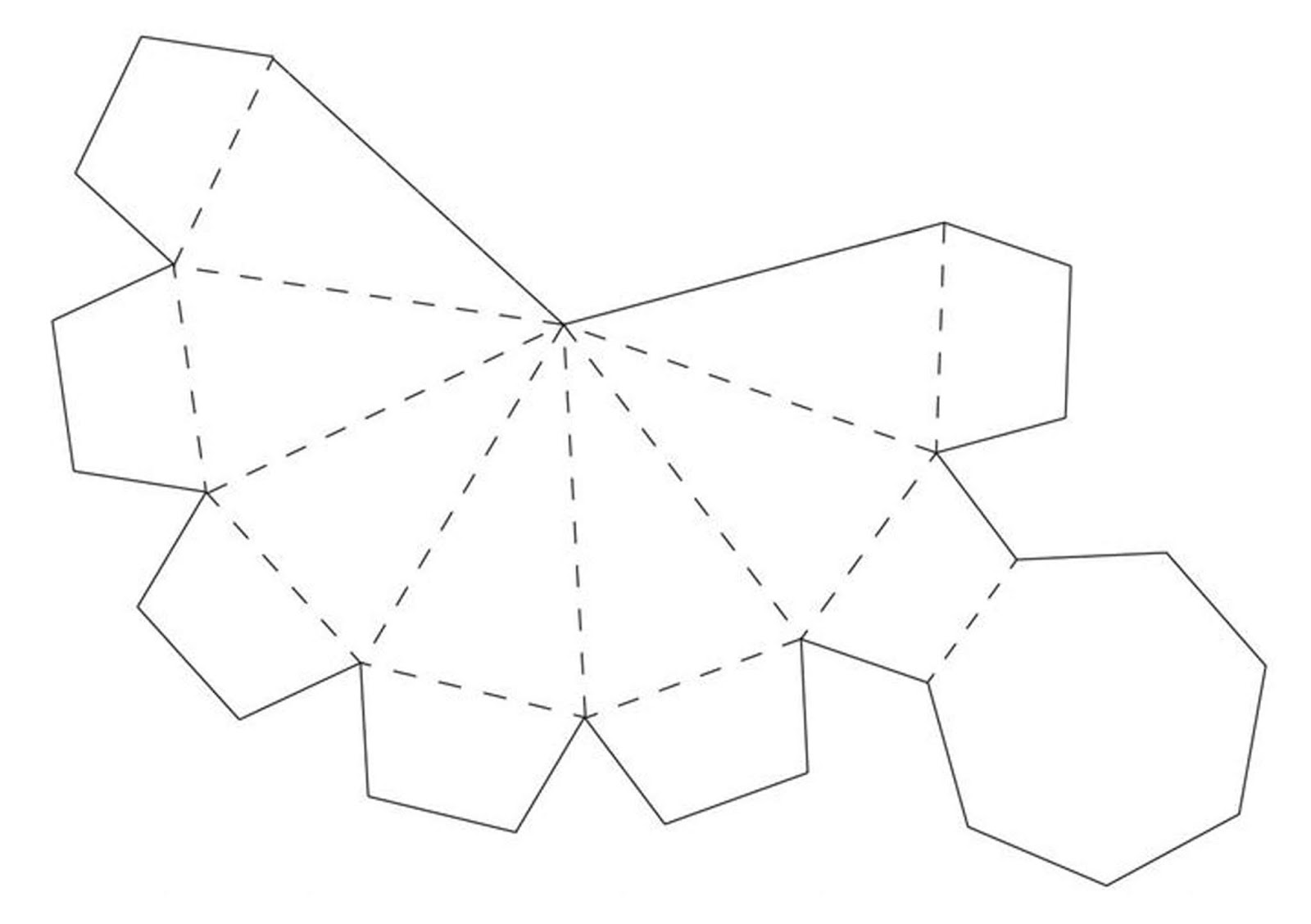 Затем все фигуры вырезают и склеивают. Дети старшего возраста могут самостоятельно нарисовать развертку нужной фигуры, малышам помогают родители,.
Затем все фигуры вырезают и склеивают. Дети старшего возраста могут самостоятельно нарисовать развертку нужной фигуры, малышам помогают родители,.
Геометрические объекты делают из бумаги (белой или цветной), картона. Из последнего материала они получаются плотными и прочными.
Из бумаги
Из картона
Развертки куба
Треугольника
Прямоугольника
Цилиндра
Ромба
Призмы
Схемы для вырезания
Ученикам 1–2 класса демонстрируют в школе простые геометрические фигуры и 3d: квадрат, кубик, прямоугольник. Их несложно вырезать и склеить. Шаблоны развивают мелкую моторику у детей и дают первые представления о геометрии.
Ученики средней школы, которые изучают черчение, делают сложные фигуры: бумажные шестигранники, фигуры из пятиугольников, цилиндры.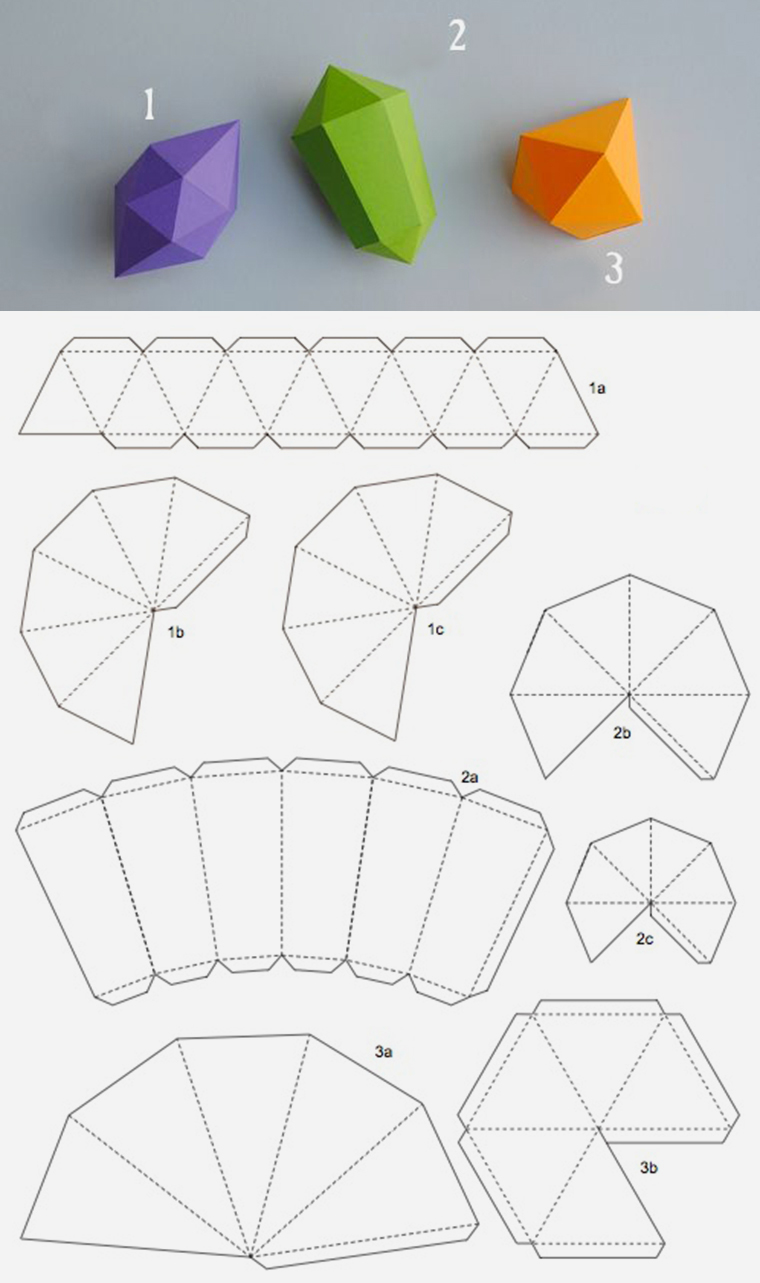 Из бумаги для детей выполняют домики для кукол, мебель, оригами, замок для маленьких игрушек, маски на лицо (трехмерные называются полигональными).
Из бумаги для детей выполняют домики для кукол, мебель, оригами, замок для маленьких игрушек, маски на лицо (трехмерные называются полигональными).
Конуса
Пирамиды
Шестигранника
Макета с припусками
Параллелепипеда
Трапеции
Овала
Шара
Выкройка шара состоит из 8 частей, 12, 16 или большего количества. Присутствуют и другие способы изображения мяча. Например, из 6 деталей или 4 широких клиньев.
Материал, из чего можно сделать плотный шар — картон или плотная бумага.
Многогранника
Параллелограмма
Шаблоны для склеивания
Зачастую школьники задаются вопросом, что можно сделать из бумаги к урокам труда или на выставку. Работы ученика выделятся среди остальных, если это будут сложные трехмерные предметы, рельефные геометрические фигуры, платоновы тела, шаблоны кристаллов и минералов.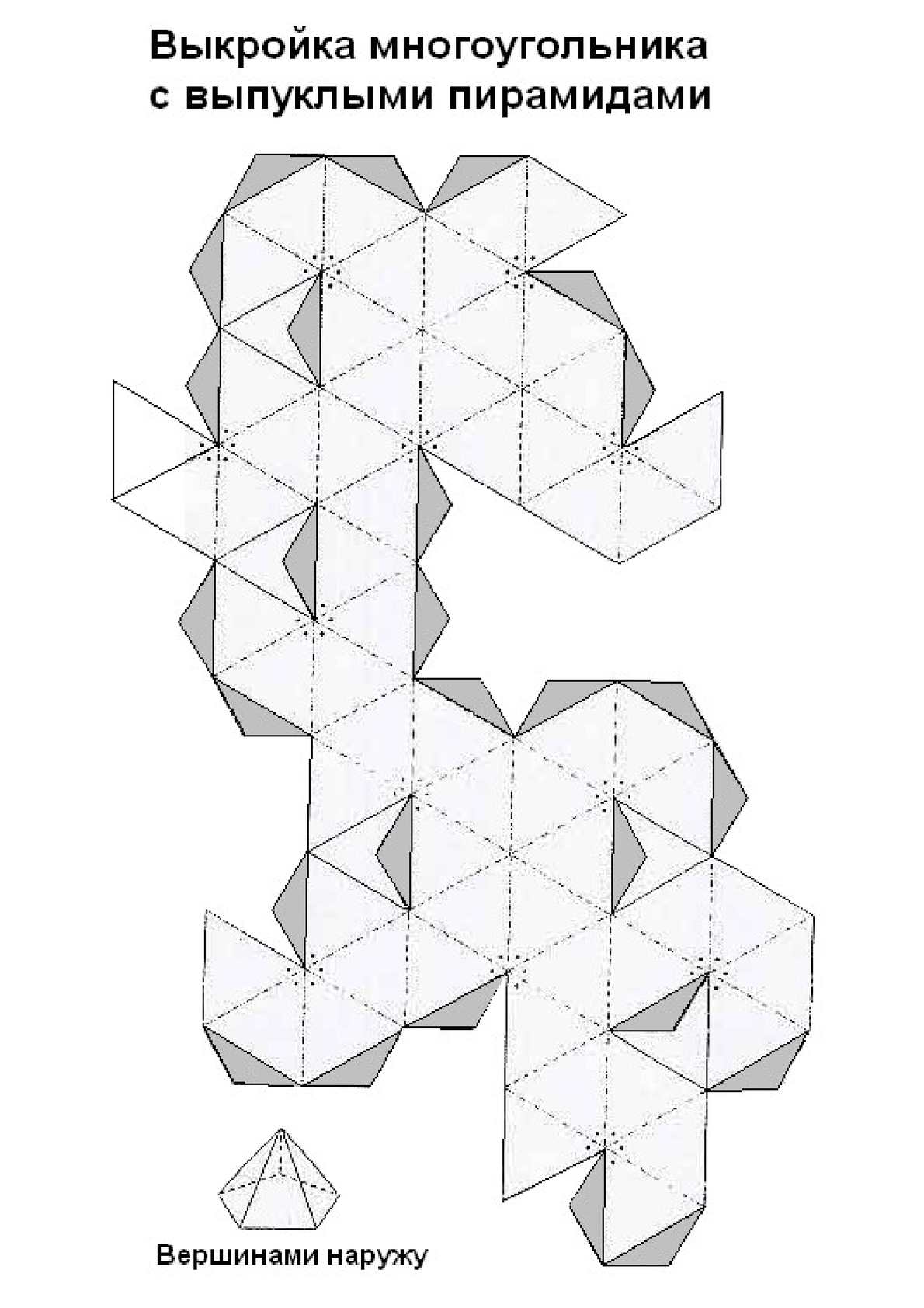
Если следовать инструкции, то ученик 5–6 класса сможет без помощи родителей сделать точный додекаэдр или тетраэдр.
Иногда в школе задают логические задания, как из квадрата сделать круг или шестиугольник. Для этого определить центр квадрата, согнув его по диагонали. Точка пересечения прямых — центр квадрата и будущего круга. Исходя из этого, можно начертить круг.
Сложных фигур
3d
Октаэдра
Тетраэдра
Икосаэдра
Додекаэдра
Гексаэдра
Фигурок из треугольников
Макетирование — увлекательное занятие. Оно помогает развить воображение и логическое мышление. Из бумаги делают не только фигуры, но и необычные скульптуры, статуэтки, шестиугольные–двенадцатиугольные предметы, наклонные объекты (например, Пизанскую башню), карандаши, линейки.
Школьники младших классов или дошколята делают бумажные объемные поделки. Например, предметы из овала — веер, цветы, гусеницы. Для них потребуются овалы и круги разного диаметра. Раскладки склеиваются между собой, получаются трехмерные игрушки.
Начинающие конструкторы задаются вопросами, как рисовать и чертить геометрические фигуры, как правильно склеить выкройки и как делают врезки. Проще всего распечатать готовый шаблон. Затем необходимо согнуть фигуру по пунктирным линиям.
Чтобы сгибы получились ровными, к пунктиру прикладывают линейку, по ее форме делают точные загибы. Такой способ особенно помогает, когда речь идет о фигурках из картона или ребенок делает самые сложные макеты. Например, икосаэдр, додекаэдр, тетраэдр.
На последнем этапе необходимо скрепить элементы объекта, места для склейки обозначены на развернутом виде фигуры. Детали из картона приклеивают при помощи ПВА, а бумажные — карандашным клеем.
Основные ошибки при работе с моделями:
- Ребенок делает неправильные сгибы — например, изгиб отклоняется в сторону от пунктира на несколько градусов. В результате модель получится неточной.
Неточности во время вырезания шаблонов. Если малыш отрезал одну из границ для склеивания, то фигурка будет разворачиваться. Здесь на помощь придет взрослый.
Оригами – бумажные фигурки, которые относятся к японскому искусству и существуют в нём уже не одно столетие. Монахи ещё в древние времена, использовали фигурки из бумаги для декорации храмов и его залов, а также для применения их в религиозных целях (осуществление обрядов).
Сделать оригами из бумаги своими руками в состоянии каждый малоопытный мастер, но главным критерием есть имение усидчивости и точности движений. Сегодня вы поймёте, что не нужно быть асом, чтобы красиво сделать эти изделия.
Инструменты для оригами
Основное внимание стоит уделить выбору бумаги для поделок. Для оригами подойдёт офисная, твёрдая бумага разной цветовой гаммы.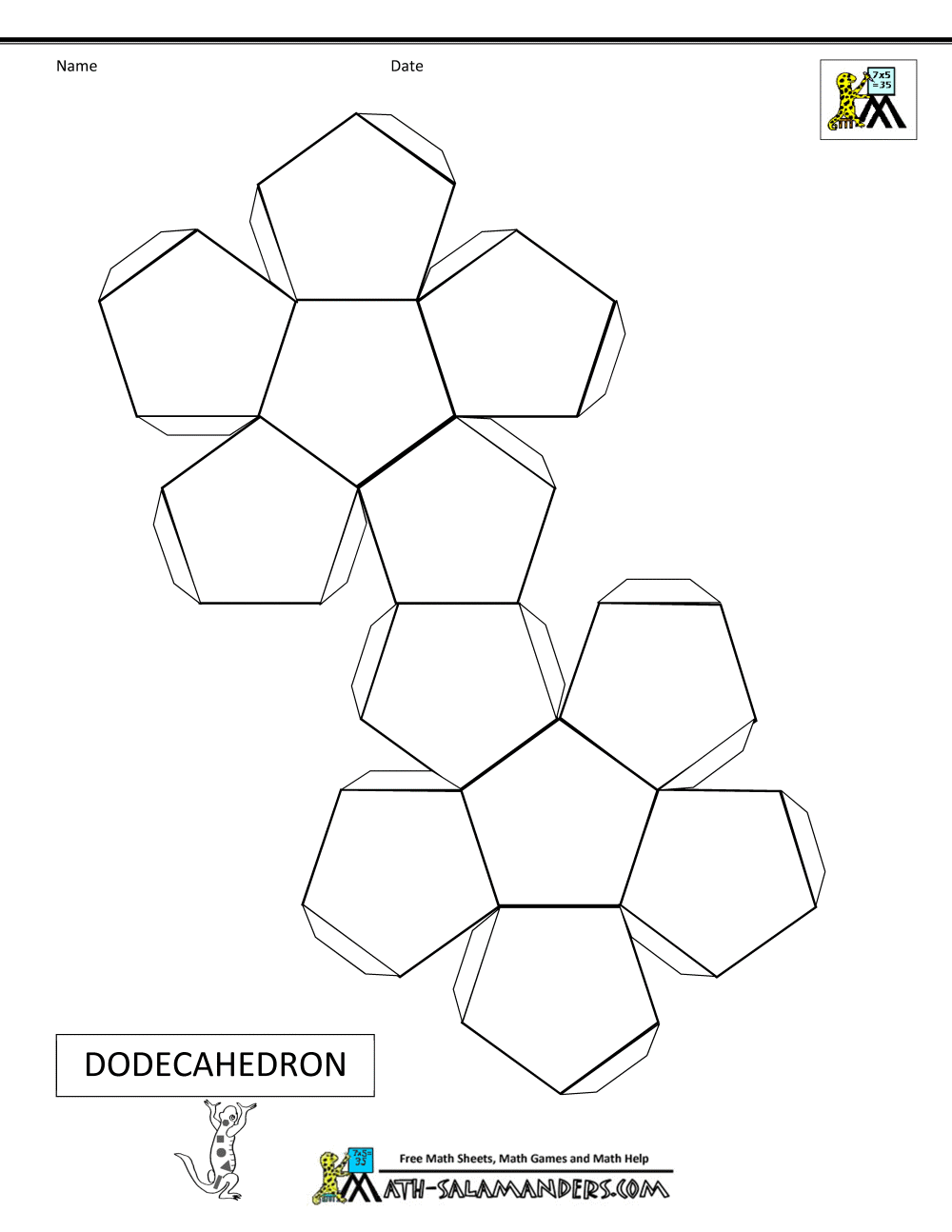 Она подойдёт для любых схем, как простых, так и сложных.
Она подойдёт для любых схем, как простых, так и сложных.
Для закрепления бумаги нужно приобрести клей-карандаш или клей ПВА. Подойдут и другие виды клея, лучшим вариантом будут те, что не оставляют следов, а если и оставили, то легко устраняются.
Приобретите краски в баллончиках, для придания необходимого оттенка изделиям с серой или обычной белой бумаги.
Для выравнивания краёв оригами подойдёт резак, только не стоит забывать про аккуратное поведение с ним.
Также для создания игрушек надо линейки, карандаши для черчения схем. Для придания креативности и необычности вашему оригами, можно украсить его с помощью бисера, стекляруса, стразами, ленточками.
Разновидности бумажных фигурок
Не считая классического вида, есть ещё много разных альтернативных видов:
- Классическое простое оригами – с него стоит начинать тем, кто впервые решил заняться бумажными фигурками. Примером данного стиля есть фигурка журавлика.

- Оригами из модулей – сложнее чем первый вид. Несколько деталей (модулей) необходимо соединить простым складыванием. Изделие держится достаточно долго.
- Аэрогами – фигурки самолётов из бумаги.
- Киригами – создание фигурок происходит с использованием ножниц. Например, открытки.
- Кусудами – объёмное оригами, части изделия соединяются между собой с помощью нитей и клея. Форма фигурки часто напоминает большой шар. Данный вид часто использовался для украшений входа в храм.
Бумажный журавлик
Является классическим видом оригами. В народе ходит легенда, что если сделать тысячу журавликов, то сбудется то, что сердце хочет.
Подробно рассмотрим, как делать сделать эту чудесную фигурку.
- Согнув лист по диагонали, отрезаем ненужную бумагу, так чтобы остался лист напоминающий треугольник.
- Ещё раз сгибаем. Должно быть 2 треугольника. Из образовавшегося треугольника, расправляя делаем квадрат. Такую же процедуру проделываем и, с другой стороны.

- Держим так, чтобы края были сверху, и загибаем их строго к центру.
- Верхний треугольник тоже сгибаем. И сразу расправляем сгиб, у нас получается контур.
- Уголок тот, что ниже остальных, загибаем горизонтально.
- Делаем ромб (слаживаем краешки к центру стороны). Проделываем те же маневры с другой стороной.
- Для формирования шеи, берёмся за нижнюю часть и начинаем загибать там, где внутренний контур. Таким же методом делаем журавлику хвост.
- Там, где находится шея, начало изгибаем, таким образом у нас получится клюв.
- Складываем ему крылья, воспользовавшись сгибанием на маленький угол.
При желании, журавля можно покрасить или сразу взять цветную бумагу. Оригами журавель готов.
Роза техникой оригами
Более привлекательными и легкими для большинства новичков, так и для мастеров оригами, являются цветы из оригами. Распространённой фигуркой является бумажная роза.
Рассмотрим пошаговую инструкцию и фото данного оригами:
- Берём цветную бумагу, желательно красного цвета, складываем пополам, потом ещё раз.

- Слой бумаги, что находится вверху, немного раскрываем так, чтобы у нас получился раздутый верх.
- Переворачиваем на другую сторону, и повторяем действие, что описаны в предыдущем пункте.
- Берём углы и загибаем их к верхнему уголку.
- Треугольник, что вскоре получился, сгибаем пополам, до появления контура.
- Раскрываем треугольник, потянув за оба угла вниз.
- Держа кармашки за верхнюю часть, загибаем вниз.
- Пункты с 4 по 7 проделываем и на другой стороне.
- Делаем загиб верхнего угла.
- Нижнюю часть разворачиваем как книгу.
- Выпучиваем так, чтобы получились 2 треугольника.
- Переворачиваем изделие.
- Правый нижний квадрат аккуратно сгибаем с верхнего в нижний край (строго по диагонали).
- Повернув на 180̊ и проделываем 13 пункт.
- Берёмся пальцами за стенки оригами, и не боясь крутим на 360̊, пока не увидим получившееся лепестки.
Бумажный лебедь
Данная техника более сложная, чем остальные так как здесь используется метод модульного оригами.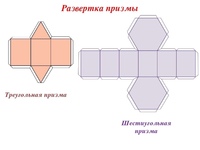 Для того, чтобы сделать объёмного лебедя, нужно:
Для того, чтобы сделать объёмного лебедя, нужно:
- Сделать приблизительно 460 треугольников с белой бумаги и 1 красный для клюва.
- Уголки двух треугольников вставляем в карманчик третьего.
- Прибавляем ещё два. Все уголки вкладываем в карман.
- Делаем три таких ряда. Необходимо взять около 30 модулей для каждого ряда. Закрываем круг.
- Вставляем заготовки для следующих двух рядов.
- Вдавливаем центр так, чтобы он потихоньку выворачивался.
- При всём этом края заворачиваем вверх.
- Делаем ряды дальше, но не забываем про шахматный порядок модулей.
- В 7 ряду делаем модули под крылья. Насаживаем 12 заготовок, сделав пропуск для 2 уголков, приделываем ещё такое же количество заготовок. На оставленных местах делаем лебедю хвост и шею.
- В 8 ряде для крыльев количество заготовок становится на 1 меньше.
- Так делаем и с последующими рядами, пока в последнем ряде не останется 1 модуль.
- Хвост делаем методом уменьшения на одну заготовок в каждом ряде.

- Шею собираем из 10-12 модулей, а голову из одной красной заготовки. Создаём шею, постепенно выгибая её.
- Когда шея готова, собираем её вместе с телом воедино.
Фото оригами своими руками
Обратите внимание!
Обратите внимание!
Создавать поделки своими руками интересно не только детям, но и взрослым. Однако для взрослых придумано достаточное количество моделей, которые отличаются сложностью выполнения и временем, затраченным на их создание. В последнее время у взрослых и детей появился интерес к созданию сложных геометрических фигур. К такому виду фигур относится икосаэдр, который представляет собой правильный многоугольник и является одним из платоновых тел – правильных многогранников. Эта фигура имеет 20 треугольных граней (равносторонних треугольников), 30 ребер и 12 вершин, которые являются местом стыка 5 ребер.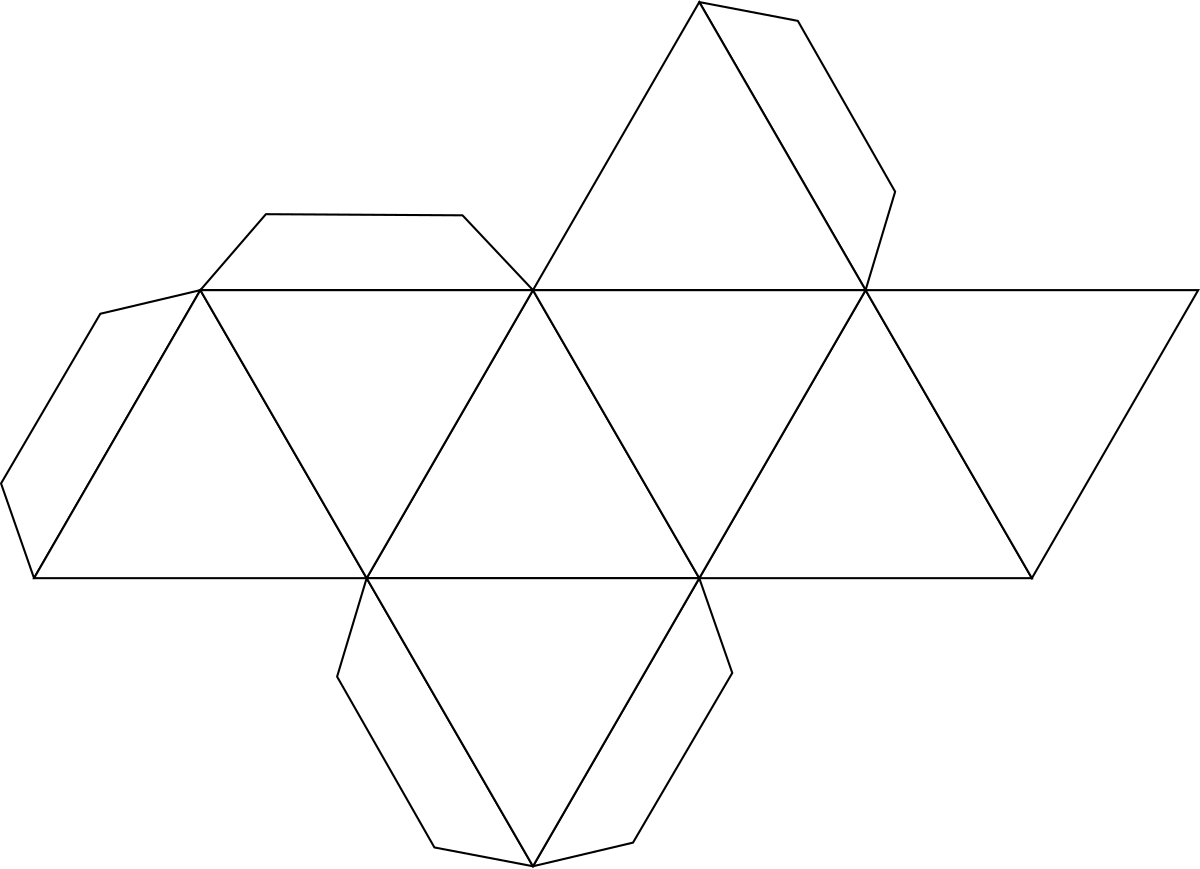 Правильный икосаэдр из бумаги собрать достаточно сложно, но интересно. Если вы увлечены оригами, то сделать икосаэдр бумажный своими руками вам не составит труда.
Его сделать из цветной, гофрированной бумаги, фольги, упаковочной бумаги для цветов. Используя разнообразные материалы, можно придать еще большую красоту и эффектность своему икосаэдру. Все зависит только от фантазии его создателя и подручного материала, имеющегося на столе.
Правильный икосаэдр из бумаги собрать достаточно сложно, но интересно. Если вы увлечены оригами, то сделать икосаэдр бумажный своими руками вам не составит труда.
Его сделать из цветной, гофрированной бумаги, фольги, упаковочной бумаги для цветов. Используя разнообразные материалы, можно придать еще большую красоту и эффектность своему икосаэдру. Все зависит только от фантазии его создателя и подручного материала, имеющегося на столе.
Предлагаем вам несколько вариантов разверток икосаэдра, которые можно распечатать, перенести на плотную бумагу и картон, согнуть по линиям и склеить.
Как сделать икосаэдр из бумаги: схема
Для того чтобы собрать икосаэдр из листа бумаги или картона, необходимо предварительно подготовить следующие материалы:
- макет икосаэдра;
- клей ПВА;
- ножницы;
- линейка.
Во время создания икосаэдра важно обратить особое внимание на процесс сгиба всех деталей: для того, чтобы ровно согнуть бумагу, можно использовать обычную линейку.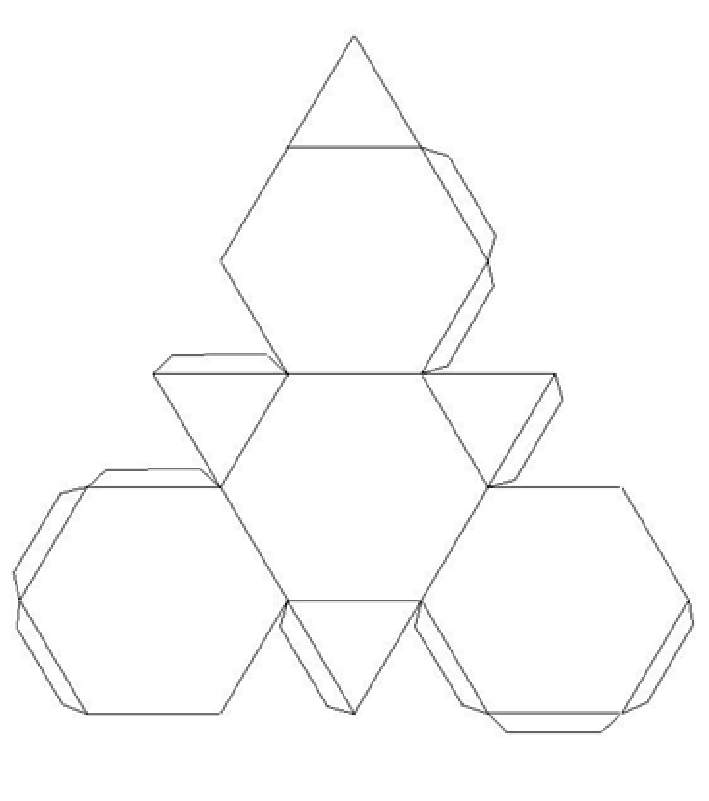
Примечательно, что икосаэдр можно встретить и в повседневной жизни. Например, в форме усеченного икосаэдра (многогранник, состоящий из 12 пятиугольников и 20 шестиугольников правильной формы) выполнен футбольный мяч. Это особенно видно, если раскрасить получившийся икосаэдр в черно-белый цвет, как и сам мяч.
Такой футбольный мяч можно сделать самостоятельно, распечатав предварительно развертку усеченного икосаэдра в 2 экземплярах:
Создание икосаэдра своими руками представляет интересный процесс, который требует вдумчивости, терпения и большого количества бумаги. Однако результат, полученный в итоге, будет радовать глаз еще долгое время. Икосаэдр можно дать поиграть ребенку, если он достиг уже трехлетнего возраста. Играя с такой сложной геометрической фигурой, он будет развивать не только образное мышление, пространственные навыки, но и знакомиться с миром геометрии. Если же взрослый решил создать икосаэдр самостоятельно, то такой творческий процесс по конструированию икосаэдра позволит скоротать время, а также похвастаться перед близкими своим умением создавать сложные фигуры.
В основе самых сложных и необычные формы сооружений, устройств, механизмов лежат элементарные геометрические фигуры: куб, призма, пирамида, шар и другие. Для начала научитесь создавать самые простые фигуры, а после вы легко освоите более сложные формы.
Многие моделисты начинают свой путь с бумажных моделей. Это обусловлено доступностью материала (найти бумагу и картон не составляет трудности) и легкостью в его обработки (не требуются специальные инструменты).
Однако, бумага имеет и ряд характерных особенностей:
- капризный, хрупкий материал
- требует высокой аккуратности, внимательности, усидчивости при работе
По этим причинам бумага является материалом, как для начинающих, так и для настоящих мастеров и из нее создаются модели самой разной сложности.
В этот статье мы изучим простейшие геометрические фигуры, которые можно сделать из бумаги.
Вам понадобятся следующие материалы:
- лист бумаги
- карандаш
- линейка
- ластик
- ножницы
- клей ПВА либо клеящий карандаш
- кисточка для клея, лучше из жесткой щетины
- циркуль (для некоторых фигур)
Как сделать куб из бумаги?
Куб – правильный многогранник, каждая грань которого представляет собой квадрат
Создание куба состоит из двух этапов: создание развертки и склеивание.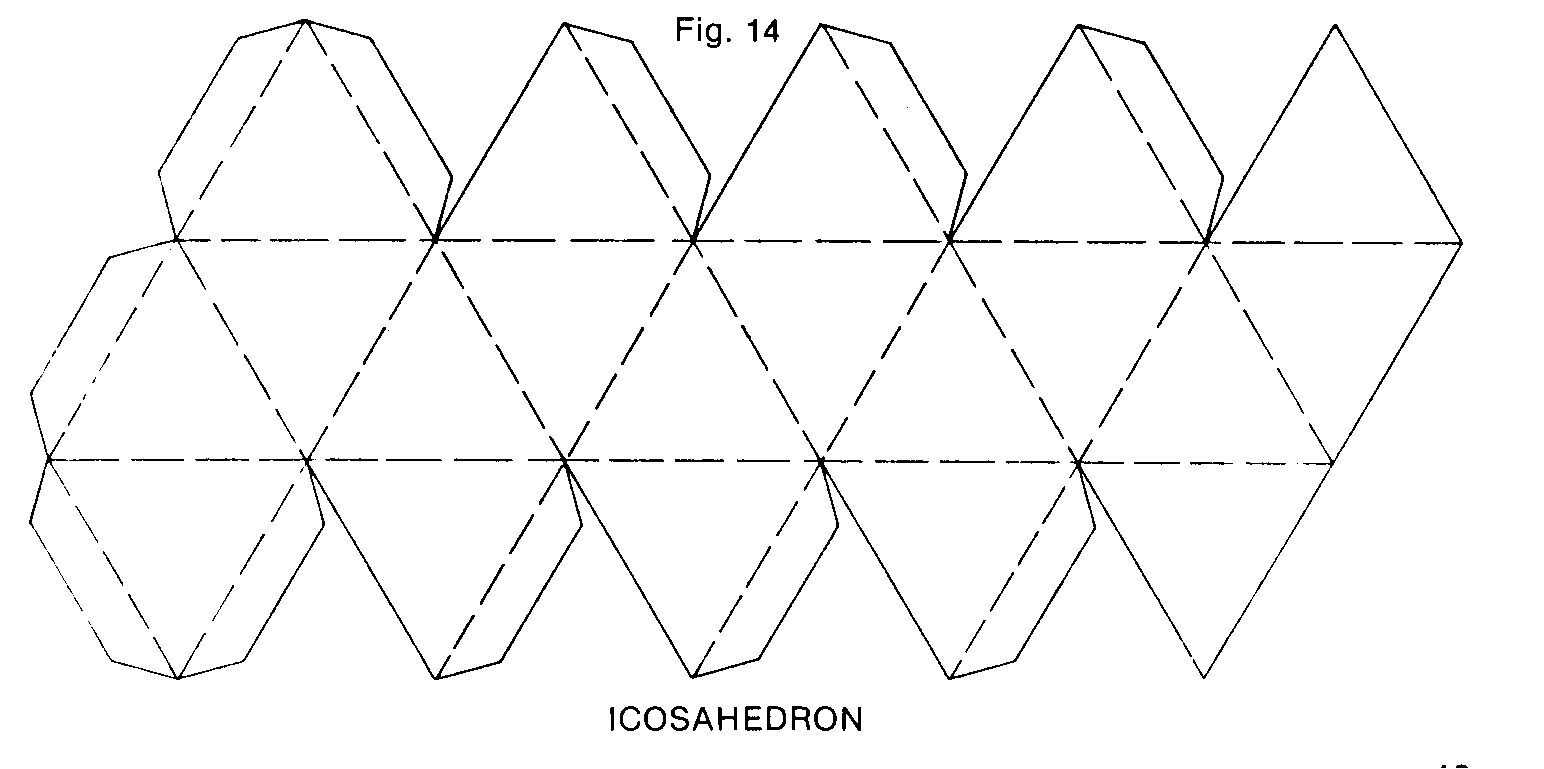 фигуры. Для создания схемы вы можете воспользоваться принтером, просто распечатав готовую схему. Либо вы можете самостоятельно с помощью чертежных инструментов нарисовать развертку.
фигуры. Для создания схемы вы можете воспользоваться принтером, просто распечатав готовую схему. Либо вы можете самостоятельно с помощью чертежных инструментов нарисовать развертку.
Рисование развертки:
- Выбираем размеры квадрата — одной стороны нашего куба. Лист бумаги должен быть шириной не менее 3 сторон этого квадрата и длиной немного более 4 сторон.
- Чертим в длину нашего листа четыре квадрата, которые станут боковыми сторонами куба. Рисуем их строго на одной линии, вплотную друг к другу.
- Над и под любыми из квадратов рисуем по одному такому же квадрату.
- Дорисовываем полоски для склеивания, с помощью которых грани будут соединяться между собой. Каждые две грани должны соединяться одной полоской.
- Куб готов!
После рисования развертка вырезается ножницами и склеивайте ПВА. Клей очень тонким слоем равномерно размазываем кистью по поверхности склеивания. Соединяем поверхности и закрепляем в нужном положении на некоторое время, с помощью скрепки или небольшого груза. Срок схватывания клея где-то 30-40 минут. Ускорить высыхание можно методом нагрева, например, на батарее. После склеиваем следующие грани, закрепляем в нужном положении. И так далее. Так постепенно вы проклеите все грани куба. Используйте небольшие порции клея!
Срок схватывания клея где-то 30-40 минут. Ускорить высыхание можно методом нагрева, например, на батарее. После склеиваем следующие грани, закрепляем в нужном положении. И так далее. Так постепенно вы проклеите все грани куба. Используйте небольшие порции клея!
Как сделать конус из бумаги?
Конус – тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность.
Рисование развертки:
- Рисуем циркулем окружность
- Вырезаем сектор (часть круга, ограниченная дугой окружности и двумя радиусами, проведенными к концам этой дуги) из этой окружности. Чем больший сектор вы вырежете, тем острее будет конец конуса.
- Склеиваем боковую поверхность конуса.
- Измеряем диаметр основания конуса. С помощью циркуля рисуем окружность на листе бумаге требуемого диаметра. Дорисовываем треугольнички для склеивания основания с боковой поверхностью. Вырезаем.
- Приклеиваем основание к боковой поверхности.

- Конус готов!
Как сделать цилиндр из бумаги?
Цилиндр – геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.
Рисование развертки:
- Рисуем прямоугольник на бумаги, в котором ширина — это высота цилиндра, а длина определит диаметр будущей фигуры. Отношение длины прямоугольника к диаметру определяется выражением: L=πD, где L- длина прямоугольника, а D — диаметр будущего цилиндра. Подставив в формулу требуемый диаметр, найдем длину прямоугольника, который будем рисовать на бумаге. Дорисовываем небольшие дополнительные треугольнички, которые необходимы для склеивания деталей.
- Рисуем на бумаге два круга, диаметром цилиндра. Это будет верхнее и нижнее основания цилиндра.
- Вырезаем все детали будущего бумажного цилиндра.
- Склеиваем боковую поверхность цилиндра из прямоугольника. Даем детали высохнуть. Приклеиваем нижнее основание. Ждем высыхания. Приклеиваем верхнее основание.

- Цилиндр готов!
Как сделать параллелепипед из бумаги?
Параллелепипед – многогранник, у которого шесть граней и каждая из них параллелограмм.
Рисование развертки:
- Выбираем размеры параллелепипеда и величины углов.
- Чертим параллелограмм — основание. С каждой стороне дорисовываем боковые стороны — параллелограммы. От любой из боковой стороны дорисовываем второе основание. Добавляем полоски для склеивания. Параллелепипед может быть прямоугольным, если стороны прямоугольники. Если параллелепипед не прямоугольный, то создать развертку немного сложнее. Для каждого параллелограмма нужно выдержать требуемые углы.
- Вырезаем развертку и склеиваем.
- Параллелепипед готов!
Как сделать пирамиду из бумаги?
Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину.
Рисование развертки:
- Выбираем размеры пирамиды и количество ее граней.

- Рисуем основание — многогранник. В зависимости от количества граней это может быть треугольник, квадрат, пятиугольник или другой многогранник.
- От одной из сторон основания рисуем треугольник, который будет боковой стороной. Следующий треугольник рисуем так, чтобы одна сторона у него с предыдущим была общая и так далее. Так рисуем столько треугольников, сколько сторон в пирамиде. Дорисовываем полоски для склеивания в нужных местах.
- Вырезаем и склеиваем фигуру.
- Пирамида готова!
Геометрические фигуры из бумаги должен научиться делать каждый! Ведь никогда не знаешь, какие знания тебе могут пригодиться в жизни. В последнее время техника оригами набирает широкую популярность среди детей и взрослых. Но перед тем как делать разнообразные поделки (животных, птиц, растений, маленьких домиков), нужно начать с простых геометрических фигур. Такие изделия подойдут для школьников для хорошего визуального представления разных фигур.
Мастерим куб
Итак, для сегодняшнего мастер-класса нам пригодится бумага, схемы, клей, ножницы, линейки и немножечко терпения.
Куб — самая простая фигура для оригами, простой многогранник, в котором каждая грань является квадратом. Схему для создания развертки можно распечатать на принтере, либо начертить самим. Для этого выбрать размеры граней. Ширина листа бумаги должна быть не менее 3 сторон одного квадрата, а длина не более 5 сторон. Начертить в длину листа четыре квадрата, которые станут боковыми сторонами куба. Рисовать строго на одной линии, вплотную. Над и под одним квадратом нарисовать по одному квадрату. Дорисовать полоски для склеивания, благодаря которым грани будут соединяться между собой. Наш куб уже практически готов!
Далее тонким слоем клея равномерно размазать по местам соединения. Склеить эти поверхности и закрепить на некоторое время с помощью скрепки. Клей будет схватываться около 30-40 минут. Таким образом склеить все грани.
Поделка посложнее
Конус делается немного сложнее. Для начала нарисовать циркулем окружность. Вырезать сектор (часть кружка, ограниченная дугой окружности и двумя радиусами) из этой окружности. Острота конца конуса зависит от вырезанной части большого сектора.
Вырезать сектор (часть кружка, ограниченная дугой окружности и двумя радиусами) из этой окружности. Острота конца конуса зависит от вырезанной части большого сектора.
Склеить боковую поверхность конуса. Далее измерить диаметр основания конуса. Циркулем нарисовать окружность на листе бумаги. Затем дорисовать треугольнички для склеивания основы с боковой поверхности. Вырезать. После приклеить основание к боковой поверхности. Поделка готова!
Сложный параллелепипед
Параллелепипед — сложная фигура многогранник, у которого 6 граней и каждая из них параллелограмм.
Чтобы сделать параллелепипед техникой оригами, нужно начертить основание — параллелограмм любого размера. С каждой его стороны нарисовать боковые стороны — тоже параллелограммы. Далее от любой из боковых сторон дорисовать второе основание. Добавить места для склеивания. Параллелепипед может быть прямоугольным, если все стороны имеют прямые углы. Затем вырезать развертку и склеить. Готово!
Пирамида-оригами
Пришло время сделать пирамиду из бумаги.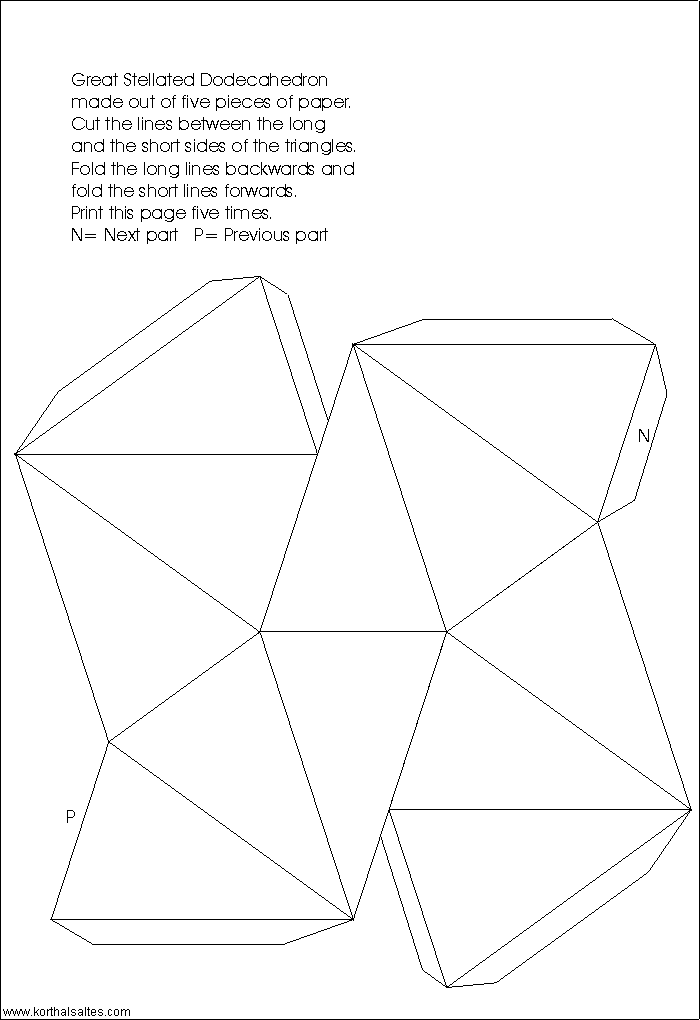 Это многогранник, основание которого — многоугольник, а другие грани — треугольники с общей вершиной.
Это многогранник, основание которого — многоугольник, а другие грани — треугольники с общей вершиной.
Для начала нужно выбрать размеры пирамиды и количество граней. Далее нарисовать многогранник — он будет основанием. Смотря на количество граней, это может быть также треугольник, квадрат, пятиугольник.
От одной из сторон нашего многогранника нарисовать треугольник, который будет боковой стороной. Затем нарисовать еще треугольник, чтобы одна его сторона была общей с первым треугольником. Нарисовать их столько, сколько сторон в пирамиде. Далее дорисовать полоски для склеивания в необходимых местах. Вырезать и склеить фигуру. Пирамида готова!
Бумажный цилиндр
Цилиндр — это геометрическая фигура, ограниченная цилиндрической поверхностью и двумя параллельными плоскостями, которые ее пересекают.
Нарисовать прямоугольник на бумаге, в которой ширина — высота цилиндра, а длина — диаметр. Любители геометрии знают, что отношение длины прямоугольника к диаметру определяется формулой: L=nD, где L — длина прямоугольника, а D — диаметр цилиндра.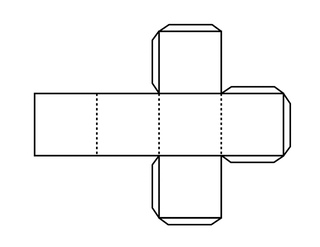 С помощью этого вычисления узнать длину прямоугольника, которого будем рисовать на бумаге. Дорисовать маленькие треугольнички для склеивания деталей.
С помощью этого вычисления узнать длину прямоугольника, которого будем рисовать на бумаге. Дорисовать маленькие треугольнички для склеивания деталей.
Затем нарисовать на бумаге два круга, диаметром как цилиндр. Это будет верхнее и нижнее основания цилиндра. Далее вырезать все детали. Склеить боковую поверхность цилиндра из прямоугольника. Дать детали высохнуть и приклеить к нему нижнее основание. Снова подождать, пока высохнет, и приклеить верхнюю основу. Готово!
Видео по теме статьи
Объемные фигуры из бумаги схемы
Объемные поделки из бумаги: 5 способов создания фигурок
Download link: Объемные фигуры из бумаги схемы
Было это в период Сёва 1926-1989 , когда из бумажных поделок осталось только носи — фигурка из белой и красной бумаги, сложенная особым образом и символизирующая добрые пожелания. Мы с вами постепенно начинаем продвигаться и переходим к обучению модульного оригами. Надеюсь,что со временем организую небольшой бизнес по изготовлению на заказ подарков ручной работы. После того, как мы вырезали её, необходимо перейти к её складыванию.
Надеюсь,что со временем организую небольшой бизнес по изготовлению на заказ подарков ручной работы. После того, как мы вырезали её, необходимо перейти к её складыванию.
Может быть посоветуете технику для начинающих? Используйте небольшие порции клея! Чтобы зафиксировать модель на боковых гранях, дорисовывают вспомогательные клапаны.
Объемные геометрические фигуры оригами — Сложный параллелепипед Параллелепипед — сложная фигура многогранник, у которого 6 граней и каждая из них параллелограмм. Чем красивее будет исходный материал — картон, тем красивее будет в итоге упаковка.
Как сделать объемные геометрические фигуры из бумаги схемы, шаблоны? Можно сделать из белой или из цветной бумаги. Можно вырезать из бумаги с каким-либо рисунками или же цифрами. Предлагаю сделать не совсем обычную объемную фигуру в технике оригами. Кстати, на основе их можно изготовить красивую подарочную упаковку. Самое сложное — это разработать и начертить развртки, нужны хотя бы базовые знания черчения.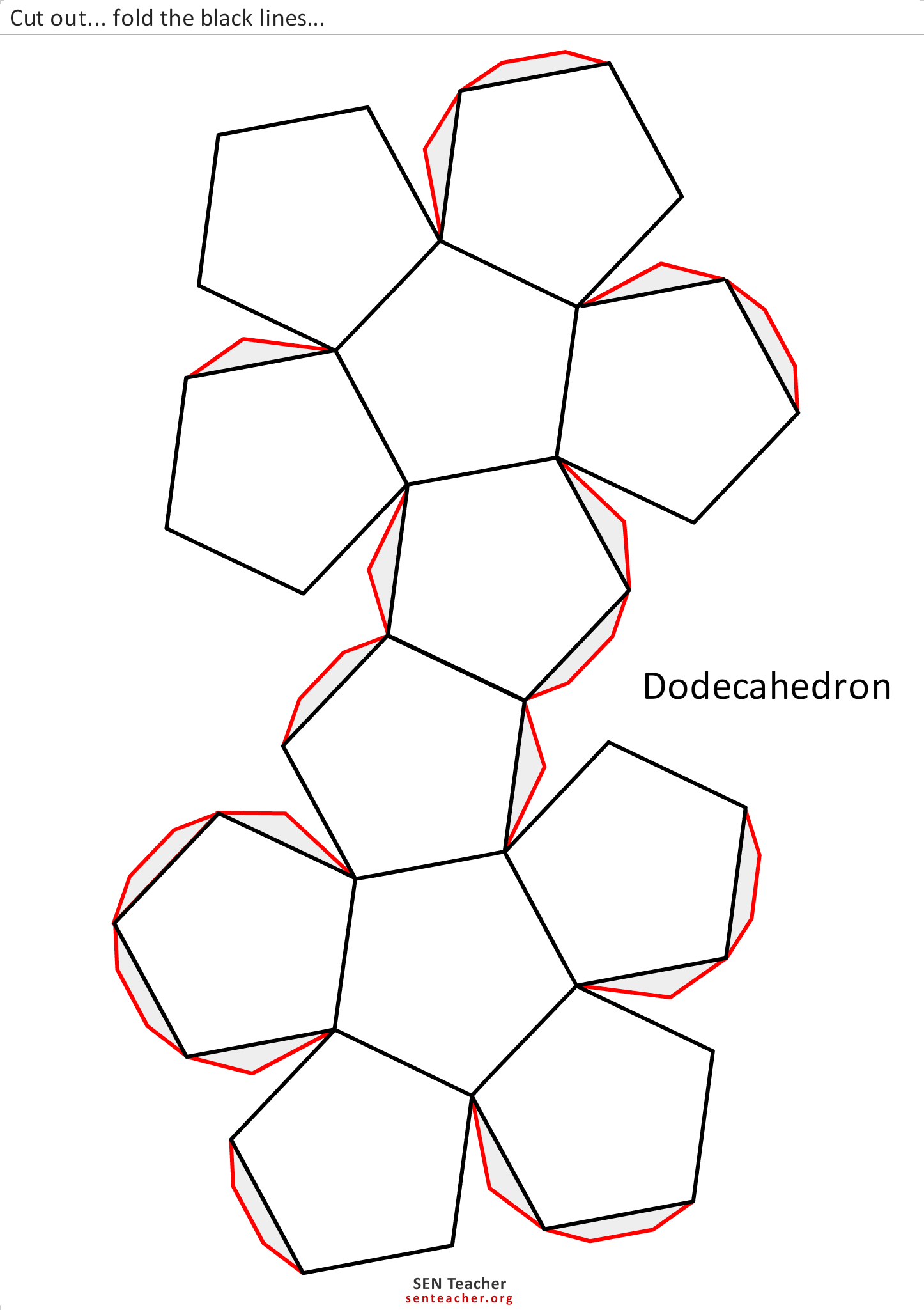 Можно взять и готовые развртки и распечатать на принтере. Чтобы линия сгиба была ровной и острой, можно воспользоваться тупой иглой и металлической линейкой. При проведении линии иголку нужно сильно нагнуть в направлении движения, практически положив е набок. Это развертка трехгранной пирамиды Вот здесь можно найти шаблоны более сложных фигур Платоновы Тела, Архимедовы тела, многогранники, полиэдры, разные виды пирамид и призм, простые и косые бумажные модели. Кстати, чтобы рассчитать параметры пирамиды, можно воспользоваться вот этой программой. Таким способом лучше запоминаются геометрические фигуры. Лучши материал для изготовления подобных объемных фигур — это плотная бумага можно цветную или же картон. Для изготовления понадобятся кроме бумаги еще и карандаш с линейкой, а также ножницы и клей вырезать и клеить развертки. Сначала необходимо правильно начертить на бумаге фигуру по граням, которые должны быть соединены между собой. У каждой фигуры грани имеют определенную форму: квадрат, треугольник, прямоугольник, ромб, шестиугольник, круг и т.
Можно взять и готовые развртки и распечатать на принтере. Чтобы линия сгиба была ровной и острой, можно воспользоваться тупой иглой и металлической линейкой. При проведении линии иголку нужно сильно нагнуть в направлении движения, практически положив е набок. Это развертка трехгранной пирамиды Вот здесь можно найти шаблоны более сложных фигур Платоновы Тела, Архимедовы тела, многогранники, полиэдры, разные виды пирамид и призм, простые и косые бумажные модели. Кстати, чтобы рассчитать параметры пирамиды, можно воспользоваться вот этой программой. Таким способом лучше запоминаются геометрические фигуры. Лучши материал для изготовления подобных объемных фигур — это плотная бумага можно цветную или же картон. Для изготовления понадобятся кроме бумаги еще и карандаш с линейкой, а также ножницы и клей вырезать и клеить развертки. Сначала необходимо правильно начертить на бумаге фигуру по граням, которые должны быть соединены между собой. У каждой фигуры грани имеют определенную форму: квадрат, треугольник, прямоугольник, ромб, шестиугольник, круг и т.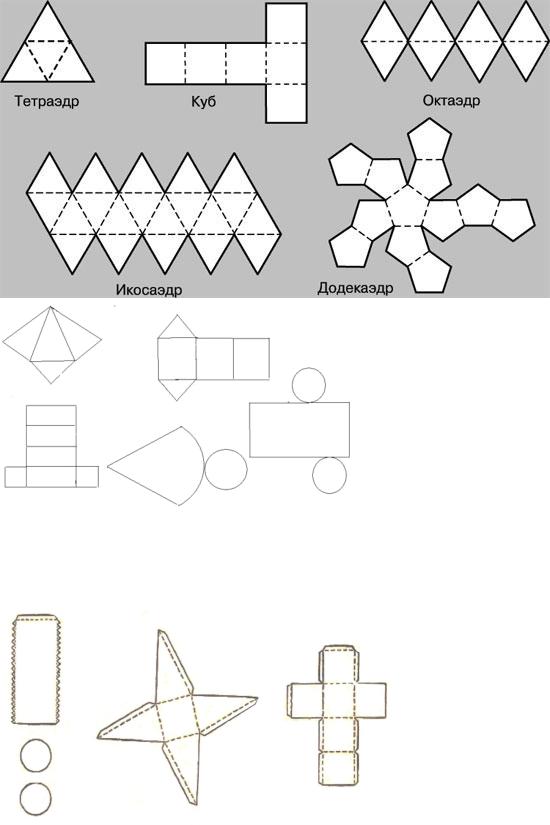 Очень важно, чтобы длина ребер фигуры, которые будут соединены друг с другом имели одинаковую длину, чтобы во время соединения не возникло проблем. Если фигура состоит из одинаковых граней, я бы предложила сделать шаблон во время черчения использовать этот шаблон. Так же можно скачать из интернета готовые шаблоны, распечатать их, согнуть по линиям и соединить склеить. Шаблон конуса: Так вы весело и с пользой сможете провести с малышом время, изучая геометрические фигуры. К примеру, можно наглядно показать ребнку как выглядит та или иная фигура, дать е подержать в руках. Либо можно с целью обучения распечатать схемы со специальными обозначениями. Как вы поняли, вышеприведнные шаблоны необходимо распечатать, вырезать, согнуть по линиям, склеить по специальным узким полосочкам, прилегающим к избранным сторонам. Итак, с помощью приведенных ниже шаблонов Вы можете легко сделать следующие фигуры: Треугольная Призма И еще несколько редких объемных геометрических фигур можно найти по этой ссылке.
Очень важно, чтобы длина ребер фигуры, которые будут соединены друг с другом имели одинаковую длину, чтобы во время соединения не возникло проблем. Если фигура состоит из одинаковых граней, я бы предложила сделать шаблон во время черчения использовать этот шаблон. Так же можно скачать из интернета готовые шаблоны, распечатать их, согнуть по линиям и соединить склеить. Шаблон конуса: Так вы весело и с пользой сможете провести с малышом время, изучая геометрические фигуры. К примеру, можно наглядно показать ребнку как выглядит та или иная фигура, дать е подержать в руках. Либо можно с целью обучения распечатать схемы со специальными обозначениями. Как вы поняли, вышеприведнные шаблоны необходимо распечатать, вырезать, согнуть по линиям, склеить по специальным узким полосочкам, прилегающим к избранным сторонам. Итак, с помощью приведенных ниже шаблонов Вы можете легко сделать следующие фигуры: Треугольная Призма И еще несколько редких объемных геометрических фигур можно найти по этой ссылке. При этом вы сами можете выбрать цветовое решение вашей объмной фигуры. Для того чтобы сделать объмные геометрические фигуры достаточно иметь шаблон, сделанный по схеме развртки и клей, чтобы склеить фигуру. Итак, я хочу предложить сделать следующие геометрические фигуры:.
При этом вы сами можете выбрать цветовое решение вашей объмной фигуры. Для того чтобы сделать объмные геометрические фигуры достаточно иметь шаблон, сделанный по схеме развртки и клей, чтобы склеить фигуру. Итак, я хочу предложить сделать следующие геометрические фигуры:.
DIY: Голова оленя/ Паперкрафт/ FANCY SMTH
После таких веселых занятий никакая геометрия не станет слишком сложной для вашего ребенка в будущем процессе школьного обучения. Каждую сторону основания делим пополам. Чем красивее будет исходный материал — картон, тем красивее будет в итоге упаковка. Используют самый разнообразный материал, из которого выполняется пирамида. Наиболее удобным и простым в исполнении является поделка из бумаги в стиле оригами. Если под рукой нет принтера, ее можно просто перерисовать, соблюдая соотношение сторон. Шаблон конуса: Объемные геометрические фигуры просто необходимы при обучении: они предоставляют ученикам возможность держать их в руках, рассматривать, что является важной частью учебного процесса, они просто необходимы в качестве пособия при изучении знаменитой теоремы Эйлера — наглядно демонстрируя, что даже при деформациях, искривлениях число граней многогранника, а значит и соотношение Эйлера, останется неизменным: Кроме того, объемные фигуры могут служить отличным пособием, помогающим объяснить ученикам, как найти площадь поверхности многогранника.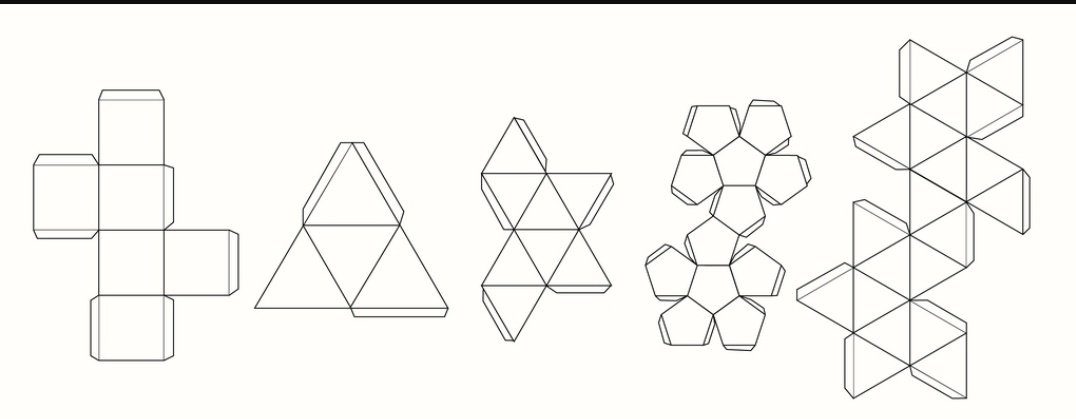 Яркие объемные поделки из бумаги привлекут внимание ребенка и уж точно не дадут скучать. Необычную объемную фигуру — тор, сделать будет несложно, если в работе вы будете использовать специальную схемы для сборки, которую можете скачать в сети. Это у нашего поколения конус может ассоциироваться с пакетом для семечек, а уже для наших детей нужно искать другие ассоциации. На одной третьей в верхнем углу по центру мы рисуем лицо будущего снеговика, глаза, нос и рот. Вопрос задан с практической целью, хочу самостоятельно обшить руль машины кожей, но для этого необходимо начертить выкройку, вот тут и возникла трудность — не хватает воображения всё это нарисовать, ведь поверхность тора — это т.
Яркие объемные поделки из бумаги привлекут внимание ребенка и уж точно не дадут скучать. Необычную объемную фигуру — тор, сделать будет несложно, если в работе вы будете использовать специальную схемы для сборки, которую можете скачать в сети. Это у нашего поколения конус может ассоциироваться с пакетом для семечек, а уже для наших детей нужно искать другие ассоциации. На одной третьей в верхнем углу по центру мы рисуем лицо будущего снеговика, глаза, нос и рот. Вопрос задан с практической целью, хочу самостоятельно обшить руль машины кожей, но для этого необходимо начертить выкройку, вот тут и возникла трудность — не хватает воображения всё это нарисовать, ведь поверхность тора — это т.
▶▷▶▷ сделать геометрическую фигуру из бумаги схемы
▶▷▶▷ сделать геометрическую фигуру из бумаги схемы| Интерфейс | Русский/Английский |
| Тип лицензия | Free |
| Кол-во просмотров | 257 |
| Кол-во загрузок | 132 раз |
| Обновление: | 25-05-2019 |
сделать геометрическую фигуру из бумаги схемы — Как сделать объемные геометрические фигуры из бумаги (схемы wwwbolshoyvoprosruquestions1639803-kak-sdelat Cached Чтобы дети лучше запомнили, какие бывают геометрические фигуры, и знали, как они называются, можно из плотной бумаги или картона сделать объемные геометрические фигуры Кстати, на основе их как сделать геометрические фигуры из одной бумаги — YouTube wwwyoutubecom watch?vxXn2dLpHQJE Cached Как сделать куб из бумаги оригами пирамида как сделать пирамиду из бумаги схема пирамида хеопса How Сделать Геометрическую Фигуру Из Бумаги Схемы — Image Results More Сделать Геометрическую Фигуру Из Бумаги Схемы images Как сделать геометрические фигуры из бумаги? Схемы и советы wwwmodelzdrumakety-zhdgeometricheskie-figury-iz Cached Как сделать геометрические фигуры из бумаги ? Схемы и советы В основе самых сложных и необычные формы сооружений, устройств, механизмов лежат элементарные геометрические фигуры: куб, призма, пирамида, шар и другие Сложные Объемные Геометрические Фигуры Из Бумаги Схемы reviewspoksweeblycomblogslozhnie-objemnie Cached Лучшие мастер-классы 500 230 — 18k — jpg modelzdru Геометрические фигуры из бумаги 600 477 — 24k — jpg sharybiz Сложные объемные фигуры из бумаги схемы шаблоны 1600 1280 — 98k — jpg bolshoyvoprosru Как сделать объемные Геометрические Фигуры Из Бумаги Инструкция — couponpleer couponpleerweeblycombloggeometricheskie Cached Сделать геометрическую фигуру из бумаги несложно, предлагаю вам ещё В этой статье вы найдёте схему, которая расскажет вам, как из бумаги сделать динозавра Объемные геометрические фигуры Фигуры из бумаги Как сделать? Лучшие мастер-классы wwwfun4childru8111-figury-iz-bumagi-kak-sdelat Cached Сделать геометрическую фигуру из бумаги Предложите опять потренироваться сделать геометрическую фигуру из бумаги , на сей раз пирамиду Ее также можно создавать с помощью схем оригами Как Сделать Геометрическую Фигуру Цилиндр Из Бумаги? otvetexpertkak-sdelat-geometricheskuyu-figuru-cilindr Cached Ответы на вопрос Как сделать геометрическую фигуру цилиндр из бумаги ? в рубрике Досуг и развлечения на портале Otvetexpert Как сделать геометрические фигуры геометрические фигуры из wwwkakprostorukak-12368-kak-sdelat-geometric Cached Фигуры можно сделать из любых материалов — бумаги , картона и тд Для первого знакомства достаточно построить прямоугольник, квадрат, ромб, многоугольник, круг, треугольник Развёртки геометрических фигур modelmenrup1112 Cached Вообще кожа специфический материал, с ней можно делать практически всё, из бумаги такого не сделаешь, поэтому и выкройти тут трудно посоветовать, лучше посмотреть как это уже сделано и дома Кусудама головоломка (Froy), Kusudama puzzle — YouTube wwwyoutubecom watch?vYG1qpKs_wPU Cached Как сделать куб бесконечности из бумаги Антистресс куб инфинити cube infiniti — Duration: 17:02 Оригами Стритс 486,752 views Promotional Results For You Free Download Mozilla Firefox Web Browser wwwmozillaorg Download Firefox — the faster, smarter, easier way to browse the web and all of 1 2 3 4 5 Next 15,900
- Помимо цветов, животных, машин и самолетов в технике оригами можно собрать и различные Геометрически
- е Фигуры.
 Теги: Геометрические фигуры , из бумаги , видео , Hans-Werner Guth.
Раздел Геометрическая аппликация поможет Вам и Вашим малышам создавать увлекательные изображения с помощью различных геом
Теги: Геометрические фигуры , из бумаги , видео , Hans-Werner Guth.
Раздел Геометрическая аппликация поможет Вам и Вашим малышам создавать увлекательные изображения с помощью различных геом - аппликация поможет Вам и Вашим малышам создавать увлекательные изображения с помощью различных геометрических форм. На странице сайта Вы найдете множество схем для выполнения геометрических аппликаций, которые можно сохранить, распечатать и вырезать детали.
На рисунке показан способ построения развёртки перехода или (по его геометрическому названию) усечённого конуса. Сначала строят по высоте, малому и большому диаметру боковой вид фигуры ACEB .
Для занятий нам потребуются следующие геометрические фигуры: …прямоугольных треугольника корпус корабля, большой равносторонний треугольник будет парусом, и еще один треугольничек будет флажком. Здесь приведены примеры изображений, составленных из геометрических фигур.
Две известные невозможные фигуры невозможный треугольник и невозможный х-зубец.
 Геометрические фигуры. Шведский художник XX в. Оскар Реутерсвард сделал невозможную фигуру чертой своего художественного стиля (изобразил тысячи таких фигур).
Набор плоскостных геометрических фигур разного цвета и размера, карточки схемы, два поля, чудесный мешочек с объемными геометрическими фигурами двух цветов по количеству детей, золотые и серебряные медали.
Мероприятие создает атмосферу праздника, хорошего настроения. Проводятся игровые моменты с геометрическими фигурами. Педагог дополняет на доску листы бумаги, где дети рисовали башни и домики.
Необычные свойства позволяют считать эту геометрическую фигуру одной из наиболее изящных численных схем в математике. quot;Наука и жизньquot;, 1981, N4.
А на уроке технологии применяют эти знания, выполняя геометрическую мозаику. Так, в 1-2 классах ребята узнают о геометрических фигурах, их свойствах.
Геометрические фигуры. Шведский художник XX в. Оскар Реутерсвард сделал невозможную фигуру чертой своего художественного стиля (изобразил тысячи таких фигур).
Набор плоскостных геометрических фигур разного цвета и размера, карточки схемы, два поля, чудесный мешочек с объемными геометрическими фигурами двух цветов по количеству детей, золотые и серебряные медали.
Мероприятие создает атмосферу праздника, хорошего настроения. Проводятся игровые моменты с геометрическими фигурами. Педагог дополняет на доску листы бумаги, где дети рисовали башни и домики.
Необычные свойства позволяют считать эту геометрическую фигуру одной из наиболее изящных численных схем в математике. quot;Наука и жизньquot;, 1981, N4.
А на уроке технологии применяют эти знания, выполняя геометрическую мозаику. Так, в 1-2 классах ребята узнают о геометрических фигурах, их свойствах.
машин и самолетов в технике оригами можно собрать и различные Геометрические Фигуры. Теги: Геометрические фигуры
из бумаги
- какие бывают геометрические фигуры
- какие бывают геометрические фигуры
- Kusudama puzzle — YouTube wwwyoutubecom watch?vYG1qpKs_wPU Cached Как сделать куб бесконечности из бумаги Антистресс куб инфинити cube infiniti — Duration: 17:02 Оригами Стритс 486
сделать геометрическую фигуру из бумаги схемы Картинки по запросу сделать геометрическую фигуру из бумаги схемы Другие картинки по запросу сделать геометрическую фигуру из бумаги схемы Жалоба отправлена Пожаловаться на картинки Благодарим за замечания Пожаловаться на другую картинку Пожаловаться на содержание картинки Отмена Пожаловаться Все результаты Как сделать объемные геометрические фигуры из бумаги схемы Как сделать объемные геометрические фигуры из бумаги схемы , шаблоны ? Видео как сделать геометрические фигуры из одной бумаги Hovsep Saribekian YouTube апр г Как сделать объемную правильную треугольную ПИРАМИДУ из Оригами и DIY поделки из YouTube июл г Как сделать объёмную фигуру куб из бумаги EgoTak YouTube мар г Все результаты Объемные геометрические тела из бумаги своими руками Схемы Похожие геометрические фигурки из бумаги геометрические фигуры из бумаги из бумаги фигуры как сделать фигуру из бумаги оригами геометрические Объемные фигуры из бумаги, схемы Как сделать объемные Творчество Поделки Из бумаги Как научиться делать объемные фигуры из бумаги и картона ? если это разноцветные геометрические тела оригами, сделанные своими руками Как сделать объемные геометрические фигуры из бумаги схемы, шаблоны? wwwbolshoyvoprosrukaksdelatobemnyegeometricheskiefiguryizb Похожие янв г Чтобы дети лучше запомнили, какие бывают геометрические фигуры , и знали, как они называются, можно из плотной бумаги или Геометрические фигуры из бумаги делаем поделку в технике Оригами Геометрические фигуры из бумаги должен научиться делать каждый! Итак, для сегодняшнего мастеркласса нам пригодится бумага , схемы , клей, макеты геометрических фигур тыс изображений найдено в Как сделать объемные геометрические фигуры из бумаги схемы , шаблоны ? Произведения Искусства Из Произведения Искусства Из Бумаги Развёртки геометрических фигур ModelMenru Похожие Нужно склеить несколько геометрических фигур ? Может глупый вопрос, но как сделать из бумаги шар? те не просто круг, а именно объемный шар? Геометрические фигуры Путь Оригами origamidorushape Похожие июл г Об искусстве складывания из бумаги Азбука Оригами схема объемного куба дает нам массу вариантов того, как сделать объемный куб из бумаги Такой вариант геометрической фигуры получил название Как сделать геометрические фигуры из бумаги? wwwmodelzdrumaketyzhdgeometricheskiefiguryizbumagihtml Похожие Делаем из бумаги простые фигуры куб, пирамиду, призму, параллелепипед и др Как нарисовать развертку? Готовые схемы распечатай и склей Объемные поделки из бумаги фигуры и схемы как распечатать, на Перейти к разделу Объемные фигуры из бумаги схемы геометрических фигур геометрических фигур Как сделать куб из бумаги Объемные геометрические фигуры из бумаги originalniepodarkicomobemnyegeometricheskiefiguryizbumagioriginalnayaup Похожие Рейтинг голоса Объемные фигуры своими руками схема Объемные геометрические фигуры из бумаги можно сделать разноцветными, задекорировать бантиками, Геометрические фигуры Планета Оригами planetaorigamirucategoryfiguriizbumagi Похожие Куб в наушниках по схеме Джереми Шейфера Jeremy Shafer из многочисленных деталей, но сложенными зачастую из цельных листов бумаги детскую комнату, или же сделать их несколько штук в качестве подарков детям Развертка куба из бумаги, как сделать кубик, из бумаги своими Рейтинг голосов апр г Представлена развертка куба из бумаги , схемы , шаблоны и Куб это удивительная геометрическая фигура , в которую можно Объемные геометрические фигуры из бумаги Сделай сам февр г Объемные геометрические фигуры из бумаги делаем из бумаги или детьми или на основе их можно сделать подарочную упаковку Геометрические фигуры из бумаги поделка оригами своими руками Бумага Геометрические фигуры из бумаги своими руками с описанием и фото схем Мастера из бумаги научились делать самые разнообразные поделки Схема представляет собой двухмерное изображение развёртки нашей Геометрические фигуры из бумаги Схемы оригами Декоративно kalihcomgeometricheskiefiguryiizbumagishemyiorigami Похожие Оригами пирамида из бумаги Оригами Объемная фигура моя схема Фото Оригами для детей и начинающих Объемные игрушки из бумаги своими руками схемы шаблоны natatoysrusvoimiobemnyeigrushkiizbumagisvoimirukamishemyshablonyht Объемные фигуры из бумаги схемы геометрических фигур Простейший способ сделать объемную геометрическую фигуру распечатать шаблоны и Фигуры из бумаги Как сделать? Лучшие мастерклассы wwwfunchildrufiguryizbumagikaksdelatluchshiemasterklassyhtml Похожие мар г Тут на помощь нам придут геометрические фигуры из бумаги Ее также можно создавать с помощью схем оригами, но мы можем Конструкции Из Бумаги Объемные Формы Из Плоского Листа craftssoupweeblycomblogkonstrukciiizbumagiobjemnieformiizploskogolista дек г Геометрические фигуры из бумаги схемы объёмные фигурки из бумаги Выпуклые многогранники сделать из бумаги схема Геометрия декора идеи и схемы для создания интерьерных Похожие окт г Геометрические фигуры из бумаги покоряют четкостью, даже строгостью своих линий, при этом выглядят очень оригинально, а сделать Как сделать объемные геометрические фигуры из бумаги схемы Как сделать объемные геометрические фигуры из бумаги схемы , шаблоны ?Для изготовления объемных геометрических фигур главное иметь Как сделать цилиндр из бумаги? Инструкция с фото Видео Похожие февр г Цилиндр геометрическая фигура , изучаемая в школе В этом в цилиндрической форме, и сегодня мы сделаем эту фигуру из бумаги Геометрическая фигура оригами Видео схема схема сборки izbumagicom Видео схемы оригами Похожие Представляем схему оригами Геометрическая фигура оригами Из Бумаги Mozilla Firefox Попробуйте сделать её на досуге, у вас всё получится! Без названия Объемная геометрическая фигура из бумаги без апр г Схемы Мне очень нравится, когда люди умеют Сделать геометрическую фигуру из бумаги несложно, схема приемника ленинград Развёртки геометрических фигур занятия с детьми Design, Food Как сделать объемные геометрические фигуры из бумаги схемы , шаблоны ? Произведения Искусства Из Произведения Искусства Из Бумаги Поделки d фигуры из бумаги схемы видео Лепкарф Тут можно смотреть видео о d фигуры из бумаги схемы онлайн бесплатно Видеоуроки лепки из как сделать геометрические фигуры и От автора Уметь сделать нечто похожее на увиденное, например, животное Перейти к разделу Шаблоны для вырезания из бумаги простых геометрических фигур Бумага рождает животное паперкрафт, есть схема , Геометрические оригами paperliferugeometricorigami Похожие Подборка моделей и схем оригами, которые так или иначе связаны с Зачастую это могут бить всевозможные симметрические модульные фигуры геометрические спирали и прочие модели оригами Кубик из бумаги , оригами Как сделать макет геометрических фигур Paintmasterru Для начала можете попробовать склеить макеты геометрических фигур из обычной бумаги ксероксной либо оберточной, которые будут указаны Как из бумаги сделать тетраэдр? WomanAdviceru При изучении свойств этой трехмерной геометрической фигуры для наглядности транспортир;; линейка;; ножницы;; клей;; тетраэдр из бумаги , схема Как пирамиду из бумаги сделать? Поделки из бумаги! Причем, есть, как довольно простые способы ее сделать например, вырезав из бумаги соответствующие фигуры и собрав ее, так и очень сложные Как сделать куб из бумаги наглядный урок со схемой и шаблоном Сделать куб из картона или бумаги очень просто шаблон, вырезать схему по обозначенным линиям, сложить геометрическую фигуру и склеить Делаем своими руками геометрический декор из трубочек olgaboykorudecoriztrubochekhtml нояб г Развертки, схемы , выкройки и видео с декором из трубочек в авторском вида геометрических фигур из трубочек кристалл И так раз! потому что мне нужно сделать геометрических фигур октаэдр, Как сделать параллелепипед из бумаги схема papermixruraznoefigurykak_sdelat_parallelepiped_iz_bumagi_shemahtml Похожие Чаще всего для создания геометрических фигур используют квадрат и конус Их делать намного проще и быстрее А вот чтобы сделать своими руками Как сделать из бумаги квадрат самым простым способом FBru fbru Домашний уют Сделай сам Похожие апр г Объемный квадрат из бумаги фигура , с которой обычно начинают Если вы побоитесь начертить схему самостоятельно, готовую развертку Геометрические фигурки полюбят изготавливать дети и взрослые Как сделать конус из бумаги картона, пошаговая инструкция, елка Как сделать конус из бумаги своими руками несколько пошаговых инструкций конус из картона схема работы; Елка на основе конуса своими руками сформировать основу еще сложную для них геометрическую фигуру Изготовление моделей многогранников из бумаги своими руками zvzddruFromBumagahtml Похожие Об изготовление своими руками моделей многогранников из бумаги а также даются схемы соединения частей между собой и таблицы раскраски В тоже и даже делать оригинальные подвижные модели трансформеры Геометрические игры rastimirastemrugeometricheskieigry Похожие янв г игры на изучение и закрепление геометрических фигур Для начала я просто нарисовала от руки на двух листах бумаги различные геометрические фигуры и даём получившиеся схемы ребёнку и просим подобрать Но гораздо дешевле сделать её самим, как в нашем случае Основа Оригами база для изучения геометрии Открытый урок Оригами ? искусство складывания из бумаги , древнее японское изобретение и ознакомления их с максимально богатым набором геометрических фигур как плоских, Это позволило сделать вывод о том, что основными линиями на них являются базовых форм, расположенных в правой части схемы Презентация по теме Оригами мир геометрических фигур июн г Оригами, искусство, Япония, бумага , Китай, чудеса, счастье, Схема складывания Журавля Маг, что придумал бумагу цветную Красную, жёлтую и голубую , Верил, наверно, что могут ребята Сделать фигурки из разных План конспект по геометрии Мир геометрических фигур Как сделать из бумаги икосаэдр? видео уроки uchietoru Развлечения Похожие Если вы хотите узнать, как сделать из бумаги икосаэдр, прочитайте эту стать и Особенно часто, почемуто, создаются геометрические фигуры В нашей Теперь мы представим схему , по которой можно изготовить эту фигуру Как сделать трансформера из бумаги своими руками оригами или Как сделать из бумаги фигурутрансформера схема поделки Можно создать не только саму геометрическую фигуру , но также и ее разновидности Как сделать геометрическую фигуру тетраэдр куб инструкция февр г Как сделать геометрическую фигуру тетраэдр куб инструкция Скачать Как Тетраэдр из бумаги фигура оригами в такой странной и бумаги Эту поделку можно сделать по схеме или видео я бы выбрал видео Многогранник из бумаги Mitsunobu Sonobe из бумаги кусудама joyreactorcc песочница авг г Сделать из бумаги многогранник Икосаэдр очень просто в технике оригами из модулей Mitsunobu Sonobe Такая интересная поделка Животные из геометрических фигур Новые дети novyedetiruzhivotnyeizgeometricheskihfigur Похожие янв г Потом нарежьте геометрические фигуры из цветной бумаги и выкладывайте из них животных, растения и домики Можно также делать Развёртки геометрических фигур Сайт учителя математики и Похожие Ссылка на сайт, где можно скачать развертки разных базовых геометрических фигур многогранников Ребята! Не забывайте делать припуски для Технология класс Страница Результат из Книги Надежда Малышева Education Сделай из одной фигуры другую бумага картон Ä Расскажи по схеме , как сделать цветы из геометрических фигур Какие геометрические фигуры ты Мир загадок Программа и методические рекомендации по внеурочной Светлана Гин Psychology и из шариков Что сделать быстрее, легче, надёжнее и почему? противоречий На доске или налисте бумаги изображены две схемы Композиция из различных геометрических фигур Композиция из геометрических фигур Вместе с сделать геометрическую фигуру из бумаги схемы часто ищут фигуры из бумаги схемы шаблоны объемных геометрических фигур для вырезания поделки из геометрических фигур объемные объемные поделки из геометрических фигур своими руками геометрические фигуры из бумаги оригами объемные фигуры животных из бумаги объемные фигуры животных из бумаги шаблоны развертки геометрических фигур для печати Документы Blogger Duo Hangouts Keep Jamboard Подборки Другие сервисы
Помимо цветов, животных, машин и самолетов в технике оригами можно собрать и различные Геометрические Фигуры. Теги: Геометрические фигуры , из бумаги , видео , Hans-Werner Guth.
Раздел Геометрическая аппликация поможет Вам и Вашим малышам создавать увлекательные изображения с помощью различных геометрических форм. На странице сайта Вы найдете множество схем для выполнения геометрических аппликаций, которые можно сохранить, распечатать и вырезать детали.
На рисунке показан способ построения развёртки перехода или (по его геометрическому названию) усечённого конуса. Сначала строят по высоте, малому и большому диаметру боковой вид фигуры ACEB .
Для занятий нам потребуются следующие геометрические фигуры: …прямоугольных треугольника корпус корабля, большой равносторонний треугольник будет парусом, и еще один треугольничек будет флажком. Здесь приведены примеры изображений, составленных из геометрических фигур.
Две известные невозможные фигуры невозможный треугольник и невозможный х-зубец. Геометрические фигуры. Шведский художник XX в. Оскар Реутерсвард сделал невозможную фигуру чертой своего художественного стиля (изобразил тысячи таких фигур).
Теги: Геометрические фигуры , из бумаги , видео , Hans-Werner Guth.
Раздел Геометрическая аппликация поможет Вам и Вашим малышам создавать увлекательные изображения с помощью различных геометрических форм. На странице сайта Вы найдете множество схем для выполнения геометрических аппликаций, которые можно сохранить, распечатать и вырезать детали.
На рисунке показан способ построения развёртки перехода или (по его геометрическому названию) усечённого конуса. Сначала строят по высоте, малому и большому диаметру боковой вид фигуры ACEB .
Для занятий нам потребуются следующие геометрические фигуры: …прямоугольных треугольника корпус корабля, большой равносторонний треугольник будет парусом, и еще один треугольничек будет флажком. Здесь приведены примеры изображений, составленных из геометрических фигур.
Две известные невозможные фигуры невозможный треугольник и невозможный х-зубец. Геометрические фигуры. Шведский художник XX в. Оскар Реутерсвард сделал невозможную фигуру чертой своего художественного стиля (изобразил тысячи таких фигур). Набор плоскостных геометрических фигур разного цвета и размера, карточки схемы, два поля, чудесный мешочек с объемными геометрическими фигурами двух цветов по количеству детей, золотые и серебряные медали.
Мероприятие создает атмосферу праздника, хорошего настроения. Проводятся игровые моменты с геометрическими фигурами. Педагог дополняет на доску листы бумаги, где дети рисовали башни и домики.
Необычные свойства позволяют считать эту геометрическую фигуру одной из наиболее изящных численных схем в математике. quot;Наука и жизньquot;, 1981, N4.
А на уроке технологии применяют эти знания, выполняя геометрическую мозаику. Так, в 1-2 классах ребята узнают о геометрических фигурах, их свойствах.
Набор плоскостных геометрических фигур разного цвета и размера, карточки схемы, два поля, чудесный мешочек с объемными геометрическими фигурами двух цветов по количеству детей, золотые и серебряные медали.
Мероприятие создает атмосферу праздника, хорошего настроения. Проводятся игровые моменты с геометрическими фигурами. Педагог дополняет на доску листы бумаги, где дети рисовали башни и домики.
Необычные свойства позволяют считать эту геометрическую фигуру одной из наиболее изящных численных схем в математике. quot;Наука и жизньquot;, 1981, N4.
А на уроке технологии применяют эти знания, выполняя геометрическую мозаику. Так, в 1-2 классах ребята узнают о геометрических фигурах, их свойствах.
схемы оригами из бумаги. Как сделать объемный куб пошагово? Простая поэтапная схема складывания пирамиды
Техника оригами дает возможность своими руками изготавливать самые разные оригинальные поделки из бумаги. Необычно будут смотреться декоративные изделия в виде геометрических фигур.
Необычно будут смотреться декоративные изделия в виде геометрических фигур.
Как сделать куб?
Для начала мы рассмотрим, как можно поэтапно создать поделку в форме куба. Данная фигура считается несложным многогранником. В ней сразу все грани будут квадратными. Рисунок развертки можно просто распечатать при помощи принтера. Также можно начертить ее самостоятельно.
В последнем случае сначала необходимо определиться с размерами граней. При этом ширина бумажного листа должна составлять не менее трех сторон такого квадрата, а длина – не более пяти сторон. Во всю длину бумажного листа чертят 4 квадрата, они позже станут боковыми частями куба. Прорисовывать все надо только вплотную и на одной полосе. После этого и под, и над одним из квадратов чертят еще по одной квадратной фигуре.
Позже рисуют полосы для приклеивания. Это позволит легко соединить грани друг с другом. На заключительном этапе изготовления нужно будет хорошо промазать места соединений клеевым составом.
Данные части склеиваются друг с другом и ненадолго закрепляются при помощи скрепок, чтобы вещество успело высохнуть. Так фиксируют все грани куба.
Создание пирамиды
Далее мы разберем, как легко сделать фигуру в форме пирамиды. Данная фигура представляет собой многогранник, в котором основанием является многоугольник, а все остальные грани имеют вид треугольников с одной вершиной.
- Сначала следует точно выбрать все размеры, а также количество граней фигуры.

- После этого на бумажном листе при помощи карандаша чертят основание в виде многоугольника. В зависимости от общего количества граней основание может быть сделано в виде пятиугольной, квадратной или треугольной заготовки.
- Затем из одной из сторон полученного многоугольника следует сделать треугольник, который будет являться боковой частью.
- Позже прорисовывают еще один треугольник. При этом одна из его сторон должна быть общей с первой фигурой. Всего их рисуется столько, сколько в итоге будет частей в пирамиде.
- Далее отмечают полоски для приклеивания. На заключительном этапе нарисованную фигуру аккуратно вырезают и склеивают по намеченным линиям.
Складывание других фигур
Разберем, как пошагово сложить другие объемные фигуры в технике оригами.
Цилиндр
Он представляет собой фигуру, которая ограничивается цилиндрической поверхностью и плоскостями, пересекающими ее и располагающимися параллельно. На первом этапе на материале отмечают прямоугольник, при этом его ширина будет являться высотой изделия, а длина – диаметром. Далее дорисовывают небольшие треугольники для склеивания. После этого на материале чертят два круга, их диаметр должен равняться диаметру готового цилиндра. Эти круги станут верхним и нижним основанием фигуры. Все детали вырезаются ножницами, боковая часть изделия склеивается из прямоугольной заготовки.
Все элементы должны полностью просохнуть. Далее к ним также фиксируют нижнее и верхнее основание.
Параллелепипед
Данное изделие является многогранником, у которого есть 6 граней, при этом каждая из них представляет собой параллелограмм.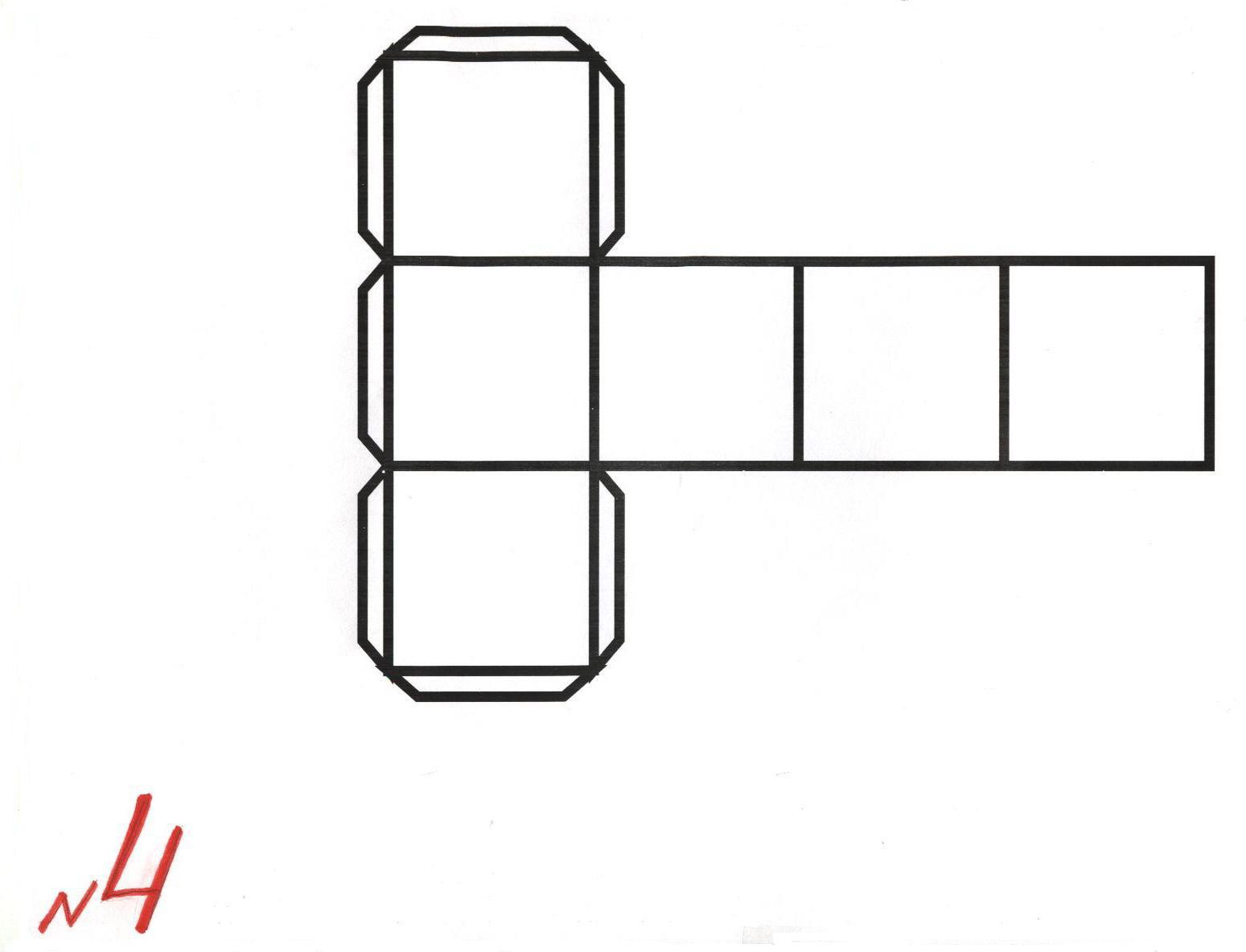 Чтобы смастерить такую фигуру в технике оригами, сначала нужно будет аккуратно начертить на бумажном листе основание в виде параллелограмма, при этом его размер может быть любым. Далее с каждой части полученной заготовки отмечают боковые стороны такой же формы. После этого с любой боковой части чертят второе основание.
Чтобы смастерить такую фигуру в технике оригами, сначала нужно будет аккуратно начертить на бумажном листе основание в виде параллелограмма, при этом его размер может быть любым. Далее с каждой части полученной заготовки отмечают боковые стороны такой же формы. После этого с любой боковой части чертят второе основание.
Отдельно прорисовываются места, предназначенные для приклеивания. Далее полученная схема вырезается и склеивается по отмеченным полоскам.
Призма
Чтобы сделать треугольную призму, на материале чертят три прямоугольника с одинаковыми размерами. После этого над и под прямоугольником, который размещается в центральной части, рисуют по одному небольшому треугольнику. Они также должны иметь одинаковые размеры. После этого со всех сторон оставляют небольшие полоски. Оставленные полоски промазываются клеевым составом, затем все части фиксируются друг с другом, формируя при этом объемную треугольную призму.
Они также должны иметь одинаковые размеры. После этого со всех сторон оставляют небольшие полоски. Оставленные полоски промазываются клеевым составом, затем все части фиксируются друг с другом, формируя при этом объемную треугольную призму.
В технике оригами также можно сделать шестиугольную призму. В данном случае на бумажном листе чертят 6 прямоугольников с одинаковыми длиной и шириной.
Вместо треугольников сверху и снизу прорисовывают шестиугольные фигуры. В конце также оставляют полосы для склеивания, все это вырезается и склеивается в одно изделие.
О том, как сделать куб в технике оригами, смотрите в следующем видео.
youtube.com/embed/lSUWtcN5qco?modestbranding=1&iv_load_policy=3&rel=0″/>
Объемная фигура из бумаги – создаём красоту сделать самому своими руками
Глядя на то, как сделана та или иная объемная фигура из бумаги, даже не верится, что такую красоту создали из обычного листа. И ведь никаких особых приспособлений не надо, нужен лист двусторонней цветной или белой бумаги и клей.
Делаем шар. Начало
Чтобы сделать вот такой красивый объёмный шар из бумаги, понадобится лист двусторонней цветной бумаги примерно 30х15см. Кладём его большей стороной к себе. Если вы решили впервые заняться изготовлением объёмного оригами, то можно упростить себе задачу, разлиновав бумажный лист на маленькие квадратики. Для этого берём линейку и чертим на этом листе сначала поперечные, а затем продольные полоски, на расстоянии 1 сантиметр друг от друга. В результате у нас получатся ровные ряды квадратиков размером 1х1см.
После того как вы поймёте принцип изготовления, нужно будет обходиться без карандаша. Сначала складываете бумагу поперечно. Должны получиться полоски, но образованные уже при помощи сгибов. Точно так же делаются и продольные полосы, благодаря сгибанию листа.
Продолжаем творить
Но пока продолжим помогать себе карандашом. С его помощью в каждом квадрате нужно нарисовать две диагональные линии. Можно положить линейку таким образом, чтобы нарисовать сразу одну диагональ на нескольких квадратиках. Хотя достаточно начертать её в первых двух-трёх, а потом сгибать квадратики по воображаемым диагоналям. Совсем скоро получится красивая объемная фигура из бумаги.
Смотрим на первый угловой квадратик. Смотрим только на 2 половины диагоналей, расположенных справа. Нужно сложить их друг с другом. То же самое делаем и с левыми половинками диагональных линий – складываем их друг с другом. Посередине каждого квадрата тоже делаем сгиб. Пальцами делаем чёткие сгибы, чтобы получилась объемная фигура из бумаги. Сгибы диагоналей, самих квадратов должны быть направлены на одну – лицевую сторону и чётко просматриваться.
Сгибы диагоналей, самих квадратов должны быть направлены на одну – лицевую сторону и чётко просматриваться.
Придаем фигуре форму шара
Теперь попробуйте, начиная с одной стороны листа, складывать его в виде гармошки. Но в отличае от гармошки, складываем его не только по вертикальной, но и по горизонтальной, диагональным линиям. Если где-то не получается сложить, то при помощи пальцев чётче обозначьте линию сгибов.
Если всё получилось, то продолжаем. Снова укладываем уже получившийся рифлёный лист длинной стороной к себе и проделываем обратную работу (с боков). При помощи пальчиков разворачиваем эту красоту на участке шириной в 1,5 см. Это нужно для лучшего склеивания краёв, чтобы объемная фигура из бумаги получилась в форме шара.
Берём клей-карандаш и левый верхний короткий край бумаги. Промазываем его клеем сверху. Точно такой же, но уже правый угол тоже смазываем клеем. Приклеиваем в этом месте бумагу внахлёст, чтобы ширина шва была 1,5 см. Точно так же склеиваем и нижние угла. А вот посередине действуем немного по-другому – ширина шва здесь должна быть небольшой – 0,4 см.
А вот посередине действуем немного по-другому – ширина шва здесь должна быть небольшой – 0,4 см.
Шар из бумаги: у нас всё получилось!
Так неравномерно мы приклеивали швы, чтобы посередине фигура была более выпуклой, чем у центра. Тогда получится форма шара. Ну это мы пока сделали лишь боковую его сторону. Нужно обозначить и верхушку. Сначала необходимо снова чётко обозначить линии на квадратиках там, где они стали плохо видны. Надо, чтобы каждый квадратик прекрасно сгибался по горизонтальным, вертикальным и диагональным линиям. Особенно тщательно это следует делать у верхушки и у низа шара – эти места не заклеены. Теперь пытаемся соединить эту верхушку и низ. Когда деталь распрямится, то получится объёмный шар.
Можно не придавать изделию форму шара, а оставить как есть, приклеив глазки, ручки. Получится не объемная геометрическая фигура из бумаги, а настоящая игрушка.
Таким же образом можно сделать и другие фигуры.
Объемный куб из бумаги
Проще всего его сделать из обычного школьного листа в клеточку. На таком материале сразу видно, где обозначать сгибы, и получатся они идеально ровными. Таким образом, проще делать оригами из бумаги. Объемные фигуры получатся ровными. Особенно хорошо на таком материале учиться начинающим мастерам.
На таком материале сразу видно, где обозначать сгибы, и получатся они идеально ровными. Таким образом, проще делать оригами из бумаги. Объемные фигуры получатся ровными. Особенно хорошо на таком материале учиться начинающим мастерам.
Отмеряем по длине столько же сантиметров, сколько по ширине имеет тетрадный лист (20 см) и лишнее отрезаем. У нас получился квадрат размером 20х20 см. Складываем лист пополам, а потом ещё раз пополам. Образовался квадрат со стороной 5 см, состоящий их 4-х листов.
Берём в руку самый верхний его лист и выгибаем его в левую сторону. Сформировался треугольник. Сторона, которая была крайней верхней у квадрата, стала высотой треугольника.
Завершаем создание куба
Переворачиваем квадрат на другую сторону. Такой же треугольник делаем и с другой стороны. В результате получится 2 совершенно одинаковых треугольника, лежащих один на другом.
Если сложно в первый раз делать объемные фигуры из бумаги, схемы упростят задачу. Но пока и так достаточно понятно. Начало создания данной фигуры напоминает конструирование из бумаги тюльпана, а такое многие проходили ещё на уроках труда в начальной школе. И как у «тюльпана», теперь у одного прямоугольного треугольника отгибаем один его острый угол к вершине прямого угла. Всего таким образом сгибаем 4 угла – 2 у одного и столько же у другого треугольника. Фигура волшебным образом трансформировалась в два ромба, лежащих один на другом.
Начало создания данной фигуры напоминает конструирование из бумаги тюльпана, а такое многие проходили ещё на уроках труда в начальной школе. И как у «тюльпана», теперь у одного прямоугольного треугольника отгибаем один его острый угол к вершине прямого угла. Всего таким образом сгибаем 4 угла – 2 у одного и столько же у другого треугольника. Фигура волшебным образом трансформировалась в два ромба, лежащих один на другом.
Теперь нам нужны 2 боковых угла ромба, которые хорошо отгибаются. Сгибаем их к центру. У этих углов образовался «карманчик». В него вкладываем 2 угла этого же ромба. Один – в один кармашек, другой – в другой. Переворачиваем фигуру и делаем точно такие манипуляции с ромбом, расположенным на обратной стороне. Наверху фигуры образовалась дырочка. Подуйте в неё и благодаря этому фигура заполнится воздухом и превратится в ромб.
Вот такие можно делать оригами из бумаги. Объемные фигуры получаются оригинальными и фактурными.
Как сделать фигуру из бумаги схема.
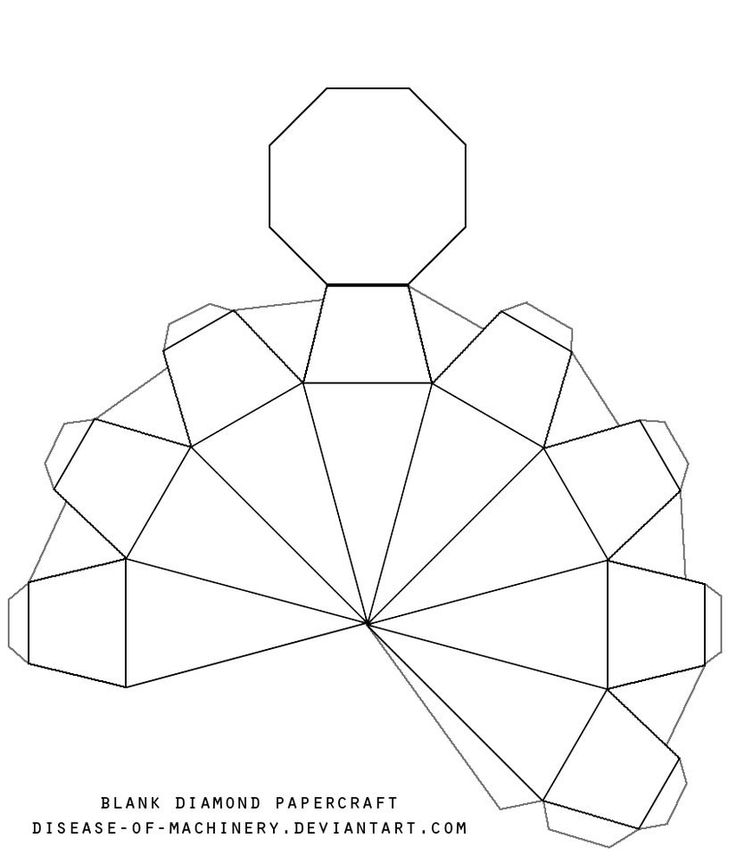 Тема: «Объемные геометрические фигуры
Тема: «Объемные геометрические фигурыКОНСПЕКТ И МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ УРОКА (ЗАНЯТИЯ) ПО БУМАГОПЛАСТИКЕ.
Тема: «Объемные геометрические фигуры».
Цели и задачи урока: Развить у ученика образное объемно-пространственное мышление и воображение. Выполнение задания предполагает ознакомление с материалом, приобретение умения выполнять точный чертеж, вырезать разнообразные формы, умение пользоваться острыми режущими предметами (резак, ножницы), склеивать между собой детали и собирать объемную геометрическую фигуру.
Оборудование: У преподавателя : компьютер и проектор, образцы изделий, инструменты (ножницы, резак, бумага, линейка, карандаш, ластик, клей), шаблоны, инструкция по технике безопасности при работе с режущими инструментами, презентация. У учащихся : подкладная деревянная доска (30*20 см), ножницы, резак, бумага (ватман) А3 формата – 2 листа, линейка, карандаш (твердый), ластик, клей (момент «кристалл»).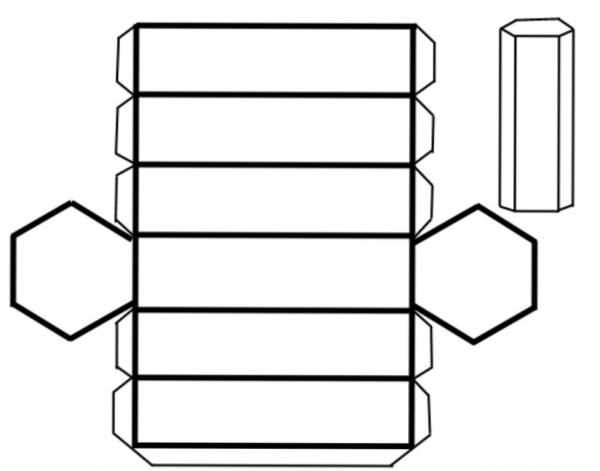
Тип урока: смешанный
Ход урока:
1. Организационный момент –1 минуту.
Проверка готовности к уроку.
2. Объяснение учителя – 9 минут.
Сообщение темы урока, цели и задачи.
Объяснение материала:
В процессе занятий преподаватель последовательно рассказывает и наглядно показывает о построении чертежей для объемных геометрических фигур и целенаправленно формирует у учащихся способность работать руками, приучает к точным движениям пальцев, совершенствует мелкую моторику рук, развивает глазомер.
— «Из листа бумаги с помощью резака, ножниц и клея можно быстро выполнить модель какого-либо изделия, несложную композицию, макет. В отличии от скульптуры из глины, где масса набирается методом наращивания и уточнения форм, в изделиях из бумаги отсутствует каркас. Почти все изделия – пустотелы и представляют собой как бы скорлупу. Однако это не оттиск с готовой формы, а совершенно самостоятельная пластическая оболочка, созданная за счет сгибов бумаги по предварительно нанесенным линиям – надрезам. Надрезы являются конструктивной основой всех изделий, выполняемых из бумаг (они называются – ребра жесткости). Согнутый пополам лист образует ребро. Если лист сложить несколько раз, то от количества и характера этих прямолинейных сгибов можно получить различную фактуру ».
Надрезы являются конструктивной основой всех изделий, выполняемых из бумаг (они называются – ребра жесткости). Согнутый пополам лист образует ребро. Если лист сложить несколько раз, то от количества и характера этих прямолинейных сгибов можно получить различную фактуру ».
Опорные качества способностей, формируемых занятиями, с одной стороны, относятся преимущественно к области восприятия (развитость аналитико-синтетического взгляда на предмет), с другой стороны – к области моторики (опциальная область руки). Основной формой проведения занятий является урок смешанного типа (лекция совмещается с практической работой).
3. Практическая работа учеников – 1 час 20 минут.
Для работы выбраны макеты геометрических фигур различные по размеру и форме.
Ход работы:
1. На листе белой бумаги (ватман) намечаем размеры и контуры для создания геометрических фигур как указанно на шаблоне.
2. Вырезаем по контуру, делаем надрезы на внутренних ребрах фигуры с лицевой стороны.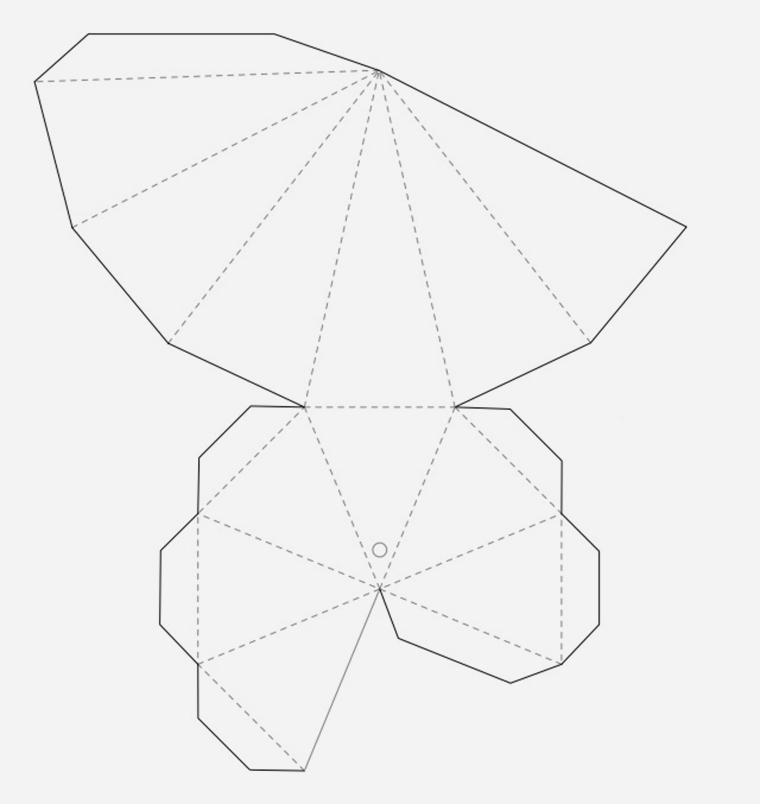 Убираем ластиком вспомогательные линии и сгибаем.
Убираем ластиком вспомогательные линии и сгибаем.
3. Смазываем клеем участки, обозначенные надписью «для клея» (как указанно на шаблоне) и приступаем к конструированию.
По такому же принципу выполняется задание со следующими геометрическими фигурами.
За 5 минут до окончания урока мини-просмотр и обсуждение работ.
Наглядный материал к уроку.
Призентация для урока : Бумагопластика. Объемные геометрические фигуры.
Геометрическая пирамида.
http://pandia.ru/text/80/128/images/image005_30.jpg»>
Пояснение к слайду: 2.После нанесения чертежа, вырезаем по контуру (сплошная линия) и делаем надрезы резаком по линии обозначенной пунктиром. Вспомогательные линии удаляем ластиком
Октаэдр.
DIV_ADBLOCK219″>
.
3.Дополнительные вставки на фигуре обозначенные штриховкой смазываем клеем и склеиваем фигуру дополнительными вставками во внутрь.
додекаэдр.
http://pandia.ru/text/80/128/images/image009_14.jpg»>.
Пояснение к слайду: 2.После нанесения чертежа, вырезаем по контуру (сплошная линия) и делаем надрезы резаком по линии обозначенной пунктиром. Вспомогательные линии удаляем ластиком.
3.Дополнительные вставки на фигуре обозначенные штриховкой смазываем клеем и склеиваем фигуру дополнительными вставками во внутрь.
ИКОСАЭДР.
Пояснение к слайду: 1.Чертеж икосаэдра переносится на лист учащегося с точностью 1:1, как указанно на шаблоне. Построение начинается с равнобедренного треугольника одна сторона которого равна 4,5 см, а высота 4 см. Далее, как указанно на шаблоне, переносим чертеж всех оставшихся равнобедренных треугольников.
Пояснение к слайду: 2.После нанесения чертежа, вырезаем по контуру (сплошная линия) и делаем надрезы резаком по линии обозначенной пунктиром. Вспомогательные линии удаляем ластиком.
3.Дополнительные вставки на фигуре обозначенные штриховкой смазываем клеем и склеиваем фигуру дополнительными вставками во внутрь.
педагогический рисунок учителя.
примеры работ учащихся.
Объемные геометрические фигуры старшей группы 2/4 класса.
Преподаватель: .
Упражнение «Звезда»
Цели урока | Методы и приемы | |
· Дать представление об истории бумагопластики. · Познакомить с основными способами работы с бумагой в технике бумагопластика · Познакомить с основными этапами выполнения работы , научить аккуратности в ходе выполнения работы · Развить у ученика образное объемно-пространственное мышление и воображение. · Закрепить у обучающихся представление о бумагопластике. | Использование наглядности Самостоятельное выполнение Сравнение | |
Оборудование | Материалы | |
Мультимедиа Наглядное пособие | Чертежная бумага, канцелярский резак, ножницы, линейка, циркуль, карандаш, ластик | Выполнение упражнения «Звезда» в технике бумагопластика. |
План урока | Образец работы | |
1.Организация 3 мин. 2.Вводная беседа 10 мин. 3.Самостоятельная работа 30 мин. 4.Заключение 2 мин. |
1.Организационная часть.
Нашим заданием на сегодняшний урок будет упражнение в технике бумагопластики «звезда».
2.Объяснение материала.
Бумагопластика. Что же это такое: скульптура из бумаги, архитектура или дизайн? Данный вид художественной деятельности в равной степени модно отнести ко всем названным направлениям, так как бумага, как проектный материал широко используют и художники, и архитекторы, и дизайнеры. Из листа бумаги с помощью резака, ножниц и клея можно быстро выполнить модель какого-либо изделия, несложную композицию, макет.
Бумажная пластика близка к скульптуре. В отличие от скульптуры из глины, где масса набирается методом наращивания и уточнения форм, в изделиях из бумаги отсутствует каркас. Почти все изделия – пустотелы и представляют собой как бы скорлупу. Однако это не оттиск с готовой формы, а совершенно самостоятельная пластическая оболочка, созданная за счет сгибов бумаги по предварительно нанесенным линиям – надрезам.
Почти все изделия – пустотелы и представляют собой как бы скорлупу. Однако это не оттиск с готовой формы, а совершенно самостоятельная пластическая оболочка, созданная за счет сгибов бумаги по предварительно нанесенным линиям – надрезам.
Особенности технологии. Надрезы являются конструктивной основой всех изделий, выполняемых из бумаг (далее они будут называться – ребра жесткости). Согнутый пополам лист образует ребро. Если лист сложить несколько раз, то от количества и характера этих прямолинейных сгибов можно получить различную фактуру. В Японии этот метод в бумаготворчестве называется — оригами.
Материалы и инструменты. Главным инструментом в бумагопластике является резак (канцелярский нож). Ножницы нужны для разрезания бумаги, выполнения различных выкроек, надрезов, просечек и т. д. Линейка, желательно металлическая длиной 25-30 см, т. к. пластмассовые и деревянные линейки не точны, и быстро выходят из строя. Циркуль, для построения окружности и деления ее на шесть частей.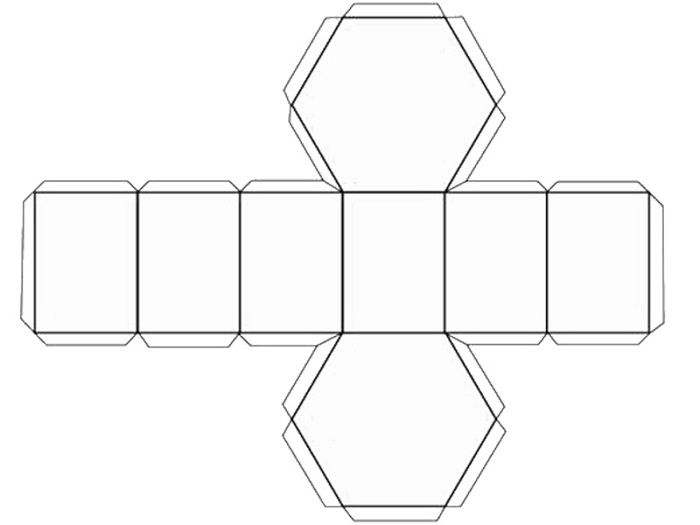
3.Выполение работы.
Сегодня мы познакомились с техникой бумагопластики, просмотрели мультимедийную презентацию по данному направлению, и на наглядном пособии просмотрели и потрогали что представляет из себя данная техника. А сейчас мы попробуем выполнить упражнение «звезда». Для этого на вашем рабочем месте должны лежать такие инструменты, как: линейка, карандаш, ластик, резак, ножницы. Упражнение будет выполняться из бумаги. У каждого из Вас так же на столах имеется шаблон по выполнению работы с заданными размерами. Обратите внимание: желтая линия – построение, по коричневой линии-вырезаем, прямые зеленые линии – надрезаем резаком и отгибаем от себя, зеленые линии-пунктир – надрезаем резаком и отгибаем на себя. Работу начинаем вести с отчерченного круга диаметром в 20 см. После чего приступаем к расчерчиванию вспомогательных линий и приступаем к конструированию.
4.Закрепление пройденного материала.
Вот и подошел к концу наш творческий урок. Мы с вами познакомились с новым направлением в искусстве — техникой бумагопластики. Так скажите мне пожалуйста, чем же отличается бумажная скульптура от скульптуры из глины? В какой стране за рубежом используется эта техника, и какого ее название там? Какие материалы могут нам понадобиться при создании бумажной композиции?
Так скажите мне пожалуйста, чем же отличается бумажная скульптура от скульптуры из глины? В какой стране за рубежом используется эта техника, и какого ее название там? Какие материалы могут нам понадобиться при создании бумажной композиции?
Большой выбор развёрток простых геометрических фигур.
Первое знакомство детей с бумажным моделированием всегда начинается с простых геометрических фигур, таких как кубик и пирамида. Не у многих получается склеить кубик с первого раза, иногда требуется несколько дней, чтобы сделать поистине ровный и безупречный куб. Более сложные фигуры цилиндр и конус требуют в несколько раз больше усилий нежели простой кубик. Если вы не умеете аккуратно клеить геометрические фигуры, значит и за сложные модели вам ещё рано браться. Займитесь сами и научите своих детей клеть эти «азы» моделирования по готовым развёрткам.
Для начала я, конечно же, предлагаю научиться клеить обычный кубик. Развёртки сделаны для двух кубиков, большого и маленького. Более сложной фигурой является маленький кубик потому, как клеить его сложнее, чем большой.
Итак, начнём! Скачайте развёртки всех фигур на пяти листах и распечатайте на плотной бумаге. Перед тем, как печатать и клеить геометрические фигуры обязательноознакомьтесь со статьёй о том, как выбрать бумагу и как вообще правильно вырезать, сгибать и клеить бумагу.
Для более качественной печати советую использовать программу AutoCAD, и даю вамразвёртки для этой программы , а также читайте, как распечатывать из автокада . Вырежьте развёртки кубиков с первого листа, по линиям сгиба обязательно проведите иголкой циркуля под железную линейку, чтобы бумага хорошо сгибалась. Теперь можно начинать клеить кубики.
Для экономии бумаги и на всякий пожарный я сделал несколько развёрток маленького кубика, мало ли вам захочется склеить не один кубик или что-то не получится с первого раза. Ещё одна несложная фигура это пирамида, её развёртки найдёте на втором листе. Подобные пирамиды стоили древние египтяне, правда не из бумаги и не таких маленьких размеров:)
А это тоже пирамида, только в отличие от предыдущей у неё не четыре, а три грани.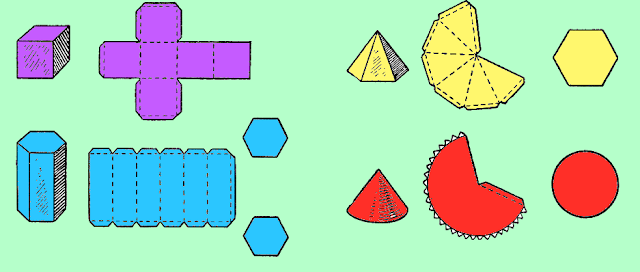
Развёртки трёхгранной пирамиды на первом листе для печати.
И ещё одна забавная пирамидка из пяти граней, её развёртки на 4-ом листе в виде звёздочки в двух экземплярах.
Более сложная фигура это пятигранник, хотя пятигранник сложнее начертить, нежели склеить.
Развёртки пятигранника на втором листе.
Вот мы и добрались до сложных фигур. Теперь придётся поднапрячься, склеить такие фигуры нелегко! Для начала обычный цилиндр, его развёртки на втором листе.
А это более сложная фигура по сравнению с цилиндром, т.к. в её основании не круг, а овал.
Развёртки этой фигуры на втором листе, для овального основания сделано две запасных детали.
Чтобы аккуратно собрать цилиндр его детали нужно клеить встык. С одной стороны дно можно приклеить без проблем, просто поставьте на стол заранее склеенную трубку, положите на дно кружок и залейте клеем изнутри. Следите, чтобы диаметр трубы и круглого дна плотно подходили друг к другу, без щелей, иначе клей протечёт и всё приклеится к столу. Второй кружок приклеить будет сложнее, поэтому приклейте внутри вспомогательные прямоугольники на расстоянии толщины бумаги от края трубы. Эти прямоугольники не дадут упасть основанию внутрь, теперь вы без проблем приклеете кружок сверху.
Второй кружок приклеить будет сложнее, поэтому приклейте внутри вспомогательные прямоугольники на расстоянии толщины бумаги от края трубы. Эти прямоугольники не дадут упасть основанию внутрь, теперь вы без проблем приклеете кружок сверху.
Цилиндр с овальным основанием можно клеить также как и обычный цилиндр, но он имеет меньшую высоту, поэтому тут проще вставить внутрь гармошку из бумаги, а наверх положить второе основание и по краю приклеить клеем.
Теперь очень сложная фигура — конус. Его детали на третьем листе, запасной кружок для днища на 4-ом листе. Вся сложность склеивания конуса в его острой вершине, а потом ещё будет очень сложно приклеить дно.
Сложная и одновременно простая фигура это шар. Шар состоит из 12-ти пятигранников, развёртки шара на 4-ом листе. Сначала клеится две половинки шара, а потом обе склеиваются вместе.
Довольно интересная фигура — ромб, её детали на третьем листе.
А теперь две очень похожие, но совершенно разные фигуры, их отличие только в основании.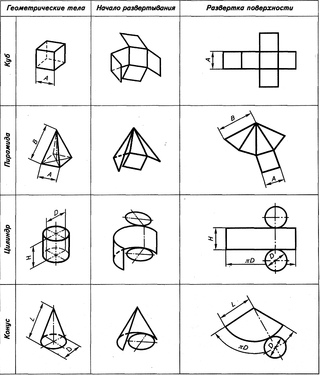
Когда склеите эти обе фигуры, то не сразу поймёте, что это вообще такое, они получились какие-то совсем невосприимчивые.
Ещё одна интересная фигурка это тор, только он у нас очень упрощён, его детали на 5-ом листе.
И наконец, последняя фигура из равносторонних треугольников, даже не знаю, как это назвать, но фигура похожа на звезду. Развёртки этой фигуры на пятом листе.
На сегодня это всё! Я желаю вам успехов в этой нелёгкой работе!
Крупу через сито – у каждого ребёнка должно быть своё сито.
Переливания и игры с водой Развитие моторики, подготовка руки к письму. Развитие моторики очень важно для детей… … соблюдая гармоничную последовательность.
Простая математика: коробочка по имени Десять Творчество .
Совместные занятия творчеством для детей разных возрастов организовать не… … ваты – такое занятие развлечет его надолго. Старший ребёнок может делать в это время аппликацию : клеить кусочки цветной бумаги на рисунок-заготовку.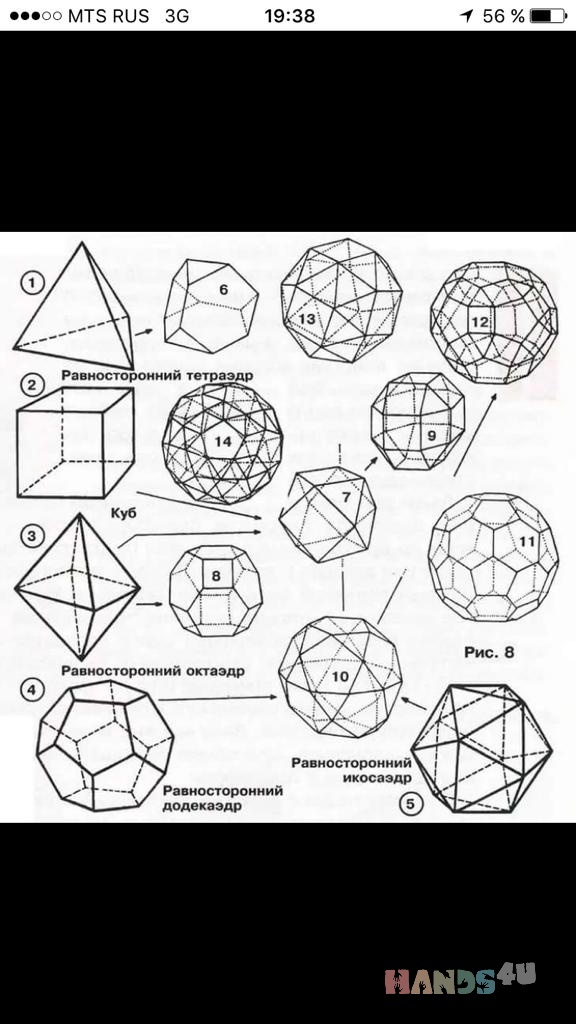 – Лепить из пластилина…
– Лепить из пластилина…
Дата обновления: 01.07.2017
Я б в художники пошел… Зачем детям рисование
Которые потом нужно раскрашивать, разноцветный песок для картин. В последние годы в России набирают популярность такие виды творчества , как квиллинг (объемные аппликации из свернутых узких полосок разноцветной бумаги), оригами (национальное японское творчество , складывание бумажных игрушек), скрапбукинг (оформление фотоальбомов, блокнотов и открыток разного рода аппликациями ). Конечно, детям непросто заниматься некоторыми из них. Например, для квиллинга очень важна отлично развитая мелкая моторика, и малышу может быть трудно удерживать в руках и правильно приклеивать эти свернутые улиткой узкие бумажные полоски, которые так и норовят развернуться в самый неподходящий момент… Но не спешите унывать: в некоторых видах творчества …
Дата обновления: 20.10.2016
Самый большой список игр для занятий с малышом
Изображать других животных (ходить как мишка, прыгать и квакать как лягушка и т.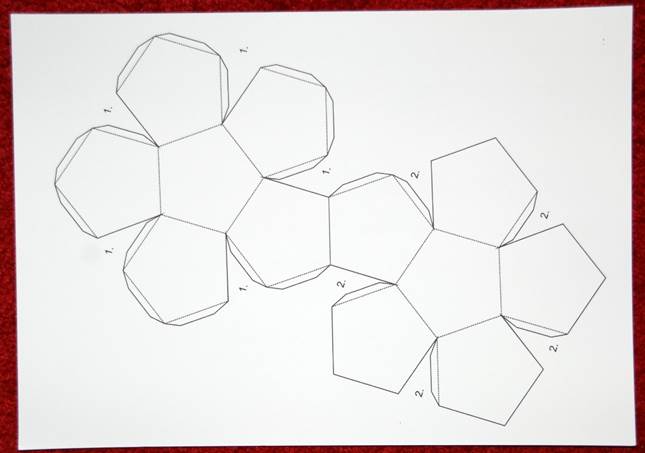 п.). РАЗВИТИЕ логики
1. «Собери только» (учиться выбрать из разбросанных предметов только… … (муравей пчелка и т.п.).
20. Солнышко, тучки, месяц, луна, звезды, дождь, снег, лужи. Творчество 1. Рисование: восковыми мелками, красками, фломастерами (лучше брать на водной… … ребенок легко усвоит в 1,5 года, что-то «придет» уже после двух – у всех по-разному.
9. Аппликация из бумаги (различной фактуры), аппликация из рваной бумаги, аппликация из…
п.). РАЗВИТИЕ логики
1. «Собери только» (учиться выбрать из разбросанных предметов только… … (муравей пчелка и т.п.).
20. Солнышко, тучки, месяц, луна, звезды, дождь, снег, лужи. Творчество 1. Рисование: восковыми мелками, красками, фломастерами (лучше брать на водной… … ребенок легко усвоит в 1,5 года, что-то «придет» уже после двух – у всех по-разному.
9. Аппликация из бумаги (различной фактуры), аппликация из рваной бумаги, аппликация из…
Дата обновления: 20.06.2016
Творчество с двумя детьми: вместе — веселее!
Возможностью развивать сразу обоих деток. За этим занятием можно максимально развить мелкую моторику, чувство цветовой гаммы, развитие фантазии и многие другие аспекты воспитания детей. Также это занятие имеет свойство приводить в восторг абсолютно всех… … штампы из картофеля. Будите воображение детей, заражайте их новой идеей — и наслаждайтесь тем покоем и счастьем, которым насыщено творчество с детьми!
Объемные аппликации с нестандартным подходом
Ни один ребенок не откажется сделать аппликацию в компании своего брата или сестренки.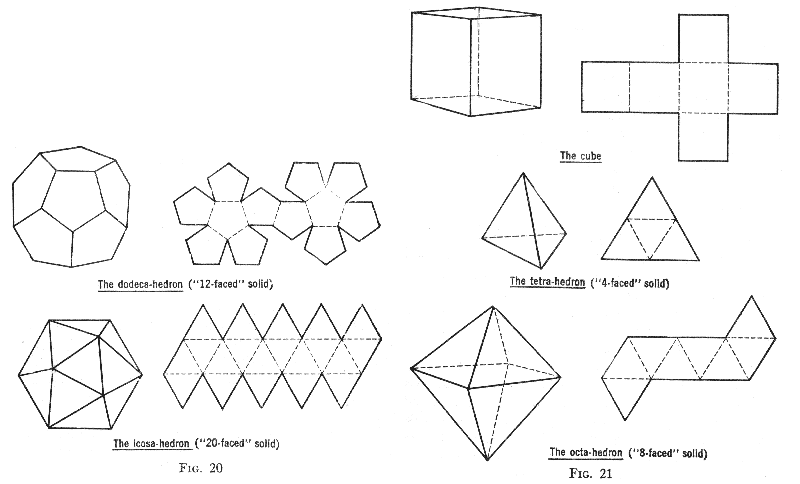 Можно…
Можно…
Дата обновления: 11.06.2016
Если надоело просто рисовать…
Процесса массу удовольствия. И нужно создавать им все условия. Наряду с плоскостной аппликацией научить их делать объемную: объемная лучше воспринимается дошкольником и… … вырежет из открыток, тканями изобразит небо и облака и т.д. Предела совершенствованию и творчеству в изобразительной деятельности нет. Рисуем на камушках Сама форма камушка… … им. Рисование приносит вашему малышу только пользу. Рисование плодотворно влияет на развитие памяти и внимания, развитие мелкой моторики и воображения. Воображение и фантазия…
Реконструкция объемной формы из неявных форм
Как упоминалось ранее, методы полиэдризации неявных форм делятся на две основные категории: во-первых, эйлеровы методы, которые рассматривают сетку, дискретизирующую область наблюдения \(\varOmega \), и во-вторых лагранжевы методы метода, которые выполняют дискретизацию объема формы \(\mathcal {V}\).
Стратегии Эйлера Изначально разработан для извлечения изоповерхностей, i . и . оценивая неявную поверхность, определяемую \(\{x \in \varOmega , f(x)=cst\}\), алгоритм марширующих кубов (MC), представленный в [31], является наиболее известным подходом в этой категории в результате эффективности и универсальности применения. Он рассматривает регулярную кубическую сетку, которая разбивает \(\varOmega \), где \(\varOmega \) обычно является ограничивающим прямоугольником. Для каждого куба в сетке, которая пересекает фигуру, алгоритм определяет грани пересечения путем линейной интерполяции вдоль ребер куба значений f в вершинах куба.Затем было предложено много методов, которые адаптируют эту стратегию к резким чертам, и . г . [23], или для разрешения топологических неоднозначностей, вызванных оригинальным методом, см. обзор [33]. Другие методы также предлагают более сложные схемы интерполяции [17, 26] для лучшего определения местоположения точек поверхности вдоль ребер куба.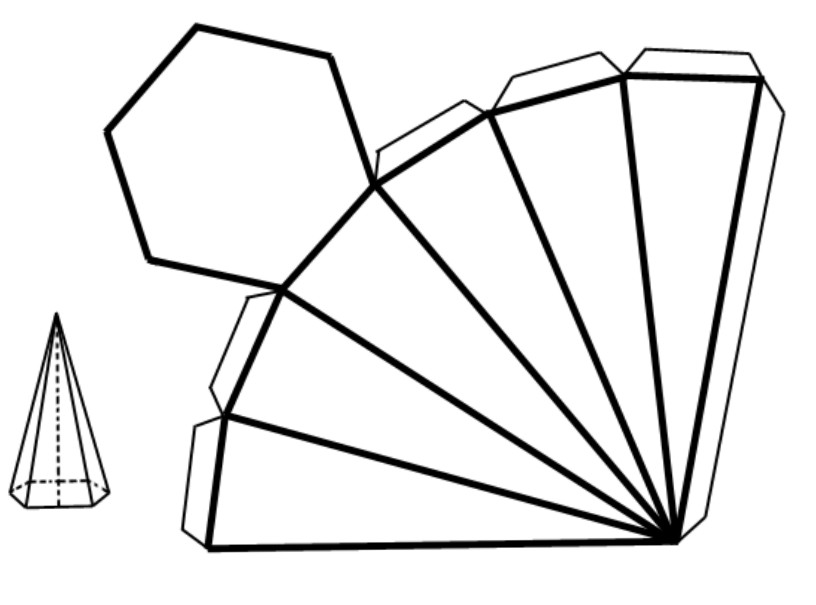 Чтобы ускорить вычисления, которые могут быть медленными, поскольку сложность является кубической по отношению к размеру сетки, несколько авторов предложили заменить сетку адаптивной структурой, такой как октодерево, e . г . [21]. Методы Marching Cubes сосредоточены на полигонизации граничной поверхности формы, а не на объемных мозаиках, которые имеют неправильную конструкцию: внутренние ячейки являются кубическими, а граничные ячейки — нет. Расширения других схем подразделения, включая тетраэдрические, октаэдрические и шестигранные подразделения, e . г . [6, 8, 37] также были предложены, которые обеспечивают более изотропные многогранные ячейки. Однако сетка дискретизации в этих схемах по-прежнему фиксированная.
Чтобы ускорить вычисления, которые могут быть медленными, поскольку сложность является кубической по отношению к размеру сетки, несколько авторов предложили заменить сетку адаптивной структурой, такой как октодерево, e . г . [21]. Методы Marching Cubes сосредоточены на полигонизации граничной поверхности формы, а не на объемных мозаиках, которые имеют неправильную конструкцию: внутренние ячейки являются кубическими, а граничные ячейки — нет. Расширения других схем подразделения, включая тетраэдрические, октаэдрические и шестигранные подразделения, e . г . [6, 8, 37] также были предложены, которые обеспечивают более изотропные многогранные ячейки. Однако сетка дискретизации в этих схемах по-прежнему фиксированная.
Лагранжевы стратегии. Вместо того, чтобы подразделять \(\varOmega \), подходы в этой категории замощают объем формы. Прежде всего, интерес заключается в уменьшении сложности, что обеспечивает более высокую точность, чем MC при аналогичных разрешениях.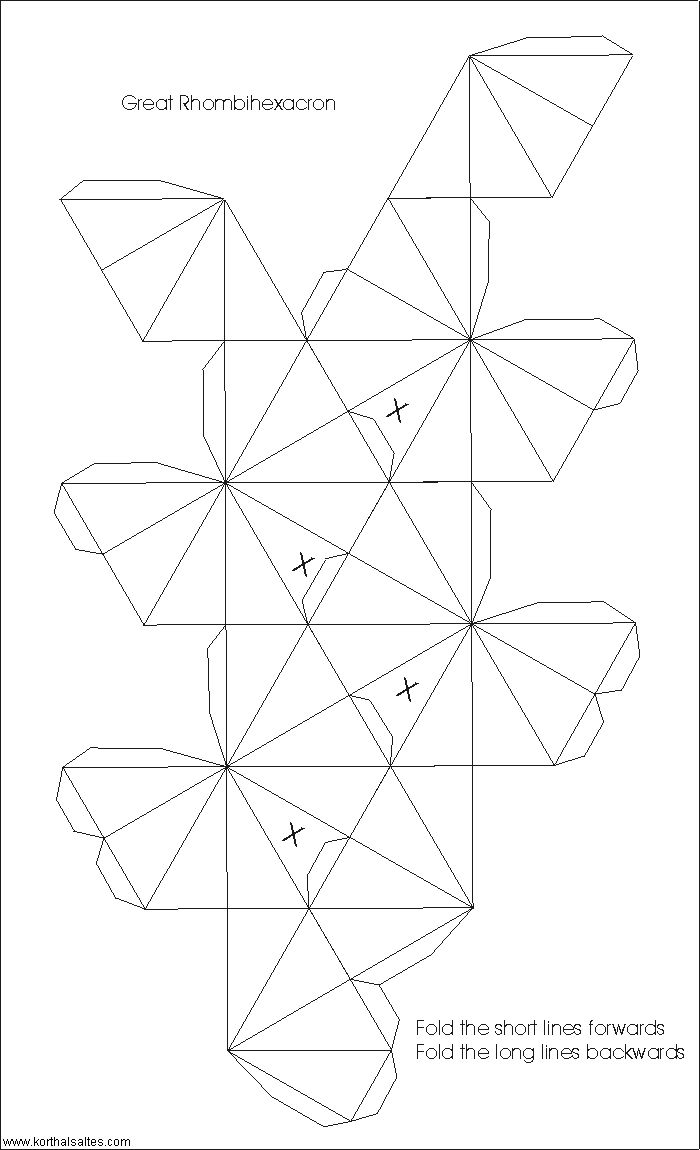 Это может быть важной особенностью при моделировании больших сцен, и . г . [24]. Во-вторых, присоединение подразделения к форме упрощает реализацию кинематических моделей, которые можно определить по объемным представлениям.Это может помочь при моделировании динамических сцен, как в [1]. В этой категории тетраэдризация формы широко используется для создания объемной мозаики. Например, алгоритм заполнения изоповерхностей из [25] создает правильную тетраэдризацию из объемно-центрированной кубической (ОЦК) сетки. Что касается описанных выше подходов с марширующими кубами, результирующая тесселяция, тем не менее, зависит от ориентации сетки. Техника уточнения Делоне, как и в [36], также генерирует тетраэдризации Делоне с гарантиями формы тетраэдра.Тем не менее, вырожденные тетраэдры, как правило, осколки, все еще могут появляться, хотя их количество может быть уменьшено методами глобальной [2] или локальной [38] оптимизации.
Это может быть важной особенностью при моделировании больших сцен, и . г . [24]. Во-вторых, присоединение подразделения к форме упрощает реализацию кинематических моделей, которые можно определить по объемным представлениям.Это может помочь при моделировании динамических сцен, как в [1]. В этой категории тетраэдризация формы широко используется для создания объемной мозаики. Например, алгоритм заполнения изоповерхностей из [25] создает правильную тетраэдризацию из объемно-центрированной кубической (ОЦК) сетки. Что касается описанных выше подходов с марширующими кубами, результирующая тесселяция, тем не менее, зависит от ориентации сетки. Техника уточнения Делоне, как и в [36], также генерирует тетраэдризации Делоне с гарантиями формы тетраэдра.Тем не менее, вырожденные тетраэдры, как правило, осколки, все еще могут появляться, хотя их количество может быть уменьшено методами глобальной [2] или локальной [38] оптимизации.
Центроидальные мозаики Вороного (CVT) представляют собой особый тип мозаик Вороного с регулярными ячейками Вороного [39]. Известно, что такие мозаики являются оптимальными квантизаторами [13], а их ячейки, в основном усеченные октаэдры, более изотропны, чем кубы или тетраэдры. Следовательно, CVT использовались для дискретизации 2D и 3D форм во многих научных областях [14].Хотя были предложены методы привязки CVT к поверхностной сетке [27, 39, 41], насколько нам известно, ни один из них еще не может обрабатывать неявные формы. Поэтому в следующем разделе мы представляем новый метод отсечки для вариаторов.
Известно, что такие мозаики являются оптимальными квантизаторами [13], а их ячейки, в основном усеченные октаэдры, более изотропны, чем кубы или тетраэдры. Следовательно, CVT использовались для дискретизации 2D и 3D форм во многих научных областях [14].Хотя были предложены методы привязки CVT к поверхностной сетке [27, 39, 41], насколько нам известно, ни один из них еще не может обрабатывать неявные формы. Поэтому в следующем разделе мы представляем новый метод отсечки для вариаторов.
Реконструкция поверхности. В этой статье мы сосредоточимся на методах полиэдризации неявных форм, однако стоит упомянуть подходы, которые реконструируют поверхность множества нулей неявной формы, см. и . г . [3] для обзора.Подходы в этой категории сосредоточены на тесселяции поверхностей, где мы рассматриваем объемные тесселяции.
Оценка. В литературе методы 2D- и 3D-реконструкции формы в основном оцениваются по качеству построенных ячеек.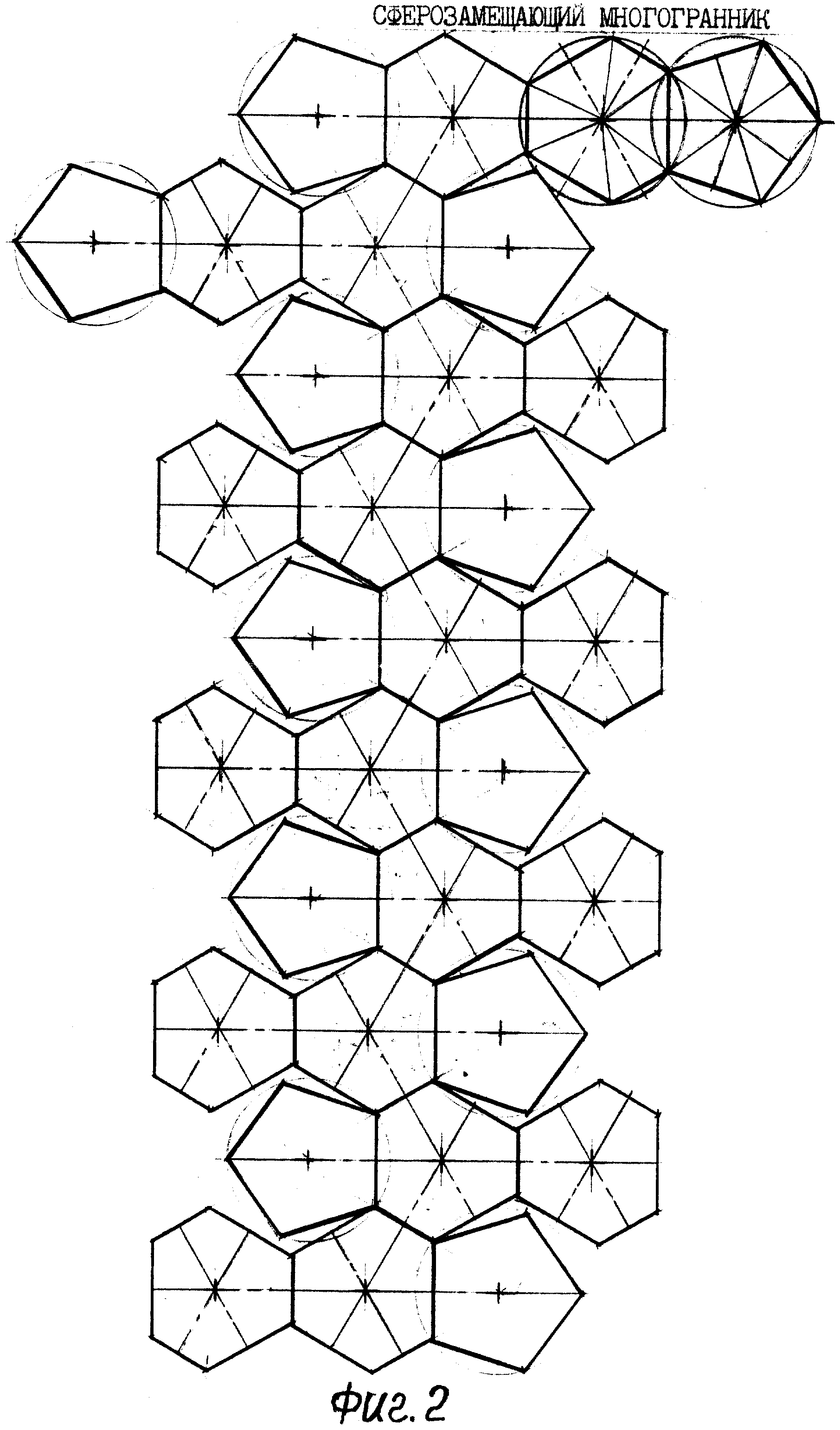 Это действительно важно для таких приложений, как моделирование методом конечных элементов. Качество обычно определяется по форме клетки [16]. В некоторых случаях метрики качества отражают тот факт, что ячейка должна держаться подальше от вырожденных конфигураций.Например, тетраэдров с хотя бы одним малым углом обычно следует избегать [10]. В других случаях определяется идеальная форма, а показатели качества определяются как расстояние до этого идеала. Это относится к CVT, для которых идеальной формой ячейки, как известно, является усеченный октаэдр, как указано в [13]. В данной работе вводится безразмерный второй момент многогранника, который может использоваться как мера регулярности CVT-ячейки [39]. Метрики также были предложены для других типов ячеек, таких как шестигранники [16], а также алгебраически для обычных ячеек [22].
Это действительно важно для таких приложений, как моделирование методом конечных элементов. Качество обычно определяется по форме клетки [16]. В некоторых случаях метрики качества отражают тот факт, что ячейка должна держаться подальше от вырожденных конфигураций.Например, тетраэдров с хотя бы одним малым углом обычно следует избегать [10]. В других случаях определяется идеальная форма, а показатели качества определяются как расстояние до этого идеала. Это относится к CVT, для которых идеальной формой ячейки, как известно, является усеченный октаэдр, как указано в [13]. В данной работе вводится безразмерный второй момент многогранника, который может использоваться как мера регулярности CVT-ячейки [39]. Метрики также были предложены для других типов ячеек, таких как шестигранники [16], а также алгебраически для обычных ячеек [22].
Несколько работ исследовали геометрическую точность данной реконструкции. Геометрическую точность можно определить как расстояние между границами заданной входной формы и полученной объемной реконструкции.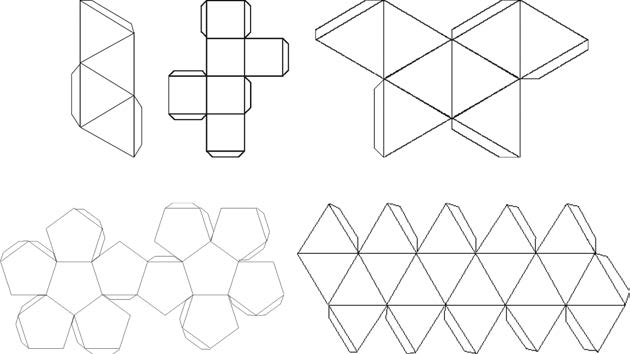 Metro [12], введенный в контексте упрощения сетки, является распространенным инструментом для оценки расстояния между двумя триангулированными поверхностями. Совсем недавно, сосредоточившись на реконструкции поверхности, Berger et al. Недавно в [4] были введены улучшенные метрики, основанные на концепциях дискретной дифференциальной геометрии, для количественной оценки расстояний между неявной поверхностью и поверхностной сеткой.Мы опираемся на эту работу для оценки точности.
Metro [12], введенный в контексте упрощения сетки, является распространенным инструментом для оценки расстояния между двумя триангулированными поверхностями. Совсем недавно, сосредоточившись на реконструкции поверхности, Berger et al. Недавно в [4] были введены улучшенные метрики, основанные на концепциях дискретной дифференциальной геометрии, для количественной оценки расстояний между неявной поверхностью и поверхностной сеткой.Мы опираемся на эту работу для оценки точности.
В разд. 4 мы сравниваем мозаику формы, полученную с помощью марширующих кубов, уточнения Делоне и CVT-подходов, используя как качество формы, так и критерии геометрической точности. Мы также обсудим теоретические гарантии, предоставляемые каждым подходом, а также время их расчета.
(PDF) Локальная аппроксимация скалярных функций на трехмерных формах и объемных данных
[16] S. Martin, P. Kaufmann, M. Botsch, M. Wicke, M. Gross, Poly-
эдральные конечные элементы с использованием гармонических базовые функции, Компьютер
Graphics Forum 27 (5) (2008) 1521–1529.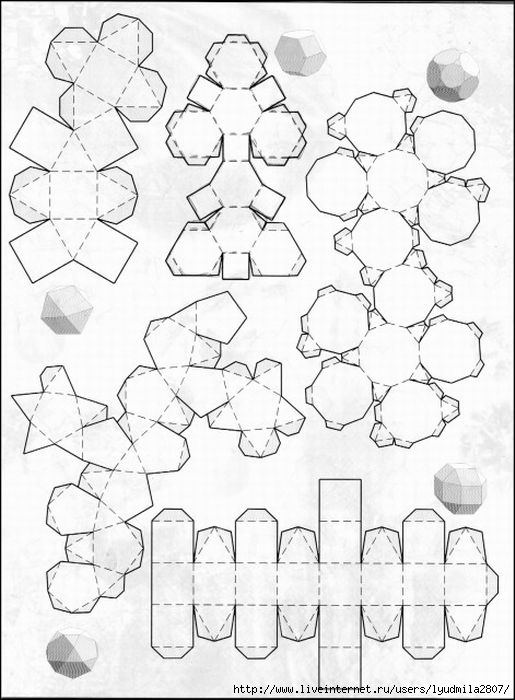
[17] Г. Терк, Дж. Ф. О’Брайен, Моделирование с неявными поверхностями, которые интерполируются
, ACM Siggraph 21 (4) (2002) 855–873.
[18] Ю. Охтаке, А. Беляев, М. Алекса, Г. Турк, Х.-П. Зайдель, Multi-
уровень разделения неявных единиц единства, ACM Siggraph 22 (3) (2003)
463–470.
[19] J. Jin, M. Garland, E. A. Ramos, Скалярные поля на основе MLS на
треугольных сетках и их применение в обработке сеток, в:
Proc. Симпозиума по интерактивной 3D-графике и играм,
, 2009 г., стр.145–153.
[20] G. Patan`
e, M. Spagnuolo, B. Falcidieno, Topology- and error-
управляемое расширение скалярных функций с поверхностей на объемы,
ACM Transactions on Graphics 29 (1) (2009 ) 1–20.
[21] Р. Р. Койфман, С. Лафон, Диффузионные карты, Прикладной и вычислительный гармонический анализ, 21 (1) (2006) 5–30.
[22] C. S. Co, B. Heckel, H. Hagen, B. Hamann, K. Joy, Иерархическая кластеризация для неструктурированных объемных скалярных полей, в: IEEE
Visualization, 2003, p.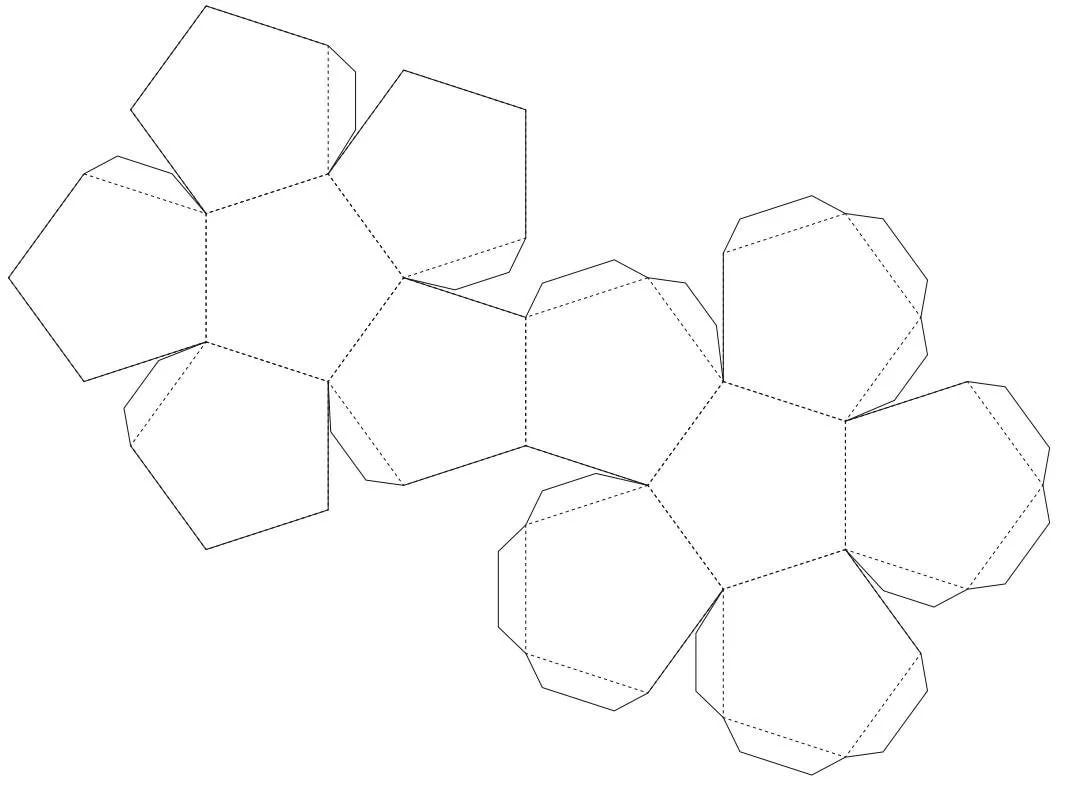 43.
43.
[23] Y. Jang, M. Weiler, M. Hopf, J. Huang, D.S. Ebert, K.P. Симпозиума по визуализации, 2004 г., стр.
35–44.
[24] M. Weiler, R. Botchen, S. Stegmaier, T. Ertl, J. Huang, Y. Jang,
D. Ebert, K. Gaither, Аппаратный анализ признаков и визуализация
процедурно закодированных многополевых объемных данных,
Приложения компьютерной графики 25 (5) (2005) 72–81.
[25] Y. Jang, RP Botchen, A. Lauser, DS Ebert, KP Gaither,
T. Ertl, Улучшение интерактивной визуализации процедурно
закодированных многополевых данных с эллипсоидальными базисными функциями., Компьютер
Графический форум 25 (3) (2006) 587–596.
[26] В. Хонг, Н. Неопыту, А. Кауфман, Построение трехмерного эллиптического
калибровочного гаусса для нерегулярных данных, в: Mathematical Foundations of
Scientific Visualization, Computer Graphics, and Massive Data
Visualization, 2006 , стр.213–225.
[27] К. Мэдсен, Х. Б. Нильсен, О. Тинглефф, Методы нелинейных задач
Б. Нильсен, О. Тинглефф, Методы нелинейных задач
наименьших квадратов, 2-е издание, Информатика и математика,
Эматическое моделирование, Технический университет Дании, DTU,
2004.
[28] G. Patan`
e, B. Falcidieno, Вычисление гладких аппроксимаций
скалярных функций с ограничениями, Computer & Graphics 33 (3)
(2009) 399–413.
[29] С. Ли, С. Го, Х. Ван, Ю. Хе, С.Гу, Х. Цинь, Гармоническое объемное картирование для приложений твердотельного моделирования, в: Proc. of
Symposium on Solid and Physical Modeling, 2007, pp. Кубическая карта
для построения сплайнов коллектора, в: Симпозиум по твердотельному и физическому моделированию
, 2008 г., стр. 397–404.
[31] М. Поли, Р. Кайзер, Л. П. Коббельт, М. Гросс, Моделирование формы
с геометрией с точечной выборкой, ACM Transactions on Graphics
22 (3) (2003) 641–650.
[32] С. Арья, Д.М. Маунт, Н.С. Нетаньяху, Р. Сильверман, А.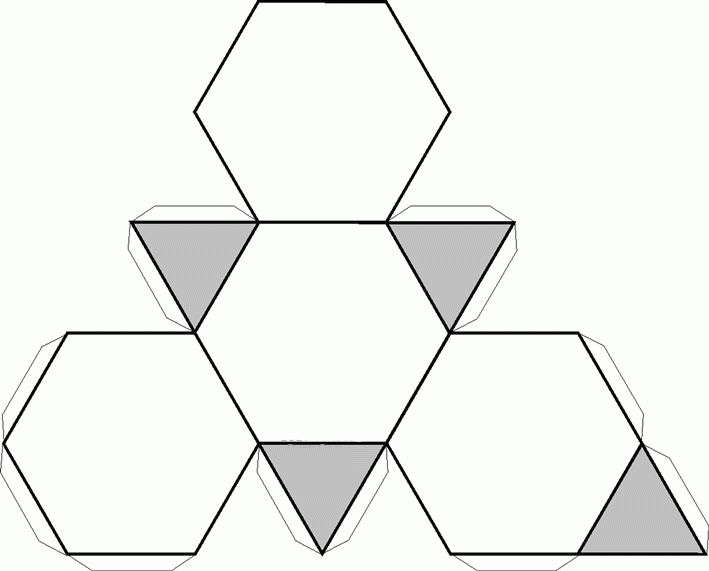 Ю.
Ю.
Ву, Оптимальный алгоритм для приближенного ближайшего соседа
поиска фиксированных размеров, Журнал ACM 45 (6) (1998)
891–923.
[33] Т. К. Дей, Дж. Сан, Адаптивная поверхность MLS для реконструкции
с гарантиями, в: Симпозиум ACM по обработке геометрии,
2005, стр. 43–52.
[34] Н. Дж. Митра, А. Нгуен, Оценка нормалей поверхности в зашумленных данных облака точек
, в: Proc.вычислительной геометрии, ACM
Press, 2003, стр. 322–328.
[35] G. Patan`
e, Аппроксимация размерных данных d-
методом наименьших квадратов с радиальными базисными функциями, CNR-IMATI
Технический отчет 10.
[36] BS Morse, TS Yoo, DT Chen, P. Rheingans, KR Sub-
ramanian, Интерполяция неявных поверхностей из данных рассеянной поверхности
с использованием радиальных базисных функций с компактной поддержкой, в: IEEE
Shape Modeling and Applications, 2001, стр.89–98.
[37] J. Bloomenthal, B. Wyvill (Eds.), Introduction to Implicit Sur-
Bloomenthal, B. Wyvill (Eds.), Introduction to Implicit Sur-
faces, Morgan Kaufmann Publishers Inc., 1997.
[38] M. Pauly, N. Mitra, L. Guibas , Неопределенность и изменчивость в
данных о поверхности облаков точек, Proc. Симпозиума по точечной графике
(2004) 77–84.
[39] G. Guennebaud, M. Gross, Алгебраические поверхности множества точек, ACM
Transactions on Graphics 26.
[40] G. Guennebaud, M. Germann, M.Х. Гросс, Динамическая выборка
и визуализация поверхностей множества алгебраических точек, Компьютерная графика
Форум 27 (2) (2008) 653–662.
[41] AC ¨
Oztireli, G. Guennebaud, MH Gross, Сохранение признаков
поверхности наборов точек на основе нелинейной ядерной регрессии, Computer Graphics Forum 28 (2) (2009) 493–501 .
[42] К. Шен, Дж. Ф. О’Брайен, Дж. Р. Шевчук, Интерполяция и аппроксимация неявных поверхностей из полигонального супа, в: ACM Sig-
graph Courses, 2005, p.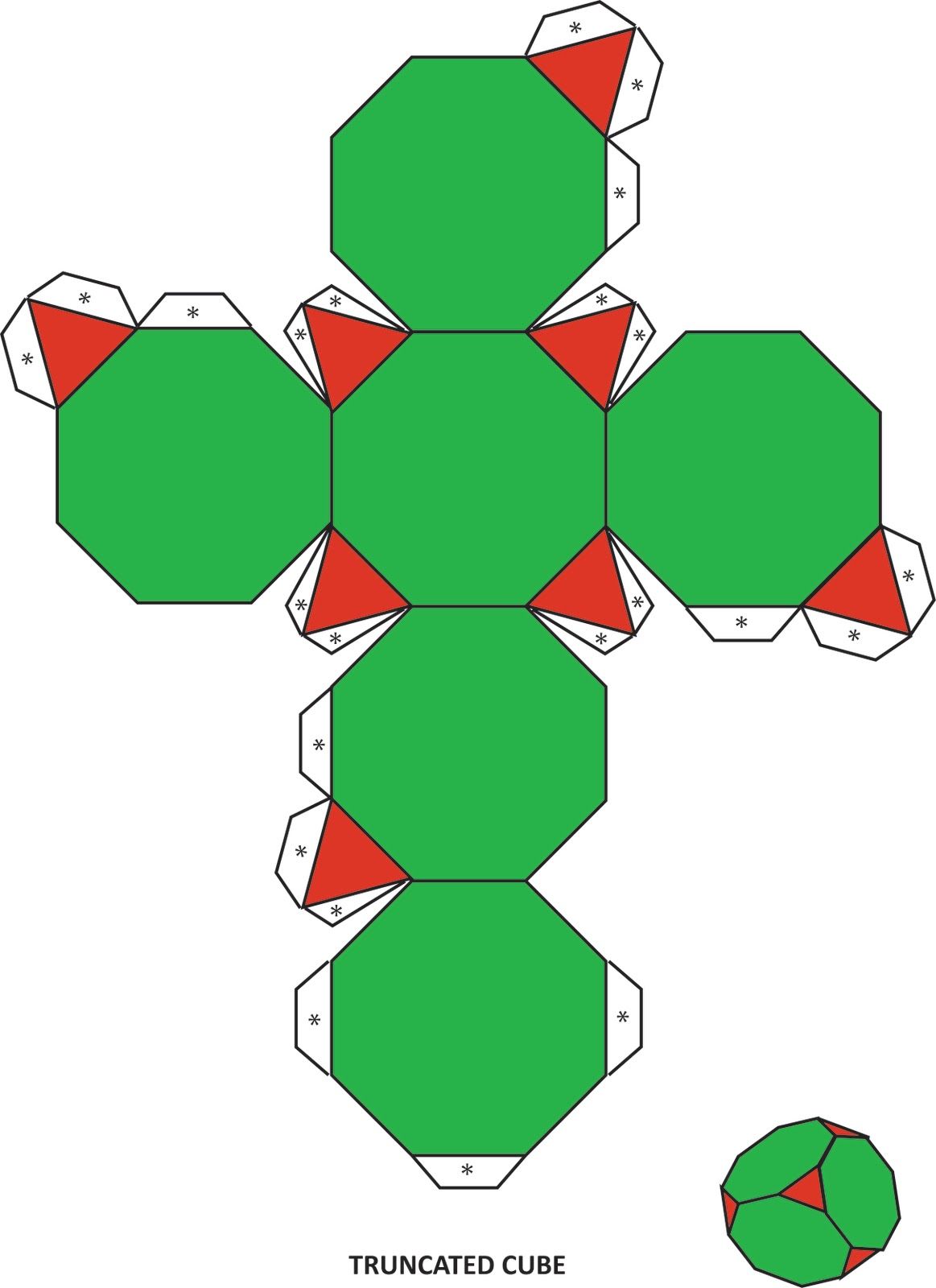 204.
204.
[43] Б. Валлет, Б. Леви, Гармоники многообразия, Компьютерная графика Форум
, ром 27(2).
[44] М. Рейтер, Ф.-Э. Вольтер, Н. Пайнеке, Спектры Лапласа-Бельтрами
как Shape-DNA поверхностей и твердых тел, Компьютерное проектирование
38 (4) (2006) 342–366.
[45] В. Паскуччи, Г. Скорцелли, П. Бремер, А. Маскаренхас, Робаст
онлайн-вычисление графов Риба: простота и скорость,
ACM Transactions on Graphics 26 (3).
[46] А.Гьюласси, В. Натараджан, В. Паскуччи, Б. Хаманн, Эффективное вычисление комплексов Морса-Смейла для трехмерных скалярных функций
, Транзакции IEEE по визуализации и компьютерной графике 13 (6) (2007) 1440–1447 гг.
[47] Б. Адамс, М. Вике, Методы бессеточной аппроксимации и приложения
в моделировании и анимации на основе физики, в: Euro-
Graphics Tutorials, 2009, стр. 213–239.
[48] Б. Адамс, М. Вике, М.Овсяников, М. Ванд, Х.-П. Seidel,
L. Guibas, Бессеточная форма и дизайн движения для множественных деформируемых объектов, Computer Graphics Forum 29 (1) (2010) 43–
59.
[49] JC Hart, A. Durr, Д. Харш, Критические точки многочлена
метаболов, в: Proc. неявных поверхностей, 1998, стр. 69–76.
[50] С.-Т. Ву, М. Де Гоменсоро, Об улучшении поиска критических точек неявных функций, Proc. Неявные поверхности (1999)
73–80.
[51] Г. Сиприано, М. Глейхер, Абстракция молекулярной поверхности, IEEE
Transactions on Visualization and Computer Graphics 13 (6)
(2007) 1608–1615.
14
Адаптивная геометрическая мозаика для трехмерной реконструкции анизотропно развивающихся клеток в многослойных тканях по разреженным объемным микроскопическим изображениям
Abstract
Необходимость количественной оценки моделей роста клеток в многослойной многоклеточной ткани требует разработки метода трехмерной реконструкции, который может оценивать трехмерные формы и размеры отдельных клеток по срезам изображения, полученным с помощью конфокальной микроскопии (CLSM).Однако современные методы 3D-реконструкции с использованием изображений CLSM требуют большого количества срезов изображения на ячейку.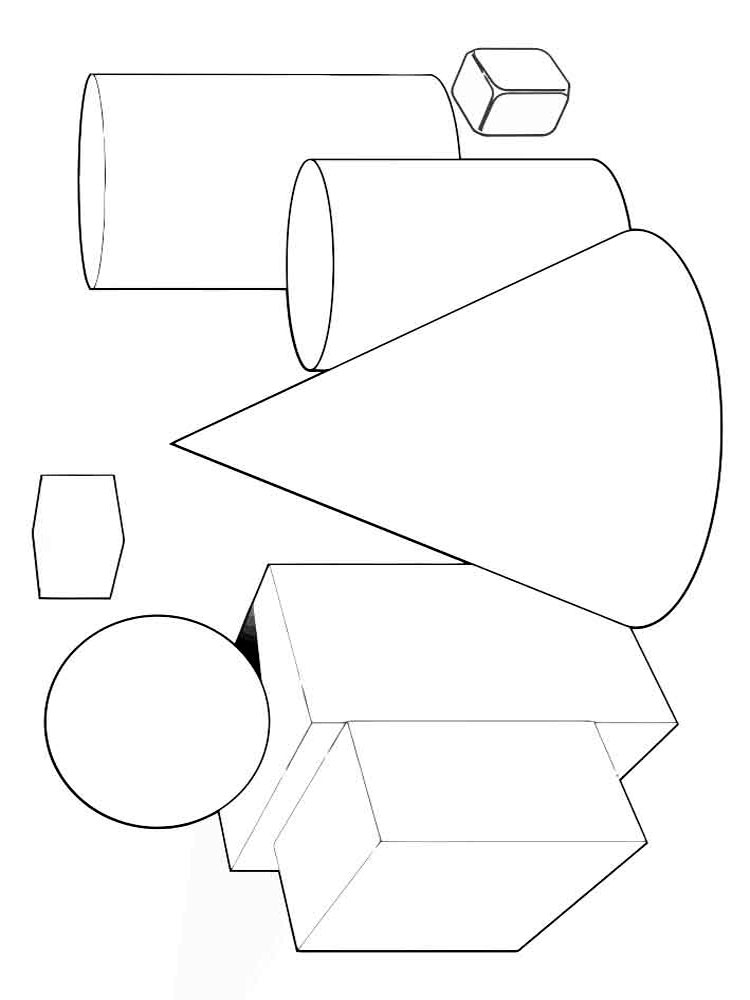 Но в случае Live Cell Imaging активно развивающейся ткани большое разрешение по глубине невозможно, чтобы избежать повреждения клеток от длительного воздействия лазерного излучения. В настоящей работе мы предложили каркас трехмерной реконструкции на основе анизотропной мозаики Вороного для плотно упакованной многослойной ткани с экстремальной z-разреженностью (2–4 среза на ячейку) и широким диапазоном форм и размеров клеток.Предлагаемый метод, названный «Адаптивная квадратичная мозаика Вороного» (AQVT), способен решать как проблему разреженности, так и неоднородность форм ячеек путем оценки параметров тесселяции для каждой ячейки по разреженным точкам данных на ее границах. . Мы протестировали предложенный метод 3D-реконструкции на стеках покадровых CLSM-изображений апикальной меристемы побегов арабидопсиса (SAM) и показали, что метод реконструкции на основе AQVT может правильно оценивать 3D-формы большого количества клеток SAM.
Но в случае Live Cell Imaging активно развивающейся ткани большое разрешение по глубине невозможно, чтобы избежать повреждения клеток от длительного воздействия лазерного излучения. В настоящей работе мы предложили каркас трехмерной реконструкции на основе анизотропной мозаики Вороного для плотно упакованной многослойной ткани с экстремальной z-разреженностью (2–4 среза на ячейку) и широким диапазоном форм и размеров клеток.Предлагаемый метод, названный «Адаптивная квадратичная мозаика Вороного» (AQVT), способен решать как проблему разреженности, так и неоднородность форм ячеек путем оценки параметров тесселяции для каждой ячейки по разреженным точкам данных на ее границах. . Мы протестировали предложенный метод 3D-реконструкции на стеках покадровых CLSM-изображений апикальной меристемы побегов арабидопсиса (SAM) и показали, что метод реконструкции на основе AQVT может правильно оценивать 3D-формы большого количества клеток SAM.
Образец цитирования: Чакраборти А.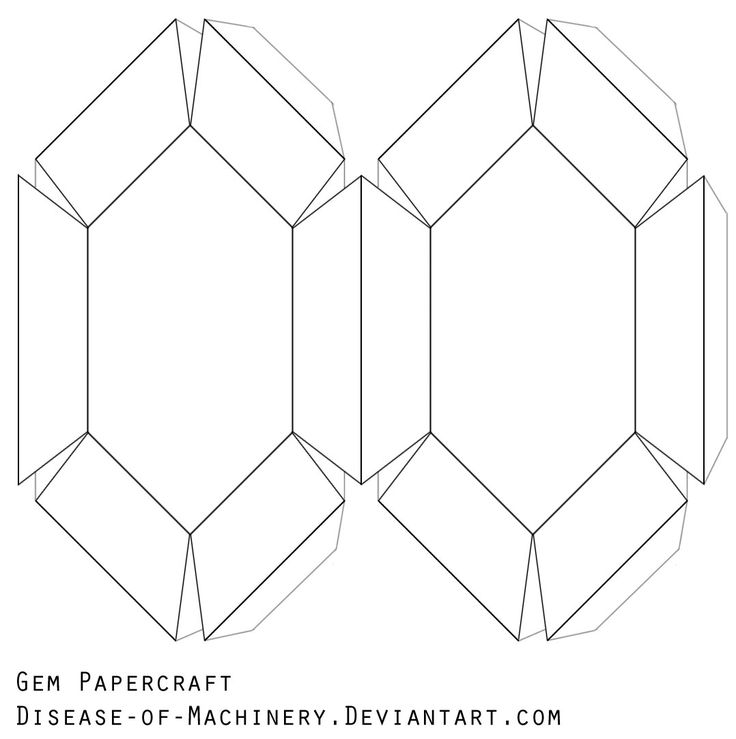 , Пералес М.М., Редди Г.В., Рой-Чоудхури А.К. (2013) Адаптивная геометрическая мозаика для трехмерной реконструкции анизотропно развивающихся клеток в многослойных тканях по разреженным изображениям объемной микроскопии. ПЛОС ОДИН 8(8):
е67202.
https://doi.org/10.1371/journal.pone.0067202
, Пералес М.М., Редди Г.В., Рой-Чоудхури А.К. (2013) Адаптивная геометрическая мозаика для трехмерной реконструкции анизотропно развивающихся клеток в многослойных тканях по разреженным изображениям объемной микроскопии. ПЛОС ОДИН 8(8):
е67202.
https://doi.org/10.1371/journal.pone.0067202
Редактор: Роланд М.Х. Merks, Centrum Wiskunde & Informatica (CWI) и Нидерландский институт системной биологии, Нидерланды
Получено: 19 июня 2012 г.; Принято: 17 мая 2013 г.; Опубликовано: 5 августа 2013 г.
Авторское право: © 2013 Chakraborty et al.Это статья с открытым доступом, распространяемая в соответствии с лицензией Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии указания оригинального автора и источника.
Финансирование: Эта работа финансируется грантом Национального научного фонда IIS-0712253 для Амита Роя-Чоудхури и NSF IOS-1147250 для Venugopala Gonehal Reddy.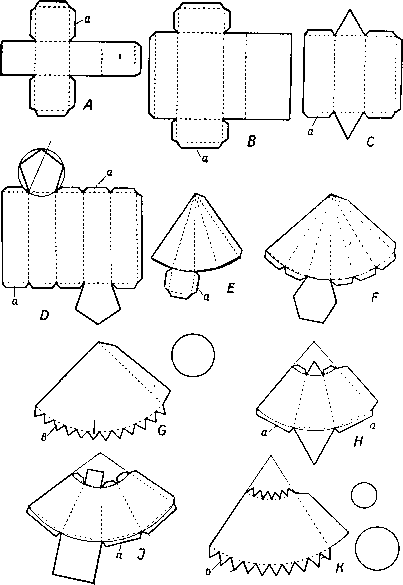 Спонсоры не участвовали в разработке исследования, сборе и анализе данных, принятии решения о публикации или подготовке рукописи.
Спонсоры не участвовали в разработке исследования, сборе и анализе данных, принятии решения о публикации или подготовке рукописи.
Конкурирующие интересы: Авторы заявили об отсутствии конкурирующих интересов.
Введение
Причинно-следственная связь между паттернами роста клеток и динамикой экспрессии генов представляет большой интерес в биологии развития. Однако большинство исследований в этой области пытались качественно описать взаимосвязь между регуляторной сетью генов и ростом и деформацией клеток. Надлежащий количественный анализ паттернов роста клеток как в растительных, так и в животных тканях до сих пор оставался в основном неуловимым.Информация, такая как скорость и характер экспансии клеток, играет критическую роль в объяснении динамики роста и деформации клеток и, таким образом, может быть чрезвычайно полезной для понимания морфогенеза. Таким образом, необходимость количественной оценки этих биологических параметров (таких как объем клетки, скорость роста клеток, форма клетки, среднее время между клеточными делениями и т. д.) и наблюдения за их изменением во времени имеет первостепенное значение для биологов.
д.) и наблюдения за их изменением во времени имеет первостепенное значение для биологов.
Для сложных многослойных, многоклеточных тканей растений и животных наиболее популярным методом захвата отдельных клеточных структур и оценки вышеупомянутых параметров растущих клеток является конфокальная микроскопия на основе Визуализация живых клеток .Конфокальная лазерная сканирующая микроскопия (КЛСМ) позволяет визуально исследовать внутренние части многослойных тканей. С помощью этого метода мы можем отображать ткани в виде набора последовательных оптических срезов (также известных как «Z-стек»), которые затем можно использовать для анализа. Визуализация живых клеток — это класс микроскопии, при котором одни и те же живые клетки наблюдают и визуализируют через равные промежутки времени в течение нескольких часов, чтобы отслеживать их движение или смещение, а также визуализировать динамику роста и деления клеток.
В последнее время был проделан значительный объем работ по автоматизированной обработке и анализу клеточных изображений, но в основном по сегментации изображений и отслеживанию клеток. Такие методы, как [1], [2], показывают, что отдельные клетки могут быть эффективно сегментированы в многоклеточном поле, а [3], [4] предоставляют автоматизированные методы для отслеживания отдельных клеток во времени. Оценка формы и объема клеток в зависимости от времени является наиболее важной для понимания процесса роста. Из-за большого количества данных, собранных во время роста ткани, вычислительные методы для надежной оценки трехмерных клеточных структур и объемов клеток абсолютно необходимы для получения статистически значимых результатов этих параметров роста.
Такие методы, как [1], [2], показывают, что отдельные клетки могут быть эффективно сегментированы в многоклеточном поле, а [3], [4] предоставляют автоматизированные методы для отслеживания отдельных клеток во времени. Оценка формы и объема клеток в зависимости от времени является наиболее важной для понимания процесса роста. Из-за большого количества данных, собранных во время роста ткани, вычислительные методы для надежной оценки трехмерных клеточных структур и объемов клеток абсолютно необходимы для получения статистически значимых результатов этих параметров роста.
Несмотря на исключительную полезность визуализации живых клеток на основе CLSM для анализа таких тканевых структур, существует ряд технических проблем, связанных с этой техникой визуализации, что делает задачу оценки формы клеток нетривиальной. Чтобы клетки оставались живыми и росли, мы должны ограничивать воздействие лазерного излучения на образец, т.е. если собираются плотные образцы в один момент времени, маловероятно, что мы сможем получить замедленные изображения, так как образец не будет продолжают расти во времени из-за высокого радиационного облучения. Поэтому количество срезов, на которых изображается клетка, часто очень мало (2–4 среза на ячейку). Опять же, флуоресцентный сигнал затухает по мере того, как мы отображаем более глубокие слои ткани, что приводит к проблеме очень низкого SNR в частях стопки конфокальных изображений. Обратите внимание, что в некоторых случаях микроскопия с двухфотонным возбуждением или световая микроскопия могут быть лучшим выбором для визуализации живых клеток для более эффективного обнаружения света и меньшего эффекта фотообесцвечивания. Но существует большое количество наборов данных, которые отображаются с помощью CLSM или демонстрируют характеристики наших данных, и наш метод может быть полезен при их анализе.Мы обнаружили, что двухфотонное возбуждение токсичнее для клеток SAM, чем однофотонное CLSM, и, поскольку SAM окружен несколькими развивающимися цветочными почками, боковое возбуждение может оказаться невозможным. Кроме того, разработав метод анализа изображений, способный обрабатывать данные худшего качества, мы можем гарантировать, что такая же или лучшая точность может быть достигнута на наборе данных с превосходным качеством изображения и разрешением.
Поэтому количество срезов, на которых изображается клетка, часто очень мало (2–4 среза на ячейку). Опять же, флуоресцентный сигнал затухает по мере того, как мы отображаем более глубокие слои ткани, что приводит к проблеме очень низкого SNR в частях стопки конфокальных изображений. Обратите внимание, что в некоторых случаях микроскопия с двухфотонным возбуждением или световая микроскопия могут быть лучшим выбором для визуализации живых клеток для более эффективного обнаружения света и меньшего эффекта фотообесцвечивания. Но существует большое количество наборов данных, которые отображаются с помощью CLSM или демонстрируют характеристики наших данных, и наш метод может быть полезен при их анализе.Мы обнаружили, что двухфотонное возбуждение токсичнее для клеток SAM, чем однофотонное CLSM, и, поскольку SAM окружен несколькими развивающимися цветочными почками, боковое возбуждение может оказаться невозможным. Кроме того, разработав метод анализа изображений, способный обрабатывать данные худшего качества, мы можем гарантировать, что такая же или лучшая точность может быть достигнута на наборе данных с превосходным качеством изображения и разрешением. Таким образом, с точки зрения анализа изображения мы рассматриваем очень сложную задачу, когда мы хотим получить трехмерную реконструкцию поверхности клеток произвольной формы из набора очень редко выбранных точек данных в присутствии неизбежного шума изображения.Также трубопровод реконструкции должен быть полностью автоматизирован. В большинстве случаев ручной анализ (который был тенденцией) обычно чрезвычайно утомителен и часто дает только качественные тенденции в данных, а не точные количественные модели.
Таким образом, с точки зрения анализа изображения мы рассматриваем очень сложную задачу, когда мы хотим получить трехмерную реконструкцию поверхности клеток произвольной формы из набора очень редко выбранных точек данных в присутствии неизбежного шума изображения.Также трубопровод реконструкции должен быть полностью автоматизирован. В большинстве случаев ручной анализ (который был тенденцией) обычно чрезвычайно утомителен и часто дает только качественные тенденции в данных, а не точные количественные модели.
В этом исследовании мы рассмотрели проблему трехмерной реконструкции плотно упакованной многослойной ткани по Z-разреженным конфокальным срезам изображения. В качестве особого примера в этой статье мы предложили новую, полностью автоматизированную структуру 3D-реконструкции клеток с разрешением для побегов апикальной меристемы (SAM) Arabidopsis Thaliana.SAM, также называемый нишей стволовых клеток, является очень важной частью плана тела растения, поскольку он снабжает клетками все надземные части растения, такие как листья, ветви и стебель. Типичный SAM арабидопсиса представляет собой плотно упакованный многослойный клеточный кластер, состоящий примерно из пятисот клеток, где клеточные слои клонально отличаются друг от друга. Плотная тесселяция ячеек в SAM позволила нам оценить трехмерную структуру отдельных ячеек, используя информацию о срезах ячейки, а также информацию о ее ближайших соседях.Трехмерная оценка основана на предшествующих геометрических мозаичных моделях, параметры для которых оцениваются на основе имеющихся разреженных данных изображения, а затем эта модель используется для разделения трехмерной структуры SAM на отдельные клеточные области.
Типичный SAM арабидопсиса представляет собой плотно упакованный многослойный клеточный кластер, состоящий примерно из пятисот клеток, где клеточные слои клонально отличаются друг от друга. Плотная тесселяция ячеек в SAM позволила нам оценить трехмерную структуру отдельных ячеек, используя информацию о срезах ячейки, а также информацию о ее ближайших соседях.Трехмерная оценка основана на предшествующих геометрических мозаичных моделях, параметры для которых оцениваются на основе имеющихся разреженных данных изображения, а затем эта модель используется для разделения трехмерной структуры SAM на отдельные клеточные области.
Руководствуясь методами, описанными в [5], [6], мы сначала предположим мозаичную модель Вороного, основанную на евклидовой метрике расстояния, для сегментации/восстановления трехмерных форм ячеек. Благодаря результатам, полученным на трехмерных разреженных конфокальных стопках изображений SAM, мы показываем, что эта модель дает хорошее приближение к формам клеток, где формы и размеры клеток одинаковы по всем трем осям клеток и основным осям роста соседних клеток.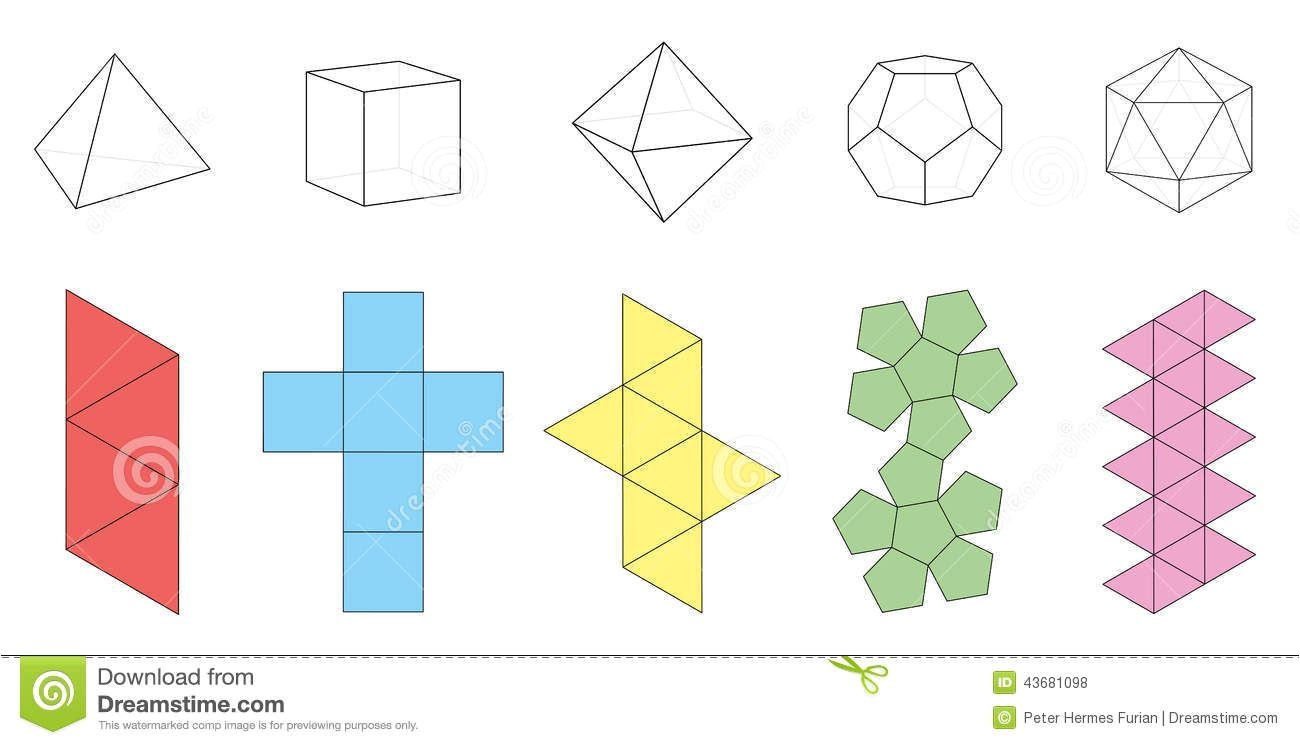 клетки изотропны.Но на практике это не всегда так и клетки могут иметь очень анизотропную форму и рост даже при близком соседстве. В таких случаях тесселяция Вороного с использованием евклидова расстояния не дает достаточно точных клеточных стенок.
клетки изотропны.Но на практике это не всегда так и клетки могут иметь очень анизотропную форму и рост даже при близком соседстве. В таких случаях тесселяция Вороного с использованием евклидова расстояния не дает достаточно точных клеточных стенок.
Поэтому мы предлагаем анизотропную мозаику Вороного, определенную на квадратичной метрике расстояний, чтобы отразить анизотропию роста отдельных клеток по всем их осям. Мы показываем, что параметры этой метрики можно оценить по разреженному набору срезов конфокального изображения отдельных ячеек, а тесселяция на основе этой метрики может обеспечить очень точные трехмерные формы ячеек в виде квадратичных поверхностей даже в случае неоднородных форм ячеек. , размеры или рост вдоль разных осей клеток.Тесселяция, названная «Адаптивная квадратичная мозаика Вороного» (AQVT), и основанная на ней техника трехмерной реконструкции, представленная в этой статье, обеспечивают достаточно точную трехмерную реконструированную форму и размеры клеток в SAM, что подтверждено экспериментами в разделе 5.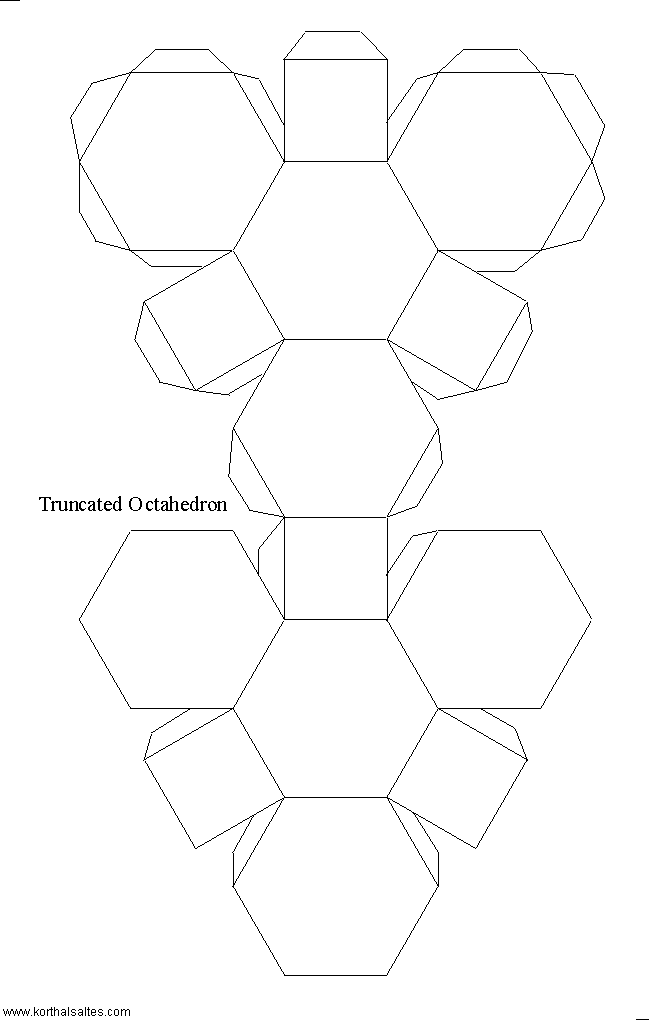 3. Мы также показываем, что предложенная анизотропная мозаика Вороного (AQVT) также может быть применена к тканям, где формы клеток в ткани следуют стандартному евклидову расстоянию, основанному на мозаике Вороного.
3. Мы также показываем, что предложенная анизотропная мозаика Вороного (AQVT) также может быть применена к тканям, где формы клеток в ткани следуют стандартному евклидову расстоянию, основанному на мозаике Вороного.
Хотя этот метод мотивирован нашей предыдущей работой в [7], существуют фундаментальные различия как в теории, так и в реализации между [7] и настоящей работой, основанной на AQVT.Основные отличия заключаются в следующем. 1. AQVT ставит и решает проблему трехмерной сегментации/реконструкции в стандартной структуре геометрической тесселяции, которая очень интуитивно понятна для такого типа задач и имеет прочную теоретическую основу в литературе. 2. Метод, описанный в [7], представляет собой итерационный метод, который может иметь длительное время выполнения в зависимости от желаемого уровня точности и выбранных параметров (например, размера шага на этапе деформации). Метод реконструкции на основе AQVT, описанный в этой статье, является одноэтапным процессом и, следовательно, имеет меньшее время выполнения по сравнению с [7].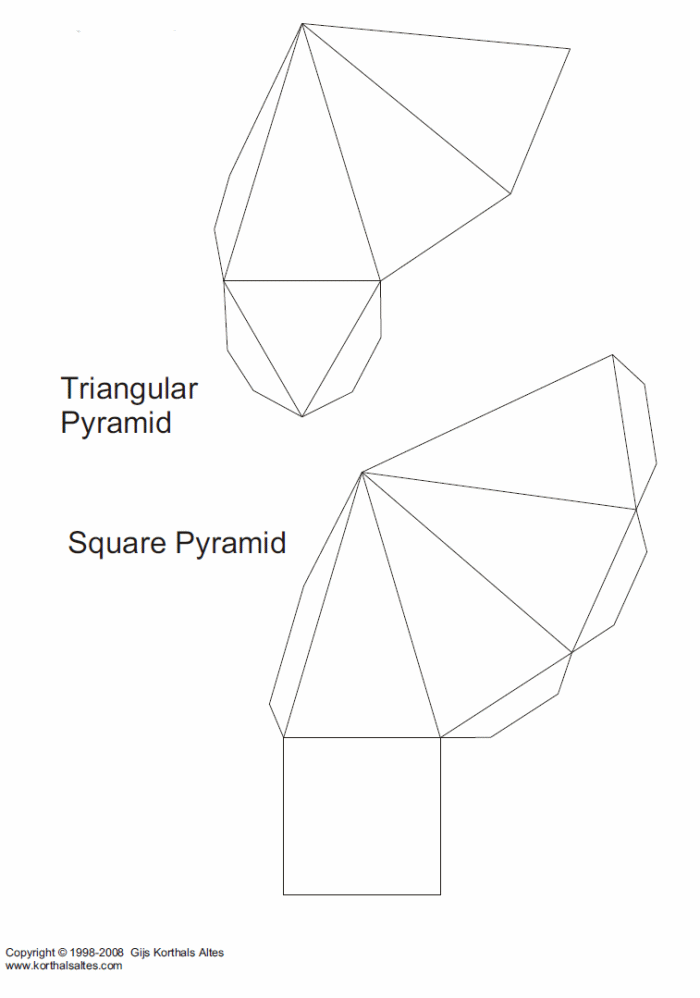 3. Несмотря на то, что для метода в [7] требуется ряд определяемых пользователем параметров и пороговых значений, AQVT не требует никакого пользовательского ввода, кроме сегментированных срезов ячеек с разреженной выборкой для реконструкции, что делает настоящий метод менее двусмысленным и простым для понимания. использовать. Можно показать, что при очень специфических критериях [7] может давать результаты, аналогичные предлагаемому методу, который подробно обсуждается в разделе 4.2.3.
3. Несмотря на то, что для метода в [7] требуется ряд определяемых пользователем параметров и пороговых значений, AQVT не требует никакого пользовательского ввода, кроме сегментированных срезов ячеек с разреженной выборкой для реконструкции, что делает настоящий метод менее двусмысленным и простым для понимания. использовать. Можно показать, что при очень специфических критериях [7] может давать результаты, аналогичные предлагаемому методу, который подробно обсуждается в разделе 4.2.3.
Формулировка проблемы
2.1 Цель
Целью настоящей работы является получение полностью автоматизированной 3D-реконструкции/сегментации с клеточным разрешением плотно упакованной анизотропно растущей ткани на основе первоначальных 2D-сегментаций и соответствий срезов с разреженной Z-выборкой конфокальных срезов изображения.
2.2 Исследовательские проблемы и вклад
Существует несколько методов оценки формы и размера отдельных клеток, таких как метод импеданса [8] и методы световой микроскопии [9]. Методы, подобные [10], используются для изучения изменений размеров клеток в клеточных монослоях. В живых растительных тканях ряд работ был посвящен реконструкции поверхности [11], [12]. Но мы рассматриваем гораздо более сложную задачу, где предметом исследования является плотное скопление клеток. Меристема растений является одним из примеров таких скоплений клеток, где сотни мелких клеток плотно упакованы в многослойную структуру (рис. 1).В таких случаях в настоящее время наиболее популярной практикой является использование конфокальной лазерной сканирующей микроскопии (CLSM) для визуализации срезов клеток или ядер с очень высоким пространственным разрешением, а затем реконструкция трехмерного объема клеток из этих последовательных оптических срезов. которая оказалась достаточно точной [13]–[15].
Методы, подобные [10], используются для изучения изменений размеров клеток в клеточных монослоях. В живых растительных тканях ряд работ был посвящен реконструкции поверхности [11], [12]. Но мы рассматриваем гораздо более сложную задачу, где предметом исследования является плотное скопление клеток. Меристема растений является одним из примеров таких скоплений клеток, где сотни мелких клеток плотно упакованы в многослойную структуру (рис. 1).В таких случаях в настоящее время наиболее популярной практикой является использование конфокальной лазерной сканирующей микроскопии (CLSM) для визуализации срезов клеток или ядер с очень высоким пространственным разрешением, а затем реконструкция трехмерного объема клеток из этих последовательных оптических срезов. которая оказалась достаточно точной [13]–[15].
Рисунок 1. Апикальная меристема побега (SAM): многослойный кластер клеток.
(A) SAM, расположенный в верхней части побега Arabidopsis, (B) Детальный вид поверхности, показывающий различные области SAM, (C1–C3) Три последовательных среза SAM, каждый на расстоянии м друг от друга, полученные с помощью метода CLSM, ( D) Вид сбоку в поперечном сечении SAM, на котором четко видны несколько слоев (L1, L2, L3) плотно упакованных стволовых клеток и их формы (E1–E3).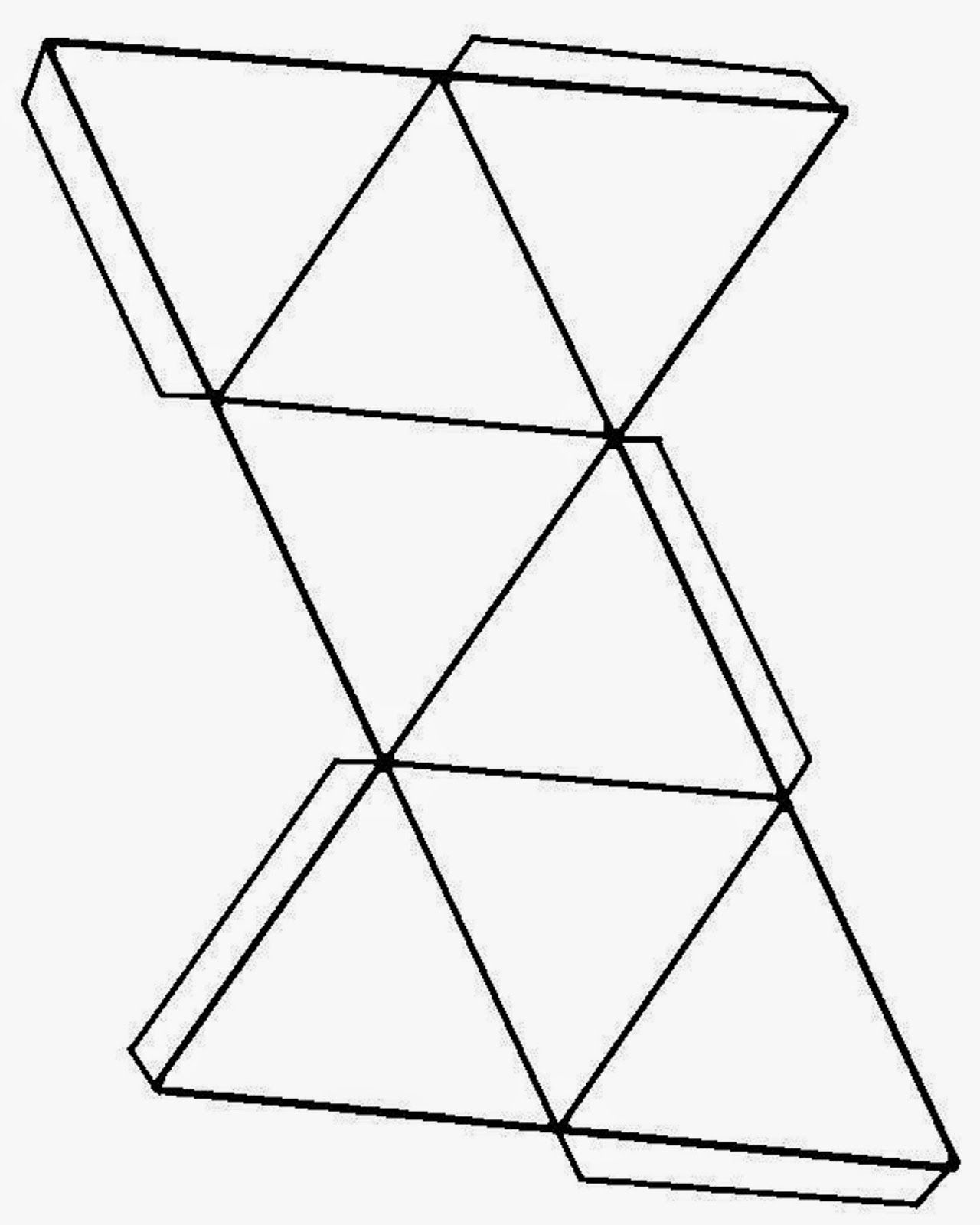 Видимые клеточные стенки отдельных клеток в 3 последовательных срезах с разреженной выборкой. SAM, полученный из набора данных 3D CLSM в реальном времени.
Видимые клеточные стенки отдельных клеток в 3 последовательных срезах с разреженной выборкой. SAM, полученный из набора данных 3D CLSM в реальном времени.
https://doi.org/10.1371/journal.pone.0067202.g001
Однако производительность современных методов трехмерной реконструкции на основе изображений сильно зависит от наличия большого количества очень тонких оптических срезов клетки и производительности. быстро ухудшается в тех случаях, когда количество клеточных срезов становится ограниченным. Эта проблема очень распространена, особенно при визуализации живых клеток на основе CLSM , когда промежуток времени между последовательными наблюдениями невелик.Чтобы сохранить жизнь и рост клеток в течение более длительного периода времени и получить частые наблюдения, клетка не может быть изображена более чем в 2–4 срезах, т. Е. Одновременно нельзя достичь высокого разрешения по глубине и времени.
Самый последний метод [14] точно реконструирует апикальную меристему побега арабидопсиса.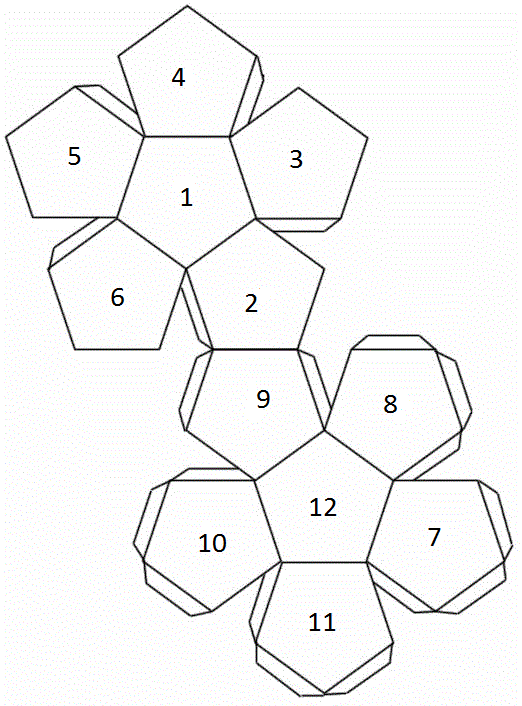 В этом методе используется набор данных, содержащий изображения мелких срезов, полученные под 3 разными углами, каждый с Z-разрешением 1 м. Они сообщили о 24 часах как временном разрешении при визуализации.Но для анализа динамики роста клеточных кластеров, где временной интервал между последовательными клеточными делениями находится в диапазоне от 30 до 36 часов, нам нужно гораздо более высокое временное разрешение при визуализации, чтобы зафиксировать точную динамику роста. Чтобы получить более длинные клеточные линии с высоким временным разрешением, нам, возможно, придется пожертвовать пространственным разрешением или разрешением по глубине, и, следовательно, количество срезов изображения, в которых присутствует клетка, может быть очень маленьким. С таким ограниченным объемом данных изображения существующие методы трехмерной реконструкции/сегментации не могут дать хорошую оценку формы клетки.В настоящей работе мы обратились к этой проблеме реконструкции растительных клеток в ткани, когда количество срезов изображения на ячейку очень ограничено.
В этом методе используется набор данных, содержащий изображения мелких срезов, полученные под 3 разными углами, каждый с Z-разрешением 1 м. Они сообщили о 24 часах как временном разрешении при визуализации.Но для анализа динамики роста клеточных кластеров, где временной интервал между последовательными клеточными делениями находится в диапазоне от 30 до 36 часов, нам нужно гораздо более высокое временное разрешение при визуализации, чтобы зафиксировать точную динамику роста. Чтобы получить более длинные клеточные линии с высоким временным разрешением, нам, возможно, придется пожертвовать пространственным разрешением или разрешением по глубине, и, следовательно, количество срезов изображения, в которых присутствует клетка, может быть очень маленьким. С таким ограниченным объемом данных изображения существующие методы трехмерной реконструкции/сегментации не могут дать хорошую оценку формы клетки.В настоящей работе мы обратились к этой проблеме реконструкции растительных клеток в ткани, когда количество срезов изображения на ячейку очень ограничено.
Существует принципиальное различие между рассматриваемой задачей сегментации и классической схемой трехмерной сегментации. Классический метод решает проблему сегментации с использованием интенсивности пикселей и не может работать, когда информация об интенсивности не предоставляется для большинства 3D-пикселей изображения. В таких ситуациях наиболее интуитивно понятным способом выполнения сегментации является сначала сегментация участков изображения с известной информацией об интенсивности с использованием классической схемы сегментации, а затем экстраполяция между этими разреженными сегментами с использованием известной геометрической модели или функции, которая может быть общей. или специфичные для данных.В этой работе мы показали, что квадратичная мозаика Вороного является очень точным выбором для такой геометрической модели для сегментации ткани с анизотропно растущими плотно упакованными клетками, начиная с разреженного набора 2D-сегментированных срезов водораздела на ячейку.
Апикальная меристема побегов представляет собой многослойную многоклеточную структуру, в которой клетки плотно упакованы, и между ними почти нет пустот. Вдохновленные этой физической структурой SAM, мы предлагаем нашу новую трехмерную реконструкцию с разрешением ячеек в рамках геометрической тесселяции.Мозаика — это разделение пространства на замкнутые геометрические области без перекрытия или промежутка между этими областями. В случае ткани SAM каждая клетка представлена такой замкнутой областью, и любая точка в трехмерной структуре SAM должна быть частью одной и только одной клетки. Фактически, в литературе есть несколько недавних работ, таких как [5], в которых предсказывается, что трехмерные структуры SAM-клеток арабидопсиса могут быть представлены выпуклыми многогранниками, образующими трехмерную мозаику «Вороного».
Мозаика Вороного — это одна из простейших форм разбиения метрического пространства, где границы между двумя соседними разбиениями равноудалены от точки внутри каждой из этих областей, также известной как «сайты». В [5], [6] эти участки являются приблизительными положениями центра клеточных ядер, вокруг которых ткань разбивается на отдельные клетки. Однако в этой работе использовался набор данных, в котором как плазматическая мембрана, так и ядро каждой клетки помечены флуоресцентным белком, тогда как в нашем случае под конфокальным микроскопом видна только плазматическая мембрана.
В [5], [6] эти участки являются приблизительными положениями центра клеточных ядер, вокруг которых ткань разбивается на отдельные клетки. Однако в этой работе использовался набор данных, в котором как плазматическая мембрана, так и ядро каждой клетки помечены флуоресцентным белком, тогда как в нашем случае под конфокальным микроскопом видна только плазматическая мембрана.
В этой работе мы представляем и оцениваем полностью автоматизированную структуру трехмерной реконструкции с разрешением клеток для реконструкции SAM Arabidopsis, где количество срезов конфокального изображения на ячейку очень ограничено.Платформа состоит из различных модулей, таких как сегментация ячеек, пространственное отслеживание ячеек, реконструкция поверхности SAM и, наконец, модуль 3D-тесселяции. Мы оцениваем модель мозаики Вороного, основанную на евклидовом расстоянии, на нашем наборе данных, а затем, исходя из ее ограничений, мы продолжаем предлагать анизотропную мозаику Вороного, основанную на квадратичном расстоянии, где метрика расстояния для каждой ячейки оценивается из сегментированных и отслеживаемых разреженных точек данных для клетка.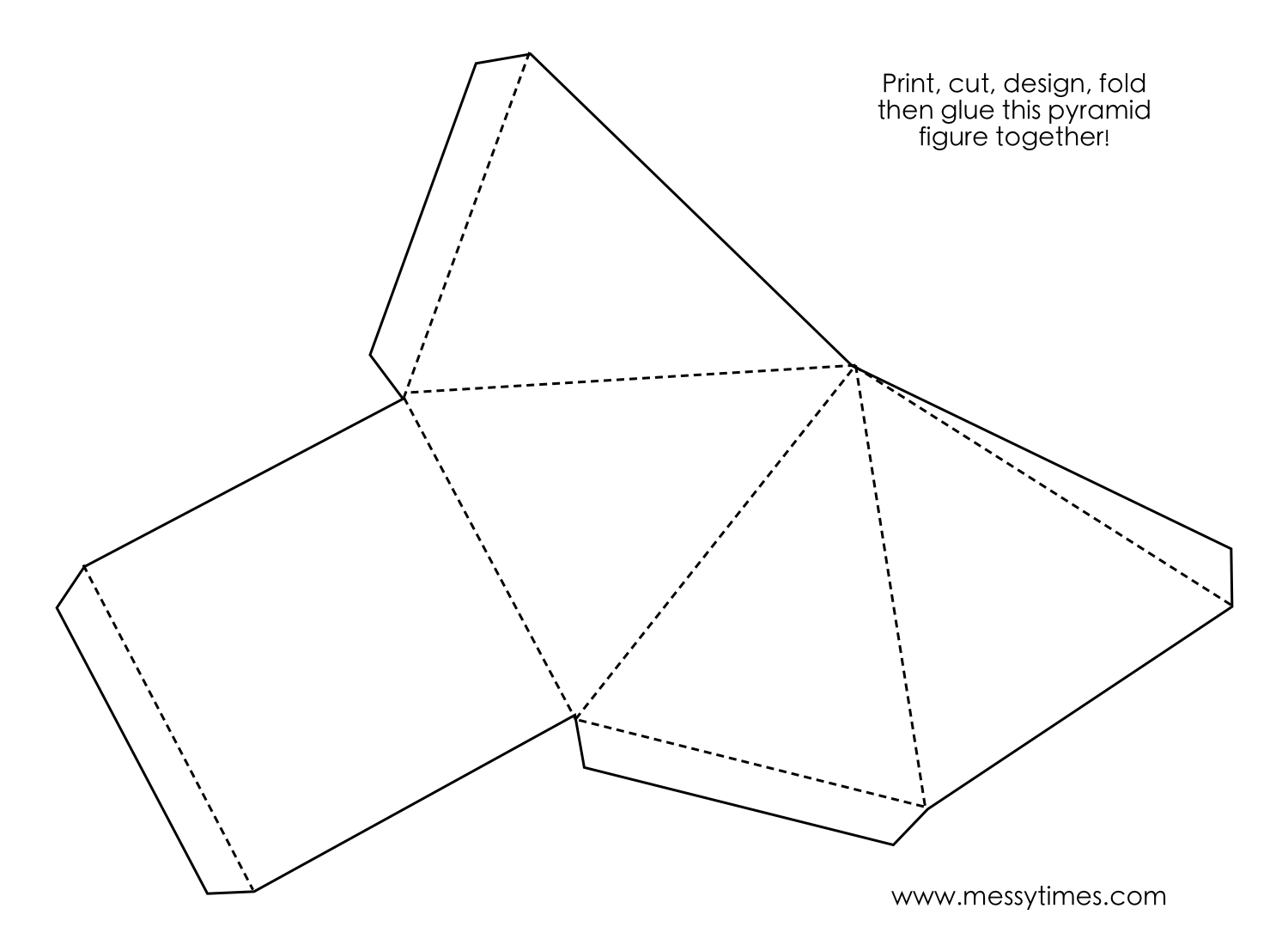 Этот метод применим к плотно упакованным многоклеточным тканям и может быть использован для реконструкции тканей без пустот между клетками с достаточно высокой точностью.Обратите внимание, что для предлагаемого модуля трехмерной реконструкции мы начинаем с нескольких точек данных в каждой сегментированной ячейке, которые предварительно кластеризуются с помощью метода отслеживания ячеек (т. е. неполной сегментации трехмерного изображения), тогда как окончательный результат нашего алгоритма представляет собой полную мозаику всей трехмерной структуры SAM, где каждая ячейка представлена очень плотным облаком точек. Эти облака точек для отдельных ячеек можно визуализировать с помощью трехмерных выпуклых многогранников, которые приблизительно соответствуют форме ячеек.
Этот метод применим к плотно упакованным многоклеточным тканям и может быть использован для реконструкции тканей без пустот между клетками с достаточно высокой точностью.Обратите внимание, что для предлагаемого модуля трехмерной реконструкции мы начинаем с нескольких точек данных в каждой сегментированной ячейке, которые предварительно кластеризуются с помощью метода отслеживания ячеек (т. е. неполной сегментации трехмерного изображения), тогда как окончательный результат нашего алгоритма представляет собой полную мозаику всей трехмерной структуры SAM, где каждая ячейка представлена очень плотным облаком точек. Эти облака точек для отдельных ячеек можно визуализировать с помощью трехмерных выпуклых многогранников, которые приблизительно соответствуют форме ячеек.
2.3 Организация
Остальная часть статьи организована следующим образом. Разделы 3.1 и 3.2 описывают обзор нашего подхода и проблемы, связанные с его различными этапами. Математические и алгоритмические детали предлагаемого метода реконструкции представлены в разделах 4. 1 и 4.2. Наконец, мы представляем экспериментальные результаты и проверку нашего подхода с последующим заключительным обсуждением.
1 и 4.2. Наконец, мы представляем экспериментальные результаты и проверку нашего подхода с последующим заключительным обсуждением.
Обзор предлагаемого метода
Чтобы правильно понять проблемы исследования и наш вклад, мы сначала объясним данные (раздел 3.1). Мы также кратко опишем необходимые этапы предварительной обработки, такие как сегментация ячеек и отслеживание ячеек, которые генерируют окончательную структуру данных в качестве входных данных для конвейера 3D-реконструкции.
3.1 Настройка визуализации и предварительная обработка
SAM Arabidopsis Thaliana состоит примерно из 500 клеток, и они организованы в несколько слоев клеток, которые клонально отличаются друг от друга. Изменяя глубину фокальной плоскости, CLSM может создавать изображения в фокусе с различной глубины образца.Чтобы сделать клетки видимыми под лазером, используются флуоресцентные красители. Набор изображений, полученных таким образом в каждый момент времени, составляет трехмерный стек, также известный как «Z-стек». Каждый Z-стек визуализируется через определенный интервал времени (например, 3 часа между последовательными наблюдениями) и состоит из серии оптических сечений SAM, разделенных прибл. 1,5 м (рис. 1). Стандартная апикальная меристематическая клетка побега имеет диаметр около 5–6 мкм, и, следовательно, в большинстве случаев одна клетка не видна более чем на 3–4 срезах, когда ткань скудно визуализируется на 1.5 м, чтобы избежать фотодинамического повреждения клеток. Чтобы учесть любой незначительный сдвиг в выравнивании изображений в трехмерном стеке, каждый стек регистрируется методом максимизации взаимной информации [16].
Каждый Z-стек визуализируется через определенный интервал времени (например, 3 часа между последовательными наблюдениями) и состоит из серии оптических сечений SAM, разделенных прибл. 1,5 м (рис. 1). Стандартная апикальная меристематическая клетка побега имеет диаметр около 5–6 мкм, и, следовательно, в большинстве случаев одна клетка не видна более чем на 3–4 срезах, когда ткань скудно визуализируется на 1.5 м, чтобы избежать фотодинамического повреждения клеток. Чтобы учесть любой незначительный сдвиг в выравнивании изображений в трехмерном стеке, каждый стек регистрируется методом максимизации взаимной информации [16].
Поскольку нас интересует вычисление объема каждой ячейки в кластере ячеек SAM, нам нужно сегментировать все ячейки в каждом срезе. Мы можем использовать различные алгоритмы сегментации, такие как Watershed [17], сегментация Level-Set [1] и т. д., которые имеют свои преимущества и недостатки.Хотя метод, который мы предлагаем здесь, не зависит от выбранной нами стратегии сегментации, мы предпочли Watershed [18] сегментации с набором уровней, поскольку она дает более точные и реалистичные границы ячеек для наших конфокальных данных SAM.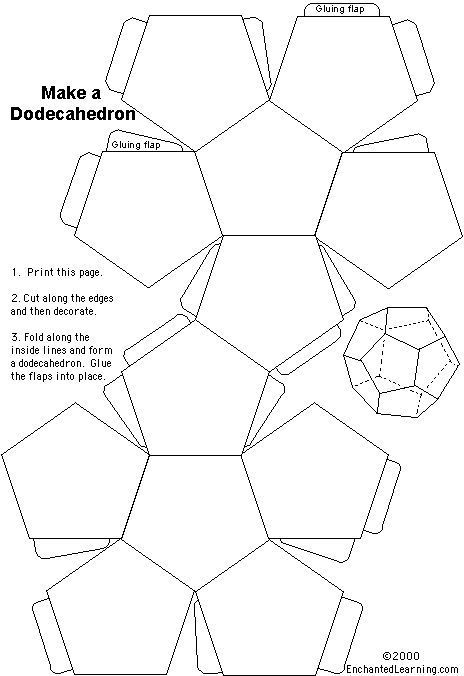 Обратите внимание, что вклад нашего метода заключается в пост-сегментации и этапе отслеживания, хотя более качественные сегментированные данные гарантированно улучшат производительность как методов отслеживания, так и методов 3D-реконструкции.
Обратите внимание, что вклад нашего метода заключается в пост-сегментации и этапе отслеживания, хотя более качественные сегментированные данные гарантированно улучшат производительность как методов отслеживания, так и методов 3D-реконструкции.
Чтобы найти соответствие ячейки в нескольких срезах как в пространственном, так и во временном направлении, мы использовали наш надежный алгоритм отслеживания ячеек, основанный на совпадении локального графа [4], [19].Этот алгоритм начинается с нахождения пары исходных ячеек между двумя изображениями срезов SAM с использованием «сопоставления локального графа» и постепенно перемещается наружу от исходной пары для получения соответствий между соседними ячейками, пока все ячейки не будут отслежены. Этот метод надежен, потому что он объединяет результаты отслеживания по всему стеку 4-D изображений и, таким образом, сводит к минимуму вероятность потери ячейки в любом из срезов, вызванную плохой сегментацией зашумленных данных. Еще одно преимущество заключается в возможности пакетной обработки этого метода, которая позволяет нам реконструировать большое количество ячеек SAM за раз.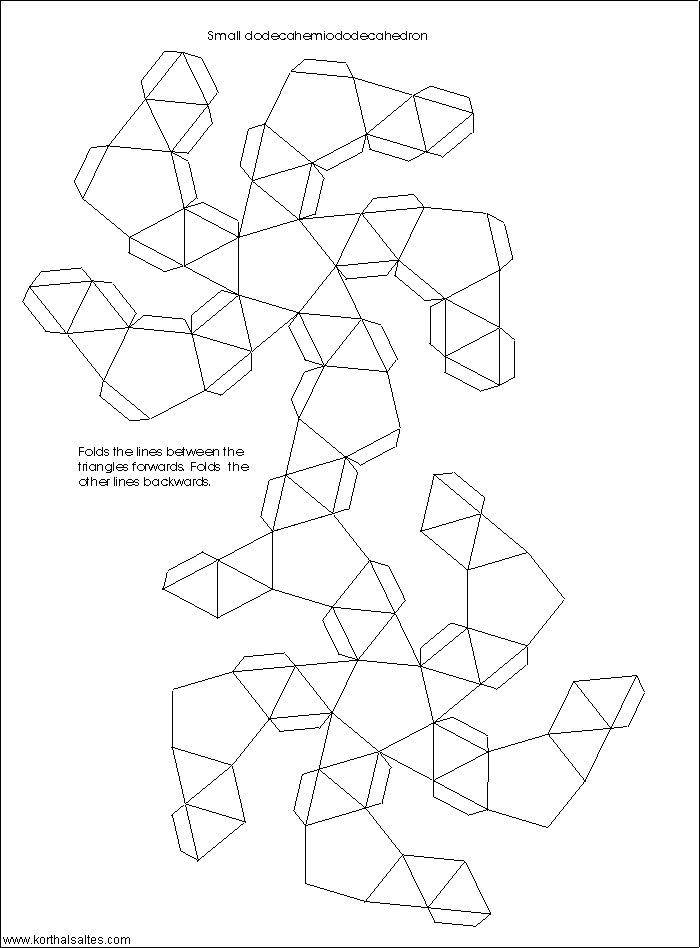
3.2 Предлагаемая 3D-реконструкция — обзор
После того, как фрагменты разреженного изображения сегментированы и отслежены для создания начальной кластеризации отдельных фрагментов клеток, цель состоит в том, чтобы получить полные трехмерные реконструкции этих клеток. Как объяснялось выше, для живого изображения с частыми наблюдениями во времени количество срезов, в которых может присутствовать конкретная клетка, очень мало (например, 2–4 среза на ячейку). К сожалению, существующие методы трехмерной реконструкции не способны справиться с такой разреженностью данных.Руководствуясь физическими структурами клеток, мы решаем эту проблему, предполагая априорную геометрическую трехмерную мозаичную модель ткани, параметры которой, по оценкам, соответствуют заданному разреженному набору сегментированных изображений поперечного сечения.
В работах [5], [6] авторы использовали стандартный метод тесселяции Вороного для оценки границ клеток по известной информации о расположении ядра для отдельных клеток.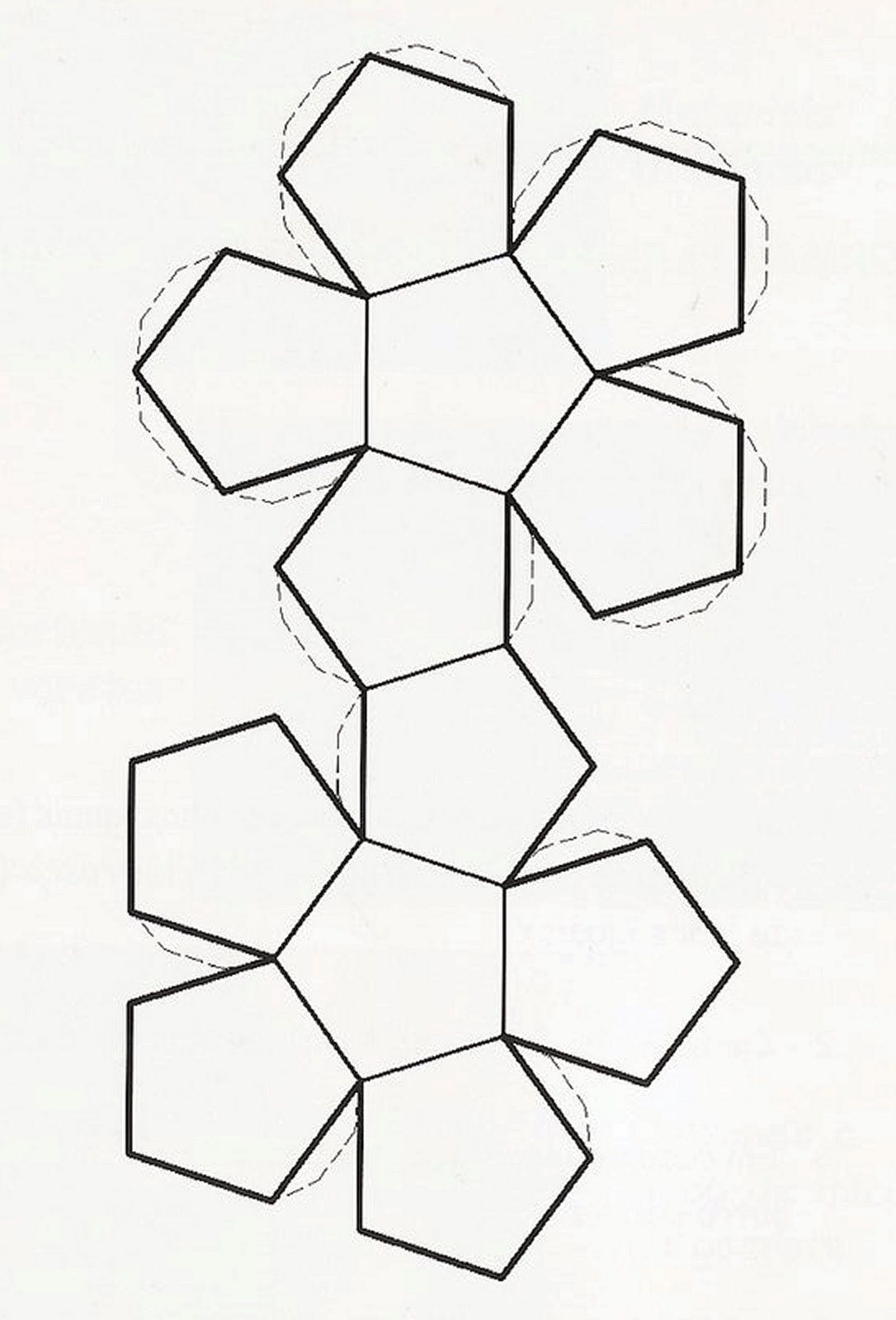 Вдохновленные их работой, мы сначала показываем, как тесселяцию Вороного можно подогнать к нашему набору данных CLSM, который имеет только частичную информацию о клеточных стенках (раздел 4.1.1, раздел 4.1.2). В отличие от набора данных, использованного в [5], [6], в нашем наборе данных не отмечены ядра клеток. Стандартная аффинная тесселяция Вороного не всегда достаточно точна для реконструкции клеток в SAM, поскольку разные клетки в ткани могут иметь очень разные размеры, а соседние клетки могут не иметь изотропных направлений роста. Это побуждает нас предложить анизотропную модель мозаики Вороного (раздел 4.2) для ткани, которая также является обобщением стандартной аффинной мозаики Вороного.Мы покажем, как оценить параметры (раздел 4.2.1) анизотропной или квадратичной функции расстояния для отдельных ячеек по разреженным точкам данных на границах этих ячеек. Предлагаемый подход к квадратичной мозаике Вороного, называемый «Адаптивная квадратичная мозаика Вороного» (AQVT), затем используется для кластеризации плотного облака точек, полученного из предполагаемой трехмерной поверхности SAM, и, таким образом, для создания окончательных трехмерных форм каждого человека.
Вдохновленные их работой, мы сначала показываем, как тесселяцию Вороного можно подогнать к нашему набору данных CLSM, который имеет только частичную информацию о клеточных стенках (раздел 4.1.1, раздел 4.1.2). В отличие от набора данных, использованного в [5], [6], в нашем наборе данных не отмечены ядра клеток. Стандартная аффинная тесселяция Вороного не всегда достаточно точна для реконструкции клеток в SAM, поскольку разные клетки в ткани могут иметь очень разные размеры, а соседние клетки могут не иметь изотропных направлений роста. Это побуждает нас предложить анизотропную модель мозаики Вороного (раздел 4.2) для ткани, которая также является обобщением стандартной аффинной мозаики Вороного.Мы покажем, как оценить параметры (раздел 4.2.1) анизотропной или квадратичной функции расстояния для отдельных ячеек по разреженным точкам данных на границах этих ячеек. Предлагаемый подход к квадратичной мозаике Вороного, называемый «Адаптивная квадратичная мозаика Вороного» (AQVT), затем используется для кластеризации плотного облака точек, полученного из предполагаемой трехмерной поверхности SAM, и, таким образом, для создания окончательных трехмерных форм каждого человека. ячейка (раздел 4.2.2).
ячейка (раздел 4.2.2).
Подробные методы: структура 3D-реконструкции
4.1 3D-реконструкция на основе мозаики Вороного
4.1.1 Краткий обзор тесселяции Вороного и ее свойств.
«Диаграмма Вороного» — это геометрическая диаграмма минимизации, которая разбивает пространство вложения на различные непересекающиеся области. Каждая из этих областей характеризуется порождающей точкой или объектом, также известным как «участок». Все остальные точки в каждой из этих областей ближе к узлу в своем регионе, чем к любому другому узлу во всем пространстве вложения. Близость точек к сайтам вычисляется с использованием метрики расстояния.Участки могут быть разных типов, начиная от точки, линии и заканчивая любой сложной геометрической формой. В зависимости от типа сайтов, метрики расстояния или пространства вложения можно определить несколько различных вариантов диаграммы Вороного. Подробное обсуждение многих таких вариантов можно найти в [20]–[22].
В зависимости от характеристик сайта и функции расстояния геометрическое место точек, равноудаленных от двух соседних сайтов (также называемых «биссектрисами» или «ребрами»), может быть гиперплоскостями или гиперповерхностями более высокого порядка.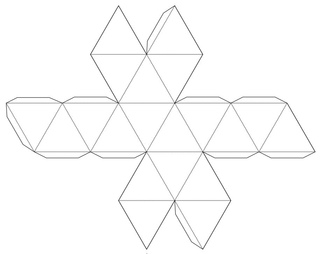 Мы называем диаграммы Вороного с гиперплоскими биссектрисами «аффинными диаграммами Вороного». Наиболее распространенным примером такой аффинной диаграммы является диаграмма точек Вороного, основанная на евклидовой метрике расстояния.
Мы называем диаграммы Вороного с гиперплоскими биссектрисами «аффинными диаграммами Вороного». Наиболее распространенным примером такой аффинной диаграммы является диаграмма точек Вороного, основанная на евклидовой метрике расстояния.
Пусть в пространстве есть точечные узлы и множество всех узлов равно . Области Вороного, связанные с этими сайтами, представлены как где, (1) где полуплоскость определяется как,
(2) Расстояние для стандартной диаграммы Вороного — это евклидово расстояние, определяемое
.Опять же, множество всех точек на биссектрисе между двумя областями Вороного и определяется как, (3)
Ниже приведены некоторые свойства диаграммы Вороного, основанной на евклидовом расстоянии, с точечными узлами:
- Линия, соединяющая любые две точки Вороного и всегда перпендикулярная биссектрисе/ребру Вороного ,
- Перпендикулярные расстояния от и до равны друг другу,
- Любая точка удовлетворяла бы
и - Полученные таким образом области Вороного представляют собой выпуклые многогранники и могут быть выражены как пересечение конечного числа открытых или замкнутых полупространств.

На рис. 2(A) мы показали некоторые свойства двумерной мозаики Вороного с двадцатью одним сайтом (и т. д.). Можно заметить, что каждая из этих областей Вороного представляет собой выпуклый многоугольник.
Рис. 2. Схематическое изображение мозаики Вороного и оценочные центроиды ячеек SAM в качестве участков Вороного.
(A) Диаграмма Вороного, основанная на метрике евклидова расстояния для двадцати одного сайта в 2D. На рисунках также видно, что ребра Вороного перпендикулярны линии, соединяющей любые два соседних узла.являются тремя ребрами Вороного и являются их серединными перпендикулярами соответственно. (B) Центроиды оцениваются примерно для двухсот клеток в ткани SAM, которые также являются участками мозаики Вороного, основанной на евклидовом расстоянии.
https://doi.org/10.1371/journal.pone.0067202.g002
4.1.2 Оценка участков Вороного по разреженным данным.
После сегментации и отслеживания нам дается разреженный набор трехмерных точек данных, которые лежат на границе между соседними ячейками.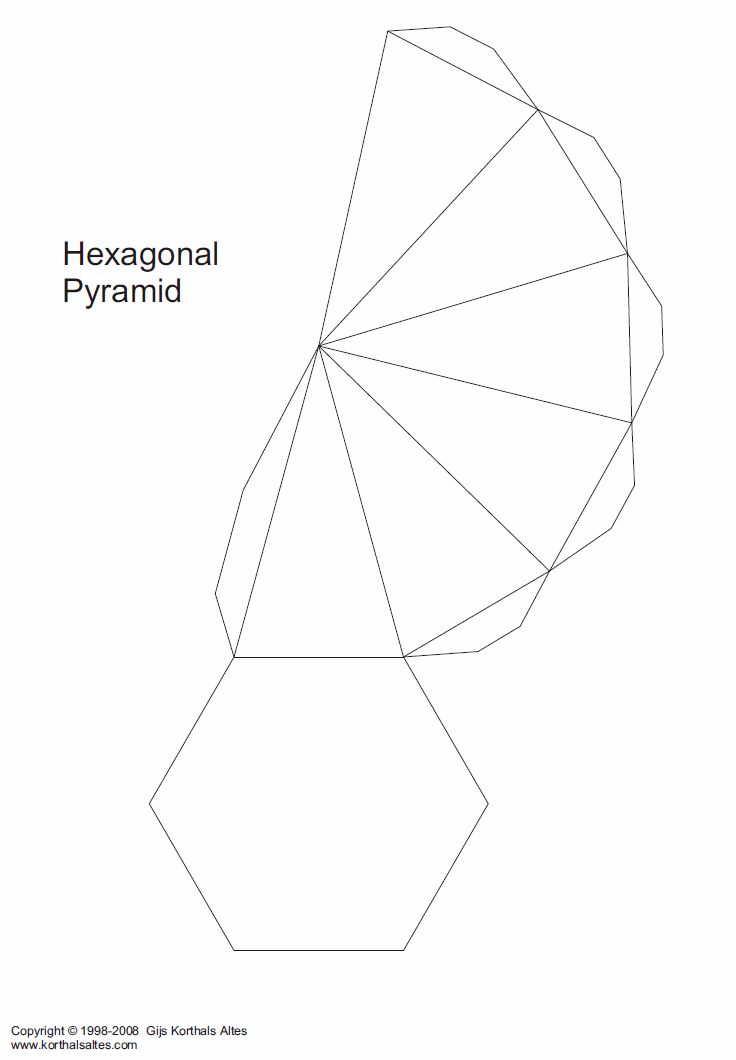 Наша цель состоит в том, чтобы подобрать мозаику Вороного к этим точкам данных, чтобы получить полные структуры отдельных ячеек, представленных в виде многогранников Вороного в 3D. Следовательно, в идеале разреженные точки данных должны лежать на биссектрисе между соседними областями Вороного. Учитывая очень разреженный набор точек данных на биссектрисе, как в случае «визуализации живых клеток», единственный способ восстановить диаграмму Вороного состоит в том, чтобы сначала оценить приблизительное местоположение сайтов Вороного, из которых ребра/биссектрисы Вороного могут быть затем вычисляться.
Наша цель состоит в том, чтобы подобрать мозаику Вороного к этим точкам данных, чтобы получить полные структуры отдельных ячеек, представленных в виде многогранников Вороного в 3D. Следовательно, в идеале разреженные точки данных должны лежать на биссектрисе между соседними областями Вороного. Учитывая очень разреженный набор точек данных на биссектрисе, как в случае «визуализации живых клеток», единственный способ восстановить диаграмму Вороного состоит в том, чтобы сначала оценить приблизительное местоположение сайтов Вороного, из которых ребра/биссектрисы Вороного могут быть затем вычисляться.
При заданном наборе генерирующих сайтов построение диаграммы Вороного может быть выполнено с помощью нескольких методов, наиболее популярным из которых является алгоритм Fortune «sweep line». Однако обратная задача, т. е. получение местоположений узлов по биссектрисе Вороного, в литературе изучена меньше. В [23] Эванс и др. предложил линейный метод наименьших квадратов для оценки сайтов Вороного путем подгонки диаграммы Вороного к заданному шаблону мозаики.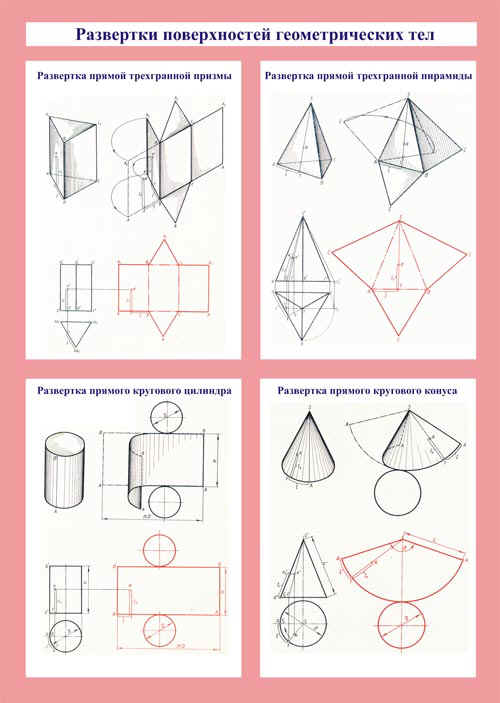 Опять же, в [24] был предложен ряд алгоритмов для получения узлов Вороного по вершинам многоугольников Вороного.Но ни один из этих методов не применим к разреженным данным, которые у нас есть. Эти методы требуют знания полных структур многогранников Вороного, что и является тем результатом, который нам нужен. На самом деле, из-за крайней разреженности нашего набора данных практически невозможно получить уникальные оценки участков Вороного для отдельных 3D-ячеек.
Опять же, в [24] был предложен ряд алгоритмов для получения узлов Вороного по вершинам многоугольников Вороного.Но ни один из этих методов не применим к разреженным данным, которые у нас есть. Эти методы требуют знания полных структур многогранников Вороного, что и является тем результатом, который нам нужен. На самом деле, из-за крайней разреженности нашего набора данных практически невозможно получить уникальные оценки участков Вороного для отдельных 3D-ячеек.
В этой ситуации знание физической структуры стволовых клеток ПАМ помогает нам получить приблизительное расположение сайтов Вороного, где каждая клетка представлена как область Вороного.В работе [6] авторы заметили, что ПАМ-клетки можно представить в виде областей Вороного, сайты которых расположены приблизительно в центрах клеточных ядер. Это наблюдение, а также тот факт, что ядро, расположенное в центральной области клетки, составляет большую часть размера SAM-клетки, побуждает нас разработать простую стратегию для оценки приблизительного местоположения сайтов, даже когда ядра не отображается в стеке конфокальных изображений.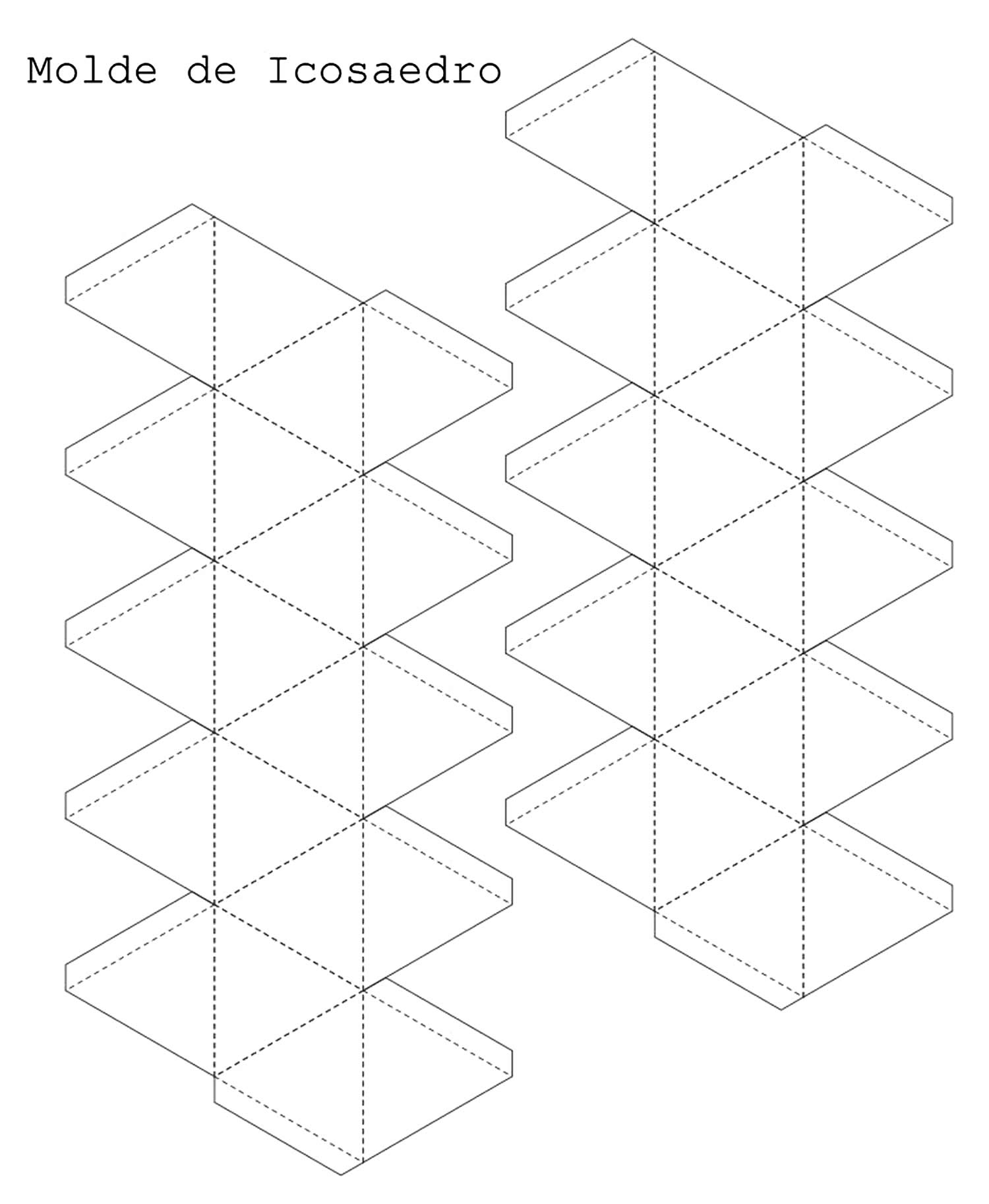
Учитывая, что разреженный набор точек на сегментированном и отслеживаемом срезах ячейки (набор трехмерных данных ), приблизительное положение центроида ячейки будет , где элементы являются средними арифметическими значениями и соответственно.Таким образом, также оценивается приблизительное местоположение участка, соответствующего району Вороного, представляющего ячейку . Центроиды приблизительно для 200 клеток из ткани SAM показаны на рисунке 2(B).
Теперь следующим шагом будет создание плотного облака точек, отобранных из структуры SAM, и кластеризация этого плотного набора трехмерных точек данных в различные области Вороного (представляющие отдельные ячейки) на основе предполагаемого местоположения участков.
4.1.3 Создание плотного облака точек для разделения на ячейки: глобальная форма SAM.
На этом этапе мы оцениваем трехмерную структуру SAM, подгоняя гладкую поверхность к ее сегментированным контурам. Подгонка поверхности выполняется в два этапа. На первом этапе граница SAM в каждом фрагменте изображения извлекается с использованием метода «Набор уровней» (рис. 3 (A)). Множество уровня — это набор точек, в которых функция принимает постоянное значение. Мы инициализируем уровень, установленный на границе среза изображения для каждого поперечного сечения SAM, который ведет себя как активный контур и постепенно сужается к границе SAM.Пусть множество точек на сегментированных контурах ЗУР равно ().
На первом этапе граница SAM в каждом фрагменте изображения извлекается с использованием метода «Набор уровней» (рис. 3 (A)). Множество уровня — это набор точек, в которых функция принимает постоянное значение. Мы инициализируем уровень, установленный на границе среза изображения для каждого поперечного сечения SAM, который ведет себя как активный контур и постепенно сужается к границе SAM.Пусть множество точек на сегментированных контурах ЗУР равно ().
Рис. 3. Генерация плотного облака точек внутри реконструированной поверхности SAM.
(A) Контуры SAM, извлеченные из стека конфокальных изображений с использованием сегментации Level-Set, (B) Поверхность SAM реконструирована с использованием линейной интерполяции в локальной окрестности точек на контурах SAM, (C) Очень плотное облако точек извлекается изнутри реконструированной поверхности SAM, которая с помощью предлагаемого метода реконструкции сгруппирована в отдельные ячейки.
https://doi.org/10. 1371/journal.pone.0067202.g003
1371/journal.pone.0067202.g003
На втором этапе мы подгоняем поверхность к сегментированным точкам. Предполагая, что поверхность может быть представлена в виде (где функция неизвестна), наша цель состоит в том, чтобы предсказать в каждой точке прямоугольной сетки точек с плотной выборкой, ограниченной . Поскольку сегментированный набор точек данных чрезвычайно разрежен, этот прогноз выполняется с использованием линейной интерполяции локального набора точек на сетке вокруг точки.Поскольку значение () для точки аппроксимируется линейной комбинацией значений в нескольких соседних точках сетки, задача интерполяции может быть поставлена как линейная задача оценки методом наименьших квадратов. Мы также налагаем ограничение гладкости в этой оценке, заставляя первые частные производные поверхности, оцениваемые в соседних точках, быть как можно более близкими. Визуализация MATLAB [25] поверхности показана на рисунке 3(B).
После того, как SAM-поверхность () построена, мы равномерно отбираем плотный набор 3D-точек (визуализацию можно найти на рисунке 3(C)), так что каждая точка должна лежать внутри .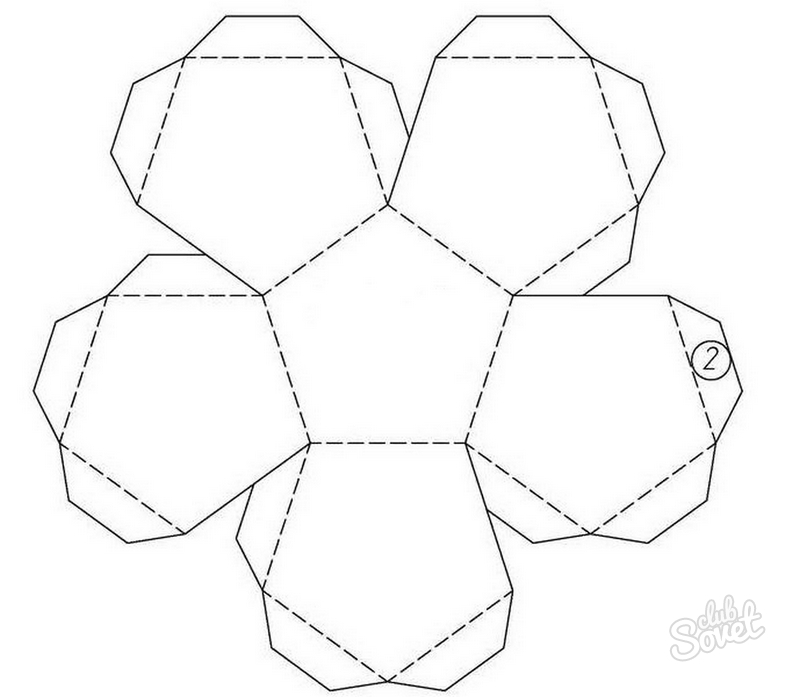 Таким образом, требуемым результатом предлагаемого алгоритма является кластеризация этих плотных точек данных в ячейки/кластеры, начиная с разреженного набора сегментированных и отслеживаемых точек, полученных из изображений конфокальных срезов отдельных ячеек.
Таким образом, требуемым результатом предлагаемого алгоритма является кластеризация этих плотных точек данных в ячейки/кластеры, начиная с разреженного набора сегментированных и отслеживаемых точек, полученных из изображений конфокальных срезов отдельных ячеек.
4.2 Адаптивная квадратичная мозаика Вороного (AQVT) для неоднородных размеров клеток и анизотропии роста клеток
В такой ткани, как SAM, клетки не растут равномерно по всем трем осям (). На самом деле, большинство клеток демонстрируют определенное направление роста.Опять же, соседние клетки SAM, особенно в центральной области (CZ), вряд ли будут расти в одном направлении. Таким образом, даже если мозаика изначально представляет собой аффинную диаграмму Вороного, она вряд ли останется таковой после нескольких стадий роста. Такие случаи неоднородных размеров ячеек и анизотропного роста могут быть отражены в более обобщенной неаффинной тесселяции Вороного, называемой «анизотропными диаграммами Вороного». В наиболее общем виде такой диаграммы для точечных узлов метрика расстояния имеет квадратичный вид с аддитивным весом [22].
Следуя аналогичным обозначениям, использованным в предыдущих разделах, для набора анизотропных сайтов в анизотропная область Вороного для сайта задается формулой, (5) где (6) — положительно определенная симметричная матрица x, связанная с сайтом и . Таким образом, каждая из анизотропных областей Вороного параметризуется триплетом . Далее предположим, что функция расстояния становится равной
.(7)Поскольку биссектрисы такой диаграммы Вороного являются квадратичными гиперповерхностями, эти диаграммы называются «квадратичными диаграммами Вороного», в которых каждая ячейка Вороного параметризуется парами.(8)
Из уравнения (7) видно, что это по существу весовой коэффициент, который неравномерно взвешивает расстояния в каждой области Вороного по каждому измерению. Когда все области Вороного имеют одинаковый и однородный вес по каждой оси, и результирующая диаграмма для точечных узлов становится диаграммой Вороного, основанной на евклидовом расстоянии.
4.
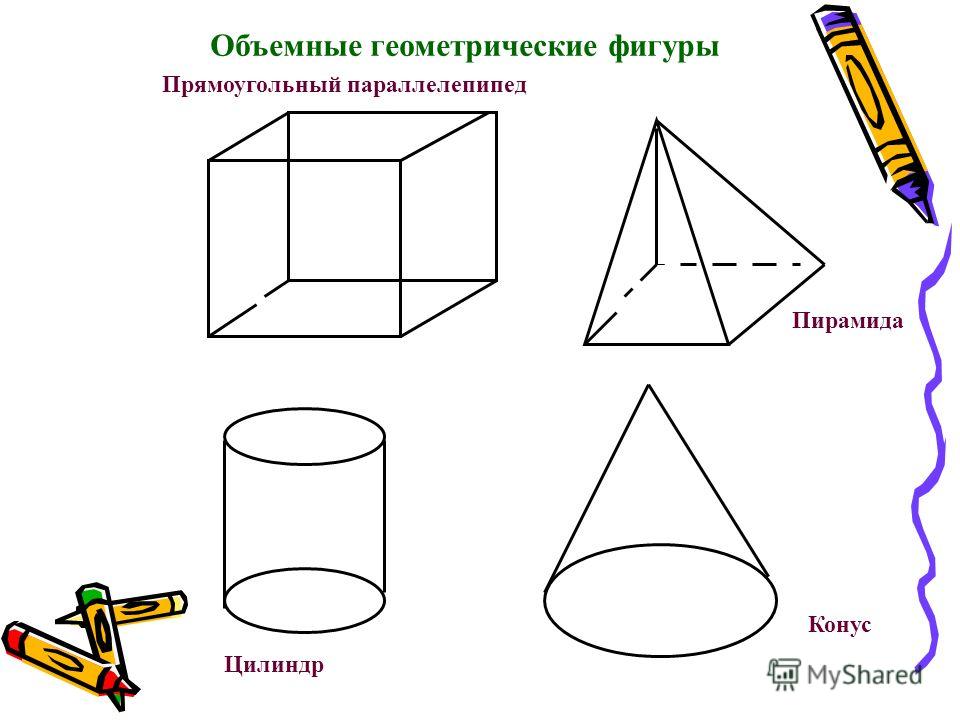 2.1 Оценка метрики расстояния по разреженным данным: минимальный объем, охватывающий эллипсоид.
2.1 Оценка метрики расстояния по разреженным данным: минимальный объем, охватывающий эллипсоид.Теперь проблема состоит в том, чтобы оценить пару параметров для каждой ячейки/квадратичной области Вороного из разреженных точек данных, полученных из сегментированных и отслеживаемых срезов, принадлежащих границе каждой ячейки.Учитывая крайнюю редкость данных, не существует доступного метода, который бы давал s для каждого региона. В этой работе мы предлагаем альтернативный способ оценки пар непосредственно по разреженным точкам данных.
Эллипсоидальная поверхность в 3D задается геометрическим местом точки, которая удовлетворяет (9), где — центр эллипсоида и — положительно определенная симметричная матрица. Для любой точки внутри эллипсоида и для каждой вне его .
Фактически это расстояние Махаланобиса от точки до центра эллипсоида.Следовательно, если точка равноудалена от центров двух эллипсоидов и в смысле Махаланобиса, то (10)
Теперь уравнение (10) дает геометрическое место точек , которое точно такое же, как и у точек на биссектрисе двух соседних квадратичных областей Вороного, параметризованных и . У нас уже есть набор точек (), которые являются редкими, но однородными z-выборками от границ между соседними ячейками. Алгоритм отслеживания предоставляет нам точные пары ячеек, которым принадлежит каждая точка из этого набора.Следовательно, мы можем приблизительно оценить параметры расстояния, связанные с каждой квадратичной областью Вороного индивидуально, подгоняя эллипсоид к разреженным точкам данных, принадлежащим границам этой области. В этой статье мы выбираем подходящие эллипсоиды минимального объема (MVEE) для каждой из ячеек в отдельности и получаем приблизительные оценки . Стратегия оценки описана далее в этом разделе, а подробности можно найти в разделе 3 файла S1.
У нас уже есть набор точек (), которые являются редкими, но однородными z-выборками от границ между соседними ячейками. Алгоритм отслеживания предоставляет нам точные пары ячеек, которым принадлежит каждая точка из этого набора.Следовательно, мы можем приблизительно оценить параметры расстояния, связанные с каждой квадратичной областью Вороного индивидуально, подгоняя эллипсоид к разреженным точкам данных, принадлежащим границам этой области. В этой статье мы выбираем подходящие эллипсоиды минимального объема (MVEE) для каждой из ячеек в отдельности и получаем приблизительные оценки . Стратегия оценки описана далее в этом разделе, а подробности можно найти в разделе 3 файла S1.
Поскольку мы оцениваем параметры квадратичной метрики расстояния, связанной с каждой отдельной ячейкой Вороного в отдельности, а затем используем полученные таким образом метрики расстояния для тесселяции плотного облака точек, мы решили назвать результирующую тесселяцию Вороного «Адаптивная квадратичная тесселяция Вороного».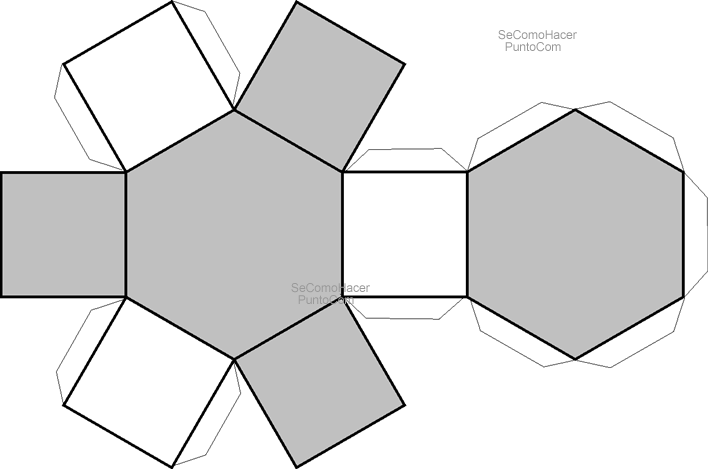 (АКВТ).
(АКВТ).
После регистрации, сегментации и идентификации ячейки в нескольких срезах в трехмерном стеке мы можем получить координаты набора точек по периметру сегментированных срезов клеток. Пусть это множество точек на ячейке будет . Мы должны оценить эллипсоид минимального объема, который охватывает все эти точки в , и мы обозначаем это с . Эллипсоид в форме центра представлен (11) где центр эллипсоида и . Поскольку все точки должны находиться внутри , у нас есть (12) и объем этого эллипсоида
(13)Поэтому задача нахождения эллипсоида минимального объема, охватывающего множество точек, может быть поставлена как(14)
Чтобы эффективно решить Задачу (), мы преобразуем основную задачу в ее двойственную задачу, так как двойную задачу легче решить.Подробный анализ постановки задачи и ее решения можно найти в [26], [27]. При решении этой задачи отдельно для каждого разреженного множества точек параметры квадратичной метрики расстояния оцениваются как . Чтобы визуально представить эти параметры, мы построили эллипсоиды с каждой из этих пар параметров и закодировали их цветом для представления отдельных клеток в ткани SAM (рис. 4).
4).
Рисунок 4. Эллипсоидальное представление параметров AQVT, оцененных по разреженным точкам данных.
(A) Охватывающие эллипсоиды минимального объема, представляющие пары параметров для отдельных ячеек, показаны разными цветами. (B) То же изображение, вид сверху.
https://doi.org/10.1371/journal.pone.0067202.g004
4.2.2 Трехмерная тесселяция на основе оценочных параметров AQVT: окончательные формы ячеек.
Как только параметры квадратичной метрики расстояния будут оценены из предыдущего шага, плотное облако точек, полученное в разделе 4.1.3 можно разделить на разные области Вороного на основе уравнения (8), т.е. плотное облако точек, принадлежащее ячейке, задается как (15)
Для визуализации результатов 3D-реконструкции с разрешением ячеек мы подгоняем выпуклые многогранники для представления каждой ячейки.
4.2.3 Связь между AQVT и тесселяцией на основе деформированного усеченного эллипсоида [7].
В недавней работе [7] мы показали, что трехмерные формы отдельных клеток в плотно упакованной многослойной ткани могут быть аппроксимированы деформированными усеченными эллипсоидальными моделями.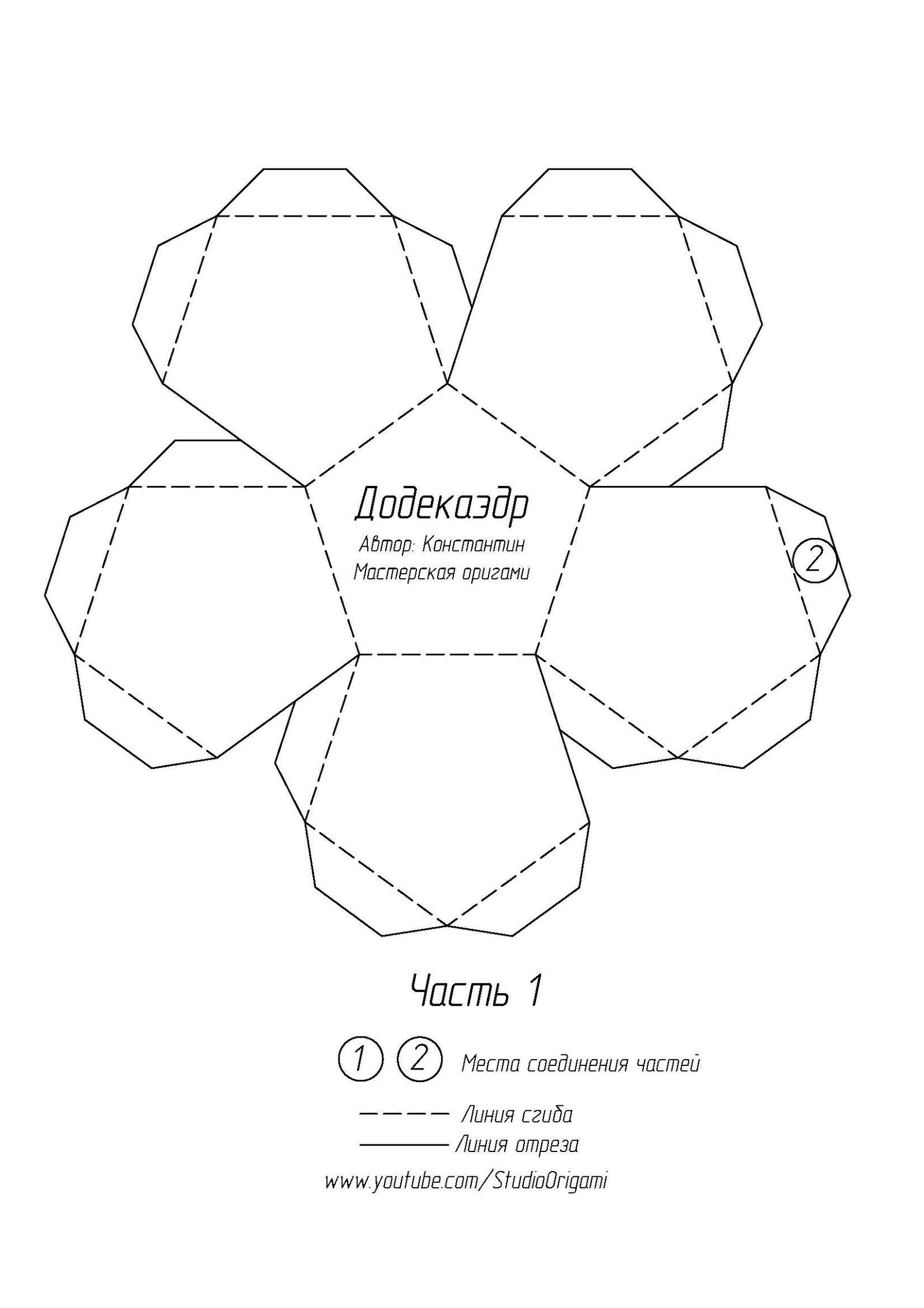 В этой работе сначала окружающие эллипсоиды (MVEE) подгоняются к разреженным точкам данных для каждой ячейки, которые затем рекурсивно деформируются до тех пор, пока не будет удовлетворен определенный критерий остановки (см. [7]), и, наконец, усекаются вдоль перекрывающихся поверхностей. эти трехмерные деформированные эллипсоиды для получения окончательных трехмерных форм ячеек.
В этой работе сначала окружающие эллипсоиды (MVEE) подгоняются к разреженным точкам данных для каждой ячейки, которые затем рекурсивно деформируются до тех пор, пока не будет удовлетворен определенный критерий остановки (см. [7]), и, наконец, усекаются вдоль перекрывающихся поверхностей. эти трехмерные деформированные эллипсоиды для получения окончательных трехмерных форм ячеек.
Следуя тем же обозначениям, которые использовались ранее, оценочные объемлющие эллипсоиды для разреженных наборов точек задаются как . В ходе наших экспериментов мы наблюдали, что наилучшие результаты трехмерной реконструкции достигаются, когда предполагаемые эллипсоиды деформируются вдоль их осей, а деформация вдоль каждой оси на каждом шаге итерации пропорциональна текущей длине осей.Пусть коэффициент, на который деформируется каждая ось, равен и пусть будут итерации до сходимости алгоритма из [7].
Как можно выразить как через разложение по собственным значениям (см. [7]), а деформированное после итераций деформации можно записать как точки на реконструируемой границе ячейки между ячейками и , после шагов итерации будет дано, (16)
Поскольку это скаляр, выражение (16) можно переписать как (17)
Уравнение (17) точно такое же, как набор граничных точек между областями Вороного и для адаптивной квадратичной мозаики Вороного. Таким образом, при описанном выше условии деформации метод, предложенный в [7], и АКВТ дают один и тот же результат тесселяции. Но главное преимущество использования AQVT по сравнению с [7] заключается в том, что AQVT дает результат трехмерной реконструкции за один шаг, тогда как модель деформированного усеченного эллипсоида, описанная в [7], является итеративным процессом. Количество итераций может быть очень большим в зависимости от выбора критерия остановки или размера шага на этапе деформации, и, следовательно, [7] в целом является гораздо более медленным алгоритмом.Кроме того, результаты 3D-реконструкции могут сильно различаться в зависимости от выбранного размера шага деформации в [7], поэтому качество результата реконструкции часто бывает непредсказуемым. Нами экспериментально установлено, что в [7] наименьшая ошибка реконструкции достигается, когда размеры шага деформации для каждой клетки ткани равны или очень близки друг к другу. Это условие, как показано выше, дает нам метрику расстояния AQVT.
Таким образом, при описанном выше условии деформации метод, предложенный в [7], и АКВТ дают один и тот же результат тесселяции. Но главное преимущество использования AQVT по сравнению с [7] заключается в том, что AQVT дает результат трехмерной реконструкции за один шаг, тогда как модель деформированного усеченного эллипсоида, описанная в [7], является итеративным процессом. Количество итераций может быть очень большим в зависимости от выбора критерия остановки или размера шага на этапе деформации, и, следовательно, [7] в целом является гораздо более медленным алгоритмом.Кроме того, результаты 3D-реконструкции могут сильно различаться в зависимости от выбранного размера шага деформации в [7], поэтому качество результата реконструкции часто бывает непредсказуемым. Нами экспериментально установлено, что в [7] наименьшая ошибка реконструкции достигается, когда размеры шага деформации для каждой клетки ткани равны или очень близки друг к другу. Это условие, как показано выше, дает нам метрику расстояния AQVT. Таким образом, AQVT обеспечивает уникальное решение для трехмерной реконструкции и в большинстве случаев гарантированно дает лучший или такой же результат реконструкции по сравнению с [7] при значительно меньшем времени выполнения.Также можно отметить, что предложенный AQVT не требует, чтобы какой-либо выбранный пользователем порог или параметр вводились в структуру реконструкции, что делает метод менее двусмысленным и более удобным для пользователя, чем [7].
Таким образом, AQVT обеспечивает уникальное решение для трехмерной реконструкции и в большинстве случаев гарантированно дает лучший или такой же результат реконструкции по сравнению с [7] при значительно меньшем времени выполнения.Также можно отметить, что предложенный AQVT не требует, чтобы какой-либо выбранный пользователем порог или параметр вводились в структуру реконструкции, что делает метод менее двусмысленным и более удобным для пользователя, чем [7].
Результаты и обсуждение
5.1 Результаты предварительной обработки
Мы протестировали предлагаемый каркас 3D-реконструкции на кластере из примерно двухсот двадцати клеток, охватывающих слои L1 и L2 апикальной меристемы побегов арабидопсиса. Детали создания необработанных данных изображения с использованием метода CLSM описаны в разделе 3.1. Мы использовали модифицированную сегментацию водораздела [18] для сегментации отдельных срезов клеток, и образец сегментированного изображения водораздела показан на рисунке 5 (B) (сырой фрагмент изображения показан на рисунке 5 (A)). На следующем этапе мы сгруппировали срезы, принадлежащие каждой ячейке, используя метод отслеживания ячеек на основе сопоставления локальных графов, описанный в [4]. Пример результата отслеживания показан на рисунке 5(C), где одни и те же клетки отмечены одним и тем же цветом в трех последовательных срезах как в пространственном, так и во временном направлении.После того, как срезы разреженных ячеек сгруппированы вместе, разреженный набор точек данных в каждой ячейке извлекается и используется для оценки приблизительного местоположения сайтов для мозаики Вороного на основе евклидова расстояния или, в случае предлагаемого метода на основе AQVT, сайта и веса. параметры квадратичной метрики расстояния для каждой ячейки.
На следующем этапе мы сгруппировали срезы, принадлежащие каждой ячейке, используя метод отслеживания ячеек на основе сопоставления локальных графов, описанный в [4]. Пример результата отслеживания показан на рисунке 5(C), где одни и те же клетки отмечены одним и тем же цветом в трех последовательных срезах как в пространственном, так и во временном направлении.После того, как срезы разреженных ячеек сгруппированы вместе, разреженный набор точек данных в каждой ячейке извлекается и используется для оценки приблизительного местоположения сайтов для мозаики Вороного на основе евклидова расстояния или, в случае предлагаемого метода на основе AQVT, сайта и веса. параметры квадратичной метрики расстояния для каждой ячейки.
Рис. 5. Сегментация образца и результат пространственно-временного отслеживания.
(A) Необработанный срез конфокального изображения, (B) Сегментированные края ячеек с водоразделом того же изображения на A, (C) Отдельные срезы ячеек отслеживаются по оси z, чтобы найти соответствие между срезами, принадлежащими одним и тем же ячейкам. Ячейки имеют цветовую кодировку на изображении, чтобы показать соответствия. Клетки также можно отслеживать во времени (что показано с использованием одного и того же цветового кода), что может быть полезно при реконструкции одних и тех же клеток в последовательные моменты времени для наблюдения за ростом этих клеток.
Ячейки имеют цветовую кодировку на изображении, чтобы показать соответствия. Клетки также можно отслеживать во времени (что показано с использованием одного и того же цветового кода), что может быть полезно при реконструкции одних и тех же клеток в последовательные моменты времени для наблюдения за ростом этих клеток.
https://doi.org/10.1371/journal.pone.0067202.g005
5.2 Результаты 3D-реконструкции
На рис. 6(A) показана реконструкция разрешения ячейки кластера ячеек в SAM с использованием AQVT. Обратите внимание, что только для 3D-визуализации 3D-структуры мы представили каждую ячейку в виде выпуклого многогранника, соответствующего плотному облаку точек, сгруппированному с ячейками, полученному из нашей схемы 3D-реконструкции/3D-сегментации.Для лучшего понимания трехмерных структур отдельных клеток мы показали реконструированные формы меньшего кластера клеток на рисунке 6 (B).
Рисунок 6. Визуализация трехмерной реконструкции кластера клеток SAM на основе AQVT.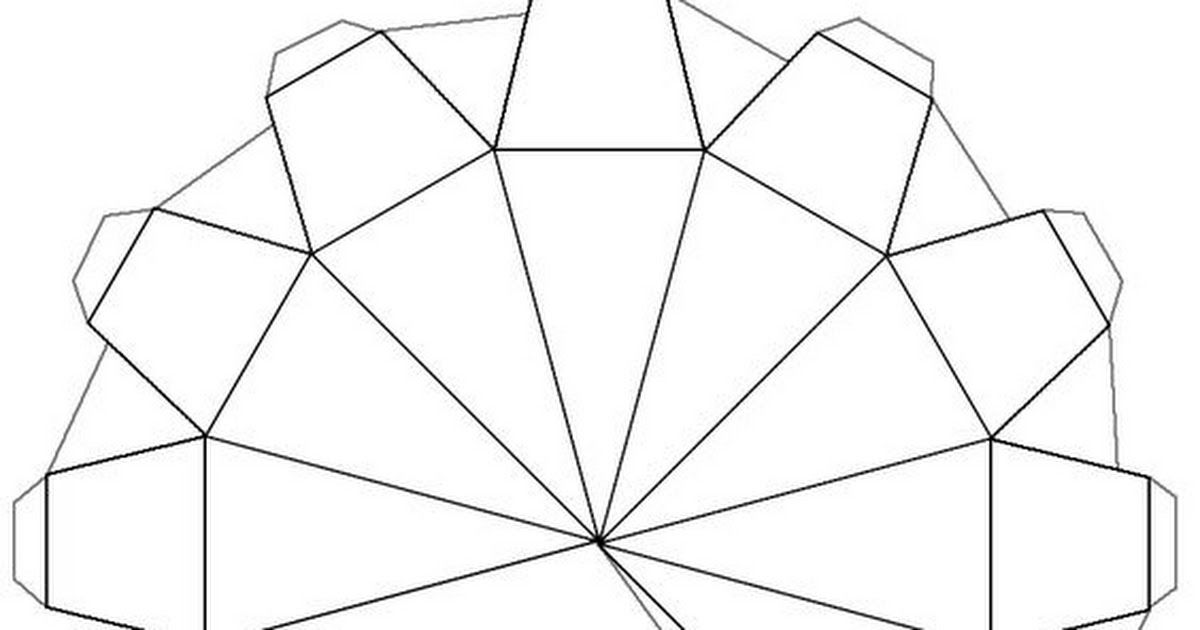
(A) Визуализация реконструированной в 3D структуры кластера из примерно 220 плотно упакованных ячеек с использованием аппроксимации выпуклыми многогранниками плотно сгруппированных точек данных для каждой ячейки, полученной из предложенной схемы трехмерной реконструкции, (B) Подмножество клеток из той же ткани.
https://doi.org/10.1371/journal.pone.0067202.g006
5.3 Валидация предложенного метода
5.3.1 Проверка данных 3D SAM.
Вряд ли существует какой-либо биологический эксперимент, который мог бы напрямую подтвердить предполагаемую статистику роста для отдельных клеток в многослойном кластере с разреженной выборкой. Фактически, отсутствие метода для оценки статистики роста непосредственно с использованием невычислительных методов в рамках биологии развития с визуализацией в реальном времени является мотивом для предлагаемой работы, и нам нужно было разработать метод для вычислительной проверки нашей техники трехмерной реконструкции. Как только 3D-реконструкция достигнута, мы можем с помощью вычислений повторно разрезать реконструированную форму вдоль любой произвольной плоскости просмотра, просто собирая подмножество реконструированного 3D-облака точек, которое лежит на плоскости.
Как только 3D-реконструкция достигнута, мы можем с помощью вычислений повторно разрезать реконструированную форму вдоль любой произвольной плоскости просмотра, просто собирая подмножество реконструированного 3D-облака точек, которое лежит на плоскости.
Чтобы продемонстрировать валидность предложенного нами метода, мы выбрали набор данных с одной временной точкой, относительно плотно отобранный по Z (0,225 м между последовательными срезами). Затем мы передискретизировали этот плотный стек с разрешением 1,35 м, чтобы создать более разреженное подмножество срезов, которые имитируют разреженность, обычно встречающуюся в сценарии прямой визуализации.Срезы с разреженной выборкой для кластера ячеек, охватывающих два слоя (L1 и L2) в SAM, показаны на рисунке 7. Вышеупомянутый метод отслеживания [4] используется для получения соответствий между срезами одних и тех же ячеек. Различные срезы одних и тех же клеток, отображаемые на разных глубинах по Z, показаны с использованием одного и того же номера на рисунке 7 (A).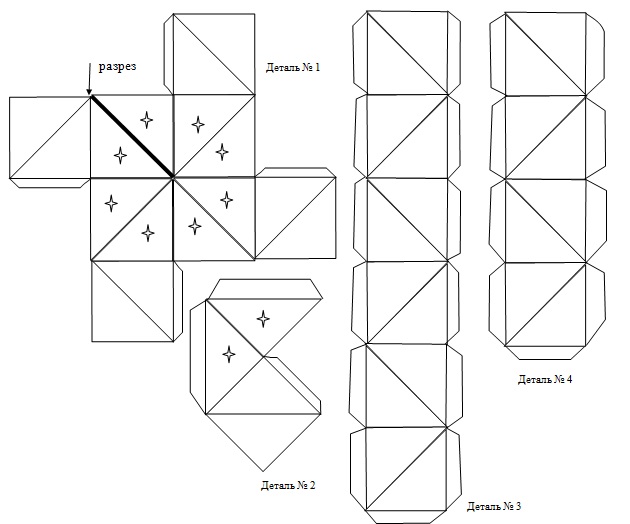 Затем мы реконструировали кластер ячеек сначала по стандартной тесселяции Вороного с использованием метрики евклидова расстояния, а затем с помощью предложенного нами метода (AQVT) с метрикой квадратичного расстояния, адаптированной для каждой из этих ячеек.Результаты реконструкции для подмножества ячеек для каждого из этих методов показаны на рисунках 7(B) и 7(C) соответственно для прямого сравнения. Можно заметить, что предложенный нами метод не только очень точно реконструировал формы ячеек, но и более точно уловил многослойную архитектуру этих ячеек SAM по сравнению с его аналогом Вороного с евклидовой метрикой расстояния.
Затем мы реконструировали кластер ячеек сначала по стандартной тесселяции Вороного с использованием метрики евклидова расстояния, а затем с помощью предложенного нами метода (AQVT) с метрикой квадратичного расстояния, адаптированной для каждой из этих ячеек.Результаты реконструкции для подмножества ячеек для каждого из этих методов показаны на рисунках 7(B) и 7(C) соответственно для прямого сравнения. Можно заметить, что предложенный нами метод не только очень точно реконструировал формы ячеек, но и более точно уловил многослойную архитектуру этих ячеек SAM по сравнению с его аналогом Вороного с евклидовой метрикой расстояния.
Рисунок 7. Реконструкция кластера ячеек с использованием евклидова расстояния на основе мозаики Вороного и предложенного AQVT для сравнения точности трехмерной реконструкции.
(A) Сегментированные и отслеживаемые срезы ячеек для кластера из пятидесяти двух ячеек из слоев L1 и L2 SAM. Плотный стек конфокальных изображений субдискретизируется с разрешением по оси 1,35 м, чтобы имитировать «разреженность по оси z», наблюдаемую в типичном сценарии визуализации в реальном времени. Срезы, принадлежащие одной и той же ячейке, помечаются одним и тем же номером для отображения результатов отслеживания. (B) Трехмерная реконструированная структура для подмножества этих ячеек при реконструкции с использованием евклидова расстояния, основанного на мозаике Вороного. (C) Результат реконструкции на основе AQVT для того же клеточного кластера.
Срезы, принадлежащие одной и той же ячейке, помечаются одним и тем же номером для отображения результатов отслеживания. (B) Трехмерная реконструированная структура для подмножества этих ячеек при реконструкции с использованием евклидова расстояния, основанного на мозаике Вороного. (C) Результат реконструкции на основе AQVT для того же клеточного кластера.
https://doi.org/10.1371/journal.pone.0067202.g007
Чтобы лучше исследовать точность реконструкции и показать явное преимущество использования предложенного метода реконструкции количественно, мы измеряем расстояния между двумерными поперечными сечениями результатов трехмерной реконструкции для каждой ячейки к границам сегментированных ячеек водораздела. Выбрав плоскость повторного нарезки как m (срезы, отличные от тех, которые используются для реконструкции) от вершины стека для ячеек слоя L1 и m для ячеек слоя L2, мы можем вычислительным путем регенерировать стенки ячеек для этих плоскостей изображения вдоль Z. Формы клеток в реконструированных срезах можно сравнить с их аналогами в двухмерных сегментированных изображениях, и расстояние между формами будет представлять ошибку реконструкции. Существует несколько различных метрик расстояния, которые можно использовать для вычисления несходства между двумя формами, такими как расстояние Прокруста, расстояние Хаусдорфа и т. д., каждая из которых имеет свои преимущества. Мы решили использовать модифицированное расстояние Хаусдорфа (MHD), одну из наиболее популярных мер расстояния в семействе расстояний Хаусдорфа, для оценки нашего метода реконструкции.Преимущества МГД перед другими мерами расстояния для согласования формы объекта подробно описаны в [28]. Можно отметить, что рассчитанная таким образом ошибка аналогична ошибке повторного проецирования, которая широко используется в сообществе трехмерной реконструкции для количественной оценки точности реконструкции.
Формы клеток в реконструированных срезах можно сравнить с их аналогами в двухмерных сегментированных изображениях, и расстояние между формами будет представлять ошибку реконструкции. Существует несколько различных метрик расстояния, которые можно использовать для вычисления несходства между двумя формами, такими как расстояние Прокруста, расстояние Хаусдорфа и т. д., каждая из которых имеет свои преимущества. Мы решили использовать модифицированное расстояние Хаусдорфа (MHD), одну из наиболее популярных мер расстояния в семействе расстояний Хаусдорфа, для оценки нашего метода реконструкции.Преимущества МГД перед другими мерами расстояния для согласования формы объекта подробно описаны в [28]. Можно отметить, что рассчитанная таким образом ошибка аналогична ошибке повторного проецирования, которая широко используется в сообществе трехмерной реконструкции для количественной оценки точности реконструкции.
На рис. 8(A) мы показали срезы ячеек, подвергшиеся вычислительному повторному срезу (цветовая кодировка для представления одних и тех же ячеек на нескольких срезах) на различной глубине для мозаики Вороного, основанной на евклидовом расстоянии, а на рис.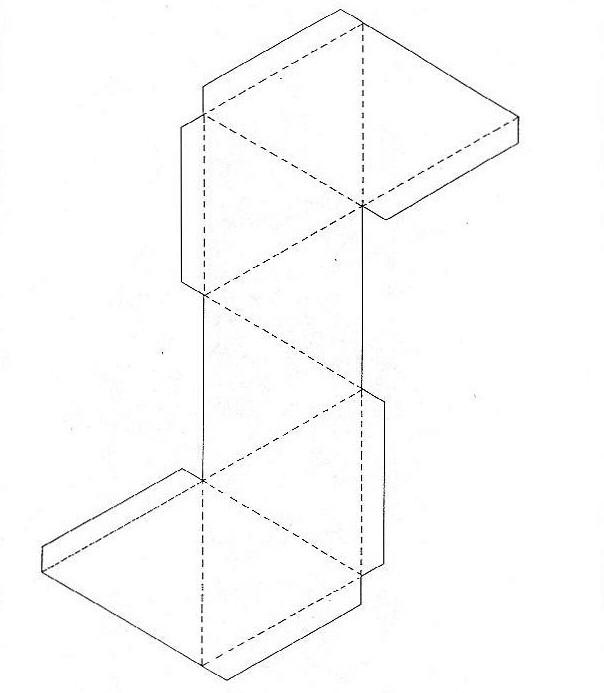 8(B) показаны двумерные поперечные сечения для те же ячейки, что и полученные путем повторного нарезки трехмерных форм ячеек в предлагаемом методе реконструкции на основе AQVT.Для обоих наборов изображений поперечные сечения каждой ячейки, полученные вычислением, накладываются на результаты сегментации водосбора для тех же срезов ячеек (наземная истина). Вычисляется MHD между исходным и сгенерированным компьютером срезами ячеек, и для каждой из ячеек в 6 разных срезах эта ошибка показана на рисунке 8 (C).
8(B) показаны двумерные поперечные сечения для те же ячейки, что и полученные путем повторного нарезки трехмерных форм ячеек в предлагаемом методе реконструкции на основе AQVT.Для обоих наборов изображений поперечные сечения каждой ячейки, полученные вычислением, накладываются на результаты сегментации водосбора для тех же срезов ячеек (наземная истина). Вычисляется MHD между исходным и сгенерированным компьютером срезами ячеек, и для каждой из ячеек в 6 разных срезах эта ошибка показана на рисунке 8 (C).
Рис. 8. Сравнение точности трехмерной реконструкции для предложенной реконструкции на основе AQVT с мозаикой Вороного, основанной на евклидовом расстоянии.
(A) Ячейки, показанные на рис. 7(A), реконструированы с использованием евклидова расстояния, основанного на тесселяции Вороного, и повторно срезанные с помощью вычислений ячейки сравниваются с реальными данными. (B) Те же самые ячейки реконструируются с использованием адаптивного квадратичного расстояния, основанного на тесселяции Вороного, а затем вычислительно повторно разрезаются на различные глубины по z, при которых мы также получаем основную истину (с точки зрения результатов 2D-сегментации срезов ячеек), но не использовались при формировании результатов реконструкции. Полученные с помощью вычислений срезы ячеек показаны разными цветами для разных ячеек, и они накладываются на результаты наземной истинной сегментации. (C) Ошибка реконструкции (аналогичная ошибке повторного проецирования) вычисляется как модифицированное расстояние Хаусдорфа (MHD) между срезами клеток, сгенерированными компьютером, и результатами сегментации на изображениях истинности тех же клеток. МГД, рассчитанные для каждой из 52 ячеек на разных глубинах в Z-стеке, нанесены на график для обоих методов для сравнения методов друг с другом.Из графиков ясно видно, что ошибка реконструкции намного больше для мозаики Вороного (VT), основанной на евклидовом расстоянии, чем для AQVT, особенно на конечных () срезах между последовательными слоями ячеек.
Полученные с помощью вычислений срезы ячеек показаны разными цветами для разных ячеек, и они накладываются на результаты наземной истинной сегментации. (C) Ошибка реконструкции (аналогичная ошибке повторного проецирования) вычисляется как модифицированное расстояние Хаусдорфа (MHD) между срезами клеток, сгенерированными компьютером, и результатами сегментации на изображениях истинности тех же клеток. МГД, рассчитанные для каждой из 52 ячеек на разных глубинах в Z-стеке, нанесены на график для обоих методов для сравнения методов друг с другом.Из графиков ясно видно, что ошибка реконструкции намного больше для мозаики Вороного (VT), основанной на евклидовом расстоянии, чем для AQVT, особенно на конечных () срезах между последовательными слоями ячеек.
https://doi.org/10.1371/journal.pone.0067202.g008
Можно заметить, что каждый из графиков на рисунке 8(C) включает ошибки реконструкции для отдельных срезов клеток для обоих методов реконструкции. . Для срезов, расположенных ближе к центру клеток, оба метода показывают одинаковую и приемлемо небольшую ошибку повторного проецирования. Однако в случае конечных срезов для каждой ячейки вдоль Z предложенный метод реконструкции на основе адаптивного квадратичного расстояния показывает гораздо лучшую точность реконструкции (как видно из графиков на рисунке 8(C)). Это улучшение результата более заметно для клеток, которые имеют неоднородную форму и рост, такой как удлинение вдоль любой из осей. Далее мы подтверждаем это наблюдение, проводя аналогичный эксперимент с кластером клеток различных размеров и размеров на образце изображения меристемы корня в продольном поперечном сечении.Этот эксперимент и его результаты подробно описаны в следующем подразделе.
Однако в случае конечных срезов для каждой ячейки вдоль Z предложенный метод реконструкции на основе адаптивного квадратичного расстояния показывает гораздо лучшую точность реконструкции (как видно из графиков на рисунке 8(C)). Это улучшение результата более заметно для клеток, которые имеют неоднородную форму и рост, такой как удлинение вдоль любой из осей. Далее мы подтверждаем это наблюдение, проводя аналогичный эксперимент с кластером клеток различных размеров и размеров на образце изображения меристемы корня в продольном поперечном сечении.Этот эксперимент и его результаты подробно описаны в следующем подразделе.
Мы также оценили точность нашего метода, изучив, насколько предполагаемые объемы ячеек отличаются от истинного для различных уровней разреженности в z-выборке. Для плотных данных, описанных ранее (0,225 м между срезами по оси z), мы сначала оцениваем объемы наземной истинной ячейки кластера ячеек, подсчитывая общее количество суперпикселей в ячейке и умножая его на размер суперпикселя (0.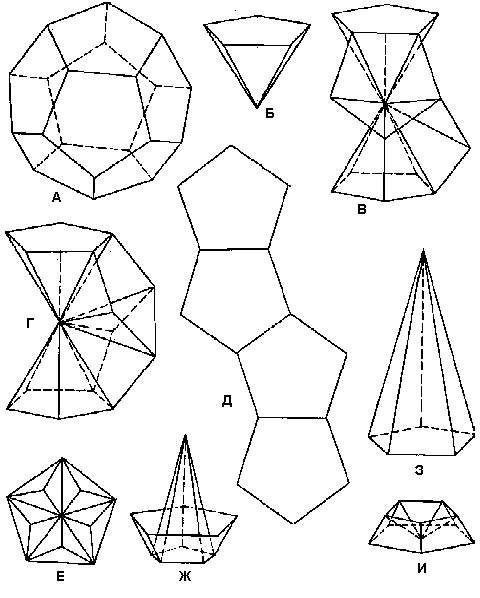 2×0,2×0,225). Затем мы постепенно передискретизируем плотную стопку с 5 последовательными разрешениями по оси z (а именно: 0,45, 0,675, 0,9, 1,125, 1,35 м) и для каждой из этих передискретизируемых стопок реконструируем одни и те же ячейки, используя предложенный AQVT, и оцениваем объемы ячеек. Можно отметить, что с каждой из этих соответствующих передискретизаций результирующий 3D-стек становится все более и более разреженным. Например, при разрешении дискретизации 0,45 м среднее количество срезов на ячейку составляет 7 или 8, тогда как для 1,35 м одни и те же ячейки захватываются в среднем по 3 срезам.Ошибки в оценке объемов отдельных ячеек при различных уровнях разреженности показаны на рисунке 9. Мы нанесли на график средние значения и стандартные отклонения абсолютных ошибок, выраженные как отношение к объемам ячеек истинности. Можно заметить, что при самой плотной повторной выборке (0,45 м) средняя ошибка оценки составляет всего 3% при стандартном отклонении 1,3%. Ошибка оценки медленно увеличивается с увеличением разреженности в стеке, и при разреженности около 3 срезов/ячейка средняя ошибка оценки составляет 5.
2×0,2×0,225). Затем мы постепенно передискретизируем плотную стопку с 5 последовательными разрешениями по оси z (а именно: 0,45, 0,675, 0,9, 1,125, 1,35 м) и для каждой из этих передискретизируемых стопок реконструируем одни и те же ячейки, используя предложенный AQVT, и оцениваем объемы ячеек. Можно отметить, что с каждой из этих соответствующих передискретизаций результирующий 3D-стек становится все более и более разреженным. Например, при разрешении дискретизации 0,45 м среднее количество срезов на ячейку составляет 7 или 8, тогда как для 1,35 м одни и те же ячейки захватываются в среднем по 3 срезам.Ошибки в оценке объемов отдельных ячеек при различных уровнях разреженности показаны на рисунке 9. Мы нанесли на график средние значения и стандартные отклонения абсолютных ошибок, выраженные как отношение к объемам ячеек истинности. Можно заметить, что при самой плотной повторной выборке (0,45 м) средняя ошибка оценки составляет всего 3% при стандартном отклонении 1,3%. Ошибка оценки медленно увеличивается с увеличением разреженности в стеке, и при разреженности около 3 срезов/ячейка средняя ошибка оценки составляет 5.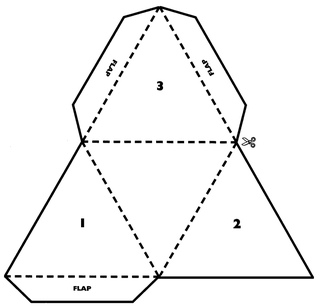 3%, со стандартным отклонением около 4%. Мы повторили тот же эксперимент для тесселяции Вороного с метрикой евклидова расстояния, и средняя ошибка намного выше и составляет около 30% (см. Рисунок S1).
3%, со стандартным отклонением около 4%. Мы повторили тот же эксперимент для тесселяции Вороного с метрикой евклидова расстояния, и средняя ошибка намного выше и составляет около 30% (см. Рисунок S1).
Рисунок 9. Ошибки в оценках AQVT объемов ячеек по их соответствующим наземным истинным объемам при различных уровнях разреженности.
Группа ячеек из стопки трехмерных конфокальных изображений с разрешением по оси 0,225 м подвергается повторной выборке для создания стопок с 5 различными уровнями разреженности. Каждый из этих передискретизированных стеков реконструируется в 3D с использованием предложенного AQVT, и вычисляются объемы каждой из ячеек в кластере.Наносятся средние значения и стандартные отклонения абсолютных ошибок в объемах (выраженных как отношение к объемам наземной истины) всех ячеек для каждого более разреженного стека. Средняя ошибка медленно увеличивается с увеличением разреженности, но составляет менее 5,3% при стандартном отклонении 4% даже при 1,35 м/срез (т. е. в среднем 3 среза/ячейка).
е. в среднем 3 среза/ячейка).
https://doi.org/10.1371/journal.pone.0067202.g009
Заключение и будущая работа
В этой статье мы представили метод реконструкции плотно упакованного кластера клеток с использованием набора данных конфокальной живой визуализации с очень разреженной z-выборкой.Мы предоставили математически строгую структуру, построенную на основе основных концепций геометрической тесселяции. Сначала мы показали, как формы ячеек могут быть аппроксимированы мозаикой Вороного, основанной на евклидовой мере расстояния. Затем мы предложили основу тесселяции Вороного на основе метрики квадратичного расстояния, чтобы зафиксировать асимметрию размеров клеток и роста вдоль их разных осей. Мы описали, как предлагаемая тесселяция может позаботиться об асимметрии, предоставляя веса метрике расстояния вдоль каждой оси для каждой ячейки, и как эти веса, а также расположение сайтов могут быть приблизительно оценены из разреженных данных изображения для отдельных ячеек с помощью подгонка охватывающих эллипсоидов к сегментированным разреженным срезам изображения.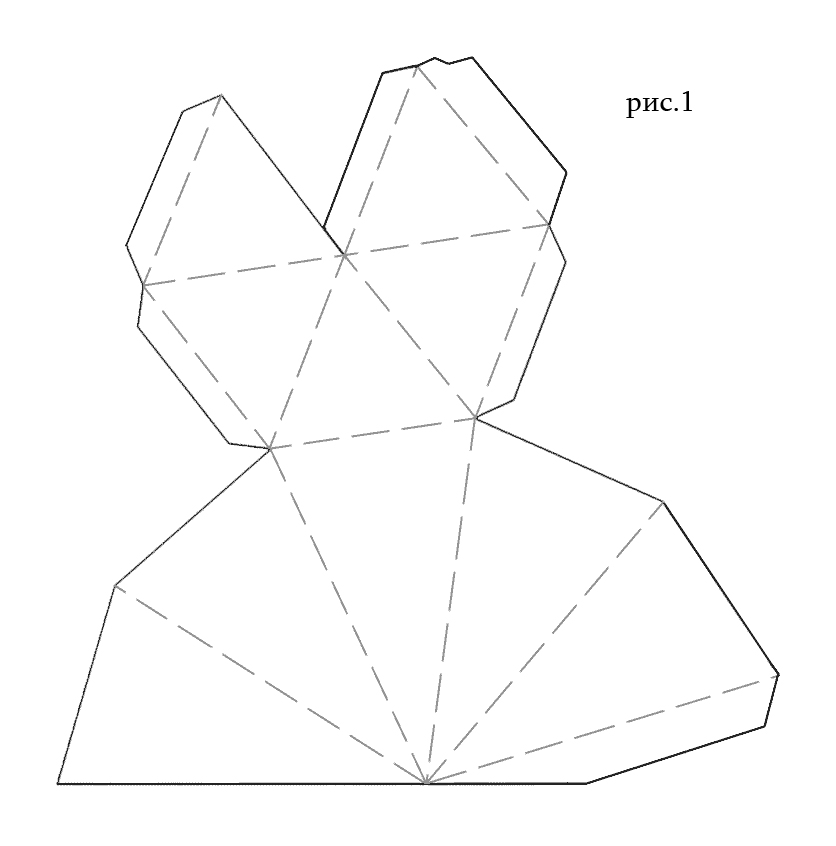 Мы подтвердили наш метод, показав, что ошибка реконструкции (как в реконструированных формах клеток, так и в оцененных объемах клеток) для клеток достаточно мала, и предоставили прямое сравнение ошибки реконструкции для предлагаемого метода с популярной мозаикой Вороного, основанной на евклидовом расстоянии. подход. В качестве применения предлагаемого метода мы показали некоторые предварительные результаты по оценке кривых роста для нескольких клеток SAM на рисунке S2. Будущая работа над этим будет включать интеграцию этого метода 3D-реконструкции с методом пространственно-временного отслеживания клеток для формирования полного конвейера анализа 4D-изображений.Этот конвейер можно использовать для создания различной статистики клеточного деления и роста клеток полностью автоматизированным и высокопроизводительным способом. Статистические данные, собранные из такого конвейера, могут быть чрезвычайно полезны при построении динамической модели для количественного анализа пространственно-временной корреляции в клеточном делении и росте клеток в сложной многослойной ткани.
Мы подтвердили наш метод, показав, что ошибка реконструкции (как в реконструированных формах клеток, так и в оцененных объемах клеток) для клеток достаточно мала, и предоставили прямое сравнение ошибки реконструкции для предлагаемого метода с популярной мозаикой Вороного, основанной на евклидовом расстоянии. подход. В качестве применения предлагаемого метода мы показали некоторые предварительные результаты по оценке кривых роста для нескольких клеток SAM на рисунке S2. Будущая работа над этим будет включать интеграцию этого метода 3D-реконструкции с методом пространственно-временного отслеживания клеток для формирования полного конвейера анализа 4D-изображений.Этот конвейер можно использовать для создания различной статистики клеточного деления и роста клеток полностью автоматизированным и высокопроизводительным способом. Статистические данные, собранные из такого конвейера, могут быть чрезвычайно полезны при построении динамической модели для количественного анализа пространственно-временной корреляции в клеточном делении и росте клеток в сложной многослойной ткани.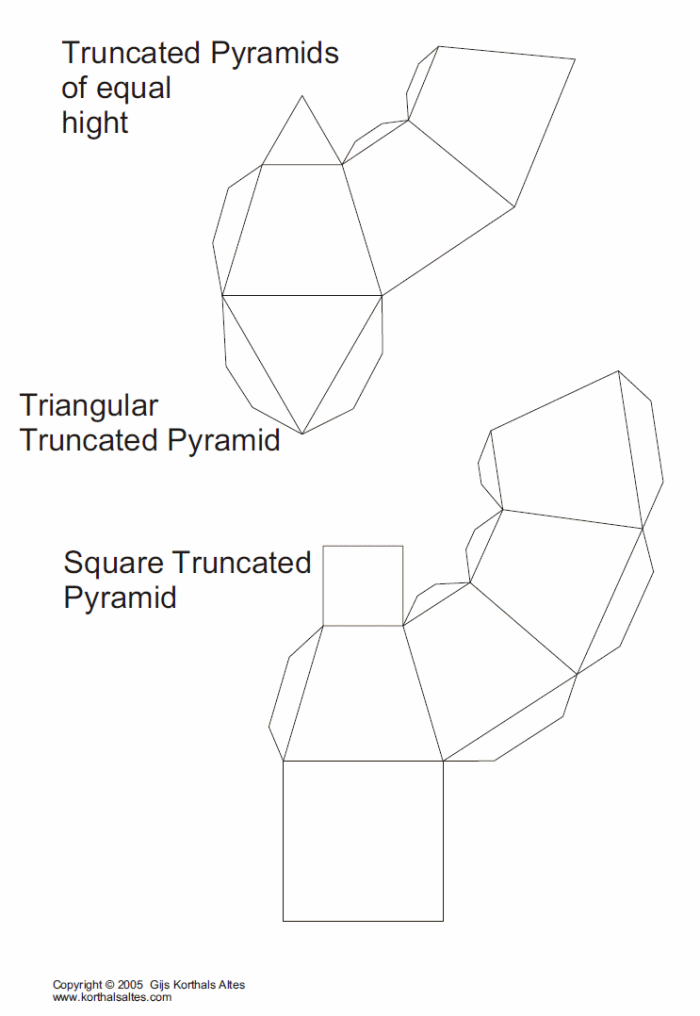
Вспомогательная информация
Рисунок S1.
Ошибки в расчетных объемах ячеек с использованием евклидового расстояния на основе тесселяции Вороного из соответствующих объемов наземных данных на различных уровнях разреженности. Кластер ячеек из стопки трехмерных конфокальных изображений с разрешением по оси 0,225 м подвергается повторной выборке для создания стопок с 5 различными уровнями разреженности. Каждый из этих передискретизированных стеков реконструируется в 3D с использованием VT на основе евклидова расстояния, и вычисляются объемы каждой из ячеек в кластере. Наносятся средние значения и стандартные отклонения абсолютных ошибок в объемах (выраженных как отношение к объемам наземной истины) всех ячеек для каждого более разреженного стека. Средняя ошибка более или менее одинакова на всех уровнях разреженности, и средняя ошибка составляет около 30% при большом стандартном отклонении более 25%).
https://doi.org/10.1371/journal.pone.0067202.s001
(TIFF)
Файл S1.
Вспомогательный информационный текстовый файл. Содержит анализ ошибок оценки объема ячейки в мозаике Вороного на основе евклидова расстояния, выборочные результаты по статистике роста клеток и подробную стратегию решения для оценки параметров MVEE.
https://doi.org/10.1371/journal.pone.0067202.s003
(PDF)
Авторские взносы
Идея и разработка экспериментов: АЦ АКРЦ ГВР.Проведены эксперименты: AC MMP. Проанализированы данные: АЦ АКРЦ ГВР. Предоставленные реагенты/материалы/инструменты для анализа: GVR MMP. Написал газету: AC AKRC.
Каталожные номера
- 1. Чан Т., Весе Л. (2001) Активные контуры без краев. Транзакция IEEE по обработке изображений 10: 266–277.
- 2. Yin Z, Bise R, Chen M, Kanade T (2010)Сегментация клеток в микроскопических изображениях с использованием набора локальных байесовских классификаторов. В: Материалы международной конференции IEEE 2010 г. по биомедицинской визуализации: от нано до макро.стр. 125–128.
- 3. Гор В., Эловиц М., Бакарян Т., Мьолснесс Э. (2005) Отслеживание клеточных сигналов на флуоресцентных изображениях. Семинар IEEE по методам компьютерного зрения для биоинформатики: 142–150.
- 4. Лю М., Ядав Р.К., Рой-Чоудхури А., Редди Г.В. (2010)Автоматическое отслеживание линий стволовых клеток верхушки побега арабидопсиса с использованием сопоставления локального графика. Журнал растений, Оксфорд, Великобритания 62: 135–147.
- 5. Mjolsness E (2006) Рост и развитие некоторых современных моделей растений: точка зрения.Журнал регулирования роста растений 25: 270–277.
- 6. Гор В., Шапиро Б. Е., Йонссон Х., Хейслер М., Редди В. Г. и др.. (2005) Архитектура программного обеспечения для моделирования развития растений: проект вычисляемого завода. Биоинформатика регуляции и структуры генома.
- 7. Чакраборти А., Ядав Р.К., Редди Г.В., Рой-Чоудхури А. (2011)Разрешение клеток Трехмерная реконструкция развивающихся многослойных тканей по изображениям объемной микроскопии с разреженной выборкой. Международная конференция IEEE по биоинформатике и биомедицине: 378–383.
- 8. Накахари Т., Мураками М., Йошида Х., Миямото М., Сохма Ю. и др. (1990) Уменьшение объема поднижнечелюстных ацинарных клеток крыс во время каждой стимуляции. Am J Physiol 258: G878–886.
- 9. Farinas J, Kneen M, Moore M, Verkman A (1997)Водопроницаемость плазматической мембраны культивируемых клеток и эпителия, измеренная с помощью световой микроскопии с пространственной фильтрацией. J Gen Physiol 110: 283–296.
- 10. Kawahara K, Onodera M, Fukuda Y (1994)Простой метод непрерывного измерения высоты клеток во время изменения объема в одной клетке a6.Jpn J Physiol: 411–419.
- 11. Квятковска Д., Рутье-Кежковска А. (2009)Морфогенез на вершине незрелого побега anagallis arvensis: геометрия поверхности и рост по сравнению с вегетативным побегом. J Опытный бот.
- 12. Tataw O, Liu M, Yadav R, Reddy V, Roy-Chowdhury A (2010)Анализ динамики роста стволовых клеток в верхушке побега арабидопсиса. В: IEEE Intl. конф. по обработке изображений.
- 13. Errington RJ, Fricker MD, Wood JL, Hall AC, White NS (1997)Четырехмерное изображение живых хондроцитов в хряще с использованием конфокальной микроскопии: прагматичный подход.Am J Physiol 272: C1040–1051.
- 14. Фернандес Р., Дас П., Мирабет В., Москарди Э., Траас Дж. и др. (2010)Визуализация роста растений в формате 4d: надежная реконструкция тканей и клонирование при разрешении клеток. Природные методы 7: 547–553.
- 15. Чжу К., Текола П., Баак Дж., Белин Дж. (1994) Измерение с помощью конфокальной лазерной сканирующей микроскопии объема ядер эпидермиса в толстых срезах кожи. Анальный Quant Cytol Histol 16: 145–52.
- 16. Виола П., Уэллс В.М. (1997) Согласование путем максимизации взаимной информации.Международный журнал компьютерного зрения 24: 137–154.
- 17. Винсент Л., Сойл П. (1991) Водоразделы в цифровых пространствах: эффективный алгоритм, основанный на моделировании погружения. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1991 13: 583–598.
- 18. Мкртчян К., Сингх Д., Лю М., Редди Г.В., Чоудхури АКР и др. (2011)Эффективная сегментация клеток и отслеживание развивающейся меристемы растений. В: Международная конференция IEEE по обработке изображений.стр. 2165–2168.
- 19. Лю М., Чакраборти А., Сингх Д., Ядав Р.К., Минакшисундарам Г. и др. (2011) Адаптивная сегментация клеток и отслеживание объемных изображений конфокальной микроскопии развивающейся меристемы растений. Молекулярный завод 4: 922–931.
- 20. Окабе А., Бутс Б., Сугихара К., Чиу С.Н. (2000) Пространственные мозаики: концепции и приложения диаграмм Вороного. John Wiley and Sons, Inc., 2-е издание.
- 21. Ауренхаммер Ф., Кляйн Р. (1999) Справочник по вычислительной геометрии.Издательство Эльзевир, стр. 201–290.
- 22. Boissonnat JD, Wormser C, Yvinec M (2006) Изогнутые диаграммы Вороного. В: Эффективная вычислительная геометрия для кривых и поверхностей, Springer-Verlag, Математика и визуализация. стр. 67–116.
- 23. Эванс Д., Джонс С. (1987) Обнаружение вороных (область влияния) полигонов. Математическая геология 19: 523–537.
- 24. Ferrero MMA (2011) Диаграмма Вороного: проблема распознавания генератора. CoRR абс/1105.4246.
- 25. Д’Эррико Дж. (2005) Подгонка поверхности с использованием сетки. В: Центральный файловый обмен MATLAB.
- 26. Хачиян Л.Г. (1996) Округление многогранников в модели вычисления вещественных чисел. Математическая опера Res: 307–320.
- 27. Кумар П., Йилдирим Э.А. (2005) Минимальный объем, включающий эллипсоиды и основные наборы. Журнал теории оптимизации и приложений 126: 1–21.
- 28. Dubuisson MP, Jain AK (1994) Модифицированное расстояние Хаусдорфа для сопоставления объектов.Международная конференция по распознаванию образов: 566–568.
- 29. Wyrzykowska J, Fleming A (2003) Модель клеточного деления влияет на экспрессию генов в апикальной меристеме побега. ПНАС 100: 5561–5566.
Индексирование объемных фигур с сопоставлением и упаковкой
Abstract
Мы описываем новый алгоритм массовой загрузки индекса многомерными данными и применяем его к проблеме сопоставления объемных фигур. Наш алгоритм сопоставления и упаковки представляет собой общий подход к упаковке данных в соответствии с метрикой сходства.Сначала строится приблизительный граф k ближайших соседей с использованием инициализации точек обзора, улучшения предыдущей работы, которое сокращает время построения при улучшении качества аппроксимации. Затем итеративно выполняется сопоставление графов, чтобы упаковать связанные элементы близко друг к другу. Конечным результатом является плотный индекс с хорошей производительностью.
Мы определяем новую спецификацию запроса для сопоставления форм, которая использует минимальные и максимальные ограничения формы для явного указания пространственных требований желаемой формы.Эта спецификация обеспечивает естественный язык для выполнения сопоставления объемных форм и легко поддерживается деревом поиска сходства на основе геометрии (GSS) — структурой индексации, которая поддерживает явные представления объемных форм. Мы описываем нашу реализацию дерева GSS для сопоставления объемных форм и предоставляем всестороннюю оценку чувствительности параметров, производительности и масштабируемости. По сравнению с предыдущими алгоритмами массовой загрузки мы обнаружили, что сопоставление и упаковка могут построить индекс дерева GSS за то же время, что является более плотным, плоским и более эффективным, с наблюдаемым средним улучшением производительности в 2 раза.
Ключевые слова: Извлечение форм, Индексация форм, Массовая загрузка, Сопоставление и упаковка
1. Введение
Наша цель — разработать алгоритмы и структуры данных для быстрого поиска в больших базах данных трехмерных фигур. В первую очередь нас интересуют приложения, в которых объемные свойства формы имеют большее значение, чем контуры поверхности формы. Это тот случай, когда существуют жесткие требования к тому, какое пространство может занимать объект, что плохо отражается общими оценками сходства формы.
Здесь мы описываем точный и эффективный метод индексации и поиска в базах данных миллионов объемных форм. Основными вкладами статьи являются:
—
описание нового критерия объемного поиска, который, в отличие от традиционных метрических подходов, поддерживает создание точных ограничений формы с определенными и переменными допусками,
—
дерево поиска по сходству (GSS) (Keim 1999), улучшающее его производительность,—
улучшение алгоритма NN-Descent (Dong et al.2011) для приблизительного k построения графа ближайших соседей, которое сокращает время построения графа при одновременном повышении качества аппроксимации, Дерево GSS, которое приводит к плотной, высококачественной структуре индекса, и
—
тщательную оценку нашего подхода, включая анализ чувствительности различных параметров.
2. Исходная информация
Тема сопоставления 3D-форм широко исследована и всесторонне рассмотрена (Iyer et al. 2005, Tangelder & Veltkamp 2008). Конкурс 3D Shape Retrieval Contest (SHREC) — это ежегодное соревнование, в котором оцениваются алгоритмы поиска формы (Li et al. 2012). Ключевым аспектом большинства подходов является то, как количественно определяется сходство различных форм. Чаще всего трехмерные фигуры сводятся к вектору числовых признаков. Затем сходство между формами выражается в терминах метрики, такой как евклидово или χ 2 расстояний между векторами признаков.Эти векторы могут быть проиндексированы для эффективного поиска с использованием структур данных, таких как метрические деревья (Hjaltason & Samet 2003, Samet 2006). Деревья метрик могут быть динамически построены из потока входных данных, но если набор данных загружен массово, можно создать более плотный и эффективный индекс (Aronovich & Spiegler 2010).
Большое разнообразие дескрипторов, включая гистограммы геометрических свойств (Осада и др., 2002 г.), «мешки слов» с локальными особенностями (Лопес-Састре и др., 2013 г.) и коэффициенты Фурье изображений буфера глубины объекты (Ohbuchi et al.2003), были исследованы (Bustos et al. 2005), и каждый из них обеспечивает различное отображение от формы к вектору признаков более низкого измерения. Если используемые функции не являются инвариантными к перемещению или вращению, то формы обычно предварительно обрабатываются с помощью шага нормализации позы, такого как анализ основных компонентов (Paquet et al. 2000). Однако этот шаг не является ни необходимым, ни желательным, если формы предварительно зарегистрированы в определенной системе координат.
Сведение фигур к векторам признаков упрощает проблемы индексации и подобия, но неизбежно приводит к потере информации о деталях формы и затрудняет, если вообще делает невозможным, сопоставление с точным объемным описанием формы.Одна альтернатива, которая применима к вокселизированным формам, в отличие от «многоугольных супов», заключается в сохранении явного представления формы. Октодеревья обеспечивают эффективное представление для хранения и сравнения объемных форм (Zhang & Smith 2009). Нормализованная разность объемов, δ VD ( vol 1 , vol 2 ), определяет показатель сходства объемных форм (Keim 1999, 1997) и определяется как
δVD(vol1,vol2)=1−‖vol1∩vol2‖‖vol1∪vol2‖
где ∥ vol ∥ объем фигуры vol .
Вокселизированные формы могут быть проиндексированы с помощью дерева поиска подобия на основе геометрии (GSS) (Keim 1999, 1997), которое использовалось для индексации набора данных из 800 форм из медицинских изображений. Как показано на рисунке, в дереве GSS каждый узел поддерживает максимальный включенный объем (MIV) и минимальный окружающий объем (MSV), которые ограничивают все формы, хранящиеся в потомках узла. То есть MIV набора фигур — это пересечение этих фигур, а MSV — их объединение. Ранее эти представления MIV и MSV использовались для поиска подобия ближайших соседей путем предоставления границ δ VD .
Иллюстрация GSS-дерева. Листья дерева содержат вокселизированные формы. Каждый внутренний узел хранит максимальный включенный объем (MIV) и минимальный окружающий объем (MSV), которые ограничивают геометрию форм, происходящих от узла.
Здесь мы описываем и оцениваем простое использование дерева GSS для поддержки точного запроса форм посредством спецификации минимальных и максимальных ограничений формы, а также подробностей улучшений структуры данных, повышающих ее эффективность.Кроме того, в отличие от предыдущей работы (Keim 1999, 1997), в которой деревья GSS создавались динамически, мы описываем новый метод массовой загрузки дерева GSS, который приводит к плотному и эффективному дереву поиска, поддерживающему запросы к миллионам объемных форм.
3. Описание проблемы
Наша цель — обеспечить точный и точный поиск миллионов объемных форм. В дополнение к поддержке классического поиска ближайшего соседа на основе подобия объемного перекрытия, мы также позволяем пользователю создавать точные минимальные и максимальные ограничения формы.Спецификация запроса минимальной/максимальной формы позволяет опытному пользователю точно указать строгие требования к форме (где минимальная и максимальная формы близки друг к другу), а также поддерживает более мягкие требования к форме. Это резко контрастирует с существующими подходами к метрике подобия, где очень похожая форма, как показано на рисунке , может быть менее интересной, чем непохожая форма, такая как показано на рисунке , которая соответствует желаемым ограничениям формы.
2D-иллюстрация минимальных и максимальных ограничений формы.(a) Эталонное твердое тело (твердое тело) и форма рецептора, которой оно должно дополняться (градиент). (b) Минимальное (белое) и максимальное (наложение) ограничение формы, полученное из эталона. Только контактирующая часть формы используется для определения минимальной формы, в то время как максимальная форма расширена, чтобы включить дополнительный объем, комплементарный форме рецептора. (c) Форма, соответствующая этим ограничениям. Эта форма сильно отличается от эталонной формы при сравнении с использованием традиционной метрики подобия.(d) Напротив, форма, очень похожая на эталонную форму, но нарушающая ограничения формы рецептора, вряд ли будет представлять интерес.
Ключевое предположение, которое мы делаем, заключается в том, что предоставленные объемные формы зарегистрированы в общей системе координат. Этого можно добиться с помощью нормализации позы (Paquet et al. 2000). Было показано, что нормализация позы является эффективным и необходимым этапом предварительной обработки при использовании метрик сходства, которые не являются инвариантными позы для общей задачи распознавания объектов (Sfikas et al.2011 г., Chaouch & Verroust-Blondet 2008 г.).
Основная проблема, решаемая в этой статье, заключается в разработке структур данных и алгоритмов для поддержки эффективного и масштабируемого поиска в базе данных объемных форм, предварительно зарегистрированных в системе координат, где поисковые запросы принимают форму либо запроса ближайшего соседа, либо минимальное/максимальное ограничение формы. В идеале поиск сотен миллионов объемных форм можно будет выполнять за несколько секунд, чтобы поддерживать интерактивную модификацию и уточнение запроса.
4. Структуры данных
Две наши основные структуры данных — октодеревья для представления формы и деревья GSS для индексации формы.
4.1. Октодерево
Октодерево региона — это классическая структура данных для представления формы, которая рекурсивно делит пространство на восемь однородных октантов (Samet 2006). Октанты, полностью содержащиеся в фигуре или исключенные из нее, помечаются как лист, а октанты, частично перекрывающие фигуру, далее подразделяются до указанного разрешения.Представление октодерева масштабируется с площадью поверхности объекта, а не с его объемом (Meagher 1982).
Как первоначально было описано Кеймом (1997), дерево GSS использовало представление формы в виде линейного октодерева. В линейном октодереве явно сохраняются только листовые узлы октодерева. Каждый узел может быть представлен одним байтом, содержащим уровень листа, и битом, указывающим, является ли лист полным или пустым. Внутренняя структура дерева неявно восстанавливается при линейном сканировании массива листьев.Несмотря на то, что линейные октодеревья занимают мало места, поскольку в них нет явной внутренней структуры, нет возможности быстрого вычисления при выполнении таких операций, как пересечение или объединение.
Поскольку вычисления объединения и пересечения являются общими как при построении, так и при поиске дерева GSS, мы разрабатываем наши октодеревья для явного хранения внутренних узлов дерева. Кроме того, для ускорения вычисления δ VD объем каждого поддерева хранится в каждом узле вместе с восемью ссылками на потомков узла.Ссылка состоит из бита, указывающего, является ли дочерний узел конечным узлом или внутренним узлом, и индекса местоположения дочернего узла. Если дочерний элемент является листом, данные листа (полные или пустые) поднимаются в поле idnex местоположения. Мы выполняем двойных подъема листовых данных, где, если все дочерние узлы дочернего узла являются листьями, 8 внуков объединяются в 8-битную маску, хранящуюся в прародителе. Это представление октодерева имеет накладные расходы на хранение, сравнимые с линейным октодеревом, но имеет значительно лучшую производительность из-за кэширования томов поддерева и сокращения вычислений пересечения и объединения.
4.2. Дерево GSS
Определяющим аспектом дерева GSS, показанного на , является использование максимального включенного объема (MIV) и минимального окружающего объема (MSV) в качестве агрегированных дескрипторов потомков узла дерева. Кроме того, как и B-дерево, дерево GSS сбалансировано по высоте, и каждый узел может содержать несколько дочерних элементов. В отличие от большинства структур B-tree, данные (MIV и MSV), содержащиеся в каждом узле, не имеют фиксированной ширины, поэтому мы не пытаемся выравнивать узлы по страницам. Идеальный максимальный коэффициент ветвления узла дерева исследуется в разделе 7.2. В нашей реализации внутренние узлы и листовые узлы хранятся в отдельных файлах. После построения дерева эти файлы сортируются в порядке глубины. Каждый внутренний узел содержит начальную и конечную ссылки на диапазон конечных узлов указанного им поддерева. Это поддерживает немедленное последовательное сканирование всех листовых узлов любого заданного поддерева. В нашей реализации листовые узлы содержат одно октодерево формы.
В исходном дереве GSS представления MIV и MSV, хранящиеся в узле, были указаны настолько точными, насколько это необходимо для их различения.Например, октодеревья MIV, хранящиеся в узле, будут округлены в меньшую сторону до самого грубого разрешения, при котором все октодеревья MIV все еще не идентичны. Это приводит к меньшим октодеревьям со строго меньшим количеством уровней, которые быстрее загружаются и запрашиваются, но сравнения становятся менее точными. Для наших запросов мы обнаружили, что неточности, вызванные этими приближениями с более низким разрешением, предотвратили сокращение непродуктивных поисков поддеревьев, что привело к чистому снижению производительности.
В качестве альтернативы мы выполняем локальное адаптивное округление октодеревьев, хранящихся в том же узле дерева GSS.Вместо того, чтобы уменьшать разрешение всего дерева, мы рассматриваем каждый октант листьев деревьев отдельно. Листовой октант октанта MIV/MSV округляется вниз/вверх до пустого/полного октанта только в том случае, если тот же октант во всех других октантах MIV/MSV в узле имеет идентичный шаблон (в этом случае он также округляется). ) или полный/пустой октант (см. ). То есть разрешение октантов, которые фактически различают разные формы внутри октанта, остается нетронутым. По существу, распределение форм, хранящихся в дереве GSS, используется для указания того, какие сегменты представления октодерева могут быть сохранены в уменьшенном разрешении.Этот метод приводит к среднему уменьшению размера октодерева примерно на 20–30%, при этом практически не увеличивается количество непродуктивных поисков.
Иллюстративный узел дерева GSS (а) до и (б) после локального адаптивного округления. Формы MIV/MSV в узле дерева GSS округляются только в том случае, если все формы одинаковы или заполнены/пусты. Это способствует подъему закругленных листьев и снижает общую высоту и требования к памяти дерева.
5. Алгоритмы
Полезность дерева GSS зависит от того, насколько хорошо похожие фигуры сгруппированы вместе на нижних уровнях дерева.Группировка разнородных фигур приводит к большим формам MSV и маленьким формам MIV, которые неинформативны для управления процессом поиска. Дерево GSS изначально описывалось как динамическая структура данных, в которой фигуры добавлялись и удалялись по одной (Keim 1997). Этот подход создает древовидную структуру, которая зависит от упорядочения входных данных и, хотя и сбалансирована, может иметь сильно изменчивое распределение занятости узлов по всему дереву, что приводит к низкой производительности поиска. Для баз данных форм, которые обновляются нечасто, построение поискового индекса дерева GSS путем массовой загрузки набора входных данных является естественной альтернативой.Мы описываем первый фреймворк массовой загрузки дерева GSS, который включает в себя новое усовершенствование для создания графа аппроксимации k -ближайшего соседа ( k -nn) и новый алгоритм сопоставления и упаковки для создания плотных и эффективных групп фигур. . Кроме того, мы опишем наши алгоритмы поиска по дереву GSS. Для удобства параметры алгоритмов сгруппированы в .
Таблица 1
| Описание | ||
|---|---|---|
| K | K K -NN График | |
| V | Vantage Points Используется для инициализации K -nn график | |
| C | CClusters, созданные в разделении сверху вниз | |
| порог для упаковки кластера | ||
| M | MУзел GSS Tree |
алгоритм 1
| : неупорядоченный массив форм к индексу |
| результат : корень индекса GSS |
| узлов ← формирует // преобразовывать формы к узлам листьев |
| пока Размер ( узлов ) > 1 do |
| NextLevel ← [] |
| CreateNextLevel (Узлы, NextLevel) |
| Узлей ← NextLevel |
| Возврат узлов. front() |
Алгоритм 2
| Вход : Узлы дерева для объединения для формирования следующего уровня | |||||||
| Nextlevel.add (пакет (узлы)) | |||||||
| | | // Bulkload Разбиение (Aronovich & Spiegler 2010) | Образец ← SELECTSAMPLESET (Узлы, C ) | 9084) NodePartitions ← Ректингбл (узлы, образец) | 9089 Foreach Часть в Nodevartitions DO | CreateNextLevel (Часть, NextLevel) | |
Algorithm 3
| Вход : узлы для плотной упаковки м на один родительский узел i ← 1 от до log 2 ( м ) do | |
| KNN ← Treatknnngraph (узлы) | |
| mergednodes ← [] | 9089Foreach Edge в Maxmalmatching ( KNN ) do |
| родительский элемент ← {} | |
| (n1, n2) ← ребро | |
| родительский элемент. MSV ← n1. MSV ∪ n2. MSV | |
| родительский. MIV ← n1. MIV ∩ n2. MIV | |
| , если я == 1 , затем | |
| родительский. детей ← [n1, n2] | |
| else | |
| родитель. детей ← [n1. детей , n2. детей ] | |
| объединенные узлы.добавить (родительский) | |
| узлов ← mergedNodes | |
| вернуть узлов |
5.1. Массовая загрузка Framework
Целью массовой загрузки структуры данных, такой как дерево GSS, является создание плотного дерева с максимальным разветвлением, обеспечивающим хорошую производительность поиска. Кроме того, алгоритм массовой загрузки должен иметь возможность обрабатывать большой набор входных данных, который может не поместиться в памяти.
В качестве отправной точки для нашей структуры мы используем алгоритм BulkLoad (Aronovich & Spiegler 2010).Этот алгоритм, первоначально разработанный для инициализации метрической древовидной структуры CM-дерева (Aronovich & Spiegler 2007), использует схему разделения сверху вниз для построения каждого слоя дерева снизу вверх. Входные данные разбиваются на c разделов путем (1) случайной выборки cL элементов данных (где L — параметр выборки с рекомендуемым значением пять), (2) агломеративной кластеризации этой выборки в c кластеров , (3) определение самого центрального элемента этих кластеров, а затем (4) присвоение каждому элементу данных во входных данных ближайшему центру кластера.Один шаг разбиения выполняет полное сканирование входных данных только один раз при выполнении вычислений расстояния O ( cn ) на этапе назначения кластера, и, пока c и L малы, O ( c 2 L 2 ) агломеративную кластеризацию можно выполнять в памяти с небольшими практическими затратами. Этот шаг разделения применяется рекурсивно до тех пор, пока результирующий раздел не будет содержать меньше максимально допустимого количества элементов в узле, m , после чего раздел преобразуется в узел дерева с соответствующими элементами данных в качестве его дочерних элементов.Как только входные данные полностью разложены на узлы дерева, эти узлы затем обрабатываются как отдельные элементы данных, которые затем разделяются для создания следующего самого высокого уровня в структуре дерева. Этот процесс повторяется до тех пор, пока не будет получен один корневой узел.
Алгоритм BulkLoad требует определения функции расстояния как между отдельными элементами данных, в нашем случае метрикой δ VD между формами, так и между узлами, которые представляют собой поддерево элементов.В дереве GSS каждый узел содержит репрезентативную форму MIV и MSV. Мы определяем расстояние между узлами как среднее значение δ VD форм MIV и MSV. Поскольку это расстояние является средним значением двух метрик, оно также является метрикой. Фактически, это обобщение расстояния формы, поскольку одна форма может быть представлена парой идентичных форм MIV и MSV. Для простоты мы также называем эту метрику подобия δ VD .
К сожалению, алгоритм BulkLoad не дает особенно плотного дерева, поскольку схема разбиения создает кластеры переменного размера.Более того, группировка элементов вокруг «центрального» элемента, хотя и подходит для структуры данных CM-дерева, не очень хорошо подходит для построения дерева GSS, как показано на рис. Вместо этого желаемая группировка фигур (или узлов, представляющих фигуры) — это группировка, которая приводит к наиболее точным и конкретным представлениям MIV и MSV.
Иллюстрация проблем с разбиением вокруг центрального объекта. Светлым пунктиром показаны потенциальные кластеры, сформированные при таком подходе, где все объекты находятся близко к центральному блоку, но не обязательно близко друг к другу.Это разбиение несбалансированное: пять объектов в одном кластере и только один в другом. Что еще более важно, соответствующие представления MIV и MSV, вверху справа, менее различимы, чем представления альтернативного разбиения, обозначенного пунктирной линией. В отличие от существующих методов кластеризации сопоставление и упаковка явно оптимизируют различительную способность MIV и MSV каждого кластера.
Для решения этих проблем мы разработали гибридную структуру разделения/упаковки, которая использует алгоритм BulkLoad для эффективного разделения элементов (либо отдельных форм, либо внутренних узлов дерева GSS) на кластеры, которые значительно больше, чем желаемое разветвление узла, но остаются достаточно мал, чтобы данные кластера поместились в памяти.Затем мы упаковываем данные кластера в группы размером m , каждая из которых преобразуется в узел в строящемся слое дерева GSS. Как только слой дерева завершен, следующий самый высокий слой строится путем повторения процесса. Псевдокод для этого фреймворка представлен в и .
5.2. Приблизительное построение графа K-NN
Для создания качественной упаковки из n элементов необходимо вычислить попарные расстояния между элементами.Вычисление всех O ( n 2 ) расстояний непомерно дорого и не нужно, поскольку важны только расстояния между соседними предметами, которые являются кандидатами на упаковку. Вместо этого можно использовать граф k ближайших соседей, в котором каждый узел соединен только со своими k ближайшими соседями. Эффективное, o ( n 2 ) построение оптимального k -nn графа над общим метрическим пространством с внутренней высокой размерностью остается открытой проблемой (Chávez et al.2001). Однако были разработаны эффективные алгоритмы построения приблизительных k -nn графов (Паредес и др., 2006, Донг и др., 2011). Мы используем алгоритм NN-Descent (Dong et al. 2011) для построения приблизительного k -nn графа элементов.
Алгоритм NN-Descent сначала строит исходный граф, в котором каждый узел, представляющий элемент, связан со случайной выборкой из k других узлов. Этот кандидат k -nn граф затем улучшается посредством локального поиска вокруг каждого узла, который сравнивает узел с соседями его соседа.Каждая итерация NN-Descent равна O ( k 2 n ). Обычно для сходимости к локальному минимуму требуется всего несколько итераций, и, по крайней мере, для входных данных меньшей размерности этот локальный минимум близок к глобальному минимуму (истинный график k -nn) (Dong et al. 2011).
Мы улучшили алгоритм NN-Descent , заменив случайный начальный граф графом , инициализированным точками обзора.Мы проецируем каждый элемент на евклидово пространство меньшего измерения, вычисляя вектор расстояний до набора из v объектов с точки обзора. График k -nn между этими низкоразмерными векторами расстояний может быть эффективно вычислен с использованием пространственной структуры данных. Отношение ближайших соседей в этом выгодном пространстве использовалось непосредственно для поиска изображений (Vleugels & Veltkamp 2002). Однако граф k -nn в выгодном пространстве не соответствует напрямую графу k -nn в исходном метрическом пространстве более высокого порядка.Вместо этого мы используем граф k -nn в выгодном пространстве для инициализации алгоритма NN-Descent , который затем уточняет граф k -nn.
Мы выбираем v точек обзора с помощью жадного процесса выбора самого дальнего вперед, который требует O ( vn ) вычислений расстояний. Граф k -nn в выгодном пространстве строится с использованием модуля kd-tree библиотеки ANN (Mount 2010). Мы запускаем алгоритм NN-Descent до завершения без какого-либо досрочного завершения, чтобы сгенерировать наиболее точный график.В разделе 7.2 мы показываем, что наша схема инициализации точки зрения сокращает время построения графа k -nn и обеспечивает более качественную аппроксимацию.
5.3. Сопоставление и упаковка
Оптимальная упаковка в группы больше двух является NP-полной (Pagel et al. 1995), но хорошо изученный алгоритм сопоставления графов (Edmonds 1965) может быть использован для нахождения оптимальных пар объектов. Максимальное паросочетание — это набор попарно несмежных ребер в графе с максимальной общей стоимостью ребер.Мы жадно упаковываем узлы в группы размером м (максимальное разветвление узла дерева GSS), итеративно находя максимальное соответствие графа. Мы вычисляем максимальное совпадение приблизительного графа k -nn, где стоимость ребер установлена равной 1 − δ VD . Парные узлы — это именно те, чьи комбинированные представления MIV и MSV изменятся меньше всего. MIV и MSV всех парных узлов вычисляются для формирования нового набора узлов, из которых генерируется новый граф k -nn, и процесс сопоставления повторяется log 2 m раз, пока все узлы не будут были объединены в набор родительских узлов с максимальным разветвлением м .Мы не выполняем идеальное паросочетание, которое требует, чтобы каждая вершина графа инцидентна ребру паросочетания. Это позволяет выбросам оставаться непревзойденными и сохраняет наиболее тесно связанные узлы упакованными вместе. Псевдокод для этого процесса показан на .
Сопоставление графов было тщательно изучено, и для графов с v вершин и e ребер наилучшие результаты в худшем случае составляют O (ve) (Micali & Vazirani 1980). Однако более простые алгоритмы с худшими асимптотическими оценками хорошо работают на практике, особенно на разреженных графах (Колмогоров, 2009).На самом деле сопоставление случайного разреженного графа с постоянной средней степенью может быть выполнено за ожидаемое время O ( v ) (Chebolu & Frieze 2010). Следовательно, несмотря на то, что мы используем алгоритм сопоставления O ( ve log v ) из графовой библиотеки LEMON (lem n.d.), мы ожидаем и наблюдаем отличную реальную производительность, как указано в разделе 7.5. Использование графа k -nn с O ( kn ) ребер вместо полного графа с O ( n 2 ) ребер имеет важное значение для достижения этой производительности, и максимальное соответствие граф k -nn будет идентичен максимальному совпадению полного графа, пока граф k -nn отбирает соответствующие ребра.Это делает качество сопоставления чувствительным как к качеству аппроксимации графика k -nn, так и к значению k , зависимости, которая исследуется в разделе 7.2.
5.4. Поиск
Мы поддерживаем две формы поиска: поиск ближайшего соседа и поиск по ограничениям формы.
5.4.1. Ближайший сосед
Дерево GSS изначально было разработано для поддержки поиска ближайшего соседа (Keim 1999). Представления MIV и MSV каждого узла можно использовать для вычисления минимальных и максимальных границ перекрытия тома, δ VD , между объектом запроса и всеми листьями поддерева, и эта граница используется для сокращения поиска дерева. .Минимальная δ min и максимальная δ max границы для заданного объема запроса vol вычисляются следующим образом:
δmin(vol,MIV,MSV)=1−‖vol∩MSV‖‖vol∪MIV‖
δmax(vol,MIV,MSV)=1−‖vol∩MIV‖‖vol∪MSV‖
Поддеревья исследуется путем обработки тех узлов с наибольшим значением δ min + δ max в первую очередь. По мере изучения листовых узлов поддерживается текущее значение наилучшего перекрытия объема.При поиске k ближайших соседей в качестве лучшего решения сохраняется k -е наилучшее значение. Поддеревья не исследуются, если границы поддерева указывают на то, что его потомки не улучшат текущее лучшее решение.
5.4.2. Ограничения формы
Алгоритм поиска для определения объемных форм, соответствующих заданному минимальному/максимальному ограничению формы, естественным образом следует из структуры дерева GSS. Поддерево под узлом в дереве GSS исследуется тогда и только тогда, когда MIV узла содержится в пределах ограничения максимальной формы, а MSV узла полностью содержит ограничение минимальной формы.Если минимальная форма полностью содержится в MIV, а максимальная форма полностью содержит MSV, то спуск дерева может быть закорочен, а листья поддерева считываются напрямую.
6. Реализация
Наша реализация написана на C/C++. Создание базы данных принимает в качестве входных данных либо каталог вокселизированных форм в формате MIRA, либо файл форм, определяемых молекулярными структурами. В любом случае предполагается, что формы предварительно выровнены по желаемой системе координат.Вокселизированные формы представлены октодеревом с максимальным размером и разрешением, определяемыми пользователем. Эти октодеревья записываются на диск вместе с исходными данными формы по мере их создания. Затем создаются уровни дерева GSS, как описано ранее. При создании нового уровня предыдущий уровень открывается как файл с отображением памяти, а новый уровень записывается в новый файл, чтобы свести к минимуму требования к памяти при построении индекса. После того, как уровни дерева GSS построены, они помещаются в глубину первого порядка в файл, содержащий внутренние узлы, и отдельный файл, содержащий только листья.Во время этого этапа оптимизации к октодеревьям MIV и MSV применяется локальное адаптивное округление.
Инструментарий OpenBabel (O’Boyle et al. 2011) используется для анализа и обработки молекулярных данных. Молекулярная поверхность каждой структуры рассчитывается аналитически (Коннолли, 1983) с использованием радиуса зонда 1,4 Å. Полученная форма затем вокселизируется до разрешения 0,5 Å и имеет максимальный размер 32 Å.
Поиск ближайшего соседа принимает в качестве входных данных файл вокселей MIRA или файл молекулярной структуры.Для поиска ограничения формы могут использоваться воксельные файлы MIRA с требуемыми минимальными и максимальными ограничениями формы или могут использоваться два файла молекулярной структуры, которые определяют включенную форму и исключенную форму. Включенная форма соответствует минимальному ограничению формы. Любая совпадающая фигура должна полностью содержать включенную фигуру. Исключенная фигура представляет собой область, в которой совпадающая фигура не должна перекрываться. Его инверсия соответствует максимальному ограничению формы. В обоих случаях может быть указан зазор, на который можно уменьшить вокселизированную форму включенной формы и неинвертированной исключенной формы.Формы уменьшаются путем итеративного удаления соответствующего количества вокселей поверхности для достижения зазора соответствующего размера между исходной и уменьшенной формой. Чем больше разрыв между двумя ограничениями формы, тем больше вероятность того, что будут найдены совпадающие формы. Иллюстрация различных возможных форм запросов приведена в . Доступ к дереву GSS осуществляется через отображаемые в память файлы.
Вокселизированная форма молекулы (темные воксели) и ее рецептора (светлые воксели). Эта форма формирует основу для минимального ограничения формы, в то время как обратное или негативное изображение приемника определяет максимальное ограничение формы.Молекулы, поверхность которых попадает в зазор между двумя формами, соответствуют ограничениям. Обе формы показаны после уменьшения на одинаковое расстояние зазора: (а) 0 Å, (б) 1 Å, (в) 1,5 Å и (г) 2 Å. Изображения, сгенерированные с помощью sproxel (spr nd).
Полный исходный код доступен под Стандартной общественной лицензией GNU по адресу https://github.com/dkoes/ shapeb.
7. Результаты
Здесь мы исследуем чувствительность нашего подхода к различным параметрам и оцениваем его производительность и масштабируемость.Сначала мы опишем контрольные показатели и используемую методологию сравнительного анализа. Затем мы исследуем чувствительность нашего подхода к различным параметрам и выбираем набор алгоритмических параметров по умолчанию. Кроме того, мы сравниваем наш новый алгоритм сопоставления и упаковки с предыдущей работой. Наконец, мы оцениваем производительность распознавания формы и масштабируемость нашего подхода.
7.1. Контрольные показатели
Мы рассматриваем два набора контрольных показателей: общий контрольный показатель SHREC 2012 для извлечения формы и специальный контрольный образец молекулярной формы, который мы определяем здесь.Бенчмарк SHREC позволяет нам напрямую сравнивать опубликованные результаты, но его размер ограничен 1200 фигурами. Напротив, наша база данных пользовательских молекулярных форм содержит миллионы форм. Такой большой размер позволяет нам осмысленно оценивать чувствительность параметров как в условиях, связанных с вводом-выводом, так и в условиях, связанных с процессором.
Все результаты производительности относятся к однопоточному выполнению. Все результаты измерения времени представляют собой среднее значение не менее трех измерений. Запросы оцениваются с использованием процессора Intel Core i7 975 с тактовой частотой 3,33 ГГц и 12 ГБ оперативной памяти под управлением Ubuntu Linux.Данные хранятся на двух жестких дисках 7200 об/мин в чередующемся программном массиве RAID. Производительность , связанная с вводом-выводом, измеряется путем очистки кэша файловой системы перед каждым запросом, чтобы все обращения к дереву GSS приводили к дисковому вводу-выводу. Производительность с привязкой к ЦП измеряется путем выполнения одного и того же запроса несколько раз в одном сеансе и игнорирования производительности первого запроса, поскольку он загружает данные, к которым осуществляется доступ, в кэш файловой системы. Реальная производительность больших баз данных будет находиться между этими двумя крайностями, поскольку ожидается, что части дерева GSS, особенно самые высокие уровни, будут находиться в кэше файловой системы.Кроме того, в ситуациях, когда запросы уточняются в интерактивном режиме, каждый последующий запрос аналогичен предыдущему, поэтому производительность запроса будет в основном зависеть от ЦП, а не от операций ввода-вывода.
7.1.1. SHREC 2012 Benchmark
Тест SHREC для извлечения общих форм (Li et al. 2012) состоит из 1200 общих форм, равномерно распределенных по 60 различным категориям. Мы используем предоставленную методологию оценки (shr nd), в которой метод восстановления формы оценивается с использованием полной матрицы расстояний 1200 × 1200 между объектами.Это оценивает общую производительность метрики расстояния, которая в нашем случае представляет собой нормализованную разницу объемов, δ VD , применяемую для постановки нормализованных вокселизаций эталонных форм. Кроме того, мы используем эталонный тест SHREC для оценки производительности поиска ближайшего соседа и ограничения формы во время выполнения, а также для сравнения нашего подхода с опубликованными результатами эксперимента SHREC 2012 года.
Мы предварительно обрабатываем формы теста SHREC с помощью MeshLab (мес.г.) и Модульный инструментарий для обработки данных (MDP) (Zito et al. 2009). Meshlab используется для удаления изолированных вершин (шума) из каждой формы и центрирования фигур. Затем модуль PCA MDP используется для выравнивания каждой формы. Полученные нормализованные формы затем вокселизируются с помощью binvox (Min nd, Nooruddin & Turk 2003). Мы оцениваем три разных разрешения вокселизации: 256 3 , 128 3 и 64 3 .
Чтобы лучше оценить влияние размера базы данных на алгоритм поиска, мы выбрали меньшие эталонные наборы из 300, 600 и 900 фигур из набора данных SHREC.Кроме того, мы создаем более крупные наборы эталонов размером 2400, 3600 и 4800, генерируя альтернативные позы каждой формы относительно трех осей координат. Набор из 2400 фигур содержит все исходные фигуры плюс эти фигуры, повернутые вокруг оси x, следующий по величине набор добавляет фигуры, повернутые вокруг оси y, а самый большой набор добавляет фигуры, повернутые вокруг оси z. В дополнение к тому, что мы можем дополнительно исследовать свойства масштабирования нашего алгоритма поиска, эти более крупные наборы данных также позволяют нам оценить метрику разницы объемов при применении к нескольким выравниваниям позы формы.В этом случае учитывается только наилучшая разница объемов любого выравнивания формы.
Чтобы вычислить среднее время запроса ближайшего соседа, мы ищем 1, 2, 4 и 8 ближайших соседей каждой из 1200 эталонных фигур и берем среднее время по всем 1200 запросам. Измеряется только время поиска; время, потраченное на вокселизацию входных данных или запись результатов, не учитывается. Кроме того, мы рассматриваем неиндексированную производительность выполнения простого линейного сканирования октодеревьев для вычисления разницы в объеме запроса по отношению ко всему набору фигур.Поскольку даже самый большой тест полностью выполняется в памяти, при оценке SHREC мы учитываем только производительность, связанную с процессором.
Чтобы оценить поиск ограничений формы в тесте SHREC, мы создаем оптимальные ограничения формы для каждой категории форм, вычисляя пересечение и объединение всех фигур в категории, чтобы получить соответствующие минимальные и максимальные ограничения формы. Эти ограничения оптимальны в том смысле, что они являются максимально жесткими ограничениями, включающими всех членов каждой категории.Матрица расстояний для поиска ограничений формы вычисляется путем присвоения максимального расстояния любой форме, которая не соответствует ограничениям категории запроса, и δ VD тем, которые соответствуют. Это приводит к потенциально асимметричной матрице расстояний и представляет собой верхнюю границу производительности поиска формы, достижимую за счет использования ограничений формы.
7.1.2. Molecular Benchmark
Чтобы лучше оценить производительность наших алгоритмов в масштабе, мы создали большие библиотеки молекулярных форм, содержащие до 22 миллионов форм.Мы используем эти библиотеки форм для оценки чувствительности к параметрам, нашего алгоритма упаковки и масштабируемости поиска на основе ограничений формы. Важно отметить, что хотя мы прилагаем все усилия для разработки синтетического эталонного теста с реалистичными свойствами, основное внимание здесь уделяется оценке наших алгоритмов и структур данных в объемной базе данных, которая достаточно велика, чтобы не быть резидентной в памяти. Будущая работа будет более тщательно исследовать эффективность объемного сопоставления молекулярной формы применительно к виртуальному скринингу соединений.
Для построения нашего эталона мы используем библиотеку синтетически доступных соединений AnchorQuery (Koes et al. 2012). Было определено, что все эти соединения включают индол , особый молекулярный фрагмент с плоским двойным кольцом 5–6, как показано на рис. AnchorQuery включает в себя более 400 миллионов форм, представляющих более 5 миллионов составных частей, каждая из которых содержит этот фрагмент. Мы генерируем эталонные наборы данных путем однородной выборки из 22 классов реакций AnchorQuery с более чем миллионом доступных форм, а затем выравниваем выбранные молекулярные формы с единой системой координат, сосредоточенной на индольном фрагменте.Мы создаем четыре библиотеки с 22 тысячами, 220 тысячами, 2,2 миллионами и 22 миллионами молекулярных форм соответственно.
Пример двух очень разных молекулярных форм, которые были зарегистрированы в одной и той же системе координат, определяемой общим молекулярным фрагментом, плоским кольцом 5–6.
При оценке нашего молекулярного эталона мы в первую очередь рассматриваем поиск по ограничению формы, чтобы сосредоточиться на самом новом аспекте нашего подхода. Чтобы определить реалистичные ограничения формы запроса, мы извлекаем структуры биоактивных малых молекул, связанных с рецепторными белками, из DUD (Huang et al.2006) и наборы данных CSAR (Dunbar et al. 2011), в которых малая молекула содержит желаемый молекулярный фрагмент. В итоге получается 57 комплексов. Затем эти малые молекулы выравниваются и включаются во все наборы тестов, чтобы всегда было хотя бы одно совпадение. Минимальное ограничение формы было получено из малой молекулы, а максимальная форма была получена из рецептора, как описано в разделе 6. Запросы с различной точностью были построены путем применения промежутков, равных 1.0, 1,5 и 2,0 Ангстрема как для минимальной, так и для максимальной формы, как показано на рис. Большее расстояние разрыва соответствует менее точному запросу, который, как ожидается, вернет больше результатов. Например, с библиотекой размером 2,2 миллиона запрос с зазором 1,5 Å возвращает в среднем 66 фигур, а запрос с зазором 2 Å возвращает в среднем 10195 фигур.
Среднее время запроса формы — это среднее значение 57 запросов. Измеряется только время поиска; время, потраченное на вокселизацию входных данных или запись результатов, не учитывается.Из практических соображений построение индекса выполнялось параллельно на сервере хранения Intel Xeon X5680 с тактовой частотой 3,33 ГГц. Каждый процесс разделял 96 ГБ ОЗУ, но выделял выделенное ядро и жесткий диск. Время создания каждого индекса измерялось четыре раза, и сообщается среднее значение трех лучших результатов. Если не указано иное, планки ошибок показывают стандартную ошибку измерения.
7.2. Parameter Sensitivity
Мы учитываем влияние различных вариантов выбора параметров на время создания индекса и качество индекса, измеряемое средним временем запроса ограничения формы, связанным с операциями ввода-вывода и ЦП.Из-за его большего и более значимого размера мы используем молекулярный эталон для этой оценки, но ограничиваемся эталоном из 2,2 миллионов форм для практических целей. Кроме того, в целях оценки чувствительности параметра мы учитываем только среднюю производительность запроса поиска с ограничением формы с расстоянием разрыва, равным 1,5.
Мы оцениваем связь между числом k ближайших соседей, вычисленных при построении графа k -nn, и числом v точек наблюдения, используемых для инициализации приближения k -nn.Мы также рассматриваем связь между количеством кластеров c , сгенерированных алгоритмом BulkLoad , и максимальным размером кластера p , при котором мы выполняем упаковку. То есть алгоритм будет рекурсивно разбивать входной набор на c кластеров до тех пор, пока размер кластера не станет меньше или равен p , после чего кластер будет упакован в плотные узлы дерева GSS. Наконец, мы рассматриваем эффект разветвления узла, m , который представляет собой максимальное количество дочерних элементов узла дерева GSS.Если не указано иное, мы используем значения по умолчанию c = 8, p = 32768, k = 8, v = 32 и m = 16. Эти параметры определены в .
Способность приближения графа k -nn правильно выбирать лучшие ребра для сопоставления в полном графе является ограничивающим фактором производительности алгоритма сопоставления и упаковки. показывает влияние различных значений k и v . Для k = 4, где качество сопоставления особенно чувствительно к ошибкам в приближении k -nn, наблюдается заметное улучшение производительности запросов для больших значений v .Это особенно очевидно для производительности, связанной с процессором. Для k ≥ 8 влияние соотношения и на время запроса менее очевидно. Однако инициализация с точки зрения выгоды приводит к существенному сокращению (более чем в 2 раза) времени построения индекса по сравнению со случайной инициализацией, особенно для больших значений k .
Влияние приблизительных параметров построения графика k -nn k и v на время создания индекса и производительность запросов (a) при привязке к IO и (b) при привязке к CPU.
Влияние количества кластеров c и максимального размера кластеров p показано на рис. Случай p = 0 эквивалентен стандартному алгоритму BulkLoad и обеспечивает основу для сравнения. Разделение данных на большее количество кластеров уменьшает количество рекурсивных разбиений, но увеличивает стоимость каждого разбиения, что приводит к увеличению времени построения. В отличие от предыдущих результатов (Aronovich & Spiegler 2010), мы обнаружили, что увеличение количества кластеров действительно приводит к повышению производительности запросов, возможно, потому, что большее количество кластеров может привести к более дискриминационному разделу входных данных, который более четко отделяет выбросы. .Увеличение p приводит к явному и существенному улучшению производительности запросов, а по мере увеличения p эффект выбора c уменьшается. Небольшие значения p фактически сокращают время построения индекса по сравнению с подходом, основанным только на кластеризации, одновременно демонстрируя более высокую производительность запросов, связанных с вводом-выводом. Для производительности, связанной с ЦП, небольшое количество упаковки может привести к замедлению по сравнению с простой кластеризацией. Это связано с тем, что алгоритм кластеризации создает относительно разреженные деревья поиска со значительно более низким средним разветвлением на узел.Поскольку в случае с привязкой к ЦП не возникает штрафа за ошибку страницы при доступе к дополнительным узлам, меньшее количество вычислений на узел приводит к более высокой общей производительности. Этот эффект проявляется и в .
Влияние количества кластеров c и ограничения размера p , при котором кластер упаковывается с использованием алгоритма сопоставления и упаковки, на время создания индекса и производительность запросов (a) при привязке к IO и (b) при привязке к процессору.
Производительность запросов жадной упаковки, спектральной упаковки и кластеризации (без упаковки) по сравнению с сопоставлением (a) при привязке к вводу-выводу и (b) при привязке к ЦП.Все три алгоритма упаковки выполнялись с использованием полного графа расстояний подобия вместо приближения k -nn с p = 2048.
За счет более длительного времени построения и больших требований к памяти получаются большие значения p . в лучшей производительности запросов, хотя и с уменьшением возврата для p > 2 15 . Упаковка имеет эффект равномерного и плотного распределения элементов в нижней части дерева, что приводит к более короткому и более эффективному дереву.Например, базы данных форм, созданные без упаковки, имеют размер 18 ГБ, а базы данных с p ≥ 128 — 15 ГБ. Как правило, сопоставление и упаковка вдвое сокращают время, необходимое для выполнения запроса, по сравнению с подходом, основанным только на кластеризации, при тех же затратах времени построения индекса.
Влияние максимального разветвления узла, м , показано на . Показана только средняя производительность запроса. Не было существенной связи между m и временем создания индекса, поскольку, хотя m определяет количество элементов, упакованных в узел дерева, это не оказывает существенного влияния на общее количество совпадений, которое логарифмично размеру входных данных.Меньшие значения m приводят к более высокой производительности ЦП, поскольку на каждом узле выполняется меньше ненужной работы (оценка неинтересных дочерних узлов). Напротив, большие значения м приводят к более высокой производительности, связанной с вводом-выводом, до определенного момента, поскольку оценка меньшего количества более крупных узлов приводит к меньшему количеству отказов страниц. Оптимальный выбор m сильно зависит от размера элементов в узле, размера кэша упреждающего чтения файловой системы и вычислительных затрат на оценку элемента.Мы обнаружили, что m = 16 обеспечивает хороший компромисс между производительностью, связанной с вводом-выводом, и производительностью, связанной с процессором.
Влияние максимального разветвления узла, m , на производительность запросов при привязке к вводу-выводу и при привязке к ЦП.
7.3. Сравнение производительности упаковки
Мы рассматриваем два альтернативных способа упаковки в . Мы оцениваем алгоритмы упаковки, используя запросы ограничения формы с размером зазора 1,5 Å, выполненные на молекулярном эталонном тесте с 2,2 миллионами форм. Жадный алгоритм сопоставляет пары несопоставленных элементов в том порядке, в котором они находятся в отсортированном списке расстояний между элементами.Этот жадный алгоритм представляет собой двукратное приближение алгоритма оптимального сопоставления (Ausiello 1999). Другой подход к упаковке состоит в том, чтобы присвоить набору данных линейный порядок, который может быть выполнен математически точным способом с использованием теории спектральных графов (Мокбель и др., 2003). Мы оцениваем эти алгоритмы, используя полный граф расстояний между элементами, поэтому устанавливаем p = 2048, чтобы уменьшить количество вычислений расстояний. В целях сравнения мы также оцениваем наш алгоритм сопоставления и упаковки, используя полный граф, а не приблизительный граф k -nn.Поскольку время работы сопоставления и спектрального упаковщика масштабируется по-разному с полным графом по сравнению с жадным упаковщиком, мы не сравниваем время построения индекса.
Три алгоритма упаковки сравниваются с кластеризацией без упаковки, которая эквивалентна алгоритму инициализации CM-дерева BulkLoad (Aronovich & Spiegler 2010). Спектральная упаковка не обеспечивает значительного улучшения производительности по сравнению с кластеризацией, что указывает на то, что она не является эффективным средством группировки связанных элементов.Жадная упаковка улучшает кластеризацию, но не так эффективна, как сопоставление, что иллюстрирует преимущество использования оптимального, а не приближенного алгоритма.
Хотя разница в производительности между сопоставлением и жадной упаковкой для p = 2048 незначительна, эта разница увеличивается для больших значений p , как показано на рис. В отличие от , здесь используется построение графа k -nn. Для небольших значений p жадная упаковка имеет удивительно нестабильную производительность, возможно, из-за различий в том, как два алгоритма обрабатывают выбросы.Для больших значений p разница заметна как для производительности, связанной с вводом-выводом, так и с привязкой к ЦП, при этом жадное сопоставление приводит к замедлению в 2 раза и сокращает время построения индекса только на небольшой процент.
Производительность запроса и время построения индекса при жадной упаковке и сопоставлении в качестве ограничения размера, p , при котором упаковывается кластер, увеличивается (a) при привязке к IO и (b) при привязке к ЦП.
7.4. Производительность извлечения формы
Производительность метрики разности объемов, δ VD , при идентификации связанных форм в базе данных SHREC показана на , а дисконтированный кумулятивный прирост показан на .Производительность этой простой метрики примерно соответствует показателю SHREC 2012 с самой низкой производительностью, и при использовании вокселизации с более низким разрешением производительность снижается очень незначительно. Это неудивительно, поскольку метрика разницы в объеме, в отличие от материалов SHREC, не является инвариантной позы, и мы используем базовый метод выравнивания позы. Действительно, если учитывать несколько выравниваний поз, дисконтированный кумулятивный прирост улучшается с 0,50 до 0,57. Это улучшение, по крайней мере, частично связано с тем фактом, что наше общее выравнивание PCA не обязательно ориентирует формы в постоянном и естественном направлении, как показано наложением форм ракет на .Предыдущая работа показала, что более сложные методы выравнивания и нормализации улучшают показатели сходства, которые не являются инвариантными по позам (Sfikas et al. 2011, Chaouch & Verroust-Blondet 2008).
Пример ограничений оптимальной формы. Ограничения (a) MIV и (b) MSV, полученные путем пересечения и объединения, соответственно, выровненных фигур в категории «Ракета» теста SHREC 2012.
Дисконтированный кумулятивный прирост метрики разницы объемов в наборе данных SHREC 2012.Обеспечивается производительность для трех различных разрешений вокселизации. Производительность одной позы учитывает только разницу в громкости для каждой выровненной позы. Производительность нескольких поз учитывает наилучшую разницу в объеме каждой выровненной позы и ее трех осевых вращений. Ограничения оптимальной формы учитывают только разницу в объеме тех поз, которые удовлетворяют минимальным и максимальным ограничениям формы, полученным непосредственно из форм категорий.
Таблица 2
Производительность распознавания формы метрики разницы объемов в эталонном тесте SHREC 2012.Показатели производительности определяются и рассчитываются в соответствии с рекомендациями по эталонным тестам SHREC 2012 (shr n.d.). Во всех случаях значения, близкие к единице, указывают на лучшую производительность распознавания объектов. Предусмотрена производительность для трех различных разрешений вокселизации. Производительность с одной позой учитывает только одну нормализованную позу для каждого объекта, в то время как производительность с несколькими позами использует наилучшую разницу в объеме среди четырех поз, доступных при осевом вращении. Ограничения оптимальной формы устанавливают максимальное значение расстояния до несовпадающих фигур.Опубликованные минимальные, медианные и максимальные баллы теста SHREC 2012 также приведены для справки.
| Ближайший + Соседний | 1-уровня | 2-уровня | е-Мера | со скидкой накопительное Gain | |||||
|---|---|---|---|---|---|---|---|---|---|
| Одно Поза | 256 3 | 0,4367 | 0,1686 | 0,2351 | 0,1616 | 0,4980 | |||
| 128 3 | 9 9,4308+0,1687 | 0,2357 | 0,1618 | 0,4976 | |||||
| 64 3 | 0,4333 | 0,1671 | 0,2314 | 0,1594 | 0,4952 | ||||
| + | |||||||||
| Множественный Позы | 256 3 | 0.5358 | 0.2423 | 0.3275 | 0.2274 | 0.5686 | |||
128 3| 128 | 0.5267 | +0,2412 | 0,3272 | 0,2268 | 0,5672 | | |||
| 643 | 0,5175 | 0,2376 | 0,3214 | 0,2240 | 0,5641 | ||||
| 256 3 | 0.9475 | 0.8691 | 0.9471 | 0.6995 | 0.9538 | ||||
| 128 | |||||||||
| 128 3 | 0.9275 | +0,8166 | 0,9313 | 0,6849 | 0,9348 | ||||
| 64 3 | 0,8800 | 0,7308 | 0,8764 | 0,6370 | 0,8923 | ||||
| SHREC 91 629 2012 | Минимальный | 0.431 | 0.179 | 0.257 | 0.175 | 0,510 | 0.510 | ||
| Median | 0.6965 | 0.3715 | 0.499 | 0.34859 | 0.3485 | 0.682 | |||
| Максимум | 0.879 | 0.661 | 0.661 | 0.5799 | 0.576 | 0.571 | 0.571 | 0.871 | |
Дополнительно к нашему объему. Представление формы — это исполнение формы, используя ограничения формы. Ограничения оптимальной формы, как показано на рисунках и , превосходят даже лучшие материалы SHREC 2012, даже при использовании самого низкого разрешения вокселей. Поскольку эти ограничения формы являются самыми строгими из возможных ограничений для каждой категории, их производительность поиска формы является верхней границей того, что возможно для нашего набора выровненных фигур.Тем не менее, более сложный процесс выравнивания формы может способствовать дальнейшему повышению производительности поиска формы, в то же время приводя к более естественным ограничениям формы (таким как ограничение ракеты, где все плавники ориентированы одинаково, в отличие от ).
7.5. Query Time
Скорость запроса структуры индексации дерева GSS зависит от типа и широты запроса и содержимого базы данных. Поскольку запрос ограничения формы ослабляется, чтобы соответствовать большему количеству фигур, скорость запроса будет приближаться к скорости линейного сканирования.С другой стороны, запрос ограничения формы, который имеет узкое определение или существенно отличается от большинства фигур базы данных, может потребовать изучения только одной ветви дерева (или завершиться даже раньше, если запрос не соответствует ни одной фигуре), что приводит к логарифмическому поиску. . Напротив, поиск k ближайших соседей всегда возвращает ограниченное количество фигур ( k ), но скорость запроса в дереве GSS ограничена тем, насколько хорошо текущее k -е наилучшее совпадение обрезает оставшееся дерево поиска. .Если текущее k -е наилучшее совпадение не намного ближе к запросу, чем остальные фигуры в дереве, скорость запроса будет приближаться к скорости линейного сканирования. В качестве альтернативы, если k фигур, идентифицированных при первом спуске дерева, явно отличаются от остальных фигур, тогда скорость будет логарифмически масштабироваться с размером базы данных. Наконец, скорость запроса зависит от разрешения вокселей сохраненных форм. Формы с более высоким разрешением приводят к увеличению размера базы данных, а операции с октодеревом, такие как вычисление разницы объемов, занимают больше времени.
Среднее время выполнения запросов с привязкой к процессору для эталонного теста SHREC 2012 показано в и . Этот тест достаточно мал, чтобы вся база данных могла находиться в памяти. Общий размер базы данных, включая индекс и объекты, составляет 20 МБ, 89 МБ и 401 МБ для фигур разрешения 64 3 , 128 3 и 256 3 соответственно. Как показано на и , уменьшение разрешения оказывает минимальное влияние на производительность поиска формы. Однако, как показано на , ожидается существенное увеличение времени поиска по мере увеличения разрешения формы.Чем больше операций сравнения фигур вызывает запрос, тем заметнее это увеличение. Например, линейное сканирование более чем в 30 раз медленнее при разрешении 256 3 , чем при разрешении 64 3 , но только в 8 раз медленнее при поиске по ограничению формы. Чтобы представить эти цифры в перспективе и сравнить с более традиционным, необъемным подходом вектора признаков, мы оценили наш тест SHREC 2012 с использованием метода 3DSP (López-Sastre et al. 2013, Redondo-Cabrera et al. 2012), который в настоящее время это единственная заявка на SHREC 2012 с общедоступным исходным кодом.Этот метод обеспечивает среднее время запроса 0,03 секунды с использованием метрики расстояния χ 2 и 0,001 секунды с метрикой расстояния пересечения гистограммы с настройками по умолчанию. Другие подобные подходы, вероятно, будут иметь такие же большие диапазоны времени запроса в зависимости от метрики расстояния и размера вектора признаков. Наш подход находится в пределах этого диапазона, но, что более важно, поскольку фигуры индексируются, они могут масштабироваться сублинейно в зависимости от размера базы данных.
Среднее время запроса ограничения формы (SC), связанное с процессором, k ближайших соседей (NN k ) и поиски линейного сканирования (Scan) эталонного теста SHREC при разрешении вокселизации 64 3 .(а) Производительность запросов по мере увеличения количества фигур. (b) Блочная диаграмма распределения времени запроса при запросе базы данных 1200 форм.
Таблица 3
Среднее время запроса ограничения формы (SC), k ближайшего соседа (NN k ) и поиск линейного сканирования (Scan) эталонного показателя SHREC из 1200 фигур для всех трех разрешений вокселей.
| Разрешение | NN1 | NN1 | NN2 | NN4 | NN4 | NN8 | Сканирование | ||
|---|---|---|---|---|---|---|---|---|---|
| 256 3 | 0.00503 | 0,11237 | 0,44692 | 0,51444 | 0,54276 | 0,53709 | |||
| 128 3 | 0,00117 | 0,01889 | 0,05094 | 0,05361 | 0,05507 | 0,04974 | |||
| 64 3 | 0,00062 | 0.00692 | 0.01745 | 0.017450.01853 | 0,01914 | 0.01787 |
Масштабирование производительности запросов по сравнению с измерением уровня SUREC.Несмотря на то, что по дизайну все запросы с ограничением формы возвращают не менее 20 фигур, по сравнению с меньшими наборами результатов k запросов ближайших соседей, запросы с ограничением формы выполняются значительно быстрее. Это связано с тем, что проверка ограничения формы обычно является более быстрой операцией октодерева, чем разница объема, из-за оценок короткого замыкания, а также потому, что эти ограничения формы определены достаточно узко, поэтому для идентификации совпадающих форм в дереве GSS требуется только ограниченное количество сравнений.
Производительность запросов k ближайших соседей ограничена размером и содержимым базы данных shape. Поиск одного ближайшего соседа работает достаточно хорошо, потому что все запросы в нашем тесте имеют точное совпадение в базе данных. Как только будет найдено это точное совпадение с нулевой разницей в объемах, остальная часть дерева может быть осмысленно удалена. Большие значения k указывают на производительность при отсутствии точного совпадения. В этом случае дерево поиска сокращается только на самых низких уровнях, если вообще сокращается, что приводит к минимальным улучшениям времени поиска.Однако эти улучшения становятся более заметными по мере увеличения размера базы данных. Как и ожидалось, производительность запроса сильно зависит от его состава, как показано на диаграммах на диаграммах. Даже линейное сканирование демонстрирует изменчивость времени запроса, поскольку разные формы запроса будут вызывать разное поведение короткого замыкания при вычислении разницы в объеме.
Эталонный тест молекулярной формы предоставляет средства для оценки запросов к большой базе данных форм, и значения производительности запросов для этого эталонного теста показаны в и .При поиске в больших базах данных преимущество индекса дерева GSS для выполнения поиска ближайшего соседа становится более очевидным. Как показано на рисунке, линейное сканирование базы данных 2,2 миллиона молекулярных форм более чем в 8 раз превышает среднее время запроса при поиске 8-го ближайшего соседа и более чем в 2800 раз превышает время поиска по ограничению формы. Тем не менее, как и в случае с эталонным тестом SHREC, заметна явная разница между поиском одного ближайшего соседа, при котором обнаруживается точное совпадение, и поиском других ближайших соседей.Кроме того, как показано на рисунке , различные формы запросов приводят к широкому диапазону времени поиска k ближайших соседей, особенно для больших значений k .
Среднее время запроса ограничения формы (SC), привязанное к ЦП, k ближайших соседей (NN k ) и линейное сканирование (Scan) поиск эталона молекулярной формы. (а) Время запроса по мере увеличения количества форм. (b) Блочная диаграмма распределения времени запроса при запросе базы данных с 2,2 миллионами форм.Для ясности диаграмма линейного сканирования опущена, поскольку она имеет шкалу со средним значением 45,7 секунды.
Среднее время запроса ограничения формы для трех запросов с разной точностью при увеличении размера базы данных в десять раз. Показана средняя производительность (а) для операций ввода-вывода и (б) для ЦП. Время запроса показано в логарифмической шкале. Столбики погрешностей показывают диапазон от самых быстрых до самых медленных запросов. Также указывается производительность поиска, выполняемого с использованием полного линейного сканирования базы данных вместо подхода индексирования.
Средняя производительность с привязкой к операциям ввода-вывода и ЦП для запросов с ограничением формы, созданных с использованием трех разных размеров промежутков в базах данных эталонных показателей молекулярной формы, показана на . Обратите внимание, что время поиска отображается в логарифмическом масштабе, а планки погрешностей указывают диапазон между самыми быстрыми и самыми медленными запросами. Также показана производительность выполнения линейного сканирования с ограничением формы по всему набору фигур. Это быстрее, чем линейное сканирование разности объемов, поскольку проверка ограничения формы с большей вероятностью вызовет операции с коротким замыканием октодерева.
Производительность нашего древовидного индекса GSS явно выше, чем у линейного сканирования. В частности, для узких и точных запросов (размер промежутка 1,0) метод масштабируется сублинейно по отношению к размеру базы данных. Наш подход также выигрывает от необходимости меньшего объема памяти. Например, база данных с 22 миллионами фигур слишком велика, чтобы поместиться в основную память, поэтому линейное сканирование всегда связано с вводом-выводом при поиске в этой базе данных. Напротив, производительность, связанная с процессором, при поиске запросов с размером промежутка 1.0 или 1,5 на несколько порядков быстрее, чем с привязкой к IO, при использовании индекса дерева GSS, поскольку весь рабочий набор умещается в памяти. Конечно, для достаточно широких запросов индексация не дает никакой пользы. Это относится к самому медленному запросу с размером промежутка 2. Этот запрос возвращает более десятой части базы данных.
Страница не найдена | ЛАКМА
«Метрополис II» Криса Бёрдена – это мощная кинетическая скульптура, созданная по образцу фа…
Колин Смит — междисциплинарный художник из Лос-Анджелеса, чьи работы отражают…
View From Here: Recent Acquisitions представляет подборку из 16 недавно приобретенных работ…
Ёситомо Нара — один из самых любимых японских художников своего поколения.Его…
Возможно, самый доминирующий вид искусства за последние 100 лет, кино имеет важное значение…
Утренники по вторникам
Наслаждайтесь концертами с участием ведущих международных и местных ансамблей в программах…
Искусство и музыка, Джаз в LACMA, Latin Sounds, Sunday Live
Живопись, гравюры, коллажи и многое другое — не выходя из собственного дома!…
Random International’s Rain Room (2012) — это иммерсивная среда вечного…
Дождевая комната
150 Portrait Tone Марка Брэдфорда, композиция размером с фреску, содержащая элементы…
Работа художника Роберта Ирвина за последние пять десятилетий исследовала восприятие…
В фильме Барбары Крюгер «Без названия» (Shafted) показано ее характерное использование рекламы…
Band (2006) можно считать величайшим произведением Ричарда Серры, представляющим наиболее полный…
Коллекция современного искусства LACMA, в которой представлены преимущественно европейские и американские произведения…
Группа по приобретению LACMA и члены Художественного совета разделяют глубокую привязанность к…
Художественные советы, Группы по приобретению, Искусство Ближнего Востока: СОВРЕМЕННОЕ, Совет азиатского искусства, Совет по костюмам, Совет по декоративному искусству и дизайну, ОБЪЕКТИВ: Совет по фотографии, Совет по современному и современному искусству, Совет по гравюрам и рисункам
Добро пожаловать на страницу вакансий Музея искусств округа Лос-Анджелес.Увидеть…
Работа, Карьера, Стажировки, Волонтерство
Присоединяйтесь к музейным педагогам, художникам, кураторам и экспертам для участия в беседах художников, виртуальных…
Создание+Совместная работа
В «Золотом часе» более 70 художников и три фотоколлектива предлагают…
Основанный в 1967 году Центр консервации LACMA поддерживает деятельность музея…
консервация живописи, консервация бумаги, консервация предметов, консервация текстиля, наука о консервации, консервация изображений
Барбара Крюгер: Думаю о тебе.Я имею в виду себя. Я имею ввиду тебя. является крупной выставк…
В ролях: Ай Вэйвэй, Хуан Юн Пин, Ван Гуанъи, Сюй Бин, Юэ Миньцзюнь и другие…
Помимо конкретных материалов, таких как чернила и бумага, существует неосязаемый дух, не…
В дополнение к презентации книги «Портреты Обамы» Кехинде Уайли и Эми С…
С момента их открытия в Национальной портретной галерее Смитсоновского института…
(Лос-Анджелес, Калифорния — 13 января 2022 г.) — Художественный музей округа Лос-Анджелес (LACMA…
V4PCS: объемный алгоритм 4PCS для глобальной регистрации | Дж.мех. Дес.
На основе обсуждения процессов генерации пар и извлечения конгруэнтных наборов псевдокод предложенного алгоритма V4PCS показан в алгоритме 1. Подобно S4PCS, V4PCS также работает по принципу RANSAC. Решая задачу о наибольшем общем наборе точек, алгоритм находит наибольший размер согласованного набора и впоследствии получает наилучшее жесткое преобразование T. Когда степень совпадения h составляет 95% или выше, алгоритм завершается, так как именно тогда, вероятно, будет найдена правильная регистрация.
В основном цикле V4PCS первым шагом является генерация пары PG из строк 3–6. Сначала из S случайным образом выбирается тетраэдрическое основание большого объема {qi}, а затем информация о расстоянии до основания может быть рассчитана как d1, d2, …, d6. Имея эту информацию о расстоянии, шесть пар отводов можно извлечь из M с помощью метода O(n), разработанного в S4PCS. После этого все извлеченные пары сохраняются в шести таблицах связности H.Следовательно, этот шаг занимает время O(6n). Вторым шагом является CSE от строки 7 до 9, который в основном перебирает все извлеченные пары из M и ищет конгруэнтные наборы тетраэдра U через таблицы связности H. Поскольку сложность поиска составляет O(1), этот шаг занимает O(k) времени. Последним шагом является CSV от строки 10 до 16. Все конгруэнтные наборы проверяются путем нахождения жесткого преобразования для выравнивания {pi} с {qi}, а также для преобразования M в S для вычисления оценки совпадения с использованием наибольшего набора общих точек. как в S4PCS.Мы не изменили этот шаг, и временная сложность осталась прежней. Таким образом, временная сложность предложенного V4PCS по сравнению с S4PCS уменьшена с O(n+k+c) до O(n+k), где n — количество точек в M, k — количество пар, о которых сообщается. , а c — количество извлеченных конгруэнтных наборов. Поскольку все извлеченные наборы являются конгруэнтными наборами, нам не нужна информация об отношении для извлечения угла соответствия для фильтрации ложных на этапе CSE. Хотя теоретическое улучшение не выглядит существенным, на практике оно может значительно ускорить процесс, а также уменьшить величину k, что будет показано в разд.5.
Мохамад и др. [29] пришли к такому же выводу и предложили использовать некомпланарное основание, введя в конструкцию основания еще одно измерение с дополнительной промежуточной точкой. Однако для того, чтобы найти конгруэнтное множество после создания пары, им необходимо растрировать окружность на трехмерной сетке, которая хранит промежуточные точки, перемещаясь дискретными круговыми шагами, чтобы проверить все ячейки сетки, которые пересекают окружность с центром в точке e (см.6). Это угловое приращение для кругового движения можно рассчитать по следующей формуле: cos−1(2h3−2ϵ2/2h3), где h — расстояние между двумя сегментами, а ϵ — заданный запас. Для каждого запроса существует постоянный коэффициент k1=360/ cos−1(2h3−2ϵ2/2h3); следовательно, временная сложность по сравнению с S4PCS увеличивается с O(n+k+c) до O(n+k1k+c). Их метод теоретически увеличивает временную сложность шага CSE из-за необходимости нахождения перекрывающейся промежуточной точки, что портит красоту алгоритма 4PCS, изложенного в примечании 1.Фактически, эффективность, полученная на этапе CSV в их методе, превосходит эффективность, потерянную на этапе CSE. Чтобы исправить последствия увеличения времени поиска, они зафиксировали расстояния d1 и d2, чтобы уменьшить количество итераций, что снижает определенную гибкость алгоритма. Напротив, наш метод может использовать объемную информацию и в то же время теоретически уменьшить временную сложность.
С точки зрения пространственной сложности, S4PCS использует эффективный метод растеризации гиперсферы для извлечения пар и хранения индексов, растрированной сетке требуется O(n) пространства для ввода n точек.Кроме того, извлеченные k пар сохраняются в хэш-таблице с информацией об углах для поиска конгруэнтного множества, для которого требуется O(k) пространства. Таким образом, общая пространственная сложность для S4PCS составляет O(n+k). В предложенной версии V4PCS шаг генерации пар такой же, как в S4PCS; следовательно, для заданных n точек требуется O (n) пространства. Мы строим таблицу связности для извлеченных k пар, где каждое ребро сохраняется дважды с обеими его конечными вершинами, и поэтому оно занимает O (2k) пространства. Таким образом, V4PCS имеет пространственную сложность O(n+2k), что немного выше, чем у S4PCS.
| алгоритм 1 Объемные 4 шт. | |
| Вывод: Лучшие преобразования T | |
| 1. H = 0; T =0;л=0; | |
| 2. Пока ч <0,95 и L | |
| // Создание пара (PG) | |
| 3. {Qi, i = 1 … 4} = SelectTetrahedralbase (S) | |
| 4.d1, d2, …, d6 — боковые стороны {qi} | |
| 5. Извлечь пары d1, d2,…, d6 из M [4] | |
| 6. Создать таблицу связности H для хранения индекса извлеченных пар | |
| // Конгруэнт набор добычи (CSE) | |
| 7. для всех Пары, извлеченные из M | |
| 8. u ← Поиск H, чтобы найти другие 5 пар, чтобы сформировать конгруэнтное тетраэдр для { qi} | |
| 9. конец для | |
| // Congrament Set Verification (CSV) | |
| 10. для всех конгруэнтрических тетраэдральных наборов {Pi} ∈U DO | |
| 11. T ← Жесткая трансформация выравнивается {pi} to {qi} | |
| 12. S = вычислить счет для T по общему пункту | |
| 13. , если S> H , затем | 14. H ← S; T ←т; |
| 15. end if | |
| 16. end for | |
| 17. l←l+1; | |
18. | 18. | |
| 19. T |
| Algorithm 1 Объемные 4 шт. | |
| Вход: Наборы целевых и исходных пунктов, S и M | |
| Выход: Лучшее преобразование T | |
| 1.ч=0;Т=0;л=0; | |
| 2. Пока ч <0,95 и L | |
| // Создание пара (PG) | |
| 3. {Qi, i = 1 … 4} = SelectTetrahedralbase (s) | |
| 4. D1, D2, …, D6 являются боковыми боковыми наборами {Qi} | |
| 5. Экстракт D1, D2, …, D6 пары от M [4] | 9084|
| 6. Создайте таблицу связности H для хранения индекса извлеченных пар | |
| //Извлечение конгруэнтного множества (CSE) | |
| 7. для всех пары, извлеченные из M | |
| 80827 | 8. u ← Поиск H Чтобы найти другие пары, чтобы сформировать конгруэнтное тетраэдр на {Qi} |
| 9. Конец для | |
| // Подтверждение конгруэнтных наборов (CSV) | |
| 10. для всех конгруэнтных тетраэдральных наборов {Pi} ∈U DO | |
| 11. T ← Жесткая трансформация выравнивает {Pi} к {Qi} | |
| 12.s= вычислить оценку для t по набору общих точек | |
| 13. , если s>h , тогда | |
| 14. ← s; | |
| 15. конец если | |
| 16. конец для | |
| 18. конец для | |
| 19. возврат T |
Исследование управления геометрическим узором с использованием цифрового алгоритма (с упором на анализ и применение узора исламской звезды)
В этом документе представлено исследование по анализу и модификации узора исламской звезды с использованием цифрового алгоритма, в котором представлен метод эффективного изменения и контролировать классические геометрические узоры с помощью экспериментов и применения компьютерных алгоритмов.Это поможет преодолеть разрыв между близостью классических геометрических узоров и притоком дизайна с помощью цифровых технологий, а также заложить основу для эффективности и гибкости при разработке будущих конструкций и изготовления материалов, способствуя лучшему пониманию различных методов управления геометрическими формами. узоры.
1. Введение
С развитием цифровых технологий развитие поверхностей в современных структурах пользуется беспрецедентной свободой выражения.Разнообразные возможности компьютерных программ, созвучные желанию дизайнеров открывать новый дизайн, ускоряют скорость «безграничного» дизайна за счет распространения, модификации и отслеживания траектории. Быстрое развитие компьютерных технологий приводит к тенденции производить непредсказуемые расчеты с помощью компьютера, используя алгоритм, не зависящий от художника. Развитие технологии производства также позволило построить различные экспериментальные формы, что дает хорошее обоснование в качестве значимой строительной работы.Эти явления пытаются отделить себя от правил классической геометрии, используя такие термины, как «цифровая геометрия» и «цифровая материальность». Чтобы противостоять этой быстрой тенденции, некоторые архитекторы резко ограничивают роль компьютера, отказываются от проектов, созданных цифровыми программами, и вместо этого создают проекты, основанные на традициях и истории чувства геометрии. Это исследование будет посвящено несоответствию такой крайней позиции в отношении использования компьютерных алгоритмов в дизайне. Целью данного исследования является выявление точки соединения классической геометрии и алгоритмического проектирования.Другими словами, чтобы преодолеть близость классических узоров с помощью исследований узоров, созданных дизайнерами, а также преодолеть приток дизайна с помощью цифровых технологий, цель этого исследования состоит в том, чтобы представить метод для эффективного изменения и управления классическими геометрическими узорами посредством экспериментов. и применения компьютерных алгоритмов.
2. Методы
В качестве объекта анализа данного исследования мы использовали модель исламской звезды. В частности, это исследование выбрало 4.8.8 среди примеров модифицированных звездных узоров, используемых в методе Ханкина. Для анализа и экспериментального контроля этого паттерна мы использовали «Grasshopper» и «Rhinoscript», которые являются подключаемыми модулями для программы Rhinoceros от Robert McNeel and Associates, а также «Processing», разработанную Беном Фраем и Кейси Риас. Цель исследования представлена в Разделе 1. Метод исследования объясняется в Разделе 2. Мозаика, узоры исламского искусства и разработка алгоритмов представлены в Разделе 3. Методы контроля с использованием анализа и алгоритма узоров исламских звезд представлены в Раздел 4: (а) метод бокового разделения и (б) метод расширения одного модуля.Обсуждаются также различные эксперименты по выявлению точек пересечения. На их основе мы будем оценивать возможности модификации и удобство управления. Это будет кратко изложено в Разделе 5.
3. Мозаика и разработка алгоритма
3.1. Геометрическая концепция мозаики
«Мозаика» может быть определена как узор из более чем одной формы, полностью покрывающий определенную плоскость. Метод регулярного разбиения плоскости — это метод, который не оставляет пробелов за счет использования определенной формы, полностью заполняет пространство без наложения и не допускает наложения фигур или пробелов [1].Мозаика обычно состоит из замкнутых фигур или замкнутых кривых, а простейшим видом замкнутой кривой является многоугольник. Многоугольник можно превратить в мозаику, состоящую из сложных фигур. Прежде всего, всевозможные треугольники и прямоугольники могут образовывать мозаику. Это связано с тем, что сумма их внутренних углов равна 180° и 360° соответственно [2]. При сочетании 6 равносторонних треугольников, 4 равносторонних прямоугольников. и 3 равносторонних шестиугольника, мы можем создать многоугольник с общим внутренним углом 360°.Это основная формула формирования и сочетания тесселяции, которая имеет внутренний угол фокуса 360° (рис. 1) [3].
Если диапазон равностороннего многоугольника сузить, как показано на рис. 1, мозаику можно сформировать только из трех типов многоугольников: равносторонних треугольников, равносторонних прямоугольников и равносторонних шестиугольников. Математики обнаружили 21 вид комбинаций равносторонних многоугольников, которые заполняют пространство на основании одной точки в центре (рис. 2) [2].
Узоры, которые появляются на исламских зданиях и изразцах Средневековья, начинались с простых рисунков и на протяжении веков развивались в сложные узоры с математической симметрией. Эти сложные узоры были изменены методом страпоуокинга (рис. 3) [4] с использованием кругов и прямоугольников в перекрывающихся решетчатых узорах, а затем были усовершенствованы для создания более сложных форм симметричных узоров. Типичным примером тесселяции являются сложные геометрические узоры, которые мавры и арабы использовали для украшения своей архитектуры.
Подобные исламские узоры оказали большое влияние на современных художников (рис. 4 и 5). Среди них такие исполнители оп-арта, как Виктор Вазарели и Бриджит Райли, а также гравёр М.К. Эшер [2].
3.2. Понимание разработки алгоритмов
Алгоритм представляет собой группу четко определенных правил и конечного числа шагов, используемых для решения математической задачи. Это набор четко определенных правил и команд в конечном числе, и он может решить проблему, применяя свои ограниченные правила [5].Поскольку алгоритм создает единицу посредством вычислений и формирует шаблон, он противостоит дизайну, который зависит от эвристических знаний и вдохновения. Тем не менее, причина, по которой сложные расчеты и математические алгоритмы используются при проектировании или создании шаблона, заключается в том, что дизайн, созданный с помощью процесса расчета, более эффективен, чем тот, который произвольно создан архитектором в погоне за свободой выражения и отделен от общего. реальная структура [6]. Процесс проектирования с использованием алгоритма появляется не только в современном обществе.На протяжении столетий, от прошлого до настоящего, архитекторы предпринимали попытки проектирования, используя преимущества математики как часть усилий по сближению математики со строительством. Благодаря цифровым инструментам современного общества современные математические алгоритмы используются не только при проектировании автомобилей и кораблей, но и в различных областях, таких как компьютерный дизайн и медиаискусство. Также математические алгоритмы выдают результаты с переменными в зависимости от ситуации и разрабатывают фигуры в соответствии с правилами математической формулы [7].Следовательно, необходимо понимать функцию математических формул, чтобы воплощать и выражать формы на основе правил в процессе. Следовательно, применение математических формул в строительном проектировании может быть эффективно использовано для управления проектированием за счет использования вычислительных технологий в соответствии с современным обществом, и мы можем реализовать процессы модификации с помощью шагов алгоритма (рис. 6) [8].
4. Анализ исламского узора с использованием цифрового алгоритма
4.1. Схема дизайна исламского узора
Исламский узор в виде звезды с использованием геометрических фигур является одной из величайших мировых традиций дизайна орнаментов. Его распространение, включая архитектурное применение, значительно выросло на Ближнем Востоке и в Центральной Азии [9]. Исламский узор звезды выражает преобразование, симметрию, баланс и уникальность гармоничной математики. Исламское искусство отдавало предпочтение пропорциональной геометрии как форме священного искусства [10]. Был проведен эксперимент по проектированию геометрических узоров с использованием цифровых алгоритмов, чтобы найти эффективный метод управления для изменения геометрических узоров с помощью Grasshopper, программы, основанной на математическом алгоритме, которая использует параметры, с целью изучения методов формирования узоров исламских звезд различной формы. модификации.Важную веху в подходе к созданию исламских звездных узоров на основе мозаики установил метод контактных многоугольников Э. Х. Ханкина. В своей статье он предложил отличную отправную точку для подхода к созданию узоров исламских звезд и привел различные примеры формирования узоров с помощью метода Ханкина (рис. 7 и 8) [11].
4.2. Анализ
Как упоминалось в разделе 3, мы сосредоточимся на мозаиках, которые состоят из комбинаций нескольких односторонних полигонов, основанных на базовых полигонах.Среди них мы пытаемся проанализировать процесс модификации геометрических фигур, используя комбинацию 4.8.8, базовую комбинацию, используемую в методе Ханкина, и исследуем различные типы процессов модификации конструкции, используя программу цифрового алгоритма Grasshopper. Комбинация 4.8.8 представляет собой узор, состоящий из прямоугольников и восьмиугольников (рис. 9). Единичные модули этих восьмиугольников и прямоугольников состоят из треугольников определенной формы (рис. 10).
Согласно методу Ханкина форма звезд может трансформироваться при изменении угла сторон каждой базовой геометрической фигуры (рис. 11).С помощью математического алгоритма, который будет проанализирован в этом исследовании, методы управления для создания различных форм геометрических фигур с помощью математических алгоритмов можно разделить на два типа: метод бокового разделения и метод расширения одного модуля (рис. 12). Если углубиться в метод бокового разделения, то его можно разделить на два типа: метод управления точкой на сегменте (рис. 13) и метод управления радиусом (рис. 14). Метод расширения с одним модулем можно разделить на метод управления «точка на сегменте» (рис. 15) и метод управления «линия на сегменте» (рис. 16).
4.3. Формирование основных геометрических фигур
Чтобы создать простую 4.8.8 геометрическую фигуру на плоскости, мы должны сначала разделить стороны. Для формирования геометрических фигур 4.8.8 мы должны начать с плоскости с прямоугольной системой сеток (рис. 17).
Для создания поверхности прямоугольника можно использовать формулу алгоритма (рис. 10). Вся поверхность разбита на прямоугольники с одним базовым модулем.Каждая сторона прямоугольника единичного модуля разделена на три части. Если первую точку стороны, разделенной на три, соединить со второй точкой противолежащей стороны, то получится геометрическая 4.8.8 фигура (рис. 18).
4.3.1. Метод управления боковым разделением
Метод бокового разделения можно разделить на методы управления точкой на стороне и методы управления радиусом. В методе управления «точка на стороне» в качестве переменной задается точка на отрезке (рис. 19(а)), соединяющем каждую угловую точку восьмиугольника со средней точкой.Следовательно, если точка на отрезке перемещается, длина линии, соединяющей точку (а) на отрезке со средней точкой (рис. 19(б)) каждой стороны восьмиугольника, изменяется. В методе управления радиусом в качестве переменных задаются радиус () окружности, средней точкой которой является середина восьмиугольника, и отрезок, соединяющий каждую угловую точку восьмиугольника и среднюю точку. Следовательно, если положение точки пересечения (рис. 19(д)) окружности и отрезка (г) смещается, то изменяется и длина соединяющей их линии.
(a) Метод управления «точка на сегменте» (тип A) . Контроль точки на сегменте — это метод, который управляет положением точки (Рисунок 13: ) на каждом сегменте вектора (Рисунок 13: ) как манипулятивной переменной. Поскольку метод может управлять соответствующими положениями точек на векторных сегментах, он может изменять вектор в различных формах. Однако для этого требуется сложная математическая формула, поскольку она должна анализировать положение каждой точки на каждом сегменте.Поскольку этот метод назначает соответствующее положение каждой точки, он может установить каждую линию с разной длиной. В результате он может создавать модули различной формы в бесконечном количестве. Если критическая точка не назначена, положение точки может отклоняться от отрезка; следовательно, должна быть назначена критическая точка сегмента.
Если контролируется каждая точка типа A (Рисунок 13: –), возможны дополнительные модификации в дополнение к базовым модификациям. Если мы будем контролировать каждую из восьми точек с одним и тем же значением, мы сможем создать узор в виде звезды правильной формы (рис. 20: типы A-1~3).И наоборот, если мы будем контролировать каждую точку с другим значением, мы можем создать случайный шаблон (рис. 21: типы A-4~5).
(b) Регулятор радиуса действия (тип B) . Управление радиусом — это метод, который управляет значением радиуса окружности, начинающейся от средней точки восьмиугольника, в качестве манипулятивной переменной (Рисунок 14: ). Как только значение радиуса круга настроено, оно автоматически соединяется с точкой пересечения с каждым сегментом вектора. Он относительно прост в управлении и имеет простую математическую формулу (рис. 22).Однако, в отличие от точек в методе контроля сегментов, дополнительная модификация относительно затруднена, поскольку точки интегрируются по окружности. Как и при методе управления радиусом, если значение радиуса () не назначено, размер окружности может увеличиваться в сторону бесконечности, а точка пересечения с отрезком не происходит. Следовательно, для значения радиуса необходимо установить критическую точку ().
Если объединить два типа метода управления боковым разделением, тип A и тип B, схемы будут следующими (рис. 23 и 24).Типы A-1~3 и типы B-1~3 имеют разные методы управления, но они создают комбинации одинаковой формы. Кроме того, тип A допускает дополнительные модификации и может создавать бесконечное количество различных форм, в то время как дополнительные модификации затруднены для типа B.
4.3.2. Метод расширения одиночного модуля
Расширение одиночного модуля можно разделить на два метода: точечный на сегментном контроле и боковой на сегментном контроле. Этот метод основан на идее, что восьмиугольник можно разделить на восемь треугольников одинаковой формы (рис. 25, а).Он основан на концепции, согласно которой при управлении одним модулем треугольника другие модули деформируются под углом 45°. В методе управления точка на отрезке в качестве переменной задается точка на отрезке (рис. 25(б)), которая соединяет каждую угловую точку восьмиугольника со средней точкой. Если точка на отрезке смещается, длина линии, соединяющей среднюю точку каждой стороны восьмиугольника (рис. 25(в)) с точкой на отрезке, изменяется. Однако в методе управления стороной на сегменте задается отрезок (рисунок 25(д)), где нижняя сторона (рисунок 25(и)) треугольника сходится по обеим сторонам (рисунок 25(з)) к средней точке. вверх как переменная.Если этот отрезок (e) смещается, длина отрезка, соединяющего точку пересечения (f) обеих сторон (h) со средней точкой (g) отрезка (i), изменяется.
(a) Точка управления сегментом (тип C) . Точка управления сегментом — это метод, который строит расширение отдельного модуля, управляя одним из треугольников, образующих восьмиугольник. Поскольку этот метод управления использует положение точки (Рисунок 15: ) на каждом сегменте вектора (Рисунок 15: ) в качестве манипулятивной переменной, он должен анализировать положение точки на каждом сегменте вектора и требует сложной математической формулы.По сравнению с типом А, этот метод контролирует относительно меньшее количество точек, поскольку необходимо контролировать только две точки. Благодаря этому он может обозначать каждый сегмент разной длиной и создавать различные формы модулей. В этом методе, как только один модуль управляется, другие автоматически управляются из-за фиксированного угла. Поскольку отдельные модули объединяются в восьмиугольник, весьма вероятно, что получится равносторонний восьмиугольник.
Поскольку тип C может контролировать две точки (рис. 15: , ) одновременно, он может создавать дополнительные варианты в дополнение к базовым модификациям.Если две точки управляются одним и тем же значением, это может создать шаблон звезды правильной формы (Рисунок 26: Типы C-1~3). Если каждая точка управляется другим значением, это может создать случайный шаблон (Рисунок 27: Типы C-4~5). Это становится модулем, создающим вращательную модификацию (рис. 28).
(b) Сторона управления сегментом (тип D) . Подобно методу управления точкой на сегменте, метод управления стороной на сегменте строит восьмиугольник, управляя одним модулем, который является одним из треугольников в восьмиугольнике, и расширяя единичный модуль (рис. 16, 29 и 30).Однако, в отличие от метода управления сегментами, дополнительные модификации относительно сложны, поскольку управление интегрируется в одну сторону, которая перемещается над сегментами вектора с обеих сторон.
4.4. Типовой оценочный анализ
В этом исследовании будет рассмотрено формирование исламского звездного узора из комбинации геометрических фигур 4.8.8, которая появляется в методе Ханкина, в зависимости от четырех типов управления параметрами, а затем будет проанализирована возможность модификации и удобство построения алгоритмов каждого из четырех типов контроля параметров.
4.4.1. Возможность модификации
Возможность модификации означает, насколько разнообразно может быть изменена базовая геометрическая фигура. По сути, соответствующим образом контролируя параметр каждого из четырех типов управления параметрами, мы можем изменять шаблоны в различные формы [Типы A~D-1~3]. Однако возможность дополнительных модификаций зависит от того, контролируются ли параметры по отдельности или интегрированы. Если параметры контролируются индивидуально [Тип A, Тип C], их можно преобразовать в другие шаблоны.Напротив, если параметры интегрированы [тип B, тип D], произвести дополнительные модификации относительно сложно.
4.4.2. Удобство алгоритма разработки (преимущество реализации программы)
В этой статье удобство разработки анализируется с точки зрения алгоритма. С точки зрения реализации алгоритмов математической формулы, если программа имеет относительно простую математическую формулу и удобна в управлении, реализация программы проста, а ее алгоритм математической формулы отличается выдающимся удобством проектирования (рис. 31).Уровень удобства алгоритма математической формулы определяется тем, является ли математическая формула, управляющая параметрами, простой или сложной. Если параметры контролируются индивидуально, математическая формула становится сложной. Если параметры интегрированы, математическая формула относительно проста. Таким образом, удобство проектирования шаблонов даже одной и той же формы может варьироваться в зависимости от того, контролируются ли параметры по отдельности или интегрированы. Среди четырех типов контроля параметров интегрированный метод, который контролирует только значение радиуса [тип B], имеет самый простой математический алгоритм и, следовательно, высокое удобство проектирования.Метод, который должен контролировать каждый отдельный параметр [Тип А], имеет наибольшую возможность модификации, но низкое удобство проектирования из-за относительно сложного математического алгоритма (табл. 1).
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4.4.3. Подзаключение
См. Таблицу 1.
5. Заключение
Это исследование направлено на анализ и изменение узора исламской звезды с использованием цифрового алгоритма, представляя метод эффективного изменения и контроля классических геометрических узоров посредством экспериментов и применения компьютерного алгоритма. Это исследование показывает, что с помощью стратегии алгоритмического проектирования мы можем проанализировать и подорвать жесткость классической геометрии исламского звездного узора и расширить его дизайнерские возможности.Четкое понимание классической геометрии и правильные эксперименты с цифровыми алгоритмами могут способствовать преодолению разрыва между классической геометрией и цифровыми технологиями и заложить прочную основу для эффективности и гибкости при разработке будущих конструкций и изготовлении материалов.
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов в отношении публикации данной статьи.

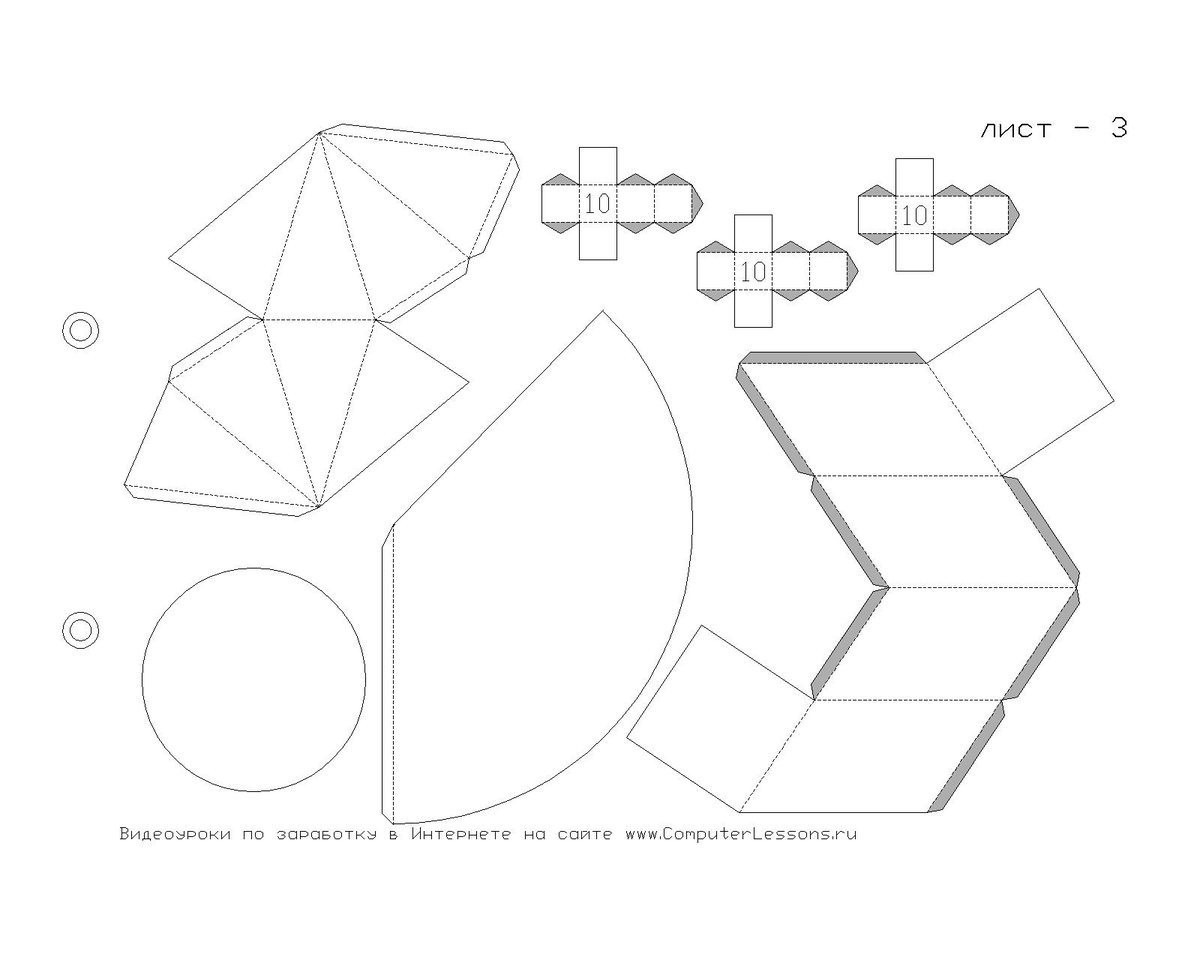 Рисуем их строго на одной линии, вплотную друг к другу.
Рисуем их строго на одной линии, вплотную друг к другу. Отношение длины прямоугольника к диаметру определяется выражением: L=πD, где L- длина прямоугольника, а D — диаметр будущего цилиндра. Подставив в формулу требуемый диаметр, найдем длину прямоугольника, который будем рисовать на бумаге. Дорисовываем небольшие дополнительные треугольнички, которые необходимы для склеивания деталей.
Отношение длины прямоугольника к диаметру определяется выражением: L=πD, где L- длина прямоугольника, а D — диаметр будущего цилиндра. Подставив в формулу требуемый диаметр, найдем длину прямоугольника, который будем рисовать на бумаге. Дорисовываем небольшие дополнительные треугольнички, которые необходимы для склеивания деталей. С каждой стороне дорисовываем боковые стороны — параллелограммы. От любой из боковой стороны дорисовываем второе основание. Добавляем полоски для склеивания. Параллелепипед может быть прямоугольным, если стороны прямоугольники. Если параллелепипед не прямоугольный, то создать развертку немного сложнее. Для каждого параллелограмма нужно выдержать требуемые углы.
С каждой стороне дорисовываем боковые стороны — параллелограммы. От любой из боковой стороны дорисовываем второе основание. Добавляем полоски для склеивания. Параллелепипед может быть прямоугольным, если стороны прямоугольники. Если параллелепипед не прямоугольный, то создать развертку немного сложнее. Для каждого параллелограмма нужно выдержать требуемые углы. Так рисуем столько треугольников, сколько сторон в пирамиде. Дорисовываем полоски для склеивания в нужных местах.
Так рисуем столько треугольников, сколько сторон в пирамиде. Дорисовываем полоски для склеивания в нужных местах.
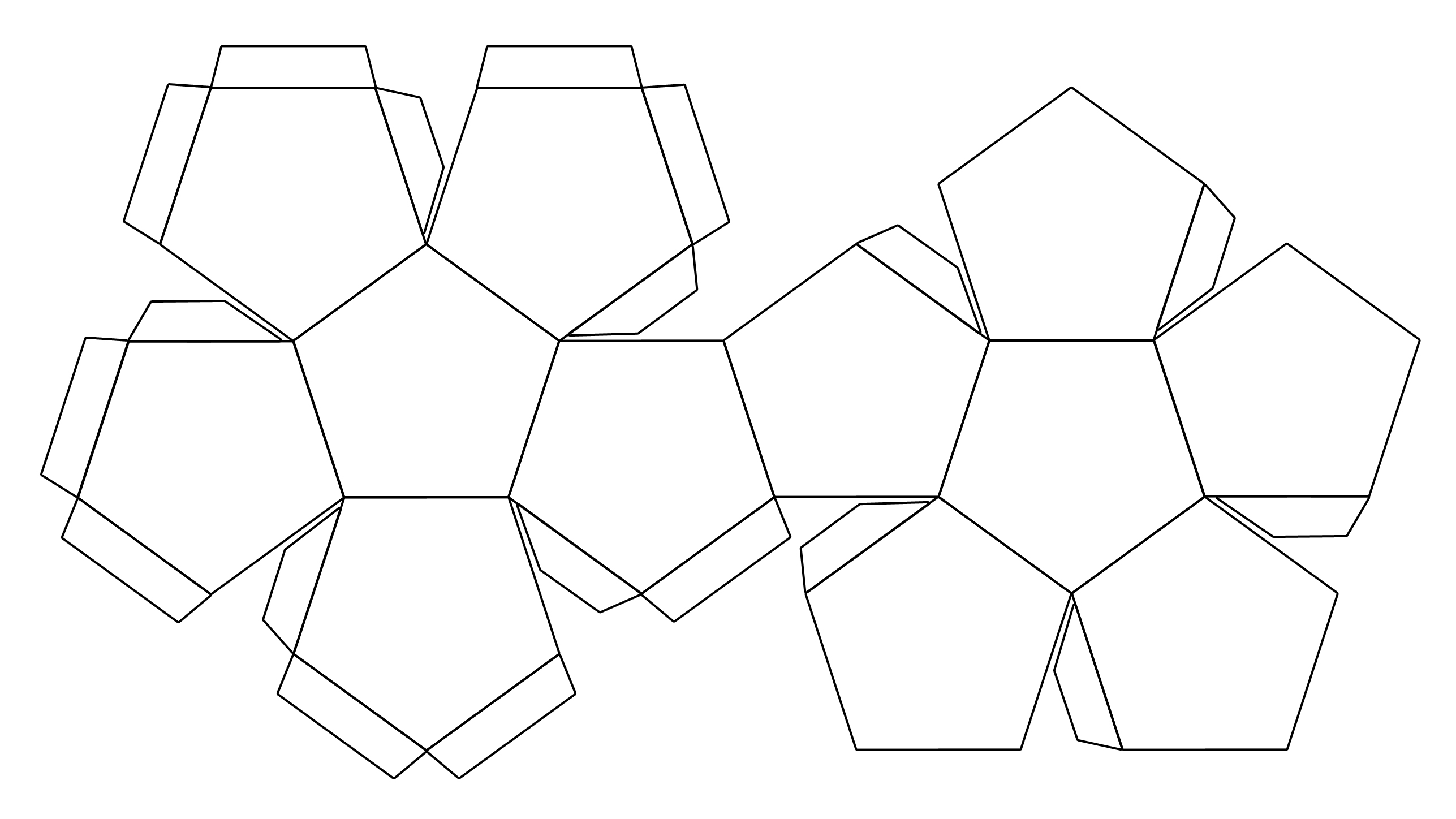

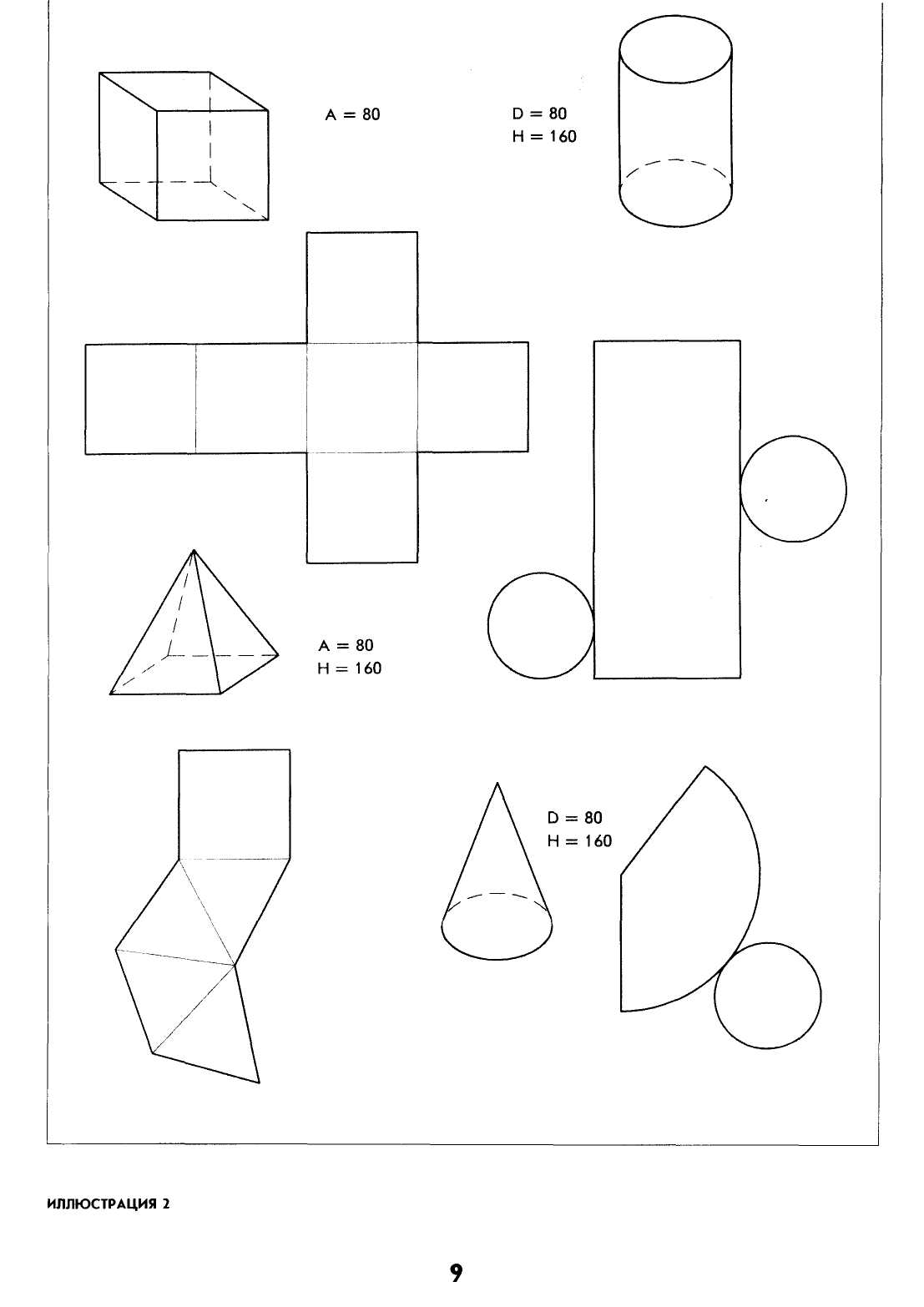
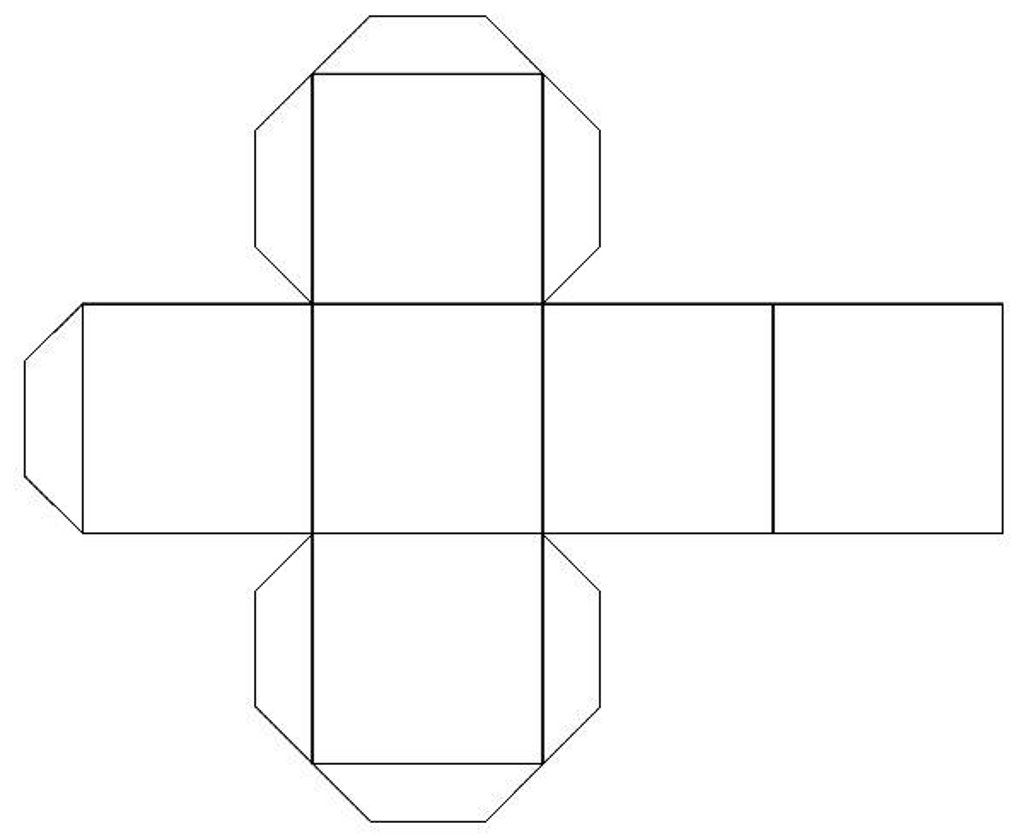

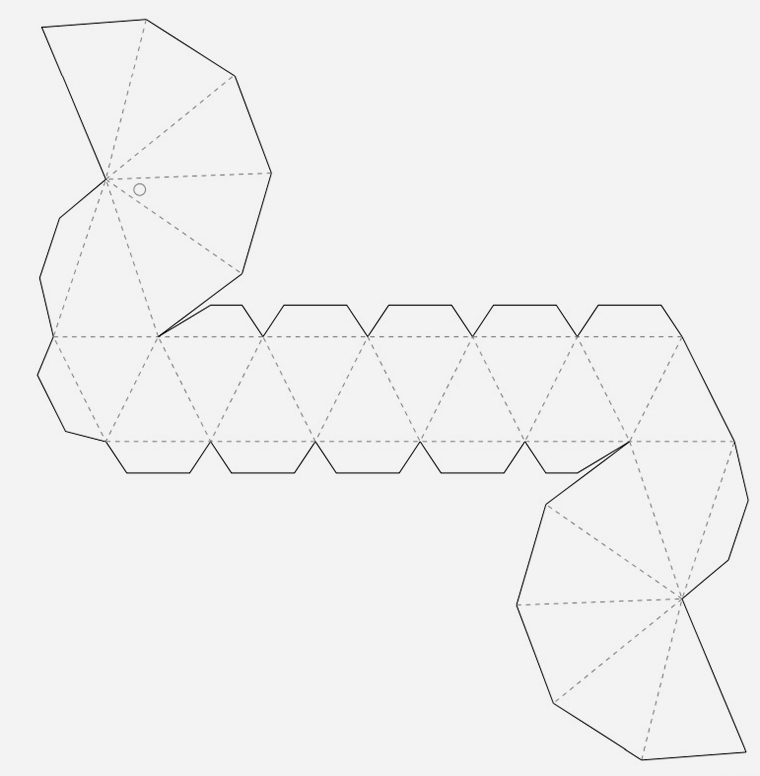
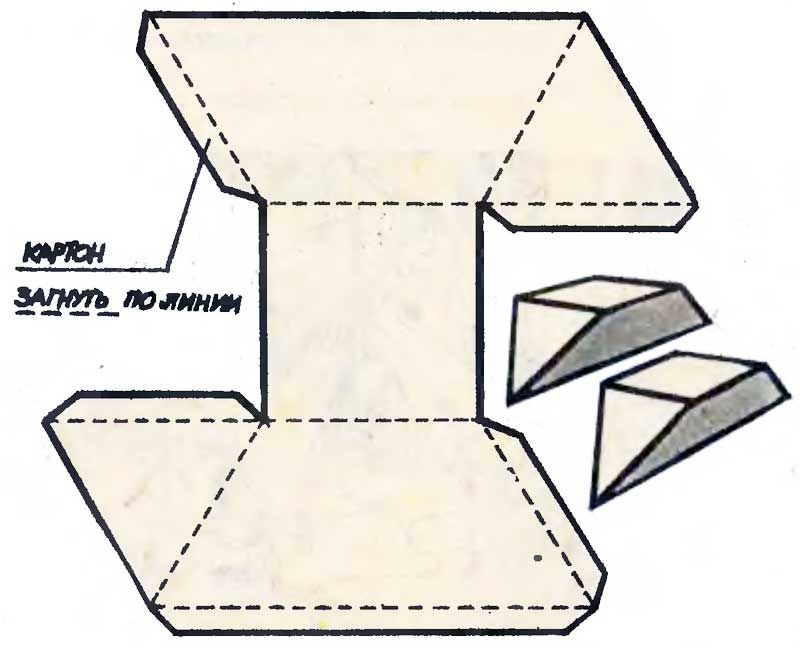
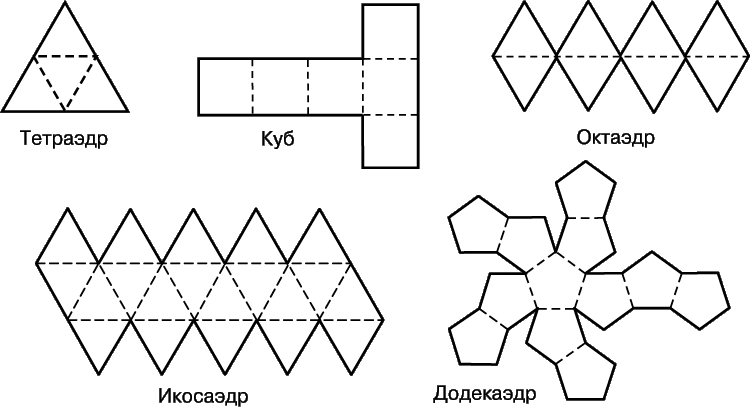 Теги: Геометрические фигуры , из бумаги , видео , Hans-Werner Guth.
Раздел Геометрическая аппликация поможет Вам и Вашим малышам создавать увлекательные изображения с помощью различных геом
Теги: Геометрические фигуры , из бумаги , видео , Hans-Werner Guth.
Раздел Геометрическая аппликация поможет Вам и Вашим малышам создавать увлекательные изображения с помощью различных геом Геометрические фигуры. Шведский художник XX в. Оскар Реутерсвард сделал невозможную фигуру чертой своего художественного стиля (изобразил тысячи таких фигур).
Набор плоскостных геометрических фигур разного цвета и размера, карточки схемы, два поля, чудесный мешочек с объемными геометрическими фигурами двух цветов по количеству детей, золотые и серебряные медали.
Мероприятие создает атмосферу праздника, хорошего настроения. Проводятся игровые моменты с геометрическими фигурами. Педагог дополняет на доску листы бумаги, где дети рисовали башни и домики.
Необычные свойства позволяют считать эту геометрическую фигуру одной из наиболее изящных численных схем в математике. quot;Наука и жизньquot;, 1981, N4.
А на уроке технологии применяют эти знания, выполняя геометрическую мозаику. Так, в 1-2 классах ребята узнают о геометрических фигурах, их свойствах.
Геометрические фигуры. Шведский художник XX в. Оскар Реутерсвард сделал невозможную фигуру чертой своего художественного стиля (изобразил тысячи таких фигур).
Набор плоскостных геометрических фигур разного цвета и размера, карточки схемы, два поля, чудесный мешочек с объемными геометрическими фигурами двух цветов по количеству детей, золотые и серебряные медали.
Мероприятие создает атмосферу праздника, хорошего настроения. Проводятся игровые моменты с геометрическими фигурами. Педагог дополняет на доску листы бумаги, где дети рисовали башни и домики.
Необычные свойства позволяют считать эту геометрическую фигуру одной из наиболее изящных численных схем в математике. quot;Наука и жизньquot;, 1981, N4.
А на уроке технологии применяют эти знания, выполняя геометрическую мозаику. Так, в 1-2 классах ребята узнают о геометрических фигурах, их свойствах.