Оригами открывает невероятные широты для фантазии и творчества. Мастера из бумаги научились делать самые разнообразные поделки. Это разные животные, птицы да даже растения. Но сегодня мы подробно рассмотрим, как делать геометрические фигуры быстро и легко из бумаги.
Такие фигуры помогут развить представление о трёхмерных фигурах, а также общее представления о них. Лучше всего они подойдут тем, у кого возникают сложности с тригонометрией, так как этот раздел геометрии требует очень хорошего визуального представления разных фигур.
Оригами в большинстве случаев заключается в складывании разнообразных форм из бумаги. В нашем же случае будет похоже, но немного иначе.
Схема или как её ещё называют развёртка – является обязательным элементом при изготовлении любой геометрической фигуры. Схема представляет собой двухмерное изображение «развёртки» нашей фигуры на бумаге.
Представим куб. И мы развернули его, что в итоге получилось? Столбик из четырёх одинаковых квадратов и два таких же квадрата сбоку. Своеобразная буква «Т».
После того, как вы сделали или нашли развёртку, вам необходимо сложить её в фигуру и очень аккуратно проклеить все элементы.
Без развёртки невозможно сделать ни одной правильной геометрической фигуры, которая была бы максимально ровная и не содержала бы погрешностей. В интернете можно найти огромное количество разнообразных схем, для самых разных фигур. Мы же рассмотрим в качестве примера изготовление цилиндр и шляпу.
Солидный цилиндр.
Цилиндр является одной из самых простых фигур в оригами. С его изготовлением справится даже новичок. И так, приступим к первому нашему творению.
Для начала ищем или делаем сами схему. Схема цилиндра представляет собой прямоугольник, длина которого вычисляется по формуле 2ПиR, где R – это радиус вашего цилиндра, то есть если вы хотите получить цилиндр диаметром 10 сантиметров, то его радиус будет равен пяти.
И тут же обратная зависимость: если вы уже нарисовали прямоугольник, длинной, например, 40 сантиметров, то радиус окружности соответственно будет равен 40/2Пи. Примерно 6,2 сантиметра.
На схеме, проводим аккуратную линию ровно по центру прямоугольника. Продолжаем нашу линию за его стороны, то есть, линия должна пересекать прямоугольник. Дальше мы должны точно знать диаметр цилиндра, чтобы вычислить радиус окружности, если же вы сначала нарисовали прямоугольник, то пользуйтесь формулой l/2Пи, где l – длина вашего прямоугольника. После того, как вы определили радиус, берём циркуль и размещаем на пересечении нашей линии симметрии и стороны прямоугольника. Начинам образно проводить окружность и смотрим, где будет вторая точка пересечения с линией симметрии, она должна находиться за пределами прямоугольника. Именно эта точка и будет центром окружности. Повторяем действия с другой стороны. Наша поделка, например, делалась по такой схеме:
Если же вы нашли схему в интернете, то достаточно распечатать её.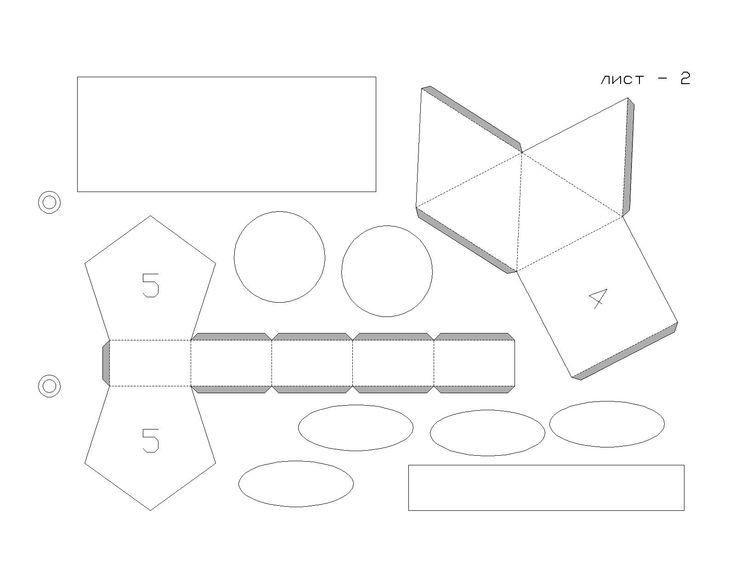
И вырезать её.
После того, как мы вырезали её, необходимо перейти к её складыванию. Начинаем складывать наш цилиндр с его основной части. Для этого сворачиваем в трубочку прямоугольник. Сворачиваем сразу с двух концов, то есть, берём один конец прямоугольника и другой, и тянем их друг к другу. Что бы получилась своеобразная труба, у которой «открыты» два кружочка.
Потом загибаем оба «окошка» внутрь и меняем по необходимости толщину трубочки, что бы эти окошки идеально вошли внутрь. Потом склеиваем получившийся цилиндр.
Шляпа из бумаги.
Шляпа – такой же цилиндр, но у него нижнее окно будет открыто на во внешнюю сторону. Нам потребуется картон, ножницы, тарелка, клей. Начнём!
Для начала разрезаем лист картона на две полосы, ширина которых будет равна высоте цилиндра.
Длина полосок будет зависеть от того, какого диаметра вы хотите получить шляпу. Если вы хотите одевать шляпу на голову, то следует измерить обхват головы и полученное число поделить на два.
Склеиваем детали так, чтобы получить единую длинную полосу.
Сворачиваем полосу в цилиндр и скрепляем его.
Выбираем, по вашему вкусу, одну из круглых сторон и делаем на ней ровные надрезы, глубина которых равна двумя сантиметрам. Отгибаем получившиеся лепестки и откладываем цилиндр в сторону.
Берём ещё небольшой кусочек картона и обводим, заготовленную ранее, тарелку. В центр получившейся окружности поставьте ваш цилиндр и обведите его. Вырезаем из листа сначала большую окружность, а потом маленькую. В итоге мы должны получить кольцо.
Ставим цилиндр на устойчивую, ровную поверхность вниз лепестками и к каждому из них приклеиваем кусочки двухстороннего скотча.
Шляпа готова!
youtube.com/embed/jbi1II6FPc8?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»> Что будет, если плоскую геометрическую фигуру, например прямоугольник, начать быстро вращать относительно одной из его сторон?
Одним лишь вращением мы можем создать новое геометрическое тело в пространстве.
Боковые поверхности цилиндра образуются за счет сторон вращающегося прямоугольника.
Официальное определение для таких геометрических тел, звучит следующим образом:
И здесь важно то, что плоская геометрическая фигура может быть совершенно произвольной формы.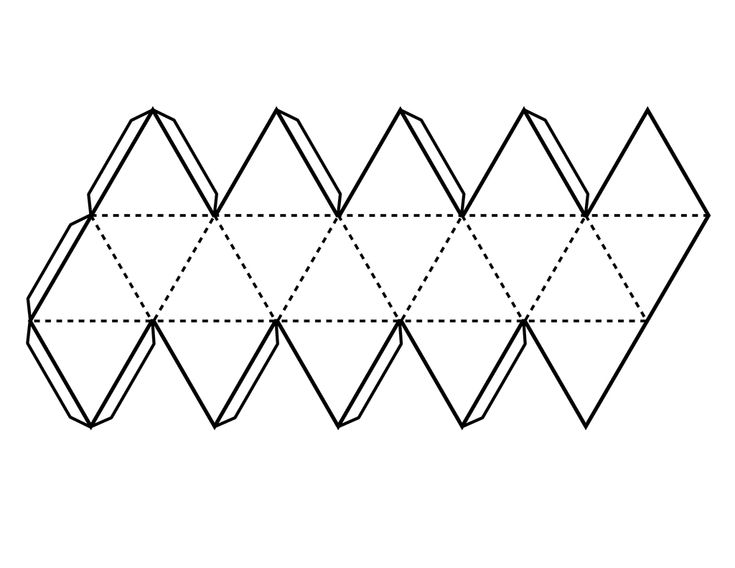
Например, кривая, которая при вращении будет образовывать вазу или лампочку. Такие инструменты создания тел вращения очень популярны у тех, кто работает в программах 3D-проектирования.
Но с математической точки зрения, для нас, прежде всего, интересны следующие геометрические тела вращения:
Цилиндр — образован прямоугольником, вращающимся вокруг одной из сторон.
Конус — образован прямоугольным треугольником, вращающимся вокруг одного из катетов.
Усечённый конус — часть конуса, расположенная между его основанием и секущей плоскостью, параллельной основанию.
Образуется при вращении прямоугольной трапеции вокруг ее боковой стороны, перпендикулярной основаниям трапеции.
Шар — образован полукругом, вращающимся вокруг диаметра разреза.
При вращении контуров фигур возникает поверхность вращения (например, сфера, образованная окружностью), в то время как при вращении заполненных контуров возникают тела (как шар, образованный кругом).
Эллипсоид
— поверхность в трёхмерном пространстве, полученная деформацией сферы вдоль трёх взаимно перпендикулярных осей.
Тор — образован окружностью, вращающейся вокруг прямой, не пересекающей его.
В обычном понимании тор — это «бублик».
Параболоид — это поверхность, которая образуется в результате вращения вокруг оси кривой образованной графиком параболы. Отсюда и название параб-о-лоид.
Гиперболоид — это поверхность, которая образуется в результате вращения вокруг оси кривой образованной графиком гиперболы. Соответственно название гиперб-о-лоид.
Для сопоставимости размеров получающихся моделей тел вращения мы постарались собрать их на одной поверхности вместе с призмами из выпуска «Волшебные грани № 16».
Получился целый математический город из бумаги, умещающийся на столе!
Двойственные пары многогранников
Что общего между додекаэдром и икосаэдром?
Многогранники в кино
Современный кинематограф постарался привлечь внимание зрителя, используя геометрические формы «инопланетного происхождения».
Разрезание Дьюдени — неразрывная цепочка разрезания
Можно ли разрезать треугольник на такое количество частей, чтобы из них можно было сложить квадрат?
Головоломка звёздчатый октаэдр
Это новый, весьма необычный способ создать модель Звёздчатого многогранника открытого 1619 году немецким математиком и астрономом Иоганном Кеплером.
Домик для птиц
Студией Артемия Лебедева (https://www.artlebedev.ru/) была предложена форма скворечника в виде многогранника. В качестве геометрической…
Как школе приобрести Волшебные грани?
В этой статье мы постараемся ответить на вопрос: «Можно ли купить для класса Волшебные грани используя бюджетные средства»?
Правильные многогранники
Правильные многогранники, их всего пять: тетраэдр, октаэдр, куб (другое название гексаэдр),…
Изучение свойств трехмерных фигур — развлечение для всех возрастов ! Поскольку дети знакомятся с трехмерными фигурами на раннем этапе, вы можете создавать их вместе с маленькими детьми или использовать их со старшеклассниками для изучения более сложной математики. Независимо от того, как вы их используете, этот набор складных 3D-фигур обязательно станет хитом!
* Обратите внимание : Этот пост содержит партнерские ссылки, которые помогают поддерживать работу этого сайта.
Ознакомьтесь с нашей полной политикой раскрытия информации здесь.*
Я настоятельно рекомендую печатать сети на стандартной бумаге , а не на обычной бумаге. Я пробовал и то, и другое, но обычная бумага слишком тонкая.
После печати просто вырежьте трехмерные сетки по сплошным линиям.
Если вы печатали на белом картоне, как я, найдите время, чтобы проявить творческий подход и раскрасить или украсить фигуры , прежде чем собирать их! Из этого мог бы получиться отличный математический арт-проект !
Если ваши ученики старше, попросите их пометить различные части фигуры (грань, край, основание) перед сборкой, чтобы использовать их в качестве эталона при изучении фигур! 🙂
Это поможет им увидеть и выучить математический словарь.
Затем осторожно согните каждый язычок так, чтобы его можно было использовать для склеивания фигуры, и согните каждую сторону фигуры.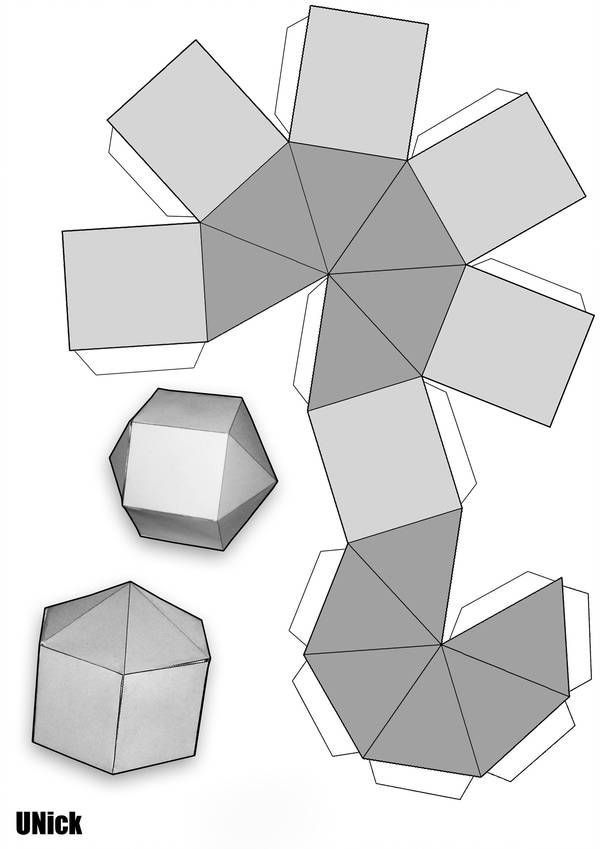
Наконец, склейте каждую сторону вместе . Я предлагаю добавить несколько мазков клея на каждый язычок, а затем подержать его на месте в течение нескольких секунд, прежде чем приклеивать следующий язычок. Это поможет убедиться, что он остается вместе.
Вы также можете использовать скотч, если вам так проще (или у вас нет клея).
Когда все фигуры собраны, вы можете использовать их по своему усмотрению, в зависимости от возраста ваших детей!
Учебные идеи для складных трехмерных фигур:
дополнительные бесплатные ресурсы для использования с книгой здесь!)Этот набор из геометрических сетей БЕСПЛАТНО загружается и содержит следующие трехмерные фигуры :
Кроме того, этот набор включает складная копия (с выступами), позволяющая учащимся дошкольного возраста создавать свои собственные модели, а также геометрические сетки без выступов для любых других целей в классе геометрии!
Например, позвольте учащимся измерить сети, чтобы исследовать площадь поверхности с помощью этих БЕСПЛАТНЫХ уроков площади поверхности (площадь поверхности призм и цилиндров и площадь поверхности пирамид и конусов)!
{Нажмите ЗДЕСЬ, чтобы перейти в мой магазин и приобрести набор для печати складных 3D-фигур!}Надеюсь, вы найдете их полезными и забавными, когда будете исследовать трехмерные формы !
Хотите больше удовольствия от 3D-фигур? Попробуйте один из этих ресурсов:
Если вам понравился этот пост, вам понравится быть частью сообщества Math Geek Mama! Каждую неделю я отправляю электронное письмо с забавными и увлекательными математическими идеями, бесплатными ресурсами и специальными предложениями.
Присоединяйтесь к более чем 163 000 читателей, поскольку мы помогаем каждому ребенку добиться успеха и преуспеть в математике! ПЛЮС, получи мою БЕСПЛАТНУЮ электронную книгу, 5 математических игр, в которые можно играть СЕГОДНЯ , в подарок вам !
Воспользуйтесь всеми преимуществами нашего сайта, включив JavaScript.
(
1000+ релевантных результатов,
с рекламой
Продавцы, желающие расширить свой бизнес и привлечь больше заинтересованных покупателей, могут использовать рекламную платформу Etsy для продвижения своих товаров.